Weighted Rooted Trees: Fat or Tall?

Abstract

Let V be a countable set, let T be a rooted tree on the vertex set V, and let ${\mathcal M}=(V,2^V, \mu )$ be a finite signed measure space. How can we describe the “shape” of the weighted rooted tree $(T, {\mathcal M})$? Is there a natural criterion for calling it “fat” or “tall”? We provide a series of such criteria and show that every “heavy” weighted rooted tree is either fat or tall, as we wish. This leads us to seek hypergraphs such that regardless of how we assign a finite signed measure on their vertex sets, the resulting weighted hypergraphs have either a “heavy” large matching or a “heavy” vertex subset that induces a subhypergraph with small matching number. Here we also must develop an appropriate definition of what it means for a set to be heavy in a signed measure space.

Supported by NSFC (11671258, 11971305) and STCSM (17690740800).

1 Background

Roughly speaking, Heisenberg’s uncertainty principle for position and momentum says that, for a good function on the real line, either its variance is large or the variance of its Fourier transform is large [15, Theorem 4.1]. This kind of weak duality or orthogonality [7] also happens in combinatorics. The most famous example may be the Erdös-Szekeres subsequence theorem [6], which says that each sequence of $rs+1$ real terms contains an increasing subsequence of $r+1$ terms or a decreasing subsequence of $s+1$ terms or both. Though the Erdös-Szekeres subsequence theorem has a short self-contained proof, it also easily follows from either Dilworth’s Theorem [3] or Mirsky’s Theorem [11]. The two equalities results, Dilworth’s Theorem and Mirsky’s Theorem, are generalized from posets to digraphs as two inequalities results, the Gallai–Milgram theorem [9] and the Gallai-Roy Theorem [8, 12]. As a consequence of the Gallai–Milgram theorem or the Gallai-Roy Theorem, we know that $\lambda (D)\alpha (D)\ge | \mathrm {V} (D)|$ for any finite digraph D, where we use $\mathrm {V} (D)$, $\lambda (D)$ and $\alpha (D)$ for the vertex set of D, the length of a longest path in D and the maximum size of an independent set in D. This means that, we either have a ‘long’ path or a ‘large’ independent set in D, provided we define ‘long’ and ‘large’ in an appropriate way. Note that $\lambda (D)$ measures the length of a path by giving each vertex of the path a weight 1 while $\alpha (D)$ measures the size of a stable set by giving each vertex in the stable set a weight 1. Are there similar orthogonality results in which we assign weight to a set by something other than the usual cardinality function? For Dilworth’s Theorem, a weighted version is recently discovered by Hujdurović, Husić, Milanič, Rizzi and Tomescu [10, Theorem 3.3]. Recall that a poset is just a transitive acyclic digraph and a rooted tree poset is a poset in which there is a special root vertex and a unique saturated path from the root vertex to any other vertex. Among the very few such weighted results which we are aware of, another one is a result of Song, Ward and York [14, Theorem 1.2], which improves a result of Bonamy, Bousquet and Thomassé [2, Lemma 3]: for any weighted rooted tree poset, either there is a long path or there are two heavy vertex subsets A and B for which there are no arcs between A and B. In some sense, this conforms to the above-mentioned result about the orthogonality of independent sets and paths: we are now considering vertex subsets which are pairwise independent of each other, instead of merely considering a set of pairwise nonadjacent vertices. We will present a vast generalization of the result of Song et al. (see Corollary 1) and discuss the possibility of going further along this line. Note that our proof strategy is totally different with the approach of Song et al.

2 Fat or Tall?

A graph G consists of a pair $( \mathrm {V} (G), \mathrm {E} (G))$ where $\mathrm {E} (G)\subseteq \left( {\begin{array}{c} \mathrm {V} (G)\\ 2\end{array}}\right)$. We call $\mathrm {V} (G)$ and $\mathrm {E} (G)$ the vertex set and edge set of G, respectively. A graph G is countable if $\mathrm {V} (G)$ is a countable set and is finite if $\mathrm {V} (G)$ is finite. Recall that each countable set is either finite or denumerable (infinite). Let V be a countable set and let ${\mathcal M}=(V,2^V, \mu )$ be a finite signed measure space, that is, $\sum _{v\in V}|\mu (v)|<\infty$ and $\mu (A)=\sum _{a\in A}\mu (a)$ holds for all $A\subseteq V$. If G is a graph with $\mathrm {V} (G)=V$, the graph G together with the finite signed measure space ${\mathcal M}$ gives us a weighted graph, in which we think of $\mu$ as the weighting function. If $r\in V= \mathrm {V} (G)$, we call the triple ${\mathbb G}=(G,r,\mu )$ a weighted rooted graph, where r is the root of ${\mathbb G}$ and $\mu$, as known to be the weighting function of $(G,\mu )$, is also referred to as the weighting function of $\mathbb G$. In the case that G is a tree, $(G,\mu )$ is called a weighted tree and $(G,r,\mu )$ is called a weighted rooted tree.

For any integer k, we use [k] for the set of positive integers between 1 and k. For any two vertices u and v of a tree T, the set of vertices on the unique path connecting u and v in T is denoted by T[u, v]. A down-set of a rooted tree (T, r) is a subset A of $\mathrm {V} (T)$ such that, for each $a\in A$, the set A contains all components of $T-a$ to which r does not belong. A chain in a rooted tree (T, r) is a subset A of $\mathrm {V} (T)$ such that T[u, r] and T[v, r] are comparable elements in the Boolean lattice $2^{ \mathrm {V} (T)}$ for every $u,v\in A$. A down-set of a rooted tree is a union of geodesic rays to the ends of the tree; A chain in a rooted tree is a subset of one geodesic ray.

Given a weighted rooted tree, when would you call it a “tall” tree and when would you call it a “fat” tree? If you think of being tall and being fat as two interesting properties, when do you expect to see an interesting weighted rooted tree? We suggest the following definitions so that you will not encounter any boring tree.

Definition 1

Let ${\mathbb T}=(T, r, \mu )$ be a weighted rooted tree and let $d_1,\ldots , d_k, c$ be $k+1$ reals. We call ${\mathbb T}$ $(d_1,\ldots ,d_k)$-fat provided we can find k disjoint down-sets $D_1,\ldots ,D_k$ of (T, r) such that $\mu (D_i)\ge d_i$ for $i\in [k]$. We call $\mathbb T$ c-tall provided we can find a chain C in (T, r) such that $\mu (C)\ge c$.

The next result says that as long as your weighted rooted tree is heavy enough, it is inevitable for it to be either fat or tall. It illustrates the spirit of Ramsey theory: You always find interesting structures when you are entering a large but otherwise arbitrary space. Note that Theorem 1 just recalls [14, Theorem 1.2] when $\mu$ is a probability measure, $k=2$ and $d_1=d_2=c=\frac{1}{3}$.

Theorem 1

Let ${\mathbb T}=(T, r, \mu )$ be a weighted rooted tree and let k be a positive integer. If $d_1,\ldots , d_k, c$ are $k+1$ positive reals such that

$$\begin{aligned} \mu ( \mathrm {V} (T))\ge \sum _{i=1}^kd_i +(k-1)c, \end{aligned}$$

(1)

then ${\mathbb T}$ is either $(d_1,\ldots ,d_k)$-fat or c-tall or both.

Let k be a positive integer and let $d_1,\ldots , d_k, c$ be $k+1$ positive reals. If $d_1,\ldots ,d_k$ take at least two different values, we are not aware of any general way of constructing a weighted rooted tree ${\mathbb T}=(T, r, \mu )$ with

$$\begin{aligned} \mu ( \mathrm {V} (T)) < \sum _{i=1}^kd_i +(k-1)c, \end{aligned}$$

which is neither $(d_1,\ldots ,d_k)$-fat nor c-tall. However, if we assume that $d_1,\ldots ,d_k$ take a constant value, we can give one such construction below, demonstrating the tightness of (1) in Theorem 1.

Fig. 1.

A weighted rooted tree with weights indicated on the left of each node.

Fig. 2.

A weighted rooted tree.

Example 1

Let k be a positive integer and let $d_1,\ldots , d_k, c$ and $\delta$ be $k+2$ positive reals. Let $K=\sum _{i=1}^kd_i$ and assume that $K +(k-1)c\ge \delta$.

Case 1. $k=1$.

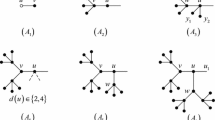
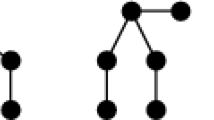
Take a positive integer m such that $mc>K-\delta$ and let $\epsilon =\frac{K-\delta }{m}$. The weighted rooted tree ${\mathbb T}=(T, r, \mu )$ as shown in Fig. 1 satisfies

$$\begin{aligned} \mu ( \mathrm {V} (T))=m\epsilon =K -\delta = K +(k-1)c-\delta \end{aligned}$$

and is neither $(d_1,\ldots ,d_k)$-fat nor c-tall.

Case 2. $k=\ell +1\ge 2$.

Pick a positive integer m such that $(m+1) \delta >2K$. Let $\epsilon =c -\frac{\delta }{2\ell }$ and $\xi = \frac{2K-\delta }{2m\ell }$. We now consider the weighted rooted tree ${\mathbb T}=(T,r,\mu )$ as displayed in Fig. 2. Note that

$$\begin{aligned} \mu ( \mathrm {V} (T))=\ell (m\xi + \epsilon )= (K -\frac{\delta }{2})+(\ell c-\frac{\delta }{2})= K +(k-1)c- \delta . \end{aligned}$$

Firstly, every chain C in (T, r) satisfies $\mu (C)\le \epsilon +\xi = c -\frac{\delta }{2\ell }+ \frac{2K-\delta }{2m\ell } <c$, showing that ${\mathbb T}$ is not c-tall.

Secondly, we assume that $D_1,\ldots D_k$ are k disjoint down-sets of (T, r). Under the additional condition that $d_i$ takes a constant value d for each $i\in [k]$, let us show that $d_j=d>\mu (D_j)$ holds for at least one $j\in [k]$, which says that $\mathbb T$ is not $(d_1,\ldots ,d_k)$-fat.

For $i\in [\ell ]$, we denote the set $\{x^i_j:\ j\in [m]\}$ by $L_i$. Note that, for all $i\in [\ell ]$, a down-set of (T, r) containing $x^i$ must also contain $L_i$. By the pigeonhole principle, without loss of generality, we assume that $\bigcup _{j\in [t]} D_{j}\subseteq \bigcup _{i\in [t-1]} L_i$ holds for some integer t satisfying $2\le t\le k$. This gives

$$\begin{aligned}&\frac{dt}{{m(t-1)}}\ge \frac{ d(\ell +1)}{{m\ell }}=\frac{dk}{m\ell }>\frac{2dk-\delta }{2m\ell }\\ =&\frac{2K-\delta }{2m\ell }= \xi =\frac{\mu (\bigcup _{i\in [t-1]} L_i)}{m(t-1)}\ge \frac{\sum _{j\in [t]}\mu (D_j)}{{m(t-1)}} , \end{aligned}$$

yielding that, for at least one $j\in [t]$, it happens $d_j=d>\mu (D_j)$, as desired.    $\square$

In Theorem 1, we can surely allow any one of $d_1,\ldots ,d_k,c$ to be zero. This does not make any real difference, as the empty set, which is both a chain and a down-set, has measure zero. But Theorem 1 may not hold if we allow any of $d_1,\ldots ,d_k,c$ to take a negative value. This can be seen from the following easy example.

Example 2

Let $V=\{r\}$, let T be the unique tree on V and let $\mu$ be the measure on V such that $\mu (r)=0$. Let $c=d_1=1$ and $d_2=-2$. Note that $\mu ( \mathrm {V} (T))=0\ge 0= (d_1+d_2) +(2-1)c$. For $(T,r,\mu )$, surely the $\mu$-measure of each chain is less than $c=1$ and the $\mu$-measure of each down-set is less than $d_1=1$.

Question 1

A function $\mu$ on $2^V$ is submodular provided $\mu (A\cup B)+\mu (A\cap B)\le \mu (A)+\mu (B)$. In Theorem 1, what will happen if $\mu$ is not a measure but only a submodular function?

A hypergraph H is a pair $( \mathrm {V} (H), \mathrm {E} (H))$, where $\mathrm {V} (H)$ is the vertex set of H and $\mathrm {E} (H)\subseteq 2^{ \mathrm {V} (H)}$ is known as the edge set of H. To emphasize that we are considering a hypergraph, we often call each edge of the hypergraph H an hyperedge of H. For each positive integer k, a k-matching of H is a set of k disjoint hyeredges of H, while a k-antimatching of H is a subset C of $\mathrm {V} (H)$ which is disjoint from at least one member of any $(k+1)$-matching of H. Note that a k-antimatching is just a set which cannot be a transversal of any $(k+1)$-matching.

Let V be a countable set and let $(V,2^V,\mu )$ be a finite signed measure space. Let H be a hypergraph with $\mathrm {V} (H)=V$ and $\mathrm {E} (H)\subseteq 2^V$. For real numbers $d_1,\ldots ,d_k$, we say that $(H,\mu )$ is $(d_1,\ldots ,d_k)$-fat provided we can find a k-matching of H, say $\{e_1,\ldots ,e_k\}$, such that $\mu (e_i)\ge d_i$ for $i\in [k]$. For any real number c and positive integer t, we say that $(H,\mu )$ is (c, t)-tall provided we can find a t-antimatching W of H such that $\mu (W)\ge c.$ These concepts allow us to formulate the next conjecture, which coincides with Theorem 1 when $t=1$.

Conjecture 1

Let ${\mathbb T}=(T, r, \mu )$ be a weighted rooted tree and let k, t be two positive integers. Let H be the hypergraph with $\mathrm {V} (H)= \mathrm {V} (T)$ and with the set of all down-sets of (T, r) as $\mathrm {E} (H)$. If $d_1,\ldots , d_k, c$ are $k+1$ positive reals such that

$$\begin{aligned} \mu ( \mathrm {V} (T))\ge \sum _{i=1}^k d_i+ \lceil \frac{k-1}{t}\rceil c, \end{aligned}$$

then $(H,\mu )$ is either $(d_1,\ldots ,d_k)$-fat or (c, t)-tall or both.

Let $(X, \mu )$ be a Borel measure space, namely X is a topological space and $\mu$ a Borel measure on the Borel sets of X. For the rooted tree case, we are indeed considering the topological space on its vertex set with all down-sets as open sets. In general, you can consider an Alexandroff space, which is essentially the same as a poset antimatroid¹, and a corresponding Borel measure space. Can we go further to talk about the hypergraph consisting of all open sets of X and conclude under certain assumption that it is fat or tall or both as in Conjecture 1?

Let P be a poset of countablely many elements. For any $x\in P$, we write $x\downarrow _P$ for the set of elements which are less than or equal to x in P and we write $x\uparrow _P$ for the set of elements which are greater than or equal to x in P. A down-set of P is a subset A of P such that $x\downarrow _P\subseteq A$ for all $x\in P$, and an up-set of P is the complement set of a down-set of P. When the poset is finite, sending a down-set to its set of maximal elements yields a one-to-one correspondence between down-sets and antichains of the poset. If $(P,2^P, \mu )$ is a finite signed measure space, we call $(P, \mu )$ a weighted poset. Each rooted tree (T, r) naturally gives rise to a poset $( \mathrm {V} (T),\prec )$, called its ancestral poset, in which $x \prec y$ if and only if $y\in T[x,r]\setminus \{x\}$. One natural question is to ask to what extent Theorem 1 can be extended to general weighted posets. A filter in a poset $(Q,\prec )$ is a nonempty subset F such that

• if $x \in F$ and $x \prec y$, then $y \in F$;

• if $x, y \in F$, then there exists $z \in F$ with $z \prec x$ and $z \prec y$.

Note that each filter in the ancestral poset of a rooted tree has to be a path. The next example tells us that we cannot always expect to see either a heavy antimatching/filter or a heavy matching in a general weighted poset.

Example 3

Take two positive integers k and n. Let $V_1= [k]\times [n]$ and $V_0=[n]^{[k]}$. You can think of $V_0$ as the set of all vertices (atoms) of the n-ary k-dimensional cube and think of $V_1$ as the set of all facets (coatoms) of the n-ary k-dimensional cube. Let P be the poset on $V_0\cup V_1$ in which $x>y$ if and only if $x=(\ell , h)\in V_1$ and $y\in V_0$ is a function satisfying $y(\ell )=h$. Let H be the hypergraph consisting of all downsets of P. Choose any nonnegative real $\delta$. We define a signed measure $\mu$ on P such that

$$\begin{aligned} \mu (x) = {\left\{ \begin{array}{ll} \frac{1-n^k\delta }{nk} &{} \text {if } \ x \in V_1;\\ \delta &{} \text {if } \ x \in V_0. \end{array}\right. } \end{aligned}$$

A subset of $V_0\cup V_1$ is a 1-antimatching of H if and only if it is a filter in P if and only if it is of the form $x\uparrow _P$ for some $x\in P$. But for any $x\in P$, it holds $\mu (x\uparrow _P)\le \delta +\frac{1-n^k\delta }{n}=\frac{1}{n}+\delta (1-n^{k-1})\le \frac{1}{n}$.

Let $\{Q_1, Q_2\}$ be a 2-matching in H. If one of them is contained in $V_0$, then $\min (\mu (Q_1), \mu (Q_2))\le \mu (V_0)=n^k\delta$. If both $Q_1$ and $Q_2$ are not contained in $V_0$, then there exists $\ell \in [k]$ such that $Q_1\cup Q_2\subseteq V_0\cup ( \{\ell \}\times [n])$. This means that $\mu (Q_1\cup Q_2)\le n \frac{1-n^k\delta }{nk} +n^k\delta =\frac{1}{k}+\frac{(k-1)n^k\delta }{k}$ and so $\min (\mu (Q_1), \mu (Q_2))\le \frac{1}{2k}+\frac{(k-1)n^k\delta }{2k}$. To summarize, when $\delta$ is small enough, say $\delta =0$, we have $\min (\mu (Q_1), \mu (Q_2))\le \frac{1}{k}$.    $\square$

One reason that we like to study trees is that they are really visible so that we may easily say many simple facts on them and then there are many directions to go for possible generalizations. For a rooted tree and a measure on its vertex set, we can add a new root vertex and join it to the old root vertex and then naturally produce a measure on the edge set of the new graph from the existing measure on the old tree. This operation allows us view the claim in Theorem 1 as a statement on an undirected branching greedoid [1, 13]. We think that we should be quite close to a proof of the following conjecture. Besides branching greedoid addressed in Conjecture 2, one may even consider possible generalizations to multiply-rooted graphs [4].

Conjecture 2

Let $\mathcal F$ be an undirected branching greedoid on a countable ground set E. Let H be the hypergraph on E whose edge set is $\{E-X:\ X\in {\mathcal F}\}$. Let $\mu$ be a measure on the power set of E and let k be a positive integer. If $d_1,\ldots , d_k, c$ are $k+1$ positive reals such that

$$\begin{aligned}\mu ( E)\ge \sum _{i=1}^kd_i +(k-1)c, \end{aligned}$$

then $(H,\mu )$ is either $(d_1,\ldots ,d_k)$-fat or c-tall or both.

We mention that Theorem 1 is self-strengthening. The next two easy corollaries of Theorem 1 both have it as a special case.

Corollary 1

Let $(P,\mu )$ be a weighted poset and $r\in P$. Assume that, for each $y\in r\downarrow _P$, the number of saturated chains from r to y, denoted by $\mathrm {n} _y$, is a finite number. For any $k+1$ nonnegative reals $c,d_1,\ldots ,d_k$ satisfying $(k-1)c + \sum _{i = 1}^{k} d_k \le \mu (r\downarrow _P)$, either there exists a saturated chain C of $r\downarrow _P$ starting from its maximum element r such that $\sum _{u\in C}\frac{\mu (u)}{ \mathrm {n} _u}\ge c$, or there exist pairwise disjoint down-sets $D_1, \ldots , D_k$ of $r\downarrow _P$ such that $\sum _{u\in D_i}\frac{\mu (u)}{ \mathrm {n} _u} \ge d_i$ for all $i \in [k]$.

Corollary 2

Let V be a countable set and let $(V,2^V,\mu )$ be a finite signed measure space. Let W be a subset of V and let T be a tree on V. Let $d_1,\ldots , d_k, c$ be $k+1$ positive reals such that Eq. (1) holds. Then there are either k disjoint subsets $D_1,\ldots ,D_k$ such that $\mu (D_i)\ge d_i$ and $T-D_i$ is a tree containing W for all $i\in [k]$, or there is a vertex u such that $\mu (C)\ge c$ where C is the the convex hull of $\{u\}\cup W$ in T.

Erdős and Hajnal [5] conjectured that for every graph H, there exists a constant $c_H$ such that every graph G on n vertices which does not contain an induced copy of H has a clique or a stable set of size $n^{c_H}$. Since clique and stable set of a graph correspond to chain and antichain in a poset, this conjecture is also in the spirit of Dilworth’s Theorem which we discuss in Sect. 1. The work of Song et al. [14, Theorem 1.2] is to verify a conjecture posed by Bonamy et al. in their study of the Erdös-Hajnal Conjecture [2]. We finally present a result, Theorem 2, as an application of Theorem 1. Note that the proof can be done by following the proof of [2, Theorem 6] with our Theorem 1 playing the role of [2, Lemma 3] there.

Let G be a graph. For any $X\subseteq \mathrm {V} (G)$, the neighborhood of X in G, denoted by $\mathrm {N} _G(X)$, is the set of vertices from $\mathrm {V} (G)\setminus X$ which are adjacent to at least one element of X in G, and the closed neighborhood of X in G, denoted by $\overline{ \mathrm {N} }_G(X)$, is defined to be $\mathrm {N} _G(X) \cup X$.

Theorem 2

Let k be a positive integer and let $(G,\mu )$ be a connected countable weighted graph. If $d_1, \ldots , d_k, c$ are $k+1$ positive integers such that

$$\begin{aligned} \mu ( \mathrm {V} (G)) \ge \sum _{i=1}^{k}d_i + (k-1)c, \end{aligned}$$

then either there exists a subset A of $\mathrm {V} (G)$ such that G[A] is a path and $\mu (\overline{ \mathrm {N} }_G(A))\ge c$, or there are k disjoint subsets $X_1, \ldots , X_k$ of $\mathrm {V} (G)$ such that $\mu (X_i ) \ge d_i$ for all $i \in [k]$ and that there are no edges between $X_i$ and $X_j$ for all $\{i,j\}\in \left( {\begin{array}{c}[k]\\ 2\end{array}}\right)$.

3 Up and Down in a Rooted Tree

The purpose of this section is to prove Theorem 1.

For each poset P and each subset D of P, we write $D \uparrow _{P}$ for the minimum up-set of P which contains D and we write $D \downarrow _{P}$ for the minimum down-set of P which contains D. Let ${\mathcal T}=(T,r)$ be a rooted tree. We will naturally regard ${\mathcal T}$ as a poset in which $x>y$ if and only if $x\in T[y,r]\setminus \{y\}$. For any $x\in \mathrm {V} (T)$, let $\mathrm {S} _{\mathcal T}(x)$ be the set of neighbors y of x in T such that $x\in T[y,r]$, which we call the shadow of x in $\mathcal T$. Surely, it holds $x \downarrow _{\mathcal T}\supseteq \mathrm {S} _{\mathcal T}(x)$ for all $x\in \mathrm {V} (T)$.

Definition 2

Let $(P,\mu )$ be a weighted poset. For any two nonnegative real numbers $\alpha$ and $\beta$, we say that a down-set D of P is an $(\alpha , \beta )$ down-set of $(P, \mu )$ provided $\mu (D) \ge \beta$ and $\mu (D \uparrow _{P}) \le \alpha + \beta$.

An $(\alpha , \beta )$ down-set D is like a good watermelon, where D really stands for the pulp of the watermelon and $D \uparrow _{P}$ represents its closure, namely the pulp together with the peel.

Let us explore the condition under which we can find an $(\alpha , \beta )$ down-set in a weighted rooted tree. We first do this for finite trees in Lemma 1. Then we strengthen Lemma 1 to Lemma 3, which makes the same statement for countable trees.

Lemma 1

Let ${\mathcal T}=(T,r)$ be a finite rooted tree and let $\mu$ be a weighting function on T. Let $\alpha$ and $\beta$ be two nonnegative reals such that $\mu ( \mathrm {V} (T)) \ge \alpha + \beta$ and $\mu (x \uparrow _{\mathcal T}) \le \alpha$ for all $x \in \mathrm {V} (T)$. Then the weighted rooted tree ${\mathbb T}=({\mathcal T}, \mu )$ has an $(\alpha , \beta )$ down-set.

Proof

We intend to find a down-set D of ${\mathcal T}$ such that $\mu (D) \ge \beta$ and ${\mu (D \uparrow _{\mathcal T})}\le \alpha + \beta$. We will demonstrate its existence by induction on $| \mathrm {V} (T)|$.

If $| \mathrm {V} (T)|=1$, then $\beta = 0$ and we can set $D = \{r\}$.

Assume now $| \mathrm {V} (T)|>1$ and that the result holds when $| \mathrm {V} (T)|$ is smaller. List the elements in $\mathrm {S} _{\mathcal T}(r)$ as $x_1, \ldots , x_s$. Let $V_i := x_i \downarrow _{\mathcal T}$ for $i \in [s]$ and put $\epsilon := \alpha - \mu (r)\ge 0$. There are three cases to consider.

Case 1. $\beta \le \mu (V_1) \le \beta + \epsilon$.

Take $D=V_1$, which is a down-set of $\mathcal T$. Then $\mu (D) = \mu (V_1) \ge \beta$ and $\mu (D \uparrow _{\mathcal T}) =\mu (V_1) + \mu (r) \le (\beta + \epsilon ) +(\alpha - \epsilon ) = \alpha + \beta$.

Case 2. $\beta + \epsilon < \mu (V_1)$.

Define a signed measure space $(V_1, 2^{V_1}, \mu ')$ by requiring

$$\begin{aligned} \mu '(A) = {\left\{ \begin{array}{ll} \mu (A) + \mu (r) &{} \text {if } x_1\in A\subseteq V_1,\\ \mu (A) &{} \text {if } A\subseteq V_1\setminus \{x_1\}. \end{array}\right. } \end{aligned}$$

Let $T'$ be the subtree of T induced by $V_1$. Note that

$$\begin{aligned} \mu ' ( \mathrm {V} (T'))=\mu ' (V_1)=\mu (V_1)+\mu (r)> (\beta + \epsilon ) +(\alpha - \epsilon ) = \alpha + \beta . \end{aligned}$$

(2)

By induction hypothesis for $(T', x_1, \mu ')$, we have a down-set D of $(T', x_1)$ such that

$$\begin{aligned} \mu '(D ) \ge \beta \ \text { and } \mu ' (D\uparrow _{T', x_1}) \le \alpha + \beta . \end{aligned}$$

(3)

Comparing (3) with (2) yields $D\uparrow _{T', x_1}\subsetneq V_1=x_1\downarrow _{T,x}$ and so $x_1 \notin D$ follows. We now see that $D=D\downarrow _{T,r}$ satisfies $\mu (D) = \mu '(D)\ge \beta$ and $\mu (D \uparrow _{T,r}) = \mu '(D \uparrow _{T',x_1})\le \alpha +\beta$.

Case 3. $\mu (V_1) < \beta$.

Let $T'$ be the tree obtained from T by deleting $V_1$ and let $\mu '$ be the restriction of $\mu$ on $2^{ \mathrm {V} (T)\setminus V_1}$. Let $\alpha ' = \alpha$ and $\beta ' = \beta - \mu (V_1) > 0$. Note that $\mu ' ( \mathrm {V} (T'))= \mu ( \mathrm {V} (T))-\mu (V_1) \ge \alpha '+\beta '$. Applying induction assumption on $(T', r, \mu ')$, we can find a down-set $D'$ of $(T',r)$ such that $\mu (D') \ge \beta ' = \beta - \mu (V_1)$ and ${\mu (D' \uparrow _{T',r})} \le \alpha ' + \beta ' = \alpha + \beta - \mu (V_1)$. We thus see that $D = D' \cup V_1$ is a down-set of ${\mathcal T}$, as required.    $\square$

Lemma 2

Let ${\mathcal T}=(T,r)$ be a countable rooted tree and let $\mu$ be a weighting function on T. Take $x\in \mathrm {V} (T)$ and any positive real $\epsilon$. Then $\mathrm {S} _{\mathcal T}(x)$ can be partitioned into two sets A and B such that $|B|<\infty$ and $|\mu (A\downarrow _{\mathcal T})|<\epsilon$.

Proof

If $\mathrm {S} _{\mathcal T}(x)$ is a finite set, we can choose $A=\emptyset$ and $B= \mathrm {S} _{\mathcal T}(x)$. Otherwise, we can enumerate the elements of $\mathrm {S} _{\mathcal T}(x)$ as $x_1, x_2, \ldots$. Note that $\sum _{i=1}^\infty {|\mu (x_i\downarrow _{\mathcal T})|}<\infty$ and so there exists a positive integer N such that $\sum _{i=N}^\infty |\mu (x_i\downarrow _{\mathcal T})|< \epsilon$. Now, let $A=\{x_i:\ i\ge N\}$ and $B=\{x_i:\ i\in [N-1]\}$.    $\square$

Lemma 3

Let ${\mathcal T}=(T,r)$ be a countable rooted tree. Let $\alpha$ and $\beta$ be two nonnegative real numbers. Consider a weighted rooted tree ${\mathbb T}=({\mathcal T}, \mu )$ satisfying $\mu ( \mathrm {V} (T)) \ge \alpha + \beta$ while $\mu (x \uparrow _{\mathcal T}) \le \alpha$ for all $x \in \mathrm {V} (T)$. Then ${\mathbb T}$ has an $(\alpha , \beta )$ down-set.

Proof

If $\mu ( \mathrm {V} (T))=\alpha +\beta$, clearly $D= \mathrm {V} (T)$ itself is an $(\alpha , \beta )$ down-set of $\mathbb T$.

In the sequel, we turn to the case that $\mu ( \mathrm {V} (T)) > \alpha + \beta$. Take any $\epsilon$ such that $0<\epsilon \le \mu ( \mathrm {V} (T)) - \alpha - \beta$. We claim that we can find an $(\alpha +\epsilon , \beta )$ down-set $D_\epsilon$ of $\mathbb T$. If this really holds, a compactness argument tells us that there exists an $(\alpha , \beta )$ downset D of $\mathbb T$, as wanted.

For any nonnegative integer i, let $L_i$ be the set of vertices of T which are of distance i from r in T. By assumption,

$$\begin{aligned} \sum _{x\in \mathrm {V} (T)}|\mu (x)|<\infty . \end{aligned}$$

Consequently, there exists a nonnegative integer N such that

$$\begin{aligned} \sum _{i=N}^\infty \sum _{x\in L_i}|\mu (x)|<\ \epsilon . \end{aligned}$$

(4)

By Lemma 2, we can associate to each $x\in \mathrm {V} (T)$ a partition of $\mathrm {S} _{\mathcal T}(x)$ into two sets $A_x$ and $B_x$ such that $|B_x|$ is finite and $|\mu (A_x\downarrow _{\mathcal T}))|<\epsilon$. In view of (4), we will require that $B_x=\emptyset$ for $x\in L_{N-1}$. For all $x\in \mathrm {V} (T)$, we denote the set $A_x\downarrow _{\mathcal T}$ by $\varLambda _x$. Let $\mathcal A$ be the set system

$$\begin{aligned} \{ \varLambda _x:\ x\in \bigcup _{i=0}^{N-1} L_i \}.\end{aligned}$$

Observe that $\mathcal A$ forms a hierarchy, namely $A\cap A'\in \{\emptyset , A, A'\}$ for all $A,A'\in \mathcal A$. Let $\overline{\mathcal A}$ be the set of maximal elements of $\mathcal A$, namely

$$\begin{aligned} \begin{array}{lll} \overline{\mathcal A}&{}=&{} \{A\in {\mathcal A}: \not \exists A'\in {\mathcal A}, A'\supsetneq A\}\\ &{}= &{} \{A\in {\mathcal A}:\ A'\cap A\in \{ A', \emptyset \}, \forall A'\in {\mathcal A}\}. \end{array}\end{aligned}$$

It is clear that the elements of $\overline{\mathcal A}$ are pairwise disjoint and we write $\varSigma$ for the union of them. Let

$$\begin{aligned} W=\left( \bigcup _{i=0}^{N-1} L_i\right) \setminus \varSigma \end{aligned}$$

and let $T^*$ be the subtree of T induced by W. For each element $\varLambda _x\in \overline{\mathcal A}$, we add a new vertex $\lambda _x$ and connect it to $x\in W$ and thus obtain from $(T^*, r)$ a new rooted tree $(T^\circ , r)$.

For $i=0,\ldots ,N-1$, let $W_i=W\cap L_i$. Of course, $W_0=\{r\}$ is a finite set. For each integer $\ell$ satisfying $0\le \ell \le N-2$, we have $W_{\ell +1}=\bigcup _{x\in W_\ell } B_x$ and so the finiteness of $W_{\ell +1}$ is guaranteed by the finiteness of $W_\ell$. We can thus conclude now that W is a finite set, and henceforth $(T^\circ , r)$ is a finite rooted tree.

We let $\mu ^\circ$ be the weighting of $T^\circ$ such that

$$ {\left\{ \begin{array}{ll} \mu ^\circ (x)=\mu (x) &{} \text {if } x \in W,\\ \mu ^\circ (\lambda _x)=\mu (\varLambda _x ) &{} \text {if } \varLambda _x\in \overline{\mathcal A}. \end{array}\right. } $$

We can see that $\mu ^\circ ( \mathrm {V} (T^\circ ))=\mu ( \mathrm {V} (T))\ge \alpha +\beta +\epsilon$ and that $\mu ^\circ (x\uparrow _{\mathcal T^\circ })\le \alpha +\epsilon$ for all $x\in \mathrm {V} (T^\circ )$. Applying Lemma 1 yields the claim that we can find an $(\alpha +\epsilon , \beta )$ down-set $D^\circ$ of $(\mathcal T^\circ , \mu ^\circ )$. Finally, letting ${\mathcal D}$ be the subset of $D^\circ$ consisting of all elements of the form $\lambda _x$, the required $(\alpha +\epsilon , \beta )$ down-set $D_\epsilon$ of $\mathbb T$ can be chosen to be

$$\begin{aligned} D_\epsilon = (D^\circ \setminus {\mathcal D})\cup \left( \bigcup _{\lambda _x\in {\mathcal D}} \varLambda _x\right) . \end{aligned}$$

This is the end of the proof.    $\square$

Proof (of Theorem 1)

We prove the statement by induction on k. Let ${\mathcal T}=(T, r).$

When $k=1$, we can simply choose $D_1$ to be the down-set $\mathrm {V} (T)$. Since $\mu (D_1)\ge d_1$, we see that $(T,r,\mu )$ is $d_1$-fat, and so the base case holds true.

Assume now $k>1$ and the result holds for smaller k. Let us suppose that $(T,r,\mu )$ is not c-tall and try to find k disjoint down-sets $D_1, \ldots , D_k$ of ${\mathcal T}$ such that $\mu (D_i) \ge d_i$ for all $i \in [k]$.

Taking $\alpha = c$ and $\beta = d_k$, it follows from Lemma 3 that there exists a down-set D of $\mathcal T$ such that $\mu (D) \ge \beta = d_k$ and $\mu (D \uparrow _{\mathcal T}) \le \alpha +\beta = c + d_k$. Consider the finite measure space $( \mathrm {V} (T), 2^{ \mathrm {V} (T)}, \mu ')$ where

$$ \mu '(x) :={\left\{ \begin{array}{ll} 0 &{} \text { if } x \in D \uparrow _{\mathcal T};\\ \mu (x) &{} \text { if } x \in \mathrm {V} (T)\setminus (D \uparrow _{\mathcal T}). \end{array}\right. } $$

Note that $(k-2)c + \sum _{i = 1}^{k-1}d_i \le \mu '( \mathrm {V} (T)$. By induction hypothesis, there exist $k-1$ down-sets of $\mathcal T$, say $D'_1, \ldots , D'_{k-1}$, such that $\mu '(D'_i) \ge d_i$ holds for all $i \in [k-1]$. For $i \in [k]$, define

$$ D_i :={\left\{ \begin{array}{ll} D'_i \setminus (D \uparrow _{\mathcal T}) &{} \text {if } i \in [k-1];\\ D &{} \text {if } i=k. \end{array}\right. } $$

Clearly, $D_1, \ldots , D_k$ are pairwise disjoint sets with $\mu (D_i) \ge d_i$ for all $i \in [k]$. To verify that $D_1, \ldots , D_k$ are what we need, it is sufficient to show that $D_i$ is a down-set of $\mathcal T$ for every $i\in [k-1]$. Pick $i \in [k-1]$ and $x \in D_i \downarrow _{\mathcal T}\subseteq D'_i$. Then there exists $x' \in D_i$ such that $x'\in T[x,r]$. Since $D_i = D'_i \setminus D \uparrow _{\mathcal T}$, we have $x' \notin D \uparrow _{\mathcal T}$ and therefore $x \notin D\uparrow _{\mathcal T}$. Consequently, we arrive at $x \in D'_i \setminus (D\uparrow _{\mathcal T} )= D_i$, finishing the proof.    $\square$

We have been playing up and down in a tree to deduce our main result. It is interesting to see for which structure more general than trees we can play up and down analogously. We conclude the paper by giving a couterexample for the “poset version” of Lemma 1.

Fig. 3.

Hasse diagram of a poset in which x covers y when x is depicted higher than y and xy is drawn as an edge. See Example 4.

Example 4

Let $\epsilon$ be a positive real such that $\epsilon < \frac{1}{12}$, let $\alpha =\frac{3}{4}$ and let $\beta$ be a number inside the open interval $( \epsilon , \frac{1}{4}-2\epsilon )$. For the weighted poset depicted in Fig. 3, $\mu ( P)=1-\epsilon > \alpha + \beta$ and $\mu (x \uparrow _{\mathcal T}) \le \frac{3}{4}-2\epsilon \le \alpha$ for all $x \in \mathrm {V} (T)$. But there is no $(\alpha , \beta )$ down-set in P.    $\square$