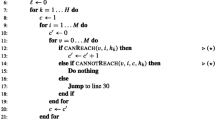Randomized and Symmetric Catalytic Computation

Abstract

A catalytic Turing machine is a model of computation that is created by equipping a Turing machine with an additional auxiliary tape which is initially filled with arbitrary content; the machine can read or write on auxiliary tape during the computation but when it halts auxiliary tape’s initial content must be restored. In this paper, we study the power of catalytic Turing machines with $O(\log n)$-sized clean tape and a polynomial-sized auxiliary tape.

We introduce the notion of randomized catalytic Turing machine and show that the resulting complexity class $\mathsf {CBPL}$ is contained in the class $\mathsf {ZPP}$. We also introduce the notion of symmetricity in the context of catalytic computation and prove that, under a widely believed assumption, in the logspace setting the power of a randomized catalytic Turing machine and a symmetric catalytic Turing machine is equal to a deterministic catalytic Turing machine which runs in polynomial time.

The first author was partially funded by a grant from Infosys foundation and SERB-MATRICS grant MTR/2017/000480. The second and fourth author were supported by Visvesvaraya PhD Scheme.

1 Introduction

Buhrman et al. [1] first introduced the catalytic computational model. This model of computation has an auxiliary tape filled with arbitrary content in addition to the clean tape of a standard Turing machine. The machine during the computation can use this auxiliary tape to read or write, but at the end of the computation, it is constrained to have the same content in the auxiliary tape as initial. The central question here is, whether catalytic computational model is more powerful than the traditional Turing machine model or not. It seems intuitive that the content of auxiliary tape must be stored in one form or another at each step of the computation, making the auxiliary tape useless if the original auxiliary tape content is incompressible. However, Buhrman et al. [1] showed that problems that are not known to be solvable by a standard Turing machine using $O(\log n)$ space (Logspace, $\mathsf {L}$) can be solved by a catalytic Turing machine with $O(\log n)$ clean space and $n^{O(1)}$ auxiliary space (Catalytic logspace, $\mathsf {CL}$). Specifically, they showed that the circuit class uniform $\mathsf {TC}_1$, which contains $\mathsf {L}$ is contained in $\mathsf {CL}$. This result gives evidence that the auxiliary tape might not be useless.

Since its introduction, researchers have tried to understand the power and limitation of catalytic Turing machine. Buhrman et al. [2] also introduced a nondeterministic version of the catalytic Turing machine and proved that nondeterministic catalytic logspace class $\mathsf {CNL}$ is closed under complement. They also showed that $\mathsf {CNL}$ is contained in $\mathsf {ZPP}$. Girard et al. [3] studied catalytic computation in a nonuniform setting. More recently, Gupta et al. [4] studied the notion of unambiguity in catalytic logspace and proved that unambiguous catalytic Turing machines are as powerful as nondeterministic catalytic Turing machines in the logspace setting.

In this paper, we study the notion of randomized computation and symmetric computation in the context of catalytic Turing machines. Following the earlier results in the field of catalytic computation, we define the classes of problems by limiting the catalytic Turing machine to $O(\log n)$-size clean tape and $n^{O(1)}$-sized auxiliary tape. We thus get the classes $\mathsf {CBPL}$ and $\mathsf {CSL}$ for randomized and symmetric logspace catalytic Turing machine respectively (see Sect. 2 for complete definitions). We show that $\mathsf {CBPL}\subseteq \mathsf {ZPP}$. We also prove that under a widely believed assumption, not only $\mathsf {CBPL}$ is equal to $\mathsf {CSL}$, but they are also equal to the class of problems that can be solved by a deterministic catalytic Turing machine running in polynomial time with $O(\log n)$-size clean (or work) tape and $n^{O(1)}$-sized auxiliary tape ($\mathsf {CSC}_1$). Formally, we prove the following.

Theorem 1 (Main Theorem)

[Main Theorem] If there exists a constant $\epsilon > 0$ such that we have $\mathsf {DSPACE}(n)\not \subseteq \mathsf {SIZE}(2^{\epsilon n})$, then $\mathsf {CBPL}= \mathsf {CL}= \mathsf {CSL}= \mathsf {CSC}_1$.

Our result requires (i) a pseudorandom generator to get a small size configuration graph of a catalytic machine, and (ii) universal exploration sequence to traverse those small size configuration graphs. The required pseudorandom generator was used in [2] and [4] as well. Universal exploration sequence was first introduced by Koucky [7]. Reingold [9] presented a logspace algorithm to construct a polynomially-long universal exploration sequence for undirected graphs. Since the catalytic Turing machines we study have $O(\log n)$ size clean space, we can use Reingold’s algorithm to construct those sequences in catalytic machines as well.

1.1 Outline of the Paper

In Sect. 2, we give preliminary definitions of various catalytic classes and state the lemmas on the pseudorandom generator and universal exploration sequences used by us. In Sect. 3, we prove $\mathsf {CBPL}\subseteq \mathsf {ZPP}$. In Sect. 4, we prove our main result Theorem 1. Finally, in Sect. 5, without using the class $\mathsf {CSL}$ we give an alternative proof of $\mathsf {CL}= \mathsf {CSC}_1$ under the same assumption as in Theorem 1.

2 Preliminaries

We start with the brief definitions of a few well-known complexity classes.

$\mathsf {ZPP}$, $\mathsf {DSPACE}(n)$, $\mathsf {SIZE}(k)$: $\mathsf {ZPP}$ denotes the set of the languages which are decidable in expected polynomial time. $\mathsf {DSPACE}(n)$ denotes the set of the languages which are decidable in linear space. $\mathsf {SIZE}(k)$ denotes the set of the languages which are decidable by circuits of size k.

The deterministic catalytic Turing machine was formally defined by Buhrman et al. [2] in the following way.

Definition 2

Let $\mathcal {M}$ be a deterministic Turing machine with four tapes: one input and one output tape, one work-tape, and one auxiliary tape (or aux-tape).

$\mathcal {M}$ is said to be a deterministic catalytic Turing machine using workspace s(n) and auxiliary space $s_a(n)$ if for all inputs $x \in \{0, 1\}^n$ and auxiliary tape contents $w \in \{0, 1\}^{s_a(n)}$, the following three properties hold.

• 1. Space bound. The machine $\mathcal {M}$ uses space s(n) on its work tape and space $s_a(n)$ on its auxiliary tape.

• 2. Catalytic condition. $\mathcal {M}$ halts with w on its auxiliary tape.

• 3. Consistency. $\mathcal {M}$ either accepts x for all choices of w or it rejects for all choices of w.

Definition 3

$\mathsf {CSPACE}(s(n))$ is the set of languages that can be solved by a deterministic catalytic Turing machine that uses at most s(n) size workspace and $2^{s(n)}$ size auxiliary space on all inputs $x \in \{0, 1\}^n$. $\mathsf {CL}$ denotes the class $\mathsf {CSPACE}(O(\log n))$.

Definition 4

$\mathsf {CTISP}(t(n),s(n))$ is the set of languages that can be solved by a deterministic catalytic Turing machine that halts in at most t(n) steps and uses at most s(n) size workspace and $2^{s(n)}$ size auxiliary space on all inputs $x \in \{0, 1\}^n$. $\mathsf {CSC}_\mathsf {i}$ denotes the class $\mathsf {CTISP}(poly(n), O((\log n)^i))$.

A configuration of a catalytic machine $\mathcal {M}$ with s(n) workspace and $s_a(n)$ auxiliary space consists of the state, at most s(n) size work tape content, at most $s_a(n)$ size auxiliary tape content, and the head positions of all the three tapes. We will use the notion of configuration graph in our results, which is often used in proving space-bounded computation results for traditional Turing machines. In the context of catalytic Turing machines, the configuration graph was defined in [1, 2] in a slightly different manner than traditional Turing machines.

Definition 5

For a deterministic catalytic Turing machine $\mathcal {M}$, input x, and initial auxiliary content w, the configuration graph denoted by $\mathcal {G}_{\mathcal {M},x,w}$ is a directed acyclic graph in which every vertex is a configuration which is reachable when $\mathcal {M}$ runs on (x, w). $\mathcal {G}_{\mathcal {M},x,w}$ has a directed edge from a vertex u to a vertex v if $\mathcal {M}$ in one step can move to v from u.

$|\mathcal {G}_{\mathcal {M},x,w}|$ denotes the number of the vertices in $\mathcal {G}_{\mathcal {M},x,w}$. We call a configuration in which a machine accepts (rejects) the input an accepting (rejecting) configuration. We note that the configuration graph of a deterministic catalytic Turing machine is a line graph.

Motivated by the symmetric Turing machines defined in [8], we study the notion of symmetricity in catalytic computation. We define the symmetric catalytic Turing machine below.

Definition 6

A symmetric catalytic Turing machine is a catalytic Turing machine with two sets of transitions $\delta _0$ and $\delta _1$. At each step, the machine uses either $\delta _0$ or $\delta _1$ arbitrarily. $\delta _0$ and $\delta _1$ are the finite set of transitions of the following form. (For simplicity, we have described these transitions for a single tape machine.)

• (p, a, 0, b, q): If machine’s current state is p, the head is on a cell containing a, then in one step machine changes the state to q, a is changed to b, and the head doesn’t move.

• (p, ab, L, cd, q): If machine’s current state is p, the head is on a cell containing b and the cell left to it contains a, then in one step machine changes the state to q, the head moves to the left, and both a and b are changed to c and d respectively.

• (p, ab, R, cd, q): If machine’s current state is p, the head is on a cell containing a and the cell right to it contains b, then in one step machine changes the state to q, the head moves to the right, and both a and b are changed to c and d respectively.

Additionally, the following two properties hold:

• Every transition has its inverse, i.e. each of $\delta _0$ and $\delta _1$ has (p, ab, L, cd, q) if and only if it has (q, cd, R, ab, p) and (p, a, 0, b, q) if and only if it has (q, b, 0, a, p).

• The machine has two special states $q_{start}$ and $q_{accept}$. The machine in the beginning is in the state $q_{start}$. During the run, at every configuration where the state is $q_{start}$ or $q_{accept}$, the machine is constrained to have the same auxiliary content as initial.

The notion of the configuration graph extends to symmetric catalytic machines as well. Due to inverse transitions, configuration graphs of a symmetric catalytic machine are bidirectional, i.e. for any two vertices in a configuration graph, say u and v, an edge goes from u to v if and only if an edge goes from v to u.

We say a symmetric catalytic Turing machine $\mathcal {M}$ decides or solves a language L if on every input x and every initial auxiliary content w, an accepting configuration (i.e., configuration with $q_{accept}$) is reachable when $\mathcal {M}$ runs on (x, w) if and only if $x \in L$.

Definition 7

$\mathsf {CSSPACE}(s(n))$ is the set of languages that can be solved by a symmetric catalytic Turing machine that uses at most s(n) size workspace and $2^{s(n)}$ size auxiliary space on all inputs $x \in \{0, 1\}^n$. $\mathsf {CSL}$ denotes the class $\mathsf {CSSPACE}(O(\log n))$.

The following lemma follows from Theorem 1 of [8].

Lemma 8

$\mathsf {CL}\subseteq \mathsf {CSL}$.

In this paper, we also study randomized catalytic computation. We define the randomized catalytic Turing machine as follows.

Definition 9

A randomized catalytic Turing machine is a catalytic Turing machine with two transition functions $\delta _0$ and $\delta _1$. At each step the machine applies $\delta _0$ with $\frac{1}{2}$ probability and $\delta _1$ with $\frac{1}{2}$ probability, independent of the previous choices. On all possible choices of transition functions $\delta _0$ and $\delta _1$, the machine is constrained to have the same auxiliary content as initial when it halts.

We say a randomized catalytic Turing machine $\mathcal {M}$ decides or solves a language L if for every input x and initial auxiliary content w, $\mathcal {M}$ accepts x with probability at least $\frac{2}{3}$ if $x \in L$ and rejects x with probability at least $\frac{2}{3}$ if $x \notin L$.

Definition 10

$\mathsf {CBPSPACE}(s(n))$ is the set of languages that can be solved by a randomized catalytic Turing machine that uses at most s(n) size workspace and $2^{s(n)}$ size auxiliary space on all inputs $x \in \{0, 1\}^n$. $\mathsf {CBPL}$ denotes the class $\mathsf {CBPSPACE}(O(\log n))$.

The class $\mathsf {CBPL}$ is the catalytic equivalent of the well-known complexity class $\mathsf {BPL}$. Configuration graph for a randomized catalytic Turing machine is defined in the same way it was defined for a deterministic catalytic Turing machine. Although note here that non-halting configurations have out-degree two in a configuration graph of a randomized catalytic machine.

For a deterministic catalytic machine $\mathcal {M}$ with $c \log n$ size workspace and $n^c$ size auxiliary space, an input x and initial auxiliary content w, $|\mathcal {G}_{\mathcal {M}, x, w}|$ can be as large as exponential in |x|. But in [1, 2], authors showed that the average size of the configuration graphs over all possible initial auxiliary contents for a particular x and $\mathcal {M}$ is only polynomial in |x|. This observation holds for symmetric and randomized catalytic Turing machines as well. The following lemma is a direct adaption of Lemma 8 from [2] for symmetric and randomized catalytic machines.

Lemma 11

Let $\mathcal {M}$ be a symmetric or randomized catalytic Turing machine with $c\log n$ size workspace and $n^c$ size auxiliary space. Then for all x,

$$\mathop {\mathbb {E}}_{w \in _R \{0,1\}^{{n^c}}}[|\mathcal {G}_{\mathcal {M},x,w}|] \le O(n^{2c+2}),$$

where $\mathbb {E}$ is the expectation symbol.

In Sect. 4, we will prove $\mathsf {CBPL}= \mathsf {CL}= \mathsf {CSL}= \mathsf {CSC}_1$ under the same assumption the following standard derandomization result holds.

Lemma 12

[5, 6] If there exists a constant $\epsilon > 0$ such that $\mathsf {DSPACE}(n) \nsubseteq \mathsf {SIZE}(2^{\epsilon n})$ then for all constants c there exists a constant $c'$ and a function $G:\{0,1\}^{c'\log n} \rightarrow \{0,1\}^n$ computable in $O(\log n)$ space, such that for any circuit C of size $n^c$

$$ \Bigl | \mathop {Pr}_{r\in \{0,1\}^n} [C(r) = 1] - \mathop {Pr}_{s\in \{0,1\}^{c'\log n}} [C(G(s)) = 1] \Bigr | < \frac{1}{n}.$$

We will use a pseudorandom generator to produce small size configuration graphs of symmetric and randomized catalytic machines. From [2] we know that such a pseudorandom generator exists for nondeterministic catalytic Turing machines under the same assumption as that of Lemma 12. Their result trivially implies the following lemma.

Lemma 13

Let $\mathcal {M}$ be a symmetric or randomized catalytic Turing machine using $c\log n$ size workspace and $n^c$ size auxiliary space. If there exists a constant $\epsilon > 0$ such that $\mathsf {DSPACE}(n) \nsubseteq \mathsf {SIZE}(2^{\epsilon n})$, then there exists a function $G:\{0,1\}^{O(\log n)} \rightarrow \{0,1\}^{n^{c}}$, such that on every input x and initial auxiliary content w, for more than half of the seeds $s \in \{0,1\}^{O(\log n)}$, $|\mathcal {G}_{\mathcal {M},x,w \oplus G(s)}| \le n^{2c+3}$. Moreover, G is logspace computable. $(w \oplus G(s)$ denotes the bitwise XOR of w and G(s).)

We will also need universal exploration sequences. Let $\mathcal {G}$ be an undirected graph, then labelling is a function where every edge uv leaving a vertex u is mapped to an integer $\{0, 1, \dots , degree(u) - 1\}$ in such a way that any two distinct edges leaving a common vertex get different labels. Note that, in such a labelling an undirected edge, say uv, gets two labels, one with respect to u and another with respect to v.

An (n, d)-universal exploration sequence of length m is a sequence of integers $(s_1, s_2, \dots ,s_m)$ where each $s_i \in \{0, 1, \dots , d - 1\}$, which can be used to visit all the vertices of any connected undirected graph $\mathcal {G}$ of n vertices and maximum degree d in the following way. Let $\mathcal {G}$ has a labelling l, in the first step we pick a vertex u and take an edge e leaving u labeled by $s_1$ mod degree(u) to move to the next vertex, after this, in the ith step if we arrived at a vertex, say v, through an edge labeled with p with respect to v then we take an edge with label $(p + s_i)$ mod degree(v) with respect to v to move to the next vertex. Reingold [9] proved that an (n, d)-universal exploration sequence can be constructed in $O(\log n)$ space.

An essential property of universal exploration sequences that we will use in our result is that at any point during the traversal using a universal exploration sequence we can stop and traverse back the vertices visited so far in the exact reverse order that they were visited.

3 $\mathsf {CBPL}\,\subseteq \,\mathsf {ZPP}$

In this section, we will prove that $\mathsf {CBPL}$ is contained in $\mathsf {ZPP}$. Our proof, similar to the proof of $\mathsf {CNL}\subseteq \mathsf {ZPP}$, uses the observation that the average size of the configuration graphs over all possible auxiliary content is polynomial in the length of the input.

Theorem 14

$\mathsf {CBPL}\subseteq \mathsf {ZPP}$.

Proof

Let $\mathcal {M}$ be a $\mathsf {CBPL}$ machine with $c\log n$ size workspace and $n^c$ size auxiliary space. We construct a $\mathsf {ZPP}$ machine $\mathcal {M'}$ such that $L(\mathcal {M}) = L(\mathcal {M'})$. On input x, $\mathcal {M'}$ first randomly generates a string w of size $|x|^c$ and constructs the configuration graph $\mathcal {G}_{\mathcal {M}, x, w}$.

For every $v \in \mathcal {G}_{\mathcal {M}, x, w}$, let $\mathsf {prob}(v)$ denote the probability of reaching an accepting configuration from v. $\mathcal {M'}$ computes the $\mathsf {prob}(v)$ for every vertex in the following way.

• 1. Set $\mathsf {prob}(v) = 1$ if v is an accepting configuration and $\mathsf {prob}(v) = 0$ if v is a rejecting configuration.

• 2. For every vertex v whose $\mathsf {prob}(v)$ is still not computed, if $\mathsf {prob}(v_1)$ and $\mathsf {prob}(v_2)$ are already computed and there is an edge from v to both $v_1$ and $v_2$, set $\mathsf {prob}(v) = \frac{1}{2}\cdot \mathsf {prob}(v_1) + \frac{1}{2}\cdot \mathsf {prob}(v_2)$.

• 3. Repeat 2 until $\mathsf {prob}(v)$ is computed for all $v \in \mathcal {G}_{\mathcal {M}, x, w}$.

In the end, $\mathcal {M'}$ accepts x if and only if $\mathsf {prob}(v_{init}) \ge \frac{2}{3}$, where $v_{init}$ is the initial configuration. The procedure to compute $\mathsf {prob}(v)$ can easily be done by $\mathcal {M'}$ in time polynomial in $|\mathcal {G}_{\mathcal {M}, x, w}|$. Since from Lemma 11 we know that ${\mathbb {E}}_{w \in _R \{0,1\}^{{n^c}}}[|\mathcal {G}_{\mathcal {M},x,w}|] \le O(n^{2c+2})$, the machine runs in expected polytime.     $\square$

4 Proof of Main Theorem

Since we know $\mathsf {CL}\subseteq \mathsf {CSL}$ from Lemma 8 and $\mathsf {CSC}_1\subseteq \mathsf {CBPL}$ follows from the definition, it is enough to prove $\mathsf {CBPL}\subseteq \mathsf {CL}$ and $\mathsf {CSL}\subseteq \mathsf {CSC}_1$.

Proof of $\mathsf {CBPL}\subseteq \mathsf {CL}$ :

Let $\mathcal {M}$ be a $\mathsf {CBPL}$ machine with $c\log n$ size workspace and $n^c$ size auxiliary space. We will construct a $\mathsf {CL}$ machine $\mathcal {M'}$ such that $L(\mathcal {M}) = L(\mathcal {M'})$.

From Lemma 13, we know that there exists a logspace computable function $G:\{0,1\}^{O(\log n)} \rightarrow \{0,1\}^{n^{c}}$, such that on every input x and initial auxiliary content w, for more than half of the seeds $s \in \{0,1\}^{O(\log n)}$, $|\mathcal {G}_{\mathcal {M},x,w \oplus G(s)}| \le n^{2c+3}$. We call a seed s good, if $|\mathcal {G}_{\mathcal {M},x,w \oplus G(s)}| \le n^{2c+3}$.

We first prove the existence of another pseudorandom generator which $\mathcal {M'}$ will use to deterministically find $\mathcal {M}$’s output in case of a good seed. Let $\tilde{s}$ be a good seed and $C_{x,w\oplus G(\tilde{s})}$ be a polynomial size boolean circuit which on input $r \in \{0,1\}^{n^{2c+3}}$ traverses $\mathcal {G}_{\mathcal {M},x,w \oplus G(\tilde{s})}$ using r in the following way. Assume a label on every edge of $\mathcal {G}_{\mathcal {M},x,w \oplus G(\tilde{s})}$, such that an edge uv is labeled by 0 if u changes to v using $\delta _0$ or 1 if u changes to v using $\delta _1$. $C_{x,w \oplus G(\tilde{s})}$ starts from the initial vertex and in the ith step moves to the next vertex using the outgoing edge with label same as the ith bit of r. $C_{x,w \oplus G(\tilde{s})}$ outputs 1 if it reaches an accepting vertex while traversing $\mathcal {G}_{\mathcal {M},x,w \oplus G(\tilde{s})}$, else it outputs 0.

From Lemma 12, we know that there exists a logspace computable function $F:\{0,1\}^{(O \log n)} \rightarrow \{0,1\}^{n^{2c+3}}$ such that,

$$ \Bigl | \mathop {Pr}_{r\in \{0,1\}^{n^{2c+3}}} [C_{x, w \oplus G(\tilde{s})}(r) = 0] - \mathop {Pr}_{s'\in \{0,1\}^{O(\log n)}} [C_{x,w \oplus G(\tilde{s})}(F(s')) = 0] \Bigr | < \frac{1}{n}.$$

For sufficiently large n, if $x \in L(\mathcal {M})$, then

$$\begin{aligned} \mathop {Pr}_{s'\in \{0,1\}^{O(\log n)}} [C_{x,w \oplus G(\tilde{s})}(F(s')) = 0] \Bigr |< \frac{1}{3} + \frac{1}{n} < \frac{1}{2} \end{aligned}$$

(1)

Similarly, we can prove that, if $x \notin L(\mathcal {M})$, then

$$\begin{aligned} \mathop {Pr}_{s'\in \{0,1\}^{O(\log n)}} [C_{x,w \oplus G(\tilde{s})}(F(s')) = 1] \Bigr |< \frac{1}{3} + \frac{1}{n} < \frac{1}{2} \end{aligned}$$

(2)

Equations (1) and (2) together prove that on less than half of the seeds $s' \in \{0,1\}^{O(\log n)}$, the simulation of $\mathcal {M}$ on (x, $w \oplus G(\tilde{s})$) by picking $\delta _0$ or $\delta _1$ according to $F(s')$ gives the wrong answer.

We now present the algorithm of $\mathcal {M'}$.

If $x \in L(\mathcal {M})$, then on every good seed s of G, $cnt_{acc} > \frac{|S'|}{2}$. Since more than half of G’s seeds are good, $cnt_{final}$ is incremented in line 16 more than $\frac{|S|}{2}$ times. Hence, in line 21 $\mathcal {M'}$ will Accept after checking $cnt_{final} > \frac{|S|}{2}$. On the other hand, if $x \notin L(\mathcal {M})$, then on every good seed s, $cnt_{acc} < \frac{|S'|}{2}$. So $cnt_{final}$ is not incremented in line 16 more than $\frac{|S|}{2}$ times. Hence, $\mathcal {M'}$ will Reject in line 23.

Proof of $\mathsf {CSL}\subseteq \mathsf {CSC}_1$ :

Let $\mathcal {M}$ be a $\mathsf {CSL}$ machine with $c\log n$ size workspace and $n^c$ size auxiliary space. We will construct a $\mathsf {CSC}_1$ machine $\mathcal {M'}$ such that $L(\mathcal {M}) = L(\mathcal {M'})$.

We will again use the pseudorandom generator G of Lemma 13 with the property that on every input x and initial auxiliary content w, for more than half of the seeds $s \in \{0,1\}^{O(\log n)}$, $|\mathcal {G}_{\mathcal {M},x,w \oplus G(s)}| \le n^{2c+3}$.

We will also use universal exploration sequence to traverse all the vertices of $\mathcal {G}_{\mathcal {M},x,w \oplus G(s)}$ on good seeds s. Let seq denote a $\left( n^{2c+3},d\right)$-universal exploration sequence, where d is a constant upper bound on the maximum degree of $\mathcal {G}_{\mathcal {M},x,w \oplus G(s)}$. We now present the algorithm of $\mathcal {M'}$.

$\mathcal {M'}$ uses a flag variable accept which it sets to TRUE when it finds an accepting configuration while traversing $\mathcal {G}_{\mathcal {M},x,w}$ using seq. If $x \in L(\mathcal {M})$, then $\mathcal {M'}$ on a good seed s must visit all the vertices of $\mathcal {G}_{\mathcal {M},x,w}$ in the simulation of line 5, and hence also visit an accepting configuration. In which case, it sets $accept =$ TRUE in line 6 and later Accepts in line 10. If $x \notin L(\mathcal {M})$, then clearly $\mathcal {M'}$ can never reach an accepting configuration during any simulation. Therefore, $\mathcal {M'}$ never sets accept to TRUE and finally, Rejects in line 13.

$\mathcal {M'}$ takes polynomial time because there are only polynomially many seeds of G, and for every seed of G, it runs two simulations using polynomially-long seq.

We note here that our proof works even for a relaxed definition of $\mathsf {CSL}$, in which a $\mathsf {CSL}$ machine is constrained to have the original auxiliary content only when it enters a configuration with $q_{start}$, not $q_{accept}$.

5 An Alternative Proof of $\mathsf {CL}= \mathsf {CSC}_1$

Under the assumption that $\mathsf {DSPACE}(n) \not \subseteq \mathsf {SIZE}(2^{\epsilon n})$, we provide an alternative proof of $\mathsf {CL}= \mathsf {CSC}_1$, without using the class $\mathsf {CSL}$. For this we need to define the notion of undirected configuration graph for the deterministic catalytic machines.

Definition 15

For a deterministic catalytic Turing machine $\mathcal {M}$, input x, and initial auxiliary content w, the undirected configuration graph denoted by $\mathcal {\widetilde{G}}_{\mathcal {M},x,w}$ contains the two types of vertices.

• Type 1: A vertex for every configuration which is reachable when $\mathcal {M}$ runs on (x,w).

• Type 2: A vertex for every configuration which is not reachable when $\mathcal {M}$ runs on (x,w) but which can reach some configuration which is reachable when $\mathcal {M}$ runs on (x,w) by applying the transition function of $\mathcal {M}$.

$\mathcal {\widetilde{G}}_{\mathcal {M},x,w}$ has an undirected edge between a vertex $v_1$ and a vertex $v_2$ if $\mathcal {M}$ in one step can move to $v_2$ from $v_1$ or to $v_1$ from $v_2$.

In the following lemma, we prove a result similar to Lemma 11 for undirected configuration graphs of a $\mathsf {CL}$ machine.

Lemma 16

Let $\mathcal {M}$ be a deterministic catalytic Turing machine with $c\log n$ size workspace and $n^c$ size auxiliary space. Then for all x,

$$\mathop {\mathbb {E}}_{w \in _R \{0,1\}^{{n^c}}}[|\mathcal {\widetilde{G}}_{\mathcal {M},x,w}|] \le O(n^{2c+2}).$$

Proof

We first show that for an input x and any two different initial auxiliary contents w and $w'$, $\mathcal {\widetilde{G}}_{\mathcal {M},x,w}$ and $\mathcal {\widetilde{G}}_{\mathcal {M},x,w'}$ cannot have a common vertex (or configuration). Let’s assume for the sake of contradiction that $\mathcal {\widetilde{G}}_{\mathcal {M},x,w}$ and $\mathcal {\widetilde{G}}_{\mathcal {M},x,w'}$ have a common vertex v. Then, the following two cases are possible for v:

Case 1: v is a Type 1 vertex in both $\mathcal {\widetilde{G}}_{\mathcal {M},x,w}$ and $\mathcal {\widetilde{G}}_{\mathcal {M},x,w'}$.

First note that if v is a Type 1 vertex in both $\mathcal {\widetilde{G}}_{\mathcal {M},x,w}$ and $\mathcal {\widetilde{G}}_{\mathcal {M},x,w}$, then v is also a common vertex of $\mathcal {G}_{\mathcal {M},x,w}$ and $\mathcal {G}_{\mathcal {M},x,w'}$. Buhrman et al. [1] proved that two different configuration graphs $\mathcal {G}_{\mathcal {M},x,w}$ and $\mathcal {G}_{\mathcal {M},x,w'}$ cannot have a common vertex. We present their argument here for the sake of completion.

If v is a common vertex of $\mathcal {G}_{\mathcal {M},x,w}$ and $\mathcal {G}_{\mathcal {M},x,w'}$, then v is reachable both the times when $\mathcal {M}$ runs on (x, w) and when $\mathcal {M}$ runs on $(x,w')$. Since $\mathcal {M}$ is a deterministic machine, its run on (x, w) and $(x,w')$ must go through the same sequence of configurations after reaching v. This implies that $\mathcal {M}$ on (x, w) has the same halting configuration as $\mathcal {M}$ on $(x, w')$, which is not possible because in such a halting configuration auxiliary content can either be w or $w'$ violating the property that $\mathcal {M}$ restores the initial auxiliary content when it halts. This proves that v cannot be a common vertex of $\mathcal {G}_{\mathcal {M},x,w}$ and $\mathcal {G}_{\mathcal {M},x,w'}$, hence, v can also not be a Type 1 vertex in both $\mathcal {\widetilde{G}}_{\mathcal {M},x,w}$ and $\mathcal {\widetilde{G}}_{\mathcal {M},x,w'}$.

Case 2: v is either a Type 2 vertex in $\mathcal {\widetilde{G}}_{\mathcal {M},x,w}$ or a Type 2 vertex in $\mathcal {\widetilde{G}}_{\mathcal {M},x,w'}$.

For simplicity we only consider the case where v is a Type 2 vertex in both $\mathcal {\widetilde{G}}_{\mathcal {M},x,w}$ and $\mathcal {\widetilde{G}}_{\mathcal {M},x,w'}$, the other cases can be analysed similarly.

If v is a Type 2 vertex in $\mathcal {\widetilde{G}}_{\mathcal {M},x,w}$, then there must be a sequence of configurations, say $S_1 = v \rightarrow C_1 \rightarrow C_2 \dots \rightarrow C_{k_1}$, where every configuration in the sequence yields the next configuration in the sequence, and $C_{k_1}$ is reachable when $\mathcal {M}$ runs on (x, w). Similarly, since v is also a Type 2 vertex in $\mathcal {\widetilde{G}}_{\mathcal {M},x,w'}$, there must also be a sequence of configurations, say $S_2 = v \rightarrow C'_1 \rightarrow C'_2 \dots \rightarrow C_{k_2}$, where every configuration in the sequence yields the next configuration in the sequence, and $C_{k_2}$ is reachable when $\mathcal {M}$ runs on (x, $w'$). Existence of $S_1$ and $S_2$ follows from Definition 15.

Without loss of generality, assume that $k_1 < k_2$. Since $\mathcal {M}$ is a deterministic machine where a configuration can yield at most one configuration, $C_i = C'_i$ for i = 1 to $k_1$. This implies that $C_{k_1}$ is present in $S_2$, and therefore, $C_{k_2}$ is also reachable when $\mathcal {M}$ runs on (x,w). Therefore, $C_{k_2}$ must be a common Type 1 vertex of $\mathcal {G}_{\mathcal {M},x,w}$ and $\mathcal {G}_{\mathcal {M},x,w'}$, which is not possible as we proved in Case 1.

A configuration of $\mathcal {M}$ can be described with at most $c \log n + n^c + \log n + \log (c \log n) + \log n^c + O(1)$ bits, where we need $c \log n + n^c$ bits for work and auxiliary tape content, $\log n + \log (c \log n) + \log n^c$ bits for the tape heads, and O(1) bits for the state. Since no two different undirected configuration graphs for $\mathcal {M}$ and x can have a common vertex, the total number of possible configurations bounds the sum of the size of all the undirected configuration graphs for $\mathcal {M}$ and x.

$$\sum _{w \in \{0,1\}^{{n^c}}} |\mathcal {\widetilde{G}}_{\mathcal {M},x,w}| \le O(2^{c \log n}.2^{n^c}.n.c\log n.n^c).$$

This implies:

$$\mathop {\mathbb {E}}_{w \in _R \{0,1\}^{{n^c}}}[|\mathcal {\widetilde{G}}_{\mathcal {M},x,w}|] \le O(n^{2c+2}).$$

.

    $\square$

Here again, we will use a pseudorandom generator to create an auxiliary content on which a $\mathsf {CL}$ machine produces a small size undirected configuration graph. Lemma 16 and the assumption of Lemma 12 gives us such a pseudorandom generator. We are omitting the proof here as it is similar to the proof of Lemma 10 of [2].

Lemma 17

Let $\mathcal {M}$ be a deterministic catalytic Turing machine using $c\log n$ size workspace and $n^c$ size auxiliary space. If there exists a constant $\epsilon > 0$ such that $\mathsf {DSPACE}(n) \nsubseteq \mathsf {SIZE}(2^{\epsilon n})$, then there exists a function $G:\{0,1\}^{O(\log n)} \rightarrow \{0,1\}^{n^{c}}$, such that on every input x and initial auxiliary content w, for more than half of the seeds $s \in \{0,1\}^{O(\log n)}$, $|\mathcal {\tilde{G}}_{\mathcal {M},x,w \oplus G(s)}| \le n^{2c+3}$. Moreover, G is logspace computable. $(w \oplus G(s)$ represents the bitwise XOR of w and G(s)).

Now to complete the proof we will construct a $\mathsf {CSC}_1$ machine $\mathcal {M'}$ for a deterministic catalytic machine $\mathcal {M}$ with $c\log n$ size workspace and $n^c$ size auxiliary space, such that $L(\mathcal {M}) = L(\mathcal {M'})$.

On an input x and initial auxiliary content w, $\mathcal {M'}$ uses the pseudorandom generator G of Lemma 17 and a universal exploration sequence to traverse the vertices of $\mathcal {\tilde{G}}_{\mathcal {M},x,w \oplus G(s)}$. Let seq denote a logspace computable $\left( n^{2c+3}, d\right)$-universal exploration sequence, where d is a constant upper bound on the degree of every vertex in $\widetilde{\mathcal {G}}_{\mathcal {M},x,w \oplus G(s)}$.

The algorithm of $\mathcal {M'}$ is same as Algorithm 2, except in line 5 instead of traversing $\mathcal {G}_{\mathcal {M},x,w \oplus G(s)}$ it traverses the vertices of $\mathcal {\tilde{G}}_{\mathcal {M},x,w \oplus G(s)}$ using seq.

If $x \in L(\mathcal {M})$, then $\mathcal {M'}$ on a good seed s must reach an accepting configuration while simulating $\mathcal {M}$ using seq. In this case it will set $accept =$ TRUE in line 6 and finally Accept in line 10.

If $x \notin L(\mathcal {M})$, then clearly a Type 1 vertex of $\mathcal {\tilde{G}}_{\mathcal {M},x,w \oplus G(s)}$ cannot be an accepting configuration for any seed s of G. Observe that a Type 2 vertex of $\mathcal {\tilde{G}}_{\mathcal {M},x,w \oplus G(s)}$ can also not be an accepting configuration because configurations corresponding to Type 2 vertices are non-halting by definition. Therefore, $\mathcal {M'}$ cannot reach an accepting configuration during any simulation if $x \notin L(\mathcal {M})$, due to which $\mathcal {M'}$ never sets accept to TRUE and finally Rejects in line 13.