1 Introduction

Proposed earlier procedure of simulation the fatigue process based on the due finite element modeling of the affected area of a structure, application of the damage summation technique and appropriate criterion for fatigue failure of material allowed assessment of fatigue life from the onset of service loading up to development of a critical state, e.g. of the through crack growth in a structural component [1, 2], etc. Also, it was shown that the simulation scheme was capable of account the heterogeneity of the material structure fatigue resistance, the crack closure effects and elastic-plastic material response when the Strain-life criterion for fatigue failure was applied (e.g., [3]). Meanwhile, fatigue reliability assessment of metallic structures subjected to intensive alternating service loading in various applications according current design codes (e.g., [4]) is based mostly on the Stress-life (S-N) criteria which formally indicate the crack initiation at critical locations. In case the crack is detected in a component the residual service life as recommended may be estimated by applying the Linear fracture mechanics techniques, however, with certain limitations in defining conditions of the crack growth and exhaustion of life.

It was shown [5, 6], that for the fatigue design purposes, in particular, application of the S-N curves collected by testing \(\ll \)classed\(\gg \) specimens (including typified welded joints [7]) terminated at almost complete failure could not provide identity of fatigue damage in structural details necessarily related to purposes of the design. Apart from that, application of different models of fatigue process (crack initiation defined by S-N criteria and crack growth assessed by the Linear fracture mechanics model) mechanically continuous is leading to uncertainties in defining fatigue life of structural components, partly, due to the uncertain gap between the states of the fatigue process at the \(\ll \)crack initiation\(\gg \) and \(\ll \)growth\(\gg \) assessed by different models.

However, the mentioned in above modeling of the fatigue process as a continuous one which allowed assessment of fatigue process from initiation of service loading up to development of a critical state may be applied for fatigue analysis purposes using the unique S-N criteria to \(\ll \)close\(\gg \) the mentioned gap. At the same time, application of the modeling principles in conjunction with the Stress-life criteria offering a certain consistency would necessarily need in comparing with proven, although far but exhausting, modeling based on using the Strain-life criteria.

The mentioned in above approaches and comparison of simulation results are commented in more details in the below focused on problems of practical application.

2 Description of the Approach

According the approach, the fatigue process in a structural component assessment is based on application of the finite element model of the component designed with the due attention to the mesh fineness in the area of expected crack initiation and propagation. The finite elements with respect to the polycrystalline material structure are assumed the grain clusters with approximately close (or, alternatively, random) slip resistance.

In the first procedure step the stress field at the expected crack extensions is analyzed in the ascending and descending half-cycles of loading and the stress range \(S_{i}\) = 2\(\sigma _{ai}\) is obtained in every i-th element.

The cyclic elastic-plastic properties of material are characterized by Ramberg-Osgood approximation; the kinematic hardening and von Mises’ criterion for plasticity are applied. The strain amplitude in finite elements (considered structural elements) is defined, respectively by:

$$\begin{aligned} \varepsilon _{a} = \sigma _{a}/E + (\sigma _{a}/K') ^{1/n'}, \end{aligned}$$
(1)

where E - elasticity modulus, \(n'\) - cyclic strain hardening exponent and \(K'\) - cyclic strength coefficient.

The number of load cycles prior to failure of elements at the initial step of the procedure is obtained by applying the Strain-life criterion:

$$\begin{aligned} \varepsilon _{a} = (\sigma '_{f}/E)(2N) ^{b} + \varepsilon '_{f} (2N) ^{c}, \end{aligned}$$
(2)

where \(\sigma ' _{f}\) - fatigue strength coefficient, \(\varepsilon '_{f}\) - fatigue ductility coefficient, b - fatigue strength exponent, c - fatigue ductility exponent.

Further, when the Stress-life criterion is applied, the S-N curve is formulated as:

$$\begin{aligned} \sigma _{a}={\left\{ \begin{array}{ll} \sigma ' _{f1}(2N) ^{b_{1}},&{}2N\le 2N _{s}\\ \sigma ' _{f2}(2N) ^{b_{2}},&{}2N>2N _{s} \end{array}\right. }, \end{aligned}$$
(3)

where \(b_{1}, b_{2}\) - fatigue strength exponent values in the bi-linear S-N curve, \(\sigma ' _{f1},\sigma ' _{f2}\) - fatigue strength coefficients in the curve model; 2\(N _{s}\) - is the “kink” number of cycles of the two-slope curve.

In further analyses the criterion (2) with description of cyclic properties of material (1) is presented in the form of Stress-life, N(S), as the criterion (3). The damage accumulated at random loading estimated by the Palmgren-Miner rule is assumed uniformly distributed within elements. The damage accumulation in finite (structural) elements in the approach is provided by the loading history at the crack initiation site and in elements located at the crack path; it results also from the loading pre-history evolution in the course of failure (crack) extension through the preceding elements (from the initiation location). The linear damage accumulation rule, Bolotin’s version [8]):

$$\begin{aligned} D=\sum _{i}^{} n_{i}(S) /N_{i}(S) = N^{*}\int _{ S_{min}}^{S_{max}} (p(S)/N(S)) dS, \end{aligned}$$
(4)

where \(p(S)=(S/\sigma _{s}^{2})\exp (-S^{2}/2\sigma _{s}^{2})\) - probability density function of the Rayleigh distribution of the stress ranges, \(\sigma _{s}\) - stress scale parameter.

Number of cycles to failure of each element at the first step can be expressed by equating the accumulated damage to unity:

$$\begin{aligned} N_{i}^{1}(S_{i}, \sigma _{si})=1/\int _{ S_{min}}^{S_{max}} (p(S, \sigma _{si})/N(S)) dS, \end{aligned}$$
(5)

where \(S_{min}=2\cdot 0.55\sigma _{-1}\) - minimum stress range in distribution, corresponding to reduced fatigue limit \(\sigma _{-1}\) due to irregular loading; \(S_{max}=S_{i}\) – maximum stress range in the distribution, corresponding to i-th element. Stress ranges below \(S_{min}\) are assumed non-damaging. As mentioned in above, the Raleigh stress range probability exceedance is defined by: \(Q(S_{i})=\exp (-S_{i}^{2}/2\sigma _{si}^{2})\). Respectively, the scale parameter of stress in the stress probability distribution for each element is: \(\sigma _{si}=S_{i}/\sqrt{-2\ln (Q)}\). Correspondingly, the number of cycles in the form  (5) takes into account the irregular loading of each element at the first step of the procedure. Then the minimum number of cycles to failure of first element at the first step of the fatigue simulation procedure is calculated: \(N_{min}^{1}=\min \{ N_{i}^{1}(S_{i}, \sigma _{si})\}\).

According the damage linear summation rule when the damage in an element reaches the critical unity, its compliance is artificially increased by several decimal orders, and nodal forces are step-wise redistributed in the surrounding elements. Damage of each element at the first step is defined as \(d_{i}^{1} = N_{min}^{1} / N_{i}\).

The damage calculation is repeated considering for the renewing stress (stress-strain) state ahead the crack tip. Respectively, an element damage criterion related to the critical load step number \(j_{cr}\):

$$\begin{aligned} d_{i}^{j_{cr}} = \sum _{j=1}^{ j_{cr}-1} d_{i}^{j}+N_{min}^{j_{cr}}/ N_{i}^{j_{cr}}=1. \end{aligned}$$
(6)

When this condition is attained at an element, its stiffness is decreased by several decimal orders and \(\ll \)killed\(\gg \) by this procedure elements form the crack front progress.

This idea was first suggested in pioneering studies of Glinka and Ellyin focused on analysis of crack extensions in thin plates at the plane stress [9, 10]; further analyses had shown that the procedure may be applied in assessment of fatigue process including the crack initiation and growth of plane cracks in arbitrary bodies [1,2,3], etc.

For the purposes of the present study the fatigue failure criteria parameters, S-N and Strain-Life, should be in principle obtained by testing specimens prepared from the same material, say, from the same rolled plate, the same location in it (edge or the mid-part) to consider the peculiarities of the material microstructure. What is essential for the purposes of the comparative study, the means of evaluation of the failure may be different in experimental definition of the criteria parameters: S-N testing of standard specimens (e.g. IIW recommended [7]) is terminated typically prior to failure of specimens controlled by the rapid acceleration of the crack growth while in the strain-controlled testing the stress-strain diagram ascending part (in the tensile phase) distortion indicates the crack initiation and is used to complete the test.

3 Results and Discussion

Implementation of the approach was illustrated by simulation of failure of a thin plate with central elliptic hole fabricated from AlMg4.5Mn alloy (\(\sigma _{y}\)= 298 MPa; (\(\sigma _{u}\) = 363 MPa). The quarter part of the plate with dimensions 2h = 800 mm; 2W = 400 mm is shown in Fig. 1, hole dimensions: 2b = 50 mm; 2R = 100 mm. Plate was loaded by pulsating tension with maximum stress \(\sigma \) in load cycle. Two maximum nominal stress ranges in the random loading successions in the illustrative example were assumed as 100 MPa and 110 MPa. Maximum stress range probability exceedance was accepted Q = 0.0001 in both cases.

Material parameters for (1): \({E} = 0.71\cdot 10^{5}\) MPa, K\(^{\prime }\)= 693 MPa, n\(^{\prime }\) = 0.125, \(\sigma '_{u}\) = 654 MPa. Strain-Life criterion (2) constants: \(\varepsilon '_{f}\) = 0.45, b = −0.089, c = −0.755 [11]. Criterion (2) was approximated by two curves with minimal interpolation error of 5%:

$$\begin{aligned} N={\left\{ \begin{array}{ll} 0.5(0.1/(\varepsilon _{a}-2.852\cdot 10^{-3}))^{1/0.45},&{}\varepsilon _{a}>3.53\cdot 10^{-3}\\ 0.5(1.052\cdot 10^{-2}/(\varepsilon _{a}-3.92\cdot 10^{-4}))^{1/0.11},&{}\varepsilon _{a}\le 3.53\cdot 10^{-3} \end{array}\right. }, \end{aligned}$$
(7)

where the Stress-life criterion (3) constants are: \(\sigma '_{f1}\) = 526 MPa, \(\sigma '_{f2}\) = 719 MPa, \(b_{1}\)= −0.06, \(b_{2}\)= −0.096, 2\(N_{s}\)= 5897 [11]. Fatigue limit of the alloy is: \(\sigma _{-1}\) = 103.4 MPa.

The crack nucleates in stress concentration area and propagates in horizontal direction following up the maximum principal stress plane. Finite-element mesh was refined in the crack growth area; the minimal element size (crack propagation increment) was designed equal to 0.3 mm (Fig. 1). In this illustration of the approach application the plane strain problem is considered and the course of \(\ll \)failure\(\gg \) of material elements the nodes of finite-element mesh are uncoupled to simulate the crack propagation.

The results of crack growth assesment are given in Figs. 2, 3 and 4. As seen, the crack growth rate increases rapidly after the crack becomes 2 mm long in both loading schemes characterized by (maximum) stress ranges. Also, the crack nucleation stage duration is practically identical in case of loading with maximum stress range 100 MPa when the Stress-Life or the Strain-Life criteria are applied (approximately \(3.9\cdot 10^{7}\) cycles).

Fig. 1.
figure 1

The FE-model of the quarter part of the plate

Full size image

In the case of more intensive loading (maximum stress range 110 MPa) the crack initiation stage estimated by the Strain-life criterion occurs shorter than in previous example. In both cases the crack propagation rate and stage duration predicted by this criterion, as seen, are substantially different from those assessed by the Stress-life scheme.

Fig. 2.
figure 2

Crack growth (initiation and propagation) vs the loading cycles number dependence on the maximum nominal stress range in the Raleigh’s distribution: 100 MPa (a) and 110 MPa (b)

Full size image
Fig. 3.
figure 3

Crack extension (initiation and growth) depending on the non-dimensional number of cycles and the maximum nominal stress range in the Raleigh’s distribution: 100 MPa (a) and 110 MPa (b)

Full size image
Fig. 4.
figure 4

Crack extension (from initial 0.3 mm size) depending on the number of load cycles and the maximum nominal stress range in the Raleigh’s distribution: 100 MPa (a) and 110 MPa (b)

Full size image

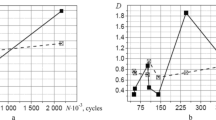
In Fig. 3 the crack growth is presented as related to the non-dimensional number of load cycles. The number of load cycles is divided by the fatigue life \(N_{0}\) corresponding to failure of the first mesh node, meaning the crack nucleation. It is seen, that crack propapation stage in both examples is relatively short and extends over 10–15% of the crack nucleation stage. Using crack propagation extrapolation you can see that crack growth phase is no more than 25% of the total fatigue life.

Figure 4 illustrates results of the crack propagation simulation from 0.3 mm-deep initial crack at the hole. It is seen that the crack growth stage assessed by applying the Strain-Life criterion occures two times shorter than that obtained when the Stress-Life criterion was used.

The discrepancies in the crack initiation and growth stages may be explained by the difference of typical testing specimens procedures, as mentioned in above: the S-N curve addressed testing is terminated when the compliance of the cracked specimen and acceleration of the loading frame is rapidly increasing, whereas when the parameters of Strain-Life criterion are obtained the test is terminated when the ascending part of the cyclic stress-strain hysterezis loop is distorted due to nucleation of macroscopic crack.

The further development of the FE modeling-based procedure of modeling fatigue process in structural components would need in comparison of simulated and observed fatigue damage in structural details with known loading histories similarly to attempted in [11].

4 Conclusions

The previously developed simulation of fatigue damage and crack growth based on respective FE modeling of a structural component, Strain-life criterion for fatigue and the damage accumulation procedure was extended into the same scheme where the Stress-life criterion typically used in current design and fatigue assessment codes was applied. The scheme of simulation fatigue process where the loading was assumed a cyclic one was completed with the means of considering the random loading histories.

The both versions of the procedure were tested in example of the randomly loaded plate with elliptic hole as the stress raiser and the fatigue damage and crack growth initiator. The crack initiation and growth stages predictions occurred different when the Strain-life and Strain-life criteria were applied. The discrepancies of results may be explained partly by specifics of experimental evaluation of the Strain-life and Stress-life criteria parameters, considering mechanics of material deformation and further studies are necessary in the prospect of development the unified approach to model the fatigue process in actual metallic structures.