Abstract
Based on employing the unbounded order convergence instead of the almost everywhere convergence, we identify and study a class of Banach lattices in which the Brezis–Lieb lemma holds true. This gives also a net-version of the Brezis–Lieb lemma in L p for p ∈ [1, ∞). We discuss an operator version of the Brezis–Lieb lemma in certain convergence vector lattices.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
- a.e.-convergence
- Brezis–Lieb lemma
- Banach lattice
- uo-convergence
- Brezis–Lieb space
- Pre-Brezis–Lieb property
2010 Mathematics Subject Classification
1 Introduction
Throughout this paper, ( Ω, Σ, μ) stands for a measure space in which every set A ∈ Σ of nonzero measure has a subset A 0 ⊆ A, A 0 ∈ Σ, such that 0 < μ(A 0) < ∞. It is known that the Fatou lemma is the following implication

where (f n) is a sequence in \(\mathcal {L}^0(\mu )\). The Brezis–Lieb lemma [2, Thm.2] is a refinement of the Fatou lemma.
Theorem 1 (The Brezis–Lieb Lemma)
Let \(j:\mathbb {C}\to \mathbb {C}\) be a continuous function with j(0) = 0 such that, for every ε > 0, there exist two continuous functions \(\phi _\varepsilon , \psi _\varepsilon :\mathbb {C}\to \mathbb {R}_+\) with

Let f be a
\(\mathbb {C}\)
-valued function in
\(\mathcal {L}^0(\mu )\)
and (g
n) be a sequence of
\(\mathbb {C}\)
-valued functions in
\(\mathcal {L}^0(\mu )\)
such that
 ; j(f), ϕ
ε(g
n), \(\psi _{\varepsilon }(f)\in \mathcal {L}^1(\mu )\)
for all ε > 0, \(n\in \mathbb {N}\)
; and let
; j(f), ϕ
ε(g
n), \(\psi _{\varepsilon }(f)\in \mathcal {L}^1(\mu )\)
for all ε > 0, \(n\in \mathbb {N}\)
; and let

Then
Two measure-free versions of Theorem 1 were proved in vector lattices in [5, 9].
The following fact is a corollary of Theorem 1 (see [2, Thm.1]).
Theorem 2 (The Brezis–Lieb Lemma for \(\mathcal {L}^p\) (0 < p < ∞))
Suppose
 and
and
 for all n and some p ∈ (0, ∞). Then
for all n and some p ∈ (0, ∞). Then
Proof
We reproduce short and instructive arguments from [2]. Take j(z) = ϕ ε(z) := |z|p and ψ ε(z) = C ε|z|p for a sufficiently large C ε. Theorem 1 applied to the sequence (g n), where g n = f n − f, gives
The uniform boundedness assumption on the sequence (f n) together with (5) ensure

Formula (6) allows us to rewrite (5) as (4). □
The Fatou lemma (in the case of a uniformly \(\mathcal {L}^p\)-bounded sequence (f n)) follows from Theorem 2, since

The next theorem is an immediate corollary of Theorem 2. Notice that the case p > 1 was obtained by Frigyes Riesz [11, p.59].
It is known that almost everywhere equality of measurable functions is an equivalence relation. An equivalence class is denoted by f. The notion L p means the collection of all equivalence classes f for which \(\int |f|{ }^p<\infty \), f ∈f.
Theorem 3 (The Brezis–Lieb Lemma for L
p
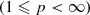 )
)
Let (f
n) be a sequence in L
p(μ) such that
 in L
p(μ) and ∥f
n∥p →∥f∥p
, where
\(\|{\mathbf {f}}_n\|{ }_p:=\bigg ({\int \limits _{\Omega }|f_n|{ }^pd\mu }\bigg )^{1/p}\)
with
\(f_n \in \mathcal {L}^p(\mu )\)
and f
n ∈f
n
. Then ∥f
n −f∥p → 0.
in L
p(μ) and ∥f
n∥p →∥f∥p
, where
\(\|{\mathbf {f}}_n\|{ }_p:=\bigg ({\int \limits _{\Omega }|f_n|{ }^pd\mu }\bigg )^{1/p}\)
with
\(f_n \in \mathcal {L}^p(\mu )\)
and f
n ∈f
n
. Then ∥f
n −f∥p → 0.
The fact that Theorem 3 becomes a Banach-lattice-result by replacing a.e.-convergence with uo-convergence, motivates investigation of the class of Banach lattices in which Theorem 2 yields for uo-convergence. One more important reason for this investigation lies at the sequential nature of a.e.-convergence, which makes obstacles in obtaining net-versions of the Brezis–Lieb lemma. To show this, we include [6, Example 1]. Let μ be the Lebesgue measure on [0, 1], \(\mathcal {P}_{fin}[0,1]\) the family of all finite subsets of [0, 1] ordered by inclusion, and \(\mathbb {I}_F\) the indicator function of \(F\in \mathcal {P}_{fin}[0,1]\). Then  and \(\int \limits _0^1|\mathbb {I}_F|d\mu =0\), however
and \(\int \limits _0^1|\mathbb {I}_F|d\mu =0\), however
Proposition 2 below may serve as a net extension of Theorem 3.
After introducing Brezis–Lieb spaces, we present and discuss an internal geometric characterization of Brezis–Lieb spaces in Theorem 4 [6, Thm.4]. Possible extensions of Theorem 4 to locally solid vector lattices are also considered. In the last part of the paper, we prove Theorem 5 which is an operator version of Theorem 1 in convergence spaces.
In the paper, we consider normed lattices over the complex field \(\mathbb {C}\) which are complexifications of uniformly complete real normed lattices. More precisely, the modulus of z = x + iy ∈ E = F ⊕ iF is defined by
and its norm is defined by ∥z∥ = ∥z∥E := ∥ |z| ∥F. We also adopt notations E + = F +, z = [z]r + i[z]i, \(x=\mathbb {Re}[z]\), and \(y=\mathbb {Im}[z]\) for z = x + iy in E. A net (v α) in a vector lattice E is said to be uo-convergent to v ∈ E whenever, for every u ∈ E +, the net (|v α − v|∧ u) converges in order to 0.
2 Brezis–Lieb Spaces
We begin with the following definition [6, Def.1] that is motivated by Theorem 3.
Definition 1
A normed lattice (E, ∥⋅∥) is said to be a Brezis–Lieb space (shortly, a
BL-space) (resp. σ-Brezis–Lieb space ( σ-BL-space) ) if, for any net (x
α) (resp, for any sequence (x
n) ) in X such that ∥x
α∥→∥x
0∥ (resp. ∥x
n∥→∥x
0∥) and  (resp.
(resp.  ), there holds ∥x
α − x
0∥→ 0 (resp. ∥x
n − x
0∥→ 0 ).
), there holds ∥x
α − x
0∥→ 0 (resp. ∥x
n − x
0∥→ 0 ).
Clearly, any BL-space is a σ-BL-space, and any finite-dimensional normed lattice is a BL-space. Since the a.e.-convergence for sequences in L
p coincides with the uo-convergence [8, Prop.3.1], Theorem 3 says that L
p is a σ-BL-space for  . The Banach lattice c
0 is not a σ-BL-space. Indeed, let (x
n) be a sequence in c
0 given by \(x_n=e_{2n}+\sum \limits _{k=1}^{n}\frac {1}{k}e_k\), and let \(x=\sum \limits _{k=1}^{\infty }\frac {1}{k}e_k\) in c
0. Then ∥x∥ = ∥x
n∥ = 1 for all \(n\in \mathbb {N}\), and
. The Banach lattice c
0 is not a σ-BL-space. Indeed, let (x
n) be a sequence in c
0 given by \(x_n=e_{2n}+\sum \limits _{k=1}^{n}\frac {1}{k}e_k\), and let \(x=\sum \limits _{k=1}^{\infty }\frac {1}{k}e_k\) in c
0. Then ∥x∥ = ∥x
n∥ = 1 for all \(n\in \mathbb {N}\), and  , however 1 = ∥x − x
n∥ does not converge to 0. A minor change of a BL-space may turn it into a normed lattice which is not even a σ-BL-space [6, EX.4]. Indeed, take any infinite dimensional BL-space E and consider \(E_1=\mathbb {R}\oplus _{\infty }E\). Take a disjoint sequence (y
n) in E such that ∥y
n∥E ≡ 1. Then
, however 1 = ∥x − x
n∥ does not converge to 0. A minor change of a BL-space may turn it into a normed lattice which is not even a σ-BL-space [6, EX.4]. Indeed, take any infinite dimensional BL-space E and consider \(E_1=\mathbb {R}\oplus _{\infty }E\). Take a disjoint sequence (y
n) in E such that ∥y
n∥E ≡ 1. Then  in E [8, Cor.3.6]. For each \(n \in \mathbb {N}\), let x
n = (1, y
n) ∈ E
1. Then \(\|x_n\|{ }_{E_1}=\sup (1,\|y_n\|{ }_E)=1\) and
in E [8, Cor.3.6]. For each \(n \in \mathbb {N}\), let x
n = (1, y
n) ∈ E
1. Then \(\|x_n\|{ }_{E_1}=\sup (1,\|y_n\|{ }_E)=1\) and  in E
1, however \(\|x_n-x\|{ }_{E_1}=\|(0,y_n)\|{ }_{E_1}=\|y_n\|{ }_E=1\) and so, (x
n) does not converge to x in \((E_1,\|\cdot \|{ }_{E_1})\). Therefore \(E_1=\mathbb {R}\oplus _{\infty }E\) is not a σ-Brezis–Lieb space. It could be interesting to construct an example of a σ-BL-space which is not a BL-space. The following result of Vladimir Troitsky gives a condition under which a σ-BL-space is a BL-space (see [6, Prop.2]).
in E
1, however \(\|x_n-x\|{ }_{E_1}=\|(0,y_n)\|{ }_{E_1}=\|y_n\|{ }_E=1\) and so, (x
n) does not converge to x in \((E_1,\|\cdot \|{ }_{E_1})\). Therefore \(E_1=\mathbb {R}\oplus _{\infty }E\) is not a σ-Brezis–Lieb space. It could be interesting to construct an example of a σ-BL-space which is not a BL-space. The following result of Vladimir Troitsky gives a condition under which a σ-BL-space is a BL-space (see [6, Prop.2]).
Proposition 1
A Banach lattice with the countable sup property and a weak unit is a BL-space iff it is a σ-BL-space.
The next definition [6, Def.2] will be used for characterizing BL-spaces.
Definition 2
A normed lattice (E, ∥⋅∥) is said to have the pre-Brezis–Lieb property (shortly, pre-BL property), whenever \(\limsup \limits _{n\to \infty }\|u_0+u_n\|>\|u_0\|\) for any disjoint normalized sequence \((u_n)_{n=1}^{\infty }\) in E + and for any u 0 ∈ E, u 0 > 0.
Every finite dimensional normed lattice has the pre-BL property. The Banach lattice c 0 obviously does not possess the pre-BL property. The mentioned modification of the norm in an infinite-dimensional Banach lattice E as above turns it to a Banach lattice \(E_1=\mathbb {R}\oplus _{\infty }E\) without pre-BL property. Indeed, take a disjoint normalized sequence \((y_n)_{n=1}^{\infty }\) in E +. Let u 0 = (1, 0) and u n = (0, y n) for \(n\geqslant 1\). Then \((u_n)_{n=0}^{\infty }\) is a disjoint normalized sequence in (E 1)+ with \(\limsup \limits _{n\to \infty }\|u_0+u_n\|=1=\|u_0\|\). The real version of the following result is included in [6, Thm.4]. Here we provide its complex version.
Theorem 4
For a σ-Dedekind complete Banach lattice E, the following conditions are equivalent:
-
(1)
E is a BL-space;
-
(2)
E is a σ-BL-space;
-
(3)
E possesses the pre-BL property and has order continuous norm.
Proof
(1) ⇒ (2) It is trivial.
(2) ⇒ (3) We show first that E has the pre-BL property. Suppose that there exist a disjoint normalized sequence \((u_n)_{n=1}^{\infty }\) in E
+ and u
0 ∈ E
+ with \(\limsup \limits _{n\to \infty }\|u_0+u_n\|=\|u_0\|\). Since \(\|u_0+u_n\|\geqslant \|u_0\|\), then \(\lim \limits _{n\to \infty }\|u_0+u_n\|=\|u_0\|\). Denote v
n := u
0 + u
n. By Gao et al. [8, Cor.3.6],  and hence
and hence  . Since E is a σ-BL-space and \(\lim \limits _{n\to \infty }\|v_n\|=\|u_0\|\), then ∥v
n − u
0∥→ 0, which is impossible in view of ∥v
n − u
0∥ = ∥u
0 + u
n − u
0∥ = ∥u
n∥ = 1. In this part of the proof, both σ-Dedekind and norm completeness of E were not used.
. Since E is a σ-BL-space and \(\lim \limits _{n\to \infty }\|v_n\|=\|u_0\|\), then ∥v
n − u
0∥→ 0, which is impossible in view of ∥v
n − u
0∥ = ∥u
0 + u
n − u
0∥ = ∥u
n∥ = 1. In this part of the proof, both σ-Dedekind and norm completeness of E were not used.
If the norm in E is not order continuous then, by the Fremlin-Meyer-Nieberg theorem (see e.g. [1, Thm.4.14]), there exist y ∈ E + and a disjoint sequence (e k) in [0, y] such that ∥e k∥↛0. Without loss of generality, we may assume ∥e k∥ = 1 for all \(k\in \mathbb {N}\). By σ-Dedekind completeness of E, for any sequence (α n) in \(\mathbb {R}_+\), there exist
Now, we choose \(\alpha _{2n}\geqslant 1\) in (7) such that ∥x
n∥ = ∥x
0∥ for all \(n\in \mathbb {N}\). Clearly,  . Since E is a σ-BL-space, then ∥x
n − x
0∥→ 0, violating
. Since E is a σ-BL-space, then ∥x
n − x
0∥→ 0, violating
The obtained contradiction shows that the norm in E is order continuous.
(3) ⇒ (1) If E is not a BL-space, then there exists a net (x
α)α ∈ A in E such that  and ∥x
α∥→∥x∥, but ∥x
α − x∥↛0. Then
and ∥x
α∥→∥x∥, but ∥x
α − x∥↛0. Then  and ∥|x
α|∥→∥|x|∥.
and ∥|x
α|∥→∥|x|∥.
Note that ∥|x
α|−|x|∥↛0. Indeed, if ∥|x
α|−|x|∥→ 0, then, for any ε > 0, (|x
α|)α ∈ A is eventually in [−|x|, |x|] + εB
E. Thus (|x
α|)α ∈ A, and hence \((\mathbb {Re}[x_\alpha ])_{\alpha \in A}\) and \((\mathbb {Im}[x_\alpha ])_{\alpha \in A}\) are both almost order bounded. Since E is order continuous and  , then
, then  and
and  . By Gao and Xanthos [7, Pop.3.7.], \(\|\mathbb {Re}[x_\alpha -x]\|\to 0\) and \(\|\mathbb {Im}[x_\alpha -x]\|\to 0\), and hence ∥x
α − x∥→ 0, that is impossible. Therefore, without loss of generality, we may assume x
α ∈ E
+ and—by normalizing—∥x
α∥ = ∥x∥ = 1 for all α.
. By Gao and Xanthos [7, Pop.3.7.], \(\|\mathbb {Re}[x_\alpha -x]\|\to 0\) and \(\|\mathbb {Im}[x_\alpha -x]\|\to 0\), and hence ∥x
α − x∥→ 0, that is impossible. Therefore, without loss of generality, we may assume x
α ∈ E
+ and—by normalizing—∥x
α∥ = ∥x∥ = 1 for all α.
Passing to a subnet, denoted by (x α) again, we may assume
Notice that  , and hence
, and hence  . Order continuity of the norm in E ensures
. Order continuity of the norm in E ensures
Denoting w α = (x α − x)+ and using (8) and (9), we assume
In view of (10), we obtain
Since  , for any fixed β
1, β
2, …, β
n,
, for any fixed β
1, β
2, …, β
n,

Since  , then
, then  and so
and so  . Due to order continuity of the norm in E, there exists an increasing sequence of indices (α
n) in A with
. Due to order continuity of the norm in E, there exists an increasing sequence of indices (α
n) in A with

By (12), we also suppose

Since

the series \(\sum \limits _{k=1,k\ne n}^{\infty }w_{\alpha _n}\wedge w_{\alpha _k}\) converges absolutely and hence in norm for any \(n\in \mathbb {N}\). Take
First, we show that the sequence \((\omega _{\alpha _n})_{n=1}^{\infty }\) is disjoint. Let m≠p, then

It follows by (13), that

Combining (14) with (11) gives
Passing to the further increasing sequence of indices, we may assume that
Now
violating the pre-BL property for u 0 = M −1 x and \(u_n=\|\omega _{\alpha _n}\|{ }^{-1}\omega _{\alpha _n}\), \(n\geqslant 1\). The obtained contradiction completes the proof. □
A special case of Theorem 4 was proved by Nakano [10, Thm.33.6]. The following result, which follows from Theorem 4, can be considered as a lemma of Brezis–Lieb type for nets in L p.
Proposition 2
Let
 and ∥f
α∥p →∥f∥p
in L
p(μ),
and ∥f
α∥p →∥f∥p
in L
p(μ),  . Then ∥f
α −f∥p → 0.
. Then ∥f
α −f∥p → 0.
It is not clear whether or not implication (2) ⇒ (3) of Theorem 4 holds without the assumption that E is σ-Dedekind complete. Since any σ-Brezis–Lieb Banach lattice has the pre-BL property, for dropping σ-Dedekind completeness assumption in Theorem 4, it is sufficient to have the positive answer to the following weaker question.
Question 1
Does the pre-BL property imply order continuity of the norm?
In the end of this section we mention some possible generalizations of Brezis–Lieb spaces and pre-Brezis–Lieb property. To avoid overloading the text, we restrict ourselves to the case of multi-normed Brezis–Lieb spaces.
A multi-normed vector lattice (shortly, MNVL) \(E=(E,\mathcal {M})\) (see [4]):
-
(a)
is said to be a Brezis–Lieb space if

-
(b)
has the pre-Brezis–Lieb property if, for any disjoint sequence \((u_n)_{n=1}^{\infty }\) in E + such that (u n) does not converge in \(\mathcal {M}\) to 0 and for any u 0 > 0, there exists \(m\in \mathcal {M}\) such that \(\limsup \limits _{n\to \infty }m(u_0+u_n)>m(u_0)\).
A σ-Brezis–Lieb MNVL is defined by replacing of nets with sequences.
By using the above definitions one can derive from Theorem 4 the following result.
Corollary 1
For an MNVL E with a separating order continuous multinorm \(\mathcal {M}\) , the following conditions are equivalent:
-
(1)
E is a BL-space;
-
(2)
E is a σ-BL-space;
-
(3)
E has the pre-BL property.
3 Operator Version of the Brezis–Lieb Lemma in Convergent Vector Spaces
In this section we discuss an operator extension of the Brezis–Lieb lemma in convergent vector spaces. Firstly, let us remind some definitions [3]. A convergence “ ” for nets in a set X is defined by the following conditions:
” for nets in a set X is defined by the following conditions:
-
(a)
 , and
, and -
(b)
 for every subnet (x
β) of (x
α).
for every subnet (x
β) of (x
α).
A mapping f from a convergence set (X, c
X) into a convergence set (Y, c
Y) is said to be c
X
c
Y-continuous (or just continuous), if  implies
implies  for every net (x
α) in X. Under a convergence vector space (X, c
X), we understand a vector space X with the convergence c
X such that the linear operations in X are c
X-continuous. (E, c
E) is a convergence vector lattice if (E, c
E) is a convergence vector space that is a vector lattice, where the lattice operations are also c
E-continuous. Motivated by the proof of the famous lemma of Brezis and Lieb [2, Thm.2], we present its operator version in convergent spaces.
for every net (x
α) in X. Under a convergence vector space (X, c
X), we understand a vector space X with the convergence c
X such that the linear operations in X are c
X-continuous. (E, c
E) is a convergence vector lattice if (E, c
E) is a convergence vector space that is a vector lattice, where the lattice operations are also c
E-continuous. Motivated by the proof of the famous lemma of Brezis and Lieb [2, Thm.2], we present its operator version in convergent spaces.
The following hypotheses will be used in the next theorem.
-
(H1)
Let (X, c X) be a convergence complex vector space.
-
(H2)
Let (E, c E) and (F, c F) be two convergence complex vector lattices, with F is Dedekind complete.
-
(H3)
Let E 0 be an order ideal in E + − E +.
-
(H4)
Let T : E 0 → F be a \(c_{E_0}o_F\)-continuous positive linear operator, where o F stands for the order convergence in F.
-
(H5)
Let J : X → E be a c X c E-continuous function with J(0) = 0.
-
(H6)
For every ε > 0, there exist two c X c E-continuous mappings Φε, Ψε : X → E + satisfying
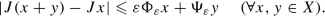 (15)
(15)
Theorem 5 (An Operator Version of the Brezis–Lieb Lemma for Nets)
Suppose hypotheses (H1) − (H6) are satisfied. Let (g
α)α ∈ A
be a net in X satisfying
 , let f ∈ X be such that |Jf|, Φ
ε
g
α, Ψ
ε
f ∈ E
0
for all ε > 0, α ∈ A, and let some u ∈ F
+
exist with
, let f ∈ X be such that |Jf|, Φ
ε
g
α, Ψ
ε
f ∈ E
0
for all ε > 0, α ∈ A, and let some u ∈ F
+
exist with
 for all ε > 0, α ∈ A. Then
for all ε > 0, α ∈ A. Then

Proof
It follows from (15) that

and hence

Thus

for all ε > 0 and α ∈ A. It follows from (16) and from c
X
c
E-continuity of J and Φε, that  as α →∞. Furthermore, (16) implies
as α →∞. Furthermore, (16) implies

Since \(T\geqslant 0\) and  , we get from (17)
, we get from (17)

for all ε > 0 and α ∈ A. Since F is Dedekind complete and T is \(c_{E_0}o_F\)-continuous,  , and in view of (18)
, and in view of (18)

Then  . □
. □
We end up by the following remarks on Theorem 5.
-
1.
Replacing nets by sequences one can obtain a sequential version of Theorem 5, whose details are left to the reader.
-
2.
In the case of \(F=\mathbb {R}\) and X = E = L 0(μ) with the almost everywhere convergence, E 0 = L 1(μ), \(Tf=\int f d\mu \), and J : X → E given by Jf = j ∘ f, where \(j:\mathbb {C}\to \mathbb {C}\) is continuous with j(0) = 0 such that for every ε > 0 there exist two continuous functions \(\phi _{\varepsilon },\psi _{\varepsilon }:\mathbb {C}\to \mathbb {R}_+\) satisfying

we obtain Theorem 1 from Theorem 5 by letting Φε(f) := ϕ ε ∘ f and Ψε(f) := ψ ε ∘ f.
References
Aliprantis, C.D., Burkinshaw, O.: Locally Solid Riesz Spaces with Applications to Economics. Mathematical Surveys and Monographs, vol. 105, 2nd edn. American Mathematical Society, Providence (2003)
Brezis, H., Lieb, E.: A relation between pointwise convergence of functions and convergence of functionals. Proc. Am. Math. Soc. 88(3), 486–490 (1983)
Dabboorasad, Y.A.M., Emelyanov, E.Y.: Survey on unbounded convergence in the convergence vector lattices. Vladikavkaz Math. J. 20(2), 49–56 (2018)
Dabboorasad, Y.A.M., Emelyanov, E.Y., Marabeh, M.A.A.: um-Topology in multi-normed vector lattices. Positivity 22(2), 653–667 (2018)
Emelyanov, E.Y., Marabeh, M.A.A.: Two measure-free versions of the Brezis–Lieb lemma. Vladikavkaz Math. J. 18(1), 21–25 (2016)
Emelyanov, E.Y., Marabeh, M.A.A.: Internal characterization of Brezis–Lieb spaces. Positivity (2019). https://doi.org/10.1007/s11117-019-00695-z
Gao, N., Xanthos, F.: Unbounded order convergence and application to martingales without probability. J. Math. Anal. Appl. 415, 931–947 (2014)
Gao, N., Troitsky, V.G., Xanthos, F.: Uo-convergence and its applications to Cesáro means in Banach lattices. Isr. J. Math. 220, 649–689 (2017)
Marabeh, M.: Brezis–Lieb lemma in convergence vector lattices. Turk. J. Math. 42, 1436–1442 (2018)
Nakano, H.: Linear Lattices. Wayne State Univ. Press, Detroit (1966)
Riesz, F.: Sur la convergence en moyenne. Acta Sci. Math. 4(1), 58–64 (1928–1929)
Acknowledgements
The research of the first author was partially supported by the Science Support Foundation Program of the Siberian Branch of the Russian Academy of Sciences; No. I.1.2, Project No. 0314-2019-0005. The second author thanks Palestine Technical University-Kadoorie (PTUK) for their support.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2021 The Editor(s) (if applicable) and The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Emelyanov, E.Y., Marabeh, M.A.A. (2021). On the Brezis–Lieb Lemma and Its Extensions. In: Kusraev, A.G., Totieva, Z.D. (eds) Operator Theory and Differential Equations. Trends in Mathematics. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-49763-7_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-49763-7_3
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-49762-0
Online ISBN: 978-3-030-49763-7
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



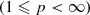 )
)
 , and
, and for every subnet (x
β) of (x
α).
for every subnet (x
β) of (x
α).