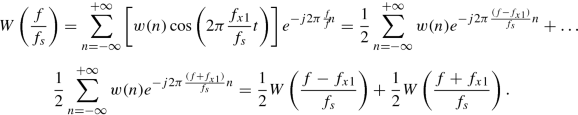4.1 Introduction

This chapter is devoted to practical computer-based frequency analysis of discrete-time signals, i.e. vectors of signal samples, by means of Fourier transform-based methods. We are assuming now that the analyzed signal is a summation of different oscillatory components with different frequencies and we are interested in finding them. From the chapter about orthogonal transforms we remember that signal analysis (decomposition into simpler components) is performed by calculation of signal similarity to some reference oscillations. The similarity coefficients are calculated as inner products of the signal vector and some reference vectors (sum of products of corresponding elements). In analog signal theory the methodology is exactly the same but the inner product has a form of infinite integral of the product of signal and reference function, calculated for an infinite number of reference frequencies. One obtains this way a signal spectrum being a continuous function of frequency. When values of this function, i.e. signal similarity measures to some reference oscillations, are multiplied by these oscillations, and all oscillations are added together in infinite integral over frequency—the signal is synthesized (reconstructed) from its spectral description. The direct and inverse continuous Fourier transform (CFT) act the same way in the analog world as discrete orthogonal transforms in discrete-time world.

When the analog signal is periodic and repeats every T seconds, the signal integration in CFT can be limited to one signal period only because all information about the signal is in this time interval. Being periodic, the signal can have only components with frequencies being multiplicities of the signal repetition frequency f 0 = 1∕T, i.e. f k = k ⋅ f 0. Thanks to this, the analyzing integration and final signal synthesizing integration from similarity coefficients are repeated not for all frequencies. In such case the CFT is taking a form of Fourier series (FS) , its special case.

When we are coming to discrete world, the CFT is changing to discrete-time Fourier transform (DtFT) and the FS are replaced with discrete Fourier transform (DFT) .

In this chapter we learn only minimum amount of information concerning CFT, FS, DtFT, and DFT. We become familiar with their definitions and primary features. The main goal is to understand, from one side, the brotherhood relation between DtFT and DFT, and, from the second side, differences in their practical usage. In frequency analysis performed on a digital computer, time-limited N-samples long signal has to be used in DtFT, similarly as in DFT. For this reason the only difference between both transforms relies on different frequency sets which are used by them. Let us assume that sampling frequency is equal to f s and the analyzed signal has N samples. In DFT one can only calculate similarity coefficients for N frequencies equal to f k = k ⋅ f 0, k = 0, 1, …, N − 1, N multiplicities of f 0 = f s∕N, while in DtFT a user does not have any restrictions in her/his frequency choice. It is interesting that DSP users very often forget about DtFT which offers better spectrum inspection than DFT.

Finally, we will make a link to the previous chapter on orthogonal transforms. DFT is a special type of N × N orthogonal transform. In contrary to orthogonal transformations discussed before, it is using complex-value, not real-value, harmonic oscillations as orthogonal basis functions to which the signal is decomposed, cosine in the real part and sine in the imaginary part. Let us repeat the definition of normalized DFT basis functions for smoother continuation (k—function number and transformation matrix row number, n—sample number and transformation matrix column number, k, n = 0, 1, 2, …, N − 1):

$$\displaystyle \begin{aligned} {{v}_{k,n}}={{v}_{k}}(n)=\frac{1}{\sqrt{N}}{{e}^{j\frac{2\pi }{N}kn}}=\frac{1}{\sqrt{N}}\left( \cos \left( \frac{2\pi }{N}kn \right)+j\cdot \sin \left( \frac{2\pi }{N}kn \right) \right). {} \end{aligned} $$
(4.1)

Due to its complexity, the transformation result is robust to signal shift in time (delay), i.e. after this modification the absolute value of the signal transform coefficients does not change after the signal shift. In this chapter we will derive the DFT equation from the Fourier series analysis and show its relation to DtFT, its older brother.

4.2 Continuous Fourier Transform and Fourier Series

Let us start from the beginning, from an analog world description. The continuous Fourier transforms (CFT) , direct and inverse, are defined as follows:

$$\displaystyle \begin{aligned} X(f)=\int\limits_{-\infty }^{\infty }{x(t){{e}^{-j2\pi ft}}dt,}\quad \ x(t)=\int\limits_{-\infty }^{\infty }{X(f){{e}^{j2\pi ft}}}{d\!f}, \quad j=\sqrt{-1}. \end{aligned} $$
(4.2)

Again, during analysis, the continuous-time signal x(t) is compared with complex-conjugated continuous-time basis functions e −j2πft, now complex-value ones. It is done by performing integration (summation) of their product. The integration is convergent for limited energy signals only, for others—concept of generalized functions (distributions) should be applied. During synthesis all basis functions e j2πft are scaled by corresponding, calculated spectral coefficients X(f) and summed (integrated). Any signal is represented as infinite summation/integration of complex-value harmonic signals of the form:

$$\displaystyle \begin{aligned} {{e}^{j2\pi ft}}=\cos (2\pi ft)+j\cdot \sin (2\pi ft) \end{aligned} $$
(4.3)

with different frequencies f. Pure cosine and sine signals with frequency f 0 have the following Fourier spectral decomposition (representation):

$$\displaystyle \begin{aligned} \cos (2\pi {{f}_{0}}t)=\frac{{{e}^{j2\pi {{f}_{0}}t}}+{{e}^{-j2\pi {{f}_{0}}t}}}{2},\quad \quad \sin (2\pi {{f}_{0}}t)=\frac{{{e}^{j2\pi {{f}_{0}}t}}-{{e}^{-j2\pi {{f}_{0}}t}}}{2j}, \end{aligned} $$
(4.4)

or:

$$\displaystyle \begin{aligned} \cos (2\pi {{f}_{0}}t)=\frac{1}{2}{{e}^{j2\pi {{f}_{0}}t}}+\frac{1}{2}{{e}^{-j2\pi {{f}_{0}}t}},\quad \quad \sin (2\pi {{f}_{0}}t)=\frac{-j}{2}{{e}^{j2\pi {{f}_{0}}t}}+\frac{j}{2}{{e}^{-j2\pi {{f}_{0}}t}}.\end{aligned} $$
(4.5)

They are summation of two harmonic signals (4.3), first with positive frequency f 0 and second with negative frequency − f 0. Fourier spectrum coefficients for cosine and sine are, respectively, equal to [1∕2, 1∕2] and [−0.5j, 0.5j], first for positive frequency, then for negative (amount of two basis signals, all remaining transform coefficients are equal to zero). We are doing here deliberately very big simplifications not mentioning the Dirac Delta functions but aiming at more intuitive, less formal presentation. Fourier spectra of pure cosine and sine with frequency f 0 are presented in Fig. 4.1.

Fig. 4.1
figure 1

Fourier spectrum of cosine (left) and sine (right)—see Eq. (4.5)

Full size image

For real-value signals, the CFT spectrum has conjugate (Hermitian) symmetry in respect to frequency f = 0 Hz, i.e. it is the same for positive and negative frequencies in its real part and negated in its imaginary part:

$$\displaystyle \begin{aligned} X(-f)={{X}^{*}}(f). {}\end{aligned} $$
(4.6)

This feature is inherited from functions of \(\cos {}()\) and \(\sin {}()\):

$$\displaystyle \begin{aligned} X(f)=\int\limits_{-\infty }^{\infty }{x(t){{e}^{-j2\pi ft}}dt}=\underbrace{\int\limits_{-\infty }^{\infty }{x(t) \cos{}(2\pi ft)dt}}_{{{X}_{\operatorname{Re}}}(-f)={{X}_{\operatorname{Re}}}(f)}-j\underbrace{\int\limits_{-\infty }^{\infty }{x(t) \sin{}(2\pi ft)dt}}_{{{X}_{Im}}(-f)=-{{X}_{Im}}(f)}\quad . {} \end{aligned} $$
(4.7)

Spectra of pure cosine and sine signals, presented in Fig. 4.1, are the best examples of the CFT spectrum symmetry.

It is very informative to calculate the Fourier spectrum of a rectangular pulse equal to 1 in the interval [−T, T] and zero elsewhere:

$$\displaystyle \begin{aligned} & {{R}_{T}}(f)=\int\limits_{-\infty }^{\infty }{{{r}_{T}}(t){{e}^{-j2\pi ft}}dt=\int\limits_{-T}^{T}{{1 \cdot {e}^{-j2\pi ft}}dt=}}\left. \frac{1}{-j2\pi f}{{e}^{-j2\pi ft}} \right|{}_{-T}^{T}=\ldots \\ & \frac{{{e}^{-j2\pi fT}}-{{e}^{j2\pi fT}}}{-j2\pi f}=\frac{-j2\sin (2\pi fT)}{-j2\pi f}=\frac{\sin (2\pi fT)}{\pi f}=2T\operatorname{sinc}(2\pi fT).{} \end{aligned} $$
(4.8)

Value for f = 0 we find calculating derivatives of nominator and denominator of the final formula in Eq. (4.8) in respect to f:

$$\displaystyle \begin{aligned} \left. {{R}_{T}}(f) \right|{}_{f=0}^{{}}={{\left. \frac{(2\pi T) \cos{}(2\pi fT)}{\pi } \right|}_{f=0}}=2T. \end{aligned} $$
(4.9)

Signal of rectangular pulse and its Fourier spectrum are presented in Fig. 4.2. The plots have been done using program 4.1.

Fig. 4.2
figure 2

Rectangular pulse and its Fourier spectrum

Full size image

Exercise 4.1 (Fourier Spectrum of the Rectangular Pulse)

Run program 4.1 which is doing the Fourier spectrum visualization of a rectangular pulse. Observe oscillatory shape of this spectrum. Around f = 0 Hz the so-called spectral main-lobe of the oscillations is located. On both sides of it the so-called oscillatory spectral side-lobes are visible. Change the pulse duration. Observe that the shorter the pulse is, the wider is its spectrum. Note also that the spectrum has values equal to zero for frequencies being multiplicities of 1∕(2T) : f = k ⋅ (1∕(2T)).

Listing 4.1 Fourier spectrum of rectangular pulse

In DSP we deal with discrete-time signals taken from real-world objects. Therefore it is very important to know which are theoretical spectra of the most popular continuous-time signals. Why? Since the same spectra should be obtained during computer calculations performed upon discrete-time signal representations. In Table 4.1 some spectra examples (definitions) are given.

Table 4.1 Continuous-time signals and their continuous-frequency CFT spectra
Full size table

We should also know which are spectral consequences of different operations performed upon the signal. To find corresponding mathematical formulas one should put the modified signal into CFT integral (4.2) and calculate it. This is a routine exercise during analog circuits and signals (or signal theory) workouts. I recommend to do it for one or two signal modifications. Examples could be found in many textbooks. The most important CFT features are listed in Table 4.2.

Table 4.2 Basic CFT features: signal processing and its spectral consequence
Full size table

At present, as an example, we will derive a few important spectral relations which will be very often used later in this book (ω = 2πf):

  1. 1.

    signal time shift —results only in signal spectrum phase change (after introducing new variable τ = t − t 0, from where t = τ + t 0):

    $$\displaystyle \begin{aligned} \int\limits_{-\infty }^{\infty }{x(t-{{t}_{0}}){{e}^{-j\omega t}}dt}=\int\limits_{-\infty }^{\infty }{x(\tau ){{e}^{-j\omega (\tau +{{t}_{0}})}}d}\tau ={{e}^{-j\omega {{t}_{0}}}}\int\limits_{-\infty }^{\infty }{x(\tau ){{e}^{-j\omega \tau }}d}\tau ={{e}^{-j\omega {{t}_{0}}}}X(\omega); {} \end{aligned} $$
    (4.10)
  2. 2.

    complex modulation —causes frequency shift of the signal spectrum to the modulation frequency:

    $$\displaystyle \begin{aligned} \int\limits_{-\infty }^{\infty }{\left( \,{{e}^{\pm j2\pi {{f}_{0}}t}}x(t) \right)\,{{e}^{-j2\pi ft}}dt}=\int\limits_{-\infty }^{\infty }{x(t){{e}^{-j2\pi (f\mp {{f}_{0}})t}}dt}=X(f\mp {{f}_{0}}); {} \end{aligned} $$
    (4.11)
  3. 3.

    convolution of two signals —results in multiplication of their spectra, which is extremely important in signal filtering (new variable λ = t − τ, from where t = τ + λ):

    $$\displaystyle \begin{aligned} & \int\limits_{-\infty }^{\infty }{\left( \int\limits_{-\infty }^{\infty }{x(\tau )y(t-\tau )d\tau } \right)}{{e}^{-j\omega t}}dt=\int\limits_{-\infty }^{\infty }{\left( \int\limits_{-\infty }^{\infty }{x(\tau ){{e}^{-j\omega \tau }}d\tau } \right)}y(\lambda ){{e}^{-j\omega \lambda }}\left( d\lambda +d\tau \right)=\ldots \\ & \left[ \int\limits_{-\infty }^{\infty }{x(\tau ){{e}^{-j\omega \tau }}d\tau } \right] \cdot \left[ \int\limits_{-\infty }^{\infty }{y(\lambda ){{e}^{-j\omega \lambda }}d\lambda } \right] = X(f)Y(f); \end{aligned} $$
    (4.12)
  4. 4.

    multiplication of two signals —results in convolution of their spectra, extremely important in spectral analysis (we show that inverse Fourier transform of convolution of two signal spectra is equal to multiplication of these signals, i.e. we will present an inverse proof; using new variable u = f − v, from where f = v + u):

    $$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \int\limits_{-\infty }^{\infty} \left( \int\limits_{-\infty}^{\infty}{X(v)}Y(f-v)dv \right){{e}^{j2\pi ft}}df= \\ &\displaystyle &\displaystyle \qquad \qquad = \left[ \int\limits_{-\infty }^{\infty }{X(\nu )}{{e}^{j2\pi \nu t}}dv \right] \cdot \left[ \int\limits_{-\infty }^{\infty}{Y(u)}{{e}^{j2\pi ut}}du \right] = {x(t)y(t)}; {} \end{array} \end{aligned} $$
    (4.13)
  5. 5.

    signal energy—Parseval’s equation —integration of squared signal in time domains is equivalent to the integration of its squared Fourier spectra in the frequency domain, important in signal power and spectral density analysis:

    $$\displaystyle \begin{aligned} \int\limits_{-\infty }^{\infty }{x(t){x^{*}(t)}dt} &= \int\limits_{-\infty }^{\infty } { \left( \int\limits_{-\infty }^{\infty } { X(f)e^{j2\pi ft}df } \right) x^{*}(t)dt } = \\ &=\int\limits_{-\infty }^{\infty } { X(f) \left( \int\limits_{-\infty }^{\infty } { x^{*}(t)e^{j2\pi ft}dt } \right)df } = \int\limits_{-\infty }^{\infty } {X(f)X^{*}(f)df}. {} \end{aligned} $$
    (4.14)

Fourier series use the same methodology as CFT but are dedicated to analysis and synthesis of periodic signals: only one signal period T is analyzed (multiplied with the reference and integrated, the result is divided by T) and only frequencies being multiplies of the signal repetition frequency \(kf_{0}=k\frac {1}{T}, k=-\infty ,\ldots ,\infty ,\) are checked:

$$\displaystyle \begin{aligned} {{X}_{k}}=\frac{1}{T}\int\limits_{0}^{T}{x(t){{e}^{-j2\pi (k{{f}_{0}})t}}dt},\quad \ x(t)=\sum_{k=-\infty }^{+\infty }{{{X}_{k}}{{e}^{j2\pi (k{{f}_{0}})t}}},\quad \ {{f}_{0}}=\frac{1}{T}. {} \end{aligned} $$
(4.15)

The Fourier series equations are written also in the so-called trigonometric version:

$$\displaystyle \begin{aligned} & {{a}_{k}}=\frac{1}{T}\int\limits_{0}^{T}{x(t)\cos\left( 2\pi (k{{f}_{0}})t \right)dt},\quad {{b}_{k}}=\frac{1}{T}\int\limits_{0}^{T}{x(t)\sin\left( 2\pi (k{{f}_{0}})t \right)dt} \end{aligned} $$
(4.16)
$$\displaystyle \begin{aligned} & x(t)={{a}_{0}}+2\sum_{k=1}^{+\infty }{\left[ {{a}_{k}}\cos\left( 2\pi (k{{f}_{0}})t \right)+{{b}_{k}}\sin\left( 2\pi (k{{f}_{0}})t \right) \right]}= \\ & \quad \ \ \ ={{X}_{0}}+2\sum_{k=1}^{+\infty }{\left| {{X}_{k}} \right|\cos \left( 2\pi (k{{f}_{0}})t+\sphericalangle {{X}_{k}} \right)} \\ & \quad \quad {{X}_{k}}={{a}_{k}}-j{{b}_{k}},\quad \left| {{X}_{k}} \right|=\sqrt{a_{k}^{2}+b_{k}^{2}},\quad \sphericalangle X=\operatorname{arctg}\left( \frac{-{{b}_{k}}}{{{a}_{k}}} \right). \end{aligned} $$
(4.17)

4.3 Discrete-Time Fourier Transform: From CFT to DtFT

Presentation of the continuous Fourier transform, given above, is very important for us because in computer-based frequency analysis a discretized CFT version is very widely used. Let us rewrite the CFT into more computer-friendly form. Denoting sampling frequency as f s, sampling period as Δt = 1∕f s, sampling time as t = n ⋅ Δt, and exchanging infinite integral with infinite summation, Eq. (4.2) of the forward CFT takes the following form:

$$\displaystyle \begin{aligned} X(f)=\int\limits_{-\infty }^{+\infty }{x(t){{e}^{-j2\pi ft}} dt \quad \Rightarrow \quad X(f)=\sum_{n=-\infty }^{+\infty }{x(n\cdot \varDelta t){{e}^{-j2\pi f(n\cdot \varDelta t)}}}}. {} \end{aligned} $$
(4.18)

Going further, we can write final equations for DtFT and its inverse as (defining \(\varOmega =2\pi \frac {f}{f_{s}}\)):

(4.19)
(4.20)

In (4.19) \(X(\frac {f}{f_{s}})\) can be calculated for any value of frequency f, being a continuous variable, but there is no need for this because the function \( {{{e}^{-j2\pi \frac {f}{{{f}_{s}}}n}}}\) is periodic in respect to f and has period f s:

$$\displaystyle \begin{aligned} {{e}^{-j2\pi \frac{(f+k\cdot {{f}_{s}})}{{{f}_{s}}}n}}={{e}^{-j2\pi \frac{f}{{{f}_{s}}}n}}\cdot {{e}^{-j2\pi kn}}={{e}^{-j2\pi \frac{f}{{{f}_{s}}}n}}. {} \end{aligned} $$
(4.21)

Therefore, it is sufficient to calculate \(X(\frac {f}{f_{s}})\) for − f s∕2 ≤ f < f s∕2 or for 0 ≤ f < f s. In the first case the inspection of the spectrum is more intuitive and easier for interpretation because pairs of positive and negative frequency components are visible in the spectrum. Going back to the sampling Exercise 1.4 presented in Chap. 1, for f s = 1000 Hz and f x = 100 Hz we see in the spectrum signal components − 100 Hz and 100 Hz, not 100 Hz and 900 Hz (see equations (1.14) and (1.15)). In fact during discretization of CFT we are sampling not only analyzed signals but also the reference functions \(\cos {}()\) and \(\sin {}()\). When their frequency is too high, the sampling theorem is not fulfilled, and the high-frequency reference signals are under-sampled and look as low-frequency ones and, as such, they fit to the analyzed low-frequency signal again. From this reason the DtFT spectrum is periodic and there is no need for its whole computation.

When we have only N signal samples, after dividing (4.19) by N, one obtains the following equation:

$$\displaystyle \begin{aligned} X \left( \frac{f}{f_{s}} \right)=\frac{1}{N}\sum_{n=0}^{N-1}{x(n){{e}^{-j2\pi \frac{f}{fs}n}}},\quad -{{f}_{s}}/2\le f<{{f}_{s}}/2, {} \end{aligned} $$
(4.22)

which offers properly scaled signal amplitude spectrum (for example, the cosine spectrum has two peaks equal to 1/2 for frequencies f 0 and − f 0). In DtFT (4.22) we can sample (discretize in frequency) the spectrum as dense as we want, significantly denser than in the DFT method, being discussed later in this chapter, where the frequency step Δf = f s∕N is always used. From this reason (4.22) should be treated as a basic tool for spectral zooming and allows us to see details invisible in DFT. It is building a bridge between digital and analog signal theory.

It is very important also to note that, analogically to CFT and its Eqs. (4.6), (4.7), the DtFT spectrum X() = X Re() + X Im() has conjugate symmetry also around the frequency f = 0 Hz—it is the same in its real part X Re() and negated in its imaginary part X Im():

$$\displaystyle \begin{aligned} {{X}_{\operatorname{Re}}}\left( \frac{-f}{{{f}_{s}}} \right)={{X}_{\operatorname{Re}}}\left( \frac{f}{{{f}_{s}}} \right),\quad \quad {{X}_{Im}}\left( \frac{-f}{{{f}_{s}}} \right)=-{{X}_{Im}}\left( \frac{f}{{{f}_{s}}} \right). {} \end{aligned} $$
(4.23)

Fundamentals of frequency analysis of signals by means of DtFT, discretized in frequency, are summarized in Fig. 4.3. A pure cosine is analyzed in it. Signals are presented on the left side, while on the right their CFT and DtFT spectra. We see on the left side, one after the other: continuous-time cosine, a continuous-time rectangular window—a function, one of many possible, used for cutting a cosine fragment, result of their multiplication, i.e. the signal fragment to be analyzed, and, finally, its time-discretized version. The CFT spectrum of a cosine \(\cos {}(2 \pi f_0 t)\) is equal to \(\frac {1}{2}\) for − f 0 and f 0 (see Eq. (4.5)). The CFT spectrum of the rectangular cutting function has an oscillatory shape described by \(\frac {\sin {}(x)}{x}\) function (see Eq. (4.8)). The CFT spectrum of a cut cosine consists of two copies of the CFT spectrum of rectangular window, shifted to frequencies − f 0 and f 0 (due to modulation feature of the CFT transform—see feature 9 in Table 4.2). After signal discretization in time with sampling frequency f s, the continuous-frequency DtFT spectrum is obtained in which the CFT spectrum is repeated with period f s—due to Eq. (4.21). Since the DtFT spectrum is periodic, only its one period can be calculated. In Fig. 4.3 this is one DtFT spectrum period from [0, f s) Hz, the same as in the discrete Fourier transform (DFT) presented in the next section. In computer implementation some sampling of the frequency axis has to be chosen, which is presented also. When different window function is used for cutting a signal fragment, the observed signal spectrum has different shapes but its peaks are still located at signal frequency components. In Exercise 4.2 we will apply and test some exemplary window functions (rectangular, Hanning, and Chebyshev) during signal DtFT analysis.

Fig. 4.3
figure 3

Graphical illustration of fundamental principles of digital spectral analysis: (left) signals, (right) their spectra. In consecutive rows: (1) infinite cosine and its theoretical Fourier spectrum, (2) rectangular window and its theoretical Fourier spectrum, (3) multiplication of cosine and rectangular window and its spectrum (convolution of two above spectra marked with “*”), (4) sampled signal and its periodic spectrum, (5) sampled one period of the repeating spectrum [11]

Full size image

Short Summary

Since during DtFT-based frequency analysis, signal is multiplied with some windowing function, the DtFT spectrum of the signal fragment is a result of convolution of the signal spectrum and spectrum of the window—see Eq. (4.13). Signal discretization causes spectrum periodic repeating (sampling frequency is the period)—due to Eq. (4.21). Therefore, the DtFT spectrum of a discrete signal should be calculated only in the frequency range \([-\frac {f_s}{2}, \frac {f_s}{2})\) for complex-value signals or in the range \([0, \frac {f_s}{2})\) for real-value signals—due to its conjugate symmetry (4.23).

In program 4.2 the Matlab code of the DtFT algorithm is presented. It will be used as a frequency detective for performing some initial experiments, recognition of DtFT features, and validation of the presented above mathematical material. We will start from the DtFT analysis of a pure cosine fragment cut by exemplary window: rectangular, Hanning, or Chebyshev. Do Exercise 4.2. Look at plots shown in Fig. 4.2, presenting DtFT spectra being solutions/results of the consecutive exercise tasks.

Listing 4.2 Matlab program for DtFT calculation

Exercise 4.2 (DtFT of a Cosine with Rectangular Window)

Use program 4.2 for computing DtFT spectrum of a simple cosine signal. Choose f x1 = 100 Hz as a signal frequency and f s = 1000 Hz as sampling frequency. Generate N = 100 signal samples. Choose x=x1.

  1. 1.

    Analyze the signal using DtFT in the frequency range \([-f_{\max },\ldots ,f_{\max }], \ f_{\max }=2.5f_s\) with the frequency step df = 10 Hz, equal to DFT step \(f_0=\frac {f_s}{N}\). We are expecting two sharp peaks at frequencies f = −100 Hz and f = 100 Hz since, due to Eq. (4.5), after discretization our signal has the form:

    $$\displaystyle \begin{aligned} \cos \left( 2\pi \frac{{{f}_{x1}}}{{{f}_{s}}}n \right)=\frac{{{e}^{j2\pi \frac{{{f}_{x1}}}{{{f}_{s}}}n}}+{{e}^{-j2\pi \frac{{{f}_{x1}}}{{{f}_{s}}}n}}}{2}. {} \end{aligned} $$
    (4.24)

    Why we see only two peaks in DFT and much more peaks in DtFT, periodically repeating around multiplies of the sampling frequency f s? Because DFT calculates the signal spectrum only in the range [0, f s) with the step f 0 and we see only two components of the cosine: f x1 = 10f 0 and f s − f x1 = f s − 10f 0. In DtFT situation is different. Due to equations (4.21), the generated reference signals of higher frequencies kf s ± f x1 have exactly the same samples as for the low frequencies ± f x1 and for them the perfect fit is valid also. Conclusion: the frequency range [−0.5f s, …, 0.5f s] is all we need. For real-value signals, having symmetrical spectra, even [0, …, 0.5f s] is enough.

  2. 2.

    Now decrease the DtFT spectrum sampling 10 times, other words set df = 1 Hz. Wow! What happens! Take it easy: now you see repeating spectrum of rectangular pulse (4.8) shown in Fig. 4.2, at present its absolute value is calculated. But why I did not see it before?! Since the rectangular pulse spectrum is oscillatory, it is crossing through zero and we before, by chance, took only samples at those zeros and at spectral peaks. But why the spectrum of rectangular pulse is present in the spectrum of the cosine? Where the rectangular pulse is hidden in math equations? We analyze not the WHOLE cosine but its N-samples long FRAGMENT, cut by the rectangular pulse. Therefore two analog time-infinite signals are multiplied: cosine and rectangular pulse, and the resultant spectrum is equal to convolution of their individual spectra (see multiplication feature in Table 4.2 and Eq. (4.13)). For this reason we see spectrum of the rectangular pulse in the position of cosine spectral peaks. We can also apply in this case the cosine modulation feature from the same table: multiplying any signal w(n) by cosine with frequency f x1 shifts the signal spectrum to cosine frequencies: f x1 and − f x1 and scale them by 1∕2. In discrete-time case:

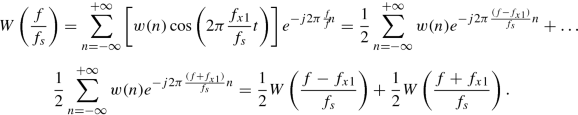    (4.25)

    Because we sample the DtFT spectrum in wider frequency range then the DFT spectrum is sampled, we have many copies of the cosine spectrum, in consequence, we see many copies of the rectangular pulse spectrum.

  3. 3.

    I do not want to watch the same film many times? No problem. We are changing frequency range of interest to [−0.5f s, …, 0.5f s] remaining the small frequency step df = 1 Hz of DtFT spectrum sampling. Run the program. Are you satisfied? Yes, but if I had the second very weak signal frequency component lying apart, I would not see it in the spectrum because it would be hidden by big spectral oscillations coming from the strong signal!

  4. 4.

    Yes, you are right! Add a second weak cosine component to the signal: x=x1+x2, for example, with frequency f x2 = 250 Hz and very small amplitude A x2 = 0.001. Run the program. The second component is not visible! I knew! I knew! Yes, as usual, you knew how to complaint but I know … how to solve the problem.

  5. 5.

    Multiply the two-component signal with samples of Hanning window function x=x.*w;, i.e. exchange the rectangular window with the Hanning window. In Matlab: w2=hanning( N) ; w=w2;. This function has lower level of spectral side-lobes than the rectangular window (look at Fig. 4.2) at the price of wider spectral main-lobe. Run the program. Now the second frequency component is visible. But if the second component would be very, very weak indeed, having only A 2 = 0.00001 (10−5 , ten micro-volts)?

  6. 6.

    No problem. We are choosing adjustable Chebyshev window function having side-lobes on the level of A sl = 10−7, 20log10(A sl) = −140 dB. In Matlab: w3=chewin( N,140) ; w=w3. Run the program. The second component is now seen. Wow! But now the spectral peaks are very wide! If the second component had a frequency very close to the first one, for example, f x2 = 110Hz, I would not see it!

  7. 7.

    No problem. Let us make use of the scaling feature of the CFT given in Table 4.2, in consequence being the feature of the DtFT also. Making the signal longer (for a < 1) leads to its spectrum narrowing. For example, the window 10 times longer has the DtFT/DFT spectrum 10 times more narrow. Therefore, we will increase now the length of our signal vector 10 times, setting N = 1000. Run the program. Yes, it works. But now … after the window usage, amplitudes of spectral peaks are not correct! For cosine 1∕2 is expected!

  8. 8.

    Yes. I admire your curiosity! Now we have to change the spectrum normalization. Since windows are reducing amplitude of oscillations in signal fragment being analyzed, we should compensate this effect! We will exchange dividing the spectrum by N, which is correct for the rectangular window, by sum of window samples, which is correct for any window (for rectangular one we have N as before). In Matlab: uncomment the line: X = N*X/sum( w) ; You see! Now the spectrum scaling is corrected.

  9. 9.

    But … Bang! Time is over! … You are the game winner. The worst thing pupil can do is not asking questions!

4.4 Window Functions

4.4.1 Practical Summary

It turned out in the previous section how important are functions used for cutting signal into fragments which are called windows! For signals being summations of pure tones we observe in their spectra only scaled and shifted copies of windows spectra (Fig. 4.4). Therefore one should choose windows very carefully: they should help us in spectral analysis, do not create troubles. The good window should have both: very narrow spectral main-lobe (similar to rectangular window) and a very big attenuation of the spectral side-lobes (in contrary to the rectangular window). The narrow spectral main-lobe allows to distinguish in the spectrum signal components having similar frequency values, while highly attenuated spectral side-lobes of the window spectrum makes possible to see in the spectrum, both, very strong and very weak components (with very large and very small amplitudes).

Fig. 4.4
figure 4

DtFT spectra calculated for signals in consecutive steps (points) of Exercise 4.2: initially for cosine 100 Hz, N = 100 samples, f s = 1000 Hz. After step 1: spectrum of rectangular window not visible, after step 2: window spectrum is visible after decreasing frequency step df from 10 Hz to 1 Hz, after step 3: reduction of frequency range due to spectrum periodicity, after step 5: addition of the second signal component with frequency 250 Hz and amplitude 0.001 and using Hanning window, after step 6: changing amplitude of the second component to 0.00001 and using Chebyshev window with side-lobes level of − 140 dB, after step 8: changing second component frequency to 110 Hz and increasing number of samples to N = 1000, additionally improving spectrum scaling

Full size image

Window tailoring is a great DSP art! There are many window functions with precisely specified, fixed shapes: rectangular, triangular (Bartlett), Hamming, Hanning, Blackman, Blackman–Harris, and many others. There are also flexible windows with adjustable shapes: Chebyshev and Kaiser windows are the most popular among them. The latter allows to change the shape of the window and its spectrum in a controlled way and make a compromise between frequency spectrum resolution (width of the window main-lobe) and amplitude spectrum resolution (attenuation of the side-lobes). A special type of windows, flat-top ones, is designed to have a very flat main-lobe peak at the cost of increasing its width. Such windows allow very precise amplitude measurements of many signal components (for example, of power voltage supply harmonics) but they require their significant separation in frequency.

In this chapter the DtFT spectrum of the rectangular window is derived and it is shown how a big family of cosine-based windows is designed (Hamming, Hanning, Blackman, etc.), summarized in Table 4.3. Design equations of Chebyshev and Kaiser windows are presented also with an explanation of their usage. In Fig. 4.5 different window shapes (up) and their DtFT spectra (down) are compared. Easy riders can skip the mathematical part, which follows, and go directly to Exercise 4.3 using program from Listing 4.3.

Fig. 4.5
figure 5

Exemplary shapes (up) and their DtFT spectra (down) for the following windows (they are becoming more peaky in the upper plot): rectangular, Hamming, Hanning, Blackman, Kaiser with β = 12 and Chebyshev − 120 dB. Windows are ordered from the lowest to the highest attenuation of spectral side-lobes (oscillatory ripples observed in window spectrum) obtained at the cost of widening the spectral main-lobe (spectral peak around 0 Hz)

Full size image
Table 4.3 Definitions and parameters of the most popular non-parametric digital window functions. Denotations: Δ ml—width of the main-lobe of the spectrum around Ω = 0 (rad/s), A sl—relative attenuation of the highest side-lobe in relation to W(0)
Full size table

4.4.2 Mathematical Description

Rectangular Window

Let us start with the rectangular window.

$$\displaystyle \begin{aligned} {{w}_{R}}(n)=\left\{ \begin{array}{*{35}{l}} 1,\quad n=\ 0,\ 1,\ 2,\ldots,\ N-1, \\ 0,\quad \text{other}\ \ n. \\ \end{array} \right. {} \end{aligned} $$
(4.26)

After introduction of a new variable—angular frequency:

$$\displaystyle \begin{aligned} \varOmega =2\pi f/{{f}_{s}}, {} \end{aligned} $$
(4.27)

and putting Eq. (4.26) into the DtFT definition (4.19), we obtain

$$\displaystyle \begin{aligned} W_{R}(\varOmega)=\sum_{n=-\infty }^{\infty }{{{w}_{R}}(n){{e}^{-j\varOmega n}}}=\sum_{n=0}^{N-1}{{{w}_{R}}(n){{e}^{-j\varOmega n}}}=\sum_{n=0}^{N-1}{{1 \cdot {e}^{-j\varOmega n}}}. {} \end{aligned} $$
(4.28)

After multiplying both sides of Eq. (4.28) by e −jΩ and rewriting the equation we have

$$\displaystyle \begin{aligned} {{e}^{-j\varOmega }}W_{R}(\varOmega)=\sum_{n=1}^{N}{{{e}^{-j\varOmega n}}}=\sum_{n=0}^{N-1}{{{e}^{-j\varOmega n}}}+{{e}^{-j\varOmega N}}-{{e}^{-j\varOmega 0}}=W_{R}(\varOmega)+{{e}^{-j\varOmega N}}-1. {} \end{aligned} $$
(4.29)

Now we can calculate the value of W R(Ω):

$$\displaystyle \begin{aligned} {{W}_{R}}(\varOmega )\cdot (1-{{e}^{-j\varOmega }})=1-{{e}^{-j\varOmega N}} {} \end{aligned} $$
(4.30)
$$\displaystyle \begin{aligned} & {{W}_{R}}\left( \varOmega \right)=\frac{1-{{e}^{-j\varOmega N}}}{1-{{e}^{-j\varOmega }}}=\frac{{{e}^{-j\varOmega N/2}}\ \left( \,{{e}^{j\varOmega N/2}}-{{e}^{-j\varOmega N/2}} \right)}{{{e}^{-j\varOmega /2}}\ \left( \,{{e}^{j\varOmega /2}}-{{e}^{-j\varOmega /2}} \right)}=\ldots \\ & \quad \quad \quad \; \, = {{e}^{-j\varOmega (N-1)/2}}\frac{\sin (\varOmega N/2)}{\sin (\varOmega /2)}. {} \end{aligned} $$
(4.31)

In a similar way it can be derived that DtFT spectrum of the odd-length rectangular window w RS(n), n = −M, …, −1, 0, 1, …, M, N = 2M + 1, symmetrical around n = 0, is equal to:

$$\displaystyle \begin{aligned} {{W}_{RS}}(\varOmega)=\frac{\sin \left( \varOmega (2M+1)/2 \right)}{\sin \left( \varOmega /2 \right)}. {} \end{aligned} $$
(4.32)

Since w RS(n) is obtained by shifting w R(n) M samples left, e.g. w R(n + M), therefore W RS(Ω) is equal to W R(Ω) multiplied by e jΩM. Of course, absolute values of both spectra are the same: |W R(Ω)| = |W RS(Ω)|. A main spectral lobe of the rectangular window (i.e. distance between first zero-crossings on both sides around Ω = 0) is equal to 4π∕N, since from Eq. (4.31) we have (first zeros of the \(\sin {}()\) function)

$$\displaystyle \begin{aligned} & {{\varOmega }_{1}}N/2=\pi \quad \quad \Rightarrow \quad \ {{\varOmega }_{1}}=2\pi /N \\ & {{\varOmega }_{2}}N/2=-\pi \quad \ \Rightarrow \quad \ {{\varOmega }_{2}}=-2\pi /N \\ & \quad \quad \quad \quad \quad \quad \quad \quad \quad \ \ \varDelta {{\varOmega }_{R}}={{\varOmega }_{1}}-{{\varOmega }_{2}}=4\pi /N. \end{aligned} $$

In practice we analyze not infinite signals but their shorter or longer fragments. Some special functions are used for cutting long signal into fragments. They are called “window” functions because we are looking at signals “through” them. The window functions are extremely important in signal theory, especially in spectral analysis and filter design.

Cosine Windows

In the beginning we ask fundamental question: what window functions are used and what are their spectra? A big family of so-called cosine-type windows is obtained by multiplication of N samples long rectangular window by sum of K cosines with different angular frequencies (Ω k) and amplitudes (A k) (n = −∞, …, −1, 0, 1, …,  + ∞):

$$\displaystyle \begin{aligned} & w(n)={{w}_{R}}(n) \; \sum_{k=0}^{K}{{{A}_{k}}\cos \left( {{\varOmega }_{k}}n \right)}={{w}_{R}}(n) \; \sum_{k=0}^{K}{{{A}_{k}}\left( \frac{1}{2}{{e}^{j{{\varOmega }_{k}}}}+\frac{1}{2}{{e}^{-j{{\varOmega }_{k}}}} \right)},\quad {{\varOmega }_{k}}=\frac{2\pi k}{N-1}. {} \end{aligned} $$
(4.33)

The DtFT (4.19) of (4.33) is equal to:

$$\displaystyle \begin{aligned} & W(\varOmega )=\sum_{k=0}^{K}{\frac{{{A}_{k}}}{2}}\left( \sum_{n=-\infty }^{+\infty }{{{w}_{R}}(n)}\cdot {{e}^{-j(\varOmega -{{\varOmega }_{k}})}}+\sum_{n=-\infty }^{+\infty }{{{w}_{R}}(n)\cdot {{e}^{-j(\varOmega +{{\varOmega }_{k}})}}} \right)= \\ & \quad \quad \ \quad \sum_{k=0}^{K}{\frac{{{A}_{k}}}{2}}\left( {{W}_{R}}(\varOmega -\varOmega_{k})+{{W}_{R}}(\varOmega +\varOmega_{k}) \right) {} \end{aligned} $$
(4.34)

due to transformation linearity: spectrum of sum of signals is equal to sum of their individual spectra. Since the window spectrum (4.34) is a sum of scaled (by A k) and shifted (Ω k = 2πk∕(N − 1)) spectra of the rectangular window (4.31), (4.32), such weights (A k) are chosen which minimizes side-lobe oscillations in final spectrum W(Ω). Definitions and spectral parameters of the most popular cosine windows are given in Table 4.3.

Window spectral features are characterized by the shape of its DtFT spectrum. The best window should have a very narrow peak around frequency 0 Hz (the so-called main-lobe) and highly attenuated spectral side-peaks, lying elsewhere (the so-called side-lobes). The first feature is measured by Δ ml (width of the main-lobe), the second by A sl (attenuation of the highest spectral side-lobe). It is impossible to fulfill both criteria at the same time. The rectangular window has the sharpest main-lobe but, unfortunately, a very high level of spectral side-lobes. Different designers of other windows have tried to increase the side-lobes attenuation at the price of making the spectral main-lobe wider, but as least as possible. In Table 4.3 a few window functions are defined and values of their Δ ml and A sl are given. We see that the more cosine terms the window has, the larger its width Δ ml is (multiplicity of 4π∕N—the size of the rectangular window is shifted K times) and the bigger attenuation A sl is. Exemplary shapes of windows (up) and their DtFT spectra (down) are presented in Fig. 4.5. Since window functions are real-value ones their spectra are always symmetrical around Ω = 0.

Special Adjustable Windows

Apart from mentioned above fixed-shape non-parametric windows having fixed spectral features there are two very important parametric windows which can change their shape and spectral characteristics. The first one is the Dolph–Chebyshev window defined as follows (N = 2M + 1):

$$\displaystyle \begin{aligned} {{w}_{DC}}\left[ m+(M+1) \right]=C\left[ \frac{1}{\gamma }+2\sum_{k=1}^{M}{{{T}_{N-1}}\left( \beta \cos \frac{\pi k}{N} \right)\cos \frac{2\pi km}{N}} \right]\,,\quad -M\le m\le M, \end{aligned} $$
(4.35)

where γ denotes the required relative height of maximum spectrum side-lode in relation to the height of the spectrum main-lobe (e.g. γ = 0,01 or 0,001, which corresponds to relative attenuation of the side-lobe A sl = 20log10(γ) = 40 dB or 60 dB) and parameter β, depending on γ, is given by

$$\displaystyle \begin{aligned} \beta =\cosh \left( \frac{1}{N-1}{{\cosh }^{-1}}\frac{1}{\gamma } \right)=\cosh \left( \frac{1}{N-1}{{\cosh }^{-1}}({{10}^{{{A}_{sl}}/20}}) \right). \end{aligned} $$
(4.36)

T N−1(x) is Chebyshev polynomial of the (N − 1)-th order:

(4.37)

The Kaiser window , for N even or odd, is defined by formula:

$$\displaystyle \begin{aligned} {{w}_{K}}(n)=\frac{{{I}_{0}}\left( \beta \sqrt{1-{{\left( \frac{n-(N-1)/2}{(N-1)/2} \right)}^{2}}} \right)}{{{I}_{0}}\left( \beta \right)}, \quad 0 \le n \le N-1, \end{aligned} $$
(4.38)

where I 0(β) denotes Bessel function of the 0-th order:

$$\displaystyle \begin{aligned} {{I}_{0}}\left( x \right)=1+{{\sum_{k=1}^{\infty }{\,\left[ \frac{{{\left( x/2 \right)}^{k}}}{k!} \right]}}^{2}}. \end{aligned} $$
(4.39)

In literature one can find equations connecting required values of Δ ml and A sl with values of Kaiser window parameters β and N:

$$\displaystyle \begin{aligned} &\beta =\left\{ \begin{array}{*{35}{l}} 0\, &\quad {{A}_{sl}}<13.26\ \text{dB} \\ 0.76609{{\left( {{A}_{sl}}-13.26 \right)}^{0.4}}+0,09834\left( {{A}_{sl}}-13.26 \right), &\quad 13.26<{{A}_{sl}}<60\ \text{dB} \\ 0.12438\left( {{A}_{sl}}+6.3 \right)\, &\quad 60<{{A}_{sl}}<120\ \text{dB} \\ \end{array} \right. \end{aligned} $$
(4.40)
$$\displaystyle \begin{aligned} &N=\left\lceil K \right\rceil ,\quad K=\frac{24\pi ({{A}_{sl}}+12)}{155\cdot {{\varDelta }_{ml}}}+1, \end{aligned} $$
(4.41)

where ⌈K⌉ denotes the smallest integer value equal to or greater than K. In Matlab we have functions kaiser( ) and chebwin( ) .

4.4.3 Application Example

Exercise 4.3 (DtFT of Different Windows)

First, choose any window and calculate its DtFT spectra for different lengths, for example, N = 50, 100, 200, 500, 1000, 2000. Plot all spectra in decibels in one figure. What is your conclusion? Next, calculate the DtFT spectra for Kaiser window for the value of β changing from 0 to 14 with step 2. Plot all spectra in decibels in one figure. What is your conclusion? Finally, repeat Exercise 4.2 using in it the Chebyshev window. Change the signal length as well as frequencies and amplitudes of its two components. Try to obtain a compromise between the Δ ml and A sl.

Listing 4.3 DtFT spectra of different windows

Windows Application Summary

The window spectrum should have narrow “main-lobe” to allow seeing in it two separate peaks for frequencies Ω k and Ω l, which can lie very close to each other. Otherwise, we might observe one broad peak instead of two narrow ones because of their fusion.

The window spectrum should also have high attenuation of side-lobes in the situation when amplitudes A k and A l of two cosine components differ a lot and spectral peak of the weaker component could be lost/missed in high spectral side-lobes (in the grass) of the stronger component.

4.5 Discrete Fourier Transform

DFT represents discretization result of the Fourier series (4.15) which is defined in analog world for periodic signals (fundamental frequency f 0 = 1∕T, T—period, T = N ⋅ Δt, t = n ⋅ Δt):

$$\displaystyle \begin{aligned} &{{X}_{k}} &={} &\frac{1}{T}\int\limits_{0}^{T}{x(t){{e}^{-j2\pi (k{{f}_{0}})t}}dt\approx \frac{1}{N\cdot \varDelta t}\sum_{n=0}^{N-1}{x(n\cdot \varDelta t){{e}^{-j2\pi (k\frac{1}{N\cdot \varDelta t})(n\cdot \varDelta t)}}}}\varDelta t=\ldots \\ &&={} &\frac{1}{N}\sum_{n=0}^{N-1}{x(n){{e}^{-j\frac{2\pi }{N}kn}}},\quad {{f}_{k}}=k\cdot {{f}_{0}}=k\frac{{{f}_{s}}}{N}, \quad k=0,1,2\ldots,N-1. {} \end{aligned} $$
(4.42)

Equation (4.42) and its inverse can be written in matrix form as orthogonal transformation pair:

(4.43)
(4.44)

well-known for us from Chap. 2. The transformation matrix F is defined as, for example, also for N = 4:

(4.45)

so it has in its rows conjugated orthogonal harmonic vectors, with different scaling than in Eq. (4.1). In non-vector form and with changed normalization, equations (4.43) and (4.44) have the following form:

(4.46)
(4.47)

In Eq. (4.46) the signal is compared (correlated) with conjugation of harmonic Fourier basis function, while in Eq. (4.47) it is represented as a sum of basic functions scaled by spectral (“similarity”) coefficients X(k), calculated in Eq. (4.46).

First, the main student problem, after calculation of the signal DFT spectrum using Eq. (4.46), is how to connect calculated spectral coefficients X k with real-world frequencies when the frequency is missing in these equations! But we know how long the signals are (N samples) and which is the sampling frequency (f s), so as a result we know also the time duration of signals: T = N ⋅ Δt = N∕f s. In first row (k = 0) of matrix F we have only ones, in the second (k = 1)—one period of cos() in real part and one period of -sin() in imaginary part, in the third (k = 2)—two periods, later three, four, five, …, N − 1 periods. Therefore, since we know T, we should deduce that X 0 is a mean value of the signal, spectral coefficient X 1 corresponds to frequency 1 ⋅ f 0 = 1∕T, X 2—to 2 ⋅ f 0, X 3—to 3 ⋅ f 0, and so on. This sounds reasonable since in Fourier series coefficients are also calculated for frequencies k ⋅ f 0.

That is it! Now a reader should do some computer experiments and … find visually with surprise conjugate symmetry of the DFT spectrum: X k, k = 0, 1, 2, …, N − 1. Yes, indeed, the spectrum of our speech has such symmetry! This is typically the second student surprise! We analyze, for example, a real-value signal having only one frequency component but in the spectrum we see two peaks: one in its first half and one in the second half. This phenomena results from the fact that for k = 1, 2, 3…, N − 1 the following relations hold:

$$\displaystyle \begin{aligned} X_{N-k}={{X}_{k}}^{*} \quad \Rightarrow \quad \operatorname{real}({{X}_{N-k}})=\operatorname{real}({{X}_{k}}),\quad \operatorname{imag}({{X}_{N-k}})=-\operatorname{imag}({{X}_{k}}) {} \end{aligned} $$
(4.48)

Additionally the DFT spectrum always has zeros in imaginary part for k = 0 and k = N∕2:

$$\displaystyle \begin{aligned} \operatorname{imag}({{X}_{0}})=\operatorname{imag}({{X}_{N/2}})=0. {} \end{aligned} $$
(4.49)

Why the DFT spectrum has conjugate symmetry? What is the sense of computing something twice? The first answer is that conjugated Fourier harmonics which are used for signal decomposition in Eq. (4.46) are the same for k and N − k, only conjugated. For the k-th harmonic we have

$$\displaystyle \begin{aligned} {{e}^{-j\frac{2\pi }{N}kn}},\quad n=0,1,2,\ldots,N-1, {} \end{aligned} $$
(4.50)

while for the (N − k)-th:

$$\displaystyle \begin{aligned} {{e}^{-j\frac{2\pi }{N}(N-k)n}}={{e}^{-j2\pi n}}\cdot {{e}^{+j\frac{2\pi }{N}kn}}={{e}^{+j\frac{2\pi }{N}kn}}. {} \end{aligned} $$
(4.51)

Therefore the calculated DFT coefficients have also the same values, only complex-conjugated:

(4.52)
(4.53)

The second explanation of the spectrum (a)symmetry phenomena is that real-value cosine and sine functions can be expressed as a summation of two Fourier harmonics used for signal decomposition:

$$\displaystyle \begin{aligned} \cos \left( \frac{2\pi }{N}kn \right)=\frac{{{e}^{j\frac{2\pi }{N}kn}}+{{e}^{-j\frac{2\pi }{N}(N-k)n}}}{2}, \end{aligned} $$
(4.54)
$$\displaystyle \begin{aligned} \sin \left( \frac{2\pi }{N}kn \right)=\frac{{{e}^{j\frac{2\pi }{N}kn}}-{{e}^{-j\frac{2\pi }{N}(N-k)n}}}{2j}, \end{aligned} $$
(4.55)

therefore, since the DFT transform is linear, when analyzing real-value signals we have two symmetrical peaks in the DFT spectrum with complex-conjugated values.

Exercise 4.4 (DFT of a Cosine with Rectangular Window)

Make use of the Matlab program 4.2 in which the DFT algorithm is also implemented. In figures generated by the program, the DFT spectra are marked with red circles and compared with the DtFT spectra, denoted by blue solid line. In the beginning, try to obtain the same plots as presented in Fig. 4.6. Set the following values of program parameters: sampling ratio f s = 1000 Hz, number of signal samples N = 50, only component x1, in the beginning with frequency 100 Hz, than with 110 Hz. Check validity of the DFT spectrum (a)symmetry (Eq. (4.48)). Next, apply different windows to the signal. Again check the DFT spectrum (a)symmetry.

Fig. 4.6
figure 6

DtFT and DFT spectra of two cosines, blue line and red dots, respectively: (up) signal with f 0 = 100 Hz: perfect DFT match to the cosine frequency, (down) signal with f 0 = 110 Hz: the worst DFT match to the cosine frequency. Values of parameters: sampling frequency f s = 1000 Hz, N = 50 samples, DFT spectrum discretization step Δf = f 0 = f s∕N = 20 Hz. Observe symmetry of the DFT spectrum marked with red circles. Notice the different shapes of correct DtFT spectrum marked with blue solid line (two shifted spectra of the rectangular window)

Full size image

4.6 Summary

Signal processing consists of two fundamental branches: frequency analysis and signal filtering (noise reduction and rejections of some signal components). This chapter has been focused on fundamentals of frequency analysis by means of Fourier transform—it has a crucial significance in our DSP course. You should understand everything in it. If you do not, I am very sorry, read this chapter again and again … before the examination. Yes, you can. Personally, some papers I was reading repeatedly even 10 years. With final success. What should be remembered?

  1. 1.

    Most frequency analysis methods are very similar: one compares a signal with reference frequency components (oscillations) multiplying it with the references and accumulating single products. This is valid in analog and digital world, done by Fourier integrals and summations.

  2. 2.

    DtFT is a discretized continuous Fourier transform and DFT is a result of the discretization of Fourier series. In computer implementation both transforms are very similar: they use the same signal samples and treat them in almost the same manner. The only difference is that in N-sample DFT the signal spectrum is computed for precisely specified set of N frequencies: f k = k ⋅ f 0, k = 0, 1, 2, …, (N − 1), where f 0 = 1∕T is the inverse of the analyzed signal duration. In DtFT the choice of frequencies is completely free. For real-value signals we are typically choosing frequency values in the range [0, f s∕2). The DtFT offers better visualization of the theoretical signal spectrum due to its possible more dense sampling.

  3. 3.

    The DtFT is more application flexible but the DFT is faster due to the existence of very fast DFT implementations (FFT algorithms are presented in the next chapter). DtFT calculation can be speed up by using fast implementations of the chirp-Z transform (usage of three FFTs, not discussed here)—never the less the method is slower than the DFT.

  4. 4.

    One should always remember that in practice frequency analysis is performed upon a signal fragment, not on the whole signal. What is the consequence of this fact? That a fragment cutting operation has a very big influence on the final result! Simply taking signal samples from–to means that we are multiplying a signal with an observation window function having a value equal to “1” from–to and “0” elsewhere.

  5. 5.

    If two signals are multiplied, the Fourier spectra are convoluted. Due to this, the signal windowing performed during signal fragment cutting causes that the theoretical spectrum of the time-infinite signal is convoluted with the window spectrum modifying it. Therefore, one should choose very carefully the window function during spectral analysis.

  6. 6.

    Increasing K-times the length of the analyzed signal, one improves K-times the DFT frequency resolution, no matter what the window function is used. As a consequence, signal components having near frequencies are better distinguished.

  7. 7.

    Using windows with a low level of spectral side-lobes, one improves amplitude resolution of the spectrum by the cost of decreasing its frequency resolution. But the frequency resolution can be always improved by signal enlargement.

  8. 8.

    There are many window functions. The best should offer the most narrow spectral main-lobe (good frequency resolution) and the lowest level of spectral side-lobes (good amplitude resolution). In practice, Kaiser and Chebyshev windows are very often used due to their adjustable shapes and changeable spectral features.

4.7 Private Investigations: Free-Style Bungee Jumps

Exercise 4.5 (Am I An Enrico Caruso? Finding Frequency of Vocal Cords Oscillation)

Use DtFT and DFT detectives for finding the frequency of your vocal cords opening and closing for different vowels.

Exercise 4.6 (In the Wonderful World of Sounds)

From the Internet web page FindSounds (https://www.findsounds.com/) take 2–3 signals of different origin and use DtFT and DFT for finding their frequency content. Scale frequency axis in hertz. Overlay two spectra in one plot.

Exercise 4.7 (Did You Break My Heart? What Is the Frequency of My Heartbeat?)

Take from the Internet an ECG heart activity signal, e.g. from the page https://archive.physionet.org/cgi-bin/atm/ATM. Calculate the frequency of the heartbeat using DtFT and DFT.

Exercise 4.8 (Steel Factory Secrets)

Analyze signals of supply voltages and currents recorded for operating arc furnace. Take them from the file load( ’UI.mat’) ; whos, given at the book web page. Do spectral DtFT analysis for interesting parts of the spectra. Estimate frequencies and amplitudes of fundamental frequency 50 Hz (close to 50) and its harmonics 100, 150, 200, 250, … Hz.

Exercise 4.9 (Clear Water, Clear Power Supply)

Please, analyze recorded power supply voltage signal tu.dat which is used for testing algorithms for monitoring electric power quality (https://grouper.ieee.org/groups/1159/). First, extract time and voltage values from matrix columns: load( ’tu.dat’) ; t=tu( :,1) ; u=tu( :,2) ; plot( t,u) ;) . Then, estimate frequencies and amplitudes of fundamental frequency 50 Hz (close to 50) and its harmonics, if they are present.

Exercise 4.10 (Mysteries of NMR Laboratory)

Do frequency analysis of pseudo-NMR signal synthesized in first additional exercise after Chap. 2.