The Linear Matching Method and Its Software Tool for Creep Fatigue Damage Assessment

Abstract

The Linear Matching Method (LMM) is a numerical procedure that has undergone extensive research and development over a number of years to conduct various structural integrity assessments, more recently, the creep-fatigue damage assessment considering full creep-cyclic plasticity interaction using the extended Direct Steady Cycle Analysis. In order to encourage the widespread implementation of the LMM throughout the industry, an Abaqus CAE plug-in has been developed that enables its use by individuals with little or no understanding of the numerical theories involved. This chapter discusses different creep-cyclic plasticity mechanisms and provides a detailed review of the latest developments within the LMM framework for its evaluation. Case studies are included to demonstrate the applicability of LMM in the evaluation of creep-cyclic plasticity response for complicated loads, varying dwell periods and multi-material structures. Further, the flexibility of LMM to couple with Reversed Plasticity Domain Method to design cyclic load levels, and with design codes for creep-fatigue damage evaluation is also presented. All the results from the case studies demonstrate the level of accuracy, efficiency and robustness of the LMM.

1 Introduction

An important consideration when designing engineering components is to determine whether the loading conditions will have a significant impact upon the length of time that a structure can remain in safe operation. This is particularly true in cases where structures are exposed to elevated temperature and cyclic loads since severe complex failure mechanisms, such as creep and fatigue and their interaction if any, must be carefully considered. Over the past few decades, efforts have been made to combine finite element analysis with continuum damage mechanics to assess the creep-fatigue damage evaluation. But for acceptable results they require numerous material parameters which are not easily available. Another limiting factor is the high computational cost involved. Recently, several direct methods have been developed which uses relatively simpler material models such as Elastic-Perfectly Plastic model (EPP) or Ramberg Osgood (RO) model. They consider a load domain that accounts for all the possible paths between the extremes. LMM is one such direct method that has been developed to include the extended Direct Steady Cycle Analysis (eDSCA) which directly calculates the stabilized response of a structure subjected to a cyclic load at high temperature. The outputs from eDSCA can be coupled with appropriate damage models to conduct creep-fatigue damage analysis.

2 Cyclically Loaded Structures

The minimum load level that a structure is able to withstand under monotonic loading condition is known as the “limit load”, loading beyond this will lead to an instantaneous collapse. When subjected to cyclic loading conditions, failure is likely to occur at lower loading levels due to the accumulation of residual stresses and plastic strains throughout the multiple cycles. In the work carried out by Bree [1], in the late 1960s, it was identified that a component subjected to a cyclic thermal load and a constant mechanical load could exhibit one of the four potential cyclic responses, namely purely elastic behaviour, elastic shakedown, reverse plasticity and ratcheting. In order to represent how the cyclic and constant loads interact with one another he proposed an interaction diagram, similar to the one presented in Fig. 1, for a thin cylindrical vessel subject to an internal pressure and a linear temperature gradient across its thickness.

Fig. 1

Classical Bree-like diagram

The cyclic thermal load is normalised with respect to the yield stress of the material and is shown on the vertical axis, while the constant mechanical load, which is also normalised against the yield stress of the structure, is shown on the horizontal axis. It can be observed that for relatively lower loading levels there is no plastic deformation and the structure exhibits purely elastic behaviour. However, for loading cases where this elastic response limit is exceeded, plastic strains begin to develop. As the cyclic thermal load is increased, the response escalates to the elastic shakedown region and then to reverse plasticity region. On increasing the mechanical load, the structure exhibits a ratcheting behaviour. Typical hysteresis loops of structures exhibiting pure elastic, elastic shakedown, reverse plastic and ratcheting mechanisms are presented in Fig. 2.

Fig. 2

Steady state structural responses to loads within a pure elastic region, b elastic shakedown region, c reverse plasticity region, d ratcheting region [2]

Elastic shakedown:

Plastic strains accumulate during the initial cycles but the response then becomes entirely elastic due to residual stresses, Fig. 2b.

Reverse plasticity:

Plastic strains occur during all cycles but there is no net increase and a closed loop is formed throughout the cycle, Fig. 2c.

Ratcheting:

Plastic strains accumulate during all cycles and this eventually leads to structural failure via incremental plastic collapse, Fig. 2d.

2.1 Creep—Cyclic Plasticity Interaction

Creep is a time-dependent damage mechanism prevalent in materials when exposed to high temperatures, generally over 30% of its melting point, for a pro-longed period. A typical creep strain curve is retraced in Fig. 3. It consists of three stages; (a) primary; (b) secondary; and (c) tertiary. During the primary phase the creep strain rate decreases. During secondary stage, the creep strain rate remains constant, and generally, the secondary stage is the longest and most prominent phase during the creep dwell. During the tertiary phase, an exponential increase in the creep strain is observed.

Fig. 3

Schematic of the standard creep curve

Under cyclic loading conditions, the introduction of creep can have severe effects on the cyclic plasticity response of the structure, such that it may introduce creep-fatigue damage mechanism in an otherwise elastic loading condition or the much more dangerous damage mechanism known as creep-ratcheting. Factors such as operating temperature, strain range, frequency of loading and duration of loading are critical and influence the creep-cyclic plasticity interaction. A typical steady state hysteresis loop of a structure under creep-cyclic plasticity mechanism is shown in Fig. 4a.

Fig. 4

Steady state hysteresis. a Creep-fatigue interaction, b cyclically enhanced creep; c creep enhanced plasticity

At steady state, if the reverse plasticity can compensate for the creep strain and the loading strain, if any, a closed hysteresis loop is obtained. On the other hand, if an open loop is obtained, the mechanism is termed as creep-ratcheting. Creep ratcheting may be broadly distinguished as “cyclic enhanced creep” and “creep enhanced plasticity”. Where the open hysteresis loop is a result of the large creep strain accumulated, it is referred to as cyclic enhanced creep (Fig. 4b). On the other hand, large reverse plastic strain may be dominated in cases with small creep strains but significant stress relaxation during the dwell, and the ratcheting mechanism in such a scenario is referred to as creep enhanced plasticity (Fig. 4c).

3 Creep-Fatigue Damage Assessment

High temperature design codes such as R5 and ASME evaluate the total damage in the following way

$$d_{c} + d_{f} \le \emptyset_{CF}$$

(1)

where $d_{c}$ and $d_{f}$ are the total creep damage and total fatigue damage; $\emptyset_{CF}$ is the allowable total creep-fatigue damage factor which is depended on the type of material and the standard considered. Essentially, both the creep and fatigue damages are individually calculated and then combined to assess the acceptance based on the code considered. The number of cycles to LCF damage is calculated using the strain-life curve (E-N) curve, for which the total stain range should be known. The fatigue damage per cycle may then be defined as:

$$d_{f}^{1c} = \frac{1}{{N\left( {\Delta \varepsilon_{tot} } \right)}}$$

(2)

where $d_{f}^{1c}$ is the fatigue damage per cycle and $N$ is the number of cycles to pure fatigue failure corresponding to the total stain range $\left( {\Delta \varepsilon_{tot} } \right)$. The two most common creep damage assessment methodologies are the time fraction (TF) rule, in line with ASME recommendation and ductility exhaustion (DE) method, which is recommended by R5. The TF rule to calculate the creep damage can be expressed as:

$$d_{c\_TF}^{1c} = \mathop \smallint \limits_{0}^{{t_{h} }} \frac{dt}{{t_{f} \left( {\sigma , T} \right)}}$$

(3)

where $t_{f}$ is the creep rupture time, and it is a function of stress and temperature. $dt$ is the time increment and $t_{h}$ is the hold time. Creep damage by DE method is calculated using:

$$d_{c\_DE}^{1c} = \mathop \smallint \limits_{0}^{{t_{h} }} \frac{{\dot{\bar{\varepsilon }}_{c} }}{{\bar{\varepsilon }_{c} \left( {\dot{\bar{\varepsilon }}_{c} , T} \right)}}dt$$

(4)

where $\dot{\bar{\varepsilon }}_{c}$ is the instantaneous creep strain rate and $\bar{\varepsilon }_{c}$ is the material creep ductility. In effect, parameters such as the total strain range, creep strain, start of dwell stress and the elastic follow up factor at steady state are critical in the assessment of creep-fatigue damage assessment. The eDSCA within the LMM frame work is capable of accurately calculating them.

4 The Linear Matching Method

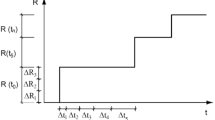
The LMM is a direct method for structural assessment that has been a part of the R5 research program for many years, having initially been developed from the Elastic Compensation Method (ECM). Over the years LMM has seen extensive theoretical and numerical development and has become one of the most successful direct methods currently available. It is based upon the premise that a non-linear material response can be simulated using a series of linear analyses during which the modulus is modified throughout the structure. Figure 5 demonstrates this concept pictorially.

Fig. 5

a Initial stress distribution, b intermediate stress redistribution, c final stress redistribution

The first stage of the LMM process is to perform a linear elastic analysis for each of the loads applied to the structure, with the modulus at each point modified such that the stress equals the yield stress (Fig. 5a). These modified values for modulus are then used in the next elastic analysis and this leads to the stress being redistributed throughout the structure (Fig. 5b). Following this the modulus is again modified and the process is repeated multiple times, thereby allowing the stresses to redistribute similarly to an elastic-plastic material (Fig. 5c). The LMM has been developed for limit analysis, shakedown analysis, ratchet analysis, and recently to include steady state cyclic behavior with full creep-cyclic plasticity interaction.

4.1 Numerical Procedures for eDSCA

A flowchart of the eDSCA evaluation procedure is presented in Fig. 6. Detailed discussions on the numerical procedure of the eDSCA has been previously presented in [3]. Revisiting the same would be beyond the scope of this chapter hence a concise discussion highlighting the major aspects of the procedure is presented here.

Fig. 6

Flow chart illustrating the eDSCA numerical procedure [4]

For a structure subjected to an arbitrary cyclic load, Chen et al. [3, 5] proposed the minimization function $I\left( {\dot{\varepsilon }_{ij}^{c} } \right) = \sum\nolimits_{l = 1}^{L} {I^{l} }$ to calculate the steady state cyclic response, where L refers to the total number of load instances, $\dot{\varepsilon }_{ij}^{c}$ indicates the kinematic admissible strain rate and l refers to the load instance considered. Further an incremental form is also suggested for the minimization function as:

$$I^{l} \left( {\Delta \varepsilon_{ij}^{l} } \right) = \int\limits_{V} {\left\{ {\sigma_{ij}^{l} \Delta \varepsilon_{ij}^{l} - \left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma }_{ij}^{l} \left( {t_{l} } \right) + \rho_{ij}^{l} \left( {t_{l} } \right)} \right]\Delta \varepsilon_{ij}^{l} } \right\}dV}$$

(5)

where $\Delta \varepsilon_{ij}^{l}$ is the strain increment and $\rho_{ij}^{l} \left( {t_{l} } \right)$ is the residual stress. Using the minimization function defined above, $\Delta \varepsilon_{ij}^{l}$ is calculated in an iterative manner. The inelastic strain and the residual stress at each increment are computed using the previously accumulated residual stress and the elastic stress. For the load instance $t_{l}$ during the loading cycle, $\Delta \varepsilon_{ij,k + 1} \left( {t_{l} } \right)$ is calculated by:

$$\Delta \varepsilon_{ij,k + 1} \left( {t_{l} } \right)^{'} = \frac{1}{{2\overline{\mu } \left( {t_{l} } \right)}}\left[ {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma }_{ij} \left( {t_{l} } \right) + \rho_{ij,k + 1} \left( {t_{l - 1} } \right) + \Delta \rho_{ij,k + 1} \left( {t_{l} } \right)} \right]^{'}$$

(6)

where $\overline{\mu }$ is the iterative shear modulus, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma }_{ij}$ is the associated elastic solution, $\rho_{ij,k + 1} \left( {t_{l - 1} } \right)$ is the prior changing residual stress history, $\Delta \rho_{ij,k + 1} \left( {t_{l} } \right)$ is the current changing residual stress associated with that inelastic strain increment and k refers to the number of sub-cycles required to attain convergence. For cyclic load with creep dwell, the accumulated creep strain can be computed by:

$$\Delta \bar{\varepsilon }^{c}_{{}} = \frac{{B\left( {n - 1} \right)\Delta t^{m + 1} \left( {\bar{\sigma }_{s} - \bar{\sigma }_{c} } \right)}}{{\left( {\frac{1}{{\bar{\sigma }_{c}^{n - 1} }} - \frac{1}{{\bar{\sigma }_{s}^{n - 1} }}} \right)\left( {m + 1} \right)}}$$

(7)

$$\bar{\sigma }_{c} = \left( {\frac{{\bar{\dot{\varepsilon }}^{F} }}{{B\Delta t^{m} }}} \right)^{{\frac{1}{n}}}$$

(8)

$$\dot{\bar{\varepsilon }}^{F\prime } = \frac{{\Delta \bar{\varepsilon }^{c} }}{\Delta t}\frac{{\left( {m + 1} \right)}}{{\left( {n - 1} \right)}}\frac{{\bar{\sigma }_{c}^{n} }}{{\left( {\bar{\sigma }_{s} - \bar{\sigma }_{c} } \right)}}\left( {\frac{1}{{\bar{\sigma }_{c}^{n - 1} }} - \frac{1}{{\bar{\sigma }_{s}^{n - 1} }}} \right)$$

(9)

where B, m and n indicate the creep parameters, $\bar{\sigma }_{c}$ refers to the creep flow stress $\bar{\sigma }_{c}$ is computed using Eq. (8), which is then used as an input in Eq. (9) to calculate the creep strain rate $\dot{\bar{\varepsilon }}^{F}$. The residual stress and an iterative shear modulus for the increment is then computed as:

$$\bar{\mu }_{k + 1} \left( {x,t_{l} } \right) = \bar{\mu }_{k} \left( {x,t{}_{l}} \right)\frac{{\sigma_{y}^{R} \left( {x,t_{l} } \right)_{k} }}{{\bar{\sigma }\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\sigma }_{ij} \left( {x,t_{l} } \right) + \rho_{ij}^{r} \left( {x,t_{l} } \right)_{k} } \right)}}$$

(10)

where $\bar{\mu }_{k} \left( {x,t_{l} } \right)$ is the iterative shear modulus at the sub-cycle k for lth load instance. $\sigma_{y}^{R} \left( {x,t_{l} } \right)_{k}$ is either an iterative von-Mises yield stress for the material model considered at load instance $t_{l}$ or the creep flow stress $\bar{\sigma }_{c}$. $\rho_{ij}^{r} \left( {x,t_{l} } \right)$ is the sum of the constant residual stress field and all previous changing residual stresses at load instance $t_{l}$. The procedure briefly detailed in this section helps in determining all the parameters required for the estimation of the saturated hysteresis loop.

4.2 The LMM Software Tool

From its inception, LMM subroutines are coded using FORTRAN language so as to facilitate its use in with Abaqus. This implies that users need to have sufficient programming experience to run the analysis efficiently. But this is not the case especially in an industrial environment. In order to counter this issue, a Graphical User Interface (GUI) and an autonomous Abaqus plug-in have been developed recently. The plug-in provides the user with an interface to select the model, chose the analysis type, define the material properties and define the load in a straight forward manner.

The LMM plug-in, on installation will appear under the “plug-in’’ menu in Abaqus CAE. A pictorial presentation of the sequence of the different dialog box the user passes through is given in Fig. 7. The first dialog box provides the user the option to select the type of LMM analysis, such as (a) strict shakedown analysis; (b) steady state cycle analysis; (c) steady state cycle and ratchet limit analysis; (d) creep rupture analysis; (e) eDSCA with creep dwell(s) analysis. The next dialog box deals with the material parameter such as the Young’s modulus, yield stress, Poisson’s ratio, the thermal expansion coefficient and creep constants for each material in the model. This enables the use of LMM in structural analysis of multi-material components such as weldments and Metal Matrix Composites (MMC). In order to achieve a higher level of accuracy, the user has the option of providing temperature dependent properties. The option to choose between EPP or RO material model is also provided. The RO material model option is coded to generate the yield stress from the RO parameters entered by the user.

Fig. 7

LMM eDSCA analysis tool procedure

Once the above steps are complete, the plug-in then presents the load cycle dialog within which a load table is provided to define the load cycle. Defining the load cycle properly is critical in the generation of accurate results. The load at each of the time point along with the corresponding temperature field can specified within the load table. It is to be noted that the user can define any number of time instances. The final dialog box helps in defining the convergence rule, name of the job and the maximum increments. In order to run larger models swiftly, the LMM software is developed to run multiple Computer Processing Units (CPUs).

On completion of the above steps, prior to running the analysis, the plug-in carries a sequence of checks to assure the applicability of LMM analysis on the model. The user is advised of the errors if any, which are to be rectified for the analysis to commence. It should be noted that at each dialog box, the values provided by the user are also checked for probable errors. In case an error is found, the plug-in produces a dialog box indicating the error and a possible solution for it.

5 LMM Cases Study

5.1 Fatigue Assessment Approach by Direct Steady Cycle Analysis (DSCA)

Recently Zheng et al. [6, 7] combined the Reversed Plasticity Domain Method (RPDM) and the DSCA within the LMM framework to design cyclic load levels for LCF experiments with predefined fatigue life ranges. The example is discussed here as it utilizes various facets within the LMM framework such as shakedown analysis, ratchet analysis, the use of temperature dependent properties and use of EPP & RO material models.

For LCF experiments of components with a predefined fatigue life range, it is critical to properly define the cyclic load levels, but this is not straight forward and is quite difficult to obtain. The DSCA option within the LMM framework may be used as an aiding tool to obtain the load levels for the experiments. The basic idea is to estimate the total strain range under the considered loading condition using the DSCA and then refine it further until the fatigue life corresponds to the LCF testing requirement. The steps may be elaborated as below:

• 1. The ratchet and shakedown limits are calculated to obtain the Reversed Plasticity Domain (RPD), and this utilizes the shakedown and ratchet plug-in.

• 2. The DSCA then calculates the total strain range of the selected load level.

• 3. The fatigue life is estimated based on the fatigue life curve and total strain range.

• 4. The above steps are repeated until the fatigue life obtained is in line with the requirements of the LCF testing.

Zheng et al. [6, 7] presented the case study of a pressurized shell made of X2CrNiMo17-12-2 steel used in nuclear power plants. The geometry and the complicated loading condition opted are presented in Fig. 8a. As indicated in Sect. 4.2, LMM has the capacity to work with both temperature dependent and temperature independent properties, though the number of iterations required is higher, as reflected in Fig. 8b.

Fig. 8

a Geometry and load applied to the pressurized shell; b comparison between the number of iterations for temperature dependent and independent material properties [6, 7]

The shakedown and ratchet limit boundaries (Fig. 9a) are generated using the relevant tools within the LMM plug-in. Load levels below the elastic limit induce HCF damage. Within the RPD, the load levels generally induce LCF damage. The total strain range is computed using the eDSCA for the opted load level (indicated as $\otimes$ in Fig. 9a) which is within the RPD. A comparison of the elastic strain range, plastic strain range, ratchet strain and total strain range computed using both the RO and EPP models are presented in Fig. 9b. The obtained total strain range, with the help of an E-N diagram is then used to compute the number of cycles (Fig. 9c). For this particular case study, the number of cycles computed by RO model is larger than that computed by EPP model, which is contrary to the normal knowledge which is that the EPP model produces the most conservative results. This unusual result is due to the lower elastic limit for the RO model compared to the EPP model. Nevertheless, this points to the high level of accuracy and the computational excellence LMM exhibits. In case the fatigue life requirements of the LCF testing are not satisfactorily met by the chosen load cycle, other load levels are analysed for their corresponding total strain ranges.

Fig. 9

a A typical shakedown-ratchet limit curve. b Calculated strains based on the temperature-dependent RO and EPP model; c fatigue life assessment based on the calculated strain range [6, 7]

5.2 Creep Fatigue Assessment on Cruciform Weldment

Y. Gorash et al. studied and presented the creep-fatigue damage assessment of a cruciform weldment (Fig. 10a) using LMM in [8,9,10], a brief overview of which is provided in this section. The loads considered include a cyclic bending moment and a uniform high temperature (Fig. 10b). A reverse pure bending moment is simulated by imposing a cyclic linear distribution of normal pressure at the end of the model. The material properties are in line with SS316 N(L) with varying properties for the PM, HAZ and WM.

Fig. 10

a Finite element model of the weldment; b loading condition of the cruciform weldment [8,9,10]

Analyses were carried out for a pure fatigue case and creep-fatigue interactions scenarios with creep dwells of 1 and 5 h. The variants of bending moments included total strains of 0.25, 0.3, 0.4, 0.6 and 1% of the parent material. The contours for total strain range, creep strain and stress from LMM analysis for a total strain of 1% and dwell time of 5 h are presented in Fig. 11. The most critical zone has been identified as the location at the weld toe near the heat affected zone. Further, Y. Gorash et al. presented a comparison between the available experimental results and the LMM simulation results, which showed a satisfactory comparison for 9 of the 11 results.

Fig. 11

For dwell time of 5 h. a Total Strain Range; b creep Strain; c start of dwell stress; d end of dwell stress [8,9,10]

5.3 Creep Fatigue Interaction of a MMC

A brief overview of the study done on MMC by Barbera et al. in [4, 11, 12] is discussed here. This case study is particularly interesting as it discusses the effect of a creep dwell on loading conditions which would otherwise resonate an elastic behavior. The loads considered for the MMC consist of a constant mechanical load and a uniform cyclic temperature load (Fig. 12a). The MMC consists of Al₂O₃ fibre and Al 2024 T3 matrix. A shakedown limit interaction curve is obtained using the LMM shakedown analysis initially to identify possible load levels that would exhibit an elastic response in the absence of creep dwell. 6 load points such as A1, A2, B1, B2, C1 and C2 as indicated in Fig. 12b were identified and studied for varying dwell times. For the load levels A1 and A2, where the primary load is relatively lower than B and C, a closed hysteresis loop is obtained for dwell holds of 1 to 100 hours, suggesting the introduction of creep-fatigue interaction. Whereas for all the other load levels considered an increment in the net strain per cycle is present suggesting creep-ratcheting mechanism. The increase in the thermal load further increased the plastic strain increment during loading and the creep strain. As an example, the hysteresis loops for B1 and B2 for dwell times 1 and 100 hours are presented in Fig. 13. It is inferred that the ratcheting mechanism is influenced by the dwell time and the mechanical load. Hence the analysis was repeated considering only cyclic thermal loads. The hysteresis loops so obtained were all closed loop though with increasing the dwell hold, the creep strain and reverse plasticity increased. Using inelastic Abaqus step-by step analysis the LMM results were verified. A comparison of the values and contours of the creep strain increment $\varepsilon_{C}^{MMC}$, plastic strain increment during loading $\varepsilon_{L}^{MMC}$ and unloading $\varepsilon_{UL}^{MMC}$ are present in Table 1 and Fig. 14 respectively.

Fig. 12

a Finite element model and the loads applied on the MMC; b shakedown limit interaction curve [4, 11, 12]

Fig. 13

Response of the steady state stress-strain path at location the critical point for load points B1 and B2 [4, 11, 12]

Table 1 Comparison between LMM and SBS analysis for different cyclic loads

Fig. 14

Comparison between LMM and SBS analysis contours [4, 11, 12]

5.4 Creep Fatigue and Creep Ratcheting of Butt Welded Pipe

The case study discussed here gives an overview of how eDSCA may be used with an appropriate damage model (introduced in Sect. 3) to conduct creep-fatigue damage analysis. Figure 15 presents the general evaluation procedure, which starts with the estimation of the saturated hysteresis loop using eDSCA. Using the total strain obtained, the fatigue damage is calculated and using the creep stresses and strains, the creep damage is calculated. The total damage is then assessed using the considered standard’s interaction diagram.

Fig. 15

Flow-chart for the general creep-fatigue evaluation procedure

The pipe geometry and loading conditions considered for the case study are presented in Fig. 16. Welding residual stresses are assumed to be minimal due to post weld heat treatment such that their effect on creep behaviour on the welded pipe can be neglected. The most critical region in terms of creep-fatigue crack initiation probability is at the interface between the WM and HAZ where the equivalent creep strain and the total strain are found to be high.

Fig. 16

a Butt welded pipe geometry. b Boundary condition and load applied; c loading condition of the pipe

The effect of creep dwell on the cyclic-creep plasticity mechanism of the pipe can be understood from Fig. 17a. Compared to the pure fatigue case, the introduction of a creep dwell increases the reverse plasticity. Increasing the dwell time further enhances the creep strain and the subsequent stress relaxation, which further enhances the plastic behaviour during the unloading phase. This results in larger total strain range, indicating a reduction in the fatigue life. It should be noted that this decrease in the fatigue life is in addition to the creep damage accumulated as a result of the creep dwell. The most significant change with respect to the accumulation of creep strain occurs from a dwell time of 10 hours to 100 hours after which it reduces as reflected in Fig. 17b.

Fig. 17

a Stabilized steady state hysteresis loops; b creep strain for increasing dwell time; c interaction between creep strain and net plastic strain; d creep-fatigue life and creep ratcheting life against dwell time

Figure 17c presents an interaction diagram between the creep strain and the net plastic strain, which is the difference between the plastic strain accumulated during loading and loading. They can be used to understand the drive of the creep-ratcheting phenomena if any. A closed hysteresis loop is obtained when the creep strain is equal to the net plastic strain. The blue line in Fig. 17c represents a closed loop. The area above this line indicates cyclically enhanced creep and the area below indicates creep enhanced plasticity. At lower dwell times, the creep ratcheting mechanism for the welded pipe is driven by creep enhanced plasticity. As the dwell time increases, the creep strain tends to dominate, with a closed loop obtained for dwell time of 100 hours, and slowly shifting towards cyclically enhanced creep mechanism for larger dwell times.

The creep-fatigue life and creep ratcheting life, calculated using the strain ductility approach [13], against dwell time are shown in Fig. 17d. The creep fatigue life decreases with increase in the dwell period, whereas an interesting trend is seen in the case of creep-ratcheting life. For shorter dwell times, creep ratcheting is dominant compared to creep-fatigue damage, which is a result of the creep enhanced plasticity mechanism. As the dwell time increases, a slight increase is observed in the creep-ratcheting life, which is because the creep strain is compensated by the net plastic strain. On further increasing the dwell time, creep ratcheting again dominates, in this case due to cyclically enhanced creep.

6 Conclusions

A complete overview of the high-temperature design and assessment capabilities of the eDSCA within the LMMF is given. The introduction of a software tool as an Abaqus CAE plug-in with an intuitive GUI makes the LMM easily accessible to a wide range of users, including those who have little theoretical understanding of the LMM and limited programming skills. Four case studies have been presented to showcase the various facets and applications for the LMM. These demonstrate the wide range of complex load interactions that the LMM is capable of assessing. Furthermore, the LMM can also be used in conjunction with other rules based methods in order to assess the component′s life in terms of creep-fatigue and creep-ratcheting failures.