Abstract
Common types of artificial neural networks have been well known to suffer from the presence of outlying measurements (outliers) in the data. However, there are only a few available robust alternatives for training common form of neural networks. In this work, we investigate robust fitting of multilayer perceptrons, i.e. alternative approaches to the most common type of feedforward neural networks. Particularly, we consider robust neural networks based on the robust loss function of the least trimmed squares, for which we express formulas for derivatives of the loss functions. Some formulas, which are however incorrect, have been already available. Further, we consider a very recently proposed multilayer perceptron based on the loss function of the least weighted squares, which appears a promising highly robust approach. We also derive the derivatives of the loss functions, which are to the best of our knowledge a novel contribution of this paper. The derivatives may find applications in implementations of the robust neural networks, if a (gradient-based) backpropagation algorithm is used.
The research was financially supported by the projects GA19-05704S (J. Kalina) and GA18-23827S (P. Vidnerová) of the Czech Science Foundation.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Neural networks represent a wide class of habitually used tools for the task of nonlinear regression. Numerous applications of estimation in nonlinear regression in various fields are nowadays solved by neural networks. Thus, they represent important exploratory tools of modern data analysis [15], particularly of exploratory data analysis (see e.g. [7]). However, the most commonly used methods for training regression neural networks based on the least squares criterion are biased under contaminated data [18] as well as vulnerable to adversarial examples.
Under the presence of outlying measurements (outliers) in the data, training multilayer perceptrons is known to be unreliable (biased). Such their non-robustness, caused by their minimization of the sum of squared residuals (see [11] for discussion), becomes even more severe for data with a very large number of regressors [3]. Therefore, researchers have recently become increasingly interested in proposing alternative robust (resistant) methods for training of multilayer perceptrons [2]. So far, only a few robust approaches for training for MLPs have been introduced and even smaller attention has been paid to a robustification of radial basis function (RBF) networks. Approaches replacing the common sum of squared residuals by a robust loss considered the loss functions corresponding to the median [1], least trimmed absolute value (LTA) estimator [17], or least trimmed squares (LTS) estimator [2, 18]. The last two estimators were proposed for the model of the so-called contaminated normal distribution, assuming the residuals to come from a mixture of normally distributed errors with outliers, typically assumed to be normally distributed as well but with a (possibly much) larger variance than the majority of the data points. Other robust loss functions within multilayer perceptrons were examined in [13]. A different robust approach to neural networks based on finding the least outlying subset of observations but exploiting the standard loss minimizing the sum of least squares of residuals was proposed in [11], where also some other previous attempts for robustification of neural networks are cited. All these robust approaches were also verified to be meaningful in numerical experiments. Robust approaches to fitting neural networks were investigated also in the context of clustering (unsupervised learning), based on replacing means of clusters by other centroids (e.g. medoids [4]).
Here, we use the idea to replace the common loss function of multilayer perceptron by a robust version. On the whole, we consider here three particular loss functions for multilayer perceptrons, corresponding to
-
Least squares (i.e. the most common form of the loss for multilayer perceptrons),
-
Least trimmed squares (see Sect. 2),
-
Least weighted squares (see Sect. 2).
As the main contribution, partial derivatives of the loss function with respect to each of the parameters are evaluated here for robust multilayer perceptrons. These are very useful, because the backpropagation algorithm for computing the robust neural networks requires them. We derive the derivatives for a particular architecture of the multilayer perceptron, while they can be extended in a straightforward way to more complex multilayer perceptrons. Nevertheless, we point out that the derivatives are difficult to find in the literature even for a standard multilayer perceptron with a loss based on minimizing the least squares criterion. Available robust estimators for linear regression and for the location model are recalled in Sect. 2 of this paper. Section 3 presents derivatives of standard as well as robust loss functions for a multilayer perceptron with one hidden layer. Section 4 concludes the paper.
2 Linear Model and Robust Estimation
This section recalls robust estimates in linear regression model (and the location model, which is its special case), which will serve as inspiration for the robust versions of neural networks studied later in Sect. 3. The standard linear regression model
considers n observations, for which a continuous response is explained by p regressors (independent variables, features) under the presence of random errors \(e_1,\dots ,e_n\). The presence of the intercept \(\beta _0\) in the model can be interpreted as the presence of a vector of ones in the design matrix X containing the elements \(X_{ij}\). As the most common least squares estimator of \(\beta =(\beta _0,\beta _1,\dots ,\beta _p)^T\) in (1) is vulnerable to the presence of outliers in the data, various robust alternatives have been proposed [8].
Robust statisticians have proposed a variety of estimation tools, which are resistant to the presence of outliers in the data. Such estimators are considered highly robust with respect to outliers, which have a high value of the breakdown point. We can say that the breakdown point, which represents a fundamental concept of robust statistics [8], is a measure of robustness of a statistical estimator of an unknown parameter. Formally, the finite-sample breakdown point evaluates the minimal fraction of data that can drive an estimator beyond all bounds when set to arbitrary values. Keeping in mind the high robustness, we decide for replacing the sum of squared residuals by loss functions of the least trimmed squares and least weighted squares estimators, which are known to yield reliable and resistant results over real data [10].
The least trimmed squares (LTS) estimator [16] represents a very popular regression estimator with a high breakdown point (cf. [8]). Consistency of the LTS and other properties were derived in [19]. Formally, the LTS estimate of \(\beta \) is obtained as

where the user must choose a fixed h fulfilling \(n/2 \le h < n\); here, \(u_i(b)\) is a residual corresponding to the i-th observation for a given b, and we consider squared values arranged in ascending order denoted as \(u_{(1)}^2(b) \le \cdots \le u_{(n)}^2(b)\). The LTS estimator may attain a high robustness but cannot achieve a high efficiency [19].
The least weighted squares (LWS) estimator [20] for the model (1), motivated by the idea to down-weight potential outliers, remains much less known compared to the LTS, although it has more appealing statistical properties. The definition of the LWS exploits the concept of weight function, which is defined as a function \(\psi : [0,1] \rightarrow [0,1]\) under technical assumptions. The LWS estimator with a given \(\psi \), which is able to much exceed the LTS in terms of efficiency, is defined as

We may refer to [20] and references cited therein for properties of the LWS; it may achieve a high breakdown point (with properly selected weights), robustness to heteroscedasticity, and efficiency for non-contaminated samples. The performance of the LWS on real data (see [9] and references cited therein) can be described as excellent. We also need to consider the location model, which is a special case of (1), in the form
with a location parameter  . The LTS and LWS estimators are meaningful (and successful [9]) also under (4), while the LWS estimator in (4) inherits the appealing properties from (1).
. The LTS and LWS estimators are meaningful (and successful [9]) also under (4), while the LWS estimator in (4) inherits the appealing properties from (1).
3 Theoretical Results
This section presents partial derivatives of three loss functions for a particular architecture of a multilayer perceptron, i.e. assuming a single hidden layer. Their usefulness is discussed in Sect. 4.
3.1 Model and Notation
We assume that a continuous response variable  and a vector of regressors (independent variables)
and a vector of regressors (independent variables)  are available for the total number of n observations. The regression modeling in the nonlinear model
are available for the total number of n observations. The regression modeling in the nonlinear model
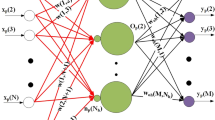
with an unknown function \(\varphi \) and random errors \(e_1,\dots ,e_n\) will be performed using a multilayer perceptron (MLP) with a single hidden layer, which contains N hidden neurons.
The MLP estimates the response \(Y_i\) of the i-th observation by
where f and g must be specified (possibly nonlinear) functions. The formula (6) for computing the fitted values of the response considers two layers only however can be generalized for more layers easily. We use here a notation following [6], although other more or less different versions of notation may be used in this context as well. If g is an identity function, then of course \(\gamma _0+c\) represents a single parameter (intercept).
We estimate parameters c, \(\gamma =(\gamma _0,\gamma _1, \dots , \gamma _N)^T\), and
of (6) exploiting a (rather complicated) nonlinear optimization of a certain (selected) loss function. To simplify the notation, we further denote
In the rest of the paper, we require that the derivatives of f and g exist. Under such (rather common) assumption, these derivatives will be denoted as \(f'\) and \(g'\), respectively. Although it is common in regression tasks to choose g in (6) as an identity function, which simplifies the computational efforts, we retain the general notation g here. Independently on the choice of the loss function we will use the notation \(u_i = Y_i - \hat{Y}_i\) for residuals of the multilayer perceptron for \(i=1,\dots ,n\).
3.2 Derivatives of Fitted Values
As a preparatory result for further computations, we now derive independently on the choice of the loss function
and
where \(i=1,\dots ,n,\) \(a=1,\dots ,N,\) and \(b=1,\dots ,p.\)
These partial derivatives of (6) were derived by a repeatedly used chain rule for computing derivatives of a composite function. They are expressed as functions, i.e. depending on their parameters c, \(\gamma \), and \(\omega \). Of course, computations with real data (e.g. within the neural network training) require to use estimated versions of these derivatives, which can be easily obtained by replacing c, \(\gamma \), and \(\omega \) by their estimates. We would like to point out that such estimates are always available within the backpropagation algorithm, because its user is required to specify initial estimates of these parameters. These partial derivatives appear in derivatives of the loss function, which will be now expressed for three different versions of the loss function, namely for the standard one based on least squares and for two robust alternatives.
3.3 Multilayer Perceptron with a Standard Loss
The most commonly used loss for multilayer perceptrons will be denoted as
which is known as the mean square error (MSE), corresponding to the least squares estimator in a location model. To estimate all parameters of (6), the common optimization criterion has the form
which is commonly solved by backpropagation. To derive the explicit expressions for partial derivatives, which are formulated below as a lemma, we will exploit the facts that e.g. it holds for \(a=1,\dots ,N\) that
Lemma 1
Under the notation of Sect. 3.1, it holds that
-
(a)
$$\begin{aligned} \frac{\partial \xi _1}{\partial c} (c, \gamma , \omega )= - \frac{2}{n}{} \sum _{i=1}^n u_i, \end{aligned}$$(17)
-
(b)
$$\begin{aligned} \frac{\partial \xi _1}{\partial \gamma _0} (c, \gamma , \omega ) = - \frac{2}{n} \sum _{i=1}^n u_i g'(\tau _i), \end{aligned}$$(18)
-
(c)
$$\begin{aligned} \frac{\partial \xi _1}{\partial \gamma _a} (c, \gamma , \omega ) = - \frac{2}{n} \sum _{i=1}^n u_i g'(\tau _i)f\, \left( \sum _{j=1}^p \omega _{aj} X_{ij} + \omega _{a0} \right) , \end{aligned}$$(19)
where \(a=1,\dots ,N,\)
-
(d)
$$\begin{aligned} \frac{\partial \xi _1}{\partial \omega _{a0}} (c, \gamma , \omega ) = - \frac{2}{n} \sum _{i=1}^n u_i \gamma _a g'(\tau _i) f' \, \left( \sum _{j=1}^p \omega _{aj}X_{ij}+\omega _{a0} \right) , \end{aligned}$$(20)
where \(a=1,\dots ,N,\)
-
(e)
$$\begin{aligned} \frac{\partial \xi _1}{\partial \omega _{ab}} (c, \gamma , \omega )= - \frac{2}{n} \sum _{i=1}^n u_i \gamma _a X_{ib} g'(\tau _i) f' \, \left( \sum _{j=1}^p \omega _{aj}X_{ij}+\omega _{a0} \right) , \end{aligned}$$(21)
where \(a=1,\dots ,N\) and \(b=1,\dots ,p\).
It is rather surprising that we are not aware of the results of Lemma 1 being available anywhere in the literature. The formulas do not appear in standard textbooks (e.g. [6]), and texts on this topic available on the internet usually contain serious mistakes. Concerning the computations of the derivatives, Lemma 1 formulates them as depending on c, \(\gamma \) and \(\omega \), while the derivatives for numerical data can be estimated by using estimates of c, \(\gamma \) and \(\omega \), respectively.
3.4 LTS-loss in Linear Regression
The loss function of the LTS estimator in (1) is defined as
To express its derivatives, we may recall the following result given on p. 7 of [19] stating that
almost everywhere, where \(u_i(\beta )=Y_i - X_i^T\beta \) for each i are residuals and \(\mathbbm {1}\) denotes an indicator function. The expression (23) contains \(p+1\) particular derivatives for individual elements of \(\beta \). In (23), the i-th squared residual is compared with the h-th largest squared residual. To conclude, the LTS estimator \(b_{LTS}\) in (1) can be computed (using now our notation) as the solution of the set of equations
where b is the \({p+1}\)-dimensional variable.
3.5 Multilayer Perceptron with an LTS-loss
An MLP with the loss function corresponding to the LTS estimator was considered already in [17], where however the derivatives of the loss function are in our opinion incorrect. The same formulas were repeated in [18]. However, we must be much more careful in deriving the derivatives, which turn out to be have more complex formulas. Let us first consider the loss
where h is a specified constant fulfilling \(n/2 \le h < n\). The loss corresponds to the LTS estimator and thus we introduce the notation LTS-MLP for the (robust) multilayer perceptron with parameters estimated by the criterion
The derivatives of \(\xi _2\) will be derived in an analogous way to the approach of Sect. 3.4.
Lemma 2
We use the notation of Sect. 3.1. To avoid confusion, let us denote the residuals of the LTS-MLP as \(\tilde{u}=\tilde{u}_i(c,\gamma ,\omega )\) for \(i=1,\dots ,n\), to stress that they are functions of \(c, \gamma \) and \(\omega \). Let us further denote \(\tilde{u}_{(1)}^2 \le \cdots \le \tilde{u}_{(n)}^2\). It holds that
-
(a)
$$\begin{aligned} \frac{\partial \xi _2}{\partial c} (c, \gamma , \omega )= - \frac{2}{h} \sum _{i=1}^n \tilde{u}_i \mathbbm {1}[\tilde{u}_i^2 \le \tilde{u}^2_{(h)}], \end{aligned}$$(27)
-
(b)
$$\begin{aligned} \frac{\partial \xi _2}{\partial \gamma _0} (c, \gamma , \omega ) = - \frac{2}{h} \sum _{i=1}^n \tilde{u}_i \mathbbm {1}[\tilde{u}_i^2 \le \tilde{u}^2_{(h)}] g'(\tau _i), \end{aligned}$$(28)
-
(c)
$$\begin{aligned} \frac{\partial \xi _2}{\partial \gamma _a} (c, \gamma , \omega ) = - \frac{2}{h} \sum _{i=1}^n \tilde{u}_i \mathbbm {1}[\tilde{u}_i^2 \le \tilde{u}^2_{(h)})] g'(\tau _i) f\, \left( \sum _{j=1}^p \omega _{aj} X_{ij} + \omega _{a0} \right) , \end{aligned}$$(29)
where \(a=1,\dots ,N,\)
-
(d)
$$\begin{aligned} \frac{\partial \xi _2}{\partial \omega _{a0}} (c, \gamma , \omega )= - \frac{2}{h} \sum _{i=1}^n \tilde{u}_i \mathbbm {1}[\tilde{u}_i^2 \le \tilde{u}^2_{(h)}] \gamma _a g'(\tau _i) f' \left( \sum _{j=1}^p \omega _{aj}X_{ij}+\omega _{a0} \right) , \end{aligned}$$(30)
where \(a=1,\dots ,N,\)
-
(e)
$$\begin{aligned} \frac{\partial \xi _2}{\partial \omega _{ab}} (c, \gamma , \omega ) = - \frac{2}{h} \sum _{i=1}^n \tilde{u}_i \mathbbm {1}[\tilde{u}_i^2 \le \tilde{u}^2_{(h)}] \gamma _a X_{ib} g'(\tau _i) f' \left( \sum _{j=1}^p \omega _{aj} X_{ij}+\omega _{a0} \right) , \end{aligned}$$(31)
where \(a=1,\dots ,N\) and \(b=1,\dots ,p.\)
3.6 LWS-Loss in Linear Regression
Let us now consider the model (1) with the loss corresponding to an LWS estimator. The loss
exploits a specified weight function \(\psi \). Equivalently, we may express
where the weights are generated by \(\psi \) under a natural requirement \(\sum _{i=1}^n w_i=1\). The LWS estimator is defined by
The set of derivatives of the loss function in (1) has the form
where \(\hat{F}^{(n)}\) denotes the empirical distribution function

a detailed proof was given on p. 183 of [20]. The special case for (4) again considers \(X_i \equiv 1\) for each i. Let us consider the empirical distribution function

The LWS estimator \(b_{LWS}\) in (1) can be obtained as the solution of
which is a set of normal equations with the variable  . Here, \(|u_i(b)|\) for each i plays the role of the threshold r from (37).
. Here, \(|u_i(b)|\) for each i plays the role of the threshold r from (37).
3.7 Multilayer Perceptron with An-LWS Loss
We introduce the notation LWS-MLP for the (robust) multilayer perceptron based on the robust loss function corresponding to the LWS estimator. Let us consider the loss
formulated using a specified weight function \(\psi \). The loss can be equivalently expressed as
if the weights are generated by \(\psi \) and again fulfil \(\sum _{i=1}^n w_i=1\). The loss corresponds to an LWS estimator and therefore we introduce the notation LWS-MLP for the (robust) multilayer perceptron with parameters given by
Our deriving the derivatives of \(\xi _3\) is analogous to the reasoning of Sect. 3.6.
Lemma 3
We use the notation of Sect. 3.1. Residuals of the multilayer perceptron will be denoted as \(\tilde{u}_i = \tilde{u}_i(c,\gamma ,\omega )\) and the corresponding empirical distribution function as

It holds that
-
(a)
$$\begin{aligned} \frac{\partial \xi _3}{\partial c} (c, \gamma , \omega ) = - 2 \sum _{i=1}^n \tilde{u}_i \psi \left( \hat{F}^{(n)}(|\tilde{u}_i|) \right) , \end{aligned}$$(43)
-
(b)
$$\begin{aligned} \frac{\partial \xi _3}{\partial \gamma _0} (c, \gamma , \omega ) = -2\sum _{i=1}^n \tilde{u}_i \psi \left( \hat{F}^{(n)}(|\tilde{u}_i|)\right) g'(\tau _i), \end{aligned}$$(44)
-
(c)
$$\begin{aligned} \frac{\partial \xi _3}{\partial \gamma _a} (c, \gamma , \omega ) = - 2 \sum _{i=1}^n \tilde{u}_i \psi \left( \hat{F}^{(n)}(|\tilde{u}_i|)\right) g'(\tau _i) f\left( \sum _{j=1}^p \omega _{aj} X_{ij} + \omega _{a0} \right) , \end{aligned}$$(45)
where \(a=1,\dots ,N,\)
-
(d)
$$\begin{aligned} \frac{\partial \xi _3}{\partial \omega _{a0}} (c, \gamma , \omega ) = - 2 \sum _{i=1}^n \tilde{u}_i \gamma _a \psi \left( \hat{F}^{(n)}(|\tilde{u}_i|)\right) g'(\tau _i) f' \left( \sum _{j=1}^p \omega _{aj} X_{ij}+\omega _{a0} \right) , \end{aligned}$$(46)
where \(a=1,\dots ,N,\)
-
(e)
$$\begin{aligned} \frac{\partial \xi _3}{\partial \omega _{ab}} (c, \gamma , \omega ) = - 2 \sum _{i=1}^n \tilde{u}_i \gamma _a X_{ib} \psi \left( \hat{F}^{(n)}(|\tilde{u}_i|)\right) g'(\tau _i) f' \left( \sum _{j=1}^p \omega _{aj} X_{ij}+\omega _{a0} \right) , \end{aligned}$$(47)
where \(a=1,\dots ,N, \quad b=1,\dots ,p.\)
3.8 Applications
Several datasets were analyzed by the presented robust neural networks (LTS-MLP and LWS-MLP) in [12]. In all datasets, which are contaminated by outliers, a robust mean square error was better (i.e. smaller) for all the robust MLPs than that of a plain MLP. This is true especially for simple artificial data and also the Boston housing dataset [5] and the Auto MPG dataset [5]. For the Boston housing dataset, some real estates in the very center of Boston are outlying, as they are small but extremely overpriced compared to those in the suburbs of the city. For the Auto MPG, we found those cars to be outlying for the model, which have a high weight and a high consumption. Other outliers can be identified as cars with a low weight, as there appears only a small percentage of them; such findings are in accordance with those of [14].
4 Conclusions
Standard training of neural networks, including their most common types, is vulnerable to the presence of outliers in the data and thus it is important to consider robustified versions instead. Due to a lack of reliable approaches, robustness in neural networks with respect to outliers remains a perspective topic in machine learning with a high potential to provide interesting applications in the analysis of contaminated data. In this paper, we focus on robust versions of multilayer perceptrons, i.e. alternative training techniques for the most common type of artificial neural networks. We propose an original robust multilayer perceptron based on the LWS loss.
We derive here derivatives of the loss functions based on the LTS and LWS estimates for a particular (rather simple) architecture of a multilayer perceptron. Our presenting this compact overview of derivatives needed for any available gradient-based optimization technique is motivated by an apparent mistake in the derivatives for a similar (although different) robust multilayer perceptron based on the LTA estimator in [18]. The main motivation for our deriving the derivatives is however their usefulness within the backpropagation algorithm, allowing to compute the robust neural networks. This paper does not however investigate any convergence issues of the proposed robust multilayer perceptron; to the best of our knowledge, convergence is not available for any other type of versions of neural networks, which are proposed as robust to the presence of outliers in the data. Implementing the LTS-MLP and LWS-MLP using the presented results is straightforward. Derivatives for more complex multilayer perceptrons, i.e. for networks with a larger number of hidden layers, can be obtained in an analogous way only with additional using the chain rule for computing derivatives.
While the presented results represent a theoretical foundation for our future research, there seems at the same time a gap of systematic comparisons of various different robust versions of neural networks over both real and simulated data. Such comparisons are intended to be a topic for our future work, because a statistical interpretation of the results of robust neural networks remains crucial.
References
Aladag, C.H., Egrioglu, E., Yolcu, U.: Robust multilayer neural network based on median neuron model. Neural Comput. Appl. 24, 945–956 (2014)
Beliakov, G., Kelarev, A., Yearwood, J.: Derivative-free optimization and neural networks for robust regression. Optimization 61, 1467–1490 (2012)
Cisse, M., Bojanowski, P., Grave, E., Dauphin, Y., Usunier, N.: Parseval networks: improving robustness to adversarial examples. In: Proceedings of the 34th International Conference on Machine Learning ICML 2017, pp. 854–863 (2017)
D’Urso, P., Leski, J.M.: Fuzzy \(c\)-ordered medoids clustering for interval-valued data. Pattern Recogn. 58, 49–67 (2016)
Frank, A., Asuncion, A.: UCI Machine Learning Repository. University of California, Irvine (2010). http://archive.ics.uci.edu/ml/
Haykin, S.O.: Neural Networks and Learning Machines: A Comprehensive Foundation, 2nd edn. Prentice Hall, Upper Saddle River (2009)
Henderson, D.J., Parmeter, C.F.: Applied Nonparametric Econometrics. Cambridge University Press, New York (2015)
Jurečková, J., Picek, J., Schindler, M.: Robust Statistical Methods with R, 2nd edn. Chapman & Hall/CRC, Boca Raton (2019)
Kalina, J.: A robust pre-processing of BeadChip microarray images. Biocybern. Biomed. Eng. 38, 556–563 (2018)
Kalina, J., Schlenker, A.: A robust supervised variable selection for noisy high-dimensional data. BioMed Res. Int. 2015, 1–10 (2015). Article no. 320385
Kalina, J., Vidnerová, P.: Robust training of radial basis function neural networks. In: Proceedings 18th International Conference ICAISC 2019. Lecture Notes in Computer Science, vol. 11508, pp. 113–124 (2019)
Kalina, J., Vidnerová, P.: On robust training of regression neural networks. In: Proceedings 5th International Workshop on Functional and Operatorial Statistics IWFOS (2020, accepted)
Kordos, M., Rusiecki, A.: Reducing noise impact on MLP training-techniques and algorithms to provide noise-robustness in MLP network training. Soft. Comput. 20, 46–65 (2016)
Paulheim, H., Meusel, R.: A decomposition of the outlier detection problem into a set of supervised learning problems. Mach. Learn. 100, 509–531 (2015)
Racine, J., Su, L., Ullah, A.: The Oxford Handbook of Applied Nonparametric and Semiparametric Econometrics and Statistics. Oxford University Press, Oxford (2014)
Rousseeuw, P.J., Van Driessen, K.: Computing LTS regression for large data sets. Data Min. Knowl. Disc. 12, 29–45 (2006)
Rusiecki, A.: Robust learning algorithm based on LTA estimator. Neurocomputing 120, 624–632 (2013)
Rusiecki, A., Kordos, M., Kamiński, T., Greń, K.: Training neural networks on noisy data. Lect. Notes Artif. Intell. 8467, 131–142 (2014)
Víšek, J.Á.: The least trimmed squares. Part I: consistency. Kybernetika 42, 1–36 (2006)
Víšek, J.Á.: Consistency of the least weighted squares under heteroscedasticity. Kybernetika 47, 179–206 (2011)
Acknowledgments
The authors would like to thank David Coufal and Jiří Tumpach for discussion.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 The Editor(s) (if applicable) and The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Kalina, J., Vidnerová, P. (2020). Robust Multilayer Perceptrons: Robust Loss Functions and Their Derivatives. In: Iliadis, L., Angelov, P., Jayne, C., Pimenidis, E. (eds) Proceedings of the 21st EANN (Engineering Applications of Neural Networks) 2020 Conference. EANN 2020. Proceedings of the International Neural Networks Society, vol 2. Springer, Cham. https://doi.org/10.1007/978-3-030-48791-1_43
Download citation
DOI: https://doi.org/10.1007/978-3-030-48791-1_43
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-48790-4
Online ISBN: 978-3-030-48791-1
eBook Packages: Computer ScienceComputer Science (R0)