Abstract
To overcome the practical limitations of partial-order runs of ‘distributed ASMs’ (Abstract State Machines) proposed by Gurevich, we have defined a concept of concurrent runs of multi-agent ASMs and could show that concurrent ASMs capture a natural language-independent axiomatic definition of concurrent algorithms, thus generalising Gurevich’s seminal ‘Sequential ASM Thesis’ from sequential to concurrent algorithms. However, we remained intrigued by the fact that Blass and Gurevich used partial-order runs of distributed ASMs to explain runs of sequential recursive algorithms. We discovered that also the inverse simulation holds: for every distributed ASM with partial order runs, these runs can be described by runs of a sequential recursive algorithm. This surprising result clarifies the difference in expressivity between partial-order and concurrent runs.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
In [8, Sect. 2–3] the concept of sequential Abstract State Machines (seq-ASMs) has been defined for which the ‘Sequential ASM Thesis’ [7]—to capture the intuitive notion of sequential algorithm—could be proved from three natural postulates, see [9]. In [8, Sect. 6] the concept of sequential ASM runs is extended by partial-order runs of a specific class of multi-agent ASMs called distributed ASMs. However, contrary to the great variety of successful applications of sequential ASMs, the use of distributed ASMs with partial-order runs turned out to be impractical to adequately model concurrent systems. It has been replaced in [4] by a language-independent axiomatic characterization of concurrent runs, adding a fourth postulate (on the intuitive meaning of concurrency), together with a definition of concurrent ASMs, based upon which the Sequential ASM Thesis and its proof could be generalized to a Concurrent ASM Thesis—to capture the proposed intuitive notion of concurrent algorithms.
In reaction to some scepticism expressed in [13], whether recursive algorithms can be adequately defined by ASMs, partial-order runs of distributed ASMs have been used in [1] to simulate the computations of recursive algorithms.Footnote 1 For a long time we have been intrigued by this proposal, since on the one side, a simple sequential extension of ASMs suffices for the specification of recursive algorithms (see for example [2]), on the other side partial-order runs of distributed ASMs turned out to be impractical for modeling truly concurrent systems (see [4]).
In Sect. 3 we review Gurevich’s description of distributed ASMs with partial-order runs and analyse the proof that the runs of recursive algorithms can be defined as partial-order runs of distributed ASMs. The analysis reveals that the distributed ASMs used to define recursive runs by partial-order runs are finitely composed concurrent ASMs with non-deterministic sequential (nd-seq) components (see the definition in Sect. 3). In Sect. 4 we show the surprising discovery that also the inverse relation holds, namely: for every finitely composed concurrent algorithm with nd-seq components, if its concurrent runs are definable by partial-order runs, then the algorithm can be simulated by a recursive algorithm. This establishes the main result of this paper.
Theorem 1.1
(Main Theorem). Recursive algorithms are behaviourally equivalent to finitely composed concurrent algorithms \(\mathcal {C}\) with nd-seq components such that all concurrent \(\mathcal {C}\)-runs are definable by partial-order runs.Footnote 2
The equivalence of runs of recursive ASMs and of partial-order runs of distributed ASMs makes it explicit in which sense concurrent ASM runs as characterized in [4] are more expressive than the ‘partial-order runs of distributed ASMs’ proposed in [8, Sect. 6].
We will also show that if the concurrent runs are restricted further to partial-order runs of a concurrent algorithm with a fixed finite number of agents and fixed non-deterministic sequential (nd-seq) programs, one can simulate them even by a non-deterministic sequential algorithm. An interesting example of this special case are partial-order runs of Petri nets and more generally of Mayr’s Process Rewrite Systems [12].
For the proofs we use an axiomatic characterization of recursive algorithms as sequential algorithms enriched by call steps,Footnote 3 such that the parent-child relationship between caller and callee defines well-defined shared locations representing input and return parameters. This characterization is reviewed in Sect. 2 and is taken from [5] where it appears as Recursion Postulate and is added to Gurevich’s three postulates for sequential ASMs [9] as basis for the proof of an ASM thesis for recursive ASMs.
We assume the knowledge of [8, 9] and [4] and use without further explanations standard textbook notations for ASMs, including ambient ASMs [3, Ch. 4.1].
2 The Recursion Postulate
We start with a characteristic example to illustrate the intuitive idea of recursion which guided the formulation of the recursion postulate below.Footnote 4 Take the mergesort algorithm, which consists of a main algorithm sort and an auxiliary algorithm merge. Every call to (a copy, we also say an instance of) sort and every call to (an instance of) the merge algorithm could give rise to a new agent. However, these agents only interact by passing input parameters and return values, but otherwise operate on disjoint sets of locations. In addition, a calling agent always waits to receive return values, which implies that only one or (in case of parallel calls) a finite number of agents are active in any state.
If one considers mutual recursion, then this becomes slightly more general, as there is a finite family of algorithms calling (instances of) each other. Furthermore, there may be several simultaneous calls. E.g. in mergesort, sort calls two copies of itself, each sorting one half of the list of given elements. Such simultaneously called copies may run sequentially in one order or the other, in parallel or even asynchronously. This give rise to non-deterministic execution of multiple sequential algorithms.
Therefore, for a characterization of recursive algorithms and their computations we can rely on the capture of non-deterministic sequential algorithms by non-deterministic sequential ASMs.Footnote 5 Thus, to axiomatically define recursive algorithms and their runs it suffices to add to the three postulates for nd-seq algorithms a Call Step Postulate and a Recursive Run Postulate defined below, which together form the Recursion Postulate.
To characterize the input/output relation between the input provided by the caller in a call step and the output computed by the callee for this input we use the ASM function classification from [6] to distinguish between input, output and local (also called controlled) function symbols in the signature, the union of pairwise disjoint sets \(\varSigma _{in}\), \(\varSigma _{out}\) and \(\varSigma _{loc}\) respectively. We call any nd-seq algorithm which comes with such a signature and also satisfies the Call Step Postulate below an algorithm with input and output (for short: i/o-algorithm). We can then define (sequential) recursive algorithms syntactically as collections of i/o-algorithms.
Definition 2.1
A recursive algorithm \(\mathcal {R}\) is a finite set of i/o-algorithms with one distinguished main algorithm. The elements of \(\mathcal {R}\) are called components of\(\mathcal {R}\).
The independency condition for (possibly parallel) computations of different instances of the given algorithms requires that for different calls, in particular for different calls of the same algorithm, the state spaces of the triggered subcomputations are separated from each other. This encapsulation of subcomputations can be made precise by the concept of ambient algorithms where each instance of an algorithm has a unique context parameter for its functions, e.g. its executing agent (see [3, Ch. 4.1]), and is started in an initial state that only depends on its input locations.Footnote 6
Now we are ready to formulate the postulate for call steps. In Sect. 3.4 we formalize this postulate by an ASM  (see Definition 3.4 and its refinement in Sect. 4).
(see Definition 3.4 and its refinement in Sect. 4).
Postulate 1
(Call Step Postulate). When an i/o-algorithm p—the caller, viewed as parent algorithm—calls a finite number of i/o-algorithms \(c_1,\ldots ,c_n\)—the callees, viewed as child algorithms CalledBy(p)—a call relationship (denoted as CalledBy(p)) holds between the caller and each callee. The caller activates a fresh instance of each callee \(c_i\) so that they can start their computations. These computations are independent of each other and the caller remains waiting—i.e. performs no step—until every callee has terminated its computation (read: has reached a final state). For each callee, the initial state of its computation is determined only by the input passed by the caller; the only other interaction of the callee with the caller is to return in its final state an output to p.
Definition 2.2
A call relationship holds for (instances of) two i/o-algorithms \(\mathcal {A}^p\) (parent) and \(\mathcal {A}^c\) (child) if and only if they satisfy the following conditions on their function classification:
-
\({\blacksquare }\) \(\varSigma ^{\mathcal {A}^c}_{in} \subseteq \varSigma ^{\mathcal {A}^p}\) so that the parent algorithm is able to update input locations of the child algorithm. Furthermore, \(\mathcal {A}^p\) never reads the input locations of \(\mathcal {A}^c\).
-
\({\blacksquare }\) \(\varSigma ^{\mathcal {A}^c}_{out} \subseteq \varSigma ^{\mathcal {A}^p}\) so that the parent algorithm can read the output locations of the child algorithm. Furthermore, \(\mathcal {A}^p\) never updates output locations of \(\mathcal {A}^c\).
-
\({\blacksquare }\) \(\varSigma ^{\mathcal {A}^c}_{loc} \cap \varSigma ^{\mathcal {A}^p} = \emptyset \) (no other common locations).
Differently from runs of a nd-seq algorithm, where in each state at most one step of the nd-seq algorithm is performed, in a recursive run a sequential recursive algorithm \(\mathcal {R}\) can perform in one step simultaneously one step of each of finitely many not terminated and not waiting called instances of its i/o-algorithms. This is expressed by the Recursive Run Postulate. In this postulate we refer to Active and not Waiting instances of components, which are defined as follows:
Definition 2.3
To be Active resp. Waiting in a state S is defined as follows:

Called collects the instances of algorithms that are called during the run. The subset of Called which contains all the children called by p is denoted by CalledBy(p). \(Called=\{main\}\) and \(CalledBy(p)=\emptyset \) are true in the initial state \(S_0\), for each i/o-algorithm \(p \in \mathcal {R}\). In particular, in \(S_0\) the original component main is considered to not be CalledBy(p), for any p.
Postulate 2
(Recursive Run Postulate). For a sequential recursive algorithm \(\mathcal {R}\) with main component main a recursive run is a sequence \(S_0,S_1,S_2, \ldots \) of statesFootnote 7 together with a sequence \(C_0,C_1,C_2, \ldots \) of sets of instances of components of \(\mathcal {R}\) which satisfy the following constraints:
-
Recursive run constraint
-
\({\blacksquare }\) \(C_0\) is the singleton set \(C_0=\{main\}\), i.e. every run starts with main,
-
\({\blacksquare }\) every \(C_i\) is a finite set of instances of components of \(\mathcal {R}\) which are Active and not Waiting in state \(S_i\),
-
\({\blacksquare }\) every \(S_{i+1}\) is obtained in one \(\mathcal {R}\)-step by performing in \(S_i\) simultaneously one step of each i/o-algorithm in \(C_i\). Such an \(\mathcal {R}\)-step is also called a recursive step of \(\mathcal {R}\).
-
-
Bounded call tree branching. There is a fixed natural number \(m>0\), depending only on \(\mathcal {R}\), which in every \(\mathcal {R}\)-run bounds the number of callees which can be called by a call step.
Remark
(on Call Trees). If in a recursive \(\mathcal {R}\)-run the main algorithm calls some i/o-algorithms, this call creates a finitely branched call tree whose nodes are labeled by the instances of the i/o-algorithms involved, with active and not waiting algorithms labeling the leaves and with the main (the parent) algorithm labeling the root of the tree and becoming waiting. When the algorithm at a leaf makes a call, this extends the tree correspondingly. When the algorithm at a child of a node has terminated its computation, we delete the child from the tree. The leaves of this (dynamic) call tree are labeled by the active not waiting algorithms in the run. When the main algorithm terminates, the call tree is reduced again to the root labeled by the initially called main algorithm.
Usually, it is expected that for recursive \(\mathcal {R}\)-runs each called i/o-algorithm reaches a final state, but in general it is not excluded that this is not the case.
In [5] the reader can find a definition of recursive ASMs together with a proof that they capture (are equivalent to) recursive algorithms as characterized by the Recursion Postulate. Here we use the postulate as a basis for the proof that recursive algorithms are captured by ‘distributed ASMs with partial-order runs’, as defined in [8].
3 Recursive ASMs Are Distributed ASMs with Partial-Order Runs
Syntactically, a multi-agent (also called concurrent) algorithm \(\mathcal {C}\) is defined as a family of algorithms alg(a), each associated with (‘indexed by’) an agent \(a \in Agent\) that executes the algorithm in a run. Each (a, alg(a)) resp. alg(a) is called a component resp. (component) program of \(\mathcal {C}\). This applies to distributed ASMs [8] as well as to recursive or concurrent algorithms and ASMs [4, 5].
To investigate the simulation of recursive runs by partial-order runs of distributed ASMs (Sect. 3.4) we must explain what are finitely composed concurrent (Gurevich’s ‘distributed’) algorithms (Sect. 3.1) and partial-order resp. concurrent runs (Sect. 3.2 resp. 3.3).
3.1 Finitely Composed Concurrent Algorithms
For recursive algorithms various restrictions on the syntactical definition of multi-agent algorithms have to be made most of which appear also for distributed ASMs in [8, Sect. 6].
First of all, although the components alg(a) of concurrent algorithms are not necessarily sequential algorithms, to simulate specific concurrent algorithms by recursive ones, which are defined as families of nd-seq algorithms, we must restrict our attention to concurrent algorithms with sequential (though possibly non-deterministic) components.Footnote 8
Second, for distributed ASMs it is stipulated in [8, p. 31] that the agents are equipped with instances of programs which are taken from ‘a finite indexed set of single-agent programs’. This leads to what we call finitely composed concurrent algorithms or ASMs \(\mathcal {C}\) where the components can only be copies (read: instances) of finitely many different nd-seq algorithms or ASMs, which we will call the program base of \(\mathcal {C}\).
Third, for distributed ASMs it is stipulated in [8, 6.2, p. 31] that in initial states there are only finitely many agents, each equipped with a program. We reflect this by the (simplifying but equivalent) condition that the runs of a finitely composed concurrent algorithm or ASM must be started by executing a distinguished main component.
Fourth, for distributed ASMs it is stipulated in [8, p. 32] that ‘An agent a can make a move at S by firing Prog(a) ... and change S accordingly. As part of the move, a may create new agents’, which then may contribute by their moves to the run in which they were created. For this purpose we use the \(\mathrel {\mathbf {new}}\) function.
We summarize these constraints for distributed ASMs by the notion of finitely composed concurrent algorithms (read: concurrent ASMs).
Definition 3.1
A concurrent algorithm \(\mathcal {C}\) is finitely composed iff (i)–(iii) hold:
-
(i)
There exists a finite set \(\mathcal {B}\) of nd-seq algorithms such that each \(\mathcal {C}\)-program is of form \(\mathbf{amb} \; a \;\mathbf{in} \; r\) for some program \(r \in \mathcal {B}\)—call \(\mathcal {B}\) the program base of\(\mathcal {C}\).
-
(ii)
There exists a distinguished agent \(a_0\) which is the only one Active in any initial state. Formally this means that in every initial state of a \(\mathcal {C}\)-run, \(Agent=\{a_0\}\) holds. We denote by main the component in \(\mathcal {B}\) of which \(a_0\) executes an instance. For partial-order runs of \(\mathcal {C}\) defined below this implies that they start with a minimal move which consists in executing the program
 .
. -
(iii)
Each program in \(\mathcal {B}\) may contain rules of form
 . Together with (ii) this implies that every agent, except the distinguished \(a_0\), before making a move in a run must have been created in the run.
. Together with (ii) this implies that every agent, except the distinguished \(a_0\), before making a move in a run must have been created in the run.
\(\mathcal {C}\) is called finite iff Agent is finite.
3.2 Partial-Order Runs
In [8] Gurevich defined (for distributed algorithms) the notion of partial-order run by a partial order on the set of single moves of the agents which execute the component algorithms. For a nd-seq algorithm \(\mathcal {A}\), to make one move means to perform one step in a state S.
Definition 3.2
Let \(\mathcal {C} = \{ (a, \text {alg}(a)) \}_{a \in Agent}\) be a concurrent algorithm, in which each \(\text {alg}(a)\) is an nd-seq algorithm. A partial-order run for \(\mathcal {C}\) is defined by a set M of moves of instances of the algorithms \(\text {alg}(a)\) (\(a \in Agent\)), a function \(\text {ag}: M \rightarrow Agent\) assigning to each move the agent performing the move, a partial order \(\le \) on M, and an initial segment function \(\sigma \) such that the following conditions are satisfied:
-
finite history. For each move \(m \in M\) its history \(\{ m^\prime \mid m^\prime \le m \}\) is finite.
-
sequentiality of agents. The moves of each agent are ordered, i.e. for any two moves m and \(m^\prime \) of one agent \(\text {ag}(m) = \text {ag}(m^\prime )\) we either have \(m \le m^\prime \) or \(m^\prime \le m\).
-
coherence. For each finite initial segment \(M^\prime \subseteq M\) (i.e. such that for \(m \in M^\prime \) and \(m^\prime \le m\) we also have \(m^\prime \in M^\prime \)) there exists a state \(\sigma (M^\prime )\) over the combined signatures of the algorithms \((a, \text {alg}(a)) \) such that for each maximum element \(m \in M^\prime \) the state \(\sigma (M^\prime )\) is the result of applying m to \(\sigma (M^\prime - \{ m \})\).
3.3 Concurrent Runs
In a concurrent run as defined in [4], multiple agents with different clocks may contribute by their single moves to define the successor state of a state. Therefore, when a successor state \(S_{i+1}\) of a state \(S_i\) is obtained by applying to \(S_i\) multiple update sets \(U_a\) with agents a in a finite set \(Agent_i \subseteq Agent\), each \(U_a\) is required to have been computed by \(a \in Agent_i \) in a preceding state \(S_j\), i.e. with \(j \le i\). It is possible that \(j<i\) holds so that for different agents different \(\text {alg}(a)\)-execution speeds (and purely local subruns to compute \(U_a\)) can be taken into account.
This can be considered as resulting from a separation of a step of an nd-seq algorithm \(\text {alg}(a)\) into a read step—which reads location values in a state \(S_j\)—followed by a write step which applies the update set \(U_a\) computed on the basis of the values read in \(S_j\) to a later state \(S_i\) (\(i \ge j\)). We say that a contributes to updating the state \(S_i\) to its successor state \(S_{i+1}\), and that a move starts in \(S_j\) and contributes to updating \(S_i\) (i.e. it finishes in \(S_{i+1}\)). This is formally expressed by the following definition of concurrent ASMs and their runs.
Definition 3.3
Let \(\mathcal {C}\) be a concurrent algorithm of component algorithms pgm(a) (read: ASM rules) with associated agents \(a \in Agent\). A concurrent run of \(\mathcal {C}\) is defined as a sequence \(S_0, S_1, \dots \) of states together with a sequence \(A_0, A_1, \dots \) of finite subsets of Agent, such that \(S_0\) is an initial state and each \(S_{i+1}\) is obtained from \(S_i\) by applying to it the updates computed by the agents in \(A_i\), where each \(a \in A_i\) computes its update set \(U_a\) on the basis of the location values (including the input and shared locations) read in some preceding state \(S_j\) (i.e. with \(j \le i\)) depending on a.
Remark
In this definition we deliberately permit the set of Agents to be infinite or dynamic and potentially infinite, growing or shrinking in a run. In Definition 3.2 above, the set of Agents is fixed by the set M of moves.
3.4 Simulation of Recursive by Partial-Order Runs
We are now ready to specify recursive algorithms by distributed ASMs, following the thought proposed in [1]. For the sake of precision and simplicity we formulate the construction in terms of ASMs; due to the characterization theorems in [5] and [4] this implies no loss of generality.
Theorem 3.1
Every recursive ASM \(\mathcal {R}\) can be simulated by a finitely composed concurrent ASM \(\mathcal {C}_{\mathcal {R}}\) with nd-seq ASM components for which every concurrent run of \(\mathcal {C}_{\mathcal {R}}\) is definable by a partial-order run.
Proof
Let \(\mathcal {R}\) be a recursive ASM given with distinguished program main. We define a finitely composed concurrent ASM \(\mathcal {C}_{\mathcal {R}}\) with program base \(\{r^* \mid r \in \mathcal {R}\}\), where \(r^*\) is defined as

In doing so, for each call rule \(r=t_0 \leftarrow N(t_1,\dots ,t_n)\) in \(\mathcal {R}\) we use for its translation the following ASM  , which rigorously defines the behavioral interpretation of the call rule r (for details see [5]):
, which rigorously defines the behavioral interpretation of the call rule r (for details see [5]):
Definition 3.4

Note that the call is a call-by-value and that \((f,(v_1^\prime ,\ldots , v_k^\prime ))\) denotes the output location whose value the caller expects to be updated by the callee with the return value.
By definition, \(r^*\) can only contribute a non-empty update set to form a state \(S_{i+1}\) in a concurrent run, if r is Active and not Waiting; this reflects that by the recursive run postulate, in every step of a recursive run of \(\mathcal {R}\) only Active and not Waiting rules are executed.
The definition of \(r^*\) obviously guarantees that \(\mathcal {C}_{\mathcal {R}}\) simulates \(\mathcal {R}\) step by step: in each run step the same Active and not Waiting rules r respectively \(r^*\) and their agents are selected for their simultaneous execution and their rules perform the same state change.
Note that by Definition 3.4 of  (i/o-rule), each agent operates in its own state space so that the view of an agent’s step as read-step followed by a write-step is equivalent to the atomic view of this step. Note also that in a concurrent run of \(\mathcal {C}_{\mathcal {R}}\) the Agent set is dynamic, in fact it grows with each execution of a call rule, together with the number of instances of \(\mathcal {R}\)-components executed during a recursive run of \(\mathcal {R}\).
(i/o-rule), each agent operates in its own state space so that the view of an agent’s step as read-step followed by a write-step is equivalent to the atomic view of this step. Note also that in a concurrent run of \(\mathcal {C}_{\mathcal {R}}\) the Agent set is dynamic, in fact it grows with each execution of a call rule, together with the number of instances of \(\mathcal {R}\)-components executed during a recursive run of \(\mathcal {R}\).
It remains to define every concurrent run \((S_0,A_0),(S_1,A_1),\ldots \) of \(\mathcal {C}_{\mathcal {R}}\) by a partial-order run. For this we define an order on the set M of moves made during a concurrent run, showing that it satisfies the constraints on finite history and the sequentiality of agents, and then relate each state \(S_i\) of the run to the state computed by the set \(M_i\) of moves performed to compute \(S_i\) (from \(S_0\)), showing that \(M_i\) is a finite initial segment of M and that the associated state \(\sigma (M_i)\) equals \(S_i\) and satisfies the coherence condition.
Each successor state \(S_{i+1}\) in a concurrent run of \(\mathcal {C}_{\mathcal {R}}\) is the result of applying to \(S_i\) the write steps of finitely many moves of agents in \(A_i\). This defines the function ag, which associates agents with moves, and the finite set \(M_i\) of all moves finished in a state belonging to the initial run segment \([S_0,\ldots ,S_i]\). Let \(M=\cup _i M_i\). The partial order \(\le \) on M is defined by \(m < m^\prime \) iff move m contributes to update some state \(S_i\) (read: finishes in \(S_i\)) and move \(m^\prime \) starts reading in a later state \(S_j\) with \(i+1 \le j\). Thus, by definition, \(M_i\) is an initial segment of M.
To prove the finite history condition, consider any \(m^\prime \in M\) and let \(S_j\) be the state in which it is started. There are only finitely many earlier states \(S_0 ,\dots , S_{j-1}\), and in each of them only finitely many moves m can be finished, contributing to update \(S_{j-1}\) or an earlier state.
The condition on the sequentiality of the agents follows directly from the definition of the order relation \(\le \) and from the fact that in a concurrent run, for every move \(m=(read_m,write_m)\) executed by an agent, this agent performs no other move between the \(read_m\)-step and the corresponding \(write_m\)-step in the run.
This leaves us to define the function \(\sigma \) for finite initial segments \(M^\prime \subseteq M\) and to show the coherence property. We define \(\sigma (M^\prime )\) as result of the application of the moves in \(M^\prime \) in any total order extending the partial order \(\le \). For the initial state \(S_0\) we have \(\sigma (\emptyset )=S_0\). This implies the definability claim \(S_i=\sigma (M_i)\).
The definition of \(\sigma \) is consistent for the following reason. Whenever two moves \(m \not = m^\prime \) are incomparable, then either they both start in the same state or say m starts earlier than \(m^\prime \). But \(m^\prime \) also starts earlier than m finishes. This is only possible for agents \(ag(m) = a\) and \(ag(m^\prime ) = a^\prime \) whose programs \(pgm(a),pgm(a^\prime )\) are not in an ancestor relationship in the call tree. Therefore these programs have disjoint signatures, so that the moves m and \(m^\prime \) could be applied in any order with the same resulting state change.
To prove the coherence property let \(M^\prime \) be a finite initial segment, and let \(M^{\prime \prime } = M^\prime {\setminus } M^\prime _{\text {max}}\), where \(M^\prime _{\text {max}}\) is the set of all maximal elements of \(M^\prime \). Then \(\sigma (M^\prime )\) is the result of applying simultaneously all moves \(m \in M^\prime _{\text {max}}\) to \(\sigma (M^{\prime \prime })\), and the order in which the maximum moves are applied is irrelevant. This implies in particular the desired coherence property. \(\square \)
The key argument in the proof exploits the Recursion Postulate whereby for recursive runs of \(\mathcal {R}\), the runs of different agents are initiated by calls and concern different state spaces with pairwise disjoint signatures, due to the function parameterization by agents, unless \(pgm(a^\prime )\) is a child (or a descendant) of pgm(a), in which case the relationship between the signatures is defined by the call relationship. Independent moves can be guaranteed in full generality only for algorithms with disjoint signatures.
4 Distributed ASMs with Partial-Order Runs Are Recursive ASMs
While Theorem 3.1 is not surprising, we will now show its less obvious inverse.
Theorem 4.1
For each finitely composed concurrent ASM \(\mathcal {C}\) with program base \( \{ r_i \mid i \in I \}\) of nd-seq ASMs such that all its concurrent runs are definable by partial-order runs, one can construct a recursive ASM \(\mathcal {R}_\mathcal {C}\) such that each concurrent run of \(\mathcal {C}\) can be simulated by a recursive run of \(\mathcal {R}_\mathcal {C}\).Footnote 9
Proof
Let a concurrent \(\mathcal {C}\)-run \((S_0,A_0),(S_1,A_1),\ldots \) be given. If it is definable by a partial-order run \((M,\le ,ag,pgm,\sigma )\), the transition from \(S_i = \sigma (M_i)\) to \(S_{i+1}\) is performed in one concurrent step by parallel independent moves \(m \in M_{i+1} {\setminus } M_i\), where \(M_i\) is the set of moves which contributed to transform \(S_0\) into \(S_i\). Let \(m \in M_{i+1} {\setminus } M_i\) be a move performed by an agent \(a=ag(m)\) with rule  , an instance of a rule r in the program base of \(\mathcal {C}\). To execute the concurrent step by means of steps of a recursive ASM \(\mathcal {R}_\mathcal {C}\), we simulate each of its moves m by letting agent a act in the \(\mathcal {R}_\mathcal {C}\)-run as caller of a named rule
, an instance of a rule r in the program base of \(\mathcal {C}\). To execute the concurrent step by means of steps of a recursive ASM \(\mathcal {R}_\mathcal {C}\), we simulate each of its moves m by letting agent a act in the \(\mathcal {R}_\mathcal {C}\)-run as caller of a named rule  . The callee agent c acts as delegate for one step of a: it executes
. The callee agent c acts as delegate for one step of a: it executes  and makes its program immediately Terminated.
and makes its program immediately Terminated.
To achieve this, we refine the  machine defined in Definition 3.4 such that upon calling
machine defined in Definition 3.4 such that upon calling  , the delegate c created by the call becomes Active so that it can make a step to execute
, the delegate c created by the call becomes Active so that it can make a step to execute  . It suffices to add to the component
. It suffices to add to the component  the update
the update  , which makes c Active.
, which makes c Active.  is defined to perform
is defined to perform  and to terminate immediately (by setting Terminated to true). For ease of exposition we add to Definition 3.4 also the update \(caller(c):=\mathrel {\mathbf {self}}\), to distinguish agents in the concurrent run—the callers of
and to terminate immediately (by setting Terminated to true). For ease of exposition we add to Definition 3.4 also the update \(caller(c):=\mathrel {\mathbf {self}}\), to distinguish agents in the concurrent run—the callers of  -machines—from the delegates each of which simulates one step of its caller and immediately terminates its life cycle.
-machines—from the delegates each of which simulates one step of its caller and immediately terminates its life cycle.
It remains to determine the input and output for calling  . For the input we exploit the existence of a bounded exploration witness \(W_r\) for r. All updates produced in a single step are determined by the values of \(W_r\) in the state, in which the call is launched. So \(W_r\) defines the input terms of the called rule
. For the input we exploit the existence of a bounded exploration witness \(W_r\) for r. All updates produced in a single step are determined by the values of \(W_r\) in the state, in which the call is launched. So \(W_r\) defines the input terms of the called rule  , combined in \(in_r\). Analogously, a single step of r provides updates to finitely many locations that are determined by terms appearing in the rule, which defines \(out_r\).
, combined in \(in_r\). Analogously, a single step of r provides updates to finitely many locations that are determined by terms appearing in the rule, which defines \(out_r\).
We summarize the explanations by the following definition:

Note that by the refined Definition 3.4,  triggers the execution of the delegate program
triggers the execution of the delegate program  . Let \(a=caller(c)\). By definition,
. Let \(a=caller(c)\). By definition,  triggers
triggers  . Furthermore, since the innermost ambient binding counts, this machine is equivalent to the simulated machine
. Furthermore, since the innermost ambient binding counts, this machine is equivalent to the simulated machine  , as was to be shown.
, as was to be shown.
Thus the recursive \(\mathcal {R}_\mathcal {C}\)-run which simulates \((S_0,A_0),(S_1,A_1),\ldots \) starts by Definition 3.1 in \(S_0\) with program  . For the sake of notational simplicity we disregard the auxiliary locations of \(\mathcal {R}_\mathcal {C}\). Let
. For the sake of notational simplicity we disregard the auxiliary locations of \(\mathcal {R}_\mathcal {C}\). Let

We use the same agents \(a_{i_j}\) for \(A_i\) in the \(\mathcal {R}_\mathcal {C}\)-run, but with program  . Their step in the recursive run leads to a state \(S_i' \) where all callers \(a_{i_j}\) are Waiting and the newly created delegates \(c_{i_j}\) are Active and not Waiting. So we can choose them for the set \(A_i'\) of agents which perform the next \(\mathcal {R}_\mathcal {C}\) step, whereby
. Their step in the recursive run leads to a state \(S_i' \) where all callers \(a_{i_j}\) are Waiting and the newly created delegates \(c_{i_j}\) are Active and not Waiting. So we can choose them for the set \(A_i'\) of agents which perform the next \(\mathcal {R}_\mathcal {C}\) step, whereby
- \({\blacksquare }\):
-
all rules \(r_{i_j}\) are performed simultaneously (as in the given concurrent run step), in the ambient of \(caller(c_{i_j})=a_{i_j}\) thus leading as desired to the state \(S_{i+1}\),
- \({\blacksquare }\):
-
the delegates make their program Terminated, whereby their callers \(a_{i_j}\) become again not Waiting and thereby ready to take part in the next step of the concurrent run. We assume for this that whenever in the \(\mathcal {C}\)-run (not in the \(\mathcal {R}_\mathcal {C}\) run) a new agent a is created, it is made not Waiting (by initializing \(CalledBy(a):=\emptyset \)).
\(\square \)
Remark
Consider an \(\mathcal {R}_\mathcal {C}\)-run where each recursive step of the concurrent caller agents in \(A_i\), which call each some  program, alternates with a recursive step of all—the just called—delegates whose program is not yet Terminated. Then this run is equivalent to a corresponding concurrent \(\mathcal {C}\)-run.
program, alternates with a recursive step of all—the just called—delegates whose program is not yet Terminated. Then this run is equivalent to a corresponding concurrent \(\mathcal {C}\)-run.
Note that Theorem 4.1 heavily depends on the prerequisite that \(\mathcal {C}\) only has partial-order runs.Footnote 10 With general concurrent runs as defined in [4] the construction would not be possible.
4.1 Partial Order Runs of Petri Nets
The semantics of Petri nets actually defines a rather special case of partial-order runs, namely runs one can describe even by a nd-seq ASM, as we show in this section.
A Petri net comes with a finite number of transition rules, each of which can be described by a nd-seq ASM (see [6, p. 297]). The special character of the computational Petri net model is due to the fact that during the runs, only exactly these rules are used. In other words there is a fixed association of each rule with an executing agent; there is no rule instantiation with new agents which could be created during a run. Therefore the states are the global markings of the net. The functions \(\sigma (I)\) associated with the po-runs of the net yield for every finite initial segment I as value the global marking obtained by firing the rules in I.
For this particular kind of concurrent ASMs with partial-order runs one can define the concurrent runs by nd-seq ASMs, as we are going to show in this section.
Theorem 4.2
For each finite concurrent ASM \(\mathcal {C} = \{ (a_i,r_i) \mid 1 \le i \le n \}\) with nd-seq ASMs \(r_i\) such that all its concurrent runs are definable by partial-order runs one can construct a nd-seq ASM \(\mathcal {M}_\mathcal {C}\) such that the concurrent runs of \(\mathcal {C}\) and the runs of \(\mathcal {M}_\mathcal {C}\) are equivalent.
Corollary 4.1
Partial-order Petri net runs can be simulated by runs of a non-deterministic sequential ASM.Footnote 11
Proof
We relate the states \(S_i\) of a given concurrent run of \(\mathcal {C} \) to the states \(\sigma (M_i)\) associated with initial segments \(M_i\) of a given corresponding partial order run \((M,\le ,ag,pgm,\sigma )\), where each step leading from \(S_i\) to \(S_{i+1}\) consists of pairwise incomparable moves in \(M_{i+1} {\setminus } M_i\). We call such a sequence \(S_0, S_1, \dots \) of states a linearised run of \(\mathcal {C}\). For \(i>0\) the initial segments \(M_i\) are non empty.
The linearized runs of \(\mathcal {C}\) can be characterized as runs of a nd-seq ASM \(\mathcal {M}_{\mathcal {C}}\): in each step this machine chooses one of finitely many non-empty subsets of rules in \(\mathcal {C}\) to execute them in parallel. Formally:

To complete the proof it suffices to show the following lemma. \(\square \)
Lemma 4.1
The linearised runs of \(\mathcal {C}\) are exactly the runs of \(\mathcal {M}_{\mathcal {C}}\).
Proof
To show that each run \(S_0, S_1, \dots \) of \(\mathcal {M}_{\mathcal {C}}\) is a linearised run of \(\mathcal {C}\) we proceed by induction to construct the partial-order run \((M,\le )\) with its finite initial segments \(M_i\). For the initial state \(S_0=\sigma (\emptyset )\) there is nothing to show, so let \(S_{i+1}\) result from \(S_i\) by applying an update set produced by  for some non-empty \(J \subseteq I\). By induction we have \(S_i = \sigma (M_i)\) for some initial segment of a partial-order run \((M,\le )\). As
for some non-empty \(J \subseteq I\). By induction we have \(S_i = \sigma (M_i)\) for some initial segment of a partial-order run \((M,\le )\). As  is a parallel composition, \(S_{i+1}\) results from applying the union of update sets \(\varDelta _{i_j} \in \varDelta _{r_{i_j}}\) for \(j = 1,\dots , |J|\) to \(S_i\). Each \(\varDelta _{i_j}\) defines a move \(m_{i_j}\) of some \(\text {ag}(m_{i_j}) = a_{i_j}\), move which finishes in state \(S_i\). We now have two cases:
is a parallel composition, \(S_{i+1}\) results from applying the union of update sets \(\varDelta _{i_j} \in \varDelta _{r_{i_j}}\) for \(j = 1,\dots , |J|\) to \(S_i\). Each \(\varDelta _{i_j}\) defines a move \(m_{i_j}\) of some \(\text {ag}(m_{i_j}) = a_{i_j}\), move which finishes in state \(S_i\). We now have two cases:
-
(i)
The moves \(m_{i_j}\) with \(j \in J\) are pairwise independent, i.e. their application in any order produces the same new state. Then \((M,\le )\) can be extended with these moves such that \(M_{i+1} = M_i \cup \{ m_{i_j} \mid j \in J \}\) becomes an initial segment and \(S_{i+1} = \sigma (M_i)\) holds.
-
(ii)
If the moves \(m_{i_j}\) with \(j \in J\) are not pairwise independent, the union of the corresponding update sets is inconsistent, hence the run terminates in state \(S_i\).
To show the converse we proceed analogously. If we have \(S_i = \sigma (M_i)\) for all \(i \ge 1\), then \(S_{i+1}\) results from \(S_i\) by applying in parallel all moves in \(M_{i+1} - M_i\). Applying a move m means to apply an update set produced by some rule \(r_j \in \mathcal {C}\) (namely the rule pgm(ag(m))) in state \(S_i\), and applying several update sets in parallel means to apply their union \(\varDelta \), which then must be consistent. So we have \(S_{i+1} = S_i + \varDelta \) with \(\varDelta = \bigcup _{j \in J} \varDelta _{i_j}\) for some J, where each \(\varDelta _{i_j}\) is an update set produced by \(r_{i_j}\), i.e. \(\varDelta \) is an update set produced by  , which implies that the linearised run \(S_0, S_1, \dots \) is a run of \(\mathcal {M}_{\mathcal {C}}\). \(\square \)
, which implies that the linearised run \(S_0, S_1, \dots \) is a run of \(\mathcal {M}_{\mathcal {C}}\). \(\square \)
For the corollary it suffices to note that each Petri net transition can be described by a nd-seq ASM (see [6, p. 297]). The functions \(\sigma (I)\) associated with the po-runs yield the global marking obtained by firing the rules in I.
5 Conclusions
While Gurevich’s Sequential ASM Thesis [9] provides an elegant and satisfactory mathematical definition of the notion of sequential algorithm plus a proof that sequential algorithms are captured by sequential ASMs, this theory does not capture recursive algorithms. It lacks an appropriate call concept. In fact, in an attempt to solve this problem Blass and Gurevich in [1] invoked the notion of partial-order runs of ‘distributed ASMs’, which has been proposed in [8] as a concurrency concept for ASMs. We showed in this paper that these ‘distributed ASMs’ are finitely composed ASMs whose partial-order runs characterize (are equivalent to) recursive runs. Thus, partial-order runs of distributed ASMs do not capture the concept of concurrent algorithms (but see [4]).
Notes
- 1.
Already the definition of recursive ASMs in [10] uses a special case of this translation of recursive into distributed computations.
- 2.
We call \(\mathcal {R}\) behaviourally equivalent to \(\mathcal {C}\) if each \(r \in \mathcal {R}\) can be simulated by a \(c \in \mathcal {C}\) and vice versa.
- 3.
To emphasize the sequential nature of recursive algorithms we sometimes use the term ‘sequential recursive algorithm’. See [5] for the technical reason for this naming policy.
- 4.
For a detailed analysis see [5].
- 5.
The proof for the Sequential ASM Thesis is easily extended from deterministic to non-deterministic algorithms, see [9, Sect. 9.2].
- 6.
More precisely, one can define an instance of an algorithm \(\mathcal {A}\) by adding a parameter a, say for an agent executing the instance \(\mathcal {A}_a=(a,\mathcal {A})\) of \(\mathcal {A}\). a can be used as environment parameter for the evaluation \(val_S(t,a)\) of a term t in state S with the given environment. This yields for different agents \(a,a^\prime \) different functions \(f_a,f_{a^\prime }\) as interpretation of the same function symbol f, so that the run-time interpretations of a common signature element f can be made to differ for different agents, due to different inputs which determine their initial states.
- 7.
For the sake of simplicity we take a state as union of the states of the component instances in the run, in other words as state over the union of the individual signatures.
- 8.
In fact it is shown in [5] that permitting the unbounded \(\mathrel {\mathbf {forall}}\) and \(\mathrel {\mathbf {choose}}\) constructs results in algorithms far more powerful than the recursive ones.
- 9.
One obtains even the behavioral equivalence via an inverse simulation of every recursive \(\mathcal {R}_\mathcal {C}\)-run by a concurrent \(\mathcal {C}\)-run if the delegates of \(\mathcal {C}\)-agents, called in the recursive run to perform the step of their caller in the concurrent run, act in an ‘eager’ way. See the remark at the end of the proof.
- 10.
The other prerequisites in Theorem 4.1 appear to be rather natural. Unbounded runs can only result, if in a single step arbitrarily many new agents are created. Also, infinitely many different rules associated with the agents are only possible, if new agents are created and added during a concurrent run. Though this is captured in the general theory of concurrency in [4], it was not intended in Gurevich’s definition of partial-order runs.
- 11.
References
Blass, A., Gurevich, Y.: Algorithms vs. machines. Bull. EATCS 77, 96–119 (2002)
Börger, E., Bolognesi, T.: Remarks on turbo ASMs for functional equations and recursion schemes. In: Börger, E., Gargantini, A., Riccobene, E. (eds.) ASM 2003. LNCS, vol. 2589, pp. 218–228. Springer, Heidelberg (2003). https://doi.org/10.1007/3-540-36498-6_12
Börger, E., Raschke, A.: Modeling Companion for Software Practitioners. Springer, Heidelberg (2018). https://doi.org/10.1007/978-3-662-56641-1
Börger, E., Schewe, K.-D.: Concurrent abstract state machines. Acta Inform. 53(5), 469–492 (2016). https://doi.org/10.1007/s00236-015-0249-7
Börger, E., Schewe, K.-D.: A behavioural theory of recursive algorithms (2020). http://arxiv.org/abs/2001.01862
Börger, E., Stärk, R.F.: Abstract State Machines: A Method for High-Level System Design and Analysis. Springer, Heidelberg (2003). https://doi.org/10.1007/978-3-642-18216-7
Gurevich, Y.: A new thesis. In: Abstracts, vol. 6, no. 4, p. 317. American Mathematical Society (1985)
Gurevich, Y.: Evolving algebras 1993: lipari guide. In: Börger, E. (ed.) Specification and Validation Methods, pp. 9–36. Oxford University Press (1995)
Gurevich, Y.: Sequential abstract-state machines capture sequential algorithms. ACM Trans. Comput. Logic 1(1), 77–111 (2000)
Gurevich, Y., Spielmann, M.: Recursive abstract state machines. J. UCS 3(4), 233–246 (1997)
Heike, C., Zimmermann, W., Both, A.: On expanding protocol conformance checking to exception handling. SOCA 8(4), 299–322 (2013). https://doi.org/10.1007/s11761-013-0146-2
Mayr, R.: Process rewrite systems. Inf. Comput. 156, 264–286 (1999)
Moschovakis, Y.N.: What is an algorithm? In: Engquist, B., Schmid, W. (eds.) Mathematics Unlimited - 2001 and Beyond, pp. 919–936. Springer, Heidelberg (2001). https://doi.org/10.1007/978-3-642-56478-9_46
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Börger, E., Schewe, KD. (2020). A Characterization of Distributed ASMs with Partial-Order Runs. In: Raschke, A., Méry, D., Houdek, F. (eds) Rigorous State-Based Methods. ABZ 2020. Lecture Notes in Computer Science(), vol 12071. Springer, Cham. https://doi.org/10.1007/978-3-030-48077-6_6
Download citation
DOI: https://doi.org/10.1007/978-3-030-48077-6_6
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-48076-9
Online ISBN: 978-3-030-48077-6
eBook Packages: Computer ScienceComputer Science (R0)


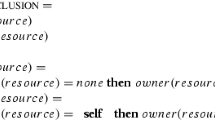


 .
. . Together with (ii) this implies that every agent, except the distinguished
. Together with (ii) this implies that every agent, except the distinguished