Abstract
PIE is a Prolog-embedded environment for automated reasoning on the basis of first-order logic. Its main focus is on formulas, as constituents of complex formalizations that are structured through formula macros, and as outputs of reasoning tasks such as second-order quantifier elimination and Craig interpolation. It supports a workflow based on documents that intersperse macro definitions, invocations of reasoners, and
 -formatted natural language text. Starting from various examples, the paper discusses features and application possibilities of PIE along with current limitations and issues for future research.
-formatted natural language text. Starting from various examples, the paper discusses features and application possibilities of PIE along with current limitations and issues for future research.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
First-order logic is used widely and in many roles in philosophy, mathematics, and artificial intelligence as well as other branches of computer science. Many practically successful reasoning approaches can be viewed as derived from reasoning in first-order logic, for example, SAT solving, logic programming, database query processing and reasoning in description logics. The overall aim of the PIE environment is to support the practical mechanized reasoning in first-order logic. Approaching this aim consequently leads from first-order theorem proving in the strict sense to tasks that compute first-order formulas, in particular second-order quantifier elimination and Craig interpolation, whose integrated support characterizes PIE. The system is written and embedded in SWI-Prolog [58] and provides, essentially as a library of Prolog predicates, a number of functionalities:
-
Support for a Prolog-readable syntax of first-order logic formulas.
-
Formula pretty-printing in Prolog syntax and in
 .
. -
A versatile formula macro processor.
-
Support for processing documents that intersperse formula macro definitions, reasoner invocations and
 -formatted natural language text.
-formatted natural language text. -
Interfaces to external first-order and propositional reasoners.
-
A built-in Prolog-based first-order theorem prover.
-
Implemented reasoning techniques that compute formulas:
-
Second-order quantifier elimination on the basis of first-order logic.
-
Computation of first-order Craig interpolants.
-
Formula conversions for use in preprocessing, inprocessing and output presentation.
-
The system is available as free software from its homepage
http://cs.christophwernhard.com/pie.
The distribution includes several example documents whose source files as well as rendered
 presentations can also be accessed directly from the system Web page. Inspecting Gödel’s Ontological Proof is there an advanced application, where the interplay of elimination and modal axioms is applied in several contexts. The system was first presented at the 2016 workshop Practical Aspects of Automated Reasoning [55]. Here we show various application possibilities, features and also issues for further research that become apparent with the system by starting from a number of examples. The paper is itself written as a PIE document and thus includes fragments generated by PIE and the included or integrated reasoners.
presentations can also be accessed directly from the system Web page. Inspecting Gödel’s Ontological Proof is there an advanced application, where the interplay of elimination and modal axioms is applied in several contexts. The system was first presented at the 2016 workshop Practical Aspects of Automated Reasoning [55]. Here we show various application possibilities, features and also issues for further research that become apparent with the system by starting from a number of examples. The paper is itself written as a PIE document and thus includes fragments generated by PIE and the included or integrated reasoners.
The rest of this paper is structured as follows: After introducing in Sect. 2 the document-oriented workflow supported by PIE, we show in Sect. 3 how it applies to the invocation of second-order quantifier elimination in the system. Section 4 provides an application example of elimination, a certain form of abduction, which is shown together with basic features of the PIE macro system. We proceed in Sect. 5 to outline how systems for theorem proving in the strict sense are embedded into PIE. In Sect. 6 the computation of circumscription is discussed as another example of second-order quantifier elimination with PIE, along with further features of the macro system and the general issue of finding good presentations of computed formulas that are essentially just characterized semantically. Section 7 sketches a further application of second-order quantifier elimination: a potential way of logic programming with second-order formulas as used for theoretical considerations in descriptive complexity. Further features of PIE are summarized in Sect. 9, and Sect. 10 concludes the paper.
Related work is discussed in the respective contexts. The bibliography is somewhat extensive, reflecting that the system relates to methods as well as implementation and application aspects in a number of areas, including first-order theorem proving, Craig interpolation, second-order quantifier elimination and knowledge representation.
2 PIE Documents
The main way to interact with PIE is by developing or modifying a PIE document, a file that intersperses definitions of formula macros, specifications of reasoning tasks, and
 -formatted natural language text in the fashion of literate programming [28]. Such a document can be loaded into the Prolog environment like a source code file. Reasoner invocations, where the defined macros are available, can then be submitted as inputs on the Prolog console. The document can also be processed, which results in a generated
-formatted natural language text in the fashion of literate programming [28]. Such a document can be loaded into the Prolog environment like a source code file. Reasoner invocations, where the defined macros are available, can then be submitted as inputs on the Prolog console. The document can also be processed, which results in a generated
 document: Macro definitions are pretty-printed in
document: Macro definitions are pretty-printed in
 , specified reasoner invocations are executed and a pretty-printed
, specified reasoner invocations are executed and a pretty-printed
 result presentation is inserted, and
result presentation is inserted, and
 fragments are inserted directly. The generated
fragments are inserted directly. The generated
 document can then be displayed in PDF format.
document can then be displayed in PDF format.
Aside of indentation, the
 pretty-printer can apply certain symbol conversions to subscripted or primed symbols. Also a compact syntax where parentheses to separate arguments from functors and commas between arguments are omitted is available as an option for both Prolog and
pretty-printer can apply certain symbol conversions to subscripted or primed symbols. Also a compact syntax where parentheses to separate arguments from functors and commas between arguments are omitted is available as an option for both Prolog and
 forms.
forms.
PIE source documents can be re-loaded into the Prolog environment such that mechanized formalizations can be developed in a workflow similar to programming in AI languages like Prolog and Lisp.
First-order reasoners are often heavily dependent on configuration settings. A PIE document specifies all information needed to reproduce the results of reasoner invocations in a convenient way. Effective configuration parameters are combined from system defaults, defaults declared in the document and options supplied with particular specifications of reasoner invocations.
3 Second-Order Quantifier Elimination in PIE
Second-order quantifier elimination is the task of computing for a given formula with second-order quantifiers, that is, quantifiers upon predicate or function symbols, an equivalent first-order formula. PIE so far just supports second-order quantification upon predicate symbols, or predicate quantification. Here is an example of PIE ’s
 representation of the invocation of a reasoner that performs second-order quantifier elimination:
representation of the invocation of a reasoner that performs second-order quantifier elimination:
Input: \(\exists p \, (\forall x \, (\mathsf {q}( x ) \rightarrow p ( x )) \wedge \forall x \, ( p ( x ) \rightarrow \mathsf {r}( x ))).\)
Result of elimination:
The source code in the PIE document that effects this output is:

The directive
 effects that its argument is evaluated at “print time”, that is, at processing, when the
effects that its argument is evaluated at “print time”, that is, at processing, when the
 presentation is generated.Footnote 1 The argument is an invocation of the elimination reasoner with the predicate
presentation is generated.Footnote 1 The argument is an invocation of the elimination reasoner with the predicate
 . It has a formula as argument, possibly with predicate quantifiers. If called at “print time” it prints inputs and outputs formatted in
. It has a formula as argument, possibly with predicate quantifiers. If called at “print time” it prints inputs and outputs formatted in
 , as shown above for the example. It can also be invoked in the context of plain Prolog processing, where it just effects that the output is pretty printed in Prolog syntax. The following interaction would, for example, be possible in the Prolog console:
, as shown above for the example. It can also be invoked in the context of plain Prolog processing, where it just effects that the output is pretty printed in Prolog syntax. The following interaction would, for example, be possible in the Prolog console:

Printing the output is performed there as a side effect. SWI-Prolog afterwards prints
 to indicate that the invocation of
to indicate that the invocation of
 was successful. To access the output formula from a program, PIE provides two alternate means: With an option list
was successful. To access the output formula from a program, PIE provides two alternate means: With an option list
 as second argument,
as second argument,
 does not effect that the elimination result is printed, but instead bound to the Prolog variable
does not effect that the elimination result is printed, but instead bound to the Prolog variable
 for further processing. The second way to access the result formula of the last reasoner invocation is with the supplied predicate
for further processing. The second way to access the result formula of the last reasoner invocation is with the supplied predicate
 . This predicate may itself be used in macro definitions.
. This predicate may itself be used in macro definitions.
Let us take a brief look at the syntax of the argument formula of
 in the example. It represents a second-order formula as a Prolog ground term. Conjunction is represented as in Prolog by
in the example. It represents a second-order formula as a Prolog ground term. Conjunction is represented as in Prolog by
 and implication by
and implication by
 , with standard operator settings from Prolog. The universal first-order quantifier is expressed by
, with standard operator settings from Prolog. The universal first-order quantifier is expressed by
 and the existential second-order quantifier by
and the existential second-order quantifier by
 .
.
PIE performs second-order quantifier elimination by an included Prolog implementation of the DLS algorithm [14], a method based on formula rewriting until second-order subformulas have a certain shape that allows elimination in one step by rewriting with Ackermann’s lemma, an equivalence due to [1]. Implementing DLS brings about many subtle and interesting issues [10, 23, 54], for example, incorporation of non-deterministic alternative courses, dealing with un-Skolemization, simplification of formulas in non-clausal form and ensuring success of the method for certain input classes. The current implementation in PIE is far from optimum solutions of these issues, but can nevertheless be used in nontrivial applications and might contribute to improvements by making experiments possible.
Of course, second-order quantifier elimination on the basis of first-order logic does not succeed in general. Nevertheless, along with variants termed forgetting, uniform interpolation or projection, it has many applications, including deciding fragments of first-order logic [3, 36], computation of frame correspondence properties from modal axioms [14, 19, 43], computation of circumscription [14], embedding nonmonotonic semantics in a classical setting [50, 51], abduction with respect to classical and to nonmonotonic semantics [15, 32, 52], forgetting in knowledge bases [13, 29, 33, 34, 49], and approaches to modularization of knowledge bases derived from the notion of conservative extension [21, 22, 35]. Further applications of second-order quantifier elimination are described in the monograph [20].
For second-order quantifier elimination and similar operations there are several implementations based on modal and description logics, but very few on first-order logic: A Web serviceFootnote 2 invokes an implementation [17] of the SCAN algorithm [19]. DLSForgetter [2] is a recent system that implements the DLS algorithm [14]. An earlier implementation [23] of DLS seems to be no longer available.
4 Abduction with Second-Order Quantifier Elimination – Basic Use of PIE Macros
In the simplest case, a PIE formula macro serves as a formula label that may be used in subformula position in other formulas and is expanded into its definiens. Here is an example of such a PIE macro definition in the
 presentation:
presentation:

The corresponding source is:

The source statement has the form
 , where
, where
 is an infix operator with lower precedence than the operators used as connectives for logical formulas. Formula \( kb _1\) is now defined as a small knowledge base that expresses a variant of a scenario often used to illustrate abduction. Actually, we use it now to show how a certain form of computing abductive explanations can be considered as second-order quantifier elimination. It is based on the notion of weakest sufficient condition [15, 32, 51], which is basically a second-order formula that expresses the weakest formula in a given vocabulary that needs to be conjoined to given axioms to make a given theorem candidate an actual theorem. This second-order formula as such is not very informative as it contains the axioms and the theorem as constituents, with disallowed symbols bound by quantifiers and possibly renamed but still present. However, the result of applying elimination to that second-order formula provides the weakest sufficient condition in the proper sense, or, considered with respect to abduction, the weakest explanation.
is an infix operator with lower precedence than the operators used as connectives for logical formulas. Formula \( kb _1\) is now defined as a small knowledge base that expresses a variant of a scenario often used to illustrate abduction. Actually, we use it now to show how a certain form of computing abductive explanations can be considered as second-order quantifier elimination. It is based on the notion of weakest sufficient condition [15, 32, 51], which is basically a second-order formula that expresses the weakest formula in a given vocabulary that needs to be conjoined to given axioms to make a given theorem candidate an actual theorem. This second-order formula as such is not very informative as it contains the axioms and the theorem as constituents, with disallowed symbols bound by quantifiers and possibly renamed but still present. However, the result of applying elimination to that second-order formula provides the weakest sufficient condition in the proper sense, or, considered with respect to abduction, the weakest explanation.
PIE allows to specify macros with parameters that are represented by Prolog variables. We utilize this to specify schematically the weakest explanation (or weakest sufficient condition) of observation Obs on the complement of Na as assumables (Na should suggest n on-assumables) within knowledge base Kb:

The corresponding source code is:

 represents the universal second-order quantifier in PIE ’s input formula syntax. The first argument of
represents the universal second-order quantifier in PIE ’s input formula syntax. The first argument of
 specifies the quantified predicates, either as a single Prolog atom or as list of atoms. In the example, there is the macro parameter \(\begin{array}{l} Na \end{array} \) that needs to be instantiated correspondingly when the macro is expanded. The expression \(\begin{array}{l} explanation ( kb_{1} ,{[}\mathsf {wet}{]},\mathsf {wet}(\mathsf {shoes})) \end{array} \) expands into the following “non-informative” version of the weakest sufficient condition:
specifies the quantified predicates, either as a single Prolog atom or as list of atoms. In the example, there is the macro parameter \(\begin{array}{l} Na \end{array} \) that needs to be instantiated correspondingly when the macro is expanded. The expression \(\begin{array}{l} explanation ( kb_{1} ,{[}\mathsf {wet}{]},\mathsf {wet}(\mathsf {shoes})) \end{array} \) expands into the following “non-informative” version of the weakest sufficient condition:

Second-order quantifier elimination applied to this formula yields the proper weakest explanation for the observation
 in which the predicate
in which the predicate
 itself does not occur, with respect to the background knowledge base \( kb _1\):
itself does not occur, with respect to the background knowledge base \( kb _1\):
Input: \( explanation ( kb_{1} ,{[}\mathsf {wet}{]},\mathsf {wet}(\mathsf {shoes})).\)
Result of elimination:
It was obtained by the following directive in the source document:

In [52] this approach to abduction has been generalized to non-monotonic semantics of logic programming, including the three-valued partial stable models semantics.
5 Invoking Theorem Provers from PIE
The abductive explanation computed in the previous section can be validated with a theorem prover. The presentation of the prover invocation and the result is in PIE as follows:
This formula is valid: \( kb_{1} \wedge (\mathsf {rained\_last\_night} \vee \mathsf {sprinkler\_was\_on}) \rightarrow \mathsf {wet}(\mathsf {shoes}).\)
The corresponding source directive is

The semicolon
 represents disjunction, as in Prolog. The reasoner invocation predicate
represents disjunction, as in Prolog. The reasoner invocation predicate
 by default first calls the model searcher Mace4 with a short timeout, and, if it can not find a “counter”-model of the negated formula, calls the prover Prover9, again with a short timeout.Footnote 3 Correspondingly,
by default first calls the model searcher Mace4 with a short timeout, and, if it can not find a “counter”-model of the negated formula, calls the prover Prover9, again with a short timeout.Footnote 3 Correspondingly,
 prints a representation of one of three result values: valid, not valid or failed to validate and in
prints a representation of one of three result values: valid, not valid or failed to validate and in
 “print time” mode also the input formula, as shown above.
“print time” mode also the input formula, as shown above.
Like
 , also
, also
 can be called with a list of options as second argument. This allows to obtain Prolog term representations of Prover9’s resolution proof or Mace4’s model, to skip the call to Mace4, modify the configuration of Mace4 and Prover9, or to specify another theorem prover to be called.
can be called with a list of options as second argument. This allows to obtain Prolog term representations of Prover9’s resolution proof or Mace4’s model, to skip the call to Mace4, modify the configuration of Mace4 and Prover9, or to specify another theorem prover to be called.
Other provers can be incorporated through a generic interface to the TPTP [47] syntax for proving problems, supported by most current first-order provers. In addition, DIMACS and QDIMACS, the common formats of SAT and QBF solvers, respectively, are supported by PIE. Large propositional formulas are handled there efficiently with an internal representation implemented with destructive term operations. Most of the support of propositional formulas is inherited from the precursor system ToyElim [53].
PIE also includes a Prolog-based first-order prover, CM, whose calculus can be understood as model elimination, clausal tableau construction [31], or the connection method [6], similar to provers of the leanCoP family [26, 27, 40]. Its implementation follows the compilation-based Prolog Technology Theorem Prover (PTTP) paradigm [46]. It computes proofs that are represented by Prolog terms and can be used to compute Craig interpolants (Sect. 8). Details and evaluation results are available at http://cs.christophwernhard.com/pie/cmprover.
6 Computing Circumscription as Second-Order Quantifier Elimination – PIE Macros with Prolog Bodies, Result Simplifications
The circumscription of a predicate P in a formula F is a formula whose models are the models I of F that are minimal with respect to P. That is, there is no model \(I'\) of F that is like I except that the extension of P in \(I'\) is a strict subset of the extension of P in I. Predicate circumscription can be expressed by a second-order schema such that the computation of circumscription is second-order quantifier elimination [14]. The second-order circumscription of predicate P in formula F can thus be defined as a PIE macro as follows:

This definition utilizes that PIE macro definitions may contain a Prolog body that permits expansions involving arbitrary computations. Utility predicates with pretty-printing templates for use in these bodies are provided for common tasks. The source of the above definition reads:

The Prolog body is introduced with the
 operator, which is defined with a precedence between
operator, which is defined with a precedence between
 and the operators used to represent logical formulas. The unary operator
and the operators used to represent logical formulas. The unary operator
 represents negation in formulas.Footnote 4 The suffix
represents negation in formulas.Footnote 4 The suffix
 used for some variable names is translated to the prime superscript in the
used for some variable names is translated to the prime superscript in the
 , rendering. We only indicate here the effects of the auxiliary predicates in the Prolog body with an example: The formula \(\begin{array}{l} circ (\mathsf {p},\mathsf {p}(\mathsf {a})) \end{array} \) expands into:
, rendering. We only indicate here the effects of the auxiliary predicates in the Prolog body with an example: The formula \(\begin{array}{l} circ (\mathsf {p},\mathsf {p}(\mathsf {a})) \end{array} \) expands into:

Second-order quantifier elimination can be applied to compute the circumscription for the example:
Input: \( circ (\mathsf {p},\mathsf {p}(\mathsf {a})).\)
Result of elimination:
As a more complex example, we consider circumscribing \(\begin{array}{l} \mathsf {wet} \end{array} \) in \(\begin{array}{l} kb_{1} \end{array} \):
Input: \( circ (\mathsf {wet}, kb_{1} ).\)
Result of elimination:

The first three implications of this output form the expansion of \(\begin{array}{l} kb_{1} \end{array} \). The last two implications are added by the circumscription. This particular form was actually obtained by applying a certain simplification to the formula returned directly by the elimination method:

The option
 supplied to
supplied to
 effects that the elimination result is postprocessed by equivalence preserving conversions with the aim to make it more readable. The conversion named
effects that the elimination result is postprocessed by equivalence preserving conversions with the aim to make it more readable. The conversion named
 chosen for this example converts to conjunctive normal form, applies various clausal simplifications and then converts back to a quantified first-order formula, involving un-Skolemization if required. That the last conjunct of the result can be replaced by the more succinct \(\forall x \, (\mathsf {wet}( x ) \rightarrow x =\mathsf {grass} \vee x =\mathsf {shoes})\) is, however, not detected by the current implementation.
chosen for this example converts to conjunctive normal form, applies various clausal simplifications and then converts back to a quantified first-order formula, involving un-Skolemization if required. That the last conjunct of the result can be replaced by the more succinct \(\forall x \, (\mathsf {wet}( x ) \rightarrow x =\mathsf {grass} \vee x =\mathsf {shoes})\) is, however, not detected by the current implementation.
Finding good presentations of formulas, in particular in presence of operations that yield formulas with essentially semantic characterizations, is a challenging topic in general.
7 Expressing Graph Colorability by a Second-Order Formula – PIE Macros with Parameters in Functor Position
One of the fundamental results of descriptive complexity is the equivalence of NP and expressibility by an existential second-order formula (with respect to finite models), that is, a first order formula prefixed with existential predicate quantifiers. This view allows, for example, to specify 2-colorabilityFootnote 5 with respect to a relation E that specifies a graph as follows:

The source of this definition is:

The macro parameter
 appears as a Prolog variable in predicate position.Footnote 6 The macro can then be used with instantiating
appears as a Prolog variable in predicate position.Footnote 6 The macro can then be used with instantiating
 to a predicate symbol, or to a \(\lambda \)-expression that describes a particular graph (we will see examples in a moment).
to a predicate symbol, or to a \(\lambda \)-expression that describes a particular graph (we will see examples in a moment).
Specifying algorithms as (existential) second-order formulas seems very elegant, but so far not established as a practical approach to logic programming. PIE in its current implementation lets become apparent related desiderata: Instantiation with a predicate symbol should be usable as basis for abstract reasoning. Instantiation with a \(\lambda \)-expression (or conjoining a definition of a graph), should permit successful elimination. If adequate, the problem should then automatically be converted to a form that can be processed by a SAT solver.
So far, in the current implementation of PIE, such steps just work in part, e.g., by decomposing the overall task manually into intermediate steps with different manually controlled formula simplifications, as illustrated by the following example. The following macro defines the inner, first-order, component of the above specification of 2-colorability:

PIE allows to instantiate E in \( fo\_col2 (E)\) with a predicate constant \(\mathsf {e}\) and eliminate one of the color predicates:Footnote 7
Input: \(\exists g \, fo\_col_{2} (\mathsf {e}).\)
Result of elimination:
2-colorability for a given graph represented by a \(\lambda \)-expression can be evaluated by PIE currently just in two steps with different elimination configurations, as performed by the following Prolog predicate:

Options
 suppress the emission of printed representations of the two invocations of the elimination reasoner. Only the input \(\lambda \)-expression and the final result are pretty-printed with calls to
suppress the emission of printed representations of the two invocations of the elimination reasoner. Only the input \(\lambda \)-expression and the final result are pretty-printed with calls to
 . Options
. Options
 and
and
 effect that preprocessing based on conversion to CNF and DNF, respectively, is applied for elimination. Invoking
effect that preprocessing based on conversion to CNF and DNF, respectively, is applied for elimination. Invoking

yields the following output:
It expresses that the graph described by the \(\lambda \)-expression is 2-colorable if and only if node 1 is not the same as node 2 and node 2 is not the same as node 3.
8 Craig Interpolation
By Craig’s interpolation theorem [11, 12], for given first-order formulas F and G such that F entails G (or, equivalently, \(F \rightarrow G\) is valid) a first-order formula H can be constructed such that F entails H, H entails G and H contains only symbols (predicates, functions, constants, free variables) that occur in both F and G. PIE supports the computation of Craig interpolants H, for given valid implications \(F \rightarrow G\). Here is a propositional example:
Input: \(\mathsf {p} \wedge \mathsf {q} \rightarrow \mathsf {p} \vee \mathsf {r}.\)
Result of interpolation:
The corresponding directive in the source document is:

The predicate
 invokes the interpolation reasoner. It takes an implication \(F \rightarrow G\) as argument and, analogously to
invokes the interpolation reasoner. It takes an implication \(F \rightarrow G\) as argument and, analogously to
 (Sect. 3), prints an interpolant of F and G.Footnote 8 Here is another example of Craig interpolation, where universal and existential quantification need to be combined:Footnote 9
(Sect. 3), prints an interpolant of F and G.Footnote 8 Here is another example of Craig interpolation, where universal and existential quantification need to be combined:Footnote 9
Input: \(\forall x \, \mathsf {p}(\mathsf {a}, x ) \wedge \mathsf {q} \rightarrow \exists x \, \mathsf {p}( x ,\mathsf {b}) \vee \mathsf {r}.\)
Result of interpolation:
Craig interpolation has many applications in logics and philosophy, as already shown in [12]. Main applications in computer science are in verification [39] and query reformulation, based on its relationship to definability and construction of definientia in terms of a given vocabulary [4, 5, 48]. For these applications, actually interpolants that are further constrained, in dependency of further restrictions on the input formulas, are relevant. We do not consider these here, but show how basic definability via Craig interpolation can be expressed in PIE.
A formula G is called definable in a formula F in terms of a set of predicates S if and only if there exists a formula H whose predicates are all in S such that
 . The formula H is then called a definiens of G. Consider, for example, the following formula:
. The formula H is then called a definiens of G. Consider, for example, the following formula:

We can invoke a first-order prover from PIE to verify that the formula \(\mathsf {p}(\mathsf {a})\) is definable in \( kb _2\) in terms of \(\{\mathsf {q},\mathsf {r}\}\):
This formula is valid: \( kb_{2} \rightarrow (\mathsf {p}(\mathsf {a}) \leftrightarrow \mathsf {q}(\mathsf {a}) \wedge \mathsf {r}(\mathsf {a})).\)
Actually, since \(\mathsf {a}\) does not occur in \( kb _2\), we can equivalently verify the following implication, whose right side is a universally quantified first-order definition:
This formula is valid: \( kb_{2} \rightarrow \forall a \, (\mathsf {p}( a ) \leftrightarrow \mathsf {q}( a ) \wedge \mathsf {r}( a )).\)
We can now utilize the features of PIE to formally characterize definability and synthesize definientia:

The interpolants of the left and right side of \( definiens (G,F,P)\) are exactly the definientia of G in F in terms of all predicates not in P. The implication is valid if and only if definability holds. The second-order quantifications in the implication are existential on the left and universal on the right side.Footnote 10 Considering that an implication can be understood as disjunction of the negated left side and the right side, if F and G are first-order, then \( definiens (G,F,P)\) is a formula whose second-order quantifiers are all universal. Such a second-order formula is valid if and only if the first-order formula obtained by renaming the quantified predicates with fresh symbols and dropping the second-order quantifiers is valid. This translation is handled automatically by PIE such that we can now we verify definability of \(\mathsf {p}(\mathsf {a})\) by invoking a first-order prover from PIE:
This formula is valid: \( definiens (\mathsf {p}(\mathsf {a}), kb_{2} ,{[}\mathsf {p},\mathsf {s}{]}).\)
And, we can apply Craig interpolation to compute a definiens:
Input: \( definiens (\mathsf {p}(\mathsf {a}), kb_{2} ,{[}\mathsf {p},\mathsf {s}{]}).\)
Result of interpolation:
The implementation of the computation of Craig interpolants in PIE operates by a novel adaption of Smullyan’s interpolation method [18, 45] to clausal tableaux [57]. Suitable clausal tableaux can be constructed by the Prolog-based prover CM that is included in PIE. The system also supports the conversion of proof terms returned by the hypertableau prover Hyper [41] to such tableaux and thus to interpolants, but this is currently at an experimental stage.Footnote 11
The interpolants H constructed by PIE strengthen the requirements for Craig interpolants in that they are actually Craig-Lyndon interpolants, that is, predicates occur in H only in polarities in which they occur in both F and G. Symmetric interpolation [38, Sect. 5] is supported in PIE, implemented by computing a conventional interpolant for each of the input formulas, corresponding to the induction suggested with [12, Lemma 2].
It seems that most other implementations of Craig interpolation are on the basis of propositional logic with theory extensions and specialized for applications in verification [4]. Craig interpolation for first-order logic is supported by Princess [8, 9] and by extensions of Vampire [24, 25]. The incompleteness indicated in footnote 9 applies to these Vampire extensions and was observed by their authors. It also appears that the Vampire extensions do not preserve the polarity constraints of Craig-Lyndon interpolants [4].
9 Further Features of PIE
In this section we briefly describe further features of PIE that were not illustrated by the examples in the previous sections. First we consider the formula macro system. It utilizes Prolog variables to mimic further features of the processing of \(\lambda \)-expressions by automatically binding a Prolog variable that is free after computing the user-specified part of the expansion to a freshly generated symbol. With a macro declaration, properties of its lexical environment, in particular configuration settings that affect the expansion, are recorded. Macros with parameters are processed by pattern matching to choose the effective declaration for expansion, allowing structural recursion in macro declarations.
A Craig interpolant for formulas F and G is extracted in PIE from a Prolog term that represents a closed clausal tableau, a proof of the validity of \(F \rightarrow G\). PIE supports the visualization of such tableaux as graph, rendered by the Graphviz tool. Here is an example:
Input: \(\forall x \, \mathsf {p}( x ) \wedge \forall x \, (\mathsf {p}( x ) \rightarrow \mathsf {q}( x )) \rightarrow \mathsf {q}(\mathsf {c}).\)
Result of interpolation:
The respective directive for this interpolation task in the source is:

The
 option effects that an image representing the tableau is generated. The
option effects that an image representing the tableau is generated. The
 option suppresses preprocessing of the interpolation input, which, in the example, would in essence be already sufficient to compute the interpolant, yielding a trivial tableau. The generated image can then be included into the PIE document with standard
option suppresses preprocessing of the interpolation input, which, in the example, would in essence be already sufficient to compute the interpolant, yielding a trivial tableau. The generated image can then be included into the PIE document with standard
 means, here, for example as Fig. 1. Siblings in the tableau represent a ground clause used in the proof. As the tableau is used for interpolant extraction, decoration indicates whether the clause stems from the left or the right side of the input formula. The decoration of the closing marks indicate the side of the connection partner. The Skolem constant \(\mathsf {sk1}\) is converted to a quantified variable in a postprocessing operation. For a description of the interpolant extraction procedure, see [57].
means, here, for example as Fig. 1. Siblings in the tableau represent a ground clause used in the proof. As the tableau is used for interpolant extraction, decoration indicates whether the clause stems from the left or the right side of the input formula. The decoration of the closing marks indicate the side of the connection partner. The Skolem constant \(\mathsf {sk1}\) is converted to a quantified variable in a postprocessing operation. For a description of the interpolant extraction procedure, see [57].
Aside of the shown representation of quantified first-order formulas by Prolog ground terms, the system also supports a representation of clausal formulas as list of lists of terms (logic literals), with variables represented by Prolog variables. The system functionality can be accessed by Prolog predicates, also without using the document processing facilities.
Practically successful reasoners usually apply in some way conversions of low complexity as far as possible: as preprocessing on inputs, potentially during reasoning, which has been termed inprocessing, and to improve the syntactic shape of output formulas as discussed in Sect. 6. Abstracting from these situations, we subsume these conversions under preprocessing operations. Also the low complexity might be taken more or less literally and, for example, be achieved simply by trying an operation within a threshold limit of resources. PIE includes a number of preprocessing operations including normal form conversions, also in variants that produce structure preserving normalizations, various simplifications of clausal formulas, and an implementation of McCune’s un-Skolemization algorithm [37]. While some of these preserve equivalence, others preserve equivalence just with respect to a set of predicates, for example, purity simplification with respect to predicates that are not deleted or structure preserving classification with respect to predicates that are not added. This can be understood as preserving the second-order equivalence
where F and G are inputs and outputs of the conversion and \(q_1, \ldots , q_n\) are those predicates that are permitted to occur in F or G whose semantics needs not to be preserved. If \(q_1,\ldots , q_n\) includes all permitted predicates, the above equivalence expresses equi-satisfiability. Some of the simplifications implemented in PIE allow to specify explicitly a set of predicates whose semantics is to be preserved, which makes them applicable for Craig interpolation and second-order quantifier elimination.
In addition to the implementation of the DLS algorithm, PIE includes further experimental implementations of variants of second-order quantifier elimination. In particular, a variant of the method shown in [33] for elimination with respect to ground atoms, which always succeeds on the basis of first-order logic. A second-order quantifier is there, so-to-speak, just upon a particular ground instance of a predicate. The Boolean solution problem or Boolean unification with predicates is a computational task related to second-order quantifier elimination [42, 44, 56]. So far, PIE includes experimental implementations for special cases: Quantifier-free formulas with a technique from [16] and a version for finding solutions with respect to ground atoms, in analogy to the elimination of ground atoms.
10 Conclusion
PIE tries to supplement what is needed to use automated first-order proving techniques for developing and analyzing formalizations. Its main focus is not on proofs but on formulas, as constituents of complex formalizations that are composed and structured through macros, and as computed outputs of second-order quantifier elimination, Craig interpolation and formula conversions that preserve semantics with respect to given predicates. All of these operations utilize some natural relationships between first- and second-order logic.
The system mediates between high-level logical presentation and detailed configuration of reasoning systems: Working practically with first-order provers typically involves experimenting with a large and developing set of related proving problems, for example with alternate axiomatizations or different candidate theorems, and is thus often accompanied with some meta-level technique to compose and relate the actual proof tasks submitted to first-order reasoners. With the macro system, the supported document-oriented workflow,
 pretty-printing, and integration into the Prolog environment, PIE offers to organize this in a systematic way through mechanisms that remain in the spirit of first-order logic, which in mathematics is actually often used with schemas.
pretty-printing, and integration into the Prolog environment, PIE offers to organize this in a systematic way through mechanisms that remain in the spirit of first-order logic, which in mathematics is actually often used with schemas.
Aside of the current suitability for non-trivial applications, PIE shows up a number of challenging and interesting open issues for research, for example improving practical realizations of second-order quantifier elimination, strengthenings of Craig interpolation that ensure application-relevant properties such as range restriction, and conversion of computed formulas that are basically just semantically characterized to comprehensible presentations. Progress in these issues can be directly experienced and verified with the system.
Notes
- 1.
The prefix
 of this and related predicates should suggest
of this and related predicates should suggest
 format.
format. - 2.
Available at http://www.mettel-prover.org/scan/.
- 3.
Prover9 and Mace4 were developed between 2005 and 2010 by William McCune. Their homepage is https://www.cs.unm.edu/~mccune/prover9/.
- 4.
The standard Prolog negation operator
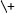 is not suited to represent classical negation as it symbolizes
is not suited to represent classical negation as it symbolizes  , non-provability.
, non-provability. - 5.
3-colorability, which is NP-complete, can be specified analogously. We consider here 2-colorability for brevity of the involved formulas.
- 6.
SWI-Prolog can be configured to permit variable names as functors, which are read in as atoms with capitalized names. The macro processor of PIE compares them to actual variable names in the macro definition.
- 7.
One color predicate can also be eliminated from an analogous specification of 3-colorability.
- 8.
In certain configurations it can also print several different interpolants.
- 9.
This is an example which involves an inference step with a constant that occurs only on the left side (\(\mathsf {a}\)) and a constant that occurs only on the right side (\(\mathsf {b}\)), which can not be handled by certain resolution-based interpolation systems. See [7, 30]. In this particular example, the order of the quantifications in the result is not relevant.
- 10.
We actually encountered right side of the implication before in Sect. 4 as the weakest sufficient condition in the macro definition of \( explanation \).
- 11.
Hypertableaux, either obtained from a hypertableau prover or obtained from a clausal tableau prover like CM by restructuring the tableau seem interesting as basis for interpolant extraction in query reformulation, as they allow to ensure that the interpolants are range restricted. Some related preliminary results are in [57].
References
Ackermann, W.: Untersuchungen über das Eliminationsproblem der mathematischen Logik. Math. Ann. 110, 390–413 (1935)
Alassaf, R., Schmidt, R.: DLS-Forgetter: an implementation of the DLS forgetting calculus for first-order logic. In: GCAI 2019. EPiC, vol. 65, pp. 127–138 (2019)
Behmann, H.: Beiträge zur Algebra der Logik, insbesondere zum Entscheidungsproblem. Math. Ann. 86(3–4), 163–229 (1922)
Benedikt, M., Kostylev, E.V., Mogavero, F., Tsamoura, E.: Reformulating queries: theory and practice. In: IJCAI 2017, pp. 837–843. ijcai.org (2017)
Benedikt, M., Leblay, J., ten Cate, B., Tsamoura, E.: Generating Plans from Proofs: The Interpolation-Based Approach to Query Reformulation. Morgan & Claypool, San Rafael (2016)
Bibel, W.: Matings in matrices. Commun. ACM 26(11), 844–852 (1983)
Bonacina, M.P., Johansson, M.: On interpolation in automated theorem proving. J. Autom. Reason. 54(1), 69–97 (2015)
Brillout, A., Kroening, D., Rümmer, P., Wahl, T.: Beyond quantifier-free interpolation in extensions of Presburger arithmetic. In: Jhala, R., Schmidt, D. (eds.) VMCAI 2011. LNCS, vol. 6538, pp. 88–102. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-18275-4_8
Brillout, A., Kroening, D., Rümmer, P., Wahl, T.: An interpolating sequent calculus for quantifier-free Presburger arithmetic. J. Autom. Reason. 47(4), 341–367 (2011)
Conradie, W.: On the strength and scope of DLS. J. Appl. Non-Classsical Logics 16(3–4), 279–296 (2006)
Craig, W.: Linear reasoning. A new form of the Herbrand-Gentzen theorem. J. Symbolic Logic 22(3), 250–268 (1957)
Craig, W.: Three uses of the Herbrand-Gentzen theorem in relating model theory and proof theory. J. Symbolic Logic 22(3), 269–285 (1957)
Delgrande, J.P.: A knowledge level account of forgetting. J. Artif. Intell. Res. 60, 1165–1213 (2017)
Doherty, P., Łukaszewicz, W., Szałas, A.: Computing circumscription revisited: a reduction algorithm. J. Autom. Reason. 18(3), 297–338 (1997)
Doherty, P., Łukaszewicz, W., Szałas, A.: Computing strongest necessary and weakest sufficient conditions of first-order formulas. In: IJCAI-01, pp. 145–151. Morgan Kaufmann (2001)
Eberhard, S., Hetzl, S., Weller, D.: Boolean unification with predicates. J. Logic Comput. 27(1), 109–128 (2017)
Engel, T.: Quantifier elimination in second-order predicate logic. Master’s thesis, Max-Planck-Institut für Informatik, Saarbrücken (1996)
Fitting, M.: First-Order Logic and Automated Theorem Proving, 2nd edn. Springer, Heidelberg (1995). https://doi.org/10.1007/978-1-4612-2360-3
Gabbay, D., Ohlbach, H.J.: Quantifier elimination in second-order predicate logic. In: KR 1992, pp. 425–435. Morgan Kaufmann (1992)
Gabbay, D.M., Schmidt, R.A., Szałas, A.: Second-Order Quantifier Elimination: Foundations, Computational Aspects and Applications. College Publications (2008)
Ghilardi, S., Lutz, C., Wolter, F.: Did I damage my ontology? A case for conservative extensions in description logics. In: KR 2006, pp. 187–197. AAAI Press (2006)
Grau, B.C., Horrocks, I., Kazakov, Y., Sattler, U.: Modular reuse of ontologies: theory and practice. J. Artif. Intell. Res. 31(1), 273–318 (2008)
Gustafsson, J.: An implementation and optimization of an algorithm for reducing formulae in second-order logic. Technical report LiTH-MAT-R-96-04, Univ. Linköping (1996)
Hoder, K., Holzer, A., Kovács, L., Voronkov, A.: Vinter: a Vampire-based tool for interpolation. In: Jhala, R., Igarashi, A. (eds.) APLAS 2012. LNCS, vol. 7705, pp. 148–156. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-35182-2_11
Hoder, K., Kovács, L., Voronkov, A.: Interpolation and symbol elimination in Vampire. In: Giesl, J., Hähnle, R. (eds.) IJCAR 2010. LNCS (LNAI), vol. 6173, pp. 188–195. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14203-1_16
Kaliszyk, C.: Efficient low-level connection tableaux. In: De Nivelle, H. (ed.) TABLEAUX 2015. LNCS (LNAI), vol. 9323, pp. 102–111. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-24312-2_8
Kaliszyk, C., Urban, J.: FEMaLeCoP: fairly efficient machine learning connection prover. In: Davis, M., Fehnker, A., McIver, A., Voronkov, A. (eds.) LPAR 2015. LNCS, vol. 9450, pp. 88–96. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48899-7_7
Knuth, D.E.: Literate programming. Comput. J. 27(2), 97–111 (1984)
Koopmann, P., Schmidt, R.A.: Uniform interpolation of \(\cal{ALC}\)-ontologies using fixpoints. In: Fontaine, P., Ringeissen, C., Schmidt, R.A. (eds.) FroCoS 2013. LNCS (LNAI), vol. 8152, pp. 87–102. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40885-4_7
Kovács, L., Voronkov, A.: First-order interpolation and interpolating proof systems. In: LPAR-21, pp. 49–64. EasyChair (2017)
Letz, R.: First-order tableau methods. In: D’Agostino, M., Gabbay, D.M., Hähnle, R., Posegga, J. (eds.) Handbook of Tableau Methods, pp. 125–196. Kluwer Academic Publishers (1999)
Lin, F.: On strongest necessary and weakest sufficient conditions. Artif. Intell. 128, 143–159 (2001)
Lin, F., Reiter, R.: Forget It! In: Working Notes, AAAI Fall Symposium on Relevance, pp. 154–159 (1994)
Ludwig, M., Konev, B.: Practical uniform interpolation and forgetting for \(\cal{ALC}\) TBoxes with applications to logical difference. In: KR 2014. AAAI Press (2014)
Lutz, C., Wolter, F.: Foundations for uniform interpolation and forgetting in expressive description logics. In: IJCAI 2011, pp. 989–995. AAAI Press (2011)
Löwenheim, L.: Über Möglichkeiten im Relativkalkül. Math. Ann. 76, 447–470 (1915)
McCune, W.: Un-Skolemizing clause sets. Inf. Process. Lett. 29(5), 257–263 (1988)
McMillan, K.L.: Applications of Craig interpolants in model checking. In: Halbwachs, N., Zuck, L.D. (eds.) TACAS 2005, pp. 1–12. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-31980-1_1
McMillan, K.L.: Interpolation and model checking. In: Clarke, E.M., Henzinger, T.A., Veith, H., Bloem, R. (eds.) Handbook of Model Checking, pp. 421–446. Springer, Heidelberg (2018). https://doi.org/10.1007/978-3-319-10575-8_14
Otten, J.: Restricting backtracking in connection calculi. AI Commun. 23(2–3), 159–182 (2010)
Pelzer, B., Wernhard, C.: System description: E-KRHyper. In: Pfenning, F. (ed.) CADE 2007. LNCS (LNAI), vol. 4603, pp. 508–513. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73595-3_37
Rudeanu, S.: Boolean Functions and Equations. Elsevier (1974)
Schmidt, R.A.: The Ackermann approach for modal logic, correspondence theory and second-order reduction. J. Appl. Logic 10(1), 52–74 (2012)
Schröder, E.: Vorlesungen über die Algebra der Logik. Teubner (1890–1905)
Smullyan, R.M.: First-Order Logic. Dover Publications, New York (1995). Corrected republication of the original edition by Springer-Verlag, New York (1968)
Stickel, M.E.: A Prolog technology theorem prover: implementation by an extended Prolog compiler. J. Autom. Reason. 4(4), 353–380 (1988)
Sutcliffe, G.: The TPTP problem library and associated infrastructure. From CNF to TH0, TPTP v6.4.0. J. Autom. Reason. 59(4), 483–502 (2017)
Toman, D., Weddell, G.: Fundamentals of Physical Design and Query Compilation. Morgan and Claypool, San Rafael (2011)
Wernhard, C.: Semantic knowledge partitioning. In: Alferes, J.J., Leite, J. (eds.) JELIA 2004. LNCS (LNAI), vol. 3229, pp. 552–564. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-30227-8_46
Wernhard, C.: Circumscription and projection as primitives of logic programming. In: Technical Communications ICLP 2010. LIPIcs, vol. 7, pp. 202–211. Schloss Dagstuhl-Leibniz-Zentrum für Informatik (2010)
Wernhard, C.: Projection and scope-determined circumscription. J. Symbolic Comput. 47, 1089–1108 (2012)
Wernhard, C.: Abduction in logic programming as second-order quantifier elimination. In: Fontaine, P., Ringeissen, C., Schmidt, R.A. (eds.) FroCoS 2013. LNCS (LNAI), vol. 8152, pp. 103–119. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40885-4_8
Wernhard, C.: Computing with logic as operator elimination: the ToyElim system. In: Tompits, H., et al. (eds.) INAP/WLP -2011. LNCS (LNAI), vol. 7773, pp. 289–296. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-41524-1_17
Wernhard, C.: Second-order quantifier elimination on relational monadic formulas – a basic method and some less expected applications. In: De Nivelle, H. (ed.) TABLEAUX 2015. LNCS (LNAI), vol. 9323, pp. 253–269. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-24312-2_18
Wernhard, C.: The PIE system for proving, interpolating and eliminating. In: PAAR 2016, pp. 125–138. CEUR-WS.org (2016)
Wernhard, C.: The Boolean solution problem from the perspective of predicate logic. In: Dixon, C., Finger, M. (eds.) FroCoS 2017. LNCS (LNAI), vol. 10483, pp. 333–350. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-66167-4_19
Wernhard, C.: Craig interpolation and access interpolation with clausal first-order tableaux. ArXiv e-prints (2018). https://arxiv.org/abs/1802.04982
Wielemaker, J., Schrijvers, T., Triska, M., Lager, T.: SWI-Prolog. Theory Practice Logic Program. 12(1–2), 67–96 (2012)
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Wernhard, C. (2020). Facets of the PIE Environment for Proving, Interpolating and Eliminating on the Basis of First-Order Logic. In: Hofstedt, P., Abreu, S., John, U., Kuchen, H., Seipel, D. (eds) Declarative Programming and Knowledge Management. INAP WLP WFLP 2019 2019 2019. Lecture Notes in Computer Science(), vol 12057. Springer, Cham. https://doi.org/10.1007/978-3-030-46714-2_11
Download citation
DOI: https://doi.org/10.1007/978-3-030-46714-2_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-46713-5
Online ISBN: 978-3-030-46714-2
eBook Packages: Computer ScienceComputer Science (R0)





 .
. -formatted natural language text.
-formatted natural language text.
 of this and related predicates should suggest
of this and related predicates should suggest
 format.
format.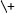 is not suited to represent classical negation as it symbolizes
is not suited to represent classical negation as it symbolizes  , non-provability.
, non-provability.