Abstract
We propose a new approach to construct general-purpose indistinguishability obfuscation (iO). Our construction is obtained via a new intermediate primitive that we call split fully-homomorphic encryption (split FHE), which we show to be sufficient for constructing iO. Specifically, split FHE is FHE where decryption takes the following two-step syntactic form: (i) A secret decryption step uses the secret key and produces a hint which is (asymptotically) shorter than the length of the encrypted message, and (ii) a public decryption step that only requires the ciphertext and the previously generated hint (and not the entire secret key), and recovers the encrypted message. In terms of security, the hints for a set of ciphertexts should not allow one to violate semantic security for any other ciphertexts.
Next, we show a generic candidate construction of split FHE based on three building blocks: (i) A standard FHE scheme with linear decrypt-and-multiply (which can be instantiated with essentially all LWE-based constructions), (ii) a linearly homomorphic encryption scheme with short decryption hints (such as the Damgård-Jurik encryption scheme, based on the DCR problem), and (iii) a cryptographic hash function (which can be based on a variety of standard assumptions). Our approach is heuristic in the sense that our construction is not provably secure and makes implicit assumptions about the interplay between these underlying primitives. We show evidence that this construction is secure by providing an argument in an appropriately defined oracle model.
We view our construction as a big departure from the state-of-the-art constructions, and it is in fact quite simple.
The full version of this paper is available at https://eprint.iacr.org/2020/394.
Z. Brakerski—Supported by the Israel Science Foundation (Grant No. 468/14), Binational Science Foundation (Grants No. 2016726, 2014276) and European Union Horizon 2020 Research and Innovation Program via ERC Project REACT (Grant 756482) and via Project PROMETHEUS (Grant 780701).
S. Garg—Supported in part from AFOSR Award FA9550-19-1-0200, AFOSR YIP Award, NSF CNS Award 1936826, DARPA and SPAWAR under contract N66001-15-C-4065, a Hellman Award and research grants by the Okawa Foundation, Visa Inc., and Center for Long-Term Cybersecurity (CLTC, UC Berkeley). The views expressed are those of the authors and do not reflect the official policy or position of the funding agencies.
G. Malavolta—Part of the work done while at the Simons Institute for the Theory of Computing.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
The goal of program obfuscation is to transform an arbitrary circuit \(C\) into an unintelligible but functionally equivalent circuit \(\tilde{C}\). The notion of program obfuscation was first studied by Hada [39] and Barak et al. [10]. However, these works showed that natural notions of obfuscation are impossible to realize for general functionalities. Specifically, Barak et al. [10] defined a very natural notion of security for program obfuscation called virtual black-box (VBB) security, which requires that an obfuscated program does not revel anything beyond what could be learned from just the input-output behavior of the original program. In the same work, they showed that this notion of program obfuscation is impossible to achieve for arbitrary circuits.
In light of this impossibility result, much of the work on obfuscation focused on realizing obfuscation for special functionalities. However, this changed with the work of Garg et al. [28] that proposed the first candidate indistinguishability obfuscation (iO) construction based on multilinear maps [26]. Furthermore, Garg et al. [28] showed powerful applications of iO to tasks such as functional encryption. Loosely speaking, iO requires that the obfuscations of two circuits \(C_0\) and \(C_1\) that have identical input output behavior are computationally indistinguishable. Subsequently, significant work on using program obfuscation (e.g., [16, 27, 55]) has shown that most cryptographic applications of interest can be realized using iO (and one-way functions), or that iO is virtually crypto-complete.
Given its importance, significant effort has been poured into realizing secure obfuscation candidates. The first approach to obfuscation relied on using new candidate constructions of multilinear maps [22, 26, 33], an algebraic object that significantly expands the structure available for cryptographic construction. Unfortunately, all multilinear map construction so far have relied on ad-hoc and new computational intractability assumptions. Furthermore, attacks [21, 40] on the multilinear map candidates and attacks [20, 51] on several of the multilinear map based iO constructions [9, 18, 28] were later found. In light of these attacks, follow up works (e.g., [31]) offered constructions that defended against these attacks by giving constructions in the so-called weak multilinear map model [51]. Several of these weak multilinear map model based iO constructions are still conjectured to be secure, however, the break-and-repair cycle of their development has left cryptographers wary, and rightly so.
Around the time when attacks on multilinear map candidates were at an all time high, cryptographers started exploring new approaches to iO without using multilinear maps (or reducing their usage). Toward this goal, Bitansky and Vaikunthanathan [15] and Ananth and Jain [4] showed that iO could be realized assuming just functional encryption. In another approach, instead of trying to remove multilinear maps completely, Lin [42] and Lin and Vaikuntanathan [47] attempted to reduce their usage, i.e., they proposed iO constructions using only constant degree multilinear maps. With the goal of ultimately basing iO constructions on standard assumptions on bilinear maps, cryptographers started developing new ideas for realizing iO candidates from smaller constant degree multilinear maps [5, 43]. Recently, Lin and Tessaro [45] described a candidate iO construction from degree-L multilinear maps for any \(L\ge 2\) and additionally assuming PRGs with certain special locality properties. Unfortunately, it was shown the needed PRGs for the case of \(L=2\) are insecure (in fact it was proved that they cannot exist) [8, 48]. Thus, still leaving a gap between bilinear maps and iO constructions which could now be based on trilinear maps [46]. Very recent works [1, 3, 41] (and cryptanalysis [12]), develop new ideas to resolve these problems and realize constructions based on bilinear maps. However, these bilinear map based constructions, which are still conjectured to be secure, additionally rely on certain pseudorandom objects with novel security properties. Finally, we note that all the other (perhaps less popular) approaches to iO (e.g., [35]) also start from new computational hardness assumptions.
Given the prior work, it is plausible that new sources of hardness are necessary for realizing iO candidates. Thus, this break-and-repair cycle would be necessary as we understand the underlying new assumptions better. In fact, there is some evidence that iO constructions based on simpler primitives [29, 30] are hard to realize. Making progress on this dilemma is the focus of this work.
1.1 Our Results
We propose a new approach to construct general-purpose indistinguishability obfuscation. Our approach is heuristic but without using any new sources of computational hardness. In other words, our constructions use well-studied cryptographic primitives in a generic way to realize obfuscation, while still being heuristic in the sense that our constructions are not provably secure and make implicit assumptions about the interplay of the underlying primitives. The primitives we use can themselves be securely realized based on standard assumptions, namely the hardness of the learning with errors (LWE) and the decisional composite residues (DCR) problem. At a high level, our heuristics are similar in flavor to (i) the random oracle heuristic that is often used in cryptographic constructions [13] and (ii) the circular security heuristic that has been widely used in the construction of fully-homomorphic encryption schemes (FHE) [32].
Split-FHE. The starting point of our work is the fact that iO can provably be based on split FHE, a new primitive that we introduce in this work. A split FHE is an FHE scheme that allows for certain special properties of the decryption algorithm. Specifically, we consider FHE schemes for which the decryption algorithm can be split into two subroutines:
-
\(\rho \leftarrow \mathsf {PDec}(\mathsf {sk},c)\): A private procedure that takes the FHE secret key and a ciphertext as input and produces a decryption hint \(\rho \), of size much smaller than the message encrypted in \(c\).
-
\(m\leftarrow \mathsf {Rec}(\rho , c)\): A public procedure that takes as input the decryption hint \(\rho \) (generated by \(\mathsf {PDec}\)) and the ciphertext \(c\) and recovers the full plaintext.
The security for a split FHE scheme requires that, for all pairs of messages \((m_0, m_1)\) and all circuits \(C\) such that \(C(m_0) = C(m_1)\), the encryption of \(m_0\) is computationally indistinguishable from the encryption of \(m_1\), even given the decryption hint for the ciphertext evaluated on \(C\).
We show that split FHE alone suffices to construct exponentially-efficient iO [44], which in turn allows us to build fully-fledged iO. Concretely, we prove the following theorem.
Theorem 1
(Informal). Assuming sub-exponentially hard LWE and the existence of sub-exponentially secure split FHE, then there exists indistinguishability obfuscation for all circuits.
A Generic Candidate. Next, we show a generic candidate construction of split FHE based on three building blocks: (i) a standard FHE scheme with linear decrypt-and-multiply (which can be instantiated with essentially all LWE-based constructions), (ii) a linearly homomorphic encryption scheme with short decryption hints (such as the Damgård-Jurik encryption scheme [23], based on the DCR problem), and (iii) a cryptographic hash functions. The security of the scheme can be based on a new conjecture on the interplay of these primitives, which we view as a natural strengthening of circular security. In this sense, it is aligned with Gentry’s heuristic step in the FHE bootstrapping theorem [32]. Additionally, our use of the cryptographic hash function has similarities to the other heuristic uses of hash functions, e.g., in the Fiat-Shamir transformation [25].
We expect that there will exist instantiations of the underlying primitives (though contrived) for which this construction is insecure. For example, if the underlying schemes are not circular secure to begin with, then the resulting split FHE would also be insecure. However, for natural instantiations of these primitives, security can be conjectured.
Evidence of Security. In order to build confidence in our construction, we show evidence that the above-mentioned conjecture on the interplay between the security holds in an appropriate oracle model, inspired by the random oracle model. Thus, pushing all the heuristic aspects of the construction to an oracle. In fact, we show that security can be proved in this oracle model.
An alternate way to think of this result is that we construct split FHE based on a obfuscation for a specific program (representing the oracle), for which we can offer a relatively simple and natural heuristic implementation.
Conceptual Simplicity. Another positive feature of our construction is its conceptual simplicity, which makes it much easier to analyze and thus have confidence in. Finally, we remark that our construction is a big departure from the previously-mentioned multilinear maps based and local PRG based iO constructions and will be accessible to readers without first understanding prior iO constructions.
1.2 Technical Overview
In the following we give an informal overview of the techniques we develop in this work and we refer the reader to the technical sections for more precise statements.
Chimeric FHE. Our starting point is the hybrid FHE scheme recently introduced by Brakerski et al. [17], which we recall in the following. The objective of their work is to build an FHE scheme with best possible rate (in an asymptotic sense) by leveraging the fact that most LWE-based FHE scheme admit an efficient linear noisy decryption. Specifically, given an FHE ciphertext \(c\) and an LWE secret key \((s_1, \dots , s_n)\) one can rewrite the decryption operation as a linear function \(L_c(\cdot )\) such that
where e is a B-bounded noise term and \(\mathsf {ECC}\) is some encoding of the plaintext (in their scheme \(m\) is packed in the high-order bits so that it does not interfere with the noise term). The idea then is to encrypt the secret key \((s_1, \dots , s_n)\) under a (high-rate) linearly homomorphic encryption (LHE) scheme, which allows one to compress evaluated FHE ciphertext by computing \(L_c(\cdot )\) homomorphically.
One interesting property of this approach is that it is completely parametric in the choice of the schemes, as long as they satisfy some simple structural requirements: More concretely, one can use any LHE scheme as long as its plaintext domain matches the LWE modulus of the FHE scheme. As an example, one can set the LHE to be the Damgård-Jurik encryption scheme [23, 52], which we briefly recall in the following. The public key of the scheme consists of a large composite \(N = pq\) and an integer \(\zeta \), and the encryption algorithm a message \(m\) computes
for some uniform  . Note that the corresponding plaintext space is \(\mathbb {Z}_{N^\zeta }\) and therefore the rate of the scheme approaches 1 as \(\zeta \) grows. Furthermore, we observe that the scheme has one additional property that we refer to as split decryption. A scheme has split decryption if the decryption algorithm can be divided into a private and a public subroutine:
. Note that the corresponding plaintext space is \(\mathbb {Z}_{N^\zeta }\) and therefore the rate of the scheme approaches 1 as \(\zeta \) grows. Furthermore, we observe that the scheme has one additional property that we refer to as split decryption. A scheme has split decryption if the decryption algorithm can be divided into a private and a public subroutine:
-
The private procedure takes as input a ciphertext \(c\) and the secret key \(\phi (N)\) and computes a decryption hint
$$\begin{aligned} \rho = c^{N^{-\zeta }} \mod N \end{aligned}$$using the extended Euclidean algorithm. It is crucial to observe that \(\rho \in \mathbb {Z}_N\) is potentially much smaller than the plaintext \(m\).
-
The public procedure takes as input a ciphertext \(c\) and the decryption hint \(\rho \) and recovers the plaintext by computing
$$ (1+N)^m= c/ \rho ^{N^\zeta } \mod N^{\zeta +1} $$and decoding \(m\) in polynomial time using the binomial theorem.
In a nutshell, the subgroup homomorphism allows one to compute a compressed version of the randomness, which can be then publicly stretched and used to unmask the plaintext. This means that \(m\) can be fully recovered by communicating a small hint of size fixed and, in particular, independent of \(|m|\). As we are going to discuss later, this property is going to be our main leverage to build general-purpose obfuscation.
Temporarily glossing over the security implications, we point out that the hybrid scheme of Brakerski et al. [17] already suffices to construct an FHE scheme with split decryption (in short, split FHE): Simply instantiate the LHE scheme with Damgård-Jurik and convert evaluated FHE ciphertexts before decryption using the algorithm described above.
Security for Split FHE. We now delve into the desired security property for a split FHE scheme. On a high level, we would like to ensure that the decryption hint does not reveal any additional information, beyond the plaintext of the corresponding ciphertext. It is instructive to observe that if we do not insist on this property, then every FHE scheme has a trivial split decryption procedure which simply outputs the secret key. We formalize this intuition as an indistinguishability definition that, roughly speaking, demands that for all plaintext pairs \((m_0, m_1)\) and every set of circuits \((C_1, \dots , C_\beta )\) such that \(C_i(m_0) = C_i(m_1)\), then the encryption of \(m_0\) and \(m_1\) are computationally indistinguishable, even given the decryption hints \(\rho _i\) of the evaluated ciphertexts. The condition \(C_i(m_0) = C_i(m_1)\) rules out trivial attacks where the distinguisher just checks the output of the evaluation. Here \(\beta = \beta (\lambda )\) is an arbitrary (but a priori bounded) polynomial in the security parameter.
Unfortunately, our candidate as described above falls short in satisfying this security notion: The central problem is that our split decryption procedure reveals the complete plaintext encoded in the Damgård-Jurik ciphertext. This means that the distinguisher learns arbitrarily many relations of the form
where \(c_i\) is the evaluated ciphertext and \(L_{c_i}\) is a publicly known linear function. Collecting a large enough sample allows the distinguisher to recompute the FHE secret key \((s_1, \dots , s_n)\) via, e.g., Gaussian elimination. A standard approach to obviate this problem is to smudge the noise \(e_i\) with some mask \(r_i\) uniformly sampled from an exponentially larger domain. Thus, a natural solution would be to compute a randomizing ciphertext \(d_i = \mathsf {DJ.Enc}(\mathsf {pk}_\mathsf {DJ}, r_i)\) and output the decryption hint for
where \(r_i\) is sampled from a domain exponentially larger than the noise bound B but small enough to allow one to decode \(\mathsf {ECC}(C_i(m_b))\). While it is possible to show that this approach indeed satisfies the security notion outlined above, it introduces an overhead in the size of the hint, which now consists of the pair \((\rho _i, d_i)\). Note that we cannot allow the distinguisher to recompute \(d_i\) locally as it is crucial that \(r_i\) remains hidden, so we have no other choice but append it to the decryption hint. However the decryption hint is now of size \(O(|c_i|)\), which does not satisfy our compactness requirement and makes our efforts purposeless (one can just set the decryption hint to be \(C_i(m_b)\) and achieve better efficiency).
Although we appear to have encountered a roadblock, a closer look reveals that we still gained something from this approach: The ciphertext \(d_i\) encodes a (somewhat small) random value and in particular is completely independent from \(c_i\). Furthermore, the decryption hint of \(c_i \cdot d_i\) can be computed using the secret key alone. Assume for the moment that we had access to an oracle \(\mathcal {O}\) that outputs uniform Damgård-Jurik encryption of bounded random values, then our idea is to delegate the sampling of \(d_i\) to \(\mathcal {O}\). This allows us to bypass the main obstacle: We do not need to include \(d_i\) in the decryption hint as it can be recomputed by querying \(\mathcal {O}\). One can think of this approach as a more structured version of the Fiat-Shamir transform [25], which allows us to state the following theorem.
Theorem 2
(Informal). Assuming the hardness of LWE and DCR, then there exists a split FHE scheme in the \(\mathcal {O}\)-hybrid model.
Looking ahead to our end goal, another interpretation of this theorem is as a universality result: Assuming the hardness of LWE and DCR, we can bootstrap an obfuscator for a specific circuit (i.e., the one that samples a uniform Damgård-Jurik encryption of a bounded random value) to an obfuscator for all circuits.
Instantiating the Oracle. The most compelling question which arises from our main theorem is whether there exist plausible instantiations for the oracle \(\mathcal {O}\). A first (flawed) attempt is to devise an oblivious sampling procedure for Damgård-Jurik ciphertext using a random oracle: Note that Damgård-Jurik ciphertexts live in a dense domain \(\mathbb {Z}_{N^\zeta +1}\) and indeed sampling a random integer  maps to a well-formed ciphertext with all but negligible probability. However, since \(c_i\) is uniform in the ciphertext domain, then so is the underlying plaintext \(r_i \in \mathbb {Z}_{N^\zeta }\). This makes \(c_i\) unusable for our purposes since we require \(r_i\) to be bounded by some value \(\tilde{q}\), which is exponentially smaller than \(N^\zeta \). If we were to sample \(r_i\) this way, then it would completely mask the term \(\mathsf {ECC}(C_i(m_b))\), thus making the plaintext impossible to decode.
maps to a well-formed ciphertext with all but negligible probability. However, since \(c_i\) is uniform in the ciphertext domain, then so is the underlying plaintext \(r_i \in \mathbb {Z}_{N^\zeta }\). This makes \(c_i\) unusable for our purposes since we require \(r_i\) to be bounded by some value \(\tilde{q}\), which is exponentially smaller than \(N^\zeta \). If we were to sample \(r_i\) this way, then it would completely mask the term \(\mathsf {ECC}(C_i(m_b))\), thus making the plaintext impossible to decode.
Ideally, we would like to restrict the oblivious sampling to ciphertexts encrypting \(\tilde{q}\)-bounded messages. Unfortunately, we are not aware of the existence of any such algorithm. Instead, our idea is to still sample \(c_i\) uniformly over the complete ciphertext domain and remove the high-order bits of \(r_i\) homomorphically: This can be done by including an FHE encryption of the Damgård-Jurik secret key, then homomorphically evaluating the circuit that decrypts \(c_i\) and computes \(- \lfloor r_i / \tilde{q} \rfloor \cdot \tilde{q}\). The evaluated ciphertext is then converted again to the Damgård-Jurik domain using the linear noisy decryption of the FHE scheme. At this point, one can obtain a well-formed encryption of a \(\tilde{q}\)-bounded value by computing
where the term \((r_i \mod \tilde{q}) + e\) is \(\tilde{q}\)-bounded with all but negligible probability by setting \(\tilde{q} \gg B\). While this approach brings us tantalizingly close to a provably secure scheme, a careful analysis highlights two lingering conjectures.
-
(1)
Circular Security: Adding and FHE encryption of the Damgård-Jurik secret key introduces a circular dependency in the security of the two schemes (recall that our construction already encodes a Damgård-Jurik encryption of the FHE secret key). While circular security falls outside of the realm of provable statements, it is widely accepted as a mild assumption and it is known to be achieved by most natural encryption schemes [11]. We stress that circular security is also inherent in the the bootstrapping theorem of Gentry [32], the only known method to construct fully (as opposed to levelled) homomorphic encryption from LWE.
-
(2)
Correlations: While the homomorphically evaluated circuit essentially ignores the low-order bits of \(r_i\), the corresponding decryption noise e might still depend on \((r_i \mod \tilde{q})\) in some intricate way. This might introduce some correlation and bias the distribution of the term \((r_i \mod \tilde{q}) + e\) with respect to a uniform
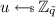 . However, the noise function is typically highly non-linear and therefore appears to be difficult to exploit. We also point out that the distinguisher has no control over the choice of e, which exclusively depends on an honest execution of the homomorphic evaluation algorithm. We therefore conjecture that the distribution of \((r_i \mod \tilde{q}) + e\) is computationally indistinguishable from u.
. However, the noise function is typically highly non-linear and therefore appears to be difficult to exploit. We also point out that the distinguisher has no control over the choice of e, which exclusively depends on an honest execution of the homomorphic evaluation algorithm. We therefore conjecture that the distribution of \((r_i \mod \tilde{q}) + e\) is computationally indistinguishable from u.
In light of the above insights, we put forward the conjecture that the proposed algorithm already gives us a secure implementation of the oracle \(\mathcal {O}\). We view this as a natural strengthening of Gentry’s heuristic for the bootstrapping theorem, which is justified by our more ambitious objective. As the conjecture pertains to standard cryptographic material (FHE and Damgård-Jurik encryption) we believe that any further insight on its veracity would substantially improve our understanding on these important and well-studied building blocks.
Finally, we mention that many heuristics can be used to weaken the correlation between the decryption noise e and the low-order bits \((r_i \mod \tilde{q})\), such as repeated applications of FHE bootstrapping [24]. We also propose a different heuristic approach to remove correlations based on binary extractors and we refer the reader to the technical sections for further details.
From Split FHE to iO. What is left to be shown is that split FHE does indeed suffice to construct program obfuscation. With this goal in mind, we recall a surprising result by Lin et al. [44] which states that, under the assumption that the LWE problem is sub-exponentially hard, iO for all circuits is implied by an obfuscator for circuits with logarithmic-size inputs with non-trivial efficiency. Here non-trivial efficiency means that the size of the obfuscated circuit \(\tilde{C}\) with input domain \(\{0,1\}^\eta \) is at most  , for some constant \(\epsilon >0\). This means that it suffices to show that split FHE implies the existence of an obfuscator (for circuits with polynomial-size input domain) with non-trivial efficiency.
, for some constant \(\epsilon >0\). This means that it suffices to show that split FHE implies the existence of an obfuscator (for circuits with polynomial-size input domain) with non-trivial efficiency.
The transformation is deceptively simple (and similar to [14]): The obfuscator computes a split FHE encryption of the circuit \(C\) and partitions the input domains in \(2^{\eta /2}\) disjoint sets \((P_1, \dots , P_{2^{\eta / 2}})\) of equal size. Then, for each partition \(P_i\), the algorithm homomorphically evaluates the universal circuit that evaluates \(C\) on all inputs in \(P_i\) and returns the concatenation of all outputs. Finally it returns the decryption hint \(\rho _i\) corresponding to the evaluated ciphertext. The obfuscated circuit consists of the public-key of the split FHE scheme, the encryption of \(C\), and all of the decryption hints \((\rho _1, \dots , \rho _{2^{\eta / 2}})\). Note that the obfuscated circuit can be evaluated efficiently: On input x, let \(P_x\) be the partition that contains x, then the evaluator recomputes the homomorphic evaluation (which is a deterministic operation) of \(C\) on \(P_x\) and recovers the output using the decryption hint \(\rho _x\). As for non-trivial efficiency, since the size of each decryption hint is that of a fixed polynomial mp, the total size of the obfuscated circuit is bounded by  , as desired.
, as desired.
Other Applications. To demonstrate that the scope of our split FHE scheme goes beyond program obfuscation, we outline two additional applications. In both cases we only rely on the hardness of the LWE and DCR problem, i.e., we do not need to introduce any new conjecture.
Two-Party Computation with Pre-Processing. We obtain a (semi-honest) two-party computation scheme for any circuit \(C:\{0,1\}^\ell \rightarrow \{0,1\}^k\) with an input- and circuit-independent pre-processing where the communication complexity of the pre-processing phase is  , whereas the communication complexity of the online phase is
, whereas the communication complexity of the online phase is  . This improves over garbled circuit-based approaches that require a pre-processing at least linear in \(|C|\). The protocol works as follows: In the pre-processing phase Alice and Bob exchange their (independently sampled) public-keys for a split FHE scheme and Alice computes a randomizing ciphertext (in the scheme defined above this corresponds to a Damgård-Jurik encryption of a bounded random value), which is sent to Bob. In the online phase, Alice and Bob exchange their inputs encrypted under their own public keys (to achieve best-possible rate this can be done using hybrid encryption) and homomorphically compute the multi-key evaluation of f over both inputs. Note that multi-key evaluation is generically possible for the case of two parties by nesting the two split FHE evaluations. Then Alice consumes the randomizing ciphertext computed in the pre-processing and sends a partial decryption of the evaluated ciphertext in the form of a decryption hint. Bob can then locally complete the partial decryption using its own secret key and recover the output.
. This improves over garbled circuit-based approaches that require a pre-processing at least linear in \(|C|\). The protocol works as follows: In the pre-processing phase Alice and Bob exchange their (independently sampled) public-keys for a split FHE scheme and Alice computes a randomizing ciphertext (in the scheme defined above this corresponds to a Damgård-Jurik encryption of a bounded random value), which is sent to Bob. In the online phase, Alice and Bob exchange their inputs encrypted under their own public keys (to achieve best-possible rate this can be done using hybrid encryption) and homomorphically compute the multi-key evaluation of f over both inputs. Note that multi-key evaluation is generically possible for the case of two parties by nesting the two split FHE evaluations. Then Alice consumes the randomizing ciphertext computed in the pre-processing and sends a partial decryption of the evaluated ciphertext in the form of a decryption hint. Bob can then locally complete the partial decryption using its own secret key and recover the output.
Rate-1 Reusable Garbled Circuits. The work of Goldwasser et al. [37] showed, assuming the hardness of the LWE problem, how to construct reusable garbled circuits where the size of the input encodings is  , where \(C:\{0,1\}^\ell \rightarrow \{0,1\}^k\) and d is the depth of \(C\). Additionally assuming the hardness of the DCR problem, we can bring down the complexity to
, where \(C:\{0,1\}^\ell \rightarrow \{0,1\}^k\) and d is the depth of \(C\). Additionally assuming the hardness of the DCR problem, we can bring down the complexity to  . This is done by using their scheme to garble the circuit that computes \(C\) homomorphically over the input encrypted under a split FHE scheme an returns the decryption hint of the evaluated ciphertext. This effectively removes the dependency of the underlying reusable garbled circuit on the output size k. However, we also need to include in the input encoding a randomizing Damgård-Jurik ciphertext, which reintroduces an additive overhead in k.
. This is done by using their scheme to garble the circuit that computes \(C\) homomorphically over the input encrypted under a split FHE scheme an returns the decryption hint of the evaluated ciphertext. This effectively removes the dependency of the underlying reusable garbled circuit on the output size k. However, we also need to include in the input encoding a randomizing Damgård-Jurik ciphertext, which reintroduces an additive overhead in k.
1.3 Related Work
In the following we discuss more in depth the relation of our approach when compared with recent candidate constructions of iO from lattices and bilinear maps [1, 3, 41]. Very informally, this line of works leverages weak pseudorandom generators (PRG) to mask the noise of the LWE decryption. However, the output domain of such a PRG is only polynomially large: This is because of the usage of bilinear groups, where the plaintext space is polynomially bounded (decryption requires one to solve a discrete logarithm). This is especially problematic because statistical/computational indistinguishability cannot hold in this regime of parameters. To circumvent this problem, all papers in this line of work assume a strict bound on the distinguisher’s success probability (e.g., 0.99) and then rely on amplification techniques. This however requires one to construct a weak PRG where the advantage of any PPT distinguisher is non-negligible but at the same time bounded by \(< 0.99\).
On the other hand, we rely on the Damgård-Jurik encryption scheme, where the message domain is exponential. This allows us to sample the smudging factor from a distribution that is exponentially larger than the noise bound, which is necessary in order to argue about statistical indistinguishability. Thus in our settings, conjecturing that the advantage of the distinguisher is negligible is, at least in principle, plausible.
2 Preliminaries
We denote by \(\lambda \in \mathbb {N}\) the security parameter. We say that a function  is negligible if it vanishes faster than any polynomial. Given a set S, we denote by
is negligible if it vanishes faster than any polynomial. Given a set S, we denote by  the uniform sampling from S. We say that an algorithm is PPT if it can be implemented by a probabilistic machine running in time
the uniform sampling from S. We say that an algorithm is PPT if it can be implemented by a probabilistic machine running in time  . We abbreviate the set \(\{1, \dots , n\}\) as [n]. We recall the smudging lemma [6, 7].
. We abbreviate the set \(\{1, \dots , n\}\) as [n]. We recall the smudging lemma [6, 7].
Lemma 1 (Smudging)
Let \(B_1 = B_1(\lambda )\) and \(B_2=B_2(\lambda )\) be positive integers and let \(e_1 \in [B_1]\) be a fixed integer. Let  chosen uniformly at random. Then the distribution of \(e_2\) is statistically indistinguishable from that of \(e_2+e_1\) as long as
chosen uniformly at random. Then the distribution of \(e_2\) is statistically indistinguishable from that of \(e_2+e_1\) as long as  .
.
2.1 Indistinguishability Obfuscation
We recall the notion of indistinguishability obfuscation (iO) from [28].
Definition 1 (Indistinguishability Obfuscation)
A PPT machine \(\mathsf {iO}\) is an indistinguishability obfuscator for a circuit class \(\{\mathcal {C}_\lambda \}_{\lambda \in \mathbb {N}}\) if the following conditions are satisfied:
(Functionality) For all \(\lambda \in \mathbb {N}\), all circuit \(C\in \mathcal {C}_\lambda \), all inputs x it holds that

(Indistinguishability) For all polynomial-size distinguishers \(\mathcal {D}\) there exists a negligible function  such that for all \(\lambda \in \mathbb {N}\), all pairs of circuit \((C_0, C_1) \in \mathcal {C}_\lambda \) such that \(|C_0| = |C_1|\) and \(C_0(x) = C_1(x)\) on all inputs x, it holds that
such that for all \(\lambda \in \mathbb {N}\), all pairs of circuit \((C_0, C_1) \in \mathcal {C}_\lambda \) such that \(|C_0| = |C_1|\) and \(C_0(x) = C_1(x)\) on all inputs x, it holds that

2.2 Learning with Errors
We recall the (decisional) learning with errors (LWE) problem as introduced by Regev [54].
Definition 2 (Learning with Errors)
The LWE problem is parametrized by a modulus q, positive integers n, m and an error distribution \(\chi \). The LWE problem is hard if for all polynomial-size distinguishers \(\mathcal {D}\) there exists a negligible function  such that for all \(\lambda \in \mathbb {N}\) it holds that
such that for all \(\lambda \in \mathbb {N}\) it holds that

where \(\mathbf {A}\) is chosen uniformly from \(\mathbb {Z}_q^{n \times m}\), \(\mathbf {s}\) is chosen uniformly from \(\mathbb {Z}_q^n\), \(\mathbf {u}\) is chosen uniformly from \(\mathbb {Z}_q^m\) and \(\mathbf {e}\) is chosen from \(\chi ^m\).
As shown in [53, 54], for any sufficiently large modulus q the LWE problem where \(\chi \) is a discrete Gaussian distribution with parameter \(\sigma = \alpha q \ge 2 \sqrt{n}\) (i.e. the distribution over \(\mathbb {Z}\) where the probability of x is proportional to \(e^{-\pi (|x|/\sigma )^2}\)), is at least as hard as approximating the shortest independent vector problem (SIVP) to within a factor of \(\gamma = \tilde{O}({n}/\alpha )\) in worst case dimension n lattices. We refer to \(\alpha = \sigma / q\) as the modulus-to-noise ratio, and by the above this quantity controls the hardness of the LWE instantiation. Hereby, LWE with polynomial \(\alpha \) is (presumably) harder than LWE with super-polynomial or sub-exponential \(\alpha \). We can truncate the discrete Gaussian distribution \(\chi \) to \(\sigma \cdot \omega (\sqrt{\log (\lambda )})\) while only introducing a negligible error. Consequently, we omit the actual distribution \(\chi \) but only use the fact that it can be bounded by a (small) value B.
3 Homomorphic Encryption
We recall the definition of homomorphic encryption in the following.
Definition 3 (Homomorphic Encryption)
A homomorphic encryption scheme consists of the following efficient algorithms.
-
\(\mathsf {KeyGen}(1^\lambda ){:}\) On input the security parameter \(1^\lambda \), the key generation algorithm returns a key pair \((\mathsf {sk}, \mathsf {pk})\).
-
\(\mathsf {Enc}(\mathsf {pk}, m){:}\) On input a public key \(\mathsf {pk}\) and a message \(m\), the encryption algorithm returns a ciphertext \(c\).
-
\(\mathsf {Eval}(\mathsf {pk}, C, (c_1, \dots , c_\ell )){:}\) On input the public key \(\mathsf {pk}\), an \(\ell \)-inputs circuit \(C\), and a vector of ciphertexts \((c_1, \dots , c_\ell )\), the evaluation algorithm returns an evaluated ciphertext \(c\).
-
\(\mathsf {Dec}(\mathsf {sk}, c){:}\) On input the secret key \(\mathsf {sk}\) and a ciphertext \(c\), the decryption algorithm returns a message \(m\).
We say that a scheme is fully-homomorphic (FHE) if it is homomorphic for all (unbounded) polynomial-size circuits. If the maximum size of the circuit that can be evaluated is bounded in the public parameters, then we call such a scheme a levelled FHE. We also consider a restricted class of homomorphism that supports linear functions and we refer to such a scheme as linearly-homomorphic encryption (LHE). We characterize correctness of a single evaluation, which suffices for our purposes. This can be extended to the more general notion of multi-hop correctness [34] if the condition specified below is required to hold for arbitrary compositions of circuits.
Definition 4 (Correctness)
A homomorphic encryption scheme \((\mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Eval}, \mathsf {Dec})\) is correct if for all \(\lambda \in \mathbb {N}\), all \(\ell \)-inputs circuits \(C\), all inputs \((m_1, \dots , m_\ell )\), all \((\mathsf {sk}, \mathsf {pk})\) in the support of \(\mathsf {KeyGen}(1^\lambda )\), and all \(c_i\) in the support of \(\mathsf {Enc}(\mathsf {pk}, m_i)\) it holds that
We require a scheme to be compact in the sense that the size of the ciphertext should not grow with the size of the evaluated circuit.
Definition 5 (Compactness)
A homomorphic encryption scheme \((\mathsf {KeyGen},\mathsf {Enc},\mathsf {Eval}, \mathsf {Dec})\) is compact if there exists a polynomial  such that for all \(\lambda \in \mathbb {N}\), all \(\ell \)-inputs circuits \(C\) in the supported family, all inputs \((m_1, \dots , m_\ell )\), all \((\mathsf {sk}, \mathsf {pk})\) in the support of \(\mathsf {KeyGen}(1^\lambda )\), and all \(c_i\) in the support of \(\mathsf {Enc}(\mathsf {pk}, m_i)\) it holds that
such that for all \(\lambda \in \mathbb {N}\), all \(\ell \)-inputs circuits \(C\) in the supported family, all inputs \((m_1, \dots , m_\ell )\), all \((\mathsf {sk}, \mathsf {pk})\) in the support of \(\mathsf {KeyGen}(1^\lambda )\), and all \(c_i\) in the support of \(\mathsf {Enc}(\mathsf {pk}, m_i)\) it holds that

We define a weak notion of security (implied by the standard semantic security [38]) which is going to be more convenient to work with.
Definition 6 (Semantic Security)
A homomorphic encryption scheme \((\mathsf {KeyGen},\mathsf {Enc},\mathsf {Eval}, \mathsf {Dec})\) is semantically secure if for all polynomial-size distinguishers \(\mathcal {D}\) there exists a negligible function  such that for all \(\lambda \in \mathbb {N}\), all pairs of message \((m_0, m_1)\), it holds that
such that for all \(\lambda \in \mathbb {N}\), all pairs of message \((m_0, m_1)\), it holds that

where \((\mathsf {sk}, \mathsf {pk}) \leftarrow \mathsf {KeyGen}(1^\lambda )\).
3.1 Linear Decrypt-and-Multiply
We consider schemes with a fine-grained correctness property. Specifically, we require that the decryption consists of the application of a linear function in the secret key, followed by some publicly computable function. Furthermore, we require that such a procedure allows us to specify an arbitrary constant \(\omega \) that is multiplied to the resulting plaintext. We refer to such schemes as linear decrypt-and-multiply schemes. This property was introduced in an oral presentation by Micciancio [50] and recently formalized by Brakerski et al. [17]. We stress that all major candidate FHE constructions satisfy (or can be adapted to) such a constraint, e.g., [2, 19, 36]. We recall the definition in the following.
Definition 7 (Decrypt-and-Multiply)
We call a homomorphic encryption scheme \((\mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Eval}, \mathsf {Dec})\) a decrypt-and-multiply scheme, if there exists bounds \(B = B(\lambda )\) and \(Q = Q(\lambda )\) and an algorithm \( \mathsf {Dec{ \& }Mult}\) such that the following holds. For every \(q \ge Q\), all \((\mathsf {sk}, \mathsf {pk})\) in the support of \(\mathsf {KeyGen}(1^\lambda ,q)\), every \(\ell \)-inputs circuit \(C\), all inputs \((m_1, \dots , m_\ell )\), all \(c_i\) in the support of \(\mathsf {Enc}(\mathsf {pk}, m_i)\) and every \(\omega \in \mathbb {Z}_q\) that
where \( \mathsf {Dec{ \& }Mult}\) is a linear function in \(\mathsf {sk}\) over \(\mathbb {Z}_q\) and \(|e| \le B\) with all but negligible probability.
In our construction, we will need some additional structure for the modulus q. Fortunately, most LWE-based FHE schemes can be instantiated with an arbitrary q that does not depend on any secret input but only on the security parameter. Moreover, LWE-based FHE schemes can be instantiated with any (sufficiently large) modulus q without affecting the worst-case hardness of the underlying LWE problem [53]. In an abuse of notation, we often write \(\mathsf {KeyGen}(1^\lambda ; q)\) to fix the modulus q in the key generation algorithm. In favor of a simpler analysis, we assume that e is always non-negative. Note that this is without loss of generality as it can be always guaranteed by adding B to the result of \( \mathsf {Dec{ \& }Mult}\) and setting a slightly looser bound \(B = 2B\).
3.2 Split Decryption
We define the notion of homomorphic encryption with split decryption, which is going to be central in our work. Loosely speaking, a scheme has split decryption if the decryption algorithm consists of two subroutines: A private algorithm (that depends on the secret key) that on input a ciphertext \(c\) computes a small hint \(\rho \), and a publicly computable algorithm that takes as input \(\rho \) and \(c\) and returns the corresponding plaintext. We henceforth refer to such schemes as split homomorphic encryption. We introduce the syntax in the following.
Definition 8 (Split Decryption)
A homomorphic encryption scheme \((\mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Eval}, \mathsf {Dec})\) has split decryption if the decryption algorithm \(\mathsf {Dec}\) consist of the following two subroutines.
-
\(\mathsf {PDec}(\mathsf {sk}, c){:}\) On input the secret key \(\mathsf {sk}\) and a ciphertext \(c\), the partial decryption algorithm returns a decryption hint \(\rho \).
-
\(\mathsf {Rec}(\rho , c){:}\) On input the hint \(\rho \) and a ciphertext \(c\), the recovery algorithm returns a message \(m\).
The notion of correctness is extended canonically.
Definition 9 (Split Correctness)
A homomorphic encryption scheme with split decryption \((\mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Eval}, \mathsf {PDec}, \mathsf {Rec})\) is correct if for all \(\lambda \in \mathbb {N}\), all \(\ell \)-inputs circuits \(C\) in the supported family, all inputs \((m_1, \dots , m_\ell )\), all \((\mathsf {sk}, \mathsf {pk})\) in the support of \(\mathsf {KeyGen}(1^\lambda )\), and all \(c_i\) in the support of \(\mathsf {Enc}(\mathsf {pk}, m_i)\) it holds that
where \(c= \mathsf {Eval}(\mathsf {pk}, C, (c_1, \dots , c_\ell ))\).
Beyond the standard compactness for homomorphic encryption, a scheme with split decryption must satisfy the additional property that the size of the decryption hint \(\rho \) is independent (or, more generally, sublinear) of the size of the message. Furthermore, the size of the public key and of a fresh encryption of a message \(m\) should depend polynomially in the security parameter and otherwise be linear in the size of the output. These are the properties that make split decryption non-trivial and that are going to be our main leverage to bootstrap this primitive into more powerful machinery. We formally characterize these requirements below.
Definition 10 (Split Compactness)
A homomorphic encryption scheme with split decryption \((\mathsf {KeyGen},\mathsf {Enc},\mathsf {Eval}, \mathsf {PDec}, \mathsf {Rec})\) is compact if there exists a polynomial  and such that for all \(\lambda \in \mathbb {N}\), all \(\ell \)-inputs circuits \(C\) in the supported family, all inputs \((m_1, \dots , m_\ell )\), all \((\mathsf {sk}, \mathsf {pk})\) in the support of \(\mathsf {KeyGen}(1^\lambda )\), and all \(c_i\) in the support of \(\mathsf {Enc}(\mathsf {pk}, m_i)\) it holds that
and such that for all \(\lambda \in \mathbb {N}\), all \(\ell \)-inputs circuits \(C\) in the supported family, all inputs \((m_1, \dots , m_\ell )\), all \((\mathsf {sk}, \mathsf {pk})\) in the support of \(\mathsf {KeyGen}(1^\lambda )\), and all \(c_i\) in the support of \(\mathsf {Enc}(\mathsf {pk}, m_i)\) it holds that
-
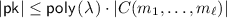 ,
, -
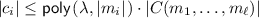 , and
, and -
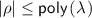
where \(\rho = \mathsf {PDec}(\mathsf {sk}, \mathsf {Eval}(\mathsf {pk}, C, (c_1, \dots , c_\ell )))\).
Finally the notion of semantic security for split schemes requires that the decryption hint \(\rho \) for a certain ciphertext does not reveal any information beyond the corresponding plaintext. Note that we define a very weak notion where the above must hold only for a bounded number of ciphertexts, and the inputs are fixed prior to the public parameters of the scheme.
Definition 11 (Split Security)
A homomorphic encryption scheme with split decryption \((\mathsf {KeyGen},\mathsf {Enc},\mathsf {Eval}, \mathsf {PDec}, \mathsf {Rec})\) is secure if for all polynomial-size distinguishers \(\mathcal {D}\) there exists a negligible function  such that for all \(\lambda \in \mathbb {N}\), all polynomials \(\beta = \beta (\lambda )\), all pairs of messages \((m_0, m_1)\), all vectors of circuits \((C_1, \dots , C_\beta )\) such that, for all \(i \in [\beta ]\), \(C_i(m_0) = C_i(m_1)\) it holds that
such that for all \(\lambda \in \mathbb {N}\), all polynomials \(\beta = \beta (\lambda )\), all pairs of messages \((m_0, m_1)\), all vectors of circuits \((C_1, \dots , C_\beta )\) such that, for all \(i \in [\beta ]\), \(C_i(m_0) = C_i(m_1)\) it holds that

where \((\mathsf {sk}, \mathsf {pk}) \leftarrow \mathsf {KeyGen}(1^\lambda )\), for all \(b\in \{0,1\}\) define \(c_b \leftarrow \mathsf {Enc}(\mathsf {pk}, m_b)\) and, for all \(i\in [\beta ]\) and all \(b\in \{0,1\}\), define \(\rho _{(i, b)} \leftarrow \mathsf {PDec}(\mathsf {sk}, \mathsf {Eval}(\mathsf {pk}, C_i, c_b))\).
3.3 Damgård-Jurik Encryption
In the following we recall a variant of the Damgård-Jurik encryption linearly homomorphic encryption scheme [23]. We present a variant of the scheme that satisfies the notion of split correctness, which is going to be instrumental for our purposes. The scheme is parametrized by a non-negative integer \(\zeta \) that we assume is given as input to all algorithms.
-
\(\mathsf {DJ.KeyGen}(1^\lambda )\): On input the security parameter \(1^\lambda \), sample a uniform Blum integer \(N = pq\), where p and q are \(\lambda \)-bits primes. Set \(\mathsf {pk}= (N, \zeta )\) and \(\mathsf {sk}= \varphi (N)\).
-
\(\mathsf {DJ.Enc}(\mathsf {pk}, m)\): On input a message \(m\in \mathbb {Z}_{N^\zeta }\), sample a random
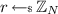 and compute $$\begin{aligned} c= r^{N^\zeta } \cdot (1+N)^{m} \mod N^{\zeta +1}. \end{aligned}$$
and compute $$\begin{aligned} c= r^{N^\zeta } \cdot (1+N)^{m} \mod N^{\zeta +1}. \end{aligned}$$ -
\(\mathsf {DJ.Eval}(\mathsf {pk}, f, (c_1, \dots , c_\ell ))\): On input a vector of ciphertexts \((c_1, \dots , c_\ell )\) and a linear function \(f = (\alpha _1, \dots , \alpha _\ell ) \in \mathbb {Z}_{N^\zeta }^\ell \), compute
$$ c= \prod ^\ell _{i=1} c_i^{\alpha _1} \mod N^{\zeta +1}. $$ -
\(\mathsf {DJ.PDec}(\mathsf {sk}, c)\): On input a ciphertext \(c\), set \(s = c\mod N\). Then compute \(N^{-\zeta }\) such that \(N^{\zeta } \cdot N^{-\zeta } = 1 \mod \varphi (N)\) using the extended Euclidean algorithm. Return
$$\begin{aligned} \rho = s^{N^{-\zeta }} \mod N. \end{aligned}$$ -
\(\mathsf {DJ.Rec}(\rho , c)\): On input a hint \(\rho \) and a ciphertext \(c\), compute
$$\begin{aligned} (1+N)^m= c/\rho ^{N^\zeta } \mod N^{\zeta +1} \end{aligned}$$and recover \(m\) using the polynomial-time algorithm described in [23].
It is well known that the scheme satisfies (standard) semantic security assuming the intractability of the decisional composite residuosity (DCR) problem, as defined in [52]. To prove correctness, we are going to use the fact that
for all non-negative integers \((x,\zeta )\). We refer the reader to [49] for a proof of this equality. Recall that \(c = r^{N^\zeta } \cdot (1+N)^m\) and that
Therefore we have that
by an application of Eq. (1). Taking the inverse on both sides of the equation above we obtain
as desired for correctness. Although such a scheme does not immediately give us a secure split LHE, we highlight a few salient properties that we are going to leverage in our main constructions.
Small Hints: The scheme satisfies a weakened notion of split compactness where the decryption hint is much smaller than the message space. The hint \(\rho \in \mathbb {Z}_N\) consists of \(\lceil \log (N)\rceil \) bits and in particular is independent of the size of the message space \(\mathbb {Z}_{N^\zeta }\), as the integer \(\zeta \) can be set to be arbitrarily large (within the range of polynomials in \(\lambda \)).
Simulatable Hints: Given a ciphertext \(c\) and a plaintext value \(m\), one can efficiently compute a ciphertext \(\tilde{c}\) such that the homomorphic sum of \(c\) and \(\tilde{c}\) results in a uniform encryption of \(m\) and the corresponding decryption hint can be computed given only the random coins used to generate \(\tilde{c}\). Concretely, let
for some  , then \(\rho = r\).
, then \(\rho = r\).
Dense Ciphertexts: Sampling a random integer in \(\mathbb {Z}_{N^{\zeta +1}}\) gives a well-formed ciphertext with all but negligible probability. This is because the group order \(\varphi (N)\cdot N^\zeta \) is close to \(N^{\zeta +1}\), i.e.,  .
.
4 Split Fully-Homomorphic Encryption
In the following we present our instantiation of FHE with split decryption. We first present a scheme from standard assumptions which assumes the existence of (a structured version of) a random oracle, then we propose plausible candidates for such an oracle.
4.1 Construction in the Presence of an Oracle
Before we delve into the details of our construction we give a definition of the oracle function that we consider. The oracle is parametrized by a pair of public keys for an FHE and an LHE scheme \((\mathsf {pk}_{\mathsf {FHE}}, \mathsf {pk}_{\mathsf {LHE}})\) and two integers \((q, \tilde{q})\). On input a bitstring \(x\in \{0,1\}^*\), the oracle returns a uniform LHE encryption of a random value in \(\mathbb {Z}_q\) and an FHE encryption of the same value rounded to the closest divisor of \(\tilde{q}\). The oracle is deterministic and it is accessible by all parties, thus on input the same x, the oracle will always output the same pair of ciphertexts. The interface is formally defined in the following.
-
\(\mathcal {O}_{(\mathsf {pk}_{\mathsf {FHE}}, \mathsf {pk}_{\mathsf {LHE}}, q, \tilde{q})}(x)\): On input a string \(x\in \{0,1\}^*\) return two uniformly distributed ciphertexts
$$\begin{aligned} \mathsf {LHE.Enc}(\mathsf {pk}_{\mathsf {LHE}}, m) \text { and } \mathsf {FHE.Enc}\left( \mathsf {pk}_\mathsf {FHE}, - \left\lfloor m/ \tilde{q}\right\rfloor \cdot \tilde{q}\right) \end{aligned}$$where
 .
.
It is useful to observe that the oracle output, along with an LHE encryption of the FHE secret key, gives us a uniformly distributed LHE encryption of a uniform value in \(\mathbb {Z}_{\tilde{q}}\). This is because we can leverage the decrypt-and-multiply algorithm \( \mathsf {Dec{ \& }Mult}\) of the FHE scheme (matching the FHE domain with the LHE paintext space appropriately) to compute \(\mathsf {LHE.Enc}\left( \mathsf {pk}_\mathsf {LHE}, - \left\lfloor m/ \tilde{q}\right\rfloor \cdot \tilde{q} + \textit{noise}\right) \), where \(\textit{noise}\) is the decryption noise of the FHE scheme. Homomorphically summing up this term with the first output of the oracle we obtain
for an appropriate choice of \(\tilde{q}\), i.e., we obtain an ciphertext which is statistically indistinguishable from an LHE encryption of a uniform element of \(\mathbb {Z}_{\tilde{q}}\).
Description. We are now in the position of giving formal description of our scheme. We assume the existence of the following primitives:
-
A fully-homomorphic encryption scheme \(\mathsf {FHE}= (\mathsf {FHE.KeyGen}, \mathsf {FHE.Enc}, \mathsf {FHE.Eval}, \mathsf {FHE.Dec})\) with linear decrypt-and-multiply and with noise bound B.
-
A linearly homomorphic encryption \(\mathsf {LHE}= (\mathsf {LHE.KeyGen}, \mathsf {LHE.Enc},\mathsf {LHE.Eval},\mathsf {LHE.PDec}, \mathsf {LHE.Rec})\) with small and simulatable decryption hints (e.g., the Damgård-Jurik encryption scheme as described in Sect. 3.3).
If the underlying FHE scheme is levelled then so is going to be the resulting split FHE. Conversely, if the FHE scheme supports the evaluation of unbounded circuits, then so does the resulting split FHE construction. The scheme is formally described in the following.

Analysis. We formally analyze our scheme in the following. During the analysis, we set the parameters on demand and we show afterwards that our choices lead to a satisfiable set of constraints for which the underlying computational problems are still conjectured to be hard. The following theorem establishes correctness.
Theorem 3
(Split Correctness). Let \(q \ge 2^k + 2^{\lceil \log (\tilde{q} + (k+1)B) \rceil }\). Let \(\mathsf {FHE}\) be a correct fully-homomorphic encryption scheme with linear decrypt-and-multiply and let \(\mathsf {LHE}\) be a split correct linearly-homomorphic encryption scheme. Then the scheme as described above satisfies split correctness.
Proof
Let us rewrite
where \(c= \mathsf {LHE.Eval}(\mathsf {pk}_\mathsf {LHE}, \tilde{g}, (c_{(\mathsf {LHE},1)}, \dots , c_{(\mathsf {LHE},n)}, d, a))\). We first expand the d term as
by the correctness of the LHE scheme, where
and \(c_i = \mathsf {FHE.Enc}(\mathsf {pk}_\mathsf {FHE}, m_i)\). Thus by the decrypt-and-multiply correctness of the FHE scheme we can rewrite
For the a variable we have that \(a = \mathsf {LHE.Enc}(\mathsf {pk}_\mathsf {LHE}, r)\), for some uniform  , by definition of the oracle \(\mathcal {O}_{(\mathsf {pk}_\mathsf {FHE}, \mathsf {pk}_\mathsf {LHE}, q, \tilde{q})}\). Recall that
, by definition of the oracle \(\mathcal {O}_{(\mathsf {pk}_\mathsf {FHE}, \mathsf {pk}_\mathsf {LHE}, q, \tilde{q})}\). Recall that
where \(\tilde{a} = \mathsf {FHE.Enc}(\mathsf {pk}_\mathsf {FHE}, -\lfloor r / \tilde{q} \rfloor \cdot \tilde{q})\). Thus \(c= \mathsf {LHE.Enc}\left( \mathsf {pk}_\mathsf {LHE}, \tilde{m}\right) \) where
by the correctness of the FHE scheme. Note that the sum \(\tilde{e}+e\) is bounded from above by \((k+1) \cdot B\), whereas the term \(\tilde{r}\) is trivially bounded from above by \(\tilde{q}\). This implies that the output of the circuit is encoded in the higher order bits of \(\tilde{m}\) with probability 1, for a large enough q.
We then argue about the split security of the scheme. We remark that we analyze security in the presence of an oracle and we refer the reader to Sect. 4.2 for concrete instantiations.
Theorem 4
(Split Security). Let \(\tilde{q} \ge 2^\lambda \cdot (k+1) \cdot B\) and let \(q \ge 2^\lambda \cdot \tilde{q}\). Let \(\mathsf {FHE}\) be a semantically secure fully-homomorphic encryption scheme and let \(\mathsf {LHE}\) be a semantically secure linearly homomorphic encryption scheme with simulatable decryption hints. Then the scheme as described above satisfies split security in the \(\mathcal {O}_{(\mathsf {pk}_\mathsf {FHE}, \mathsf {pk}_\mathsf {LHE}, q, \tilde{q})}\)-hybrid model.
Proof
Let \((m_0, m_1, C_1, \dots , C_\beta )\) be the inputs specified by the adversary at the beginning of the experiments. Consider the following series of hybrids.
Hybrid \(\mathcal {H}_0\): Is defined as the original experiment. Denote the distribution induced by the random coins of the challenger by
where
and \(\rho _i\) is computed as \(\mathsf {PDec}(\mathsf {sk}, \mathsf {Eval}(\mathsf {pk}, C_i, c))\).
Hybrids \(\mathcal {H}_1 \dots \mathcal {H}_\beta \): Let \(d^{(i)}\) be the variable d defined during the execution of \(\mathsf {Eval}(\mathsf {pk}, C_i, c)\). The i-th hybrid \(\mathcal {H}_i\) is defined to be identical to \(\mathcal {H}_{i-1}\), except that the oracle \(\mathcal {O}_{(\mathsf {pk}_\mathsf {FHE}, \mathsf {pk}_\mathsf {LHE}, q, \tilde{q})}\) on input \(d^{(i)}\) is programmed to output some a (along with a well-formed \(\tilde{a}\)) such that the resulting \(c\) is of the form
where \(\mathsf {ECC}\) is the high-order bits encoding defined in the evaluation algorithm, \(\tilde{e} + e\) is the sum of the decryption noises of the ciphertexts \((d^{(1)}, \dots , d^{(k)}, \tilde{a})\), as defined in the evaluation algorithm, and  . Then \(\tilde{\rho }_i\) is defined to be the decryption hint of \(c\) computed using the random coins of a.
. Then \(\tilde{\rho }_i\) is defined to be the decryption hint of \(c\) computed using the random coins of a.
First observe that \(\tilde{e} + e\) is efficiently computable given the secret key of the FHE scheme and therefore \(\tilde{\rho }_i\) is also computable in polynomial time. It is important to observe that the distribution of \(c\) is identical to the previous hybrid and the difference lies only in the way \(\tilde{\rho }_i\) is computed. Since the LHE scheme has simulatable hints, it follows that the distribution of \(\mathcal {H}_i\) is identical to that of \(\mathcal {H}_{i-1}\) and the change described here is only syntactical. That is,
Hybrids \(\mathcal {H}_{\beta +1} \dots \mathcal {H}_{2\beta }\): The \((\beta + i)\)-th hybrid differs from the previous one in the sense that a is programmed such that
where  . Note that the distributions induced by the two hybrids differ only in case where \(r \in R\), where \(R = \{q - (q \mod \tilde{q}), \dots , q\}\). Since \(\tilde{q} / q \le 2^{-\lambda }\) we have that the two distributions are statistically close.
. Note that the distributions induced by the two hybrids differ only in case where \(r \in R\), where \(R = \{q - (q \mod \tilde{q}), \dots , q\}\). Since \(\tilde{q} / q \le 2^{-\lambda }\) we have that the two distributions are statistically close.
Hybrids \(\mathcal {H}_{2\beta +1} \dots \mathcal {H}_{3\beta }\): The \((\beta + i)\)-th hybrid is defined to be identical to the previous ones except that a is programmed such that
I.e., the noise term \(\tilde{e}\) is omitted from the computation. Thus the only difference with respect to the previous hybrid is whether the noise term \(\tilde{e} + e\) is included in the ciphertext or not. Since \(\tilde{e} + e\) is bounded from above by \((k+1)\cdot B\) and \(\tilde{q} \ge 2^\lambda \cdot (k+1)\cdot B\), by Lemma 1 the distribution induced by this hybrid is statistically indistinguishable from that of the previous one.
Hybrids \(\mathcal {H}_{3\beta + 1} \dots \mathcal {H}_{3\beta + n}\): The \((3\beta +i)\)-th hybrid is defined as the previous one, except that the ciphertext \(c_{(\mathsf {LHE}, i)}\) in the public parameters is computed as the encryption of 0. Note that the secret key of the LHE scheme is no longer used in the computation of \((\tilde{\rho }_1, \dots , \tilde{\rho }_\beta )\) and therefore indistinguishability follows from an invocation of the semantic security of the LHE scheme. Specifically, the following distributions are computationally indistinguishable
Hybrid \(\mathcal {H}^{(b)}_{3\beta + n}\): We define the hybrid \(\mathcal {H}^{(b)}_{3\beta + n}\) as \(\mathcal {H}_{3\beta + n}\) with the challenger bit fixed to b. Note that the distribution induced by these hybrids is
where
Observe that the secret key of the FHE scheme is no longer encoded in the public parameters and is not needed to compute \((\tilde{\rho }_1, \dots , \tilde{\rho }_\beta )\) either. It follows that any advantage that the adversary has in distinguishing \(\mathcal {H}^{(0)}_{3\beta + n}\) from \(\mathcal {H}^{(1)}_{3\beta + n}\) cannot be greater than the advantage in distinguishing \(\mathsf {FHE.Enc}(\mathsf {pk}_\mathsf {FHE}, m_0)\) from \(\mathsf {FHE.Enc}(\mathsf {pk}_\mathsf {FHE}, m_1)\). Thus, computational indistinguishability follows from an invocation of the semantic security of the FHE scheme. This concludes our proof.
Parameters. When instantiating the LHE scheme with the Damgård-Jurik encryption scheme (as described in Sect. 3.3) and the FHE scheme with any LWE-based scheme with linear decrypt-and-multiply (e.g., the scheme proposed in [36]) we obtain a split FHE which satisfies the notion of split compactness: The hint \(\rho \) is of size  and in particular is arbitrarily smaller than the size of the plaintext space \(q = N^\zeta \). For essentially any choice of the LWE-based FHE scheme with modulus q, the size of the public key and fresh ciphertexts depends polynomially in \(\lambda \) and linearly in \(\log (q) = \log (N^\zeta )\), which gives us the desired bound. The analysis above sets the following additional constraints:
and in particular is arbitrarily smaller than the size of the plaintext space \(q = N^\zeta \). For essentially any choice of the LWE-based FHE scheme with modulus q, the size of the public key and fresh ciphertexts depends polynomially in \(\lambda \) and linearly in \(\log (q) = \log (N^\zeta )\), which gives us the desired bound. The analysis above sets the following additional constraints:
-
\(q \ge 2^k + 2^{\lceil \log (\tilde{q} + (k+1)B) \rceil }\),
-
\(q \ge 2^\lambda \cdot \tilde{q}\), and
-
\(\tilde{q} \ge 2^\lambda \cdot (k+1) \cdot B\)
which are always satisfied for \(q = N^\zeta \), by setting the integer \(\zeta \) to be large enough. Note that this choice of parameters fixes the modulus of the FHE with linear decrypt-and-multiply to \(\mathbb {Z}_{N^\zeta }\), which is super-polynomially larger than the noise bound B. Finally, the LWE parameter n is free and can be set to any value for which the corresponding problem (with super-polynomial modulus-to-noise ratio) is conjectured to be hard.
4.2 Instantiating the Oracle
To complete the description of our scheme, we discuss a few candidate instantiations for the oracle \(\mathcal {O}_{(\mathsf {pk}_{\mathsf {FHE}}, \mathsf {pk}_{\mathsf {LHE}}, q, \tilde{q})}\). We require the underlying LHE scheme to have a dense ciphertext domain (which is the case for the Damgård-Jurik encryption scheme). Both of our proposal introduce new circularity assumptions between the FHE and the LHE schemes.
An alternate way to think of the oracle in Theorem 4 is to see it as an obfuscation for a special program, which is sufficient for realizing split FHE. The candidate constructions that we provide below can be seen as a very natural and simple obfuscation of this special program.
A Simple Candidate. Let \(\mathfrak {C}\) be the ciphertext domain of \(\mathsf {LHE}\). Our first instantiation hardwires an FHE encryption of the LHE secret key \(c_\mathsf {FHE}\leftarrow \mathsf {FHE.Enc}(\mathsf {pk}_{\mathsf {FHE}}, \mathsf {sk}_{\mathsf {LHE}})\). We fix the random coins of the algorithm (whenever needed) by drawing them from the evaluation of a cryptographic hash function \(\mathsf {Hash}\) over the input. The intuition for our candidate is very simple: The LHE ciphertext is obliviously sampled without the knowledge of the underlying plaintext (which is the reason why we need dense ciphertexts) whereas the FHE term is computed by evaluating the decryption circuit homomorphically and rounding the resulting message to the closest multiple of \(\tilde{q}\).
-
\(\mathcal {O}_{(\mathsf {pk}_{\mathsf {FHE}}, \mathsf {pk}_{\mathsf {LHE}}, q, \tilde{q})}(x)\): On input a string \(x\in \{0,1\}^*\) sample
 , using \(\mathsf {Hash}(x)\) as the random coins, then compute $$ \tilde{y} \leftarrow \mathsf {FHE.Eval}\left( \mathsf {pk}_\mathsf {FHE}, -\left\lfloor \mathsf {LHE.Dec}(\cdot , y) / \tilde{q} \right\rfloor \cdot \tilde{q}, c_\mathsf {FHE}\right) $$
, using \(\mathsf {Hash}(x)\) as the random coins, then compute $$ \tilde{y} \leftarrow \mathsf {FHE.Eval}\left( \mathsf {pk}_\mathsf {FHE}, -\left\lfloor \mathsf {LHE.Dec}(\cdot , y) / \tilde{q} \right\rfloor \cdot \tilde{q}, c_\mathsf {FHE}\right) $$and return \((y, \tilde{y})\).
Observe that y is an element in the ciphertext domain of \(\mathsf {LHE}\) and it is of the form \(y =\mathsf {LHE.Enc}(\mathsf {pk}_\mathsf {LHE}, m)\), for some \(m\in \mathbb {Z}_q\), since \(\mathsf {LHE}\) has a dense ciphertext domain. Furthermore, by the correctness of the FHE and the LHE scheme, we have that
It follows that the pair \((y, \tilde{y})\) is syntactically well formed. However, a closer look to the oracle instantiation reveals two lingering assumptions.
-
(1)
Circular Security: The addition of \(c_\mathsf {FHE}= \mathsf {FHE.Enc}(\mathsf {pk}_{\mathsf {FHE}}, \mathsf {sk}_{\mathsf {LHE}})\) introduces a circular dependency in the security of the LHE and FHE schemes (recall that our split FHE construction includes in the public key an encryption of \(\mathsf {sk}_\mathsf {FHE}\) under \(\mathsf {pk}_\mathsf {LHE}\)). Circular security is however widely considered to be a very mild assumption and currently is the only known approach to construct plain (as opposed to levelled) FHE from LWE via the bootstrapping theorem [32].
-
(2)
Correlations: Although \(\tilde{y}\) is an FHE encryption of the correct value, it is not necessarily uniformly distributed, conditioned on y. In particular the randomness of \(\tilde{y}\) may depend in some intricate way on the low-order bits of \(m\). For the specific case of LWE-based schemes, the noise term might carry some information about \(m\mod \tilde{q}\), which could introduce some harmful correlation. However, the noise function is typically highly non-linear and therefore appears to be difficult to exploit. We also stress that we only consider honest executions of the \(\mathsf {FHE.Eval}\) algorithm.
While (1) can be regarded as a standard assumption, we view (2) as a natural conjecture which we believe holds true for any natural/known candidate instantiation of the FHE and LHE schemes. In light of these considerations, we conjecture that the implementation as describe above already leads to a secure split FHE scheme.
Towards Removing Correlations. A natural approach towards removing the correlation of the LHE and FHE ciphertexts is that of ciphertext sanitization [24]: One could expect that repeatedly bootstrapping the FHE ciphertext would decorrelate the noise from the companion LHE ciphertext. Unfortunately our settings are different than those typically considered in the literature, in the sense that the santiziation procedure must be carried out by the distinguisher and therefore cannot use private random coins. Although it appears hard to formally analyze the effectiveness of these methods in our settings, we expect that these techniques might (at least heuristically) help to obliterate harmful correlations. In this work we take a different route and we suggest a simple heuristic method to prevent correlations. In a nutshell, the idea is to sample a set of random plaintexts and define the random string as the sum of a uniformly sampled subset S of these plaintext. The key observation is that subset sum is a linear operation and therefore can be performed directly in the LHE scheme, which implies that the leakage of the FHE scheme cannot depend on S. As for the previous construction, our instantiation contains and a ciphertext \(c_\mathsf {FHE}= \mathsf {FHE.Enc}(\mathsf {pk}_{\mathsf {FHE}}, \mathsf {sk}_{\mathsf {LHE}})\). The scheme is parametrized by some  , which defines the size of the set S. In the following description we present the algorithm as randomized, although this simplification can be easily bypassed with standard techniques (e.g., computing the random coins using a cryptographic hash \(\mathsf {Hash}(x)\)).
, which defines the size of the set S. In the following description we present the algorithm as randomized, although this simplification can be easily bypassed with standard techniques (e.g., computing the random coins using a cryptographic hash \(\mathsf {Hash}(x)\)).
-
\(\mathcal {O}_{(\mathsf {pk}_{\mathsf {FHE}}, \mathsf {pk}_{\mathsf {LHE}}, q, \tilde{q})}(x)\): On input a string \(x\in \{0,1\}^*\) sample a random set
 .
.Then, for all \(i \in [\sigma ]\), do the following:
-
If \(S_i = 1\), sample a uniform
 .
. -
If \(S_i = 0\), sample a uniform encryption
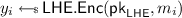 , for a random known \(m_i\).
, for a random known \(m_i\).
Then compute
$$ \tilde{y} \leftarrow \mathsf {FHE.Eval}\left( \mathsf {pk}_\mathsf {FHE}, -\sum ^\sigma _{i=1}\left\lfloor \mathsf {LHE.Dec}(\cdot , y_i) / \tilde{q} \right\rfloor \cdot \tilde{q}, c_\mathsf {FHE}\right) . $$Let f be the following linear function
$$ f(x_1, \dots , x_{|S|}) = \sum _{i \in S} x_i + \sum _{i\notin S} \lfloor m_i / \tilde{q}\rfloor \cdot \tilde{q} $$then compute \(y \leftarrow \mathsf {LHE.Eval}\left( \mathsf {pk}_{\mathsf {LHE}}, f, \left\{ y_i\right\} _{i\in S}\right) \) and return \((y, \tilde{y})\).
-
To see why the implementation is syntactically correct, observe that
by the evaluation correctness of the FHE scheme. Invoking to the correctness of the LHE scheme we have that
which is exactly what we want, except that \(\tilde{m}\) is slightly larger than \(\tilde{q}\), by a factor of at most \(\sigma \). This can still be used in our main construction by adjusting the error correcting code accordingly. The intuition why we believe that this variant is secure is that the leakage in the FHE randomness cannot depend on the set S, since the distributions of all \(y_i\) are statistically close (recall that LHE has dense ciphertexts). Thus, S (which is chosen uniformly) resembles the behavior of a binary extractor on \((m_i \mod \tilde{q})\). Nevertheless, proving a formal statement remains an interesting open question.
5 Split Fully-Homomorphic Encryption \(\implies \) Obfuscation
In order to construct fully-fledged iO from split FHE, we rely on a theorem from Lin et al. [44], which we recall in the following. Roughly speaking, the theorem states that, under the assumption that the LWE problem is sub-exponentially hard, it suffices to consider circuits with a polynomial-size input domain and obfuscators that output obfuscated circuits of size slightly sublinear in size of the truth table of the circuit.
Theorem 5
([44]). Assuming sub-exponentially hard LWE, if there exists a sub-exponentially secure indistinguishability obfuscator for \(\mathsf {P}^\mathsf {log} / \mathsf {poly}\) with non-trivial efficiency, then there exists an indistinguishability obfuscator for \(\mathsf {P} / \mathsf {poly}\) with sub-exponential security.
Here \(\mathsf {P}^\mathsf {log} / \mathsf {poly}\) denotes the class of polynomial-size circuits with inputs of length \(\eta = O(\log (\lambda ))\) and by non-trivial efficiency we mean that the size of the obfuscated circuit is bounded by  , for some constant \(\varepsilon > 0\). Note that the above theorem poses no restriction on the runtime of the obfuscator, which can be as large as
, for some constant \(\varepsilon > 0\). Note that the above theorem poses no restriction on the runtime of the obfuscator, which can be as large as  .
.
In the following we show how to construct an obfuscator for \(\mathsf {P}^\mathsf {log} / \mathsf {poly}\) with non-trivial efficiency. We assume only the existence of a (levelled) split FHE scheme \(\mathsf {sFHE}= (\mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Eval}, \mathsf {PDec}, \mathsf {Rec})\).
-
\(\mathsf {iO}(C)\): On input the description of a circuit \(C\), sample a fresh key pair \((\mathsf {sk}, \mathsf {pk}) \leftarrow \mathsf {KeyGen}(1^\lambda )\) and compute \(c\leftarrow \mathsf {Enc}(\mathsf {pk}, C)\). For all \(i \in \left[ 2^{\eta / 2}\right] \) define the universal circuit \(\mathfrak {U}_i\) as
$$ \mathfrak {U}_i(C) = C\left( (i-1) \cdot 2^{\eta / 2}\right) \Vert \dots \Vert C\left( i \cdot 2^{\eta / 2} -1\right) . $$Then compute \(c_i \leftarrow \mathsf {Eval}(\mathsf {pk}, \mathfrak {U}_i, c)\) and \(\rho _i \leftarrow \mathsf {PDec}(\mathsf {sk}, c_i)\). The obfuscated circuit is defined to be \(\left( \mathsf {pk}, c, \rho _1, \dots , \rho _{2^{\eta / 2}} \right) \).
First we discuss how to evaluate an obfuscated circuit: On input some \(x\in \{0,1\}^{\eta }\), parse it as an integer and round it to the nearest multiple of \(2^{\eta /2}\) (let such integer be \(\bar{x}\)) such that \(\bar{x} \le x\). Then compute \(c_{\bar{x}} \leftarrow \mathsf {Eval}(\mathsf {pk}, \mathfrak {U}_{\bar{x}}, c)\) and \(m\leftarrow \mathsf {Rec}(\rho _{\bar{x}}, c_{\bar{x}})\). Read the output as the \((x - \bar{x})\)-th bit of \(m\).
Analysis. Note that the runtime of the obfuscator is dominated by \(2^{\eta /2}\) evaluations of the split FHE ciphertext, where each subroutine homomorphically evaluates the circuit \(C\) \(2^{\eta / 2}\)-many times. Thus the total runtime of the obfuscator is in the order of  . We now argue that our obfuscator has non trivial efficiency in terms of output size. We analyze the size of each component of the obfuscated circuit:
. We now argue that our obfuscator has non trivial efficiency in terms of output size. We analyze the size of each component of the obfuscated circuit:
-
By the compactness of the split FHE scheme, the public key \(\mathsf {pk}\) grows linearly with the size of the output domain, i.e., \(2^{\eta /2}\), and polynomially in the security parameter.
-
The ciphertext \(c\) grows linearly with the size of the encrypted message and therefore, by the compactness of the split FHE scheme, bounded by
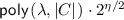 .
. -
Each decryption hint \(\rho _i\) is of size
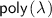 , since the underlying split FHE is compact. As an obfuscated circuit consists of \(2^{\eta /2}\)-many decryption hints, the size of the vector \((\rho _1, \dots , \rho _{2^{\eta /2}})\) is
, since the underlying split FHE is compact. As an obfuscated circuit consists of \(2^{\eta /2}\)-many decryption hints, the size of the vector \((\rho _1, \dots , \rho _{2^{\eta /2}})\) is 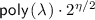 .
.
It follows that the total size of the obfuscated circuit is bounded from above by  . What is left to be shown is that our obfuscator satisfies the notion of indistinguishability obfuscation.
. What is left to be shown is that our obfuscator satisfies the notion of indistinguishability obfuscation.
Theorem 6
(Indistinguishability Obfuscation). Let \(\mathsf {sFHE}\) be a sub-exponentially secure levelled split FHE scheme. Then the scheme as described above is a sub-exponentially secure indistinguishability obfuscator.
Proof
By the perfect correctness of the split FHE scheme it follows that the obfuscated circuit is functionally equivalent to the plain circuit. Indistinguishability follows immediately from the split security of \(\mathsf {sFHE}\): If the split FHE is secure against a distinguisher running in sub-exponential time, then so is \(\mathsf {iO}\).
References
Agrawal, S.: Indistinguishability obfuscation without multilinear maps: new methods for bootstrapping and instantiation. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part I. LNCS, vol. 11476, pp. 191–225. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17653-2_7
Alperin-Sheriff, J., Peikert, C.: Faster bootstrapping with polynomial error. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 297–314. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_17
Ananth, P., Jain, A., Lin, H., Matt, C., Sahai, A.: Indistinguishability obfuscation without multilinear maps: new paradigms via low degree weak pseudorandomness and security amplification. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part III. LNCS, vol. 11694, pp. 284–332. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_10
Ananth, P., Jain, A.: Indistinguishability obfuscation from compact functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015, Part I. LNCS, vol. 9215, pp. 308–326. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-47989-6_15
Ananth, P., Sahai, A.: Projective arithmetic functional encryption and indistinguishability obfuscation from degree-5 multilinear maps. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part I. LNCS, vol. 10210, pp. 152–181. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56620-7_6
Applebaum, B., Ishai, Y., Kushilevitz, E.: How to garble arithmetic circuits. In: Ostrovsky, R. (ed.) 52nd FOCS, pp. 120–129. IEEE Computer Society Press, October 2011
Asharov, G., Jain, A., López-Alt, A., Tromer, E., Vaikuntanathan, V., Wichs, D.: Multiparty computation with low communication, computation and interaction via threshold FHE. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 483–501. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_29
Barak, B., Brakerski, Z., Komargodski, I., Kothari, P.K.: Limits on low-degree pseudorandom generators (or: sum-of-squares meets program obfuscation). Cryptology ePrint Archive, Report 2017/312 (2017). http://eprint.iacr.org/2017/312
Barak, B., Garg, S., Kalai, Y.T., Paneth, O., Sahai, A.: Protecting obfuscation against algebraic attacks. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 221–238. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-55220-5_13
Barak, B., et al.: On the (im)possibility of obfuscating programs. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 1–18. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44647-8_1
Barak, B., Haitner, I., Hofheinz, D., Ishai, Y.: Bounded key-dependent message security. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 423–444. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_22
Barak, B., Hopkins, S.B., Jain, A., Kothari, P., Sahai, A.: Sum-of-squares meets program obfuscation, revisited. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part I. LNCS, vol. 11476, pp. 226–250. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17653-2_8
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: Denning, D.E., Pyle, R., Ganesan, R., Sandhu, R.S., Ashby, V. (eds.) ACM CCS 1993, pp. 62–73. ACM Press, November 1993
Bitansky, N., Nishimaki, R., Passelègue, A., Wichs, D.: From cryptomania to obfustopia through secret-key functional encryption. In: Hirt, M., Smith, A. (eds.) TCC 2016, Part II. LNCS, vol. 9986, pp. 391–418. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_15
Bitansky, N., Vaikuntanathan, V.: Indistinguishability obfuscation from functional encryption. In: Guruswami, V. (ed.) 56th FOCS, pp. 171–190. IEEE Computer Society Press, October 2015
Boneh, D., Zhandry, M.: Multiparty key exchange, efficient traitor tracing, and more from indistinguishability obfuscation. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014, Part I. LNCS, vol. 8616, pp. 480–499. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-662-44371-2_27
Brakerski, Z., Döttling, N., Garg, S., Malavolta, G.: Leveraging linear decryption: rate-1 fully-homomorphic encryption and time-lock puzzles. Cryptology ePrint Archive, Report 2019/720 (2019)
Brakerski, Z., Rothblum, G.N.: Virtual black-box obfuscation for all circuits via generic graded encoding. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 1–25. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_1
Brakerski, Z., Vaikuntanathan, V.: Lattice-based FHE as secure as PKE. In: Naor, M. (ed.) ITCS 2014, pp. 1–12. ACM, January 2014
Chen, Y., Gentry, C., Halevi, S.: Cryptanalyses of candidate branching program obfuscators. In: Coron, J.-S., Nielsen, J.B. (eds.) EUROCRYPT 2017, Part III. LNCS, vol. 10212, pp. 278–307. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-56617-7_10
Cheon, J.H., Han, K., Lee, C., Ryu, H., Stehlé, D.: Cryptanalysis of the multilinear map over the integers. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015, Part I. LNCS, vol. 9056, pp. 3–12. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46800-5_1
Coron, J.-S., Lepoint, T., Tibouchi, M.: Practical multilinear maps over the integers. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 476–493. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_26
Damgård, I., Jurik, M.: A generalisation, a simpli.cation and some applications of Paillier’s probabilistic public-key system. In: Kim, K. (ed.) PKC 2001. LNCS, vol. 1992, pp. 119–136. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44586-2_9
Ducas, L., Stehlé, D.: Sanitization of FHE ciphertexts. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part I. LNCS, vol. 9665, pp. 294–310. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_12
Fiat, A., Shamir, A.: How to prove yourself: practical solutions to identification and signature problems. In: Odlyzko, A.M. (ed.) CRYPTO 1986. LNCS, vol. 263, pp. 186–194. Springer, Heidelberg (1987). https://doi.org/10.1007/3-540-47721-7_12
Garg, S., Gentry, C., Halevi, S.: Candidate multilinear maps from ideal lattices. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 1–17. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_1
Garg, S., Gentry, C., Halevi, S., Raykova, M.: Two-round secure MPC from indistinguishability obfuscation. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 74–94. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54242-8_4
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: 54th FOCS, pp. 40–49. IEEE Computer Society Press, October 2013
Garg, S., Mahmoody, M., Mohammed, A.: Lower bounds on obfuscation from all-or-nothing encryption primitives. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 661–695. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_22
Garg, S., Mahmoody, M., Mohammed, A.: When does functional encryption imply obfuscation? In: Kalai, Y., Reyzin, L. (eds.) TCC 2017, Part I. LNCS, vol. 10677, pp. 82–115. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_4
Garg, S., Miles, E., Mukherjee, P., Sahai, A., Srinivasan, A., Zhandry, M.: Secure obfuscation in a weak multilinear map model. In: Hirt, M., Smith, A. (eds.) TCC 2016, Part II. LNCS, vol. 9986, pp. 241–268. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53644-5_10
Gentry, C.: Fully homomorphic encryption using ideal lattices. In: Mitzenmacher, M. (ed.) 41st ACM STOC, pp. 169–178. ACM Press, May/June 2009
Gentry, C., Gorbunov, S., Halevi, S.: Graph-induced multilinear maps from lattices. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part II. LNCS, vol. 9015, pp. 498–527. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46497-7_20
Gentry, C., Halevi, S., Vaikuntanathan, V.: i-Hop homomorphic encryption and rerandomizable Yao circuits. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 155–172. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_9
Gentry, C., Jutla, C.S., Kane, D.: Obfuscation using tensor products. Cryptology ePrint Archive, Report 2018/756 (2018)
Gentry, C., Sahai, A., Waters, B.: Homomorphic encryption from learning with errors: conceptually-simpler, asymptotically-faster, attribute-based. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013, Part I. LNCS, vol. 8042, pp. 75–92. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_5
Goldwasser, S., Kalai, Y.T., Popa, R.A., Vaikuntanathan, V., Zeldovich, N.: Reusable garbled circuits and succinct functional encryption. In: Boneh, D., Roughgarden, T., Feigenbaum, J. (eds.) 45th ACM STOC, pp. 555–564. ACM Press, June 2013
Goldwasser, S., Micali, S.: Probabilistic encryption and how to play mental poker keeping secret all partial information. In: 14th ACM STOC, pp. 365–377. ACM Press, May 1982
Hada, S.: Zero-knowledge and code obfuscation. In: Okamoto, T. (ed.) ASIACRYPT 2000. LNCS, vol. 1976, pp. 443–457. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44448-3_34
Hu, Y., Jia, H.: Cryptanalysis of GGH map. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part I. LNCS, vol. 9665, pp. 537–565. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_21
Jain, A., Lin, H., Matt, C., Sahai, A.: How to leverage hardness of constant-degree expanding polynomials over \(\mathbb{R}\) to build \(i\cal{O}\). In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part I. LNCS, vol. 11476, pp. 251–281. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17653-2_9
Lin, H.: Indistinguishability obfuscation from constant-degree graded encoding schemes. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016, Part I. LNCS, vol. 9665, pp. 28–57. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49890-3_2
Lin, H.: Indistinguishability obfuscation from SXDH on 5-linear maps and locality-5 PRGs. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 599–629. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_20
Lin, H., Pass, R., Seth, K., Telang, S.: Indistinguishability obfuscation with non-trivial efficiency. In: Cheng, C.-M., Chung, K.-M., Persiano, G., Yang, B.-Y. (eds.) PKC 2016, Part II. LNCS, vol. 9615, pp. 447–462. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49387-8_17
Lin, H., Tessaro, S.: Indistinguishability obfuscation from bilinear maps and block-wise local PRGs. Cryptology ePrint Archive, Report 2017/250, Version 20170320:142653 (2017)
Lin, H., Tessaro, S.: Indistinguishability obfuscation from trilinear maps and block-wise local PRGs. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 630–660. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_21
Lin, H., Vaikuntanathan, V.: Indistinguishability obfuscation from DDH-like assumptions on constant-degree graded encodings. In: Dinur, I. (ed.) 57th FOCS, pp. 11–20. IEEE Computer Society Press, October 2016
Lombardi, A., Vaikuntanathan, V.: Limits on the locality of pseudorandom generators and applications to indistinguishability obfuscation. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017, Part I. LNCS, vol. 10677, pp. 119–137. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_5
Malavolta, G., Thyagarajan, S.A.K.: Homomorphic time-lock puzzles and applications. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part I. LNCS, vol. 11692, pp. 620–649. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26948-7_22
Micciancio, D.: From linear functions to fully homomorphic encryption. Technical report (2019). https://bacrypto.github.io/presentations/2018.11.30-Micciancio-FHE.pdf
Miles, E., Sahai, A., Zhandry, M.: Annihilation attacks for multilinear maps: cryptanalysis of indistinguishability obfuscation over GGH13. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016, Part II. LNCS, vol. 9815, pp. 629–658. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53008-5_22
Paillier, P.: Public-key cryptosystems based on composite degree residuosity classes. In: Stern, J. (ed.) EUROCRYPT 1999. LNCS, vol. 1592, pp. 223–238. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48910-X_16
Peikert, C., Regev, O., Stephens-Davidowitz, N.: Pseudorandomness of ring-LWE for any ring and modulus. In: Hatami, H., McKenzie, P., King, V. (eds.) 49th ACM STOC, pp. 461–473. ACM Press, June 2017
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Gabow, H.N., Fagin, R. (eds.) 37th ACM STOC, pp. 84–93. ACM Press, May 2005
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: Shmoys, D.B. (eds.) 46th ACM STOC, pp. 475–484. ACM Press, May/June 2014
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 International Association for Cryptologic Research
About this paper
Cite this paper
Brakerski, Z., Döttling, N., Garg, S., Malavolta, G. (2020). Candidate iO from Homomorphic Encryption Schemes. In: Canteaut, A., Ishai, Y. (eds) Advances in Cryptology – EUROCRYPT 2020. EUROCRYPT 2020. Lecture Notes in Computer Science(), vol 12105. Springer, Cham. https://doi.org/10.1007/978-3-030-45721-1_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-45721-1_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-45720-4
Online ISBN: 978-3-030-45721-1
eBook Packages: Computer ScienceComputer Science (R0)


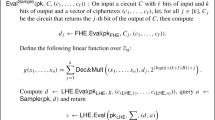


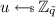 . However, the noise function is typically highly non-linear and therefore appears to be difficult to exploit. We also point out that the distinguisher has no control over the choice of e, which exclusively depends on an honest execution of the homomorphic evaluation algorithm. We therefore conjecture that the distribution of
. However, the noise function is typically highly non-linear and therefore appears to be difficult to exploit. We also point out that the distinguisher has no control over the choice of e, which exclusively depends on an honest execution of the homomorphic evaluation algorithm. We therefore conjecture that the distribution of 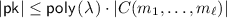 ,
,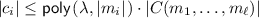 , and
, and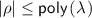
 and compute
and compute  .
. , using
, using  .
. .
.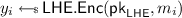 , for a random known
, for a random known 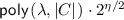 .
.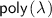 , since the underlying split FHE is compact. As an obfuscated circuit consists of
, since the underlying split FHE is compact. As an obfuscated circuit consists of 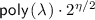 .
.