Trace Analysis Using an Event-Driven Interval Temporal Logic

Abstract

Nowadays, many critical systems can be characterized as hybrid ones, combining continuous and discrete behaviours that are closely related. Changes in the continuous dynamics are usually fired by internal or external discrete events. Due to their inherent complexity, it is a crucial but not trivial task to ensure that these systems satisfy some desirable properties. An approach to analyze them consists of the combination of model-based testing and run-time verification techniques. In this paper, we present an interval logic to specify properties of event-driven hybrid systems and an automatic transformation of the logic formulae into networks of finite-state machines. Currently, we use Promela/Spin to implement the network of finite-state machines, and analyze non-functional properties of mobile applications. We use the TRIANGLE testbed, which implements a controllable network environment for testing, to obtain the application traces and monitor network parameters.

This work has been supported by the Spanish Ministry of Science, Innovation and Universities project RTI2018-099777-B-I00 and the European Union’s Horizon 2020 research and innovation programme under grant agreement No. 777517 (EuWireless).

1 Introduction

In the last years, the improvement of sensor technology has led to the development of different software systems that monitor some physical magnitudes to control many everyday tasks. Water resource management systems [8], or aeronautics [9] are some examples of this type of systems. As it is well known, hybrid systems are composed of the so-called discrete and continuous components, which are strongly interrelated. Usually, the role of the discrete part is to control the continuous one, modifying its behaviour when necessary according to some system conditions. The continuous component may follow complex dynamics, which are usually represented by differential equations. The verification of critical properties on these systems is crucial since they may carry out critical tasks that affect the health of people or with a great economic impact. In the literature, hybrid automata constitute the best known mechanism to model hybrid systems. For example, tools like Uppaal [2] focus on the verification by model checking of some hybrid automata subclasses (timed automata). However, not all hybrid systems can be easily represented as hybrid automata, not only because of their complex dynamics but also because of their interaction with an unpredictable environment. For this reason, in the last decades, other computational hybrid models have appeared such as extended hybrid systems [4] in which the hybrid systems are parameterized to incorporate the influence of the environment, or sampled-data control systems [12] in which the continuous and discrete components alternate their execution using a fixed time duration.

Fig. 1.

Approach for testing event-driven hybrid systems

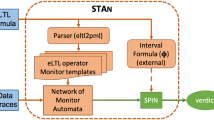
In a previous work [6], we proposed a framework to test event-driven hybrid systems using a combination of model-based testing (to automatically generate test cases) and runtime verification (to check the traces obtained against the desirable properties). The framework, shown in Fig. 1, was implemented in the context of the TRIANGLE project to analyze non-functional properties on traces produced by the execution of mobile applications. In this work, we implemented an ad-hoc trace monitoring system that was able to analyze some non-functional properties of interest.

In this paper, we concentrate on the trace analysis using runtime verification. In particular, we propose an event-driven linear temporal logic (eLTL) that allows us to extend the set of non-functional properties that can be specified and analyzed in the framework described above. The motivation for the definition of the new logic is twofold. On the one hand, we need a logic in which properties on monitored magnitudes are evaluated on time intervals determined by internal or external events that have occurred during the execution trace. For instance, in the context of mobile applications (apps), in a video streaming app, the video resolution can vary depending on network parameters (e.g. radio technology, signal strength, etc.). The exact moment when the video starts playing is a priori unknown, but during video playback, determined, for instance, by events $\texttt {vstart}$ and $\texttt {vstop}$, different network and device parameters must be monitored to determine the suitable video resolution. On the other hand, we also need a logic whose formulae can be transformed into monitors that act as listeners of the trace events to dynamically evaluate the specified property. Thus, the contributions of the paper are both the definition of the event-driven linear time logic eLTL and the transformation of the logic formulae into finite-state machines (FSM) that act as observers of the execution traces. A preliminary version of the logic was presented in a Spanish workshop [7]. With respect to this former paper, the current version has been extended with a more formal presentation of the logic, and with the implementation section which is completely new.

The paper is organized as follows. Section 2 summarizes some work related to interval logics. Section 3 presents the syntax and semantics of the event-driven interval logic. We also show its expressiveness with some examples and briefly compare eLTL and LTL. Section 4 describes the transformation of each eLTL formula into a network of FSM and proves the correctness of the transformation. Finally, Sect. 5 gives the conclusions and future work. Appendices contain the proof of all the results presented in the paper, along with the current Promela implementation of the network of FSM which allows us to check the satisfaction of eLTL formulae on traces using Spin [11].

2 Related Work

In Linear Temporal Logic (LTL) is not easy to express requirements to be held in a bounded future. Thus, the extension of LTL with intervals seems a natural idea to easily express these other type of properties. This is the approach followed in [20], where the authors use events to determine the intervals on which formulae must be evaluated, although they do not deal with real-time. The temporal logic FIL is also defined with similar purposes but the formulae are written using a graphical representation. Real-time FIL [19] is an extension of FIL that incorporates a new predicate $len(d_1,d_2]$ that bounds the length of the intervals on which properties have to be evaluated. In other context, the duration calculus [3] (DC) was defined to verify real-time systems. In DC system states have a duration in each time interval that can be measured taking into account the presence of the state in the interval. DC includes modalities (temporal operators) able to express relations between intervals and states, which constitute the basis of the logic.

The Metric Interval Logic (MITL) [1] is a real-time temporal logic that extends LTL by using modal operators of the form , where I is an open/close, bounded/unbounded interval of $\mathbb {R}$. MITL$_{[a,b]}$ [13] is a bounded version of MITL with all temporal modalities restricted to bounded intervals of the form [a, b]. MITL$_{[a,b]}$ formulae can be translated into deterministic timed automata. More recently, MITL$_{[a,b]}$ was extended to Signal Temporal Logic STL [14] including numerical predicates that allow analogue and mixed-signal properties to be specified. Lately, the MITL logic has been extended to $\textsc {xSTL}$ [16] by adding timed regular expressions to express behaviour patterns to be met by signals.

Finally, the differential dynamic logic (dL) [18] is a specification language to describe safety and liveness properties of hybrid systems. In dL, formulae are of the form $[\alpha ] \phi$ or $\langle \alpha \rangle \phi$ meaning that the behaviour of hybrid system $\alpha$ always (eventually) is inside the region defined by $\phi$.

Fig. 2.

Synchronization of trace $\pi$ and continuous variable c using $\tau (\pi )$

3 Event-Driven Systems and Logic eLTL

In this section, we introduce a general model of event-driven hybrid systems, which is characterized by containing continuous variables whose values can be monitored. From a very abstract perspective, the behaviour of such a system may be given by a transition system $P = \langle \varSigma ,{\mathop {\longmapsto }\limits ^{-}},{L},s_0 \rangle$ where $\varSigma$ is a non-enumerable set of observable states, ${L}$ is a finite set of labels, is the transition relation, and is the initial state. Transitions labels represent the external/internal system events or system instructions that make the system evolve. In addition, we assume that is an special label that represents the time passing between two successive states during which no event or instruction is executed. Thus, transitions may take place when an event arrives, when a system discrete instruction is carried out, or when a continuous transition occur in which the only change in the state is the passing of time.

We denote with $\mathcal {O}_ f (P)$ the set of execution traces of finite length determined by P. The elements of $\mathcal {O}_ f (P)$ are traces of the form $\pi = s_0 {\mathop {\longmapsto }\limits ^{l_0}}s_1 {\mathop {\longmapsto }\limits ^{l_1}} \cdots {\mathop {\longmapsto }\limits ^{l_{n-2}}}s_{n-1}$ where each is the event/instruction/$\iota$ that fired the transition. The length of a trace $\pi = s_0 {\mathop {\longmapsto }\limits ^{l_0}} s_1 {\mathop {\longmapsto }\limits ^{l_1}}\cdots {\mathop {\longmapsto }\limits ^{l_{n-2}}}s_{n-1}$ is the number of its states n. Given a trace $\pi$ of length n, we define the set $\mathcal {O}bs(\pi )$ of observable states of $\pi$; that is, $\mathcal {O}bs(\pi ) = \{s_0,\cdots , s_{n-1}\}$. It is worth noting that although event-driven hybrid systems have continuous variables, we assume that their values are only visible at observable states. In addition, we assume that the time instant in which each state occurs is given by function which relates each state s with the moment it happens .

In the following, given a trace $\pi$ of length n and , we denote with $\langle \pi ,t \rangle$ the observable state $s_i$ of the trace at time instant t. In addition, we use function $\sigma : \{\tau (s_0),\cdots \tau (s_{n-1})\} \rightarrow \mathcal {O}bs(\pi )$ as the inverse function of $\tau$, i.e., and $\sigma (\tau (s_i)) = s_i$.

Each continuous variable c of the system is a function that gives the value of c, c(t), at each time instant t. Figure 2 shows the relation between the states in a trace, the time instants where they occur and the corresponding values of continuous variable c at these instants. By abuse of notation, in the figure and in the rest of the section, we use $\tau (\pi )$ to denote set $\{\tau (s_0),\cdots \tau (s_{n-1})\}$.

We have decided to define the behaviour of event-driven hybrid systems by means of the simple notion of transition systems on purpose. The definition is highly general in the sense that it is able to capture the behaviour of hybrid event-driven systems described by hybrid automata or other formalisms. Transitions correspond to changes of the system variables producing observable states in the traces that can be the result of the system that accepts an event or executes an instruction, or the result of an internal evolution $\iota$ where time passing is the only change in the trace. Anyway, the number of observable states in each trace is finite. In practice, in our current implementation, the time instants and the value of continuous variables in traces is recorded in log files, although other time models could also be managed by the logic presented below.

3.1 Syntax and Semantics of eLTL

We consider two types of state formulae to be analyzed on states of $\varSigma$. On the one hand, we have those that can be evaluated on single states as used in propositional linear temporal logic $\textsf {LTL}$, for instance. On the other hand, we assume that events of ${L}$ are also state formulae that can be checked on states. Thus, let $\mathcal {F}$ be the set of all state formulae to be evaluated on elements of $\varSigma$. As usual, we suppose that state formulae may be constructed by combining state formulae and Boolean operators. Relation associates each state with the state formulae it satisfies, that is, given , and , $s \vdash p$ iff the state s satisfies the state formula p. In the following, given , and , we write iff . When is an event occurred at state $s_i$ that evolves to $s_{i+1}$ in trace , we assume that state $s_{i+1}$ records the fact that $l_i$ has just occurred and, in consequence, we have that , or equivalently, . Other logics such as HML [10] or ACTL [5] focus on actions versus state formulae. We have decided to keep them at the same level to allow the use of both in the logic.

In order to analyze the behaviour of continuous variables, it is useful to observe them not only in a given time instant, but also during time intervals to know, for example, whether their values hold inside some expected limits or whether they never exceed a given threshold. To this end, we use intervals of states (inside the traces) to determine the periods of time during which continuous variables should be observed. Our proposal is inspired in the interval calculus introduced by [3], where the domain of interval logic is the set of time intervals $\mathbb {I}$ defined as . Considering this, we define the so-called interval formulae as functions of the type to represent the formulae that describe the expected behaviour of continuous variables on time intervals. For instance, assume that is a continuous variable of our system. Given a constant , function given as defines an interval formula that is $true$ on an interval $[t_1,t_2]$ iff the absolute value of difference between c in the interval endpoints $t_1$ and $t_2$ is less than K. Let us denote with $\varPhi$ the set of interval formulae. We assume that $\varPhi$ contains the special interval formula that returns $true$ for all positive real intervals, that is, .

In the following, given two state formulae , we use expressions of the form [p, q], that we call event intervals, to delimit intervals of states in traces. Intuitively, given a trace $\pi = s_0 {\mathop {\longmapsto }\limits ^{l_0}} s_1 {\mathop {\longmapsto }\limits ^{l_1}}\cdots {\mathop {\longmapsto }\limits ^{l_{n-2}}} s_{n-1}$, [p, q] represents time intervals $[t_i,t_j]$ with such that and ; that is, and . We also consider simple state formulae p to denote states in $\pi$ satisfying p. Now, we formally define relation that relates event intervals with intervals of states in traces.

Definition 1

Given a trace , two state formulae and two time instants such as , we say that the time interval $[t_p,t_q]$ satisfies the event interval [p, q], and we denote it as , iff the following four conditions hold: (1) ; (2) ; (3) ; and (4) there exists no interval , verifying conditions 1–3 of this definition, such that .

That is, iff satisfies p and is the first state following $s_p$ that satisfies q. In addition, the fourth condition ensures that the interval of states from $s_p$ until $s_q$ is maximal in the sense that it is not possible to find a larger interval ending at $s_q$ satisfying the previous conditions. This notion of maximality guarantees that the evaluation of interval formulae starts at the state when event p first occurs, although it could continue being true in some following states. In the previous definition, the time instants $t_p$ and $t_q$ must be different elements of $\tau (\pi )$, that is, $[t_p,t_q]$ cannot be a point.

Example 1

The following trace ($\pi$) tries to clarify Definition 1. Given , and assuming that $\tau (s_i) = t_i$ for all states, we have that , but , since condition (4) does not hold.

Definition 2

[$\textsf {eLTL}$ formulae]. Given , and , the formulae of $\textsf {eLTL}$ logic are recursively constructed as follows:

The rest of the temporal operators are accordingly defined as:

, ,

,

The following definition gives the semantics of $\textsf {eLTL}$ formulae given above. Given a trace , and with , we use $\langle \pi ,t_i,t_ f \rangle$ to represent the subtrace of $\pi$ from state to state .

Definition 3

(Semantics of eLTL formulae). Given , , and the eLTL formulae $\psi , \psi _1, \psi _2$, the satisfaction relation is defined as follows:

(3.1)

(3.2)

(3.3)

(3.4)

(3.5)

The semantics given by is similar to that of LTL, except that manages interval formulae instead of state formulae. For instance, case 3.1 states that the subtrace $\langle \pi ,t_i, t_ f \rangle$ of $\pi$ satisfies an interval formula $\phi$ iff $\phi ([t_i,t_ f ])$ holds. Case 3.4 establishes that $\mathcal {U}_{[p,q]}$ holds on the subtrace $\langle \pi ,t_i, t_ f \rangle$ iff there exists an interval such that $\psi _1$ and $\psi _2$ hold on $[t_i,t_p]$ and $[t_p,t_q]$, respectively. Case 3.5 is similar except for the interval in which $\psi _2$ has to be true is $[t_p,t_p]$, which represents the time instant $t_p$.

Proposition 1

The semantics of operators and , given in Definition 2, is the following:

(3.6)

(3.7)

(3.8)

(3.9)

3.2 Examples

We now give some examples to show the use of the logic. In [6, 17], we proposed a model-based testing approach to test mobile applications (apps) under different network scenarios. We automatically generated app user flows, that is, different interactions of the user with the app, using model-based testing techniques. Then, we executed these app user flows in the TRIANGLE testbed, which provides a controlled mobile network environment, to obtain measurements and execution traces in order to evaluate the performance of the apps.

In this section, we make use of eLTL to describe desirable properties regarding to the values of continuous variables of the ExoPlayer app, a video streaming mobile app that implements different adaptive video streaming protocols. Using the current implementation of the eLTL operators, and with the execution traces provided by the evaluation presented in [17], we can determine if the execution traces of ExoPlayer satisfy the properties. The execution traces of the app contain the following events: the start of video playback (stt), the load of the first complete picture (fp), the end of the video playback (stp), and the changes in the video resolution (low, high). In addition, the TRIANGLE testbed measures every second (approximately) the amount and rate of transmitted and received data, as well as different parameters of the network (e.g. signal strength and signal quality) and the device (e.g. RAM, CPU and radio technology).

Property 1: We can write the property “during video playback, the first picture must be loaded at least once in all network conditions” which may be specified using the formula . The following trace satisfies this property, where the expressions over each state represent the state formulae it holds.

Property 2: We can also specify the property “during video playback, if the video resolution is high, the average received data rate is greater than 5 Mbps, and if the video resolution is low the average data rate is below 1Mbps.” The video resolution is high in the time interval between h and l events. Similarly, the video resolution is low between the events l and h. The eLTL formula is

where $\phi _1$ and $\phi _2$ are defined as: and .

This formula uses function $RxRate(t_i,t_f)$ that accesses to the file of the trace and workouts the average in the corresponding time interval. In the current implementation on Spin, it is calculated using Promela embedded C code.

Property 3: The eLTL formula for property “during video playback, if the video resolution changes from High to Low, the peak signal strength (rssi) is less than −45 dBm” can be written as:

Using this formula with different thresholds for the peak rssi, we can determine whether the adaptive protocols take into consideration the signal strength in the terminal to make a decision and change the video resolution.

Other Examples. In the health field, eLTL can also be useful. For instance, patients with type 1 diabetics should be monitored to assure that their glucose levels are always inside safe limits. Related to this problem, we could describe different properties of interest. Given the interval formula with , and events sleep, awake, run, end, break, endBreak, drink and $over\,70$ that denote when the patient goes to sleep, awakes, starts running, stops running, drinks and his/her glucose level is over 70 mg/l:

• Property “while sleeping, the glucose level is never below 70 mg/l” can be expressed as  70. Observe that in this property over70 acts as a simple interval formulae that holds on each state inside [sleep, awake] iff the glucose level is over 70.

• Property “if the patient is running more than 60 min, he/she has to make a stop of more than 5 min to drink” can be written as

  

3.3 Comparison with LTL

In this section, we briefly compare the expressiveness of logics LTL and eLTL. One important difference between both logics is that LTL is evaluated on infinite traces while, on the contrary, eLTL deals with finite traces. This makes some LTL properties hard to specify in eLTL. In addition, eLTL is thought to analyze extra-functional properties on traces, that is, properties that refer to the behaviour of certain magnitudes in subtraces (as in the examples presented above), which cannot easily be expressed in LTL. The context where eLTL formulae are checked is determined by the event intervals [p, q] associated to the modal operators. However, this context is implicit in LTL since formulae are evaluated on the whole infinite trace. In conclusion, we can say that although both logic have similarities, they are different regarding expressiveness. The following table shows some usual patterns of LTL formulae with its corresponding eLTL versions. The inverse transformation is not so easy. For instance, eLTL formula , which forces that p occurs between each pair of a and b events, is hard to write in LTL. In the table, we use interval formulae $\phi _p$ () defined as . In addition, are events used to delimit finite subtraces.

$\textsf {LTL}$	$\textsf {eLTL}$	Comments
		In both cases, p has to be $true$ eventually, but in $\textsf {eLTL}$, p must be $true$ inside of the finite trace.
		in both cases, p has to be always $true$, but in $\textsf {eLTL}$ It is limited to the states of the finite trace
		In $\textsf {LTL}$, p has to be true infinitely often. In $\textsf {eLTL}$, p has to Occur always inside the subtraces determined by [a, b].
		The $\textsf {LTL}$ formula says that p has to be always true from some unspecified state. The $\textsf {eLTL}$ says the same, but limited by the extreme states of the finite trace [a, b].
$p \ \mathcal {U} q$		In this case, the $\textsf {LTL}$ formula is clearly easier to write, since $\textsf {eLTL}$ is thought to evaluate magnitudes on subtraces.
	$(\Diamond _{p} True ) \mathcal {U}_q True$	the LTL formula could be $true$ even if p occur after p in the trace. However, in the $\textsf {eLTL}$ version, p has to occur before p.

4 Implementation

In this section, we describe the translation of eLTL formulae into a network of state machines $\mathcal {M}$ that check the satisfiability of the property on execution traces. As described in Sect. 3, formulae are evaluated against time bounded traces $\pi$ that execute in time intervals of the form . Formulae can include nested temporal operators whose evaluation can be restricted to subintervals. The implementation described below assumes that traces are analyzed offline, i.e., given a particular trace, for each state, we have stored the time instant when it occurred and the set of state formulae of $\mathcal {F}$ which it satisfies. In consequence, we can use the trace to build a simple state machine $\mathcal {T}$ that runs concurrently with the network of machines $\mathcal {M}$. $\mathcal {T}$ sends to $\mathcal {M}$ events to start and finalize the analysis, and also the events included in the formula which are of interest for the correct execution of the network.

Fig. 3.

Example of a network of state machines

We use an example to intuitively explain how the network of machines $\mathcal {M}$ is constructed. Assume we want to evaluate . The outer operator must find the different time intervals , delimited by events p and q, to check if there exists at least one satisfying the sub-formula . Similarly, given one of the time intervals $[t_p, t_q]$, the inner operator has to find all time intervals , determined by events r and s, to check whether $\phi$ holds in all of them.

The network $\mathcal {M}$ is composed of the parallel composition of finite-state machines, each one monitoring a different sub-formula. The network is hierarchized, that is, each state machine communicates through channels with the trace $\mathcal {T}$ being analysed and with the state machine of the formula in which it is nested. The state machine of the outer eLTL temporal operator starts and ends the evaluation, reporting the analysis result to $\mathcal {T}$. Each state machine has a unique identifier id which allows it to access the different input/output channels. Thus, channel cm [id] is a synchronous channel through which the state machine id is started and stopped. Channel rd [id] is used by machine id to send the result of its evaluation. Finally, ev [id] is an asynchronous channel through which each state machine receives from $\mathcal {T}$ the events in which it is interested along with the time instant they have occurred ([$t_e$,e]).

Figure 3 gives an intuition about how the network of state machines of the example is constructed. The network of the example is composed by three state machines $\mathcal {M}_0 \Vert \mathcal {M}_1 \Vert \mathcal {M}_2$. $\mathcal {M}_0$ is the highest level state machine that monitors operator . Thus, it should receive from $\mathcal {T}$ events p and q each time they occur in the trace. Similarly, $\mathcal {M}_1$ monitors , and it should be informed when events r or s occur. Finally, $\mathcal {M}_2$ is devoted to checking $\phi$. It is worth noting that all machines are initially active, although they are blocked until the reception of the start message STT. Machine $\mathcal {A}_0$ is started when $\mathcal {T}$ begins its execution. Each machine id receives the start and stop messages STT and STP though channel cm [id]. Events arrive to machine id via channel ev [id] and it returns the result of its evaluation ($true$ or $false$) using channel rd [id]. In the example, when $\mathcal {M}_0$ receives event p, it sends a STT message to the nested machine $\mathcal {M}_1$. Similarly, when $\mathcal {M}_1$ receives event r, it sends message STT to $\mathcal {M}_2$. Each time $\mathcal {M}_1$ receives event s sends STP to $\mathcal {M}_2$.When $\mathcal {M}_2$ receives STP, it ends its execution, evaluates the interval formula and sends the result through channel rd [2]. Similarly, when $\mathcal {M}_0$ receives event q via channel ev[0], it sends STP to $\mathcal {M}_1$. When a machine receives STP, it tries to finish its execution immediately. But, before stopping, it has to process all the events stored in its ev channel since they could have occurred before the STP were sent. To know this, each message contains a timestamp with the time instant when the event took place. This is needed since events and STP are sent via different channels. Thus, it is possible for a machine to read STP before reading a previous event in the trace.

Finite-State Machine Templates. We now show finite-state machines templates that implement eLTL operators. In these machines, id refers to the state machine being implemented, and c1, c2 are, respectively, the identifiers of the state machines of the first and the second nested operators, if they exist. All machines described below follow the same pattern. First, each machine starts after receiving message STT, and initiates its sub-machines, if necessary. Then, it continues processing the input events in which it is interested. These events are directly sent from the instrumented trace $\mathcal {T}$ that is being monitored. When the machine receives STP, it returns the result of its evaluation via channel rd. To simplify the diagrams, we have used sometimes guarded transitions of the form G|Action. When guard G is a message reception via a synchronous channel, it is executable iff it is possible to read the message and, as a side effect, the message is extracted from the channel. Due to lack of space, we have not included operator $\mathcal {U}_p$ since its machine is a simplified version of that of $\mathcal {U}_{[p,q]}$.

Fig. 4.

State machine of an interval formulae

Interval formula ($\phi$): Figure 4 shows the state machine for an interval formula $\phi$ without eLTL operators. An interval formula is evaluated on a time interval $[t_i, t_ f ]$ that is communicated to the process via the channel cm [id] with messages [$t_i$,STT] and [$t_ f$ ,STP]. After detecting the interval end, the state machine evaluates the expression $\phi ([t_i, t_ f ])$ and sends the result to the parent machine through rd [id].

Fig. 5.

State machine of the not operator

Negation ($\lnot \psi$): Figure 5 shows the negation operator. The state machine synchronizes with the machine of its nested formula ($\psi$) as soon as it receives the STT and STP commands. Observe that, in this case, to simplify the diagram, we have used guarded transitions. When the nested machine finishes, the machine negates the result and returns it through the rd channel.

Figure 6 shows the state machine of the or operator. This machine checks if any of the two sub-formulae $\psi _1$ and $\psi _2$ holds on the same interval $[t_i, t_ f ]$ over which the or operator is being evaluated. Similarly to the NOT machine, this machine waits the successive reception of the STT and STP messages and resends them to the machines of its sub-formulae to start and stop them.

Fig. 6.

State machine for or operator

Fig. 7.

State machine for until operator

Until ($\psi _1 \mathcal {U}_{[p, q]} \psi _2$): Figure 7 shows the state machine template of the until operator. As can be observed, it is much more complex than the previous templates. Assuming that the whole formula is evaluated on interval $[t_i,t_ f ]$, the first sub-formula $\psi _1$ must be true on an interval $[t_i,t_p]$ ($t_p$ being a time instant when event p has occurred), and the second one $\psi _2$ must be true on the time interval $[t_p,t_q]$ ($t_q$ being the time instant when event q has first occurred after p). The machine id starts accepting the message STT from its parent and, then, it resends the message to the state machine of $\psi _1$. In state wait p, the machine is waiting for the p event to occur or for the STP message to arrive. If p arrives at a correct time instant (after $t_i$), the machine sends STP to machine c1 and waits for its result in state wait c1. If $\psi _1$ is not valid in the interval $[t_i,t_p]$, machine id records $false$ in variable res1 and waits in state wait q the following event q, then it transits to wait p and restarts machine c1. This is because machine id has found that formula does not hold on a time interval determined by the occurrence of p and q and, in consequence, it starts searching for the following interval given by [p, q] in the trace. Otherwise, if $\psi _1$ holds on $[t_i,t_p]$, machine sends STT to machine c2 and waits for its result in state wait c2. In this state, machine id behaves in a similar way as in state wait p. If c2 returns $false$, it restarts again machine c1 and goes back to state wait p to search for the following time interval determined by events p and q. Conversely, if c2 returns $true$, machine id waits for message STP to send its result. Note that it only sends $true$ if event q has occurred before the end of the interval $t_ f$. Otherwise, the machine returns $false$, since $\psi _2$ could not be evaluated in time. Observe that in states wait p and wait q, message STP is only accepted when the event channel is empty (emp(ev[id])). This is to prioritize reading events p and q before STP and simplify the implementation.

Theorem 1

Let f be an eLTL formula, and $\mathcal {M}_{id}$ the network of state machines implementing f, then given a finite trace $\langle \pi ,t_i,t_ f \rangle$, if and only if $\mathcal {M}_{id}$ finishes its execution by sending $true$ via channel rd [id] (rd [id] ! $true$).

5 Conclusions

In this paper, we have presented an event-driven interval logic (eLTL) suitable for describing properties in terms of time intervals determined by trace events. We have transformed each eLTL formula into network of finite state machines to evaluate it using runtime verification procedures, and have proved the correctness of the transformation. We have constructed a prototype implementation of these machines in Promela to be executed on Spin.

Our final goal is to apply the approach to analyze execution traces of real systems against extra-functional properties, such as evaluating the performance of mobile apps in different network scenarios [17]. Currently, the transformation from eLTL formula into Promela code, and the transformation of the traces are manually done, although the automatic transformation will be carried out in the near future. We also plan to use the approach in other domains such as the EuWireless project [15]. This project is designing an architecture to dynamically create network slices to run experiments. In this context, it is of great importance to monitor the different network slices and the underlying infrastructure to ensure safety (e.g. isolation of slices) and extra-functional properties related to performance and quality of service.