Cell Motility and Locomotion by Shape Control

Abstract

Mathematical modeling and quantitative study of biological motility is producing new biophysical insight and opportunities for discoveries at the level of both fundamental science and technology. One example is the elucidation of how complex behavior of simple organisms emerges from specific (and sophisticated) body architectures, and how this is affected by environmental cues. Moreover, the two-directional interaction between biology and mechanics is promoting new approaches to problems in engineering and in the life sciences: understand biology by constructing bio-inspired machines, build new machines thanks to bio-inspiration.

This article contains an introduction to the mathematical study of swimming locomotion of unicellular organisms (e.g., unicellular algae). We use the tools of geometric control theory to identify some general principles governing life at low Reynolds numbers, that can guide the design of engineered devices trying to replicate the successes of their biological counterparts. Locomotion strategies employed by biological organism are, in fact, a rich source of inspiration for studying mechanisms for shape control. We focus on morphing mechanisms based on Gauss’ theorema egregium, which shows that the curvature of a thin shell can be controlled through lateral modulations of stretches induced in its mid-surface. We discuss some examples of this Gaussian morphing principle both in nature and technology.

1.1 Introduction

Motility refers to the ability to move spontaneously. In biology, this is related to the execution of a biological function involving the (active, purposeful) motion of the whole body of an organism or of some of its parts. At the level of individual cells or tissues, motility is crucial in many important biological processes such as cell migration, the immune system response, the establishment of neuron synapses, wound healing, just to name a few. More broadly, motility is fundamental to both the origin of life and the propagation of lethal diseases. Example are the unicellular swimming of sperm cells, the motion of bacteria and parasites in humans, animals and plants, the invasion of nearby tissues by metastatic tumor cells, and the list could continue.

Swimming locomotion of unicellular organisms has provided particularly fertile grounds for the application of mathematical/physical modeling and of quantitative methods to biology. The swimming behavior of micro-organisms has been analyzed through the lenses of mathematical models based on the physical laws of fluid dynamics, and it has attracted considerable attention in the recent biophysical literature.

Among the successes on the biology side, one can list the early discovery of the basic propulsion mechanisms in bacteria (through one rotary motor located at the proximal end of each bacterial flagellum [20]) and flagellated eukaryotes (through molecular motors distributed along the whole length of an eukaryotic flagellum [76]). These have both been discovered through arguments based on physical modeling, when direct observation of the active motors driving flagellar motion was not yet possible. More generally, numerous more recent contributions have established how complex behavior of simple organisms emerges from specific body architectures, and how this is affected by environmental cues. Unicellular organisms represent particularly valuable model systems for the study of the simplest mechanisms of sensing, decision making, and response in biology because they do not involve the intervention of a nervous system (and a brain) in the cascade of regulatory processes.

In addition to the biological motivation to study them, the proficiency exhibited by unicellular swimmers in navigating complex environments, including the human body, has fueled the hope that new bio-inspired biomedical devices can be engineered by trying to learn and replicate the mechanism that work for the biological templates. This includes miniaturized robotic systems for diagnostics, therapeutics, targeted drug delivery, minimally invasive surgery, micro-manipulation, micro-fluidics. Moreover, the two-directional interaction between biology and mechanics is promoting new approaches to engineering problems and in the life sciences: understand biology by constructing bio-inspired machines, build new machines thanks to bio-inspiration. In these notes, we will try to convey some of the excitement that this exchange of information is generating at the cross-roads of biology, physics, mathematics and engineering.

More concretely, this article contains an introduction to the mathematical study of swimming locomotion of unicellular organisms (e.g., unicellular algae). We give a mathematical formulation of the basic problem of “swimming by prescribing time-histories of shapes”, and then use the tools of geometric control theory to identify some general principles governing life at low Reynolds numbers, that can guide the design of engineered devices trying to replicate the successes of their biological counterparts. We also illustrate how these principles are at work in biological organisms, and provide a more detailed case study of the behavior of one specific organism, Euglena gracilis, which exhibits a transition from flagellar swimming to amoeboid motion (by propagation of peristaltic waves along the body) in response to increasing confinement.

Besides their primary function, which is motion, locomotion strategies employed by biological organism represent also a rich source of inspiration for studying mechanisms for shape control. They are not visible to the naked eye and revealing them by observing them with a microscope provides a golden mine for new solutions to the problem of controlling shape in order to execute a function. Function often follows from shape in biology. This is true in a wide range of phenomena and across many time-scales, from morphogenesis, to adaptability to changing requirements from an evolving environment, to functional behaviors resting on the possibility of spanning diverse shapes over time, as is the case in motility. We focus on morphing mechanisms based on Gauss’ theorema egregium, a principle we like to call Gaussian morphing [36], and that was pioneered in [67]. Here we can witness in a concrete setting the two-way interaction between biology and mechanics/engineering mentioned above, with shape morphing mechanisms of biological organisms suggesting, for example, new solutions for medical tools for minimally invasive surgery.

We end this introduction by mentioning briefly some topics that are very closely related to the subject of these notes but that, however, are not discussed explicitly here. The conceptual framework we adopt to study swimming locomotion is general, and it applies to other forms of motility besides swimming. Locomotion arises from the mechanical interactions of an active body (i.e., a body capable of changing its shape) with its surroundings, driven by the action–reaction principle. In the case of higher organisms, muscle activity selects a preferred state of deformation, the configuration that the body would acquire in the absence of external forces. Modulating this state of spontaneous deformation in time while in contact with a surrounding medium generates reactive forces from the environment that can be used as propulsive forces for locomotion, just as in the case of a fish waving a fin. Examples of reactive forces exploited for locomotion come from the interaction with a substrate, as in the case of frictional ground forces in human and animal legged locomotion [60], in the limbless undulatory locomotion of snakes [33, 59, 61], and in the peristaltic locomotion of worms [1]. Similarly, hydraulic and (non-newtonian) viscous forces arise from the interaction with a substrate in the case of snails gliding on a substrate [30, 48, 68, 69]. Viscous and inertial forces exerted by the surrounding fluid are the interaction forces with the environment in the case of swimming and flying [32, 72]. Clearly, the list could continue. Anyway, higher organisms with a nervous system, where proprioception and feedback become very important are outside of the scope of these notes. See [60, 62, 86] for some interesting ideas and references in this context.

At the level of single cell locomotion, muscle activity is replaced by activity of molecular motors exerting forces of biofilaments (actin filaments, microtubules) as in the case of the actin cortex of eukaryotic cells. Different modes of motility can arise, such as motion by blebbing, see, e.g., [31, 108], by frictional interaction with a channel or a surrounding fluid arising as a reaction to actin retrograde flow [21], or by lamellipodia protrusion thanks to cycles of attachment at the leading edge (lamellipodium), retrograde actin flow, and detachment at the trailing edge, as in the migration of adhesive cells on or within solid substrates, matrices, and tissues, see [8]. Actin-powered motility of adhesive cells is very common in biology, hence it is a vast topic with a very large literature. Conformational changes of molecular motors, polymerization of actin filaments and, more generally, growth may provide the energy required for motion via biochemical reactions [3, 16, 27, 85, 88, 109].

Modulation of adhesive forces is often crucial for this type of locomotion [94]; in more macroscopic cases, similar stick-slip effects can be obtained through directional friction: see, e.g., [47,48,49, 54]. Motility of neuronal growth cones has been analyzed in [89]. Contact guidance of adhesive cells by substrate patterning (e.g., chemical guidance with adhesive lines on an otherwise repellent surface, or guidance by curvature with adhesive tubes) is an interesting, related topic, see [25]. Here, the possibility of a statistical mechanics approach based on shape fluctuations of cells is a very attractive recent development. Further discussion on these topics can be found in the work by Lev Truskinovsky and his co-authors, and reported in another section in this volume.

The study of motion in plants [41], e.g. tropisms and nastic movements, is also closely related to the theme of these notes. The fact that the time scales associated with these plant motions are long compared with the typical human attention span does not make them any less interesting, and time-lapse photography can reveal very interesting motile behaviors: see the recent article on nutations of plant shoots [2] and the references quoted therein for an introduction. Complex helical motion motion of growing shoots or root tips is often tied to effective exploration and penetration of the subsoil, or to the search for nearby supports in the case of climbing plants. The oscillatory movements (nutations) of growing plant shoots reveal some striking similarities with the beating of eukaryotic flagella and cilia, although on very different time scales. This is a reflection of the fact that the bio-chemical process that govern the response are very different (bio-chemistry of conformational transformation of the molecular motors in the eukaryotic flagellum case, auxin transport and cell growth in the plant nutation case). However, there seems to be an interesting and yet unexplored connection between the two phenomena, at least at some level, although the details of the response mechanism are certainly very different.

The focus of these notes is on conceptual principles. These are often best extracted from the analysis of model problems arising from simplified minimal systems, that retain the richness of the original problem but can be reduced to simple calculations. As a consequence, we do not talk about numerical techniques to solve control problems associated with locomotion questions, even though this is a very important topic. The reader is referred to [10, 11, 15, 22, 24, 55, 63, 64, 70, 75, 77, 79, 96, 97, 102, 103, 107] and the references quoted therein for examples and analysis of navigation and optimal control problems in biological and bio-inspired locomotion, including numerical strategies for their solution.

1.2 Swimming at Low Reynolds Numbers

We describe the motion of a generic swimmer through a (time-dependent) shape map $t\mapsto \bar {\Phi }_t$, which specifies the way the reference configuration $\mathcal {B}$ evolves in time as seen by an observer moving with the swimmer (we identify this observer with the body-frame), and through the way the body frame moves with respect to the lab-frame. The current position of the body-frame is given by the position of the origin, c(t), while the orientation of the axes is obtained from the axes of the lab-frame through the rotation R(t). In formulas (see also Fig. 1.1),

$$\displaystyle \begin{aligned} \Phi_t(X)=\mathbf{c}(t)+\mathbf{R}(t)\bar{\Phi}_t(X)=\left(\mathbf{c}(t)+\mathbf{R}(t) {id}(X)\right) + \mathbf{R}(t)\bar{\mathbf{u}}_t(X) \end{aligned} $$

(1.1)

where, in the second identity, we have written $\bar {\Phi }_t$ as the sum of the identity map id plus a displacement $\bar {\mathbf {u}}_t$. This emphasizes that Φ_t(X) consists of a rigid motion (the one in brackets), and of a genuine change of shape associated with $\bar {\mathbf {u}}_t$.

Fig. 1.1

Reference and deformed configurations of a swimmer: parametrization of the swimmer motion in terms of position c(t), orientation R(t), and shape $\bar {\Phi }_t$. Figure reproduced from [35]

The map (1.1) gives the position x at time t of a (material) point $X\in \mathcal {B}$ of the swimmer. Given a point $x\in \mathcal {B}_t=\Phi _t(\mathcal {B})$, this is the position at time t of the point

$$\displaystyle \begin{aligned} X=\Phi^{-1}_t(x)=\bar{\Phi}^{-1}_t({\mathbf{R}}^{T}(t)(x-\mathbf{c}(t))) \end{aligned} $$

(1.2)

The (Lagrangian) velocity of a (material) point of the swimmer is the time derivative of (1.1),

$$\displaystyle \begin{aligned} \dot{\Phi}_t(X)=\dot{\mathbf{c}}(t)+\dot{\mathbf{R}}(t)\bar{\Phi}_t(X)+\mathbf{R}(t)\dot{\bar{\Phi}}_t(X) \end{aligned} $$

(1.3)

where superposed dots denote time derivatives. The (Eulerian) velocity of the point of the swimmer occupying place x at time t is

$$\displaystyle \begin{aligned} \dot{\Phi}_t\left( \Phi^{-1}_t(x) \right) =\dot{\mathbf{c}}(t)+\boldsymbol{\omega}(t)\times(x-\mathbf{c}(t))+ \mathbf{R}(t)\dot{\bar{\Phi}}_t \left( \bar{\Phi}^{-1}_t\left( {\mathbf{R}}^{T}(t)(x-\mathbf{c}(t)) \right)\right) \end{aligned} $$

(1.4)

where ω(t) is the axial vector associated with the skew-symmetric matrix $\dot {\mathbf {R}}(t){\mathbf {R}}^T(t)$.

Shape changes of the swimmer induce motion of the surrounding fluid. Dealing with microscopic scales (so that the Reynolds number is small) and assuming that the rates at which shape changes occur are not exceedingly fast (so that the Womersley number is also small), we model the flow with the stationary Stokes equations, so that the velocity u and pressure p in the fluid satisfy

$$\displaystyle \begin{aligned} \eta\Delta\mathbf{u}-\nabla p =0 \quad \text{ and } \quad \mathrm{div}\,\mathbf{u}=0\quad \text{ in } \mathbb{R}^3\setminus\mathcal{B}_t \end{aligned} $$

(1.5)

where η is the viscosity of the fluid, together with the no-slip condition at the interface between the fluid and the swimmer boundary

$$\displaystyle \begin{aligned} \mathbf{u}(x,t)|{}_{\partial\mathcal{B}_t} = \dot{\Phi}_t\left( \Phi^{-1}_t(x) \right)|{}_{\partial\mathcal{B}_t} \end{aligned} $$

(1.6)

and suitable decay conditions at infinity. This outer Stokes problem is well posed, and given the one-parameter family of Dirichlet data $t\mapsto \mathbf {u}(x,t)|{ }_{\partial \mathcal {B}_t}$ (i.e., given the maps $t\mapsto \mathbf {c}(t), \mathbf {R}(t), \bar {\Phi }_t$), the distributions of velocity u(x, t) and pressure p(x, t) in the fluid are uniquely determined.

The motion of the swimmer is governed by the balance of linear and angular momentum. We neglect inertia, and all other external forces different from those exerted by the fluid. So the balance of linear and angular momentum become the statement that the total force and torque exerted on the swimmer by the surrounding fluid vanish. Denoting the Cauchy stress in the fluid with

$$\displaystyle \begin{aligned} \mathbf{S}[\mathbf{u}](x,t)=-p(x,t)\mathbf{I}+\eta\left(\nabla \mathbf{u}(x,t) + \nabla {\mathbf{u}}^T(x,t)\right) \end{aligned} $$

(1.7)

where I is the identity, we write these as

$$\displaystyle \begin{aligned} 0=\mathbf{f}(t)=\int_{\partial\mathcal{B}_t}\mathbf{S}[\mathbf{u}](x,t)\mathbf{n}(x)\mathrm{dA} \end{aligned} $$

(1.8)

and

$$\displaystyle \begin{aligned} 0=\mathbf{g}(t)=\int_{\partial\mathcal{B}_t}(x-\mathbf{c}(t)\times\mathbf{S}[\mathbf{u}](x,t)\mathbf{n}(x)\mathrm{dA}\quad \end{aligned} $$

(1.9)

where n(x) is the outer unit normal at $x\in \partial \mathcal {B}_t$. It turns out that, given $t\mapsto \bar {\Phi }_t$, Eqs. (1.8) determine uniquely the two time-dependent vectors $\bar {\mathbf {v}}(t)={\mathbf {R}}^{T}(t)\dot {\mathbf {c}}(t)$ and $\bar {\boldsymbol {\omega }}(t)={\mathbf {R}}^{T}(t)\boldsymbol {\omega }(t)$, namely, the representations in the body-frame of $\dot {\mathbf {c}}(t)$ and ω(t). Thus, c(t) and R(t) are found by integrating the equations $\dot {\mathbf {c}}(t)=\mathbf {R}(t)\bar {\mathbf {v}}(t)$ and $\dot {\mathbf {R}}(t)=\mathbf {R}(t)[\bar {\omega }(t)]_{\times }$ (where the skew-symmetric tensor $[\bar {\omega }(t)]_{\times }$ is defined by $[\bar {\omega }(t)]_{\times } \mathbf {a}= \bar {\omega }(t)\times \mathbf {a}$ holding for every vector a). This shows that the following

Swimming Problem

given a history of swimmer shapes $t \mapsto \bar {\Phi }_t$, find the corresponding history of positions and orientations t↦c(t), R(t) has a unique solution. The reader is referred to [40] for a detailed proof of this fundamental fact.

A further interesting question is whether, given initial position and orientation c(0), R(0) and a target position c(0) +  Δc (or a target position and orientation pair), there exist a shape history $t \mapsto \bar {\Phi }_t$ such that the swimmer can reach the target. This is a typical question of control theory. In fact, swimming is a perfect example of exploiting fluid-structure interactions to control the (Navier)-Stokes equations: we use shape changes and act on the fluid to produce flows that generate exactly those forces that propel the swimmer in the desired way.

The question of whether a periodic shape change can result in a net displacement Δc in a cycle has attracted a lot of interest in the literature, starting from G.I Taylor’s educational movie on low Reynolds number flows [99] and Purcell’s seminal paper [87] popularizing some of the seemingly paradoxical aspects of life at low Reynolds numbers. This is the so-called Scallop Theorem, stating that, without inertia, a scallop-like organism that can only open and close its (rigid) valves cannot swim. More precisely, a low Reynolds swimmer varying its shape by periodically modulating the opening of its valves can only achieve Δc = 0 in one period. In the language of control theory, this is the statement that the state of the system (in particular, its position) is not controllable in terms of the rate of shape change (the input of the system). We will return to this issue in the next section.

1.3 Locomotion Principles and Minimal Swimmers

In this section, we use the framework introduced in Sect. 1.2 to discuss some general locomotion principles and to infer some prescriptions on how to design competent swimmers of minimal complexity. We do this by focusing on some simple, yet representative examples.

1.3.1 Looping in the Space of Shapes: No Looping? No Party!

A simple model system which is of great conceptual value is the three-sphere-swimmer proposed in [83]. Consider the case in which $\mathcal {B}$ consists of three rigid spheres of equal radius, whose centers are aligned and constrained to move along one line parallel to the unit vector e, only varying their mutual distances $L+\bar {u}_1(t), L+ \bar {u}_2(t)$ (see Fig. 1.2). The position of every point of the system is specified, once we know the positions of the centers of the three spheres

$$\displaystyle \begin{aligned} x_1(t)=c(t)-(L+\bar{u}_1(t))\,, \quad c(t)\,, \quad x_2(t)= c(t)+(L+\bar{u}_2(t))\,. \end{aligned} $$

(1.10)

We consider a T-periodic shape change

$$\displaystyle \begin{aligned} t\mapsto \bar{\mathbf{u}}(t)=(\bar{u}_1(t),\bar{u}_2(t)) \,, \end{aligned} $$

(1.11)

namely, a closed curve in the space of shapes which we assume to be traced in the anti-clockwise direction.

Fig. 1.2

Three-sphere-swimmer: parametrization in terms of position c(t) and shape $(\bar {u}_1(t),\bar {u}_2(t))$. Figure reproduced from [35]

Linearity of the Stokes system leads to linear dependence of the forces in (1.8) on the Dirichlet data of the outer Stokes problem, hence on $\dot {c}, \dot {\bar {u}}_1, \dot {\bar {u}}_2$. The component along e of the force balance is then written as

$$\displaystyle \begin{aligned} 0=f(t)=f_1(\bar{\mathbf{u}}(t))\dot{\bar{u}}_1(t)+ f_2(\bar{\mathbf{u}}(t))\dot{\bar{u}}_2(t)+ f_3(\bar{\mathbf{u}}(t))\dot{c}(t) \end{aligned} $$

(1.12)

where, in view of translational invariance, the force coefficients are independent of position and depend only on shape. It turns out that f ₃ ≠ 0 (in fact, f ₃ < 0 because it is the drag opposing the motion of the system when the system translates rigidly at unit speed, and the drag has direction opposite to the one of the velocity). Solving for $\dot {c}$ we obtain

$$\displaystyle \begin{aligned} \dot{c}(t)=\mathbf{V}(\bar{\mathbf{u}}(t))\cdot \dot{\bar{\mathbf{u}}}(t)\,,\quad \text{where } \quad V_i(\bar{\mathbf{u}}(t)):=-\frac{f_i(\bar{\mathbf{u}}(t))}{f_3(\bar{\mathbf{u}}(t))} \end{aligned} $$

(1.13)

Using Stokes theorem, we obtain the displacement Δc in one stroke as

$$\displaystyle \begin{aligned} \Delta c = \int_0^T \mathbf{V}(\bar{\mathbf{u}}(t))\cdot \dot{\bar{\mathbf{u}}}(t)dt = \int_{\omega} \mathrm{curl}_{\bar{\mathbf{u}}}{\mathbf{V}}(u_1,u_2)du_1du_2 \end{aligned} $$

(1.14)

where $\mathrm {curl}_{\bar {\mathbf {u}}}{\mathbf {V}}=\partial V_2/\partial {\bar {u}_1} - \partial V_1/\partial {\bar {u}_2}$ and ω is the region of shape space enclosed by the closed curve (1.11).

As emphasized in [9], formula (1.14) above summarizes several key results of low Reynolds number swimming. The first one is that, if the closed curve ∂ω spans zero area (i.e., the loop in shape space is trivial, as it happens for a reciprocal shape change), then the displacement vanish. This is the so-called Scallop Theorem of [87], already discussed in Sect. 1.2, stating that a scallop-like organism that can only change shape by opening and closing its rigid valves cannot swim in the absence of inertial forces.

The second important result is that, even when the loop in shape space is non-trivial, the displacement is zero if the integrand in (1.14) vanishes. Therefore, swimming rests on the fact that hydrodynamic resistance forces (the f _i’s defining the vector field V in (1.13)) are shape-dependent, as probed by the differential operator $\mathrm {curl}_{\bar {\mathbf {u}}}$.

The third fact following from (1.14) is that the displacement in one stroke is geometric: it only depends on the geometry of the loop (1.11) drawn in the space of shapes, not on the speed at which the loop is traced.

Finally, formula (1.14) shows that the system is fully controllable. Indeed, if Δc ≠ 0 is the displacement achieved with the loop Γ, smaller displacements of the same sign can be achieved with loops of smaller area, any positive multiple k Δc can be achieved by tracing k times the curve Γ, and − Δc can be obtained by tracing Γ in the direction opposite to the one used to obtain Δc.

We close this section by remarking that the one-dimensional nature of the swimming dynamics of the three-sphere-swimmer (one degree of freedom for the translational velocity of the swimmer) has made it possible to analyze the problem with simple tools, such as Stokes theorem from differential calculus. In the case of general swimmers (six degrees of freedom for the positional and orientational velocity of the swimmer) the main concept is exactly the same, namely, controllability needs lack of integrability of a differential form. One can obtain similar results in the more general setting by using the tools of Geometric Control Theory. The fact that the curl is non-trivial (i.e., the vector field V is not the gradient of a scalar potential) is replaced by the requirement that the coefficients of the affine control system governing the dynamics of the swimmer generate, through their Lie-brackets, the whole tangent space. In other (more technical) words, the affine control system governing the dynamics of the swimmer should be bracket-generating, and then controllability is guaranteed by Chow’s theorem, see e.g., [9, 13, 80].

1.3.2 Minimal Swimmers With or Without Directional Control

Building on the results of the previous section, we want to ask now the following question. What is the minimal number of independent motors, or controllers, that can allow the three-sphere swimmer to achieve non-zero net displacements? A superficial answer would be that two independent active elements are needed to generate nontrivial loops in the space of shapes. However, as shown in [81], the correct (and, at first sight, surprising) answer is that one active element suffices.

Indeed, by replacing one of the “arms” between two consecutive spheres with a passive spring, and actuating periodically the remaining one, one can still extract net displacements, because the two arm lengths can still describe a loop in the space of shapes. To understand how this arises, consider the two limit cases of very slow and very fast actuation frequencies. At low actuation frequencies, the viscous forces are negligible with respect to the elastic ones, and the system behaves as if it had one rigid arm (hence, no net displacements). At high actuation frequencies, elastic forces are negligible with respect to viscous ones, and the system behaves as a collection of three beads, one of which is free, while the distance between the other two is oscillating. It is relatively straightforward to show that, in this case, long range hydrodynamic interactions lead to synchronization of the three spheres, and the two distances (the arm lengths) oscillate keeping their sum constant. At intermediate actuation frequency ω, elastic and viscous forces compete, and the dynamics of the system leads to the two distances oscillating at the same frequency, but with a frequency-dependent (locked) phase difference which is controlled by the non-dimensional parameter

$$\displaystyle \begin{aligned} \Omega:=\frac{\omega \eta L }{K}\,. \end{aligned} $$

(1.15)

Here K is the stiffness of the passive spring, L its rest length, and η is the fluid viscosity. Thanks to this phase lag, the two arm lengths trace a non-trivial loop in the space of shapes, leading to non-zero (frequency dependent) net displacements in one cycle.

The gain in simplicity associated with getting rid of independent control of one the two arms comes with a cost in terms of the performance of the device, namely, loss of controllability. Indeed, since the phase lag is set by system properties that cannot be tuned, see (1.15), the loops in the space of shapes will be traced with a fixed phase lag, hence in a fixed direction. The sign of the displacement is then hard-wired into the system and the three-sphere swimmer with one passive arm can only move with the passive arm ahead, see [81]. Put differently, one motor/controller leads to the minimal system capable of achieving non-zero net displacements, but without a reverse gear. Two independent motors/controllers are necessary for a controllable system.

In closing this section, it is important to emphasize that this simple example shows in a nutshell features that are much more general. Indeed, the dependence of the net displacement in one cycle from the actuation frequency shows that, when shape is not fully prescribed but it rather emerges form the balance between hydrodynamic and elastic forces, the purely geometric picture of Sect. 1.3.1 is no longer sufficient. The behavior of the system arises form a two-way fluid-structure interaction problem, in which one needs to solve for the unknown shape variables by coupling an equilibrium problem for an elastic structure to the dynamics of the surrounding fluid (the outer Stokes problem of Sect. 1.3.1). In this context, deciding on the controllability properties of the swimmer becomes more involved. These controllability questions are very relevant. Examples of these questions are whether a sperm cell can trace curvilinear trajectories (and through which control mechanisms?), whether an artificial sperm-like robot whose flexible magnetic tail is actuated by an external oscillating magnetic field can trace any desired trajectory in space and, in particular, can proceed both forward and backward along the direction of the flagellum when the flagellum experiences small oscillations around a straight extended configuration. Some of these question are further explored below.

1.3.3 Steering by Modulation of the Actuation Speed

Section 1.3.2 has shown that when shape is not completely prescribed, but it rather emerges from the balance of elastic and viscous forces, some adjustments need to be made to the geometric picture of Sect. 1.3.1. The presence of elastically deformable parts in a swimmer makes the net displacement in a cycle frequency-dependent. This fact can be used to steer a swimmer along curved trajectories.

The swimmer studied in [34] consists of a (rigid) spherical head with an elastic tail attached to it, as schematically depicted in Fig. 1.3. We considered planar motions of the system, assuming that the swimmer can actively control only the angle α between the head and the tail. We studied the resulting swimming motion under generic periodic time histories t → α(t) of the control parameter, resulting in a periodic beating of its elastic tail.

Fig. 1.3

Swimmer with elastic tail. The moving frame of the swimmer is given by the centre c and the orientation θ of the head. The swimmer controls the angle α between its spherical head and its tail at the point of attachment. Figure reproduced from [35]

The first surprising feature of the system is the ability of the swimmer to propel itself and to “steer”, following either straight or curved trajectories (on average, after many beats), despite being actuated by only one control parameter. Secondly, the resulting displacements after each beating period are not geometric: Changing the speed of the periodic control αdoes change the resulting displacement. There is no contradiction, however, between these results and the observations in Sect. 1.3.1. The key to realize this is that, in the swimmer of Fig. 1.3, shape is not completely prescribed, because of the presence of the elastic tail. The shape of the latter is not a-priori known, and it only emerges from the balance of elastic and hydrodynamic forces arising from the actuation of the angle α. Thus, moving from systems in which shape is completely controlled to systems in which shape is partly emergent, the picture changes completely with respect to the Scallop Theorem scenario of [87].

We considered in [34] the equations of motion of the system in the local drag approximation of Resistive Force Theory, see [70], restricting our analysis to stiff-tailed swimmers. This allowed us to obtain analytical results in the small parameter regime 𝜖 ≪ 1 where 𝜖 is the ratio between the typical viscous and elastic force acting on the tail (called the Machin number in recognition of the insight contained in his seminal paper [76]). A formula that sheds light on the behavior of the system during its motion is the one proved in [34] for the (normalized) deviation y(x, t) of the tail from its straightened configuration

$$\displaystyle \begin{aligned} y(x,t) = - \epsilon p(\alpha(t),x) \dot{\alpha}(t) + \mathcal{O}(\epsilon^2) \, , {} \end{aligned} $$

(1.16)

see Fig. 1.3. The function p(α, x) in Eq. (1.16), which can be calculated explicitly, is a positive polynomial with α-dependent coefficients in the variable x. The dependence of the deviation y on the velocity $\dot {\alpha }$ of the angle α has a simple physical reason: The faster the tail beats, the larger are the viscous forces acting on it, which result in larger bending of the tail itself. The critical consequence of (1.16) follows from another simple observation: given the position of centre c and the orientation θ of the swimmer’s head (see Fig. 1.3), the configuration of the swimmer is fully determined by the angle α and the deviation y. That is, α and y determine the shape of the swimmer. What (1.16) shows, then, is that the shape of the swimmer in motion is fully determined (at least at first approximation) by the angle α and its rate-of-change $\dot {\alpha }$, which, in turn, can be considered as a shape control parameter.

Indeed, a loop in the shape-space of the elastic tail swimmer can be effectively given by the closed curve $t \to (\alpha (t),\dot {\alpha }(t))$. Consistently with the basic principles stated in Sect. 1.3.1, we showed that net displacements Δc and net rotations Δθ of the swimmer arise because of this looping. More precisely, denoting by ω the two dimensional set enclosed by the loop $t \to (\alpha (t),\dot {\alpha }(t))$, we derived the following formulas

$$\displaystyle \begin{aligned} \Delta \mathbf{c} = \epsilon \int_{\omega} \mathbf{U}(\alpha , \psi) d\alpha d\psi + \mathcal{O}(\epsilon^2) {} \end{aligned} $$

(1.17)

and

$$\displaystyle \begin{aligned} \quad \Delta \theta = \epsilon \int_{\omega} W(\alpha , \psi) d\alpha d\psi + \mathcal{O}(\epsilon^2) \, , \end{aligned} $$

(1.18)

where U and W are two non-vanishing functions (vector-valued and scalar-valued, respectively) which are independent on the loop itself. At leading order in 𝜖, formulas (1.17)–(1.18) have the exact same structure of Eq. (1.14).

From (1.17)–(1.18) we can deduce the characteristic motion control capabilities of the swimmer. First, we can conclude that propulsion is possible, since a loop $t \to (\alpha (t),\dot {\alpha }(t))$ naturally spans non-zero area, as one can see in the simple case $\alpha (t)=\sin t$. Second, (1.17)–(1.18) explain why net displacements in one cycle are not geometrical. For example, a simple time rescaling t → λt results in a deformation of the shape parameters loop $t \mapsto (\alpha (\lambda t), \lambda \dot {\alpha }(\lambda t))$, thus faster (or slower) beating results in different displacements. More general modulations of the velocity of beating can be considered, resulting in different geometries of the shape parameters loop. This gives room for motion control, so that the swimmer can couple displacements and rotation during each period (steering). In fact, one can show that the swimmer follows curved trajectories when the beating is asymmetric, namely, when for example α has a fast up-beat phase followed by a slow down-beat phase during one shape cycle.

1.3.4 Swimming by Lateral Undulations: Optimality of Traveling Waves of Bending

Swimming by lateral undulation is a very common locomotion strategy that is used by a large number of swimmers both at the macroscopic and the microscopic scale (for the latter, see Sect. 1.4 below for more details). The mechanism by which propagating a traveling wave of bending produces propulsion was analyzed in the seminal paper [98], one of the milestones of the whole literature on biological fluid dynamics at microscopic scales. The traveling waves of bending studied in this paper are of the form

$$\displaystyle \begin{aligned} \bar{v}(X,t)=b \sin (kX - \omega t) = b \cos (\omega t) \sin (kX) - b \sin (\omega t) \cos (kX)\,, \end{aligned} $$

(1.19)

which shows how they represent a non-trivial loop (in fact, a circle, since $\cos ^2(\omega t) + \sin ^2(\omega t)=1$) in a space of shapes parametrized by the two wave forms $\sin (kX)$ and $\cos (kX)$. In other words, Taylor’s waves of bending fall in the general framework of Sect. 1.3.1.

More in detail, let us consider a planar sheet infinitely extended in the z direction. Let us focus on the plane (x, y), and let X be a Lagrangian coordinate along the axis x, which is assumed to move with the sheet (hence x is the horizontal axis of the body frame). Denoting by $(\bar {u},\bar {v})$ the components of the displacement of a point (X, 0) in the body frame, we can consider the history of shapes described by a traveling wave of the form

$$\displaystyle \begin{aligned} \bar{u}(X,t)=a \cos \left( kX-\omega t -\phi \right) \end{aligned} $$

(1.20)

$$\displaystyle \begin{aligned} \bar{v}(X,t)= b \sin \left( kX-\omega t \right) \end{aligned} $$

(1.21)

These functions $\bar {u}$, $\bar {v}$ describe shape waves propagating along the body axis that can be both of stretching and of bending type, with a phase shift ϕ. Waves of stretching (a > 0, b = 0) can be assimilated to peristaltic waves, waves of bending (a = 0, b > 0) to lateral undulations. For ω > 0 and k > 0, these waves propagate in the direction of increasing x and X.

Computing velocities from positions using (1.20)–(1.21), and using these velocities as Dirichlet boundary conditions for the outer Stokes problem, one can try to solve for the velocities of the fluid and obtain the (horizontal) velocity U of the sheet. This can be done through a series expansion leading to the following expressions for the leading order term in the swimming speed U

$$\displaystyle \begin{aligned} U=-\frac 12 \omega k \left( b^2 + 2ab \cos \phi - a^2 \right) \end{aligned} $$

(1.22)

The reader is referred to [32] for a proof of these results. In particular, we have

$$\displaystyle \begin{aligned} U=\frac 12 \omega k a^2 \,,\quad \text{(peristaltic case: wave of stretching)} \end{aligned} $$

(1.23)

$$\displaystyle \begin{aligned} U= - \frac 12 \omega k b^2 \,,\quad \text{(undulation case: wave of bending)} \end{aligned} $$

(1.24)

which show that in the case of a (peristaltic) wave of stretching the motion is prograde (i.e., in the same direction of the direction of propagation of the wave) while, in the (undulatory) case of a wave of bending, the motion is retrograde (i.e., in the direction opposite to the direction of propagation of the wave). Some interesting applications of these formulas to the biological world of snails and earthworms and of bio-inspired robotic replicas can be found in [1, 47,48,49, 54] and in the references quoted therein.

Moving form the idealized case of the Taylor sheet to the analysis of a concrete swimmer, which is in particular of finite length, is not straightforward. We have studied in a series of papers the case of a planar swimmer consisting of N rigid segments of equal length, connected by rotational joints. For N = 3 this is Purcell’s three-link minimal swimmer [87], while considering the limit N →∞ we can reproduce the geometry of Taylor’s sheet discussed above. This N-link swimmer has been analyzed in the framework of Geometric Control Theory in several scenarios. One is the case in which the angles between successive links (which provide a discrete analog of the local curvature) are prescribed, i.e., we are dealing with a problem of swimming at prescribed shapes as in Sect. 1.3.1, see [12]. It turns out that the governing equations for this swimmer have the structure of an affine control system without drift, for which one can apply powerful theorems to prove controllability. Another case is obtained by assuming that the links are ferromagnetic and a time-dependent (oscillatory) external magnetic field is applied, and that elastic torsional springs are present at the joints between successive links. The resulting N-link magnetic swimmer, analyzed in [14], provides an example in which shape emerges only from the balance of elastic restoring torques, external magnetic torques, and torques arising from hydrodynamic drag, i.e., a problem conceptually analogous to the one of Sect. 1.3.2. The governing equations for this second case have the structure of an affine control system with drift, for which general sufficient conditions for controllability are not available. Loss of controllability for swimmers whose shape is only partially controlled can therefore be understood in the light of the structure of the governing equations, using the tools of Geometric Control Theory.

The N-link swimmer can also be used to probe questions of optimal control. Deformations in the form of waves traveling along the body are very common in nature (both for swimmers and crawlers), and are used very frequently in slender bio-inspired mobile robots. Are they optimal in any sense, when compared to alternative actuation strategies? We have examined this question in [15]. More precisely, we have considered the problem of finding the gait of minimal energy expenditure among all those capable of reaching a prescribed displacement in one shape cycle.

This problem of optimal control is nonlinear in the shape parameters (the angles between successive joints) and finding (even numerically, when N is large) the optimal gait explicitly is exceedingly difficult. By considering the regime of small deviations from the straight configuration, i.e., under the assumption of small-amplitude angles, and considering the approximation of the governing equations at leading order in the shape parameters, we obtain an affine control system that can be analyzed in full detail. We find that optimal gaits are always two-dimensional elliptical loops, independent of N. These gaits bridge Purcell’s loops for the two-dimensional shape space associated with N = 3, to gaits that, modulo edge effects, can be identified with Taylor’s traveling waves of bending for large N, of a type similar to (1.19).

The result above, namely, the energetic optimality of undulation waves as a swimming strategy for a swimmer differing only slightly from a straight segment only depends on structural properties and symmetries of the governing equations, which in turn reflect the geometric symmetry of the physical problem at hand. In fact, in this regime of small-amplitude joint angles, the perturbations from the rectilinear geometry of the reference configuration are small, and a slender one-dimensional swimmer with homogenous geometric and mechanical properties that interacts with a homogeneous surrounding medium is a system which is essentially invariant under shifts along the body axis. This is exactly true for an infinite or a periodic system and approximately true, modulo edge effects, for a system of finite length. The relevance of traveling waves as optimal gaits is therefore naturally suggested by the geometric symmetry of the system and, in fact, it emerges naturally from the symmetries of the governing equations. Given the generality of this argument, it is quite natural that the same conclusion holds true for other types of locomotion as well, such as the case of one-dimensional crawlers gliding on solid surfaces, see [1].

Removing the assumption of small-amplitude joint angle and exploring the case in which large deviations of the shape from the rectilinear one are allowed is difficult. Numerical simulations show that the optimal gaits (obtained for the case N = 3 and N = 5 in [15]) are planar but non-convex in the case N = 3, and non-planar with complex geometries in the case N = 5. This is not surprising because, when the restricted setting of small perturbations from the rectilinear geometry is abandoned, and large shape changes are considered, then invariance under shifts along the body axis is lost and traveling waves are no longer a natural basis for the study of the properties of optimal gaits. It would be interesting to find out whether the closed curves of high dimensionality representing the optimal gaits in the large deformation regime, that we find numerically, do exhibit special structural properties or symmetries: this question is, at present, completely open.

1.4 Biological Swimmers

It may seem surprising that the principles discussed above may be relevant in the study of the locomotion strategies of unicellular organisms, whose bodies look very different from the idealized systems of beads and springs analyzed in the previous section. In fact, this is indeed the case, as we argue in the remainder of this section. We will show that the principles discussed in Sect. 1.3 go a long way in rationalizing behaviors observed in biology.

1.4.1 Chlamydomonas’ Breaststroke

Chlamydomonas is a unicellular alga, with a round body, which swims thanks to the beating of two flexible anterior flagella, see e.g. [56, 58]. It has been used as a model organism, in particular for what concerns flagellar locomotion [51].

In one of its typical behaviors, the cell beats the two flagella in synchrony in a plane, symmetrically about a central symmetry axis of the body. With this perfect breast-stroke, the cell progresses with a rocking back-and-forth motion along the symmetry axis. Net displacements are made possible by the fact that the shape of the flagella varies during one stroke cycle. They are extended during the power phase of the stroke, when the flagella beat (say) downwards, and push the cell body upwards. They are contracted in the recovery part of the stroke, when they move upwards to recover the initial posture, and push the cell downwards (hence the rocking motion). Net upward displacement results from the fact that the hydrodynamic forces generated by the extended flagellum are higher than those generated by the retracted flagellum, moving in the opposite direction. Considering as shape variables the angle formed at the attachment of the body (localized curvature), and a measure of global curvature, we recognize that Chlamydomonas’ breast stroke consists of a loop in the space of shapes.

This mechanism, based on the non-reciprocal time-periodic beating of slender one-dimensional structures, is ubiquitous also in the self-propulsion of ciliates, which are typically covered by numerous arrays of beating cilia. Their beating is organized in periodic spatio-temporal patterns called metachronal waves. Individual cilia oscillate back and forth with a shape asymmetry between an extended configuration in the power phase of the stroke and a more bent one during the recovery phase of the stroke.

1.4.2 Sperm Cells and Flagellar Beat

Sperm cells are among the most thoroughly studied examples of unicellular swimmers, see e.g. [53]. There is hardly a more evident illustration of how cell motility is relevant to life as the highly oscillatory motion by which a sperm cell successfully swims its way until it reaches and fecundates an egg cell.

Sperm cells move by beating a flagellum, whose structure is highly conserved across all eukaryotic species. It consists of longitudinal bundles of microtubules, arranged in a precise spatial structure (the 9 + 2 architecture of microtubule doublets in the axoneme), on which molecular motors (dyneins) exert forces that cause the creation and propagation of longitudinal bending waves [8]. These bending waves generate the propulsive forces powering the motion of the cell. The same flagellar architecture and the same flagellar beat, with the resulting force-exchange with a surrounding fluid are at the basis of the locomotion strategies of all flagellates and ciliates. In addition, they are at the root of some fluid transport phenomena of great physiological relevance in humans and animals (such as muco-ciliary clearance, i.e, the self-clearing mechanism of the airways in the respiratory system, but cilia may also be involved in the flow of cerebrospinal fluid) which are driven by the beating of ciliated cells lining the walls of the organs inside which the flow takes place.

Interestingly, a basic and fundamental model for the flagellar beat in eukaryotic cilia and flagella is still lacking, in spite this being one of the most thoroughly studied topics in cell motility for the last several decades. The seminal paper by Machin [76] established that the observed wave patterns are incompatible with the hypothesis that the flagellum is a passive elastic filament set in motion by external actuation (e.g., an active process located at the proximal end, as is the case for bacterial flagella, which are driven by a rotary motor located at the proximal end of the flagellum). For eukaryotic flagella, active contractile elements must exist along the length of the flagellum. In other words, mechanics shows that the observed bending waves require the presence of internal actuation along the flagellum: distributed active forces/torques along the flagellum, which we now know to be the result of the action of molecular motors (dyneins) on microtubule bundles But how is the active beat generated? How is the frequency of the beat set? Is it affected by environmental cues and, if so, through which mechanisms? Already at its most basic level, a bending wave requires spatio-temporal patterns of curvature of variable sign along the body axis. This has led to the hypothesis there must exist some coordination mechanism between molecular motors acting on opposite sides of the flagellum: In order to generate the flagellar beat, molecular motors must switch on and off, respectively, at the opposite sides of the bending plane (this is called the ‘switch-point hypothesis’ in the biophysical literature). Whether this hypothesis is correct and, if so, what controls the switching of activation of axonemal motors is still a debated issue, and it is the subject of active ongoing research [74]. Recent advances in high resolution microscopy (cryo-electron tomography) have enabled us to observe distinctive asymmetric spatial patterns of active and inhibited motors along the length of a flagellum [73]. To date, however, there are no time-resolved observations of the beat pattern, allowing for a direct visualization of the configurations of motors and microtubules during the beat. In addition, it is not known how the beat is regulated, and it is not ruled out that oscillations simply emerge spontaneously as a resonance of the axoneme, seen as mechanical system in which motors respond to the forces transmitted by the microtubules [92]. The quest for a fundamental model of the regulation mechanism of the flagellar beat is still outstanding.

1.5 Euglena Gracilis: A Case Study in Biophysics and a Journey from Biology to Technology

We have been studying Euglenids, and Euglena gracilis in particular (see [71]), already for some years. The reason behind our interest in this protist, a unicellular flagellate, is that it exhibits two distinct forms of motility. One is through the beating of a single anterior flagellum (swimming motility). Another one is through very large, elegantly coordinated, rhythmic shape changes of the whole body (amoeboid motion or metaboly). What controls the switching between this two distinct ‘gaits’ is an interesting question, which is still open, and on which we have some hypotheses.

1.5.1 Metaboly and Mechanisms for Shape Change, Embodied Intelligence

The large shape changes associated with metaboly rely on the special body architecture of Euglena cells whose outer envelope, just like other Euglenids, has a complex structure. Indeed, underneath the plasma membrane, they have an ultra-structure called pellicle, see Fig. 1.4. This is a complex made of protinaceous strips, microtubules, and molecular motors. The strips have overlap regions and are able to slide one on another along their length. The sliding is powered by molecular motors that induce sliding in the microtubules that run parallel to the strips, along the overlap region. The large shape changes of metaboly correlate closely with geometric rearrangements of the pellicle structure. In fact, the relative sliding along the strips can be thought of as a mechanism of active surface shearing or, in the language of differential geometry, of active change in the surface metric. In view of Gauss’ Theorema Egregium, modulating the pellicle shears means modulating the surface metric along the surface, and this can produce (Gaussian) curvature. In particular, the propulsive mechanism associated with metaboly consists of the propagation of a round protruding bulge along the axis of an elongated body of approximately cylindrical shape. A surface with a bulge is one with nonzero Gaussian curvature, so that metaboly relies on the propagation of nonzero Gaussian curvature along the cell body. This can be accomplished and, as experiments show, is in fact accomplished by modulation of the pellicle shears along their lengths. And in the regions where the bulge forms, the pellicle strips acquire a characteristic helical shape. This mechanism is described in detail in [17, 18], and in Sect. 1.6 below.

Fig. 1.4

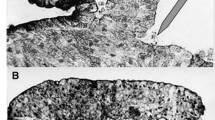
Left: a sample of Euglena gracilis imaged in bright-field, reflected light microscopy while exhibiting cell body shape changes (metaboly) concomitant with the reconfiguration of the striated cell envelope. Right: micrographs of Euglena gracilis effectively crawling in a capillary under significant spatial confinement by means of peristaltic shape changes. Notice the forward motion of the leading edge of the cell and the corresponding retrograde motion of the traveling bulge sliding against the capillary wall. Figure reproduced from [3]

Observation at the microscope of the behavior of E. gracilis in capillaries of decreasing diameter or in environments of increasing crowding suggest that metaboly may be triggered by confinement. In fact, we could confirm this hypothesis in [85] by examining swimming Euglena cells in environments of controlled crowding and geometry, see Fig. 1.4. Under these conditions of increasing confinement, metaboly allows cells to switch from unviable flagellar swimming to a new and highly robust mode of fast crawling, which can deal with variable levels of geometric confinement, even extreme ones, and turn both frictional and hydraulic resistance into propulsive forces.

To understand how a single cell can control such an adaptable and robust mode of locomotion, we developed in [85] a computational model of the motile apparatus of Euglena cells consisting of an active striated cell envelope. The activity of the motors results in tangential forces applied to the pellicle strips along their region of overlap, which causes them to slide one relative to the other. Using the energy consumed by these motors as the input, we assign spatio-temporal patterns of activation generating traveling waves of tangential forces and, in turn, traveling waves of sliding displacements which produce peristaltic waves of the cell body. One of the most striking conclusions that can be reached with the model is the following. Driving the active cell envelope inside capillaries of decreasing diameter, but with the same spatio-temporal patterns of activation, the system is capable of quickly adjusting to the increasing confinement, always finding an effective gait (a limit cycle) up to the most extreme levels of confinement. In other words, our model shows that gait adaptability does not require specific mechano-sensitive feedback but can be explained instead by the mechanical self-regulation of an elastic and extended motor system.

From an engineering point of view, the ability of the pellicle to mechanically self-adapt and maintain the locomotory function under different geometric and mechanical conditions represents a remarkable instance of mechanical or embodied intelligence, a design principle that is recently emerging in bio-inspired robotics by which part of the burden involved in controlling complex behaviors is outsourced to the mechanical compliance of the materials and mechanisms that build the device.

In conclusion, our analysis identifies a locomotory function and the operating principles of the adaptable peristaltic body deformation of Euglena cells. Further details on metaboly as a form of motility, and on the mechanisms controlling how Euglena switches under confinement from flagellar swimming to this mode of behavior are discussed in [85].

1.5.2 Flagellar Swimming, Helical Trajectories and a Principle for Self-Assembly

When left undisturbed in free space, Euglena cells swim by beating a single anterior flagellum. Contrary to what happens for Chlamydomonas, see Sect. 1.4.1, the flagellar shapes of Euglena are typically non-planar (their geometry is often referred to as ‘figure eight’ or ‘spinning lasso’). The resulting trajectories are also non-planar: Euglena cells swim with a characteristic swinging motion (Erschuetterung) with apparent sinusoidal trajectories when the cells are imaged in the two-dimensional world of optical microscopy. In fact, as it turns out, this is the typical footprint of a helical swimming motion projected on a 2D plane.

This is in fact proved in [90], where we have managed to reconstruct the three-dimensional trajectories and flagellar shapes of swimming Euglena, starting from time-sequences of two-dimensional images obtained with an optical microscope. This has been made possible thanks to the precise characterization of the orbits (the maps t↦c(t), R(t) of the swimming problem of Sect. 1.2) traced by an object propelled by a flagellum beating periodically in time. Hydrodynamics of Stokes flows dictates the following universal law of periodic flagellar (and ciliar) propulsion: the orbits of any object propelled by periodically beating flagella (or cilia), swimming far away from walls, boundaries, etc. are always generalized helices. This makes the reconstruction of three-dimensional trajectories possible: once the three-dimensional geometric structure of the orbits is known, these can be recovered from their two-dimensional projections, hence lifting the two-dimensional experimental images to three dimensions.

In fact, the same result on helical trajectories holds true if the organism is propelled by an array of cilia, beating periodically. This situation is typically modeled treating the swimmer as a squirmer, i.e. a rigid body with a distribution of slip velocities on its boundary, which represent the relative velocity of the fluid (which moves like the tips of the cilia) with respect to the base of the cilia, attached to the boundary of the body. If the slip velocity field is periodic in time, the resulting orbits are generalized helices. For the sake of simplicity, we will illustrate the results on helical swimming above by only considering the discrete curve traced by an arbitrary point of the swimmer (the origin c(t) of the body-frame), following its positions after integer multiples of the beating period T. We have the following:

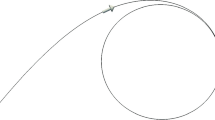
Helix Theorem

The discrete trajectory k↦c _k = c(0 + kT) traced by a micro-swimmer moving in free-space, propelled by the T-periodic beating of a flagellum or of an array of cilia, is a discrete circular helix.

This result is a special case of a more general one proved in [90], but we give here a direct proof following [35]. Assume that, at t = 0, body-frame and lab-frame coincide: c(0) = o, R(0) = I, and let d and R be the displacement and rotation at the end of one beat cycle. After each cycle, the incremental displacement and rotation in the body-frame will always be d and R since the shape change cycle is the same, and the swimming problem (written in the body-frame) is invariant by rotation and translation. Composing these (constant) translations and rotations with the motion of the body-frame, the discrete trajectory in the lab-frame will be

$$\displaystyle \begin{aligned} {\mathbf{c}}_k=\mathbf{o} + \mathbf{d} + \mathbf{R}\mathbf{d} + {\mathbf{R}}^{2}\mathbf{d} + \ldots + {\mathbf{R}}^{(k-1)}\mathbf{d}\,, \quad \text{and}\quad {\mathbf{R}}_k={\mathbf{R}}^{k}\,, \end{aligned} $$

(1.25)

where R _k = R(0 + kT) and R ⁰ = R(0) = I.

To see that (1.25)₁ is a discrete circular helix, we will use the discrete version of a well known result form differential geometry, stating that a curve with constant curvature and torsion is necessarily a circular helix. This is easy to prove by integrating Frenet’s formulas, and is sometimes referred to as Lancret’s theorem. To compute the (discrete) curvature at point c _k, consider the (osculatory) plane generated by the three points (c _k−1, c _k, c _k+1) and spanned by the (discrete) tangents R ^(k−1)d and R ^(k−1)Rd, see Fig. 1.5. By Frenet’s formulas, the curvature at c _k is 1∕|d| times the angle θ between d and Rd, which is independent of k. Similarly, to compute the torsion at point c _k, consider the binormal at c _k. This is orthogonal to the osculatory plane at c _k, hence parallel to R ^(k−1)(d ×Rd). Similarly, the binormal at c _k+1 is orthogonal to the plane spanned by R ^kd and R ^(k+1)d, hence parallel to R ^(k−1)(R(d ×Rd)). By Frenet’s formulas, the torsion at c _k is 1∕|d| times the angle ϕ between d ×Rd and R(d ×Rd), which is independent of k. Special cases are that of a straight trajectory, which arises when d is parallel to the axis of R (hence d ×Rd = 0, zero discrete curvature), and of a circular trajectory, which arises when d is perpendicular to the axis of R (so that both d ×Rd and R × (d ×Rd) are parallel to the axis of R and hence, zero discrete torsion).

Fig. 1.5

Tangents and binormals to the discrete helix to compute discrete curvature θ∕|d| and discrete torsion ϕ∕|d|. Figure reproduced from [35]

The informal discussion above can be made rigorous by using the results in [28], that show that curve (1.25)₁ can be seen as the discretization of a continuous curve having as curvature and torsion exactly the values computed from (1.25)₁.

It is interesting to give a concrete geometric representation of the helix above, see Fig. 1.6. Let e be the axis of the rotation R (the eigenvector corresponding to its eigenvalue equal to + 1) and θ the angle. We can highlight the two parameters characterising the rotation R by writing $\mathbf {R}={\mathbf {R}}_{\mathbf {e}}^{\theta }$. In a reference frame with origin o, first axis aligned with d _⊥, the projection of d on the plane perpendicular to the rotation axis e (we are assuming here that d is not parallel to e, for otherwise the trajectory is a straight line parallel to d), and third axis aligned with e, the equation of the discrete circular helix (1.25)₁ is

$$\displaystyle \begin{aligned} x_1(k)=r\, \mathrm{cos}\left(\frac{\pi-\theta}{2} \right) + r\, \mathrm{cos}\left(-\frac{\pi+\theta}{2} +k \theta \right) \end{aligned} $$

(1.26)

$$\displaystyle \begin{aligned} x_2(k)=r\, \mathrm{sin}\left(\frac{\pi-\theta}{2} \right) + r\, \mathrm{sin}\left(-\frac{\pi+\theta}{2} +k \theta \right) \end{aligned} $$

(1.27)

$$\displaystyle \begin{aligned} x_3(k)=0+k\, |{\mathbf{d}}_{//}| \end{aligned} $$

(1.28)

where

$$\displaystyle \begin{aligned} r\,=\frac{|{\mathbf{d}}_{\perp}|/2}{\mathrm{sin}(\theta/2)}\,,\quad {\mathbf{d}}_{//}= \left(\mathbf{e}\otimes \mathbf{e} \right) \mathbf{d} \,, \quad {\mathbf{d}}_{\perp}= \left(\mathbf{I}- \mathbf{e}\otimes \mathbf{e} \right) \mathbf{d} \,. \end{aligned} $$

(1.29)

Fig. 1.6

Geometric construction of the parameters of the discrete circular helix associated with shift d and rotation $\mathbf {R}={\mathbf {R}}^{\theta }_{\mathbf {e}}$ of angle θ and axis e. In the figure, d _⊥ denotes the projection of d on the plane perpendicular to the rotation axis e. Figure reproduced from [35]

Finally, it is interesting to notice that, since the axis of body rotation R is also the screw axis of the helix traced by the cell body, as the cell moves in average along the screw axis, the body rotates so that the lateral surfaces containing the eyespot (in which a light receptor is located) is periodically exposed to or shaded from light, unless the screw axis is aligned with the light source. In fact, this is a vivid example of a general biochemical mechanism, repeatedly found in nature, whereby periodic signals are used as a tool for navigation: the existence of a periodic signal implies lack of alignment [56]. Thus, the organism can react to the signal by perturbing its beat until the periodic signal is suppressed, in the aligned state. In this way, the coupling between direction of average motion and axis of body rotations could explain the navigation mechanism used by phototactic Euglena to orient with a light source.

The result contained in the Helix Theorem is remarkable in its universality, and it has far reaching consequences for the swimming of flagellated and ciliated unicellular organism: They all trace helical trajectories. This is at least true over time windows over which they exhibit stereotyped behavior (e.g., no turns), resulting on periodic beating of their cilia and flagella. As a matter of fact, the recent biophysical literature abounds with reports of discoveries of the helical structure of experimentally observed trajectories of a variety of micro-swimmers of great biological relevance (bacteria, sperm cells, etc.). Most of the previous literature had focused on the special cases of straight and circular trajectories, which are easily measured from two-dimensional images from an optical microscope, while the reconstruction of trajectories such as helices, which are spatial curves, requires that we resolve the third dimension perpendicular to the focal plane of the microscope. This entails technical problems, and only recently is it becoming possible to overcome them.

The interest and possible applications of the Helix Theorem above are not confined to trajectories of biological (and, possibly, artificial) micro-swimmers. In fact, the theorem yields a principle for the self-assembly of helical structures. Indeed, the theorem characterizes the geometry of any chain resulting from the assembly of rigid monomers, when the position and orientation of the (k + 1)-th monomer are constrained to be those arising from a shift d and a rotation R of the k-th one. In this case, a discrete circular helix will emerge. In other words, if two monomers can only bind in a precise relative position and orientation, then a self-assembled helical structure will be the outcome when they form in a chain. This simple observation provides a rationale explaining why helices are so ubiquitous in biology and nature, and why bio-polymers self-assemble into helices. For the same reason, self-assembled helical structures are frequently encountered in polymer science, chemical engineering and materials science.

1.6 Shape Control and Gaussian Morphing

The mechanism by which Euglena changes shape when executing metaboly, discussed in Sect. 1.5.1, is based on active shears of its outer envelope, which arise in turn from the sliding of its pellicle strips. To the best of our knowledge, this mechanism has never been used in engineered devices, at least until now. For this reason, it is interesting to place this mechanism within a more general discussion of shape control in biological organism, of deployable structures, of bio-inspired morphing structures, of shape programming of active materials, adaptable structures, and the various other variants of these concepts.

In fact, the active shearing explaining Euglena’s metaboly is but one example of shape control of two-dimensional thin, shell-like objects, whereby shape control is enforced through control of curvature. There are two main avenues to achieve this. The first one operates by inducing differential strains along the thickness, as in Timoshenko’s bimetallic strips [100] and in modern soft variants, see e.g. [5, 29, 38, 44, 93]. The second one operates by controlling in-plane stretches and exploiting Gauss’ theorema egregium. This second avenue, based on the fact that Gaussian curvature is associated with derivatives of the components of the metric tensor, i.e., differential stretches of the mid-surface, has received a lot of attention in the recent literature, see e.g., [67, 78, 82, 91] and many others. We call Gaussian morphing this second strategy, namely, the idea of controlling curvature (shape) of a thin two-dimensional structure through modulated stretching of the mid-surface (via prescription of the metric tensor). The mechanism used by Euglena is of this second type.

Many results are available on how this Gaussian morphing principle is at work in biological structures [6, 17, 18], and on how it can be exploited in artificial structures by using for example hydrogels or nematic elastomers, see e.g. [7, 65, 95, 106]. But, up to now, technology has mostly relied on the first principle (differential strains across the thickness), rather than on the second (differential stretches of the mid-surface). Understanding how Gaussian morphing works in specific examples may help popularize this new approach and inspire novel applications in the context of deployable or adaptive structures and devices. With these motivations in mind, we explore two concrete examples in the next sections. Further details can be found in [36].

1.6.1 Controlling the Shape of Surfaces by Prescribing Their Metric

We start by considering the reference configuration of a material surface, namely, a two-dimensional surface immersed in $\mathbb {R}^3$ and its deformations. This means that we consider a map $(u,v)\mapsto \boldsymbol {\chi }_0(u,v)\in \mathbb {R}^3$, where $(u,v)\in (L_0, H_0)\subset \mathbb {R}^2$. A deformed configuration of this material surface will be given by another map, say, $(u,v)\mapsto \boldsymbol {\chi }(u,v)\in \mathbb {R}^3$, again with $(u,v)\in (L_0, H_0)\subset \mathbb {R}^2$.

By computing the surface deformation gradient F and the right Cauchy-Green strain C = F ^TF, we obtain the metric tensors of the material surface in the reference and deformed configurations as

$$\displaystyle \begin{aligned} \boldsymbol{C}_0=g_0= \left[\begin{array}{cc} \boldsymbol{\chi}_{0,u} \cdot \boldsymbol{\chi}_{0,u}\, &\, \boldsymbol{\chi}_{0,u} \cdot \boldsymbol{\chi}_{0,v} \\ \boldsymbol{\chi}_{0,u} \cdot \boldsymbol{\chi}_{0,v}\, & \,\boldsymbol{\chi}_{0,v} \cdot \boldsymbol{\chi}_{0,v} \\ \end{array} \right] \end{aligned} $$

(1.30)

and

$$\displaystyle \begin{aligned} \boldsymbol{C}=g= \left[\begin{array}{cc} \boldsymbol{\chi}_{,u} \cdot \boldsymbol{\chi}_{,u}\, &\, \boldsymbol{\chi}_{,u} \cdot \boldsymbol{\chi}_{,v} \\ \boldsymbol{\chi}_{,u} \cdot \boldsymbol{\chi}_{,v}\, & \,\boldsymbol{\chi}_{,v} \cdot \boldsymbol{\chi}_{,v} \\ \end{array} \right] =\left[\begin{array}{cc} E & F \\ F & G \\ \end{array} \right] , \end{aligned} $$

(1.31)

where a comma denotes partial differentiation.

We are interested in inducing controlled changes of the shape of the material surface by generating changes of lengths and angles of its material fibers through actuation, described by changes of the metric tensor from its reference value g ₀ to a new value g. The possibility of changing curvature (morphing) of a surface by acting on its metric is recognized by a remarkable theorem by Gauss, his celebrated theorema egregium, stating that the Gaussian curvature K of a surface (the product of its principal curvatures) can be computed by differentiating the components of its metric tensor as

$$\displaystyle \begin{aligned} -E K = (\Gamma^2_{12})_{,u} - (\Gamma^2_{11})_{,v} + \Gamma^1_{12}\Gamma^2_{11} + \Gamma^2_{12}\Gamma^2_{12} -\Gamma^2_{11}\Gamma^2_{22} -\Gamma^1_{11}\Gamma^2_{12} \,, \end{aligned} $$

(1.32)

where $\Gamma ^\alpha _{\beta \gamma }$, α, β, γ = 1, 2, are the Christoffel symbols, see [50]. The interpretation of Gauss’ theorema egregium as a morphing scheme has been pioneered in the seminal paper [67].

We will discuss examples that are motivated by shape changes exhibited by unicellular organisms, of special relevance in the study of cell motility. Our first example, motivated by Euglena’s metaboly introduced in Sect. 1.5.1, is the local simple shear arising from the sliding of pellicle strips making up the cell envelope of euglenids. This mechanism for shape change has been analyzed in great detail in [17, 18, 84, 85], and it is described by a metric tensor of the form

$$\displaystyle \begin{aligned} g = \left[\begin{array}{cc} 1+\gamma^2 & \gamma \\ \gamma & 1 \\ \end{array} \right] \;\;\;\;\;\mbox{(shearing mechanism).} \end{aligned} $$

(1.33)

Here $\gamma =\gamma (u,v)\in \mathbb {R}$ is the local simple shear between material fibers aligned with the coordinate lines (the direction of the centerline of the pellicle strips in the case of euglenids), an area preserving deformation. Actually, the same mechanism drives the flagellar and ciliary beating in eukaryotic cells discussed in Sect. 1.4.2, where molecular motors induce relative sliding between parallel bundles of microtubules lying on the outer cylindrical envelope of the flagellum, see [36] for more details. Substituting (1.33) into (1.32) we obtain

$$\displaystyle \begin{aligned} K =\left(\gamma_{,u}- \gamma \gamma_{,v} \right)_{,v} \;\;\;\;\;\mbox{(shearing mechanism).} \end{aligned} $$

(1.34)

Our second example is motivated by the observations in [39] of the deformations of Lacrymaria olor, a unicelluar ciliate that is easily found in freshwater ponds, just as Euglena. This same mechanism is also at work in the braided sheaths of pneumatic artificial muscles of McKibben type [101]. It consists of a stretch with principal directions along the coordinate lines

$$\displaystyle \begin{aligned} g= \left[\begin{array}{cc} \lambda^2 & 0 \\ 0 & \mu^2 \\ \end{array} \right] \;\;\;\;\;\mbox{(stretching mechanism),} \end{aligned} $$

(1.35)

where λ = λ(u, v) ∈ (0, +∞) and μ = μ(u, v) ∈ (0, +∞) are the stretches along the u − and v −coordinate lines, respectively. These are typically the diagonals in the rhombus-shaped unit cell of a meshwork which deforms as a pantograph in the sheath of a McKibben actuator or, for the biological case, in the arrays of biofilaments making up the cell envelope.

The deformation associated with (1.35) is area preserving if λμ = 1, in which case it is called a pure shear. Substituting (1.35) into (1.32) we obtain

$$\displaystyle \begin{aligned} K= -\frac{1}{\lambda\mu}\left( \left(\frac{\lambda_{,v}}{\mu}\right)_{,v} + \left(\frac{\mu_{,u}}{\lambda}\right)_{,u} \right) \;\;\;\;\;\mbox{(stretching mechanism)} \end{aligned} $$

(1.36)

in the general case while, in the area-preserving case, we have

$$\displaystyle \begin{aligned} K= - \left( \lambda \lambda_{,v}\right)_{,v} - \left( \mu \mu_{,u}\right)_{,u} \quad \quad (\mbox{stretching mechanism}\,,\,\lambda\mu = 1). \end{aligned} $$

(1.37)

1.6.2 Axisymmetric Surfaces

For simplicity, we focus now on axisymmetric shape-shifting surfaces. As reference configuration S ₀, we consider the cylinder of radius R ₀ such that

$$\displaystyle \begin{aligned} \boldsymbol{\chi}_0(u,v)=\left\{ R_0 \cos \left(\frac{u}{R_0}\right), R_0 \sin \left(\frac{u}{R_0}\right), v \right\} ,\quad u\in(0,L_0), v\in (0,H_0) \,, \end{aligned} $$

(1.38)

where L ₀ = 2πR ₀. This has the identity matrix as metric tensor g ₀ and zero Gaussian curvature K ₀ = 0, in agreement with formulas for g and K in the previous section obtained by setting either γ = 0 or λ = μ = 1.

We are then interested in deformed configurations with axisymmetric shape S, which can be written by assigning a generating curve $\left \{ r(v), z(v)\right \}$ in the symmetry plane and an azimuthal displacement ψ(v), leading to

$$\displaystyle \begin{aligned} \boldsymbol{\chi}(u,v) &= \left\{ r(v) \cos \left(\frac{u}{R_0}+\psi(v)\right), r(v) \sin \left(\frac{u}{R_0}+\psi(v)\right), z(v) \right\} , \, \\ & u\in(0,L_0), v\in (0,H_0) \,. \end{aligned} $$

(1.39)

Substituting (1.39) into (1.31) we obtain

$$\displaystyle \begin{aligned} \left[\begin{array}{cc} (r/R_0)^2 & r^2\psi^{\prime}/R_0 \\ {} r^2\psi^{\prime}/R_0 & \quad r^{\prime 2} + z^{\prime 2}+ r^2\psi^{\prime 2} \end{array} \right] =\left[\begin{array}{cc} E & F \\ F & G \\ \end{array} \right] = g \, , \end{aligned} $$

(1.40)

where a prime (⋅)^′ denotes differentiation with respect to v. Clearly, since the left hand side in the last equation depends only on v, only metric tensors g = g(v) that are independent of u (axi-symmetric actuation) are compatible with (1.39). In these circumstances, Eqs. (1.34), (1.36), and (1.37) from the last section simplify to

$$\displaystyle \begin{aligned} K= - \left( \gamma \gamma_{,v} \right)_{,v} &\;\;\;\;\; \mbox{(shearing mechanism),} {} \end{aligned} $$

(1.41)

$$\displaystyle \begin{aligned} K= \frac{1}{\lambda\mu}\left( \frac{1}{\mu^2}\lambda_{,v}\mu_{,v} -\frac{1}{\mu}\lambda_{,vv} \right) &\;\;\;\;\; \mbox{(stretching mechanism),} {} \end{aligned} $$

(1.42)

$$\displaystyle \begin{aligned} K= - \left( \lambda \lambda_{,v}\right)_{,v} &\;\;\;\;\; \mbox{(stretching mechanism,}~\lambda\mu = 1 \mbox{),} {} \end{aligned} $$

(1.43)

respectively.

We would like to compute the axisymmetric shapes that can result from axisymmetric actuation patterns either in simple shear, γ = γ(v), or in pure shear λ = λ(v), λμ = 1. From Eq. (1.40) we immediately see that, since E = (r∕R ₀)², whenever the metric g is constant, then the axisymmetric surface χ is a cylinder of radius r = E ^1∕2R ₀, a special instance of a surface with zero Gaussian curvature K = 0. This case of constant metric g is the simplest to examine, and we shall consider this case first.

1.6.3 Cylinders from Cylinders

When K = K ₀ = 0, the axisymmetric morphing surface can be developed onto a plane both before and after actuation. Following [17], in order to study the shape change S ₀↦S induced by the change of metric g ₀↦g, it is useful to analyze the process by first cutting S ₀ along a direction parallel to the cylinder axis and unfolding it (isometrically) to a plane, then deform this plane with a two-dimensional affine map Φ(u, v) inducing the (spatially uniform) change of metric g ₀↦g

$$\displaystyle \begin{aligned} \left[\begin{array}{cc} \boldsymbol{\Phi}_{,u} \cdot \boldsymbol{\Phi}_{,u}\, &\, \boldsymbol{\Phi}_{,u} \cdot \boldsymbol{\Phi}_{,v} \\ \boldsymbol{\Phi}_{,u} \cdot \boldsymbol{\Phi}_{,v}\, & \,\boldsymbol{\Phi}_{,v} \cdot \boldsymbol{\Phi}_{,v} \\ \end{array} \right] =g=\left[\begin{array}{cc} E & F \\ F & G \\ \end{array} \right] , \end{aligned} $$

(1.44)

and then roll-up (isometrically) the deformed plane on a cylinder of radius r = E ^1∕2R ₀. The case associated with Euglena’s shearing mechanism is

$$\displaystyle \begin{aligned} \boldsymbol{\Phi}(u,v)= \boldsymbol{R}_{\boldsymbol{e}_3}^\phi \left( u \boldsymbol{e}_1 + (v + \gamma u) \boldsymbol{e}_2 \right) \,, \quad g= \left[\begin{array}{cc} 1+\gamma^2 & \gamma \\ \gamma & 1 \\ \end{array} \right] , \end{aligned} $$

(1.45)

where $\boldsymbol {R}_{\boldsymbol {e}_3}^\phi$ is a rotation with axis e ₃ and angle $\phi = \tan ^{-1}(\gamma )$.

The case associated with with Lacrymaria’s stretching mechanism is given instead by

$$\displaystyle \begin{aligned} \boldsymbol{\Phi}(u,v)= \lambda u \boldsymbol{e}_1 + \mu v \boldsymbol{e}_2 \,, \quad g= \left[\begin{array}{cc} \lambda^2 & 0 \\ 0 & \mu^2 \\ \end{array} \right] . \end{aligned} $$

(1.46)

The way surfaces deform as a consequence of metrics of type (1.45) is studied extensively in [17, 18], to which the reader is referred. A similar analysis can be done for metrics of type (1.46). Substituting (1.46) into (1.40) we obtain

$$\displaystyle \begin{aligned} \left[\begin{array}{cc} (r/R_0)^2 & r^2\psi^{\prime}/R_0 \\ {} r^2\psi^{\prime}/R_0 & \quad r^{\prime 2} + z^{\prime 2}+ r^2\psi^{\prime 2} \end{array} \right] = \left[\begin{array}{cc} \lambda^2 & 0 \\ 0 & \mu^2 \\ \end{array} \right] = \mathrm{constant,} \end{aligned} $$

(1.47)

which gives r = λR ₀, while the functions ψ(v) and z(v) are determined by solving the differential equations

$$\displaystyle \begin{aligned} \psi^{\prime}=0 \,, \end{aligned} $$

(1.48)

and

$$\displaystyle \begin{aligned} z^{\prime}= \pm \mu \,. \end{aligned} $$

(1.49)

Hence, by setting the integration constants ψ(0) and z(0) equal to zero and selecting the plus sign in (1.49) (solutions to (1.47) are determined up to a rigid motion allowing for translations along e ₃, rotations about e ₃, and ± inversion along e ₃, which are here fixed), we have ψ(v) = 0 and z(v) = μv.

Having in mind the arrangement of microtubules in Lacrymaria’s envelope, and also the arrangement of fibers in the braided sheaths of McKibben artificial muscles, we are interested in the conformational changes of networks of helical material curves on S ₀, when a metric change g ₀↦g transforms S ₀ into S. We consider the 2N lines

$$\displaystyle \begin{aligned} u^{(k)}(v)= k \frac{2\pi}{N} R_0 \pm \tan (\vartheta_0) v \,,\quad k=0, \dots, N-1\end{aligned} $$

(1.50)

and their images in the reference and deformed configurations

$$\displaystyle \begin{aligned} \begin{aligned} \boldsymbol{\chi}^{(k)}_0 (v)= {}& \boldsymbol{\chi}_0(u^{(k)}(v), v) \\ = {}& \left\{ R_0 \cos \left(\frac{1}{R_0} u^{(k)}(v) \right), R_0 \sin \left( \frac{1}{R_0} u^{(k)}(v) \right), v \right\} , \,\, v \in (0,H_0) \end{aligned}\end{aligned} $$

(1.51)

and

$$\displaystyle \begin{aligned} \begin{aligned} \boldsymbol{\chi}^{(k)} (v)= {}& \boldsymbol{\chi} ( u^{(k)}(v), z(v) ) \\ = {}& \left\{ \lambda R_0 \cos \left(\frac{1}{R_0} u^{(k)}(v) \right), \lambda R_0 \sin \left( \frac{1}{R_0} u^{(k)}(v) \right), \mu v \right\} , \,\, v\in (0,H_0) . \end{aligned}\end{aligned} $$

(1.52)

Curves (1.51) are circular helices with radius R ₀, screw axis parallel to e ₃, and pitch angle 𝜗 ₀. Curves (1.52) are circular helices with radius λR ₀, screw axis parallel to e ₃, and pitch angle $\tan ^{-1} (\lambda \tan {}(\vartheta _0)/\mu )$ (when 𝜗 ₀ = π∕4, the angular pitch of (1.52) is $\tan ^{-1}(\lambda /\mu )$). These are all illustrated in Fig. 1.7.

Fig. 1.7

Cylindrical surfaces obtained from a referential cylinder with H ₀∕R ₀ = 5 by exploiting the area preserving stretching morphing principle (1.35) for λ = {0.75, 1, 1.5, 2, 2.5, 3}. Cylindrical surfaces are decorated by blue and yellow material fibers for θ ₀ = π∕4 and N = 10. Figure reproduced from [36]

1.6.4 Axisymmetric Surfaces with Non-constant Metric

We turn now to more general axisymmetric surfaces S of the form (1.39), obtained by axisymmetric actuation, i.e., by a non-constant metric g depending only on the “vertical” coordinate v (the coordinate along the symmetry axis) and not on the “azimuthal” coordinate u. The case of simple shear (1.33) has been studied in detail in [17, 18, 84, 85] in connection with the morphing mechanism of the pellicle of euglenids. In particular, we refer to [17] for the complete atlas of the axisymmetric shapes of constant Gaussian curvature surfaces (cylinders, cones, spheres, spindles, and pseudo-spheres) achievable by axisymmetric shearing, and for the solution of the inverse problem of finding which shear actuation patterns, i.e., which metric of the type (1.45), are capable of realizing each given shape.

Here, we consider the stretching metric given by (1.35), restricting attention to the area-preserving case of λμ = 1 (pure shear) for simplicity. From

$$\displaystyle \begin{aligned} \left[\begin{array}{cc} (r/R_0)^2 & r^2\psi^{\prime}/R_0 \\ {} r^2\psi^{\prime}/R_0 & \quad r^{\prime 2} + z^{\prime 2}+ r^2\psi^{\prime 2} \end{array} \right] =\left[\begin{array}{cc} \lambda^2 & 0 \\ 0 & 1/\lambda^2 \\ \end{array} \right] ,\end{aligned} $$

(1.53)

where λ = λ(v) and a prime denotes derivative with respect to v, we obtain

$$\displaystyle \begin{aligned} r(v)=\lambda(v) R_0 \,,\end{aligned} $$

(1.54)

$$\displaystyle \begin{aligned} \psi^{\prime} (v) = 0 \,,\end{aligned} $$

(1.55)

and

$$\displaystyle \begin{aligned} z^{\prime}(v)= \pm \frac{1}{\lambda(v)}\sqrt{1- (R_0 \lambda \lambda^{\prime})^2} \,,\end{aligned} $$

(1.56)

which can be solved with real z(v) provided that

$$\displaystyle \begin{aligned} \lambda|\lambda^{\prime}|\le \frac{1}{R_0} \,.\end{aligned} $$

(1.57)

This is a necessary condition for a metric of the form (1.35) to be realized by an axisymmetric surface (embeddability in $\mathbb {R}^3$).

We start by seeking surfaces of zero Gaussian curvature K = 0, more general than the cylinders of the previous section, which arise when λ ^′ = 0. We thus have

$$\displaystyle \begin{aligned} 0 = - \left( \lambda \lambda^{\prime}\right)^{\prime} = - \frac 12(\lambda^2)^{\prime\prime} \,,\end{aligned} $$

(1.58)

which implies that λ(v)λ ^′(v) = C, a constant such that |C|≤ 1∕R ₀. Hence,

$$\displaystyle \begin{aligned} z^{\prime}(v)= \frac{dz}{dv} = \pm \frac{1}{\lambda(v)}\sqrt{1- R_0^2 C^2 } \end{aligned} $$

(1.59)

and, using (1.54), we deduce that

$$\displaystyle \begin{aligned} \frac{dr}{dz}=\frac{\frac{dr}{dv}}{\frac{dz}{dv}}=\pm\frac{R_0\lambda(v)\lambda^{\prime}(v)}{\sqrt{1- R_0^2 C^2}}= \pm \sqrt{ \frac{R_0^2 C^2}{1- R_0^2 C^2} } =: \pm \tan{}(\phi) \,, \end{aligned} $$

(1.60)

which shows that S is a cone with axis parallel to e ₃ and opening angle ϕ (measured clockwise from the e ₃ axis). This angle tends to zero when C → 0, and to π∕2 when C →±1∕R ₀.

Moreover, it follows from (1.58) that λ ²(v) is a linear function of v ∈ (0, H ₀). Thus, we can write λ as

$$\displaystyle \begin{aligned} \lambda=\tilde{\lambda}(\xi)= \sqrt{A(1-\xi)+B\xi}\,, \quad \xi:=\frac{v}{H_0}\in(0,1)\,,\quad \tilde{\lambda}(0)=\sqrt{A}\,,\quad \tilde{\lambda}(1)=\sqrt{B} \end{aligned} $$

(1.61)

and integrate (1.59) to obtain

$$\displaystyle \begin{aligned} z(v)=z(0)\pm H_0\sqrt{1-R_0^2 C^2}\int_0^{v/H_0}{\frac{dx}{\sqrt{A(1-x)+Bx}}} \,. \end{aligned} $$

(1.62)

Furthermore, from λλ ^′ = (λ ²)^′∕2 = C, we obtain

$$\displaystyle \begin{aligned} C=\frac{B-A}{2H_0} \,, \end{aligned} $$

(1.63)

so that the embeddability condition |C|≤ 1∕R ₀ is equivalent to

$$\displaystyle \begin{aligned} |B-A| -\frac{2H_0}{R_0}\le 0 \,. \end{aligned} $$

(1.64)

Setting all the integration constants to zero and choosing the positive sign in the previous formulas, we obtain the parametrization of S as

$$\displaystyle \begin{aligned} \lambda(v)=\sqrt{A\left(1-\frac{v}{H_0}\right)+B\frac{v}{H_0}} \,, \end{aligned} $$

(1.65)

$$\displaystyle \begin{aligned} r(v)=\lambda(v)R_0 \,, \end{aligned} $$

(1.66)

$$\displaystyle \begin{aligned} \psi(v)=0 \,, \end{aligned} $$

(1.67)

and

$$\displaystyle \begin{aligned} z(v) = \frac{\sqrt{A(1-R_0^2 C^2)}}{C}\left(\sqrt{1-\frac{v}{H_0} + \frac{B}{A}\frac{v}{H_0}} - 1\right) , \end{aligned} $$

(1.68)

which describes a truncated cone with opening angle given by (1.60) and radii at the rim of the surface equal to $r(0)=R_0\sqrt {A}$ and $r(H_0)=R_0\sqrt {B}$. Here A = λ ²(0), B = λ ²(H ₀), C = (B − A)∕(2H ₀) and A, B must be such that |B − A|− 2H ₀∕R ₀ ≤ 0.

The images of the circular helices (1.51) after deformation are obtained by substituting the previous formulas into

$$\displaystyle \begin{aligned} \begin{aligned} \boldsymbol{\chi}^{(k)} (v)= {}& \boldsymbol{\chi} ( u^{(k)}(v), z(v) ) \\ = {}& \left\{ r(v) \cos \left(\frac{1}{R_0} u^{(k)}(v) \right), r(v) \sin \left( \frac{1}{R_0} u^{(k)}(v) \right), z(v) \right\} , \,\, v\in (0,H_0) \\ \end{aligned} \end{aligned} $$

(1.69)

and are represented in Fig. 1.8.

Fig. 1.8

Truncated cones obtained from a referential cylinder with H ₀∕R ₀ = 5 by exploiting the stretching morphing principle (1.35) for r(0)∕R ₀ = {1, 1.5, 2, 2.5, 3, 3.32} and r(H ₀)∕R ₀ = 1. Conical surfaces are decorated by blue and yellow material fibers for θ ₀ = π∕4 and N = 10. Figure reproduced from [36]

Figure 1.9 shows a comparison between surfaces and networks of material lines arising form the two different actuation mechanisms. The figure shows that the same shapes can be obtained with two different metrics (one corresponding to a stretching mechanism, the other one to a shearing mechanism). The two mechanisms (not the shapes) are distinguishable because they lead to different deformations of the networks of material lines, and lead to different displacements of material points on the surfaces. On the left part of the figure, red lines suggest the evolution of the orientation of the pellicle strips of Euglenids, which deform according to the shearing mechanism (1.33). On the right side of the figure the blue and yellow lines suggest the evolution of the orientation of the network of threads in the sheath of a McKibben artificial muscle or of the microtubules in the cell envelope of Lacrymaria, which deform according to the stretching mechanism (1.35).

Fig. 1.9

A comparison between identical shapes (cylinders and truncated cones) obtained by means of either a shearing (left) or stretching (right) mechanism. All the shapes are for H ₀∕R ₀ = 5. The shorted cylinders correspond to $\gamma = \sqrt {3}$ (shearing mechanism) and to λ = 2 (stretching mechanism). Cones are both such that r(0)∕R ₀ = 2.5 and r(H ₀)∕R ₀ = 1. Surfaces are decorated by colored material fibers to highlight the embodiment of the morphing principle and to emphasize the difference between the two morphing mechanisms. Figure reproduced from [36]

We remark that the theory of shape-shifting surfaces va Gaussian morphing described in this section is purely geometric. It is clear, however, that the shape-programming path in shape space we have described may require elastic deformations of the structural elements (rod, membrane, plate, shell, and block elements) making up the morphing surface. Since these elements will be stretched and bent, the way a morphing principle works when implemented into a concrete organism or in a concrete engineered device cannot be predicted without the explicit appreciation of its embodiment into a specific body architecture (in the case of organisms) or into specific arrangement of structural elements in the case of engineered devices. In other words, the way a morphing principle works in practice is crucially affected by the mechanical compliance of the materials and mechanisms that build the body or the device.

Thus, the difference between the two mechanisms illustrated in Fig. 1.9 is not without subtleties. For each fixed value γ of the shearing metric g, there is a stretching metric delivering the same shape, through stretches along different coordinate lines, the ones along the γ-dependent eigenvectors of g. A change of coordinates transforms one metric into the other. If, however, we insist on the fact that some curves in the reference configuration have the character of material lines, and that the embodiment of the shape-shifting mechanism governs the change of lengths and angles of material lines, then the two mechanisms by shearing and stretching are no longer interchangeable. Indeed, material lines are deformed in different ways by the two mechanisms and the embodiment reveals the difference between the two. Along the one-parameter family of shapes illustrated in Fig. 1.9, material lines initially straight and vertical deform at constant length by differential lateral sliding in the shearing mechanism (shown in the left). Instead, they remain straight and are shortened by the stretching mechanism (shown in the right). A more complete discussion of this issue, and a more complete characterization of shapes that can be produced with the two mechanisms (direct problem), and of the actuation patterns needed to obtain them in specific embodiments of the underlying Gaussian morphing principle (inverse problem) will be provided elsewhere.

1.6.5 Protruding Necks and Localized Bulges

Of particular interest in biology and soft robotics is the construction of localized bulges and of protruding necks starting from an axisymmetric shape. These are commonly exhibited by biological organisms and one can think of exploiting them in artificial devices for robotic manipulation, drug delivery, surgical tools for minimally invasive surgery, etc. In the context of the shearing mechanism (1.41), they have been used to mimic the peristaltic waves and traveling bulges rationalizing metaboly in Euglenids, see [17, 85]. In the context of the stretching mechanism, (1.42) or (1.43), they can be used to mimic the neck protrusion that the unicellular predator Lacrymaria olor uses to explore the environment to search for preys and to feed on them.

Indeed, let’s consider (1.43), with the axially-symmetric stretch λ given in terms of a non-dimensional coordinate ξ along the symmetry axis by

$$\displaystyle \begin{aligned} \tilde{{\lambda}}(\xi)= 1 + A \left(1- \exp \left[ - \left(\frac{\xi-\xi_0}{D}\right)^2 \right] \right) , \quad \xi:=\frac{v}{H_0}\in (-1,1) \, , \end{aligned} $$

(1.70)

where A > −1 determines the strength of the bulge perturbation with respect to the reference cylinder (1.38), D > 0 determines its non-dimensional breadth, while ξ ₀ ∈ (−1, 1) locates the centre of the bulge along the symmetry axis.

The shapes resulting from (1.70) are shown in Fig. 1.10. They are closely reminiscent of the patterns exhibited by Lacrymaria when it protrudes its neck for feeding, see [39]. Shape changes of a similar kind are also exhibited by Euglena when it executes metaboly, even though the extent of the protrusions is less extreme. There, the shape-shifting mechanism (the metric change) and the displacements of material points on the surface (the sliding of the pellicle strips) arise from a continuous one–parameter family of shears (1.41) rather than stretches (1.43), see [17, 85]. The molecular and bio-physical details by which the two unicellular organisms control their behavior are still largely unknown.

Fig. 1.10

Deformations resembling the neck extension of Lacrymaria olor obtained by means of the stretching mechanism (1.43) from a reference cylinder. Shapes are obtained using Eq. (1.70) with A = {0, −0.17, −0.34, −0.51, −0.68, −0.85}, D = 0.28, and ξ ₀ = 0.3. The referential cylinder is such that H ₀∕R ₀ = 7. Surfaces are decorated by blue and yellow material fibers defined by Eq. (1.50) with θ ₀ = π∕4 and N = 10. Figure reproduced from [36]

1.7 Discussion and Outlook

In these notes we have followed two main threads, which are obviously intertwined.

On the one hand, we have considered biological and bio-inspired locomotion at small length scales, and swimming motility of microscopic unicellular organisms in particular. How does an organism or an artificial device move as a consequence of its mechanical interactions with the environment, if is shape varies in time? E.g., according to a periodic time-history? The main tool we have used in our mathematical approach to this navigation problem is geometric control theory. In this way, reaching position B from position A becomes a question of controllability, and doing so optimally (e.g., at minimal energetic cost) is a problem of optimal control.

On the other hand, we have considered the problem of how to control the shape of the outer envelope of biological organism or of a thin engineering structure. I.e., how can we morph surfaces according to a specified shape programming scheme? In particular, we have discussed the Gaussian morphing scheme, by which shape changes result form changes of Gaussian curvature, which are in turn induced by (active) lateral modulation of the metric of the surface.

There are cases, such as the metaboly of Euglenids, where the two threads are intertwined. Indeed, Euglena gracilis cells control the shape of their outer envelope by patterns of active pellicle shears, which represent modulations of the surface metric by surface shears.

This brings us to the issue of the practical use of the algorithmic morphing principle we have discussed, be it Gaussian morphing or more general morphing schemes, for concrete applications. Invariably, workers in the field of micro-swimmers like to mention the goal of using these principles to fabricate microscopic medical devices (micro-robots) for autonomous navigation inside the human body, capable of executing diagnostic, therapeutic, drug delivery, and minimally invasive surgery functions, in a concrete application of the visionary sequences of the movie ‘Fantastic Voyage’, or of the visionary words of R. Feynman, who was talking about surgeons that can be swallowed. More generally, robotics has shown concrete interest in concepts similar to the ones described in these notes, opening up the new field of Soft Robotics [66]. In this new paradigm, robots that are asked to interact with unstructured and rapidly changing environments can exploit the adaptability coming from compliant bodies, instead of relying only on complex control algorithms for more traditional architectures based on rigid body parts.

The community of Soft Robotics is expanding, but a key challenge to the actual deployment of robotic devices made at least in part of soft component comes from the availability of soft active materials with the right properties. Hydrogels have been used in several applications, in which actuation by solvent uptake is a feasible mechanism (see e.g. [5, 65, 67, 91] and the references cited therein). Liquid crystal elastomers (LCEs) [104] have also been identified as a very promising material, thanks to the availability of many stimuli to which they can respond to (temperature, light, electromagnetic fields, solvent uptake), and recent advances in manufacturing (that allow for a very fine resolution of the patterns of programmed director fields, which can be used to induce shape changes following Gaussian morphing principle). There is a large literature on modeling the mechanical response of LCE sheets, see [4, 7, 19, 26, 37, 43, 45, 46, 52, 78, 82, 93, 104,105,106] and the references cited therein for a small sample.

These materials pose serious challenges also at the level of mathematical modeling. Modeling the mechanics of phase transforming polymeric materials such as LCEs is highly nontrivial, since they exhibit nonlinearities in their response, for example due to domain evolution and hysteresis. Modeling these phenomena still represent a challenge, in spite of the fact that these topics having been in the forefront of research for many years, see e.g., [23, 42, 43]. Recent spectacular results on the possibility of producing low hysteresis shape memory materials, based on mathematical models (with low hysteresis behavior occurring when special compatibility relations between the metric changes in two neighboring domains are satisfied) testifies, however, that progress in this difficult subject is being made [57].