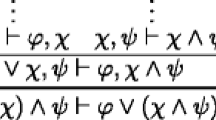Higher-Order Categorical Substructural Logic: Expanding the Horizon of Tripos Theory

Abstract

Higher-order intuitionistic logic categorically corresponds to toposes or triposes; here we address what are toposes or triposes for higher-order substructural logics. Full Lambek calculus gives a framework to uniformly represent different logical systems as extensions of it. Here we define higher-order Full Lambek calculus, which boils down to higher-order intuitionistic logic when equipped with all the structural rules, and give categorical semantics for (any extension of) it in terms of triposes or higher-order Lawvere hyperdoctrines, which were originally conceived for intuitionistic logic, and yet are flexible enough to be adapted for substructural logics. Relativising the completeness result thus obtained to different axioms, we can obtain tripos-theoretical completeness theorems for a broad variety of higher-order logics. The framework thus developed, moreover, allows us to obtain tripos-theoretical Girard and Kolmogorov translation theorems for higher-order logics.

1 Introduction

Propositional logic corresponds to a class of algebras; for example, the algebras of classical intuitionistic logic are Heyting algebras. What are, then, the algebras of predicate logic? There is seemingly no agreed concept of algebras of predicate logic. Cylindric algebras [11] give a candidate for it. It is not very clear how far and how uniformly cylindric algebraic semantics can be extended so as to treat different sorts of logical systems, especially substructural logics (linear, relevant, fuzzy, etc.). Lawvere’s hyperdoctrines [18] give another concept of algebras of predicate logic, and may be seen as a categorical extension of cylindric algebras (see, e.g., Jacobs [13], which gives a fibrational understanding of cylindric algebras; fibrations and hyperdoctrines as indexed categories are connected with each other via the Grothendieck construction). From an algebraic point of view, a hyperdoctrine is a fibred algebra, i.e., an algebra indexed by a category:

$$P:\mathbf{C}^\mathrm{op}\rightarrow \mathbf{Alg}.$$

$\mathbf{Alg}$ is a category of algebras of propositional logic (e.g., Heyting algebras or BI-algebras as in Biering et al. [2]). There are logical conditions to express quantifiers and others as we shall detail below. The intuitive meaning of the base category $\mathbf{C}$ is the category of types (aka. sorts) or domains of discourse, and then P(C) is the algebra of predicates on a type C. And P is called a predicate functor. Roughly, if a propositional logic L is complete with respect to a variety $\mathbf{Alg}_L$, then the corresponding fibred algebras $P:\mathbf{C}^\mathrm{op}\rightarrow \mathbf{Alg}_L$ yield complete semantics for the predicate logic that extends L. This may be called completeness lifting: the completeness of propositional logic with respect to $\mathbf{Alg}$ lifts to the completeness of predicate logic with respect to $P:\mathbf{C}^\mathrm{op}\rightarrow \mathbf{Alg}$. While this completeness lifting is demonstrated for first-order logic in [21], in the present paper, we demonstrate completeness lifting for higher-order logic of different sorts.

In order to represent different logical systems in a uniform setting, we rely upon the framework of substructural logics over Full Lambek calculus $\mathrm{FL}$ and their algebras (see, e.g., Galatos-Jipsen-Kowalski-Ono [8]); $\mathrm{FL}$ algebras (defined below) play the rôle of $\mathbf{Alg}$ above. Diverse logical systems can be represented as axiomatic extensions of $\mathrm{FL}$, including classical, intuitionistic, fuzzy, relevant, paraconsistent, and linear logics. In this field, there are vital developments of the correspondence between cut elimination and algebraic completion (see Ciabattoni-Galatos-Terui [3], which focus upon the propositional case, but might possibly be extended to the first-order and higher-order cases via the framework of substructural hyperdctrines). In this paper we think of higher-order Full Lambek calculus, which boils down to higher-order intuitionistic logic (as in Lambek-Scott [17]) when equipped with all the structural rules, and give hyperdoctrine semantics for (any extension of) it. Lawvere’s hyperdoctrines were originally for intuitionistic logic; yet they are flexible enough so as to be adapted for a variety of substructural logics as we shall see below. Note that, whilst toposes are impredicative, triposes can have their type theories predicative (e.g., Martin-Löf); the two-level structure of triposes allows more flexibility than toposes do.

There is a tight connection between toposes and higher-order hyperdoctrines, which are also called triposes (for triposes, see, e.g., Hyland-Johnstone-Pitts [12] and Pitts [26]; there are actually several non-equivalent definitions of triposes; we simply call higher-order hyperdoctrines triposes). Indeed, toposes and triposes correspond to each other via the two functors of taking subobject hyperdoctrines and of the tripos-to-topos construction (see, e.g., Coumans [4] and Frey [10]); note that the subobject functor $\mathrm{Sub}$ of a topos plays the rôle of a predicate functor P above. Both toposes and (intuitionistic) higher-order hyperdoctrines give complete semantics for higher-order intuitionistic logic; the completeness result of this paper generalises this classic result quite vastly in terms of higher-order substructural hyperdoctrines or triposes. The contributions of this paper may be summarised succinctly as follows: (i) higher-order completeness via Full Lambek triposes, which can be instantiated for a broad variety of logical systems; (ii) tripos-theoretical Girard’s ! translation and Kolmogorov’s $\lnot \lnot$ translation theorems for higher-order logic, in which the internal language of triposes is at work. As illustrated by the translation theorems, the general framework of the present paper allows us to compare different categorical logics within the one setting (many categorical logics have only been developed locally so far; there has been no global framework to compare them in the same setting).

The rest of the paper is organised as follows. We first present the syntax of Higher-order Full Lambek calculus $\mathrm{HoFL}$, which obtains by adapting higher-order intuitionistic logic to Full Lambek calculus $\mathrm{FL}$. And we introduce the concept of Full Lambek tripos ($\mathrm{FL}$ tripos for short; aka. higher-order $\mathrm{FL}$ hyperdoctrine; for brevity we use the former terminology), thereby obtaining the higher-order completeness theorem for $\mathrm{HoFL}$. Finally, our general framework thus developed is applied, via the internal language of $\mathrm{FL}$ triposes, to the categorical analysis of Girard’s and Kolmogorov’s translation for higher-order logics.

2 Higher-Order Full Lambek Calculus

In this section we introduce Higher-order Full Lambek calculus $\mathrm{HoFL}$, which extends quantified $\mathrm{FL}$ as in Ono [23, 24] so that $\mathrm{HoFL}$ equipped with all the structural rules boils down to higher-order intuitionistic logic, the logic of toposes (see Lambek-Scott [17], Jacobs [13], or Johnstone [15]). Our presentation of $\mathrm{HoFL}$, especially its type-theoretic part, follows the style of Pitts [25]; thus we write, e.g., “$t:\sigma \ [\varGamma ]$” and “$\varphi \ [\varGamma ]$”, rather than “$\varGamma \vdash t:\sigma$” and “$\varGamma \vdash \varphi$”, respectively, where t is a term of type $\sigma$ in context $\varGamma$, and $\varphi$ is a formula in context $\varGamma$.

$\mathrm{HoFL}$ is a so-called “logic over type theory” or “logic-enriched type theory” in Aczel’s terms; there is an underlying type theory, upon which logic is built (see, e.g., Jacobs [13]). To begin with, let us give a bird’s-eye view of the structure of $\mathrm{HoFL}$. The type theory of $\mathrm{HoFL}$ is given by simply typed $\lambda$-calculus with finite product types (i.e., 1 and $\times$; these amount to the structure of CCCs, cartesian closed categories), and moreover, with the special, distinguished type

$$\mathrm{Prop}$$

which is a “proposition” type, intended to represent a truth-value object $\varOmega$ on the categorical side. The logic of $\mathrm{HoFL}$ is given by Full Lambek calculus $\mathrm{FL}$. The $\mathrm{Prop}$ type plays the key rôle of reflecting the logical or propositional structure into the type or term structure: every formula or proposition $\varphi$ may be seen as a term of type $\mathrm{Prop}$. This is essentially what the subobject classifier $\varOmega$ of a topos $\mathbf{E}$ is required to satisfy, that is,

$$\mathrm{Sub}_\mathbf{E}(\text {-})\simeq \mathrm{Hom}_\mathbf{E}(\text {-},\varOmega ).$$

Spelling out the meaning of this axiom in logical terms, we have got

$$\mathrm{Pred}(\sigma ) \simeq \mathrm{Term}(\sigma ,\mathrm{Prop})$$

which means the structure of predicates on each type $\sigma$ (or context $\varGamma$ in general) is isomorphic to the structure of terms from $\sigma$ to $\mathrm{Prop}$. The logical meaning of $\varOmega$ may thus be summarised by a sort of reflection principle, namely the reflection of the propositional structure into the type structure, which may also be called the “propositions-as-terms” or “propositions-as-functions” correspondence, arguably lying at the heart of higher-order categorical logic, for $\varOmega$ would presumably be the raison d’être of higher-order categorical logic (toposes are CCCs with $\varOmega$).

The power type $P\sigma$ of a given type $\sigma$ can be defined in the present framework as $\sigma \rightarrow \mathrm{Prop}$; the comprehension term $\{ x:\sigma \ | \ \varphi \}: P\sigma$ and the membership predicate $s\in t : \mathrm{Prop}$ are definable via $\lambda$-abstraction or currying (categorically, transposing) and $\lambda$-application (categorically, evaluation), respectively. That is, $\{ x:\sigma \ | \ \varphi \}$ may be defined as $\lambda x:\sigma .\ \varphi$ where $\varphi$ is seen as a term of type $\mathrm{Prop}$, and also $s\in t$ may be defined as ts where $t:\sigma \rightarrow \mathrm{Prop}$ and $s:\sigma$. These definable operations allow us to express set-theoretical reasoning in higher-order logic. There is, of course, some freedom on the choice of primitives, just as toposes can be defined in terms of either subobject classifiers or power objects. All this is to facilitate an intuitive understanding of the essential features of higher-order logic; we give a formal account below.

The syntactic details of $\mathrm{HoFL}$ are as follows. $\mathrm{HoFL}$ is equipped with the following logical connectives of Full Lambek calculus:

$$\otimes , \wedge , \vee , \backslash , /, 1, 0, \top , \bot , \forall , \exists .$$

The non-commutativity of $\mathrm{HoFL}$ gives rise to two kinds of implication ($\backslash$ and $/$). We have basic variables and types, denoted by letters like x and $\sigma$, respectively. And as usual $x:\sigma$ is a formal expression to say that a variable x is of type $\sigma$. Note that every variable must be typed in $\mathrm{HoFL}$, unlike untyped $\mathrm{FL}$. A context is a finite list of typings of variables: $x_1:\sigma _1,...,x_n:\sigma _n$ which is often abbreviated as $\varGamma$. Formulae and terms are then defined within specific contexts. There are relation symbols and function symbols, both in context: $R(x_1,...,x_n) \ [x_1:\sigma _1,...,x_n:\sigma _n]$ is a formal expression to say that R is a relation symbol with variables $x_1,...,x_n$ of types $\sigma _1,...,\sigma _n$ respectively; and also $f:\tau \ [x_1:\sigma _1,...,x_n:\sigma _n]$ is a formal expression to say that f is a function symbol with its domain (the product of) $\sigma _1,...,\sigma _n$ and with its codomain $\tau$.

The type constructors of $\mathrm{HoFL}$ are product $\times$, function space $\rightarrow$, and the proposition type $\mathrm{Prop}$, which is a nullary type constructor. The term constructors of $\times$ and $\rightarrow$ are as usual: pairing $\langle \text {-}, \text {-} \rangle$ and (first and second) projections $\pi _1,\pi _2$ for product $\times$, and $\lambda$-abstraction and $\lambda$-application for function space $\rightarrow$. The term constructors of $\mathrm{Prop}$ are all the logical connectives of Full Lambek calculus as listed above, the relation symbols taken to be of type $\mathrm{Prop}$ and thus working as generators of the terms of type $\mathrm{Prop}$. Formulae in context, $\varphi \ [\varGamma ]$, and terms in context, $t:\tau \ [\varGamma ]$, are then defined in the usual, inductive manner (our terminology and notation mostly follow Pitts [25]; we are extending his framework so as to encompass higher-order substructural logics). Finally, sequents in contexts are defined as:

$$\varPhi \vdash \varphi \ [\varGamma ]$$

where $\varGamma$ is a context, $\varPhi$ is a finite list of formulae $\varphi _1,...,\varphi _n$, and all the formulae involved are in context $\varGamma$.

So far we have not touched upon any axiom (or inference rule) involved. In the following, we first give axioms for terms, and then for sequents. The axioms for $\times$ and $\rightarrow$ are as usual (see, e.g., Pitts [25]). The axiom for $\mathrm{Prop}$ is as follows:

This axiom relates the structure of propositions to that of terms, thus guaranteeing the aforementioned “propositions-as-functions” correspondence for higher-order categorical logic. There are several standard rules for contexts and substitution, which are the same as those in Pitts [25] (we do not repeat them here, referring to the Sect. 2 of Pitts [25] for the details). We now turn to inference rules for sequents. We first have the identity and cut rules as follows:

where $\psi$ may be empty; this applies to the following L (Left) rules as well. Note that $\mathrm{HoFL}$ has no structural rule other than the cut rule. The rules governing the use of the logical connectives are as follows.

There are eigenvariable conditions on the quantification rules: x must not appear as a free variable in the bottom sequents of the $\forall R$ and $\exists L$ rules. We write $\forall x$ and $\exists x$ when the type of x is obvious. These are all of the rules of $\mathrm{HoFL}$; the provability of sequents in context is defined in the usual way. The essential difference from the first-order case is the existence of function and truth value types; they are what make the logic higher-order, enabling set-theoretical reasoning.

For a collection X of axiom schemata (which we often simply call axioms), let us denote by $\mathrm{HoFL}_X$ the axiomatic extension of $\mathrm{HoFL}$ via X. In particular, we can recover higher-order intuitionistic logic as $\mathrm{HoFL}_{ecw}$, i.e., by adding to $\mathrm{HoFL}$ the exchange, weakening, and contraction rules (as axiom schemata).

Lemma 1

The following sequents-in-context are deducible in $\mathrm{HoFL}$:

• (i) $\varphi \otimes (\exists x \psi ) \vdash \exists x (\varphi \otimes \psi ) \ [\varGamma ]$ and $\exists x (\varphi \otimes \psi ) \vdash \varphi \otimes (\exists x \psi ) \ [\varGamma ]$;

• (ii) $(\exists x \psi ) \otimes \varphi \vdash \exists x (\psi \otimes \varphi ) \ [\varGamma ]$ and $\exists x (\psi \otimes \varphi ) \vdash (\exists x \psi ) \otimes \varphi \ [\varGamma ]$

where it is supposed that $\varphi$ does not contain x as a free variable, and $\varGamma$ contains type declarations on those free variables that appear in $\varphi$ and $\exists x \psi$.

As explained in [21], typed logic allows domains of discourse to be empty; they must be non-empty in the Tarski semantics. A type $\sigma$ can be interpreted as an initial object in a category. We need no ad hoc condition on domains of discourse if we work with typed logic. This is due to Joyal as noted in Marquis and Reyes [19]. Proof-theoretically, the following is not deducible in $\mathrm{HoFL}$: $\forall x \varphi \vdash \exists x \varphi \ [ ]$. Still the following is deducible: $\forall x \varphi \vdash \exists x \varphi \ [x:\sigma ,\varGamma ]$. That is, we can prove the sequent above when a type $\sigma$ is inhabited (see [21] for more details).

3 Full Lambek Tripos

The algebras of propositional $\mathrm{FL}$ are $\mathrm{FL}$ algebras, the definition of which is reviewed below. The algebras of first-order $\mathrm{FL}$ are arguably $\mathrm{FL}$ hyperdoctrines; note that complete $\mathrm{FL}$ algebras only give us completeness in the presence of the ad hoc condition of so-called safe valuations (cf. [24]), and yet $\mathrm{FL}$ hyperdoctrines allow us to prove completeness without any such ad hoc condition, and at the same time, to recover the complete $\mathrm{FL}$ algebra semantics as a special, set-theoretical instance of the $\mathrm{FL}$ hyperdoctrine semantics (in a nutshell, the condition of safe valuations is only necessary to show completeness with respect to the restricted class of $\mathrm{FL}$ hyperdoctrines with the category of sets their base categories). In this section we define $\mathrm{FL}$ triposes, which are arguably the (fibred) algebras of higher-order $\mathrm{FL}$, and prove higher-order completeness, again without any ad hoc condition such as safe valuations or Henkin-style restrictions on quantification (set-theoretical semantics is only complete under this condition).

Definition 2

$(A,\otimes ,\wedge ,\vee ,\backslash ,/,1,0,\top ,\bot )$ is an $\mathrm{FL}$ algebra iff the following hold:

• $(A,\otimes ,1)$ is a monoid; 0 is a distinguished element of A;

• $(A,\wedge ,\vee ,\top ,\bot )$ is a bounded lattice;

• for any $a\in A$, $a\backslash (\text {-}):A\rightarrow A$ is a right adjoint of $a\otimes (\text {-}):A\rightarrow A$: $a\otimes b \le c \text { iff } b\le a\backslash c$ for any $a,b,c\in A$;

• for any $b\in A$, $(\text {-})/b:A\rightarrow A$ is a right adjoint of $(\text {-})\otimes b:A\rightarrow A$: $a\otimes b \le c \text { iff } a\le c/b.$ for any $a,b,c\in A$.

A homomorphism of $\mathrm{FL}$ algebras is required to preserve all the operations of $\mathrm{FL}$ algebras. Let $\mathbf{FL}$ denote the category of $\mathrm{FL}$ algebras and their homomorphisms.

$\mathbf{FL}$ is an algebraic category (namely, a category monadic over the category of sets; see [1]), and then an axiomatic extension $\mathrm{FL}_X$ of $\mathrm{FL}$ corresponds to an algebraic subcategory of $\mathbf{FL}$, which shall be denoted $\mathbf{FL}_X$. Note that algebraic categories are called varieties or equational classes in universal algebra.

Definition 3

An $\mathrm{FL}$ (Full Lambek) hyperdoctrine is a contravariant functor

$$P:\mathbf{C}^\mathrm{op}\rightarrow \mathbf{FL}$$

such that the base category $\mathbf{C}$ of P is a category with finite products, and that the following conditions (to express quantifiers) are satisfied:

• For any projection $\pi :X\times Y\rightarrow Y$ in $\mathbf{C}$, $P(\pi ):P(Y)\rightarrow P(X\times Y)$ has a right adjoint, denoted $\forall _{\pi }:P(X\times Y)\rightarrow P(Y).$ And the corresponding Beck-Chevalley condition holds, i.e., the following diagram commutes for any arrow $f:Z\rightarrow Y$ in $\mathbf{C}$ ($\pi ':X\times Z\rightarrow Z$ below denotes a projection):

  

• For any projection $\pi :X\times Y\rightarrow Y$ in $\mathbf{C}$, $P(\pi ):P(Y)\rightarrow P(X\times Y)$ has a left adjoint, denoted $\exists _{\pi }:P(X\times Y)\rightarrow P(Y).$ The corresponding Beck-Chevalley condition holds:

  

  Furthermore, the Frobenius Reciprocity conditions hold: for any projection $\pi :X\times Y\rightarrow Y$ in $\mathbf{C}$, any $a\in P(Y)$, and any $b\in P(X\times Y)$,

  $$\begin{aligned} a\otimes (\exists _{\pi }b)= & {} \exists _{\pi }(P(\pi )(a)\otimes b) \\ (\exists _{\pi }b)\otimes a= & {} \exists _{\pi }(b\otimes P(\pi )(a)). \end{aligned}$$

The logical reading of the Beck-Chevalley conditions above is that substitution commutes with quantification.

Now, $\mathrm{FL}$ triposes are defined as $\mathrm{FL}$ hyperdoctrines with their base categories CCCs, and with truth-value objects $\varOmega$ (i.e., representability via $\varOmega \in \mathbf{C}$):

Definition 4

An $\mathrm{FL}$ (Full Lambek) tripos, or higher-order $\mathrm{FL}$ hyperdoctrine, is an $\mathrm{FL}$ hyperdoctrine $P:\mathbf{C}^\mathrm{op}\rightarrow \mathbf{FL}$ such that:

• The base category $\mathbf{C}$ is a CCC (Cartesian Closed Category);

• There is an object $\varOmega \in \mathbf{C}$ such that

  $$P\simeq \mathrm{Hom}_\mathbf{C}(\text {-},\varOmega ).$$

We then call $\varOmega$ the truth-value object of the $\mathrm{FL}$ tripos P. Given a set X of axioms, an $\mathrm{FL}_X$ tripos is defined by replacing $\mathbf{FL}$ above with $\mathbf{FL}_X$.

For an $\mathrm{FL}$ tripos P, each P(C) is called a fibre of the $\mathrm{FL}$ tripos P from a fibrational point of view; intuitively, P(C) may be seen as the algebra of propositions on a type or domain of discourse C. Note that it is also possible to define $\mathrm{FL}$ triposes in terms of fibrations, even though the present formulation in terms of indexed categories would be categorically less demanding.

$\mathrm{FL}$ tripos semantics for $\mathrm{HoFL}$ is defined as follows.

Definition 5

Let $P:\mathbf{C}^\mathrm{op}\rightarrow \mathbf{FL}$ be an $\mathrm{FL}$ tripos. An interpretation ${[\!\,\![}\text {-}{]\!\,\!]}$ of $\mathrm{HoFL}$ in the $\mathrm{FL}$ tripos P is defined as follows. Types and atomic symbols are interpreted in the following way:

• each basic type $\sigma$ is interpreted as an object ${[\!\,\![} \sigma {]\!\,\!]}$ in $\mathbf{C}$;

• product and function types, $\sigma \times \tau$ and $\sigma \rightarrow \tau$, are interpreted, as usual, by categorical product and exponentiation;

• each function symbol $f:\tau \ [\varGamma ]$ is interpreted as an arrow

  $${[\!\,\![} f:\tau \ [\varGamma ] {]\!\,\!]} : {[\!\,\![} \varGamma {]\!\,\!]} \rightarrow {[\!\,\![} \sigma {]\!\,\!]}$$

  in $\mathbf{C}$; if the context $\varGamma$ is $x_1:\sigma _1,...,x_n:\sigma _n$, then ${[\!\,\![} \varGamma {]\!\,\!]}$ denotes $[\!\,\![\sigma _1 ]\!\,\!]\times ... \times [\!\,\![\sigma _n ]\!\,\!]$;

• each relation symbol $R\ [\varGamma ]$ is interpreted as an element $[\!\,\![R\ [\varGamma ] ]\!\,\!]$ in the corresponding fibre $P([\!\,\![\varGamma ]\!\,\!])$ of the $\mathrm{FL}$ tripos P at $[\!\,\![\varGamma ]\!\,\!]$.

Terms and their equality are interpreted in the following, inductive manner:

• $[\!\,\![x:\sigma \ [\varGamma _1,x:\sigma ,\varGamma _2] ]\!\,\!]$ is defined as the following projection in $\mathbf{C}$:

  $$\pi :[\!\,\![\varGamma _1 ]\!\,\!]\times [\!\,\![\sigma ]\!\,\!]\times [\!\,\![\varGamma _2 ]\!\,\!]\rightarrow [\!\,\![\sigma ]\!\,\!].$$

• $[\!\,\![f(t_1,...,t_n):\tau \ [\varGamma ] ]\!\,\!]$ is defined as the following arrow in $\mathbf{C}$:

  $$[\!\,\![f ]\!\,\!]\circ \langle [\!\,\![t_1:\sigma _1 \ [\varGamma ] ]\!\,\!],...,[\!\,\![t_n:\sigma _n\ [\varGamma ] ]\!\,\!]\rangle $$

  where $f:\tau \ [x_1:\sigma _1,...,x_n:\sigma _n]$, and $t_1:\sigma _1 \ [\varGamma ],...,t_n:\sigma _n \ [\varGamma ]$ (note also that $\langle [\!\,\![t_1:\sigma _1 \ [\varGamma ] ]\!\,\!],...,[\!\,\![t_n:\sigma _n\ [\varGamma ] ]\!\,\!]\rangle$ denotes the product/pairing of arrows in $\mathbf{C}$).

• $\lambda$-abstraction, $\lambda$-application, projections, and pairing are interpreted, as usual, by categorical transpose, evaluation, projections, and pairing in the base CCC $\mathbf{C}$, respectively;

Formulae are interpreted in the following, inductive manner:

• $[\!\,\![R(t_1,...,t_n)\ [\varGamma ] ]\!\,\!]$ is defined as

  $$P(\langle [\!\,\![t_1:\sigma _1[\varGamma ] ]\!\,\!],..., [\!\,\![t_n:\sigma _n [\varGamma ] ]\!\,\!]\rangle )([\!\,\![R\ [x:\sigma _1,...,x_n:\sigma _n] ]\!\,\!])$$

  where R is a relation symbol in context $x_1:\sigma _1,...,x_n:\sigma _n$.

• $[\!\,\![\varphi \otimes \psi \ [\varGamma ] ]\!\,\!]$ is defined as $[\!\,\![\varphi \ [\varGamma ] ]\!\,\!]\otimes [\!\,\![\psi \ [\varGamma ] ]\!\,\!]$. The other binary connectives $\wedge ,\vee ,\backslash ,/$ are interpreted in a similar way. $[\!\,\![1 \ [\varGamma ] ]\!\,\!]$ is defined as the monoidal unit of $P([\!\,\![\varGamma ]\!\,\!])$. The other constants $0,\top ,\bot$ are interpreted in a similar way.

• $[\!\,\![\forall x \varphi \ [\varGamma ] ]\!\,\!]$ is defined as $\forall _{\pi }([\!\,\![\varphi \ [x:\sigma ,\varGamma ] ]\!\,\!])$ where $\pi :[\!\,\![\sigma ]\!\,\!]\times [\!\,\![\varGamma ]\!\,\!]\rightarrow [\!\,\![\varGamma ]\!\,\!]$ is a projection in $\mathbf{C}$, and $\varphi$ is a formula in context $[x:\sigma ,\varGamma ]$. Similarly, $[\!\,\![\exists x \varphi \ [\varGamma ] ]\!\,\!]$ is defined as $\exists _{\pi }([\!\,\![\varphi \ [x:\sigma ,\varGamma ] ]\!\,\!]).$

$\mathrm{Prop}$ and its terms are then interpreted as follows:

• $\mathrm{Prop}$ is interpreted as the truth-value object $\varOmega$ of the $\mathrm{FL}$ tripos P:

  $$[\!\,\![\mathrm{Prop} ]\!\,\!]= \varOmega ;$$

• each formula $\varphi : \mathrm{Prop} \ [\varGamma ]$, regarded as a term of type $\mathrm{Prop}$, is interpreted as the element of $\mathrm{Hom}_\mathbf{C}([\!\,\![\varGamma ]\!\,\!],\varOmega )$ which corresponds to $[\!\,\![\varphi \ [\varGamma ] ]\!\,\!]\in P([\!\,\![\varGamma ]\!\,\!])$ in the defining isomorphism $P\simeq \mathrm{Hom}_\mathbf{C}(\text {-},\varOmega )$ of the $\mathrm{FL}$ tripos P; in a nutshell, $[\!\,\![\varphi : \mathrm{Prop} \ [\varGamma ] ]\!\,\!]$’s and $[\!\,\![\varphi \ [\varGamma ] ]\!\,\!]$’s are linked via the isomorphism.

Finally, the validity of sequents in context is defined as follows:

• $\varphi _1,...,\varphi _n \vdash \psi \ [\varGamma ]$ is valid in an interpretation $[\!\,\![\text {-} ]\!\,\!]$ in an $\mathrm{FL}$ tripos P iff the following holds in $P([\!\,\![\varGamma ]\!\,\!])$:

  $$[\!\,\![\varphi _1\ [\varGamma ] ]\!\,\!]\otimes ... \otimes [\!\,\![\varphi _n \ [\varGamma ] ]\!\,\!]\le [\!\,\![\psi \ [\varGamma ] ]\!\,\!].$$

  In case the right-hand side of a sequent is empty, $\varphi _1,...,\varphi _n \vdash [\varGamma ]$ is valid in $[\!\,\![\text {-} ]\!\,\!]$ iff $[\!\,\![\varphi _1\ [\varGamma ] ]\!\,\!]\otimes ... \otimes [\!\,\![\varphi _n \ [\varGamma ] ]\!\,\!]\le 0$ in $P([\!\,\![\varGamma ]\!\,\!])$. In case the left-hand side of a sequent is empty, $\vdash \varphi \ [\varGamma ]$ is valid in $[\!\,\![\text {-} ]\!\,\!]$ iff $1\le [\!\,\![\varphi [\varGamma ] ]\!\,\!]$ in $P([\!\,\![\varGamma ]\!\,\!])$. When $\varPhi$ consists of $\varphi _1,...,\varphi _n$, let $[\!\,\![\varPhi \ [\varGamma ] ]\!\,\!]$ denote $[\!\,\![\varphi _1 \ [\varGamma ] ]\!\,\!]\otimes ... \otimes [\!\,\![\varphi _n \ [\varGamma ] ]\!\,\!]$.

An interpretation of $\mathrm{HoFL}_X$ in an $\mathrm{FL}_X$ tripos is defined by replacing $\mathbf{FL}$ and $\mathrm{HoFL}$ above with $\mathbf{FL}_X$ and $\mathrm{HoFL}_X$, respectively.

The categorical conception of interpretation encompasses set-theoretical interpretations and forcing-style model constructions. First of all, interpreting logic in the $\mathbf{2}$-valued tripos $\mathrm{Hom}_\mathbf{Set}(\text {-},\mathbf{2})$ (where $\mathbf{2}$ is the two-element Boolean algebra) is precisely equivalent to the standard Tarski semantics. Yet there is a vast generalisation of this: given a quantale $\varOmega$, the representable functor

$$\mathrm{Hom}_\mathbf{Set}(\text {-},\varOmega ): \mathbf{Set}^\mathrm{op}\rightarrow \mathbf{FL}$$

forms an $\mathrm{FL}$ tripos, which gives rise to a universe of quantale-valued sets via the generalised tripos-to-topos construction as in [21]; if $\varOmega$ is a locale in particular (i.e., complete Heyting algebra), it is known that $\mathrm{Hom}_\mathbf{Set}(\text {-},\varOmega )$ yields $\mathbf{Sh}(\varOmega )$ (i.e., the sheaf topos on $\varOmega$). This sort of $\mathrm{FL}$ tripos models of set theory could hopefully be applied to solve consistency problems for substructural set theories (especially, Cantor-Łukasiewicz set theory).

Note that the base category of an $\mathrm{FL}$ tripos is used to interpret the type theory of $\mathrm{HoFL}$, and the value category is used to interpret the logic part of $\mathrm{HoFL}$. In the following, we first prove soundness and then completeness.

Proposition 6

If $\varPhi \vdash \psi \ [\varGamma ]$ is provable in $\mathrm{HoFL}$ (resp. $\mathrm{HoFL}_X$), then it is valid in any interpretation in any $\mathrm{FL}$ (resp. $\mathrm{FL}_X$) tripos.

Proof

Let P be an $\mathrm{FL}$ or $\mathrm{FL}_X$ tripos, and $[\!\,\![\text {-} ]\!\,\!]$ an interpretation in P. Soundness for the first-order part can be proven in essentially the same way as in [21]; due to space limitations, we do not repeat it, and focus upon $\mathrm{Prop}$, which is the most distinctive part of higher-order logic. So let us prove that the rule for the $\mathrm{Prop}$ type preserves validity. Suppose that

$$[\!\,\![\varphi \ [\varGamma ] ]\!\,\!]\le [\!\,\![\psi \ [\varGamma ] ]\!\,\!]$$

and that

$$[\!\,\![\psi \ [\varGamma ] ]\!\,\!]\le [\!\,\![\varphi \ [\varGamma ] ]\!\,\!].$$

It then follows that

$$[\!\,\![\varphi \ [\varGamma ] ]\!\,\!]= [\!\,\![\psi \ [\varGamma ] ]\!\,\!].$$

Note that this is a “propositional” equality, i.e., an equality in the fibre $P([\!\,\![\varGamma ]\!\,\!])$ of propositions on $[\!\,\![\varGamma ]\!\,\!]$. Since we have the following isomorphism

$$P([\!\,\![\varGamma ]\!\,\!]) \simeq \mathrm{Hom}_\mathbf{C}([\!\,\![\varGamma ]\!\,\!],[\!\,\![\mathrm{Prop} ]\!\,\!])$$

the equality above, together with the definition of the interpretation of terms of type $\mathrm{Prop}$, tells us that

$$[\!\,\![\varphi : \mathrm{Prop} \ [\varGamma ] ]\!\,\!]= [\!\,\![\psi : \mathrm{Prop} \ [\varGamma ] ]\!\,\!].$$

Note that this is a “functional” equality, i.e., an equality in $\mathrm{Hom}_\mathbf{C}([\!\,\![\varGamma ]\!\,\!],[\!\,\![\mathrm{Prop} ]\!\,\!])$. Thus, the propositional equality implies the functional equality (via the isomorphism above), and this is exactly what it is for the $\mathrm{Prop}$ rule to preserve validity.   $\square$

For the sake of a completeness proof, let us introduce the syntactic tripos construction (for logic over type theory), which is the combination of the syntactic category construction (for type theory) and the Lindenbaum-Tarski algebra construction (for propositional logic):

Definition 7

The syntactic tripos of $\mathrm{HoFL}$ is defined as follows. Let us first define the syntactic base category $\mathbf{C}$: an object is a context $\varGamma$ (up to $\alpha$-equivalence); an arrow from $\varGamma$ to $\varGamma '$ is a list of terms (up to equality on terms)

$$[t_1,...,t_n]$$

where $t_1:\sigma _1\ [\varGamma ],...,t_n:\sigma _n\ [\varGamma ]$ and $\varGamma '$ is supposed to be $x_1:\sigma _1,...,x_n:\sigma _n$. Composition is defined via substitution. The syntactic tripos $P_\mathrm{HoFL}:\mathbf{C}^\mathrm{op}\rightarrow \mathbf{FL}$ is then defined as follows. Given an object $\varGamma$ in $\mathbf{C}$, let $\mathrm{Form}_{\varGamma }$ denote the set of formulas in context $\varGamma$, and then define

$$P_\mathrm{HoFL}(\varGamma )=\mathrm{Form}_{\varGamma }/\sim $$

where $\sim$ is an equivalence relation on $\mathrm{Form}_{\varGamma }$ defined as follows: for $\varphi ,\psi \in \mathrm{Form}_{\varGamma }$, $\varphi \sim \psi$ iff $\varphi \vdash \psi \ [\varGamma ]$ and $\psi \vdash \varphi \ [\varGamma ]$ are provable in $\mathrm{HoFL}$. The arrow part of $P_\mathrm{HoFL}$ is defined as follows. Let $[t_1,...,t_n]:\varGamma \rightarrow \varGamma '$ be an arrow in $\mathbf{C}$ where $\varGamma '$ is $x_1:\sigma _1,...,x_n:\sigma _n$. Then we define $P_\mathrm{HoFL}([t_1,...,t_n]):P_\mathrm{HoFL}(\varGamma ')\rightarrow P_\mathrm{HoFL}(\varGamma )$ by

$$P_\mathrm{HoFL}([t_1,...,t_n])(\varphi \ [\varGamma '])=\varphi [t_1/x_1,...,t_n/x_n] \ [\varGamma ]$$

where it is supposed that $t_1:\sigma _1 \ [\varGamma ],...,t_n:\sigma _n \ [\varGamma ]$, and that $\varphi$ is a formula in context $x_1:\sigma _1,...,x_n:\sigma _n$. The syntactic tripos $P_{\mathrm{HoFL}_X}$ of $\mathrm{HoFL}_X$ is defined just by replacing $\mathbf{FL}$ and $\mathrm{HoFL}$ above with $\mathbf{FL}_X$ and $\mathrm{HoFL}_X$, respectively.

The syntactic tripos of higher-order logic is the fibrational analogue of the Lindenbaum-Tarski algebra of propositional logic; each fibre $P_\mathrm{HoFL}(\varGamma )$ of the syntactic tripos $P_\mathrm{HoFL}$ is the Lindenbaum-Tarski algebra of formulae in context $\varGamma$. The syntactic tripos of $\mathrm{HoFL}$ has the universal mapping property that inherits from the syntactic base category of the underlying type theory of $\mathrm{HoFL}$, and also from the fibre-wise Lindenbaum-Tarski algebras of the logic part of $\mathrm{HoFL}$. We of course have to verify that the syntactic tripos $P_\mathrm{HoFL}$ indeed carries an $\mathrm{FL}$ tripos structure; this is the crucial part of the completeness proof.

Lemma 8

The syntactic tripos $P_\mathrm{HoFL}:\mathbf{C}^\mathrm{op}\rightarrow \mathbf{FL}$ (resp. $\mathbf{FL}_X$) defined above is an $\mathrm{FL}$ (resp. $\mathrm{FL}_X$) tripos. In particular, the base category is a CCC, and there is a truth-value object $\varOmega \in \mathbf{C}$ such that

$$P_\mathrm{HoFL}\simeq \mathrm{Hom}_\mathbf{C}(\text {-},\varOmega ).$$

Proof

The existence of products and exponentials in $\mathbf{C}$ is guaranteed by the existence of product types and function space types in the type theory of $\mathrm{HoFL}$. Substitution commutes with all the logical connectives. This means that $P([t_1,...,t_n])$ defined above is a homomorphism; so P is a contravariant functor.

P has quantifier structures as follows. Let $\pi :\varGamma \times \varGamma ' \rightarrow \varGamma '$ denote the projection in $\mathbf{C}$ defined above, and consider $P(\pi )$, which has right and left adjoints in the following way. Recall $\varGamma$ is $x:\sigma _1,...,x_n:\sigma _n$. Let $\varphi \in P(\varGamma \times \varGamma ' )$; we identify $\varphi$ with the equivalence class to which $\varphi$ belongs. Define $\forall _{\pi }:P(\varGamma \times \varGamma ' )\rightarrow P(\varGamma ' )$ by

$$\forall _{\pi }(\varphi )=\forall x_1 ... \forall x_n \varphi .$$

We also define $\exists _{\pi }:P(\varGamma \times \varGamma ' )\rightarrow P(\varGamma ' )$ by $\exists _{\pi }(\varphi )=\exists x_1 ... \exists x_n \varphi .$ Then, $\forall _{\pi }$ and $\exists _{\pi }$ give the right and left adjoints of $P(\pi )$, respectively.

We can verify the Beck-Chevalley condition for $\forall$ as follows. Let $\varphi \in P(\varGamma \times \varGamma ')$, $\pi :\varGamma \times \varGamma '\rightarrow \varGamma '$ a projection in $\mathbf{C}$, and $\pi ':\varGamma \times \varGamma ''\rightarrow \varGamma ''$ another projection in $\mathbf{C}$ for objects $\varGamma ,\varGamma ',\varGamma ''$ in $\mathbf{C}$. Then,

$$P([t_1,...,t_n])\circ \forall _{\pi }(\varphi )=(\forall x_1...\forall x_n \varphi ) [t_1/y_1,...,t_n/y_m]$$

where $\varGamma$ is supposed to be $x_1:\sigma _1,...,x_n:\sigma _n$, $\varGamma '$ is $y_1:\tau _1,...,y_m:\tau _m$, and $t_1:\tau _1\ [\varGamma ''], ..., t_m:\tau _m \ [\varGamma '']$. Likewise we have $\forall _{\pi '}\circ P( [t_1,...,t_n])(\varphi )= \forall x_1...\forall x_n (\varphi [t_1/y_1,...,t_n/y_m]).$ The Beck-Chevalley condition for $\forall$ thus follows. The Beck-Chevalley condition for $\exists$ can be verified in a similar way. The two Frobenius Reciprocity conditions for $\exists$ follow immediately from Lemma 1.

In the following we prove the existence of a truth-value object $\varOmega$. Let

$$\varOmega = x:\mathrm{Prop}.$$

Note that, since the objects of the base category are contexts rather than types, we cannot take $\varOmega$ to be $\mathrm{Prop}$ per se; yet $x:\mathrm{Prop}$ practically means the same thing as $\mathrm{Prop}$, thanks to $\alpha$-equivalence required. We now have to show that for each context $\varGamma$,

$$P(\varGamma )\simeq \mathrm{Hom}_\mathbf{C}(\varGamma ,x:\mathrm{Prop})$$

and this correspondence yields a natural transformation. The required isomorphism is given by mapping

$$\varphi \ [\varGamma ]\in P(\varGamma )$$

to

$$\varphi : \mathrm{Prop} \ [\varGamma ]\in \mathrm{Hom}_\mathbf{C}(\varGamma ,x:\mathrm{Prop}).$$

Note that $\varphi$ above is actually an equivalence class, and yet the above mapping is well defined, and also that $\varphi : \mathrm{Prop} \ [\varGamma ]$ is actually a list consisting of a single term $\varphi : \mathrm{Prop} \ [\varGamma ]$. This mapping is an isomorphism by the definition of terms of type $\mathrm{Prop}$. Let us denote the above mapping by

$$\mathrm{PaF}_{\varGamma }:P(\varGamma )\rightarrow \mathrm{Hom}_\mathbf{C}(\varGamma ,x:\mathrm{Prop})$$

with the idea of “Propositions-as-Functions” in mind. The naturality of this correspondence then means that the following diagram commutes for any arrow $[t_1,...,t_n]: \varGamma ' \rightarrow \varGamma$ in $\mathbf{C}$:

By the following calculation:

$$\begin{aligned} \mathrm{Hom}_\mathbf{C}([t_1,...,t_n],\mathrm{Prop})\circ \mathrm{PaF}_{\varGamma }(\varphi \ [\varGamma ])= & {} \mathrm{Hom}_\mathbf{C}([t_1,...,t_n],\mathrm{Prop})(\varphi : \mathrm{Prop} \ [\varGamma ]) \\= & {} \varphi [t_1/x_1,...,t_n/x_n] : \mathrm{Prop} \ [\varGamma '] \\= & {} \mathrm{PaF}_{\varGamma '}(\varphi [t_1/x_1,...,t_n/x_n] \ [\varGamma ']) \\= & {} \mathrm{PaF}_{\varGamma '}\circ P([t_1,...,t_n])(\varphi \ [\varGamma ]) \end{aligned}$$

we obtain the commutativity of the diagram and hence the naturality of the “propositions-as-functions” correspondence.   $\square$

It is straightforward to see that if $\varPhi \vdash \psi \ [\varGamma ]$ is valid in the canonical interpretation in the syntactic tripos $P_\mathrm{HoFL}$ (resp. $P_{\mathrm{HoFL}_X}$), then it is provable in $\mathrm{HoFL}$ (resp. $\mathrm{HoFL}_X$). And this immediately gives us completeness via the standard counter-model argument. Hence the higher-order completeness theorem:

Theorem 9

$\varPhi \vdash \psi \ [\varGamma ]$ is provable in $\mathrm{HoFL}$ (resp. $\mathrm{HoFL}_X$) iff it is valid in any interpretation in any $\mathrm{FL}$ (resp. $\mathrm{FL}_X$) tripos.

This higher-order completeness theorem can be applied, with a suitable choice of axioms X, for any of classical, intuitionistic, fuzzy, relevant, paraconsistent, and (both commutative and non-commutative) linear logics; higher-order completeness has not been known for these logics except the first two. The concept of (generalised) tripos, therefore, is so broadly applicable as to encompass most logical systems. Modal logics also can readily be incorporated into this framework by working with modal $\mathrm{FL}$ rather than plain $\mathrm{FL}$. Coalgebraic dualities for modal logics (see, e.g., [14, 16, 20, 22]) then yield models of modal triposes for them; these modal issues are to be addressed in subsequent papers.

4 Girard and Kolmogorov Translation for Triposes

We finally analyse Kolmogorov’s double negation $\lnot \lnot$ translation (Kolmogorov found it earlier than Gödel-Gentzen; see Ferreira and Oliva [7]) and Girard’s exponential ! translation from a tripos-theoretical point of view.

Propositional Kolmogorov translation algebraically means that, for any Heyting algebra A, the doubly negated algebra $\lnot \lnot A$, defined as $\{ a\in A \ | \ \lnot \lnot a=a \},$ always forms a Boolean algebra. This $\lnot \lnot$ construction extends to a functor from the category $\mathbf{HA}$ of Heyting algebras to the category $\mathbf{BA}$ of Boolean algebras. And then the categorical meaning of first-order Kolmogorov translation is that, for any first-order $\mathrm{IL}$ hyperdoctrine $P: \mathbf{C}^\mathrm{op}\rightarrow \mathbf{HA}$ (where $\mathrm{IL}$ denotes intuitionistic logic), the following composed functor

$$\lnot \lnot \circ P: \mathbf{C}^\mathrm{op}\rightarrow \mathbf{BA}$$

forms a first-order $\mathrm{CL}$ hyperdoctrine (where $\mathrm{CL}$ denotes classical logic) as in [21]. Yet this strategy does not extend to the higher-order case: in particular, although the base category does not change in the first-order case, in which types and propositions are separated, it must nevertheless be modified in the higher-order case, in which types and propositions interact via $\mathrm{Prop}$ or $\varOmega$. Technicalities involved get essentially more complicated in the higher-order case. Still, we can construct from a given $\mathrm{IL}$ tripos $P:\mathbf{C}^\mathrm{op}\rightarrow \mathbf{HA}$ a $\mathrm{CL}$ tripos

$$P_{\lnot \lnot }: \mathbf{C}_{\lnot \lnot }^\mathrm{op}\rightarrow \mathbf{BA}.$$

For the sake of the description of $\mathbf{C_{\lnot \lnot }}$ (and $P_{\lnot \lnot }$), however, we work within the internal language $\mathrm{HoFL}_P$ of the tripos $P:\mathbf{C}^\mathrm{op}\rightarrow \mathbf{FL}$: in $\mathrm{HoFL}_P$, we have types C and terms f corresponding to objects C and arrows f in $\mathbf{C}$, respectively, and also formulae R on a type $C \in \mathbf{C}$ corresponding to elements $R\in P(C)$.

Now we define the translation on the internal language $\mathrm{HoFL}_P$ of the tripos P which allows us to describe the double negation category $\mathbf{C}_{\lnot \lnot }$ mentioned above. The basic strategy of translation is this: we leave everything in $\mathrm{HoFL}_P$ as it is, unless it involves the proposition type $\varOmega$ of $\mathrm{HoFL}_P$; and if something involves $\varOmega$, we always put double negation on it. Formally it goes as follows:

Definition 10

We recursively define the translation on $\mathrm{HoFL}_P$ as follows.

• If $\varphi :\varOmega \ [\varGamma ]$ then we put $\lnot \lnot$ on every sub-formula of $\varphi$ (do the same for $\varphi$ seen as formulae).

• If $t :\sigma \ [\varGamma ,x:\varOmega ,\varGamma ']$ then we replace every occurrence of x in t by $\lnot \lnot x$.

• If $t:\varOmega \times \sigma \ [\varGamma ]$ then t translates into $\langle \lnot \lnot \pi _1t,\pi _2t\rangle$; if $t:\sigma \times \varOmega \ [\varGamma ]$ then t translates into $\langle \pi _1t,\lnot \lnot \pi _2t\rangle$.

• If $t:\sigma \ [\varGamma ,x:\varOmega \times \sigma ,\varGamma ']$ then we replace every occurrence of x in t by $\langle \lnot \lnot \pi _1x,\pi _2x\rangle$; if $t:\sigma \ [\varGamma ,x:\sigma \times \varOmega ,\varGamma ']$ then we replace every occurrence of x in t by $\langle \pi _1x,\lnot \lnot \pi _2x\rangle$.

• If $t:\sigma \rightarrow \varOmega \ [\varGamma ]$ then t translates into $\lambda x:\sigma . \lnot \lnot tx$; if $t:\varOmega \rightarrow \sigma \ [\varGamma ]$ then t translates into $\lambda x:\varOmega . t\lnot \lnot x$.

• If $t:\sigma \ [\varGamma ,x:\sigma \rightarrow \varOmega ,\varGamma ']$ then we replace every occurrence of x in t by $\lambda y:\sigma .(\lnot \lnot x)y$; if $t:\sigma \ [\varGamma ,x:\varOmega \rightarrow \sigma ,\varGamma ']$ then we replace every occurrence of x in t by $\lambda y:\varOmega . x\lnot \lnot y$.

• Finally, if $t :\sigma \ [\varGamma ]$ and no $\varOmega$ appears in it, then t translates into itself.

The double negation category $\mathbf{C}_{\lnot \lnot }$ is then defined as follows: the objects of $\mathbf{C}_{\lnot \lnot }$ are contexts in $\mathrm{HoFL}_P$ up to $\alpha$-equivalence (which are essentially the same as objects in $\mathbf{C}$), and the arrows of $\mathbf{C}_{\lnot \lnot }$ are the translations of lists of terms in $\mathrm{HoFL}_P$ up to equality on terms, with their composition defined via substitution as usual. This intuitively means that those arrows in $\mathbf{C}$ that involve $\varOmega$ are double negated in $\mathbf{C}_{\lnot \lnot }$ whilst the other part of $\mathbf{C}_{\lnot \lnot }$ remains the same as that of $\mathbf{C}$ (to give the rigorous definition of this, we work within the internal language). Then it is not obvious that $\mathbf{C}_{\lnot \lnot }$ forms a category again, let alone a CCC. Thus:

Lemma 11

$\mathbf{C}_{\lnot \lnot }$ defined above forms a category, in particular a CCC.

Proof

Since everything involving $\varOmega$ is doubly negated, we have to verify that all of the relevant categorical structures, that is, composition, identity, projection, paring, evaluation, and transpose, preserve or respect double negation. Here we just give several sample proofs to show essential ideas.

Consider the case of composition. We think of single terms for simplicity. The composition of arrows $t:\sigma \ [x:\varOmega ]$ and $s:\sigma ' \ [y:\sigma ]$ in $\mathbf{C}_{\lnot \lnot }$ (which may be seen as $t:\varOmega \rightarrow \sigma$ and $s:\sigma \rightarrow \sigma '$ in terms of the original category $\mathbf{C}$) is defined as $s[t/y]:\sigma ' \ [x:\varOmega ]$, where every occurrence of x in s[t/y] must have been replaced by $\lnot \lnot x$ (for s[t/y] to be in $\mathbf{C}_{\lnot \lnot }$); this is true because every occurrence of x in t is replaced by $\lnot \lnot x$ by the definition of arrows in $\mathbf{C}_{\lnot \lnot }$. Likewise, the composition of arrows $t:\sigma ' \ [x:\sigma ]$ and $s:\varOmega \ [y:\sigma ']$ in $\mathbf{C}_{\lnot \lnot }$ is defined as $s[t/y]: \varOmega \ [x:\sigma ]$, where every sub-formula of s[t/y] is doubly negated by the assumption of $s,t\in \mathbf{C}$; and hence $s[t/y]\in \mathbf{C}$. More complex cases can be proven in a similar way.

Consider the case of identity. Think of an identity on $\varOmega$, which is given by $\lnot \lnot x : \varOmega \ [x:\varOmega ]$. Given $t:\varOmega \ [y:\sigma ']$ in $\mathbf{C}_{\lnot \lnot }$, $(\lnot \lnot x) \circ t$ is defined as $(\lnot \lnot x) [t/x]: \varOmega \ [y:\sigma ']$, which equals $\lnot \lnot t: \varOmega \ [y:\sigma ']$. By $t\in \mathbf{C}_{\lnot \lnot }$, t can be written as $\lnot \lnot t'$, and so $\lnot \lnot t = \lnot \lnot \lnot \lnot t' = \lnot \lnot t' = t$. Hence $(\lnot \lnot x) \circ t = t$. Likewise, given $t:\sigma ' \ [y:\varOmega ]$ in $\mathbf{C}_{\lnot \lnot }$, $t\circ \lnot \lnot x$ is defined as $t[\lnot \lnot x/y]:\sigma ' \ [x:\varOmega ]$; since every occurrence of y in t is replaced by $\lnot \lnot y$ because $t\in \mathbf{C}_{\lnot \lnot }$ and since $\lnot \lnot \lnot \lnot$ is equivalent to $\lnot \lnot$, we have $t[\lnot \lnot x/y]=t$, whence $t\circ \lnot \lnot x=t$. More complex cases can be shown in a similar manner.

To show the existence of finite products and exponentials involving $\varOmega$ (otherwise it is trivial), it is crucial to check that doubly negated projection, pairing, evaluation, and transpose still play their own rôles, just as doubly negated identity still plays the rôle of identity as we have shown above.    $\square$

Finally we obtain the following, tripos-theoretical Kolmogorov translation theorem for higher-order logic, which may also be seen as a translation from classical set theory to intuitionistic set theory (since higher-order logic is basically set theory in logical form).

Theorem 12

Let $P:\mathbf{C}^\mathrm{op}\rightarrow \mathbf{HA}$ be an $\mathrm{IL}$ tripos, and $\mathbf{C}_{\lnot \lnot }$ the double negation category as defined above. Then, $P_{\lnot \lnot }$ defined as

$$\mathrm{Hom}_{\mathbf{C}_{\lnot \lnot }}(\text {-},\varOmega ):\mathbf{C}_{\lnot \lnot }\rightarrow \mathbf{BA}$$

forms a $\mathrm{CL}$ tripos, called the double negation tripos of P.

Proof

$\mathbf{C}_{\lnot \lnot }$ is a CCC by the lemma, and $P_{\lnot \lnot }$ is represented by $\varOmega$. This completes the higher-order part of the proof. Concerning the first-order part, the existence of quantifiers follows from this fact: if $\varphi$ admits the double negation elimination, then $\lnot \lnot \forall x \varphi$ and $\lnot \lnot \exists x \varphi$ are equivalent to $\forall x \lnot \lnot \varphi$ and $\exists x \lnot \lnot \varphi$, respectively.   $\square$

Note that the hyperdoctrinal Kolmogorov translation does not reduce to the construction of toposes via double negation topology because there are more triposes than toposes in the adjunction between them (all toposes come from triposes, but not vice versa). Moreover, our hyperdoctrinal method is designed modularly enough to be applicable to Girard’s translation as well as Kolmogorov’s. Although Glivenko-type theorems have been shown for substructural propositional and first-order logics (see Ferreira-Ono [6] and Galatos-Ono [9]), no such result is known for higher-order logic (as to the first-order case, [21] is typed and categorical while [6] is single-sorted and proof-theoretical).

An exponential ! on an $\mathrm{FL}$ algebra A is defined as a unary operation satisfying: (i) $a\le b$ implies $!a\le !b$; (ii) $!!a=!a\le a$; (iii) $!\top =1$; (iv) $!a \otimes !b = !(a\wedge b)$ (Coumans, Gehrke, and van Rooijen [5]). We denote by $\mathbf{FL}^!_c$ the category of commutative $\mathrm{FL}$ algebras with !, which are algebras for intuitionistic linear logic. $\mathrm{FL}^!_c$ triposes give sound and complete semantics for higher-order intuitionistic linear logic. The Girard category $\mathbf{C}_!$ of an $\mathrm{FL}^!_c$ tripos $P:\mathbf{C}^\mathrm{op}\rightarrow \mathbf{FL}^!_c$ is defined by replacing double negation in the above definition of $\mathbf{C}_{\lnot \lnot }$ with Girard’s exponential !. The following is the hyperdoctrinal Girard translation theorem for higher-order logic, which can be shown in basically the same way as above; no such higher-order translation has been known so far.

Theorem 13

Let $P:\mathbf{C}^\mathrm{op}\rightarrow \mathbf{FL}^!_c$ be an $\mathrm{FL}^!_c$ tripos (for intuitionistic linear logic), and $\mathbf{C}_!$ the Girard category of P. Define

$$P_{!}=\mathrm{Hom}_{\mathbf{C}_!}(\text {-},\varOmega ):\mathbf{C}_!\rightarrow \mathbf{HA}.$$

Then, $P_{!}$ forms an $\mathrm{IL}$ tripos (i.e., $\mathrm{FL}_{ecw}^!$ tripos), called the Girard tripos of P.