Dynamical Rheological Properties of In-Silico Epithelial Tissue by Vertex Models

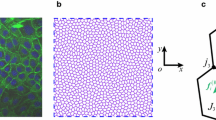
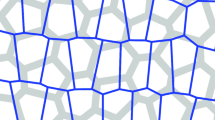
Abstract

Many biological systems including humans are made up of various cells. In addition, cells of a specific type gather together to form tissues, and organs are organized as an aggregate of multiple tissues. One of the tissues constituting organs is epithelial tissue. Epithelial tissue is composed of epithelial cells, and almost all the surfaces inside and outside the body is covered with epithelial tissue, many of which are monolayered. Mathematical models expressing morphogenesis of epithelial tissue have been developed by many researchers. One of the models, the cell vertex model [1] discusses tissue growth through polygonal approximation of cells, but it does not take into account the curvature of cell boundaries. Ishimoto et al., developed the bubbly vertex model [2] introducing the curvature into the model and studied the morphology of the epithelial tissue.

In this study, we focus on two mathematical models of epithelial tissue: the cell vertex model and the bubbly vertex model. We analyze the rheological properties of the models by simulation and aim at finding a correspondence with actual viscoelastic epithelial tissues.

1 Introduction

A number of researchers have developed mathematical models that express the morphology of epithelial tissue, which we focuses on in this research: the cell vertex model (VM) [1, 3, 4], the cell-centered model [5], the cellular Potts model [6, 7] and so on. Among them, vertex model discussed tissue growth by polygonal approximation of cells, but it does not take into account the curvature of cell boundaries. In 2014, Ishimoto et al. developed the bubbly vertex model (BVM) [2] introducing the curvature into this model and studied the morphology of the epithelial tissue.

Morphogenesis of epithelial tissues is nothing but the formation of multicellular mechanical structures by intercellular communication and intracellular activities. Computer-aided elucidation of such formation mechanisms has been awaited for further applications. However, correspondence between existing simulation models and epithelial tissues has not been established due to the complexity of even the basic physical properties of the tissues [8]. In addition, the properties may vary depending on morphogenetic stages and the affiliated organs.

In this study, we will quantify the rheological properties of the two models (VM and BVM) by simulation, aiming at establishing a correspondence with various epithelial tissues with viscoelasticity.

2 Rheology and Complex Modulus

In this study, we use some concepts of rheology to analyze the viscoelastic properties of epithelial tissue. Since epithelial tissue is a collection of epithelial cells, and the cells are composed of many proteins, epithelial tissue can be considered as a highly self-assembled macromolecular substance. Polymeric substances are said to be typical viscoelastic bodies. Since a viscoelastic body is a substance having both viscosity and elasticity, in the mechanical behavior of the tissue viscous fluid and ideal elastic responses would be combined in a complex manner.

One of the simplest viscoelastic models is the Maxwell model. The system can be represented by a dashpot and a spring arranged in series (Fig. 1).

Fig. 1.

Simple Maxwell model.

To quantify the mechanical properties of this linear viscoelastic model, the relationship between stress and strain is used when strain $\epsilon \left( t \right)$ changes periodically as in Eq. (1).

$$ \epsilon \left( t \right) = \epsilon_{0} \cdot e^{i\omega t} , $$

(1)

where $\epsilon_{0}$ is the strain amplitude and $\omega$ is the angular velocity. Since, in general, there is found a phase lag between the strain $\epsilon \left( t \right)$ and the acting stress $\tau \left( t \right)$, the stress $\tau \left( t \right)$ is represented with the phase difference $\delta$ by

$$ \tau \left( t \right) = \tau_{0} \cdot e^{{i\left( {\omega t + \delta } \right)}} , $$

(2)

where $\tau_{0}$ is the stress amplitude. Setting $\left| G \right| = \tau_{0} / \epsilon_{0}$, $G^{\prime} = \left| G \right|\cos \delta$ and $G^{\prime\prime} = \left| G \right|\sin \delta$ for simplicity, Eq. (2) becomes

$$ \tau \left( t \right) = \left| G \right| \cdot \epsilon_{0} \cdot e^{i\omega t} \cdot e^{i\delta } = \left| G \right| \cdot e^{i\delta } \cdot \epsilon . $$

(3)

Here, $\left| G \right|$ is called the absolute dynamic elastic modulus, $\left| {G^{\prime}} \right|$ is the storage modulus, $\left| {G^{\prime\prime}} \right|$ is the loss modulus, and $G^{ *}$ is expressed by the sum of $G^{\prime}$ and $G^{\prime\prime}$ as

$$ G^{ *} = G^{\prime} + iG^{\prime\prime}, $$

(4)

where $G^{ *}$ is the complex modulus. In what follows, we will quantify the complex modulus of the two models. Note that we usually do not intend to do shear test of the tissues in the lateral direction. So, we do not consider the shear modulus but the definitions of the moduli given above in what follows.

3 Numerical Analysis of In-Silico Epithelial Tissues by Mathematical Models

3.1 Vertex Model

In the VM, cells in tissue are approximated by polygons, and these polygons are expressed by vertices, and edges connecting them. Here, the vertices represent multicellular connections and the edges represent cell boundaries. In this model, the edges are defined by straight lines, and in most cases, it is assumed that each vertex is connected to only three edges. Also, the energy in the network is described as

$$ E\left( {\left\{ {\varvec{x}_{i} } \right\}} \right) = \mathop \sum \nolimits_{{\left\langle {i,j} \right\rangle }} \varLambda_{ij} l_{ij} + \mathop \sum \nolimits_{\alpha } \frac{{\varGamma_{\alpha } }}{2}L_{\alpha }^{2} + \mathop \sum \nolimits_{\alpha } \frac{{\kappa_{\alpha } }}{2}\left( {A_{\alpha } - A_{\alpha }^{0} } \right)^{2} $$

(5)

using the potential function [3], where i and j are adjacent vertices, and $\alpha$ labels a cell. $\varvec{x}_{i}$ is the 2D position of the i^th vertex, i.e., the junction of the cell boundaries. $\varLambda_{ij}$ is a constant, $\varGamma_{\alpha }$ and $\kappa_{\alpha }$ are nonnegative constants, $l_{ij}$ is the cell edge length, and $L_{\alpha }$ is the cell perimeter. $A_{\alpha }$ is the area of cell $\alpha$ and $A_{\alpha }^{0}$ is its preferred area. The area “constraint” of the third term is introduced as a “mechanism to make the cell size uniform” in [4].

The equation of motion at the vertex position is given by

$$ \eta_{i} \frac{{d\varvec{x}_{i} }}{dt} = - \frac{{\partial E\left( {\left\{ {\varvec{x}_{i} } \right\}} \right)}}{{\partial \varvec{x}_{i} }}. $$

(6)

The left hand side of Eq. (6) is the friction force, and $\eta_{i}$ represent the friction coefficient. The right hand side is the potential force, and the inertia term is ignored in this equation.

3.2 Bubbly Vertex Model

In the VM, the cell boundary is expressed by linear approximation, but one can introduce curvature to it as in the BVM [2]. In the BVM, each cell has a unique hydrostatic pressure, and each cell boundary has a unique curvature resulting from the mechanical properties of the boundary and the surrounding pressure. The general form of the potential energy function of this model is defined in [2] as

$$ \begin{aligned} & E\left( {\left\{ {\varvec{x}_{i} } \right\},\left\{ {R_{ij} } \right\}} \right) = \mathop \sum \nolimits_{{\left\langle {i,j} \right\rangle }} \varLambda_{\alpha \beta } l_{ij} + \mathop \sum \nolimits_{i,j} \frac{{\varGamma_{\alpha \beta }^{\left( l \right)} }}{2}\left( {l_{ij} } \right)^{2} + \mathop \sum \nolimits_{\alpha } \frac{{\varGamma_{\alpha }^{\left( L \right)} }}{2}L_{\alpha }^{2} + \mathop \sum \nolimits_{\alpha } \left\{ {\kappa_{\alpha }^{\left( 1 \right)} A_{\alpha } + } \right. \\ & \left. {\frac{{\kappa_{\alpha }^{\left( 2 \right)} }}{2}\left( {A_{\alpha } - A_{\alpha }^{\left( 0 \right)} } \right)^{2} } \right\} - \mathop \sum \nolimits_{\alpha } \mathop \smallint \nolimits_{{A_{\alpha }^{\left( 0 \right)} }}^{{A_{\alpha } }} dS_{\alpha }\Pi _{\alpha } \left( {S_{\alpha } } \right) - P_{outer} \left( {\mathop \sum \nolimits_{\alpha } A_{\alpha } } \right), \\ \end{aligned} $$

(7)

where $\left\{ {R_{ij} } \right\}$ is the curvature radius of the cell boundaries, $\alpha$ and $\beta$ are the cell number. The pair $\left\langle {i,j} \right\rangle$ represents the cell boundary connecting vertices i and j. $\varLambda_{\alpha \beta }$ and $\varGamma_{\alpha \beta }^{\left( l \right)}$ are constants dependent on the cells $\alpha$ and $\beta$ on both sides of the cell boundary, and $\varGamma_{\alpha }^{\left( L \right)}$ is a nonnegative constant for cell $\alpha$. $l_{ij}$ is the cell boundary length. $\kappa_{\alpha }^{{\left( {1,2} \right)}}$ is a nonnegative number depending on the cell height of epithelial tissue [4]. $dS_{\alpha }$ is the surface element of the cell $\alpha$ for the integration of the osmotic pressure $\Pi _{\alpha }$, and $P_{outer}$ is the pressure in the outer region of the tissue when the tissue boundary exists.

The equation of motion of the BVM is given by

$$ \eta_{i} \frac{{d\left( {\varvec{x}_{i} - \varvec{X}_{i} } \right)}}{dt} = - \frac{{\partial E\left( {\left\{ {\varvec{x}_{i} } \right\}} \right)}}{{\partial \varvec{x}_{i} }}. $$

(8)

The left hand side of Eq. (8) is the friction, and the right hand side is the potential force. The variable $\varvec{X}_{i}$ is introduced as a referential position to the vertex i. The noise term is suppressed for convenience, and the inertia term is neglected as in the VM.

3.3 Analysis Method and Initial Conditions

Most cell shapes in epithelial tissue show hexagonal shapes in a mechanically stable state, as Staple et al. analyzed the behavior of cell shapes in tissue based on the relationship between $\varLambda$ and $\varGamma$ in Eq. (6) [3]. In our study, in order to analyze the rheological properties of the tissue in which the hexagon seems to be in the mechanical stable state, analysis is performed by changing parameters $\varLambda_{\alpha \beta }$, $\varGamma_{\alpha \beta }^{\left( l \right)}$ and $\varGamma_{\alpha }^{\left( L \right)}$ within the parameter range for the stable hexagonal lattice in [3].

As a method of evaluating the simulation, complex modulus is used to quantify the rheological properties of the epithelial tissue, and its mechanical indications is to be analyzed (Fig. 2).

Fig. 2.

Polygon shape (left) and square shape (right) initial configurations.

We use two types initial configurations for a tissue shape (polygon and square) for different in-silico experiments, and the polygonally shaped tissue is composed of 217cells, and the square-shaped tissue is composed of 250 cells. Here, each cell is randomly arranged first by Voronoi division, and the tissue is relaxed mechanically enough to be the equilibrated initial configuration.

4 Results and Discussion

In this section, we present our simulation results of viscoelastic measurement of the polygonal stress test in the VM and BVM, and the results of the square stretch test in the VM. In these simulations, the polygonal tissue is isotopically stressed from the outside of the tissue, and in the square tissue, the left side of the tissue is fixed and the stress is applied to the right side so that a prescribed strain is achieved.

Figure 3 shows the storage and loss moduli of the polygonal stress test in the VM and BVM cases. Here, there are 5 data points, and a spline curve interpolation is applied. The complex moduli are converted from the complex compliances.

Fig. 3.

Viscoelastic properties of the VM (top) and the BVM (bottom) in the polygonal tissue.

In Fig. 3, the tissue behaves in a solid-like behavior in the range where $G^{\prime}$ is larger than $G^{\prime\prime}$, and the liquid-like behavior in the range where $G^{\prime\prime}$ is larger than $G^{\prime}$. In the VM, $G^{\prime}$ and $G^{\prime\prime}$ intersect in the vicinity of $\log_{10} \omega = - 0.5$ in each parameter, but in the BVM, it can be seen that both moduli do not intersect in the frequency range for this simulation. From this result, the BVM is considered to exhibit complex viscoelasticity in a wider area compared to the VM.

Figure 4 shows the simulation results of the VM in a square tissue. Here, there are 5 data points, and the same curve interpolation is applied. The viscoelastic properties of the square tissue by the stretch test are largely different from the properties plotted in Fig. 3. A reason why they are largely different is because, in the latter test, a tissue is adhered to a substrate such as PDMS and vibrated together. The different friction works between the substrate and the tissue.

Fig. 4.

Viscoelastic properties of the VM in the square tissue.

Among the tested parameter values in the stretch test, at $\varLambda = 0.12$ and $\varGamma = 0.03$, the loss modulus has a different response from the others. With regard to storage modulus, there is no significant change, so the test might investigate only the viscosity component of the tissue. To deepen the discussion, it would be interesting to see whether this phenomenon is unique to this set of values and, if so, the set characterizes the tissue.

5 Conclusion

We analyzed the viscoelastic properties of polygonal and square epithelial tissues using the cell vertex model and the bubbly vertex model. In this study, simulation parameters were set for the tissue to be hexagonally stable state, and the viscoelasticity of the epithelial tissue was confirmed from the rheological analysis by in-silico experiments. It would be better to continue to analyze the viscoelastic properties with more parameter values in the future.

Although the initial configurations used in these simulations are constructed from random Voronoi division, it would be more implicative to use initial configurations constructed from experimental images.