1 Introduction

Bayesian spatial modelling continues to increase in popularity, offering a suite of models with a range of strengths in various contexts. Modelling spatial effects through a Bayesian hierarchical model has many advantages, such as being able to include a range of functions to represent outcomes over space and time, as well as the capacity to incorporate data characteristics such as rare outcomes, missing information, misclassifications, measurement error and known biases [9, 47]. Moreover, direct probabilistic statements can be made, such as the probability that an area has a higher disease risk than a comparison area [20].

A popular form for a Bayesian spatial model for disease mapping uses data aggregated by area and specifies the likelihood as:

$$\displaystyle \begin{aligned} Y_i \sim \text{Poisson}\left(E_i e^{\mu_i}\right) \hspace{1.5em} \text{for }\ i = 1, \ldots, N\ \text{ areas} \end{aligned}$$

where \(\left \{Y_1, \dots ,Y_N\right \}\) are count data for a relatively uncommon disease, making a Poisson distribution appropriate. Other distributions are possible, including variants of Poisson such as negative binomial. The expected counts (E i) are commonly defined using indirect standardisation to account for population size and age structure. The modelled log standardised incidence ratio (SIR) μ i, also called log-relative risk, is often expressed as a regression equation and typically includes an overall fixed effect (intercept, denoted α), covariate effects (β) where x i denotes a vector of covariates relating to area i, and spatial random effect(s) R i, as follows:

$$\displaystyle \begin{aligned} \mu_i = \alpha + \boldsymbol{x}_i^{\text{T}}\boldsymbol{\beta} + R_i. \end{aligned}$$

Much of this chapter shall discuss options for modelling the spatial random effect(s), R i. Prior distributions are then specified for each of the unknown parameters:

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle \alpha \sim p\left(\cdot | \boldsymbol{\theta}_\alpha \right) \\ &\displaystyle \boldsymbol{\beta} \sim p\left(\cdot | \boldsymbol{\theta}_\beta \right) \\ &\displaystyle R_i \sim p\left(\cdot | \boldsymbol{\theta}_R \right). \end{array} \end{aligned} $$

The spatial random effects are given a spatial prior, which may be assumed to follow a conditional autoregressive (CAR) or alternative prior to enable spatial correlation and smoothing [8, 10]. If the parameters θ α, θ β, or θ R are unknown, then the hyperpriors represent an additional stage of the hierarchy.

Many different Bayesian spatial models have been proposed, most of which vary the representation of the spatial prior. Understanding the theoretical assumptions and appropriateness of different models is important. It is also necessary to consider how models perform in different circumstances. Therefore, this chapter discusses the theoretical underpinnings of key spatial models. Where possible and pertinent, these models were applied to typical cancer incidence mapping scenarios obtained by simulating rare and common cancer incidence data across Australia. This nation has more than 2100 small areas, with large differences in population size, demographic structure, land area size and shape.

2 Bayesian Spatial Models

Fourteen Bayesian spatial models used in disease mapping are considered. These can be divided into two broad types, namely ‘global’ spatial smoothing models that have a common spatial correlation term across the region, and ‘local’ spatial smoothing models that allow for differential spatial correlation depending on neighbourhood characteristics.

2.1 Global Spatial Smoothing

Global spatial smoothing means that the same correlation parameters are applied consistently across the entire region [26]. Although the global CAR-based models are relatively easy to implement in a range of software, disadvantages of global models include the potential to obscure genuine deviations in the underlying spatial patterns (i.e. to over-smooth), as discontinuities between adjacent areas are smoothed over.

2.1.1 Intrinsic CAR and BYM Models

The most commonly used prior for enabling spatial correlation within a Bayesian model is the intrinsic CAR distribution. This approach allows for smoothing of estimates over neighbouring areas, but it assumes a common variance for the smoothing term (and therefore a smooth spatial trend) over the whole region.

The intrinsic CAR (ICAR) model specifies the following set of conditional distributions for the spatial random effect parameter:

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle R_i = S_i \\ &\displaystyle S_i | \boldsymbol{s}_{\setminus i} \sim \mathcal{N}\left(\frac{\sum_j w_{ij}s_j}{\sum_j w_{ij}}, \frac{\sigma_s^2}{\sum_j w_{ij}}\right) \end{array} \end{aligned} $$

or in matrix notation

$$\displaystyle \begin{aligned} S_i | \boldsymbol{s}_{\setminus i} \sim \mathcal{N}\left(\left\{{\mathbf{D}}^{-1} \mathbf{W}\boldsymbol{s}\right\}_i, \sigma_s^2 \left\{\mathbf{ D}^{-1}\right\}_{ii}\right) \end{aligned}$$

where w ij is the element of a spatial weights matrix W corresponding to row i and column j [6, 10], and D is a diagonal matrix with elements \(\text{diag}\left \{\sum _j w_{ij}\right \}\). The term W determines the spatial proximity between the random effects, and it is most commonly defined as a binary, first-order, adjacency matrix, whereby

$$\displaystyle \begin{aligned} w_{ij} = \begin{cases} 1 & \mbox{if areas } i \mbox{ and } j \mbox{ are adjacent}\\ 0 & \mbox{otherwise.} \\ \end{cases} \end{aligned} $$
(10.1)

This model implies that the conditional expectation of S i is equal to the mean of the random effects at neighbouring locations.

The S i can be regarded as structured spatial random effects. If R i = S i + U i, so that unstructured spatial random effects \(U_i \sim \mathcal {N}\left (0,\sigma _U^2\right )\) are also included, the resulting model is referred to as the convolution model, or the BYM model in honour of Besag et al. [8]. However, the two separate random effects components cannot be individually identified—only their sum is identifiable [15]. Note that for all CAR-based models, the strength of the partial autocorrelation depends on the number of neighbouring areas rather than on any underlying relationship [27]. The BYM remains the most popular approach to incorporating spatial smoothing, in part due to its computational synergy with fairly standard MCMC approaches [47] and ease of implementation.

2.1.2 Proper CAR Model

The full conditionals for the ICAR prior are proper, but the joint distribution is improper since the precision matrix is singular [7]. The impropriety of the ICAR prior can be overcome by redefining the precision matrix

$$\displaystyle \begin{aligned} \mathbf{T} = \frac{1}{\sigma_s^2}\left(\mathbf{D} - \mathbf{W}\right) \end{aligned}$$

to

$$\displaystyle \begin{aligned} \mathbf{T} = \frac{1}{\sigma_s^2}\left(\mathbf{D} - \phi\mathbf{W}\right) \end{aligned}$$

such that the conditional distributions for the spatial random effect are:

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle S_i | \boldsymbol{s}_{\setminus i} \sim \mathcal{N}\left(\frac{\phi \sum_j w_{ij}s_j}{\sum_j w_{ij}}, \frac{\sigma_s^2}{\sum_j w_{ij}}\right) \end{array} \end{aligned} $$

with the constraint |ϕ| < 1, where ϕ represents the expected proportional ‘reaction’ of S i to ∑jw ijs j∕∑jw ij [5]. This ensures that the covariance matrix T −1 is positive definite and S has a proper joint distribution [19]. The proper CAR prior may have certain disadvantages, including potentially limiting the breadth of the posterior spatial pattern. Moreover, ϕ will likely need to be very close to 1 for there to be a reasonable amount of spatial association [5].

2.1.3 Leroux CAR Model

Another variant of the BYM model was proposed by Leroux et al. [29],

$$\displaystyle \begin{aligned} S_i | \boldsymbol{s}_{\setminus i} \sim \mathcal{N}\left(\frac{\rho \sum_j w_{ij}s_j}{\rho \sum_j w_{ij} + 1 - \rho}, \frac{\sigma_s^2}{\rho \sum_j w_{ij} + 1 - \rho}\right) \end{aligned}$$

which only requires a single set of random effects [24]. This avoids the difficulties in identifiability, and also the selection of hyperpriors (given that in the BYM model, the S i variance are conditional on neighbouring areas, while the U i have a marginal variance term) [41].

The precision matrix can be expressed as

$$\displaystyle \begin{aligned} \mathbf{T} = \frac{1}{\sigma_s^2}\left[\rho\left(\mathbf{D} - \mathbf{W}\right) + \left(1-\rho\right)\right]. \end{aligned}$$

This mixture representation consists of correlated smoothing of the neighbouring random effects (weighted by ρ) as well as uncorrelated smoothing to a global mean of zero (weighted by (1 − ρ)) [26]. Thus S i has a conditional expectation based on a weighted average of both the independent random effects and the spatially structured random effects. The ICAR prior is therefore a limiting case of both the proper CAR and Leroux CAR models when ρ is set to 1. The spatial autocorrelation parameter ρ is typically given either a continuous [19, 25] or a discrete [24] uniform prior

$$\displaystyle \begin{aligned} \rho \sim \mbox{Uniform}\left(0,1\right), \end{aligned}$$

where the discrete case offers gains in computational efficiency [24], although other priors have been suggested such as a diffuse Gaussian prior on the logit scale [27].

2.1.4 Geostatistical Model

Here, the residual spatial structure is modelled as a Gaussian process using a geostatistical design [11]. Because this model incorporates distance, counts are assumed to be located in the centroid of an area.

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle R_i \sim \mathcal{N}\left(S_i, \sigma^2\right) \\ &\displaystyle S_i = \exp \left( -(\lambda d_{ij})^k\right), \enspace \lambda > 0 \end{array} \end{aligned} $$

where λ controls the rate of decay, k is the “degree of spatial smoothing”, and d ij is the distance between points (e.g. centroids of areas) i and j [11]. This expression is the exponential decay function with the addition of the power k. Rather than fix decay parameter λa priori, a hyperprior is specified as a fourth stage of the hierarchy:

$$\displaystyle \begin{aligned} \lambda \sim \text{Uniform}\left(0.1, 6\right). \end{aligned}$$

The justification for the bounds 0.1 and 6 were based on the minimum and maximum separating distance in decimal degrees between area centroids to ensure that the spatial correlation was able to be high at the minimum distance, and likely to be low at the maximum distance. This choice is also able to give near zero correlation for distances within the study region, which is vital to avoid non-identifiability of the mean and correlation parameters [10].

Alternative functions are possible, including the disc model [40] (a linear decrease with increasing distance, where two discs of common radius are centred on centroids, and the correlation is proportional to the disc intersection area), or combining two parametric functions to obtain different shapes of decrease, such as the Matern class [10]. Note that often limited information is available to guide the choice of functional form, or correlation parameters, especially as complexity increases [10]. Because the covariance matrix is inverted at each iteration, these models can be computationally intensive and slow to run in a naïve algorithm, although this can be mitigated to some extent with the use of sparse matrix algebra.

2.1.5 Global Spline Models

The spline model also assumes that the cases are all located at the centroid of each area [17].

There are two main methods: smoothing splines and P-splines [32]. Smoothing splines are penalised splines which have knots on all data points. P-splines allow for a smaller number of knots, and are commonly formulated as a penalised spline regression under a ‘difference penalty’ based on the coefficients of adjacent B-spline bases or other spline bases [32].

The correlation between areas i and j can be modelled by a two-dimensional smooth surface [17]. First, define the longitude and latitude pairs representing the centroid of each area, denoted (c 1i, c 2i). Then

$$\displaystyle \begin{aligned} R_i = f(c_{1i},c_{2i}) \end{aligned}$$

where the smooth function f(⋅) is expressed as

$$\displaystyle \begin{aligned} f(c_{1i},c_{2i}) = \theta_1 B_1 (c_{1i},c_{2i}) + \cdots + \theta_k B_k (c_{1i},c_{2i}) \end{aligned}$$

which is estimated using P-splines with B-spline bases B 1, …, B k. The terms θ 1, …, θ k are unknown coefficients which are penalised to control for “wiggliness” through a penalty matrix, and k depends on the number of knots and the degree of the B-spline bases.

Define \(c_1 = \left (c_{11}, \ldots , c_{1N} \right )^{\text{T}}\) and \(c_2 = \left (c_{21}, \ldots , c_{2N} \right )^{\text{T}}\) and univariate B-spline bases \({\mathbf {B}}_1 = \left \{B_{11}(\boldsymbol {c}_1),\ldots ,B_{1{k_1}}(\boldsymbol {c}_1)\right \}\) and \({\mathbf {B}}_2 = \left \{B_{21}(\boldsymbol {c}_2),\ldots ,B_{2{k_2}}(\boldsymbol {c}_2)\right \}\). The bivariate B-spline basis is then constructed as the row-wise Kronecker product (denoted by \(\boxtimes \)) of the marginal B-spline bases:

$$\displaystyle \begin{aligned} \begin{array}{rcl} \mathbf{B} &\displaystyle =&\displaystyle {\mathbf{B}}_2 \boxtimes {\mathbf{B}}_1 \\ &\displaystyle =&\displaystyle \left({\mathbf{B}}_2\otimes {\mathbf{1}}_{k_1}^{\text{T}}\right) \odot \left({\mathbf{1}}_{k_1}^{\text{T}} \otimes {\mathbf{B}}_1\right). \end{array} \end{aligned} $$

The basis B is of dimension N × k where k = k 1k 2, the symbols ⊗ and ⊙ represent the Kronecker product and “element-wise” matrix product respectively, and \({\mathbf {1}}_{k_1}\) and \({\mathbf {1}}_{k_2}\) are column vectors of ones of length k 1 and k 2 [17].

Overall this model provides a relatively smooth surface, as the covariance structure is impacted by long distance effects that influence the smoothing. This is in contrast to the covariance structure of the CAR model where an area’s estimate depends on the mean of its neighbours [17].

The formulation of the P-spline model using the row-wise Kronecker product, or tensor product, is better suited to data which lie on a regular grid, or at least have similar distances between the centroids.

An alternative formulation [42] is to define the B-spline bases in terms of the distances,

$$\displaystyle \begin{aligned} z_{ik} = \exp \left(-\frac{d_{ik}}{\Delta}\right)\left(1+\frac{d_{ik}}{\Delta}\right) \end{aligned}$$

where d ik is the distance between the i th area and the k th knot, and Δ is a constant used to normalise the distances so that the values of B are more evenly spread between the lower and upper limits. This version of the P-spline uses a radial basis function which achieves rotational invariance [42].

2.2 Local Spatial Smoothing

In contrast to the global smoothing models, local smoothing is focused on allowing nearby areas to potentially have different amounts of spatial smoothing. Many of these are based on modifying the CAR prior to allow for discontinuous surfaces.

2.2.1 CAR Dissimilarity Models

Lee and Mitchell [26] based this model on the Leroux CAR prior, with ρ set to be 0.99 to ensure strong global spatial smoothing which could then be altered locally through estimating \(\left \{w_{ij} | i \sim j \right \}\). Here, the elements in W are modelled so the partial autocorrelations can be reduced between certain adjacent random effects. This approach can have binary or non-binary elements in W.

The similarity between areas is determined by including non-negative dissimilarity metrics in the model, i.e. z ij = (z ij1, …, z ijq) where z ijk = |z ik − z jk|∕σ k and σ k is the standard deviation of |z ik − z jk| over all pairs of contiguous areas.

The set of w ij are determined using regression parameters \(\boldsymbol {\alpha }=\left (\alpha _1, \ldots ,\alpha _q\right )\). These can be based on social or physical factors. Physical boundaries (e.g. river/railway line, or the distance between centroids) can be used if the aim is to explain the spatial pattern in the response and include covariates in the model. Alternatively, covariate information can be used to construct the dissimilarity metrics if the aim is to identify the locations of any boundaries [25].

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle R_i = S_i \\ &\displaystyle S_i | \boldsymbol{s}_{\setminus i} \sim \mathcal{N}\left(\frac{0.99\sum_j w_{ij}(\boldsymbol{\alpha})s_j + 0.01 \mu_0}{0.99\sum_j w_{ij}(\boldsymbol{\alpha})+0.01}, \frac{\sigma_s^2}{0.99\sum_j w_{ij}(\boldsymbol{\alpha})+0.01}\right). \end{array} \end{aligned} $$

The default binary formulation is:

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle w_{ij}(\boldsymbol{\alpha}) = \begin{cases} 1 &\displaystyle \mbox{if } \exp\left(-\sum_{k=1}^q z_{ijk} \alpha_k \right) \geq 0.5\ \text{ and }\ i \sim j\\ 0 &\displaystyle \mbox{otherwise} \\ \end{cases} \\ &\displaystyle \alpha_k \sim \text{Uniform}\left(0, M_k\right) \enspace \text{for }\ k = 1,\ldots, q \end{array} \end{aligned} $$

where M k is fixed so that a maximum of 50% of borders could be defined as boundaries [26]. The non-binary formulation (which does not allow identification of hard boundaries, but does allow for localised smoothing) is:

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle w_{ij}(\boldsymbol{\alpha}) = \exp\left(-\sum_{k=1}^q z_{ijk} \alpha_k \right) \\ &\displaystyle \alpha_k \sim \text{Uniform}\left(0, 50\right) \enspace \text{for }\ k = 1,\ldots, q. \end{array} \end{aligned} $$

2.2.2 Localised Autocorrelation

The spatially smooth random effects in this model are augmented with a piecewise constant intercept (cluster model). This allows for large jumps in the risk surface between adjacent areas if they are in different clusters. The approach by Lee and Sarran [28] partitions the I areas into a maximum of G clusters, each with their own intercept term (λ 1, …, λ G). The model is thus given by:

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle R_i = S_i + \lambda_{z_i} \\ &\displaystyle S_i | \boldsymbol{s}_{\setminus i} \sim \mathcal{N}\left(\frac{\sum_j w_{ij}s_j}{\sum_j w_{ij}}, \frac{\sigma_s^2}{\sum_j w_{ij}}\right) \\ &\displaystyle \lambda_g \sim \text{Uniform}\left( \lambda_{g-1}, \lambda_{g+1}\right) \enspace \text{for }\ g = 1, \ldots, G \\ &\displaystyle f(Z_i) = \frac{\exp\left(-\delta(Z_i - G^*)^2 \right)}{\sum_{r=1}^G \exp\left(-\delta(r - G^*)^2 \right)} \\ &\displaystyle \delta \sim\ \text{Uniform}(1, M) \end{array} \end{aligned} $$

where f(Z i) denotes a shrinkage prior on Z i which shrinks extreme values towards the middle intercept value. Label switching is prevented by ordering the cluster means (λ 1, …, λ G) so that λ 1 < λ 2 < ⋯ < λ G. The penalty term δ(Z i − G ∗)2 where G ∗ = (G + 1)∕2 means that if G is odd then each data point will be shrunk towards a single intercept \(\lambda _{G^*}\), but if G is even, there may be two different intercept terms used even if there is a spatially smooth residual structure. Lee and Sarran [28] thus recommend setting G to be a small odd number, such as 3 or 5. Area i is assigned to one of the G intercepts by \(Z_i \in \left \{1,\ldots ,G\right \}\), and there is no spatial smoothing imposed on the indicator vector Z. The clustering is purely non-spatial, and it is the CAR prior on the S i term that accounts for spatial autocorrelation [28].

2.2.3 Locally Adaptive Model

The locally adaptive model takes a similar approach to the above dissimilarity model, except that here the boundaries are not identified by the use of additional information and the modelled w ij are binary only. Lee and Mitchell [27] again based this on the Leroux CAR model:

$$\displaystyle \begin{aligned} S_i | \boldsymbol{s}_{\setminus i} \sim \mathcal{N}\left(\frac{\rho \sum_j w_{ij}s_j}{\rho \sum_j w_{ij} + 1 - \rho}, \frac{\sigma_s^2}{\rho \sum_j w_{ij} + 1 - \rho}\right). \end{aligned}$$

Here ρ can be estimated in the model, or fixed at a specified value. (Lee and Mitchell [27] recommend 0.99.)

The spatial weights matrix starts out as the binary, first-order, adjacency matrix given by Eq. (10.1) and is subsequently updated at each iteration which allows the weights corresponding to neighbours to be estimated as either 1 or 0 (with w ij fixed at zero for non-neighbouring areas). Because only weights corresponding to neighbouring areas are estimated, this approach should be more computationally feasible than areal wombling [30] where all values in W are estimated.

The matrix W is estimated as follows. For adjacent areas i and j: if the marginal 95% credible intervals (CIs) of s i and s j overlap, then set w ij = 1; else set w ij = 0. It is therefore not a ‘fully’ Bayesian method of estimation for these terms, as they are not considered to be random variates. For further details, refer to Lee and Mitchell [27], who implemented this using INLA.

2.2.4 Weighted Sum of Spatial Priors

The BYM model with its spatially structured component S i and its unstructured spatial component U i was extended by Lawson and Clark [23] to be able to incorporate discontinuities:

$$\displaystyle \begin{aligned} R_i = p_i S_i + (1 - p_i)Z_i + U_i. \end{aligned} $$
(10.2)

The Z component models abrupt discontinuities between areas. Although a range of options is possible, Lawson and Clark [23] based the prior for this parameter on the total absolute difference in risk between neighbouring areas, i.e.

$$\displaystyle \begin{aligned} \pi \left(Z_1, \ldots, Z_N\right) \propto \frac{1}{\sqrt{\lambda}}\exp\left(-\frac{1}{\lambda}\sum_{i\sim j} |Z_i - Z_j|\right) \end{aligned}$$

where λ acts as a constraining term.

Note that if p i = 1 in Eq. (10.2), then the model reverts to the BYM model. Conversely, if p i = 0, then the model is entirely discontinuous.

2.2.5 Leroux Scale Mixture Model

Using a scale mixture model within a Leroux prior also enables detection of abrupt changes between areas, with the advantage over the above approaches of incorporating non-normality (heavy tailed distributions). This was proposed by Congdon [12] as follows:

$$\displaystyle \begin{aligned} S_i | \boldsymbol{s}_{\setminus i} \sim \mathcal{N}\left(\frac{\rho \sum_j w_{ij}s_j}{\rho \sum_j w_{ij} + 1 - \rho}, \frac{\sigma_s^2}{\kappa_i \left[\rho \sum_j w_{ij} + 1 - \rho\right]}\right). \end{aligned}$$

If ρ = 0, this reduces to an unstructured iid scale mixture Student-t density, which is a heavy-tailed distribution. Small values of κ j(<1) will indicate areas differ from their neighbours and result in less smoothing between neighbouring areas. The scale mixture is implemented by κ i ∼Gam(0.5ν, 0.5ν), where ν is a hyperparameter.

The precision matrix has the following diagonal terms [12]:

$$\displaystyle \begin{aligned} \left\{\mathbf{T}\right\}_{ii} = \frac{1}{\sigma_s^2}\kappa_i \left[(1-\rho) + \rho \sum_{j \neq i} w_{ij} \right] \end{aligned}$$

and off-diagonal terms:

$$\displaystyle \begin{aligned} \left\{\mathbf{T}\right\}_{ij} = \frac{1}{\sigma_s^2}\rho \kappa_i \kappa_j \mathbb{I}(i \sim j). \end{aligned}$$

2.2.6 Skew-Elliptical Areal Spatial Model

Another approach that focused on incorporating skewness was introduced by Nathoo and Ghosh [36]. Here

$$\displaystyle \begin{aligned} R_i = \eta_i^{-0.5}\left(\delta|Z_i| + S_i \right) \end{aligned}$$

where δ|Z i| is the skewing component where Z i is a set of skewing variables each independently drawn from a standard normal distribution, η provides the scale mixing and S i is from the CAR model, i.e.

$$\displaystyle \begin{aligned} S_i | \boldsymbol{s}_{\setminus i} \sim \mathcal{N}\left(\kappa\frac{\sum_j w_{ij}s_j}{\sum_j w_{ij}}, \frac{\sigma_s^2}{\sum_j w_{ij}}\right) \end{aligned}$$

where κ is a spatial smoothing parameter (note that if κ is set to 0 then the distribution corresponds to uncorrelated skew-t random effects) and other terms are defined as before.

Two versions were proposed by Nathoo and Ghosh [36]. The first aims to ensure each R i has a skew-elliptical distribution, with the marginal distribution for each spatial effect belonging to the skew-t family of distributions.

The second is a semiparametric version that uses an approximation to a Dirichlet process to allow for data-driven departures from the parametric version. This accommodates uncertainty in the mixing structure, and gives greater flexibility in the tail behaviour of marginal distributions [36].

2.2.7 Hidden Potts Model

In contrast to the above approaches, this model is based on a hidden Markov field, so spatial correlation occurs in an additional latent hierarchy of the model [47]. This approach was proposed by Green and Richardson [18] and assigns each area to one of several risk categories. The spatial random effect is modelled on the log scale, as a K-component mixture model, where each component represents a different risk category, and the allocation of each area to a component follows a spatially correlated process. The number of components K is considered unknown and is estimated by the model.

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle R_i = \log (S_{z_i}) \\ &\displaystyle S_k \sim \text{Gamma}(a, b) \enspace \text{for }\ k = 1, \ldots, K \\ &\displaystyle K \sim \text{Uniform}(1, K_{\text{max}}). \end{array} \end{aligned} $$

The Potts model is proposed as the allocation model,

$$\displaystyle \begin{aligned} p(\boldsymbol{z}|\psi, K) = \exp(\psi U(z) - \delta_k(\psi)) \end{aligned}$$

where ψ > 0 is the interaction parameter to be estimated and \(U(z) = \sum _{i \sim j} \mathbb {I}(z_i = z_j)\) is the number of like labelled pairs of neighbouring areas. This model allows for discontinuities between areas in different risk categories and also for the amount of spatial correlation to vary by risk category. However, it does require careful MCMC implementation due to having an unknown number of risk categories and unknown area allocation to these categories. It is also more often implemented in high-dimensional data rather than disease mapping, as its greater flexibility generally has more advantages as data complexity increases [47].

2.2.8 Spatial Partition Model

Closely related to the above Hidden Potts model are the spatial partition models [14, 21]. These also have K non-overlapping clusters of areas, each with a constant relative risk, and K is unknown [10]. The key differences are in defining the clusters and the hyperprior specifications [10]. Specifically, the spatial partition model assigns up to K areas as cluster centres, which are allocated with a uniform prior probability, and the number of clusters is chosen according to the distribution p(K = k) ∝ (1 − c)k where c ∈ [0, 1) is fixed a priori. Smaller values of c makes this prior less informative, with the limiting case c = 0 yielding a uniform distribution. The remaining N − K areas are then assigned to their nearest cluster, according to the minimal number of boundaries that have to be crossed. Both this model and the above hidden Potts model have been criticised for forcing discontinuities into a surface, and for assuming constant relative risk within a cluster [23].

2.2.9 Local Spline Model

An extension to the global spline models described in Sect. 10.2.1 that results in a less smooth surface is the incorporation of unstructured random effects as in the penalised random individual dispersion effects (PRIDE) model, originally proposed by Perperoglou and Eilers [37]. Here

$$\displaystyle \begin{aligned} R_i = f(c_{1i}, c_{2i}) + \gamma_i \end{aligned}$$

where γ i is an area-specific random effect, whose vector follows a multivariate normal distribution [17]. This means that the covariance matrix captures the unstructured heterogeneity by containing an identity matrix multiplied by a variance component, in addition to the eigenvalues from the P-spline model component [17].

3 Case Study

3.1 Data

Since the dissemination of actual cancer data is restricted due to privacy and confidentiality requirements of the data custodians, simulated data that reflected the general distributions of actual data were generated to enable data sharing and reproduction of the presented results (see contact the authors for data and model code). Two datasets were generated that reflected the incidence of cancer types with a strong socioeconomic gradient: one with low total counts per geographical area over ten years (median of 2, range 0–19), considered a rare cancer, and one with higher counts over 10 years (median 25 cases, range 0–163), considered a common cancer. The focus on socioeconomic gradients meant we expected neighbouring areas having different socioeconomic levels would have different incidence rates.

The areas used were statistical areas 2 (SA2s) based on the 2011 Australian Statistical Geography Standard (ASGS) boundaries [4]. After excluding some areas with no/nominal resident populations, the number of areas was 2153. The median population of the included SA2s was 9055 (range: 3–50,251). Land area size varied from 0.8 to 520,000 km2, with a median of 15.6 km2.

3.2 Model Selection

Of the fourteen models introduced in Sect. 10.2 and described in Table 10.1, five were excluded from the application. Two of these were on theoretical grounds: the localised P-spline and the proper CAR models. The localised P-spline model was not investigated because implementing the P-spline had many challenges within the Australian context of vastly differing area sizes. The disadvantages of the proper CAR formulation such as the potentially limited breadth of estimates have limited appeal for spatial modelling [5]. We attempted to run a Hidden Potts model, spatial partition model and skew-elliptical areal spatial model, but were unable to successfully achieve this due to the computational complexity of the models, so they are also excluded from this section. The skew-elliptical model was unable to compile in WinBUGS [31], while the multidimensionality required for the spatial partition model and Hidden Potts model became too unwieldy.

Table 10.1 Software used for models applied to simulated data
Full size table

3.3 Model Variants

Of the nine models successfully implemented, multiple variants were considered for the global P-spline model, CAR dissimilarity models, localised autocorrelation models, and the locally adaptive models, and these are detailed below. Specifications for the geostatistical model are also documented. These resulted in a total of 13 versions of models applied to the simulated data (Table 10.1).

3.3.1 Global P-spline Model

Two formulations of the global P-spline model were implemented: the first uses a tensor product (refer to Sect. 10.2.1.5 for a definition) to define the basis, and the second uses a radial basis based on distances. No further modifications were made to the tensor product version.

The radial P-spline model had the knots evenly spaced at intervals of 5 degrees of latitude and longitude, as shown in Fig. 10.1. Knots which were too distant from the centroids of SA2 areas were subsequently dropped. A total of 47 knots were retained for modelling. Based on these knots, Δ was set to 500.

Fig. 10.1
figure 1

Location of knots (crosses) in relation to SA2 centroids (dots) for the P-spline radial model

Full size image

3.3.2 CAR Dissimilarity Model

The CAR dissimilarity model can also be applied in a variety of forms. As discussed in Sect. 10.2.2.1, the weighting matrix can be binary or non-binary, and the dissimilarity measure can be based on distance, geographical features (such as railways or mountains), or covariate information. Here we examine both binary and non-binary forms of this model based on the Socioeconomic Indexes for Areas (SEIFA) dissimilarity. This gives a continuous score for each area which is designated based on a range of socioeconomic measures, including house ownership, car ownership, employment and internet access. Several indices are available, and we used the Index of Relative Socioeconomic Disadvantage. Further details on SEIFA are available in Australian Bureau of Statistics [ABS] [3].

3.3.3 Localised Autocorrelation Models

Two variants of this model were assessed based on the value of G, the maximum number of clusters, being set to 3 or 5. See Sect. 10.2.2.2 for discussion of these choices.

3.3.4 Locally Adaptive Models

Two variants of this model were assessed based on the value of ρ, the spatial autocorrelation parameter, one being set to 0.99 (as recommended by Lee and Mitchell [27]) and the other allowed to vary between 0 and 1. The aim of fixing the value of ρ close to one is to ensure there is spatial smoothing occurring when w ij > 0. Note that if ρ = 0 then w ij vanishes from the model and cannot be used to determine if discontinuities are present. Setting ρ to 1 is not ideal, as the precision matrix would become singular.

3.3.5 Geostatistical Model

The geostatistical model had two adjustments made to provide a better fit. First, the priors for λ and k were changed according to the possible values of spatial correlation observed given different combinations of λ, k, and distances d ij. This exploratory analysis suggested using

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle \lambda \sim \text{Uniform}(0.01, 1) \\ &\displaystyle k \sim \text{Uniform}(0.1, 20). \end{array} \end{aligned} $$

To allow for further flexibility, λ and k were replaced by one of \(\left \{\lambda _1, \ldots , \lambda _5\right \}\) and \(\left \{k_1, \ldots , k_5\right \}\) respectively according to the remoteness of the area (major city, inner regional, outer regional, remote, and very remote) to allow the degree of smoothing to vary between the five levels of remoteness. Second, to make this model computationally feasible, the distance matrix \(\left \{d\right \}_{ij}\) was modified by imposing a remoteness-specific radius of influence \(\left \{r_1, \ldots , r_5\right \}\) on each area, such that areas beyond this threshold are not considered neighbours. These radii were \(\left \{50, 100, 200, 400, 800\right \}\) km respectively. This induces a Markov random field (MRF) structure which should have only a negligible effect on parameter estimation while greatly increasing computational efficiency. Some remote and very remote areas are relatively close to major city and inner regional areas, which can lead to some areas having more than 1000 neighbouring SA2s, thereby drastically reducing any computational gains. Therefore, the imposed MRF was further modified to exclude major city areas as neighbours of remote areas, and to exclude both major city and inner regional areas as neighbours of very remote areas. This is also sensible given the differences in cancer incidence and underlying influences between these areas [13]. This was achieved by setting the distances to these excluded areas to infinity. The result of these adjustments lead to

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle \left\{\mathbf{S}\right\}_{ij} = \begin{cases} \exp \left(-(\lambda_{z_i}d_{ij})^{k_{z_i}}\right) &\displaystyle \mbox{if } d_{ij} \leq r_{z_i} \\ 0 &\displaystyle \mbox{if } d_{ij} > r_{z_i} \\ \end{cases} \\ &\displaystyle S_i = f(\mathbf{S}) = \frac{1}{N_i}\sum_{j=1}^{N_r}\left\{\mathbf{S}\right\}_{ij} \end{array} \end{aligned} $$

where N i is the number of areas within a radius of \(r_{z_i}\) units from the centroid of area i (including area i), \(N_r=\underset {i}\max \left \{N_i\right \}\), and z i represents the degree of remoteness for area i, where z i = 1 corresponds to an area in a major city.

3.4 Statistical Software

Code for implementing the models in freely available software (Table 10.1) is available on request, as are the data sets.

The main software used to implement the statistical models were WinBUGS [31] and JAGS [38], which were run via R [39] using the packages R2WinBUGS [44] and R2jags [45] respectively, and also the R package CARBayes [25]. R-INLA [33] was also used for one model.

3.5 Model Comparison

Models were compared using several criteria, which are described below. The posterior SIR was calculated as \(\exp (\mu _i) = \exp (\alpha + R_i)\), as no covariates were included in these models. The median, lower and upper bounds of the 80% CIs were calculated as the 50th, 10th and 90th percentiles of the posterior, respectively.

3.5.1 Convergence

Convergence was predominately based on calculating the Geweke convergence diagnostic [16] for each area’s posterior SIR. A p-value for the test statistic below 0.01 was interpreted as suggestive evidence of non-convergence for that area. The trace and density plots for a subsample of areas were also examined for convergence.

3.5.2 Plausibility of Estimates

To determine how plausible the posterior SIR estimates were, the CI width was visually inspected, with unreasonably large CIs (with many of the 80% CIs spanning ± 5000% or more of the median estimate) providing evidence the estimate was not well-defined; while very precise estimates (the majority within ± 4%) were evidence that uncertainty was not appropriately included. The magnitude of smoothing of the median posterior SIRs in comparison to the raw SIRs was also visually examined. A smoothed SIR which was very similar to the raw SIR was suggestive of under-smoothing, particularly in areas with small populations.

3.5.3 Model Goodness-of-Fit

Three model goodness-of-fit measures were considered: Deviance information criterion (DIC) [43], Watanabe-Akaike information criterion (WAIC) [48] and Moran’s I on the residuals [35].

DIC and WAIC are both useful for comparing the predictive accuracy between models. Although DIC is a commonly used measure to compare Bayesian models, WAIC has several advantages over DIC, including that it closely approximates Bayesian cross-validation, it uses the entire posterior distribution and it is invariant to parameterisation [46]. For both these measures, smaller values indicate a better fitting model.

Moran’s I was applied to the model residuals to determine if spatial autocorrelation was present after fitting the models. This measure can be quite sensitive to the spatial weights matrix used to define the spatial dependencies between areas, and while a range of spatial weights matrices (inverse-distance, third-order neighbours etc) were considered, we used a matrix based on first-order neighbours. As values of Moran’s I close to 0 indicate very low or no residual spatial autocorrelation, here we consider values above 0.2 to be suggestive of some positive spatial autocorrelation. The closer Moran’s I is to zero, the better the model accounts for spatial autocorrelation [2].

3.5.4 Computational Time

The microbenchmark R package [34] was used to monitor computational time to run each model. The models were run on two different computers. However, the specifications of these computers were similar and any differences should have a negligible influence on computation time.

4 Results and Discussion

Substantive differences in the posterior estimates were observed between the 13 model variants applied, especially for the rare cancer (Table 10.2, Figs. 10.2, 10.3, 10.4, and 10.5). Depending on the model chosen, the modelled SIR estimates for the same geographical area could range from well below to well above the Australian average (Figs. 10.3 and 10.5).

Fig. 10.2
figure 2

Graphs of posterior SIR results by model, rare cancer. Note: Axes are consistent. Column 1 shows the 80% CI (shaded as per the tones on the maps in Fig. 10.3), the black line is the median SIR (in ascending order), the dots are the raw SIRs and the horizontal line at 1 represents the national average. For column 2, the 80% CIs are the BYM model, and the SA2s are ordered according to the BYM median SIR. The black line is the median estimate for the model named

Full size image
Fig. 10.3
figure 3

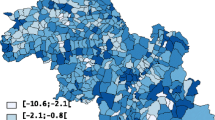
Rare cancer median posterior SIR mapped by model. (a) Raw (observed/expected), (b) BYM, (c) Leroux, (d) Geostatistical, (e) P-spline (tensor), (f) P-spline (radial), (g) CAR dissimilarity (binary), (h) CAR dissimilarity (non-binary), (i) Localised autocorrelation (G  =  3), (j) Localised autocorrelation (G = 5), (k) Locally adaptive (ρ estimated), (l) Locally adaptive (ρ = 0.99), (m) Weighted sum of spatial priors, (n) Leroux scale mixture

Full size image
Fig. 10.4
figure 4

Graphs of posterior SIR results by model, common cancer. Note: Axes are consistent. Column 1 shows the 80% CI (shaded as per the tones on the maps in Fig. 10.5), the black line is the median SIR (in ascending order), the dots are the raw SIRs and the horizontal line at 1 represents the national average. For column 2, the 80% CIs are the BYM model, and the SA2s are ordered according to the BYM median SIR. The black line is the median estimate for the model named

Full size image
Fig. 10.5
figure 5

Common cancer median posterior SIR mapped by model. (a) Raw (observed/expected), (b) BYM, (c) Leroux, (d) Geostatistical, (e) P-spline (tensor), (f) P-spline (radial), (g) CAR dissimilarity (binary), (h) CAR dissimilarity (non-binary), (i) Localised autocorrelation (G = 3), (j) Localised autocorrelation (G = 5), (k) Locally adaptive (ρ estimated), (l) Locally adaptive (ρ = 0.99), (m) Weighted sum of spatial priors, (n) Leroux scale mixture

Full size image
Table 10.2 Quantitative summary of results across model criteria
Full size table

While small numbers in geographical areas require smoothing, it remains possible that the neighbouring areas may have genuinely different incidence rates. These differences would be obscured during the smoothing process. Detecting these differences is problematic, and even many of the models designed to allow for local variation gave results similar to the BYM and Leroux models (Figs. 10.2, 10.3, 10.4, and 10.5), suggesting there was insufficient statistical power to adequately detect local differences. Of the models that obtained greater variation in the median SIR estimates between areas and less smoothing, there was often excessive uncertainty around these estimates, such as the localised autocorrelation model results (Figs. 10.2 and 10.4).

The number of area-specific SIR estimates that had evidence of non-convergence (based on Geweke p-value < 0.01) did vary between models and with the extent of data sparseness. In many cases, very wide CIs were symptomatic of non-convergence. For instance, the localised autocorrelation (G = 3) model for the rare cancer had 86% of area-specific SIRs with significant Geweke p-values, suggesting lack of convergence, and this model had among the widest CIs (Table 10.2). In contrast, models which had implausibly narrow CIs generally had very few/no areas with small Geweke p-values. However, overly narrow CIs are equally problematic as they over-exaggerate confidence in the plausibility of the estimates, which may actually be over- or under-smoothed.

In general, especially as data sparsity increased, our application of these models suggested that global models with more smoothing tended to have ‘well-behaved’, reliable estimates, while local models tended to struggle in producing plausible estimates (Figs. 10.2 and 10.4). The estimates for the binary CAR dissimilarity model (based on socioeconomic differences) in our study were often unreliable, and this is likely due to its tendency to remove too many neighbours. This is expected to also apply to other formulations, such as distance-based models.

The DIC and WAIC (Table 10.2) measures of goodness of model fit were generally in consensus for a given cancer type, apart from the localised autocorrelation models which had among the lowest DIC, but highest WAIC. Some models fit the data well for one type of simulated data, but not the other. For example, the geostatistical and P-spline models fit the common cancer quite well, but resulted in poor to average model fit for the rare cancer.

Moran’s I statistic (Table 10.2) generally indicated that the residual spatial autocorrelation is quite small. The only models with noticeable remaining correlation were the centroid based geostatistical and P-spline models, and this apparent correlation may result from using a weights matrix based on first-order neighbours when calculating Moran’s I.

Computational time varied substantially across the models, with times for the rare cancer ranging from 5 minutes (Leroux model in CARBayes) to over 20 hours (geostatistical model in JAGS). Models able to be run in CARBayes were generally very fast, while models run in JAGS or WinBUGS took longer (approximately between 0.5 and 2.5 hours, excluding the geostatistical model). Of note though, are the implications these varying computing times may have when many models need to be run, such as considering multiple cancer types, or repeating models to test different hyperprior specifications. While increasing computing specifications may reduce these times, it is still an important consideration when choosing between two (or more) otherwise well performing models.

It is a tenet of statistical research that the choice of model depends on the data characteristics and the aims of the analysis. However, when data are sparse and there is extreme variation in area size, such as are consistent with our simulated data, we found that the geostatistical or P-spline models generally had poor performance. The geostatistical model is prohibitively slow for these type of data, and when combined with the unpredictable model fit, this model is not recommended.

A previous comparison by Adin et al. [1] of the global P-spline model against the moving average and CAR models found the P-spline performed well for sparse disease mapping, although Goicoa et al. [17] found it to be more prone to detecting more false high-risk areas than either the CAR or a local P-spline model. This model is also rather complex to implement, requiring a penalty matrix and the number of knots to be specified, both of which are subjective and can have a large impact on model fit. The main concern with the P-spline model, however, was the specification of the basis matrix using the tensor product, which does not adequately address the fact that the SA2s are irregular in shape and the distances between their centroids can be vastly different. The radial basis version of the P-spline model was designed to address this, but aside from being computationally faster, it provided similar levels of smoothing and a worse model fit.

The BYM and Leroux models may be prone to over-smoothing when neighbouring areas have abrupt differences [23, 27], but they generally converged, provided a reasonable model fit with plausible estimates and were computationally efficient to implement. The Leroux model may be preferred over the BYM model to avoid the inability of the BYM model to identify both the structured and unstructured spatial random effects separately, but we found that in some cases it struggled to achieve convergence for its mixing parameter.

The locally adaptive models provided results similar to that of the BYM model, with slightly wider credible intervals. The main disadvantage was the difficulty in obtaining samples from the posterior due to the script calling up INLA from within another function.

A non-binary dissimilarity model may also provide an adequate fit, as this smooths more than a P-spline but less than BYM or Leroux. The non-binary dissimilarity formulation using the SEIFA covariate worked quite well for both cancer types, with noticeably less constraining of modelled SIR estimates than under BYM or Leroux. Whether these SIR estimates are appropriate or are under-smoothed will depend on data characteristics and the aims of the analysis.

Note that the final specification of each model requires additional sensitivity analyses to determine the influence of the priors and hyperpriors, the topic of which was outside the scope of this chapter.

5 Conclusion

The number of Bayesian spatial models available continues to increase, along with the capacity of the computing software and hardware. Determining the optimal amount of smoothing in spatial analyses remains difficult, but our study demonstrates the benefits of running a range of model types and provides insights into the relative merits of the different models for the study dataset. Comparing estimates from several different model types is important to assess consistency of results when conducting a spatial analysis

In summary, in sparse data contexts, the BYM, Leroux, locally adaptive, non-binary CAR dissimilarity models or some versions of localised autocorrelation models may outperform the other models examined. We suggest considering using centroid-based smoothing models only when areas are of similar size and shape.