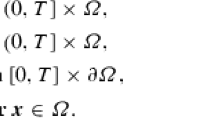Implicit LES with High-Order H(div)-Conforming FEM for Incompressible Navier-Stokes Flows

Abstract

Consider the transient incompressible Navier-Stokes flow at high Reynolds numbers. A high-order H(div)-conforming FEM with pointwise divergence-free discrete velocities is applied to implicit large-eddy-simulation in two limit cases: (1) decaying turbulence in periodic domains, (2) wall bounded channel flow.

1 H(div)-Conforming dGFEM for Navier-Stokes Problem

Consider a flow in a bounded polyhedron $\varOmega \subset {\mathbb R}^d,~ d \le 3$ with boundary ∂Ω = Γ ₀ ∪ Γ _per and outer unit normal $\mathbf {n}=(n_i)_{i=1}^d$. Set Q _T := (0, T) × Ω and denote f as source term. We want to find velocity $\mathbf {u}: Q_{T} \to {\mathbb R}^{d}$ and pressure $p: Q_T \to {\mathbb R}$ s.t.

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \partial_t \mathbf{u}- \nu \varDelta \mathbf{u} + (\mathbf{u} \cdot \nabla)\mathbf{u} + \nabla p &\displaystyle = &\displaystyle \mathbf{f} \qquad \mbox{in}~ Q_T , \end{array} \end{aligned} $$

(1)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \nabla \cdot \mathbf{u} &\displaystyle = &\displaystyle 0 \qquad \mbox{in}~ Q_T , \end{array} \end{aligned} $$

(2)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mathbf{u} &\displaystyle = &\displaystyle \mathbf{0} \qquad \mbox{on}~ (0,T) \times \varGamma_0 , \end{array} \end{aligned} $$

(3)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mathbf{u} &\displaystyle = &\displaystyle {\mathbf{u}}_0 \quad \mbox{on}~ \lbrace 0 \rbrace \times \varOmega , \end{array} \end{aligned} $$

(4)

and periodic boundary conditions on Γ _per. Let H = [L ²(Ω)]^d with inner product (⋅, ⋅)_H and assume u ₀ ∈H, f ∈ L ²(0, T;H). The inner product in L ²(Ω) is (⋅, ⋅)_Ω.

A variational formulation of the transient incompressible Navier-Stokes problem (1)–(4) is to find (u, p) ∈X × Q ⊆ [H ¹(Ω)]^d × L ²(Ω) for t ∈ (0, T) a.e. from

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} (\partial_t \mathbf{u}(t),\mathbf{v})_{\mathbf{H}} + \nu a(\mathbf{u}(t),\mathbf{v}) + c(\mathbf{u}(t),\mathbf{u}(t),\mathbf{v}) + b(p(t),\mathbf{v}) &\displaystyle = &\displaystyle (\mathbf{f}(t),\mathbf{v})_{\mathbf{H}}, \end{array} \end{aligned} $$

(5)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} -b(q,\mathbf{u}(t)) &\displaystyle = &\displaystyle 0, \end{array} \end{aligned} $$

(6)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mathbf{u}(0) &\displaystyle = &\displaystyle {\mathbf{u}}_0 . \end{array} \end{aligned} $$

(7)

with bounded bilinear resp. trilinear forms

$$\displaystyle \begin{aligned} a(\mathbf{u},\mathbf{v}):= \nu (\nabla \mathbf{u}, \nabla \mathbf{v})_\varOmega,~~ b(q,\mathbf{v}):= -(q, \nabla \cdot \mathbf{v})_\varOmega,~~ c(\mathbf{w},\mathbf{u},\mathbf{v}):= ((\mathbf{w} \cdot \nabla) \mathbf{u},\mathbf{w})_\varOmega . \end{aligned} $$

(8)

Consider H(div)-conforming, discontinuous Galerkin methods (dGFEM) with

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mathbf{H}(\text{div};\varOmega) &\displaystyle := &\displaystyle \lbrace \mathbf{w} \in \mathbf{H}:~~ \nabla \cdot \mathbf{w} \in L^2(\varOmega) \rbrace, \end{array} \end{aligned} $$

(9)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} {\mathbf{H}}_{\varGamma_0}(\text{div};\varOmega) &\displaystyle := &\displaystyle \lbrace \mathbf{v} \in \mathbf{H}(\text{div};\varOmega):~ \mathbf{v} \cdot \mathbf{n}|{}_{\varGamma_0} = 0 \rbrace . \end{array} \end{aligned} $$

(10)

Let ${\mathscr T}_h$ be a shape-regular decomposition of $\varOmega \subset {\mathbb R}^d$. Moreover, denote ${\mathscr E}_h$ the set of (open) edges (d = 2) or faces (d = 3) in ${\mathscr T}_h$. ${\mathscr E}^{\,B}_h \subset {\mathscr E}_h$ is the set of all $E \in {\mathscr E}_h$ with E ∩ Γ ₀≠∅ and ${\mathscr E}_h^{\,I} :={\mathscr E}_h \setminus {\mathscr E}^{\,B}_h$ the set of interior edges. Please note that edges/faces on Γ _per are considered as interior edges/faces. Consider adjacent elements $K, K' \in {\mathscr T}_h$ with ∂K ∩ ∂K′ = E and unit normal vector μ _E. For a scalar function v in the broken Sobolev space $H^{1}(\varOmega ,\mathscr {T}_h)$ denote jump resp. average of v across E by

$$\displaystyle \begin{aligned}{}[|v|]_E := v|{}_{\partial K\cap E}-v|{}_{\partial K'\cap E}, \qquad { \big\{\big\{ }v\big\}\big\} _E : = (v|{}_{\partial K\cap E}+v|{}_{\partial K'\cap E})/2. \end{aligned} $$

(11)

For $\mathbf {v} \in [H^{1}(\varOmega ,\mathscr {T}_h)]^d$, jump and average are understood component-wise.

Lemma 1 ([2])

Let W _h be a space of vector-valued polynomials w.r.t. ${\mathscr T}_h$. Then W _h ⊂H(div;Ω) if [|v|]_E ⋅μ _E = 0 for all v ∈W _h and all $E \in {\mathscr E}_h^{\,I}$.

Owing to Lemma 1 [|v|]_t,E = [|v − (v ⋅ μ _E)μ _E|]_E is the tangential jump across $E \in {\mathscr E}_h$.

Example 1

Examples of H(div)-conforming FEM are given in [1]. On simplicial grids one can apply Raviart-Thomas (RT) or Brezzi-Douglis-Marini (BDM) spaces

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mbox{RT}_k &\displaystyle = &\displaystyle \lbrace {\mathbf{w}}_h \in {\mathbf{H}}_{\varGamma_0}(\mbox{div};\varOmega):~ {\mathbf{w}}_h|{}_K \in {\mathbb P}_k(K) \oplus x {\mathbb P}_k(K)~ \forall K \in {\mathscr T}_h \rbrace,~ k \in {\mathbb N}_0~\qquad \end{array} \end{aligned} $$

(12)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \mbox{BDM}_k &\displaystyle = &\displaystyle \lbrace {\mathbf{w}}_h \in {\mathbf{H}}_{\varGamma_0}(\text{div};\varOmega):~ {\mathbf{w}}_h|{}_K \in {\mathbb P}_k(K)~ \forall K \in {\mathscr T}_h \rbrace,~ k \in {\mathbb N}. \end{array} \end{aligned} $$

(13)

On quadrilateral meshes, local Raviart-Thomas (RT) elements of degree $k \in {\mathbb N}_0$ are $\mbox{RT}_k(K) = ({\mathbb P}_{k+1,k}(K),{\mathbb P}_{k,k+1}(K))^t, d=2$. For d = 3, one has similarly $\mbox{RT}_k(K) = ({\mathbb P}_{k+1,k,k}(K),{\mathbb P}_{k,k+1,k}(K),{\mathbb P}_{k,k,k+1}(K))^t$. □

Let w _h ∈W _h ⊂H(div;Ω) with W _h ∈ {RT_k, BDM_k}. The spaces W _h⊄[H ¹(Ω)]^d are not [H ¹(Ω)]^d-stable, hence not directly applicable to the Navier-Stokes problem. As a remedy, we modify the diffusion bilinear form a using a symmetric interior penalty (SIP) dGFEM-approach with the broken gradient ∇_hv := ∇(v|_K): For sufficiently smooth $\mathbf {u} \in [H^s(\varOmega )]^d, s>\frac 32$, we define by adding two consistent terms

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} a_h(\mathbf{u},{\mathbf{w}}_h) &\displaystyle := &\displaystyle \int_\varOmega \nabla_h \mathbf{u}:\nabla_h {\mathbf{w}}_h~dx + \sum_{E \in {\mathscr E}_h} \sigma h_E^{-1} \int_E |[\mathbf{u}|]_t |[\mathbf{w}]|{}_t~ ds \\ &\displaystyle - &\displaystyle \sum_{E \in {\mathscr E}_h} \int_{E} \big( { \big\{\big\{ }\nabla_h \mathbf{u} \cdot \mu_E\big\}\big\} [|{\mathbf{w}}_h|]_t + { \big\{\big\{ }\nabla_h {\mathbf{w}}_h \cdot \mu_E\big\}\big\} [|\mathbf{u}|]_t~\big)~ ds~~ \forall {\mathbf{w}}_h \in {\mathbf{W}}_h \end{array} \end{aligned} $$

(14)

with h _E := diam(E) and parameter σ > 0 (to be chosen according to next lemma).

Define the following discrete H ¹-norms ∥w∥_1,h and ∥w∥_1,h,∗

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \|\mathbf{w}\|{}^2_{1,h} &\displaystyle := &\displaystyle \sum_{K \in {\mathscr T}_h} \| \nabla \mathbf{w}\|{}^2_{L^2(K)} + \sum_{E \in {\mathscr E}_h} h_E^{-1} \| [|\mathbf{w}|]_\tau\|{}^2_{L^2(E)} , \end{array} \end{aligned} $$

(15)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \|\mathbf{w}\|{}^2_{1,h,*} &\displaystyle := &\displaystyle \|\mathbf{w}\|{}^2_{1,h} + \sum_{E\in {\mathscr E}_h} h_E \|{ \big\{\big\{ }\nabla _h \mathbf{w} \cdot \mu_E\big\}\big\} \|{}^2_{L^2(E)}. \end{array} \end{aligned} $$

(16)

Lemma 2 ([2])

There exists constant σ ₀ (depending only on k and on shape regularity of ${\mathscr T}_h$) s.t. for σ ≥ σ ₀ one has:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} a_h({\mathbf{w}}_h,{\mathbf{w}}_h) &\displaystyle \ge &\displaystyle \frac 12 \|\mathbf{w}\|{}_{1,h}^2 \quad \forall {\mathbf{w}}_h \in {\mathbf{W}}_h, \end{array} \end{aligned} $$

(17)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} a_h(\mathbf{v},{\mathbf{w}}_h) &\displaystyle \le &\displaystyle C \|\mathbf{v}\|{}_{1,h,*} \|{\mathbf{w}}_h\|{}_{1,h} \quad \forall {\mathbf{w}}_h \in {\mathbf{W}}_h ~~ \mathit{\mbox{and}}~~ \mathbf{v} \in [H^s(\varOmega)]^d,~ s > \frac 32 .\qquad \end{array} \end{aligned} $$

(18)

Lemma 3 ([1])

RT- and BDM-spaces, together with appropriate discrete spaces Q _h

$$\displaystyle \begin{aligned} \begin{array}{rcl} {\mathbf{W}}_h &\displaystyle = &\displaystyle \mathit{\mbox{RT}}_k ~~\mathit{\mbox{with}}~~ Q_h := \lbrace q_h \in L^2(\varOmega):~ q_h|{}_K \in {\mathbb P}_k(K)~ \forall K \in {\mathscr T}_h \rbrace \qquad \mathit{\text{and}} \\ {\mathbf{W}}_h &\displaystyle = &\displaystyle \mathit{\mbox{BDM}}_k ~~\mathit{\mbox{with}}~~ Q_h := \lbrace q_h \in L^2(\varOmega):~ q_h|{}_K \in {\mathbb P}_{k-1}(K)~ \forall K \in {\mathscr T}_h \rbrace \end{array} \end{aligned} $$

form inf-sup stable pairs w.r.t. discrete H ¹ -norm:

$$\displaystyle \begin{aligned} \exists \beta_h \ge \beta_0 > 0~ \mathit{\mbox{s.t.}}~~ \inf_{q_h \in Q_h \setminus \lbrace 0 \rbrace } \sup_{{\mathbf{w}}_h \in {\mathbf{W}}_h \setminus \lbrace \mathbf{0} \rbrace } \frac{ (\nabla \cdot {\mathbf{w}}_h,q_h)_\varOmega}{\|{\mathbf{w}}_h\|{}_{1,h} \| q_h\|{}_{L^2(\varOmega)}} \ge \beta_h . \end{aligned} $$

(19)

By construction ∇⋅W _h = Q _h, these spaces are globally pointwise divergence-free:

$$\displaystyle \begin{aligned} \lbrace {\mathbf{w}}_h \in {\mathbf{W}}_h:~ (\nabla \cdot {\mathbf{w}}_h,q_h)_\varOmega =0~ \forall q_h \in Q_h \rbrace = \lbrace {\mathbf{w}}_h \in {\mathbf{W}}_h:~ \nabla \cdot {\mathbf{w}}_h = 0 \rbrace . \end{aligned} $$

(20)

For an exactly divergence-free field b ∈ [L ^∞(Ω)]^d ∩H(div;Ω) we modify the convective term c as in [2] by

$$\displaystyle \begin{aligned} \begin{array}{rcl} c_h(\mathbf{b};\mathbf{u},\mathbf{v}) &\displaystyle := &\displaystyle \sum_{K \in {\mathscr T}_h} ((\mathbf{b} \cdot \nabla )\mathbf{u},\mathbf{v})_K \\ {} &\displaystyle - &\displaystyle \sum_{E \in {\mathscr E}_h^{\,i}} \big( (\mathbf{b} \cdot \boldsymbol{\mu}_E) ([|\mathbf{u}|], { \big\{\big\{ }\bf v\big\}\big\} ) \big)_{\mathit{E}} + \frac 12 \sum_{\mathit{E} \in {\mathscr E}_{\mathit{h}}^{\mathit{\,i}}} \big( |\mathbf{b} \cdot \boldsymbol{\mu}_{\mathit{E}}| [|\mathbf{u}|],[|\mathbf{v}|]) \big)_{\mathit{E}}.\qquad \end{array} \end{aligned} $$

(21)

The first right-hand side terms corresponds to the standard form of the convective term. The last two facet terms, the upwind discretization, are consistent perturbations of the standard form of the convective term for u, v ∈X. The impact of these terms is included in the jump semi-norm |v|_b,upw defined via

$$\displaystyle \begin{aligned} |\mathbf{v}|{}^2_{\mathbf{b},\text{upw}} := \frac 12 \sum_{E \in {\mathscr E}_h^{\,i}} |\mathbf{b} \cdot \boldsymbol{\mu}_E|~ \| [|\mathbf{v}|] \|{}_{L^2(E)}^2.\end{aligned} $$

(22)

In case of exactly divergence-free fields b, one has $c_h(\mathbf {b};\mathbf {v},\mathbf {v}) = |\mathbf {v}|{ }^2_{\mathbf {b},\text{upw}}.$

We consider now the H(div)-conforming dGFEM for the transient Navier-Stokes problem (5)–(7) with f ∈ L ²(0, T;H). Combining the SIP-form of the diffusive term and the upwind-discretization of the convective term, one obtains:

Find (u _h, p _h) : (0, T) →W _h × Q _h with u _h(0) = u _0,h s.t. for all (v _h, q _h) ∈W _h × Q _h:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} (\partial_t {\mathbf{u}}_h,{\mathbf{v}}_h)_{\mathbf{H}} + \nu a_h({\mathbf{u}}_h,{\mathbf{v}}_h) + c_h({\mathbf{u}}_h;{\mathbf{u}}_h,{\mathbf{v}}_h) + b(p_h,{\mathbf{v}}_h) &\displaystyle = &\displaystyle (\mathbf{f},{\mathbf{v}}_h)_{\mathbf{H}} , \end{array} \end{aligned} $$

(23)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} - b(q_h,{\mathbf{u}}_h) &\displaystyle = &\displaystyle 0 . \end{array} \end{aligned} $$

(24)

All computations have been done using a hybridized variant of (23)–(24) implemented in the high-order sofware package NGSolve [9].

We will consider method (23)–(24) as tool for implicit large-eddy-simulation (ILES) in two limit cases: (i) decaying turbulence in periodic 2D and 3D domains (see Sect. 2) and (ii) wall bounded flow in a 3D-channel (see Sect. 3).

2 Decaying 2D- and 3D-Turbulent Flows

2.1 Stability and Error Analysis for Decaying Flows

Consider now decaying flows, i.e. we consider problem (23)–(24) with f ≡0. Using the mesh-dependent expressions (15) and (22) and setting v _h = u _h in the semidiscrete problem (23)–(24), one obtains with $\| \mathbf {v} \|{ }_e^2 := a_h(\mathbf {v},\mathbf {v})$ the balance

$$\displaystyle \begin{aligned} \frac{d}{dt} \left( \frac 12 \|{\mathbf{u}}_h(t)\|{}_{L^2(\varOmega)}^2 \right) + \nu \|{\mathbf{u}}_h(t)\|{}^2_e + |{\mathbf{u}}_h(t)|{}_{{\mathbf{u}}_h,\text{upw}}^2 = 0 . \end{aligned} $$

(25)

This implies existence of (u _h, p _h) and bounds for kinetic and dissipation energies:

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \frac 12 \|{\mathbf{u}}_h(t) \|{}_{L^2(\varOmega)}^2 &\displaystyle \le &\displaystyle \frac 12 \|{\mathbf{u}}_{0h}\|{}_{L^2(\varOmega)}^2 \exp (-\nu t/C_F^2) , \end{array} \end{aligned} $$

(26)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \int_0^t \Big( \frac{\nu}{2} \|{\mathbf{u}}_h(\tau)\|{}_e^2 + |{\mathbf{u}}_h(\tau)|{}_{{\mathbf{u}}_h,\text{upw}}^2 \Big) d\tau &\displaystyle \le &\displaystyle \frac 12 \|{\mathbf{u}}_{0h}\|{}_{L^2(\varOmega)}^2 . \end{array} \end{aligned} $$

(27)

In case of smooth velocity with u ∈ L ¹(0, T;[W ^{1, ∞}(Ω)]^d), we obtain the following pressure-robust and Re-semi-robust error estimate.

Theorem 1 ([10])

Let $\mathbf {u} {\,\in \,} L^2(0,T;{\mathbf {H}}^{\frac 32+\epsilon }(\varOmega )),~ \epsilon >0$, ∇u ∈ L ¹(0, T, [L ^∞(Ω)]^d) and u _h(0) = π _Su ₀ with Stokes projector π _Su, i.e. a _h(u − π _Su, v _h) = 0 ∀v _h ∈W _h; then:

$$\displaystyle \begin{aligned} \begin{array}{rcl} &\displaystyle &\displaystyle \frac 12 \|{\mathbf{u}}_h- \pi_S \mathbf{u}\|{}^2_{L^\infty(0,T;L^2(\varOmega))} + \int_0^T \big[ \frac{\nu}{2} \|{\mathbf{u}}_h- \pi_S \mathbf{u}\|{}_{1,h}^2 + | {\mathbf{u}}_h-\pi_S |{}_{{\mathbf{u}}_h,\mathit{\mbox{ upw}}}^2 \big] ~d\tau \\ &\displaystyle \le &\displaystyle e^{G_{\mathbf{u}}(T)} \int_0^T \big[ \| \partial_t \eta \|{}_{L^2(\varOmega)}^2 + \| \mathbf{u}\|{}_{L^\infty(\varOmega)} \| \nabla _h \eta \|{}^2_{L^2(\varOmega)} + h^{-2} \| \nabla \mathbf{u} \|{}_{L^\infty(\varOmega)} \| \eta \|{}^2_{L^2(\varOmega)} \big] ~d\tau \end{array} \end{aligned} $$

with η := u − π _Su and Gronwall factor

$$\displaystyle \begin{aligned}G_{\mathbf{u}}(T) := T + \| \mathbf{u} \|{}_{L^1(0,T;[L^\infty (\varOmega)]^d)} + C \| \nabla \mathbf{u} \|{}_{L^1(0,T;[L^\infty (\varOmega)]^d)} .\end{aligned}$$

The vorticity equation for ω := ∇×u describes the dynamics of decaying flows:

$$\displaystyle \begin{aligned} \partial_t \omega + \mathbf{u} \cdot \nabla \omega - \nu \varDelta \omega = \omega \cdot \nabla \mathbf{u}, \qquad \nabla \cdot \mathbf{u} = 0. \end{aligned} $$

(28)

The vortex stretching term ω ⋅∇u vanishes for d = 2 which leads to a completely different behavior for d = 2 and d = 3.

2.2 Decaying 2D-Turbulent Flow

Consider the following 2D-turbulent flow problem with a unique solution of (5)–(7).

Example 2

2D-lattice flow Consider on Ω = (−1, 1)² the following solution of the steady Euler model (ν = 0)

$$\displaystyle \begin{aligned} {\mathbf{u}}_0(x) = (- \varPsi_{x_2}(x),\varPsi_{x_1}(x))^t, \qquad \varPsi (x) := \frac{1}{2\pi} \sin (2\pi x_1)\cos (2\pi x_2) . \end{aligned}$$

The initial vorticity ω ₀ = ∇×u ₀ is shown in Fig. 1 for t = 0. The Taylor cells $\mathbf {u}(t,x) = {\mathbf {u}}_0(x) e^{-4\pi ^2 \nu t}$ are the (unique!) solution of the transient Navier-Stokes model. For this very smooth solution, a high-order FEM is preferable.

Fig. 1

Example 2: Snapshots of vorticity ω _h = ∇×u _h of high-order FEM with k = 8, N = 8 with t ∈{0, 22, 23, 26} (see first row) and t ∈{30, 35, 40, 50} (see second row)

This is a generalized Beltrami flow, since (u ⋅∇)u = −∇p. Due to pressure-robustness, a linearization via dropping (u ⋅∇)u preserves the coherent structures of the initial solution [4]. For order k = 8 and $h=\frac 14$, Fig. 1 shows snapshots of the discrete vorticity on the time interval 0 ≤ t ≤ T = 50 for ν = 10⁻⁶. We observe a self-organization of vortical structures which deviates from the unique solution.

Consider now the behavior of the kinetic energy $\frac 12\|{\mathbf {u}}_h\|{ }^2_{L^2(\varOmega )}$, enstrophy $\frac 12 \|\omega _h\|{ }^2_{L^2(\varOmega )}$ and palinstrophy $\frac 12 \|\nabla _h \omega _h\|{ }^2_{L^2(\varOmega )}$ for 0 ≤ t ≤ 50, see Fig. 2. Around t = 22.0 the solution deviates from coherent structures of the exact solution, also visible in the strong reduction of the amplitude of the kinetic energy. The exponential growth of the L ²- and H ¹-errors of the velocity (according to Theorem 1) is shown in Fig. 3. The initial condition u ₀ of the planar lattice flow induces a flow structure which, due to its saddle point structure, is “dynamically unstable so that small perturbations result in a very chaotic motion” as stated in Majda & Bertozzi [6]. A convincing discussion of self-organization in 2D-flows is given by van Groesen [12].

Fig. 2

Example 2: Temporal development of kinetic energy, enstrophy and palinstrophy

Fig. 3

Example 2: Error plots of high-order FEM for ν = 10⁻⁶, k = 8, N = 8, Δt = 10⁻³

Note that the preservation of the coherent structures (of the unique solution) can be extended in time by higher order k and/or h-refinement. Moreover, compared to standard mixed non-pressure-robust FEM, the application of pressure-robust FEM leads to much longer existence of such structures, see [4]. □

Remark 1

• (i) A similar behavior of 2D-decaying turbulent flows is known for the 2D Kelvin-Helmholtz instability. We refer to careful numerical studies in [11].

• (ii) The smallest scales depend on d. For d = 3, one has Kolmogorov-length $\lambda _{3D} \approx L Re^{-\frac 34}$ whereas for d = 2, the Kraichnan-length is $\lambda _{2D} \approx L Re^{-\frac 12}$. As conclusion, a direct numerical simulation (DNS) of 2D-flows at Re ≫ 1 is much more realistic than in 3D, see [5]. □

2.3 Decaying 3D-Turbulent Flows

From the vorticity equation (28) we concluded a completely different behavior of high Re-number flows for d = 3 as compared to d = 2. The following example highlights the effect of vortex stretching term (ω ⋅∇)u.

Example 3

3D-lattice flow

Consider the exact solution of the transient incompressible Navier-Stokes problem

$$\displaystyle \begin{aligned} \mathbf{u}(t,x) = {\mathbf{u}}_0(x) e^{-4\pi^2 \nu t}, \quad {\mathbf{u}}_0(x_1,x_2) = (-\varPsi_{x_2},\varPsi_{x_1},\sqrt{2} \varPsi )^t(x_1,x_2) \end{aligned}$$

in Ω = (0, 1)³ with stream function Ψ as in Example 2, with f = 0 and $\frac {1}{\nu }=2000$. This problem can be seen as 3D-extension of the 2D-lattice flow [6].

The snapshots of the solution in Fig. 4 show that until t ≈ 6, the numerical method tries to preserve the 2D-behavior of the 2D-lattice flow. This can be seen from the “vortex tubes” (presented by the 5.0-isocontour of the so-called Q-criterion, colored with vorticity). Then the vortex stretching starts to deform the vortex tubes until t = 7.5. Later on, i.e. around t = 10, there starts the eddy-breakdown in the inertial range. Here we observe the transition to homogeneous isotropic turbulence. Finally, in Fig. 5, we consider the influence of the Reynolds number for $\frac {1}{\nu } \in \lbrace 2000, 4000, 100000 \rbrace$. We apply again the high-order H(div)-dGFEM (here with $k=8, h=\frac {1}{8}$). In the first row, one observes the strongly decaying kinetic energy and the effect of vortex stretching in the (scaled) dissipation rate in time.

Fig. 4

Example 3: Transition to decaying homogeneous isotropic 3D-turbulence: 5.0 isocontour of Q-criterion, colored with vorticity at t ∈{0.0, 6.5, 7.0, 7.5, 10.0, 20.0}

Fig. 5

Example 3. First row: t-dependent kinetic energy and enstrophy, Second row: t-dependence of errors in L ² and H ¹, Legend: $\frac {1}{\nu }=2.0 \times 10^3$ (blue), $\frac {1}{\nu }=4.0 \times 10^3$ (red), $\frac {1}{\nu }= 1.0 \times 10^5$ (green)

The solution is still a Beltrami flow since (∇×u) ×u = 0. Thus a linearization via $p \mapsto P:=p+\frac 12 |\mathbf {u}|{ }^2$ would retain coherent structures as in 2D. This corresponds to the formal exact solution, see dashed lines. Solid lines correspond to the discrete solutions with k = 8 and $h=\frac 18$. The deviation of the discrete solution from the (formal) exact solution starts earlier for increasing Reynolds number. On the other hand, the deviation can be shifted to larger times if the FEM-order k is increased and/or an h-refinement is performed.

In the second row of Fig. 5, we consider the L ²- and H ¹-errors for u −u _h. According to the estimate in Thm. 1, one observes the exponential behavior of both errors in time. This again indicates that, after a certain time, the discrete solution deviates from the (formal) exact solution.

Example 4

3D-Taylor-Green vortex at Re = 1600

A typical LES-benchmark is the 3D-Taylor-Green vortex problem at $Re=\frac {UL}{\nu } = 1600$ with f = 0 and initial condition

$$\displaystyle \begin{aligned}{\mathbf{u}}_0 (x) = U \Big( \sin \frac{x_1}{L} \cos \frac{x_2}{L} \cos \frac{x_3}{L}, - \cos \frac{x_1}{L} \sin \frac{x_2}{L} \cos \frac{x_3}{L}, 0 \Big)^t .\end{aligned}$$

As in the previous example we observe the breakdown of large eddies into smaller and smaller eddies, see Fig. 6. This indicates that the typical behavior of homogeneous isotropic turbulence develops already for this relative small Reynolds number Re = 1600 where we set U = L = 1.

Fig. 6

Example 4. Behavior like decaying homogeneous isotropic 3D-turbulence: 0.1-isocontour of Q-criterion, coloured with velocity at t ∈{0.0, 2.0, 4.0, 9.0}

Consider now the temporal development of kinetic energy resp. the L ²-energy spectrum, see Fig. 7. For f = 0, we found in Sect. 3 a weak exponential decay of kinetic energy according to (26). As reference solution serves the solution of a spectral method with 512³ grid points (ooo). For increasing values of FEM-order k and/or increasing spatial resolution (via refinement of h = 1∕N), we observe grid convergence for the kinetic energy, see Fig. 7 (left).

Fig. 7

Example 4. Left: Temporal development of kinetic energy for 3D-Taylor-Green vortex at Re = 1600 for different values of order k and N = 1∕h; Right: Spectrum of kinetic energy at t = 10 for different values of k and h = 1∕N

In Fig. 7 (right) we plot the spectra of the kinetic energy at t = 10 for different values of k and h = 1∕N. In particular, no pile-up of the spectra for large wave numbers k occurs. The Kolmogorov rate of $E(k) = {\mathscr O}(k^{-5/3})$ is not reached since Re = 1600 is too small but will be reached at larger values of Re.

Consider now the temporal development of the kinetic energy dissipation rate for which we obtained estimate (27). This quantity is much harder to approximate. For increasing values of FEM-order k and/or increasing resolution (via refinement of h = 1∕N), we observe nearly convergence for the energy dissipation rate. In particular, we find that upwind stabilization (see solid lines) decreases the energy dissipation rate on the coarser grids, see Fig. 8 (left).

Fig. 8

Example 4. Left: Temporal development of energy dissipation rate for Taylor-Green vortex at Re = 1600 for different values of order k and N = 1∕h; Right: Balance of dissipation rates

Finally, consider the balance of dissipation rates according to

$$\displaystyle \begin{aligned} \frac{d}{dt} \Big( \frac 12 \|{\mathbf{u}}_h(t)\|{}_{L^2(\varOmega)}^2 \Big) + \nu a_h({\mathbf{u}}_h(t),{\mathbf{u}}_h(t)) + |{\mathbf{u}}_h(t)|{}_{{\mathbf{u}}_h,\text{upw}}^2 = 0 . \end{aligned}$$

The results are plotted for a relatively fine resolution with order k = 8 and h = 1∕N = 1∕16. This corresponds to 128³ grid points. We observe a very good agreement between molecular dissipation rate $\nu \| \nabla _h {\mathbf {u}}_h\|{ }^2_{L^2(\varOmega )}$ and kinetic energy dissipation rate $\frac {d}{dt} \left ( \frac 12 \|{\mathbf {u}}_h(t)\|{ }_{L^2(\varOmega )}^2 \right )$, since the numerical dissipation rate (stemming from SIP penalty and upwinding) reaches not more than 3% of the other rates around the peak rate of molecular dissipation rate, see Fig. 8 (right).

Please note that no explicit turbulence modeling has been applied. The price for such results is the H(div)-dGFEM simulation with around 9 × 10⁶ unknowns.

3 Wall-Bounded Flow

For wall-bounded turbulent flows, one striking problem is the presence of strong boundary layers, e.g. at walls. Another problem is to apply a splitting ${\mathbf {u}}_{(h)} = \langle {\mathbf {u}}_{(h)} \rangle + {\mathbf {u}}^{\prime }_{(h)}$ of the solution into an averaged velocity with some filter 〈⋅〉 and fluctuations.

Example 5 (3D Channel Flow)

Figure 9 (left) presents a laminar channel flow with a uniquely defined deterministic solution. A snapshot of the turbulent channel flow at Re _τ = 180 is shown on the right. The latter is slightly above the transition from laminar to turbulent flow. The chaotic solution of turbulent channel flow can be averaged in time and in x ₁- and x ₃-directions. One obtains, after a certain time of averaging, a relatively simple structure of the flow with 〈u ₁〉 = 〈u ₁〉(x ₂).

Fig. 9

3D channel flow: Laminar flow (left), Turbulent Re _τ = 180-flow (right)

Prandtl’s boundary layer theory leads to the so-called law of-the-wall, visible in Fig. 10. The mean viscous stress at the wall, the wall-shear stress, is $\tau _W = \nu \partial _{x_2} \langle u_1 \rangle |{ }_{x_2=0}.$ An appropriate velocity resp. length-scale in the near-wall region are the friction velocity $U_\tau = \sqrt {\tau _W}$ resp. $\eta _\nu = \nu /\sqrt {\tau _W}= \nu /U_\tau$. The friction-based Reynolds number is defined as Re _τ = U _τH∕ν with channel half width H. The layer can be characterized via the non-dimensional distance from wall in wall units $x_2^+ = x_2/\eta _\nu = U_\tau x_2/\nu$. It is characterized by the viscous wall region $x_2^+ <50$ with dominance of molecular viscosity, including the steep viscous sublayer at the wall with $x_2^+ < 5$, and by the outer layer with $x_2^+ > 50$.

Fig. 10

3D Channel flow at Re _τ = 180 with ILES: First row: k = 3, N = 4, Second row: k = 3, N = 8; Left: Mean profile U ⁺, Middle: Reynolds stress $\langle u^{\prime }_1u^{\prime }_2\rangle ^+$, Right: rms turbulence intensity $u_{RMS}^+$

The standard approach to resolve boundary layers is to use a (strongly) anisotropic mesh with refinement towards the wall(s). Very recent results with a L ²-based dGFEM-code by Fehn et al. [3] indicate that a strong anisotropic h-refinement can be relaxed to a (very) coarse h-mesh if higher-order FEM are applied. It turns out that for such (highly) under-resolved turbulent flows a “medium order” (k = 4, …, 8) is most efficient. Another point is that a purely numerical approach to stabilization is applied, i.e. no physical LES or VMS model is used.

Figure 10 shows results for the H(div)-dGFEM for the channel flow at Re _τ = 180. It turns out that a method of order k = 2 is not sufficient, but k = 3 provides good results. Very coarse grids with N = 4 resp. N = 8 elements in each x _i-direction with slightly anisotropic refinement in x ₂-direction towards the wall (indicated by vertical lines in Fig. 10) are used.

No explicit physical LES model is applied. In the ILES approach only numerical dissipation (basically from SIP and upwind) is used. The results for the averaged mean profile of U ⁺, the Reynolds stress component $\langle u^{\prime }_1u^{\prime }_2\rangle ^+$ and the rms turbulence intensity values $u_{RMS}^+$, compared to the DNS-data by Moser et al. [7], are surprisingly good on this very coarse grids with 12³ resp. 24³ grid points. □

Results in [3] indicate that such approach is also possible for larger values of Re _τ.

4 Outlook

The following features of H(div)-dGFEM are exploited in the numerical simulation of turbulent flows via implicit LES for incompressible Navier-Stokes flows:

• Minimal stabilization: Numerical dissipation may only result from the SIP term for the diffusive term a _h and upwind term in c _h.

• Simple form of convective form: There is no need to modify the convective term c _h since an exactly divergence-free FEM has a clean energy balance a priori.

• Pressure robustness: H(div)-conforming FEM have the relevant property that changing source term f to f + ∇ψ changes the solution (u _h, p _h) to (u _h, p _h + ψ).

• Re-semi-robust error estimates: Right-hand-side terms of the error estimate, see Theorem 1, including the Gronwall-term do not explicitly depend on 1∕ν.

We considered an ILES approach to simple turbulent flows with very resonable results. Turbulent flows in practice are clearly much more complex. A challenge is the flow around a high-lift airfoil, see Fig. 11, with complicated interplay of attached laminar and turbulent layers, separation, vortex structures etc. For a careful numerical study of such flows see [8]. A full DNS is still unfeasable. It would be of strong interest to develop new numerical concepts for such complex flows which clearly go beyond the limit cases (homogeneous isotropic turbulence and turbulent channel flows) under consideration. Nevertheless, the proposed ILES approach with high-order and pointwise divergence-free H(div)-dGFEM is a very promising approach. Another important point is that the flow in the previous example is governed by the compressible Navier-Stokes model. Many aspects of incompressible flows can be extended to the compressible case, e.g. the approach in boundary layer regions.

Fig. 11

Complex flow around three-element high-lift airfoil