Secure Key Encapsulation Mechanism with Compact Ciphertext and Public Key from Generalized Srivastava Code

Abstract

Code-based public key cryptosystems have been found to be an interesting option in the area of Post-Quantum Cryptography. In this work, we present a key encapsulation mechanism (KEM) using a parity check matrix of the Generalized Srivastava code as the public key matrix. Generalized Srivastava codes are privileged with the decoding technique of Alternant codes as they belong to the family of Alternant codes. We exploit the dyadic structure of the parity check matrix to reduce the storage of the public key. Our encapsulation leads to a shorter ciphertext as compared to DAGS proposed by Banegas et al. in Journal of Mathematical Cryptology which also uses Generalized Srivastava code. Our KEM provides IND-CCA security in the random oracle model. Also, our scheme can be shown to achieve post-quantum security in the quantum random oracle model.

1 Introduction

Cryptography and coding theory are at the core of implementation of telecommunication systems, computational systems and secure networks. Cryptography based on error correcting codes is one of the main approaches to guarantee secure communication in post-quantum world. The security of current widely used classical cryptosystems relies on the difficulty of number theory problems like factorization and the discrete logarithm problem. Shor [21] showed in 1994 that most of these cryptosystems can be broken once sufficiently strong quantum computers become available. Thus, it is necessary to devise alternatives that can survive quantum attacks while offering reasonable performance with solid security guarantees.

Code-based cryptosystems are usually very fast and can be implemented on several platforms, both software and hardware. They do not require special-purpose hardware, specifically no cryptographic co-processors. The security of code based cryptography mainly relies on the following two computational assumptions:

• (i) the hardness of generic decoding [8] which is NP complete and also believed to be hard on average even against quantum adversaries

• (ii) the pseudorandomness of the underlying code $\mathcal {C}$ for the construction which states that it is hard to distinguish a random matrix from a generator (or parity check) matrix of $\mathcal {C}$ used as a part of the public key of the system.

Designing practical alternative cryptosystems based on difficulty of decoding unstructured or random codes is currently a major research area. The public key indistinguishability problem strongly depends on the code family. For instance, the McEliece encryption scheme [17] uses binary Goppa codes for which this indistinguishability assumption holds. On the other hand, the assumption does not hold for other families such as Reed Solomon codes, Concatenated codes, Low Density Parity Check (LDPC) codes etc. In [12], Faugere et al. devise a distinguisher for high rate Goppa codes. One of the key challenges in code-based cryptography is to come up with families of codes for which the indistinguishability assumption holds.

Constructing efficient and secure code-based cryptographic scheme is a challenging task. The crucial fact in designing code-based cryptosystems is to use a linear error-correcting code in such a way that the public key is indistinguishable from a random key. A codeword is used as ciphertext of a carefully chosen linear error-correcting code to which random errors are added. The decryptor with the knowledge of a trapdoor can perform fast polynomial time decoding, remove the errors and recover the plaintext. Attackers are reduced to a generic decoding problem and the system remains secure against an adversary equipped with a quantum computer.

Our Contribution. In this paper, we focus on designing an IND-CCA secure efficient code-based KEM that relies on the difficulty of generic decoding problem. Our starting point is the key encapsulation mechanism DAGS [5] that uses the quasi-dyadic structure of Generalized Srivastava (GS) code. Quasi-dyadic structure reduces the public key size remarkably in DAGS while the encapsulation procedure increases the size of ciphertext. We aim to design a KEM with relatively short ciphertext. We deploy the Niederreiter framework to develop our KEM using a syndrome as ciphertext and achieve IND-CCA security in the random oracle model. More precisely, we use the parity check matrix of the Generalized Srivastava code as the public key and utilize its block dyadic structure to reduce the public key size. We consider the syndrome of a vector as the ciphertext header where the vector is formed by parsing two vectors – the first vector is an error vector that is generated by a deterministic error vector generation algorithm and the second vector is constructed from a hash value of a randomly chosen message by the encapsulator. This significantly reduces the ciphertext header size that makes the scheme useful in application with limited communication bandwidth. Also, the use of the parity check matrix directly in computing the ciphertext is more fast and efficient. For decapsulation, we form an equivalent parity check matrix using the secret key to decode the ciphertext header and then proceed to get the decapsulation key. Note that, Generalized Srivastava codes belong to the class of Alternant codes which have benefits of an efficient decoding algorithm. The complexity of decoding is $O(n \log ^2 n)$ [20] which is the same as that of Goppa codes where n is the length of the code.

In Table 1, we provide a theoretical comparison of our KEM with other recently proposed code-based KEMs. All the schemes in the table are based on finite fields having characteristic 2. We summarize the following features of our KEM.

• The closest related work to ours is DAGS [5]. Similar to DAGS, we also use quasi-dyadic form of Generalized Srivastava code. However, DAGS uses generator matrix whereas we use parity check matrix. Consequently, in our construction, the ciphertext size is reduced by $k\log _2q$ bits as compared to DAGS [5] whereas the public key and the secret key sizes remain the same. Furthermore our encapsulation is faster than DAGS.

• The public key sizes in our approach are better than NTS-KEM [2], Classic McEliece [9] and BIG QUAKE [6]. Although the BIKE variants are efficient in terms of key sizes and achieve IND-CCA security, they still suffer from small decoding failure rate. The erlier BIKE variants proposed in [3] have a non-negligible decoding failure rate and only attain IND-CPA security.

Table 1. Summary of IND-CCA secure KEMs using random oracles

In the comparison table, we mostly highlight the KEMs which rely on the error correcting codes that belong to the class of Alternant codes except BIKE variants which use QC (Quasi-Cyclic)-MDPC codes. We exclude the schemes like LEDAkem, RLCE-KEM, LAKE, Ouroboros-R, LOCKER, QC-MDPC, McNie etc. In fact, the schemes LAKE, Ouroboros-R, LOCKER use rank metric codes (Low Rank Parity Check (LRPC) codes) while RLCE-KEM is based on random linear codes and McNie relies on any error-correcting code, specially QC-LRPC codes. LEDAkem uses QC-LDPC codes and has a small decoding failure rate. Moreover, it has risks in case of keypair reuse which may cause a reaction attack [11] for some particular instances. The schemes proposed in [1] are also kept out as both HQC and RQC are constructed for any decodable linear code. Also, HQC has a decryption failure and RQC uses rank metric codes. The protocol QC-MDPC may have a high decoding failure rate for some particular parameters which enhances the risk of GJS attack [14]. The scheme CAKE is another important KEM which is merged with another independent construction Ouroboros to obtain BIKE [3].

Organization of the Paper. This rest of the paper is organized as follows. In Sect. 2, we describe necessary background related to our work. We illustrate our approach to design a KEM in Sect. 3 and discuss its security in Sect. 4. Finally, we conclude in Sect. 5.

2 Preliminaries

In this section, we provide mathematical background and preliminaries that are necessary to follow the discussion in the paper.

Notation. We use the notation $\textsf {x} \overset{ U}{\longleftarrow }X$ for choosing a random element from a set or distribution, wt(x) to denote the weight of a vector x, $(\mathbf{x} || \mathbf{y} )$ for the concatenation of the two vectors $\mathbf{x}$ and $\mathbf{y}$. The matrix $I_n$ is the $n \times n$ identity matrix. We let $\mathbb {Z}^{+}$ to represent the set $\{a \in \mathbb {Z} | a \ge 0\}$ where $\mathbb {Z}$ is the set of integers. We denote the transpose of a matrix A by $A^T$ and concatenation of the two matrices A and B by [A|B]. The uniform distribution over $(n-k) \times n$ random q-ary matrices is denoted by $U_{(n-k) \times n}$.

2.1 Hardness Assumptions

Definition 1

((Decision) (q-ary) Syndrome Decoding (SD) Problem [8]). Given a full-rank matrix $H_{(n - k) \times n}$ over $\textsf {GF}(q)$, a vector $\mathbf{e} \in (\textsf {GF}(q))^{n}$ and a non-negative integer w, is it possible to distinguish between a random syndrome $\mathbf{s}$ and the syndrome $H\mathbf{e} ^T$ associated to a w-weight vector $\mathbf{e}$?

Suppose $\mathcal {D}$ is a probabilistic polynomial time algorithm. For every positive integer $\lambda$, we define the advantage of $\mathcal {D}$ in solving the decisional SD problem by

$$\begin{aligned} \textsf {Adv}_{\mathcal {D},\textsf {SD}}^{\textsf {DEC}}(\lambda )&=|\Pr [ \mathcal {D}(H, H \mathbf{e} ^T) = 1~|~\mathbf{e} \in (\textsf {GF}(q))^{n} , H \overset{U}{\longleftarrow } U_{(n-k) \times n} ] \\&\,\,- \Pr [ \mathcal {D}(H,\mathbf{s} ) = 1~|~\mathbf{s} \overset{U}{\longleftarrow } U_{(n-k) \times 1} , H \overset{U}{\longleftarrow } U_{(n-k) \times n} ]|. \end{aligned}$$

Also, we define $\textsf {Adv}_{\textsf {SD}}^{\textsf {DEC}}(\lambda ) = \max \limits _{\mathcal {D}}[\textsf {Adv}_{\mathcal {D},\textsf {SD}}^{\textsf {DEC}}(\lambda )]$ where the maximum is taken over all $\mathcal {D}$. The decisional SD problem is said to be hard if $\textsf {Adv}_{\textsf {SD}}^{\textsf {DEC}}(\lambda ) < \delta$ where $\delta >0$ is arbitrarily small.

In addition, some code based schemes require the following computational assumption. Most of the schemes output a public key that is either a generator matrix or a parity check matrix by running key generation algorithm.

Definition 2

(Indistinguishability of public key matrix H [18]). Let $\mathcal {D}$ be a probabilistic polynomial time algorithm and $\textsf {PKE} = (\textsf {Setup}, \textsf {KeyGen}, \textsf {Enc}, \textsf {Dec})$ be a public key encryption scheme that uses an $(n-k) \times n$ matrix H as a public key over $\textsf {GF}(q)$. For every positive integer $\lambda$, we define the advantage of $\mathcal {D}$ in distinguishing the public key matrix H from a random matrix R as $\textsf {Adv}_{\mathcal {D},H}^{\textsf {IND}}(\lambda ) = \Pr [ \mathcal {D}(H) = 1| (\textsf {pk}=H,\textsf {sk}) \longleftarrow \textsf {PKE.KeyGen}(\textsf {param}), \textsf {param} \longleftarrow \textsf {PKE.Setup}(1^{\lambda } ) ] - \Pr [\mathcal {D}(R) = 1|R \overset{U}{\longleftarrow } U_{(n-k) \times n} ]$.

We define $\textsf {Adv}_{H}^{\textsf {IND}}(\lambda ) = \max \limits _{\mathcal {D}} [ \textsf {Adv}_{\mathcal {D},H}^{\textsf {IND}}(\lambda ) ]$ where the maximum is over all $\mathcal {D}$. The matrix H is said to be indistinguishable if $\textsf {Adv}_{H}^{\textsf {IND}}(\lambda ) < \delta$ where $\delta >0$ is arbitrarily small.

2.2 Basic Definitions from Coding Theory

Definition 3

(Dyadic Matrix and Quasi-Dyadic Matrix [7]). Given a ring R and a vector $\mathbf{h} = (h_0,h_1, \ldots , h_{n-1}) \in \mathbf{R} ^n$, the dyadic matrix $\varDelta (\mathbf{h} ) \in \mathbf{R} ^{n \times n}$ is a symmetric matrix having components $\varDelta _{ij} = h_{i\oplus j}$ where $\oplus$ stands for bitwise exclusive-or. The vector h is called a signature of the dyadic matrix. The signature of a dyadic matrix forms its first row. A matrix is called quasi-dyadic if it is a block matrix whose component blocks are $s \times s$ dyadic submatrices. An $s \times s$ dyadic matrix block can be generated from its first row.

Generating the dyadic signature [7]: A valid dyadic signature $\mathbf{h} =(h_0,h_1,\ldots ,h_{n-1})$ over $\mathbf{R} = \textsf {GF}(q^m)$ is derived using Algorithm 1.

Definition 4

(The Generalized Srivastava (GS) Code [16]). Let $m, n, s, t \in \mathbb {N}$ and q be a prime power. Let $\alpha _1,\alpha _2, \ldots , \alpha _n$, $w_1,w_2, \ldots , w_s$ be $n + s$ distinct elements of $\textsf {GF}(q^m)$ and $z_1,z_2, \ldots , z_n$ be nonzero elements of $\textsf {GF}(q^m)$. The Generalized Srivastava (GS) code of length n is a linear code with $st \times n$ parity-check matrix of the form $H= \begin{bmatrix} H_{1} ~ H_2~ \cdots ~ H_s \end{bmatrix}^T$ where

$$ H_{i}= \begin{bmatrix} \frac{z_{1}}{\alpha _{1}-w_{i}}&{}\frac{z_{2}}{\alpha _{2}-w_{i}} &{}\cdots &{} \frac{z_{n}}{\alpha _{n}-w_{i}}\\ \frac{z_{1}}{(\alpha _{1}-w_{i})^{2}}&{}\frac{z_{2}}{(\alpha _{2}-w_{i})^{2}} &{}\cdots &{} \frac{z_{n}}{(\alpha _{n}-w_{i})^{2}}\\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ \frac{z_{1}}{(\alpha _{1}-w_{i})^{t}}&{}\frac{z_{2}}{(\alpha _{2}-w_{i})^{t}} &{}\cdots &{} \frac{z_{n}}{(\alpha _{n}-w_{i})^{t}} \end{bmatrix} $$

is a $t \times n$ matrix block. The code is of length $n\le q^m -s$, dimension $k \ge n-mst$ and minimum distance $d \ge st + 1$. It can correct at most $\displaystyle w=\left\lfloor \frac{d-1}{2} \right\rfloor = \frac{st}{2}$ errors and is an Alternant code. In the parity check matrix

$$H= \begin{bmatrix} y_1g_1(\alpha _1) &{} y_2g_1(\alpha _2) &{} \cdots &{} y_{n}g_1(\alpha _n) \\ y_1g_2(\alpha _1) &{} y_2g_2(\alpha _2) &{} \cdots &{} y_{n}g_2(\alpha _n) \\ y_1g_3(\alpha _1) &{} y_2g_3(\alpha _2) &{} \cdots &{} y_{n}g_3(\alpha _n) \\ \ldots &{} \cdots &{} \cdots &{} \cdots \\ y_1g_r(\alpha _1) &{} y_2g_r(\alpha _2) &{} \cdots &{} y_{n}g_r(\alpha _n) \end{bmatrix} $$

where $g_i(x)= c_{i1} + c_{i2}x + \cdots + c_{ir}x^{r-1} ,~i= 1,2 , \ldots , r$ is a polynomial of degree $< r$ over $\textsf {GF}(q^m)$ for the Alternant code $\mathcal {A}(\varvec{\alpha }, \mathbf{y} )$, let $r = st$. Also set $g_{(l-1)t+k}(x)=\prod \limits _{j=1}^{s}(x-w_j)^t/(x-w_l)^k,~l=1,2,\ldots ,s \text { and }k = 1 ,2, \ldots , t$ and $y_i=z_i/\prod \limits _{j=1}^{s}(\alpha _i-w_j)^t,~ i=1,2,\ldots ,n$ so that $y_i g_{(l-1)t+k}(\alpha _i)=z_i/(\alpha _i-w_l)^k$. The resulting code will be a Generalized Srivastava code.

3 Our KEM Protocol

We construct a key encapsulation mechanism $\textsf {KEM}=(\textsf {Setup},\textsf {KeyGen},\textsf {Encaps}, \textsf {Decaps})$ as described below.

• $\textsf {KEM.Setup}(1^\lambda )$ $\longrightarrow \textsf {param}$ : Taking security parameter $\lambda$ as input, a trusted authority proceeds as follows to generate the global public parameters $\textsf {param}$.

• (i) Sample $n_0,p_1,p_2,m \in \mathbb {Z}^{+}$, set $q=2^{p_1},~s=2^{p_2}$ and $n = n_0s < q^m$.

• (ii) Select $t \in \mathbb {Z}^{+}$ such that $mst<n$. Set $w \le st/2$ and $k=n-mst$.

• (iii) Sample $k' \in \mathbb {Z}^{+}$ with $k'<k$.

• (iv) Select three cryptographically secure hash functions $\mathcal {G}:(\textsf {GF}(q))^{k^{'}}\longrightarrow (\textsf {GF}(q))^{k}$, $\mathcal {H}:(\textsf {GF}(q))^{k^{'}}\longrightarrow (\textsf {GF}(q))^{k'}$ and $\mathcal {H}' :\{0,1\}^{*} \longrightarrow \{0,1\}^r$ where $r \in \mathbb {Z}^{+}$ denotes the desired key length.

• (v) Publish the global parameters $\textsf {param} = (n,n_0, k,k',w,q,s,t,r,m,\mathcal {G}, \mathcal {H},\mathcal {H}')$.

• KEM.KeyGen(param)$\longrightarrow (\textsf {pk},\textsf {sk})$ : A user on input param, performs the following steps to generate the public key $\textsf {pk}$ and secret key $\textsf {sk}$.

• (i) Generate dyadic signature $\mathbf{h} =(h_0,h_1,\ldots ,h_{n-1})$ using Algorithm 1 where $h_i\in \textsf {GF}(q^m)$ for $i=0,1,\ldots ,n-1$.

• (ii) Select $\omega \overset{U}{\longleftarrow } \textsf {GF}(q^m)$ with $\omega \ne \frac{1}{h_j}+\frac{1}{h_0}$, $j=0,1,\ldots ,n-1$ and compute $u_i =\frac{1}{h_{i}} + \omega , ~ ~i =0,1,\ldots ,s - 1 \text { and } v_j =\frac{1}{h_{j}} +\frac{1}{h_0} + \omega ,~ j =0,1,\ldots ,n - 1.$ Set $\mathbf{u} =(u_0,u_1,\ldots ,u_{s-1})$ and $\mathbf{v} =(v_0,v_1,\ldots ,v_{n-1})$.

• (iii) Construct $st \times n$ quasi-dyadic matrix $A= \begin{bmatrix} A_1 ~ A_2 ~ \cdots ~ A_t \end{bmatrix}^T$ where

  $$\begin{aligned}&\,\, A_i=\\&\begin{bmatrix} \frac{1}{(u_{0}-v_{0})^{i}}&{}\frac{1}{(u_{0}-v_{1})^{i}} &{}\cdots &{} \frac{1}{(u_{0}-v_{n-1})^{i}}\\ \frac{1}{(u_{1}-v_{0})^{i}}&{}\frac{1}{(u_{1}-v_{1})^{i}} &{}\cdots &{} \frac{1}{(u_{1}-v_{n-1})^{i}}\\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ \frac{1}{(u_{s-1}-v_{0})^{i}}&{}\frac{1}{(u_{s-1}-v_{1})^{i}} &{}\cdots &{} \frac{1}{(u_{s-1}-v_{n-1})^{i}} \end{bmatrix}=\begin{bmatrix} \frac{1}{(v_{0}-u_{0})^{i}}&{}\frac{1}{(v_{1}-u_{0})^{i}} &{}\cdots &{} \frac{1}{(v_{n-1}-u_{0})^{i}}\\ \frac{1}{(v_{0}-u_{1})^{i}}&{}\frac{1}{(v_{1}-u_{1})^{i}} &{}\cdots &{} \frac{1}{(v_{n-1}-u_{1})^{i}}\\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ \frac{1}{(v_{0}-u_{s-1})^{i}}&{}\frac{1}{(v_{1}-u_{s-1})^{i}} &{}\cdots &{} \frac{1}{(v_{n-1}-u_{s-1})^{i}} \end{bmatrix} \end{aligned}$$

  is the $s \times n$ matrix block that can be written as $A_i=[\hat{A}_{i_1}|\hat{A}_{i_2}|\cdots |\hat{A}_{i_{n_0}}].$ Each block $\hat{A}_{i_k}$ is an $s \times s$ dyadic matrix for $k= 1,2,\ldots ,n_0$. For instance, take the first block

  $$ \hat{A}_{i_1}= \begin{bmatrix} \frac{1}{(u_{0}-v_{0})^{i}}&{}\frac{1}{(u_{0}-v_{1})^{i}} &{}\cdots &{} \frac{1}{(u_{0}-v_{s-1})^{i}}\\ \frac{1}{(u_{1}-v_{0})^{i}}&{}\frac{1}{(u_{1}-v_{1})^{i}} &{}\cdots &{} \frac{1}{(u_{1}-v_{s-1})^{i}}\\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ \frac{1}{(u_{s-1}-v_{0})^{i}}&{}\frac{1}{(u_{s-1}-v_{1})^{i}} &{}\cdots &{} \frac{1}{(u_{s-1}-v_{s-1})^{i}} \end{bmatrix}$$

  which is symmetric as $u_i-v_j=\frac{1}{h_{i}} +\frac{1}{h_{j}} +\frac{1}{h_0} =u_j-v_i$ and dyadic of order s as the $s \times s$ matrix

  $$\begin{aligned}&\begin{bmatrix} \frac{1}{(u_{0}-v_{0})}&{}\frac{1}{(u_{0}-v_{1})} &{}\frac{1}{(u_{0}-v_{2})} &{} \cdots &{} \frac{1}{(u_{0}-v_{s-1})}\\ \frac{1}{(u_{1}-v_{0})}&{}\frac{1}{(u_{1}-v_{1})} &{} \frac{1}{(u_{1}-v_{2})} &{} \cdots &{} \frac{1}{(u_{1}-v_{s-1})}\\ \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ \frac{1}{(u_{s-1}-v_{0})}&{}\frac{1}{(u_{s-1}-v_{1})^{i}} &{} \frac{1}{(u_{s-1}-v_{2})^{i}} &{} \cdots &{} \frac{1}{(u_{s-1}-v_{s-1})} \end{bmatrix}\\ =&\begin{bmatrix} h_0 &{} h_1 &{} h_2 &{} \cdots &{} h_{s-1}\\ h_1 &{} h_0 &{} h_3 &{} \cdots &{} h_{s-2}\\ \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ h_{s-1} &{} h_{s-2} &{} h_{s-3} &{} \cdots &{} h_0 \end{bmatrix} =\begin{bmatrix} h_{0 \oplus 0} &{} h_{0\oplus 1} &{} h_{0\oplus 2} &{} \cdots &{} h_{0 \oplus (s-1)}\\ h_{1\oplus 0} &{} h_{1\oplus 1} &{} h_{1\oplus 2} &{} \cdots &{} h_{1\oplus (s-1)}\\ \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ h_{(s-1) \oplus 0 } &{} h_{(s-1) \oplus 1} &{} h_{(s-1) \oplus 2} &{} \cdots &{} h_{(s-1) \oplus (s-1)} \end{bmatrix} \end{aligned}$$

  can be derived from the first row of the block using the relation $\frac{1}{h_{i\oplus j}}=\frac{1}{h_{i}}+ \frac{1}{h_{j}}+\frac{1}{h_{0}}$. Since the powering process acts on every single element, $\hat{A}_{i_1}$ preserves its dyadic structure.

• (iv) Choose $z_{is} \overset{U}{\longleftarrow }\textsf {GF}(q^m)$, $i=0,1,\ldots , n_0 - 1$ and set $z_{is+p} = z_{is}$, $p = 0,1, \ldots , s - 1$ where $n=n_0s$. Also set

  $$\begin{aligned}&\mathbf{z} =(z_{0s},z_{0s+1},\ldots ,z_{0s+s-1};z_{1s},z_{1s+1},\ldots ,z_{1s+s-1};\ldots ;z_{(n_0-1)s},z_{(n_0-1)s+1}, \\&\qquad \,\, \ldots ,z_{(n_0-1)s+s-1}) =(z_0,z_1,\ldots ,z_{n-1}) \in (\textsf {GF}(q^m))^n .\end{aligned}$$

• (v) Compute $y_j=z_j / \prod \limits _{i=0}^{s-1}(u_i-v_j)^t ~~\text {for}~j=0,1,\ldots , n-1$ and set $\mathbf{y} =(y_0,y_1,\ldots ,y_{n-1}) \in (\textsf {GF}(q^m))^n$.

• (vi) Construct $st \times n$ matrix B= $\begin{bmatrix} B_1 ~B_2 ~\cdots ~B_t \end{bmatrix}^T$ where

  $$ B_i= \begin{bmatrix} \frac{z_0}{(v_{0}-u_{0})^{i}}&{}\frac{z_1}{(v_{1}-u_{0})^{i}} &{}\cdots &{} \frac{z_{n-1}}{(v_{n-1}-u_{0})^{i}}\\ \frac{z_0}{(v_{0}-u_{1})^{i}}&{} \frac{z_1}{(v_{1}-u_{1})^{i}} &{}\cdots &{} \frac{z_{n-1}}{(v_{n-1}-u_{1})^{i}}\\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ \frac{z_0}{(v_{0}-u_{s-1})^{i}}&{}\frac{z_1}{(v_{1}-u_{s-1})^{i}} &{}\cdots &{} \frac{z_{n-1}}{(v_{n-1}-u_{s-1})^{i}} \end{bmatrix} $$

  is $s \times n$ matrix block. Sample a permutation matrix P of order st and compute $st \times n$ matrix $\overline{B}=PB$. The matrix $\overline{B}$ is a parity-check matrix of the GS code equivalent to its parity check matrix as in Definition 4, Subsect. 2.2.

• (vii) Project $\overline{B}$ onto $\textsf {GF}(q)$ using the co-trace function to form a $mst \times n$ matrix C where co-trace function converts an element of $\textsf {GF}(q^m)$ to an element of $\textsf {GF}(q)$ with respect to a basis of $\textsf {GF}(q^m)$ over $\textsf {GF}(q)$. For $\mathbf{a} \in \textsf {GF}(q^m)$, $\textsf {co-trace}(\mathbf{a} )=(a_0,a_1,\ldots ,a_{m-1})\in (\textsf {GF}(q))^m$ satisfying $<\mathbf{g} ,\mathbf{a} >=a_0+a_1q+a_2q^2+\cdots +a_{m-1}q^{m-1}$ where $a_i \in \textsf {GF}(q)$ and $\mathbf{g} =(1,q,q^2,\ldots ,q^{m-1})$ is a basis of $\textsf {GF}(q^m)$ over $\textsf {GF}(q)$. Thus if $\overline{B}=(\overline{b}_{ij})$ where $\overline{b}_{ij} \in \textsf {GF}(q^m)$, then $C=(c_{ij})$ is obtained from $\overline{B}$ by replacing $\overline{b}_{ij}$ by $\textsf {co-trace}(\overline{b}_{ij})$. Write the matrix C in the systematic form $(M | I_{n-k})$ where M is $(n-k) \times k$ matrix with $k = n - mst$. Note that, the $z_i$ are chosen to be equally having s-length block and all the operations during the row reduction are performed block-wise. Consequently, the dyadic structure is maintained in C and in particular in M. Let $M= \begin{bmatrix} M_{0,0}&{} M_{0,1}&{} \cdots &{}M_{0,\frac{k}{s}-1}\\ M_{1,0}&{} M_{1,1}&{} \cdots &{}M_{1,\frac{k}{s}-1}\\ \cdots &{} \cdots &{} \cdots &{}\cdots \\ M_{mt-1,0}&{} M_{mt-1,1}&{} \cdots &{}M_{mt-1,\frac{k}{s}-1} \end{bmatrix}$ where each block matrix $M_{i,j}$ is $s \times s$ dyadic matrix with dyadic signature $\varvec{\psi }_{i,j} \in (\textsf {GF}(q))^s$ which is the first row of $M_{i,j}$, $i=0,1,\ldots ,mt-1$, $j=0,1,\ldots ,\frac{k}{s}-1$.

• (viii) Publish the public key $\textsf {pk}$ = $\{\varvec{\psi }_{i,j}~|~ i=0,1,\ldots ,mt-1,~ j=0,1,\ldots ,\frac{k}{s}-1 \}$ and keep the secret key $\textsf {sk}=(\mathbf{v} , \mathbf{y} )$ to itself.

• KEM.Encaps($\textsf {param},\textsf {pk}$)$\longrightarrow (\textsf {CT},K$) : Given system parameters param and public key pk, an encapsulator proceeds as follows to generate a ciphertext header $\textsf {CT} \in (\textsf {GF}(q))^{n-k+k'}$ and an encapsulation key $K \in \{0,1\}^r$.

• (i) Sample $\mathbf{m} \overset{U}{\longleftarrow } (\textsf {GF}(q))^{k'}$ and compute $\mathbf{r} = \mathcal {G}(\mathbf{m} ) \in (\textsf {GF}(q))^{k}$, $\mathbf{d} = \mathcal {H}(\mathbf{m} ) \in (\textsf {GF}(q))^{k'}$ where $\mathcal {G}$ and $\mathcal {H}$ are the hash functions given in param.

• (ii) Parse $\mathbf{r}$ as $\mathbf{r}$ = $(\varvec{\rho } || \varvec{ \sigma })$ where $\varvec{\rho } \in (\textsf {GF}(q))^{k-k'}$, $\varvec{\sigma } \in (\textsf {GF}(q))^{k'}$. Set $\varvec{\mu } = (\varvec{\rho } || \mathbf{m} ) \in (\textsf {GF}(q))^{k}$.

• (iii) Run Algorithm 2 to generate a error vector $\mathbf{e}$ of length $n-k$ and weight $w-\textsf {wt}(\varvec{\mu })$ using $\varvec{\sigma }$ as a seed. Note that Algorithm 2 uses an expansion function¹. Set $\mathbf{e} '=(\mathbf{e} ||\varvec{\mu }) \in (\textsf {GF}(q))^{n}$.

• (iv) Using the public key $\textsf {pk}$=$\{\varvec{\psi }_{i,j}~|~ i=0,1,\ldots ,mt-1,~ j=0,1,\ldots ,\frac{k}{s}-1 \}$, compute $s \times s$ dyadic matrix $M_{i,j}$ with signature $\varvec{\psi }_{i,j} \in (\textsf {GF}(q))^s$ and reconstruct the parity check matrix $H=(M | I_{n-k})$ for the the GS code where $n-k=mst$ and

  $$M=\begin{bmatrix} M_{0,0}&{} M_{0,1}&{} \cdots &{}M_{0,\frac{k}{s}-1}\\ M_{1,0}&{} M_{1,1}&{} \cdots &{}M_{1,\frac{k}{s}-1}\\ \cdots &{} \cdots &{} \cdots &{}\cdots \\ M_{mt-1,0}&{} M_{mt-1,1}&{} \cdots &{}M_{mt-1,\frac{k}{s}-1} \end{bmatrix}$$

• (v) Compute the syndrome $\mathbf{c} = H(\mathbf{e} ')^T$ and the encapsulation key $K = \mathcal {H}'(\mathbf{m} )$ where $\mathcal {H}'$ is the hash function given in param.

• (vi) Publish the ciphertext header $\textsf {CT}=(\mathbf{c} , \mathbf{d} )$ and keep K as secret.

• KEM.Decaps($\textsf {param},\textsf {sk}$,$\textsf {CT}$)$\longrightarrow K$ : On receiving a ciphertext header $\textsf {CT}=(\mathbf{c} ,\mathbf{d} )$, a decapsulator executes the following steps using public parameters param and its secret key $\textsf {sk}=(\mathbf{v} ,\mathbf{y} )$ where $\mathbf{v} =(v_0,v_1,\ldots ,v_{n-1})$ and $\mathbf{y} =(y_0,y_1,\ldots ,y_{n-1}) .$

• (i) First proceed as follows to decode c and find error vector $\mathbf{e} ''$ of length n and weight w:

  (a) Use $\textsf {sk}=(\mathbf{v} ,\mathbf{y} )$ to construct $st \times n$ matrix $H'$ in the form

  $$\begin{aligned} \begin{bmatrix} y_0 &{} y_1 &{} \cdots &{}y_{n-1}\\ v_0y_0 &{} v_1y_1 &{} \cdots &{} v_{n-1}y_{n-1} \\ v_0^{2}y_0 &{} v_1^{2}y_1 &{} \cdots &{} v_{n-1}^{2}y_{n-1} \\ \cdots &{} \cdots &{} \cdots &{}\cdots \\ v_0^{st-1}y_0 &{} v_1^{st-1}y_1 &{} \cdots &{} v_{n-1}^{st-1}y_{n-1} \\ \end{bmatrix} = \begin{bmatrix} 1 &{} 1 &{} \cdots &{}1\\ v_0 &{} v_1 &{} \cdots &{} v_{n-1} \\ v_0^{2} &{} v_1^{2} &{} \cdots &{} v_{n-1}^{2} \\ \cdots &{} \cdots &{} \cdots &{} \cdots \\ v_0^{st-1} &{} v_1^{st-1} &{} \cdots &{} v_{n-1}^{st-1} \\ \end{bmatrix} \begin{bmatrix} y_0 &{} 0 &{} \cdots &{}0\\ 0 &{} y_1 &{} \cdots &{} 0 \\ 0 &{} 0 &{} y_2 &{} 0 \\ \cdots &{} \cdots &{} \cdots &{}\cdots \\ 0 &{} 0 &{} \cdots &{}y_{n-1} \\ \end{bmatrix}. \end{aligned}$$

  Note that, $H'$ is a parity check matrix in alternant form of the GS code over $\textsf {GF}(q^m)$ whereas the matrix $H=[M|I_{(n-k)}]$ constructed during KEM.KeyGen or KEM.Encaps is a parity check matrix in the systematic form of the GS code over $\textsf {GF}(q)$.

  (b) As the GS code is an Alternant code, the parity check matrix $H'$ is used to decode $\mathbf{c}$ by first computing the syndrome $S= H{'}(\mathbf{c} || \mathbf 0 )^T$ where $\mathbf 0$ represents the vector $(0,0,\ldots ,0)$ of length k and then by running decoding algorithm for the Alternant code to find the error locator polynomial $\omega (z)=\sum \limits _{\nu =1}^{w}Y_{\nu }y_{i_{\nu }}\prod \limits _{\mu =1,\mu \ne \nu }^{w} (1-X_{\mu }z)$ and error evaluator polynomial $\sigma (z)=\prod \limits _{i=1}^{w}(1-X_iz).$ Let $X_1=v_{i_1},X_2=v_{i_2},\ldots , X_w=v_{i_w}$ be the error locations and $Y_1=e_{X_1},Y_2=e_{X_2},\ldots , Y_w=e_{X_w}$ be the error values.

  (c) Set $\mathbf{e} ''=(e_1,e_2,\ldots ,e_n)$ with $e_j=$ ${\left\{ \begin{array}{ll} 0 ~~~ \text {if}~ j \ne X_i, 1 \le i \le w \\ Y_i ~\text { if} ~j = X_i, 1 \le i \le w \end{array}\right. }$.

• (ii) Let $\mathbf{e} ''=(\mathbf{e} _0||\varvec{\mu }') \in (\textsf {GF}(q))^{n}$ and $\varvec{\mu }'$=$(\varvec{\rho }' || \mathbf{m} ') \in (\textsf {GF}(q))^{k}$ where $\mathbf{e} _0 \in (\textsf {GF}(q))^{n-k}$, $\varvec{\rho }' \in (\textsf {GF}(q))^{k-k'} ,~ \mathbf{m} ' \in (\textsf {GF}(q))^{k'}$.

• (iii) Compute $\mathbf{r} ' = \mathcal {G}(\mathbf{m} ') \in (\textsf {GF}(q))^{k}$ and $\mathbf{d} ' = \mathcal {H}(\mathbf{m} ') \in (\textsf {GF}(q))^{k'}$ where $\mathcal {G}$ and $\mathcal {H}$ are the hash functions given in param.

• (iv) Parse $\mathbf{r} '$ as $\mathbf{r} '=(\varvec{\rho }'' || \varvec{\sigma }')$ where $\varvec{\rho }'' \in (\textsf {GF}(q))^{k-k'} ,~ \varvec{\sigma }' \in (\textsf {GF}(q))^{k'}$.

• (v) Run Algorithm 2 to generate deterministically an error vector $\mathbf{e} _{0}'$ of length $n-k$ and weight $w-\textsf {wt}(\varvec{\mu }')$ using $\varvec{\sigma }'$ as seed.

• (vi) If $(\mathbf{e} _0 \ne \mathbf{e} _{0}') \vee (\varvec{\rho }' \ne \varvec{\rho }'') \vee (\mathbf{d} \ne \mathbf{d} '$), output $\bot$ indicating decapsulation failure. Otherwise, compute the encapsulation key $K = \mathcal {H}'(\mathbf{m} ')$ where $\mathcal {H}'$ is the hash function given in param.

Correctness: While decoding $\mathbf{c}$, we form an $st \times n$ parity check matrix $H'$ over $\textsf {GF}(q^m)$ using the secret key $\textsf {sk}=(\mathbf{v} ,\mathbf{y} )$ and find the syndrome $H{'}(\mathbf{c} || \mathbf 0 )^T$ to estimate the error vector $\mathbf{e} '' \in (\textsf {GF}(q))^{n}$ with $\textsf {wt} (\mathbf{e} '')=w$. Note that, the ciphertext component $\mathbf{c} =H(\mathbf{e} ')^T$ is the syndrome of $\mathbf{e} '$ where the matrix H is a parity check matrix in the systemetic form over $\textsf {GF}(q)$ which is indistinguishable from a random matrix over $\textsf {GF}(q)$. At the time of decoding $\mathbf{c}$, we need a parity check matrix in alternant form over $\textsf {GF}(q^m)$. The parity check matrix H, a parity check matrix of GS code in the systemetic form derived from the public key $\textsf {pk}$, does not help to decode c as the SD problem is hard over $\textsf {GF}(q)$. The decoding algorithm in our decapsulation procedure uses the parity check matrix $H'$ (derived from the secret key $\textsf {sk}$) which is in alternant form over $\textsf {GF}(q^m)$. This procedure can correct upto st/2 errors. In our scheme, the error vector $\mathbf{e} '$ used in the procedure KEM.Encaps satisfies $\textsf {wt}(\mathbf{e} ')=w \le st/2$. Consequently, the decoding procedure will recover the correct $\mathbf{e} '$. We regenerate $\mathbf{e} _0'$ and $\varvec{\rho }''$ and compare it with $\mathbf{e} _0$ and $\varvec{\rho }'$ obtained after decoding. Since the error vector generation uses a deterministic function to get a fixed low weight error vector, $\mathbf{e} _0=\mathbf{e} _0'$ and $\varvec{\rho }'=\varvec{\rho }''$ occurs.

4 Security

4.1 Security Notions

Definition 5

(Indistinguishability under Chosen Plaintext Attack (IND-CPA) [13]). The IND-CPA game between a challenger $\mathcal {S}$ and a PPT adversary $\mathcal {A}$ for a public key encryption scheme PKE=($\mathsf {Setup}$, $\mathsf {KeyGen}$, $\mathsf {Enc}$, $\mathsf {Dec}$) is described below.

• 1. The challenger $\mathcal {S}$ generates $\textsf {param} \longleftarrow \textsf {PKE.Setup}(1^{\lambda })$, $(\textsf {pk}, \textsf {sk}) \longleftarrow \textsf {PKE.Key-} \textsf {Gen}(\textsf {param})$ where $\lambda$ is a security parameter and sends $\textsf {param},\textsf {pk}$ to $\mathcal {A}$.

• 2. The adversary $\mathcal {A}$ sends a pair of messages $\mathbf{m} _0 , \mathbf{m} _1 \in \mathcal {M}$ of the same length to $\mathcal {S}$.

• 3. The challenger $\mathcal {S}$ picks a random bit $b \in \{0, 1\}$, computes a challenge ciphertext $\textsf {CT} \longleftarrow \textsf {PKE.Enc} (\textsf {param}, \textsf {pk},\mathbf{m} _b;\mathbf{r} _b)$ and sends it to $\mathcal {A}$.

• 4. The adversary outputs a bit $b'$.

The adversary $\mathcal {A}$ wins the game if $b' = b$. We define the advantage of $\mathcal {A}$ against the above IND-CPA security game for the PKE scheme as

$$ \textsf {Adv}_{\textsf {PKE}}^{\textsf {IND-CPA}}(\mathcal {A} ) = | \Pr [b' = b] - 1/2 |.$$

A PKE scheme is IND-CPA secure if $\textsf {Adv}_{\textsf {PKE}}^{\textsf {IND-CPA}}(\mathcal {A} ) < \epsilon ~\text {where} ~\epsilon >0$ is arbitrarily small.

We also define the following four security notions for PKE scheme that are (i) One-Wayness under Chosen Plaintext Attacks (OW-CPA), (ii) One-Wayness under Plaintext Checking Attacks (OW-PCA), (iii) One-Wayness under Validity Checking Attacks (OW-VA) and (iv) One-Wayness under Plaintext and Validity Checking Attacks (OW-PCVA).

Definition 6

(OW-ATK [15]). For $\textsf {ATK} \in \{\textsf {CPA}, \textsf {PCA}, \textsf {VA}, \textsf {PCVA}\}$, the OW-ATK game between a challenger $\mathcal {S}$ and a PPT adversary $\mathcal {A}$ for a public key encryption scheme PKE = (Setup, KeyGen, Enc, Dec) is outlined below where $\mathcal {A}$ can make polynomially many queries to the oracle $O_{ \textsf {ATK}}$ given by

$$O_{ \textsf {ATK}} = {\left\{ \begin{array}{ll} - &{} \textsf {ATK} = \textsf {CPA} \\ \textsf {PCO}(\cdot ,\cdot ) &{} \textsf {ATK} = \textsf {PCA} \\ \textsf {CVO}(\cdot ) &{} \textsf {ATK} = \textsf {VA} \\ \textsf {PCO}(\cdot , \cdot ),\textsf {CVO}(\cdot ) &{} \textsf {ATK} = \textsf {PCVA} \end{array}\right. }$$

where the oracle $\textsf {PCO}(\cdot ,\cdot )$ takes a message $\mathbf{m}$ and a ciphertext CT as input and checks if the message recovered from $\textsf {CT}$ is $\mathbf{m}$ or not while the oracle $\textsf {CVO}(\cdot )$ takes a ciphertext CT as input distinct from the challenge ciphertext $\textsf {CT}^{*}$ and checks whether the message recovered from $\textsf {CT}$ belongs to the message space or not.

• 1. The challenger $\mathcal {S}$ generates $\textsf {param} \longleftarrow \textsf {PKE.Setup}(1^{\lambda })$, $(\textsf {pk}, \textsf {sk}) \longleftarrow \textsf {PKE.Key-} \textsf {Gen}(\textsf {param})$ where $\lambda$ is a security parameter and sends $\textsf {param},\textsf {pk}$ to $\mathcal {A}$.

• 2. The challenger $\mathcal {S}$ chooses a message $\mathbf{m} ^* \in \mathcal {M}$, computes the challenge ciphertext $\textsf {CT}^* \longleftarrow \textsf {PKE.Enc}(\textsf {param},\textsf {pk},\mathbf{m} ^*;\mathbf{r} ^*)$ and sends it to $\mathcal {A}$.

• 3. The adversary $\mathcal {A}$ having access to the oracle $O_{\textsf {ATK}}$, outputs $\mathbf{m} '$.

The adversary $\mathcal {A}$ wins the game if $\mathbf{m} '=\mathbf{m} ^*$. We define the advantage of $\mathcal {A}$ against the above $\textsf {OW-ATK}$ security game for PKE scheme as $\textsf {Adv}_{\textsf {PKE}}^{\textsf {OW-ATK}}(\mathcal {A}) = \Pr [\mathbf{m} '=\mathbf{m} ^*]$. The PKE scheme is said to be OW-ATK secure if $\textsf {Adv}_{\textsf {PKE}}^{\textsf {OW-ATK}}(\mathcal {A}) < \epsilon \text { for arbitrarily small non zero } \epsilon .$

Definition 7

(Indistinguishability under Chosen Ciphertext Attack (IND-CCA) [19]). The IND-CCA game between a challenger $\mathcal {S}$ and a PPT adversary $\mathcal {A}$ for a key encapsulation mechanism $\textsf {KEM}$ = ($\textsf {Setup}$, $\textsf {KeyGen}$, $\textsf {Encaps}$, $\textsf {Decaps}$) is described below.

• 1. The challenger $\mathcal {S}$ generates $\textsf {param} \longleftarrow \textsf {KEM.Setup}(1^{\lambda })$ and $(\textsf {pk}, \textsf {sk}) \longleftarrow \textsf {KEM.KeyGen}(\textsf {param})$ where $\lambda$ is a security parameter and sends $\textsf {param},\textsf {pk}$ to $\mathcal {A}$.

• 2. The PPT adversary $\mathcal {A}$ has access to the decapsulation oracle $\textsf {KEM.Decaps}$ to which $\mathcal {A}$ can make polynomially many ciphertext queries $\textsf {CT}_i$ and gets the corresponding key $K_i \in \mathcal {K}$ from $\mathcal {S}$.

• 3. The challenger $\mathcal {S}$ picks a random bit b from $\{0,1\}$, runs $\textsf {KEM.Encaps}(\textsf {param}, \textsf {pk})$ to generate a ciphertext-key pair $( \textsf {CT}^*, K_0^*)$ with $\textsf {CT}^* \ne \textsf {CT}_i$, selects randomly $K_1^* \in \mathcal {K}$ and sends the pair $(\textsf {CT}^*,K_b^*)$ to $\mathcal {A}$.

• 4. The adversary $\mathcal {A}$ having the pair $(\textsf {CT}^*,K_b^*)$ keeps performing polynomially many decapsulation queries on $\textsf {CT}_i \ne \textsf {CT}^*$ and outputs $b'$.

The adversary succeeds the game if $b' = b$. We define the advantage of $\mathcal {A}$ against the above IND-CCA security game for the KEM as

$$ \textsf {Adv}_{\textsf {KEM}}^{\textsf {IND-CCA}}(\mathcal {A} ) = | \Pr [b' = b] - 1/2 |.$$

A KEM is IND-CCA secure if $\textsf {Adv}_{\textsf {KEM}}^{\textsf {IND-CCA}}(\mathcal {A} ) < \epsilon ~~\text {where} ~\epsilon >0 ~\text {is arbitrarily small}.$

4.2 Security Proof

Our KEM provides IND-CCA security in random oracle model by Theorem 1.

Theorem 1

Assuming the hardness of decisional SD problem (Definition 1, Sect. 2.1) and indistinguishability of the public key matrix H (derived from the public key pk by running $\mathsf {KEM}.\mathsf {KeyGen}(\mathsf {param})$ where $\mathsf {param}\longleftarrow \mathsf {KEM}.\textsf {Setup}(1^{\lambda })$, $\lambda$ being the security parameter), our $\mathsf {KEM}=(\mathsf {Setup},\mathsf {KeyGen},\mathsf {Encaps}, \mathsf {Decaps})$ described in Sect. 3 provides IND-CCA security (Definition 7, Sect. 4.1) when the hash functions $\mathcal {H}'$ and $\mathcal {G}$ are modeled as random oracles.

The proof of the above theorem is the immediate consequence of Theorem 2, Corollary 1 and Theorem 4.

Fig. 1.

Scheme $\textsf {PKE}_1=(\textsf {Setup}, \textsf {KeyGen}, \textsf {Enc}, \textsf {Dec})$

Theorem 2

If the public key encryption scheme $\mathsf {PKE}_1= (\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Dec})$ described in Fig. 1 is OW-VA secure (Definition 6, Sect. 4.1) and there exist cryptographically secure hash functions, then the key encapsulation mechanism $\mathsf {KEM}=(\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Encaps}, \mathsf {Decaps})$ as described in Sect. 3 achieves IND-CCA security (Definition 7, Sect. 4.1) when the hash function $\mathcal {H}'$ is modeled as a random oracle.

Fig. 2.

Game $\mathbf{G} _0$ in the proof of Theorem 2

Fig. 3.

Sequence of games $\mathbf{G} _j,j=1,2,3$ in the proof of Theorem 2

Proof

Let $\mathcal {B}$ be a PPT adversary against the IND-CCA security of KEM providing at most $n_{D}$ queries to KEM.Decaps oracle and at most $n_{\mathcal {H}'}$ queries to the hash oracle $\mathcal {H}'$. We show that $\exists$ a PPT adversary $\mathcal {A}$ against the OW-VA security of the scheme $\textsf {PKE}_1$. We start with a sequence of games and the view of the adversary $\mathcal {B}$ is shown to be computationally indistinguishable in any of the consecutive games. Finally, we end up in a game that statistically hides the challenge bit as required. All the games are defined in Figs. 2 and 3. Let $E_j$ be the event that $b=b'$ in game $\mathbf{G} _j$, $j= 0,1,2,3$.

$\mathbf{Game} ~\mathbf{G} _0$: As usual, game $\mathbf{G} _0$ (Fig. 2) is the standard IND-CCA security game (Definition 7, Sect. 4.1) for the KEM and we have $|\Pr [E_0]-1/2|=\mathsf {Adv}^{\textsf {IND-CCA}}_{\textsf {KEM}} (\mathcal {B}).$

Fig. 4.

The hash oracles $\mathcal {H}'$ and the decapsulation oracle Decaps for games $\mathbf{G} _j,j=1,2,3$ in the proof of Theorem 2

Fig. 5.

Adversary $\mathcal {A}$ against OW-VA security of $\textsf {PKE}_1$

$\mathbf{Game} ~\mathbf{G} _1$: In game $\mathbf{G} _1$, a message $\mathbf{m} ^{*}$ is chosen randomly and the ciphertext $\textsf {CT}^{*}$ is computed by running $\textsf {PKE}_1.\textsf {Enc}(\textsf {param},\textsf {pk}, \mathbf{m} ^{*};\mathbf{r} ^{*})$. The challenger $\mathcal {S}$ maintains a hash list $Q_{\mathcal {H}'}$ (initially empty) and records all entries of the form $(\mathbf{m} , K)$ where hash oracle $\mathcal {H}'$ is queried on some message $\mathbf{m} \in \mathcal {M}$. Note that both games $\mathbf{G} _0$ and $\mathbf{G} _1$ proceed identically and we get $\Pr [E_0]=\Pr [E_1] .$

$\mathbf{Game} ~\mathbf{G} _2$: In game $\mathbf{G} _2$, the hash oracle $\mathcal {H}'$ and the decapsulation oracle Decaps are answered in such a way that they no longer make use of the secret key $\textsf {sk}$ except for testing whether $\mathsf {PKE}_1.\textsf {Dec}(\textsf {param},\textsf {sk}, \textsf {CT}) \in \mathcal {M}$ for a given ciphertext $\textsf {CT}$ (line 12 of Decaps oracle in Fig. 4). The hash list $Q_{\mathcal {H}'}$ records all entries of the form $(\mathbf{m} , K)$ where hash oracle $\mathcal {H}'$ is queried on some message $\mathbf{m} \in \mathcal {M}$. Another list $Q_D$ stores entries of the form $(\textsf {CT}, K)$ where either Decaps oracle is queried on some ciphertext $\textsf {CT}$ or the hash oracle $\mathcal {H}'$ is queried on some message $\mathbf{m} \in \mathcal {M}$ satisfying $\textsf {CT} \longleftarrow \textsf {PKE}_1.\textsf {Enc}(\textsf {param},\textsf {pk}, \mathbf{m} ;\mathbf{r} )$ with $\textsf {PKE}_1.\textsf {Dec}(\textsf {param},\textsf {sk}, \textsf {CT}) \longrightarrow \mathbf{m}$.

Let X denotes the event that a correctness error has occurred in the underlying $\textsf {PKE}_1$ scheme. More specifically, X is the event that either the list $Q_{\mathcal {H}'}$ contains an entry $(\mathbf{m} ,K)$ with the condition $\textsf {PKE}_1.\textsf {Dec}(\textsf {param}, \textsf {sk},\textsf {PKE}_1.\textsf {Enc}( \textsf {param},\textsf {pk},\mathbf{m} ; \mathbf{r} )) \ne \mathbf{m}$ or the list $Q_{D}$ contains an entry $(\textsf {CT},K)$ with the condition $\textsf {PKE}_1.\textsf {Enc} (\textsf {param}, \textsf {pk},\textsf {PKE}_1.\textsf {Dec}(\textsf {param},\textsf {sk},\textsf {CT}); \mathbf{r} ) \ne \textsf {CT}$ or both.

Claim: The view of $\mathcal {B}$ is identical in games $\mathbf{G} _1$ and $\mathbf{G} _2$ unless the event X occurs.

Proof of claim. To prove this, consider a fixed $\textsf {PKE}_1$ ciphertext $\textsf {CT}$ (placed as a Decaps query) with $\mathbf{m} \longleftarrow \textsf {PKE}_1.\textsf {Dec}(\textsf {param},\textsf {sk}, \textsf {CT})$. Note that when $\mathbf{m} \notin \mathcal {M}$, the decapsulation oracle $\textsf {Decaps}(\textsf {CT})$ returns $\bot$ in both games $\mathbf{G} _1$ and $\mathbf{G} _2$. Suppose $\mathbf{m} \in \mathcal {M}$. We now show that in game $\mathbf{G} _2$, $\mathsf {Decaps}(\textsf {CT}) \longrightarrow \mathcal {H}'(\mathbf{m} )$ for the $\textsf {PKE}_1$ ciphertext $\textsf {CT}$ of a message $\mathbf{m} \in \mathcal {M}$ with $\mathsf {PKE}_1.\textsf {Enc}(\textsf {param},\textsf {pk}, \mathbf{m} ;\mathbf{r} ) \longrightarrow \textsf {CT}$. We distinguish two cases – $\mathcal {B}$ queries hash oracle $\mathcal {H}'$ on $\mathbf{m}$ before making $\mathsf {Decaps}$ oracle on $\textsf {CT}$, or the other way round.

Case 1: Let the oracle $\mathcal {H}'$ be queried on $\mathbf{m}$ first by $\mathcal {B}$ before decapsulation query on $\textsf {PKE}_1$ ciphertext $\textsf {CT}$. Since $\mathsf {Decaps}$ oracle was not yet queried on $\textsf {CT}$, no entry of the form $(\textsf {CT}, K)$ exist in the current list $Q_D$ yet. Therefore, besides adding $(\mathbf{m} , K \overset{U}{\longleftarrow } \mathcal {K} )$ to the list $Q_{\mathcal {H}'}$(line 22 of $\mathcal {H}'$ oracle in Fig. 4), the challenger $\mathcal {S}$ also adds $(\textsf {CT}, K)$ to the list $Q_D$ (line 18 of $\mathcal {H}'$ oracle in Fig. 4), thereby defining $\mathsf {Decaps}(\textsf {CT}) \longrightarrow K = \mathcal {H}'(\mathbf{m} )$.

Case 2: Let the oracle $\mathsf {Decaps}$ be queried on $\textsf {PKE}_1$ ciphertext $\textsf {CT}$ before the hash oracle $\mathcal {H}'$ is queried on m. Then no entry of the form $(\textsf {CT}, K)$ exists in $Q_D$ yet. Otherwise, $\mathcal {H}'$ already was queried on a message $\mathbf{m} '' \ne \mathbf{m}$ (because $\mathsf {Decaps}$ oracle is assumed to be queried first on CT and the oracle $\mathcal {H}'$ was not yet queried on m) satisfying $\mathsf {PKE}_1.\textsf {Enc}(\textsf {param},\mathsf {pk}, \mathbf{m} '';\mathbf{r} '') \longrightarrow \textsf {CT}$ with $\mathsf {PKE}_1.\textsf {Dec}(\textsf {param},\mathsf {sk},\textsf {CT}) \longrightarrow \mathbf{m} ''$. This is a contradiction to the fact that the same $\textsf {PKE}_1$ ciphertext CT is generated for two different messages $\mathbf{m} '' , \mathbf{m}$ using randomness $\mathbf{r} ,\mathbf{r} ^{''}$ respectively where $\mathbf{r} =\mathcal {G}(\mathbf{m} ) \ne \mathcal {G}(\mathbf{m} '')=\mathbf{r} ''$ for a cryptographically secure hash function $\mathcal {G}$. Therefore,$\mathsf {Decaps}$ oracle adds $(\textsf {CT}, K \overset{U}{\longleftarrow } \mathcal {K})$ to the list $Q_D$, thereby defining $\mathsf {Decaps}(\textsf {CT}) \longrightarrow K$. When queried on $\mathbf{m}$ afterwards for hash oracle $\mathcal {H}'$, an entry of the form $(\textsf {CT}, K)$ already exists in the list $Q_D$ (line 15 of $\mathcal {H}'$ oracle in Fig. 4). By adding $(\mathbf{m} , K)$ to the list $Q_{\mathcal {H}'}$ and returning K, the hash oracle $\mathcal {H}'$ defines $\mathcal {H}'(\mathbf{m} ) = K \longleftarrow \textsf {Decaps}(\textsf {CT})$.

Hence, $\mathcal {B}$’s view is identical in games $\mathbf{G} _1$ and $\mathbf{G} _2$ unless a correctness error X occurs.                                                             $\square$ (of Claim)

As $\Pr [X]=0$ for our KEM, we have $\Pr [E_1] = \Pr [E_2].$

$\mathbf{Game} ~\mathbf{G} _3$: In game $\mathbf{G} _3$, the challenger $\mathcal {S}$ sets a flag $Y=\textsf {true}$ and aborts (with uniformly random output) immediately on the event when $\mathcal {B}$ queries the hash oracle $\mathcal {H}'$ on $\mathbf{m} ^{*}$. Hence, $|\Pr [E_2] -\Pr [E_3]| \le \Pr [Y=\textsf {true}].$ In game $\mathbf{G} _3$, $\mathcal {H}'(\mathbf{m} ^{*})$ will never be given to $\mathcal {B}$ neither through a query on hash oracle $\mathcal {H}'$ nor through a query on decapsulation oracle $\textsf {Decaps}$, meaning bit b is independent from $\mathcal {B}$’s view. Thus, $\Pr [E_3] = 1/2$. To bound $\Pr [Y=\textsf {true}]$, we construct an adversary $\mathcal {A}$ against the OW-VA security of $\textsf {PKE}_1$ simulating game $\mathbf{G} _3$ for $\mathcal {B}$ as in Fig. 5. Here $\mathcal {B}$ uses $\textsf {Decaps}$ oracle given in Fig. 5 with the same hash oracle $\mathcal {H}'$ for game $\mathbf{G} _2$ in Fig. 4. Consequently, the simulation is perfect until $Y=\textsf {true}$ occurs. Furthermore, $Y=\textsf {true}$ ensures that $\mathcal {B}$ has queried $\mathcal {H}'(\mathbf{m} ^{*})$, which implies that $(\mathbf{m} ^{*}, K') \in Q_{\mathcal {H}'}$ for some $K' \in \mathcal {K}$ where the list $Q_{\mathcal {H}'}$ is maintained by the adversary $\mathcal {A}$ simulating $G_3$ for $\mathcal {B}$. In this case, we have $\textsf {PKE}_1.\textsf {Enc}(\textsf {param},\textsf {pk}, \mathbf{m} ^{*};\mathbf{r} ^*) \longrightarrow \textsf {CT}^{*}$ and hence $\mathcal {A}$ returns $\mathbf{m} ^{*}$. Thus, $\Pr [Y=\textsf {true}] = \textsf {Adv}_{\textsf {PKE}_1}^{\textsf {OW-VA}} (\mathcal {A})$. Combining all the probabilities, we get $\textsf {Adv}_{\textsf {KEM}}^{\textsf {IND-CCA}}(\mathcal {B}) = |\Pr [E_0]-1/2| =|\Pr [E_1]-1/2| =|\Pr [E_2]-1/2| = |\Pr [E_2]- \Pr [E_3]| \le \Pr [Y=\text {true}] = \textsf {Adv}_{\textsf {PKE}_1}^\textsf {OW-VA}(\mathcal {A})$ which completes our proof.    $\square$

Fig. 6.

Scheme $\textsf {PKE}_2=(\textsf {Setup},\textsf {KeyGen},\textsf {Enc},\textsf {Dec})$

Theorem 3

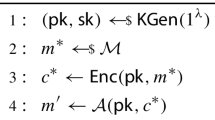
If the public key encryption scheme $\mathsf {PKE}_2$ = ($\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Dec}$) described in Fig. 6 is IND-CPA secure (Definition 5, Sect. 4.1), then the public key encryption scheme $\mathsf {PKE}_1=(\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Dec})$ as described in Fig. 1 provides OW-PCVA security (Definition 6, Sect. 4.1) when the hash function $\mathcal {G}$ is modeled as a random oracle.

The OW-PCVA security for a PKE scheme trivially implies the OW-VA security of the PKE scheme considering zero queries to the $\textsf {PCO} (\cdot ,\cdot )$ oracle. Therefore, the following corollary is an immediate consequence of Theorem 3.

Corollary 1

If the public key encryption scheme $\mathsf {PKE}_2$ =($\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Dec}$) described in Fig. 6 is IND-CPA secure (Definition 5, Sect. 4.1), then the public key encryption scheme $\mathsf {PKE}_1=(\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Dec})$ as described in Fig. 1 provides OW-VA security (Definition 6, Sect. 4.1) when the hash function $\mathcal {G}$ is modeled as a random oracle.

Theorem 4

If the decisional SD problem (Definition 1, Sect. 2.1) is hard, the public key matrix H (derived from the public key pk which is generated by running $\mathsf {PKE}_2.\mathsf {KeyGen}(\mathsf {param})$ where $\mathsf {param} \longleftarrow \mathsf {PKE}_2.\mathsf {Setup}(1^{\lambda })$) is indistinguishable (Definition 2, Sect. 2.1) and the hash function $\mathcal {G}$ is modeled as a random oracle, then the public key encryption scheme $\mathsf {PKE}_2=(\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Dec})$ presented in Fig. 6 is IND-CPA secure (Definition 5, Sect. 4.1).

Due to limited space, proofs of Theorems 3 and 4 will appear in the full version of the paper.

Remark 1

The KEM protocol also can be shown to provide security in quantum random oracle model following the work in [15] and thus we can get Theorem 5.

Theorem 5

Assuming the hardness of decisional SD problem (Definition 1, Sect. 2.1) and indistinguishability of the public key matrix H (derived from the public key pk by running $\mathsf {KEM}.\mathsf {KeyGen}(\mathsf {param})$ where $\mathsf {param}\longleftarrow \mathsf {KEM}.\mathsf {Setup}(1^{\lambda })$, $\lambda$ being the security parameter), our $\mathsf {KEM}=(\mathsf {Setup},\mathsf {KeyGen},\mathsf {Encaps}, \mathsf {Decaps})$ described in Sect. 3 provides IND-CCA security (Definition 7, Sect. 4.1) when the hash functions $\mathcal {G},\mathcal {H}$ and $\mathcal {H}'$ are modeled as quantum random oracles.

Note that, proof of Theorem 5 follows from Theorems 4, 6 and 7 along with the fact that IND-CPA security implies OW-CPA security.

Theorem 6

If the public key encryption scheme $\mathsf {PKE}_2$ = ($\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Dec}$) described in Fig. 6 is OW-CPA secure (Definition 6, Sect. 4.1), then the public key encryption scheme $\mathsf {PKE}_1=(\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Dec})$ as described in Fig. 1 provides OW-PCA security (Definition 6, Sect. 4.1) when the hash function $\mathcal {G}$ is modeled as a quantum random oracle.

Theorem 7

If the public key encryption scheme $\mathsf {PKE}_1= (\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Enc}, \mathsf {Dec})$ described in Fig. 1 is OW-PCA secure (Definition 6, Sect. 4.1) and there exist cryptographically secure hash functions, then the key encapsulation mechanism $\mathsf {KEM}=(\mathsf {Setup}, \mathsf {KeyGen}, \mathsf {Encaps}, \mathsf {Decaps})$ as described in Sect. 3 achieves IND-CCA security (Definition 7, Sect. 4.1) when the hash functions $\mathcal {H}$ and $\mathcal {H}'$ are modeled as quantum random oracles.

5 Conclusion

In this work, we give a proposal to design an IND-CCA secure key encapsulation mechanism based on Generalized Srivastava codes. In terms of storage, our work seems well as compared to some other code-based KEM protocols as shown in Table 1. The scheme instantiated with Generalized Srivastava code does not involve any correctness error like some lattice-based schemes which allows achieving a simpler and tighter security bound for the IND-CCA security. In the upcoming days, it would be desirable to devise more efficient and secure constructions using suitable error-correcting codes.