Keywords

1 Introduction

Many important applied problems of decision making can be stated as problems of searching the global minimum of a multidimensional multiextremal function subject to complicated constraints [1, 6, 13, 22, 28, 33, 38]. The property of multiextremality generates significant complexity of these problems because analytical methods are not almost applicable to solve them and numerical algorithms in general case require essential computational expenditures. This feature is explained by the fact that the global minimizer is an integral characteristic of the objective function, i.e., in order to confirm that a point is the global minimizer, it is necessary to compare the objective function value at this point with function values at all points in the region of the search. As a consequence, the global optimization method is obliged to build in the search domain a grid of trial points (the term trial means the evaluation of objective function value at a point). Such the grids can be simple enough, for example, regular rectangular or random Monte-Carlo ones [39], but efficient methods build non-uniform grids which adapt to the behavior of the objective function placing trials densely in subregions with low function values and rarely in subdomains where the function has high values. For essentially multiextremal functions like Lipschitzian ones the number of grid nodes grows exponentially when increasing the problem dimension. Just this circumstance explains the high complexity of global optimization problems.

As the main approaches to designing efficient and theoretically substantiated methods one can consider the paradigm of component methods and the idea of reducing the dimensionality of optimization problems.

The component methods [4, 21, 23, 27, 28, 30] partition the search region into several subdomains and introduce a criterion that evaluates numerically each subdomain from the point of view of its efficiency for search continuation and after that a new iteration is executed in the subdomain with the best criterion value. The methods of this class differ in the strategies of partitioning and criteria of efficiency of subdomains.

The algorithms based on the idea of dimensionality reduction can be divided into two groups. The methods of the first group replace the multidimensional problem with an equivalent univariate one applying a continuous mapping of the multidimensional search domain onto a subregion of the real axis by means of the Peano space-filling curves, or evolvents [3, 14, 24,25,26, 32, 36].

The second group of optimization algorithms is based on the known scheme of nested optimization [4]. According to this approach the initial multidimensional problems is reduced to a family one-dimensional subproblems connected recursively [5, 9,10,11,12, 17, 18, 29, 34, 36]. In the paper [9], a generalization of the classical scheme called adaptive nested optimization has been proposed and the research [18] has demonstrated that this version of the nested scheme in combination with information-statistic algorithm of univariate global search has the high efficiency being better significantly than the classical prototype and one of the most qualitative popular method DIRECT [21].

For solving relatively simple problems of global optimization characterized by a small number of local optima with regions of attraction being large enough, a so called multi-start approach [2, 5, 35] can be used when a local optimization method is launched from several starting points. This approach is clear geometrically, but, unfortunately, the methods of this type are semiheuristical and are not efficient for complicated multiextremal problems.

Another challenge in global optimization refers to problems with complicated constraints. The traditional way to solve such the problems consists in transforming the constrained problem to an equivalent problem either without constraints or, as a rule, in a simple region like a box.

There exist two main approaches in this way. The first transformation is classical in optimization and is connected with the penalty function method [7, 20, 37]. This method is sufficiently universal but it requires a tuning of its parameters (penalty constant, equalizing coefficients for constraints). In many cases this tuning is not simple and a wrong choice of parameters does not allow obtaining the correct solution of the constrained problem. For example, if the penalty constant is small the solution of the unconstrained problem can differ significantly from the solution of the initial problem. At the same time, if the penalty constant is too large then it worsens substantially the properties of the objective function in the transformed problem, in particular, the Lipschitz constant can increase essentially.

The second approach is based on building the so called index function [36] that contains no tuning parameters but generates, in general case, a discontinuous objective function in the transformed problem and requires, as a consequence, application of special global optimization techniques oriented at this class of functions.

When solving the transformed problem in the framework of both the approaches (penalty and index methods), the optimization algorithm places trial points not only in the feasible domain of the constrained problem but out of it as well.

In this paper we consider the approach which allows one to avoid performing trials at non-feasible points and does not include any tuning parameters. The core of this approach is the nested optimization scheme applied to multiextremal optimization in domains with special type of constraints, namely, in domains with computable boundaries. These domains can be very complicated, in particular, non-convex, non-simply connected, and even disconnected domains. An algorithm for Lipschitzian optimization on the base of classical nested scheme for domains with computable boundaries has been described in the paper [16]. In the present paper we propose its generalization that applies the more efficient recursive technique of global search in the framework of the adaptive nested optimization [9]. To demonstrate the advantages of the proposed constraint satisfaction approach the results of comparison with the penalty function method are given on two known test classes that are classical for estimating the efficiency of global optimization algorithms.

The rest of the paper is organized as follows. Section 2 contains statement of the multiextremal constrained problem to be studied and description of a generalization of the adaptive nested scheme for the case of computable boundaries. Section 3 is devoted to computational testing the proposed technique in comparison with the classical nested scheme and the method of penalty functions. Section 4 concludes the paper.

2 Nested Optimization and Computable Boundaries

The optimization problem under consideration is formulated in the following way. It is required to find the least value (global minimum) and its coordinates (global minimizer) of an objective function f(x) in a domain D of the N-dimensional Euclidean space \(\mathbb {R}^N\). This problem will be denoted as

$$\begin{aligned} f(x) \rightarrow \min , \; x = (x_1, \dots , x_N) \in D \subseteq \mathbb {R}^N. \end{aligned}$$
(1)

The feasible domain D is supposed to be given by constraints-inequalities

$$\begin{aligned} D = \{ x \in X : h_s(x) \le 0, \, 1 \le s \le q \}, \end{aligned}$$
(2)

where the region X is determined by simple coordinate constraints as

$$\begin{aligned} X = \{ x \in \mathbb {R}^N : a_j \le x \le b_j, \, 1 \le j \le N \}. \end{aligned}$$
(3)

The objective function f(x) and constraints \(h_s(x)\), \(1 \le s \le q\), are supposed to satisfy in the domain X the Lipschitz condition

$$\begin{aligned} | h_s(x') - h_s(x'') | \le L_s\Vert x' - x''\Vert , \; x', x'' \in X, \; 1 \le s \le q + 1, \end{aligned}$$
(4)

where the function \(h_{q+1}(x) = f(x)\), \(L_s > 0\) is a finite value called the Lipschitz constant of the function \(h_s(x)\), \(1 \le s \le q+1\), and \(\Vert \cdot \Vert \) denotes the Euclidean norm in \(\mathbb {R}^N\). In general case, the objective function and constraints of the problem  (1)–(2) are multiextremal and non-smooth.

If the problem (1) does not contain constraints (2) (\(q = 0\)), i.e., \(D = X\), for solving such the problem the known nested scheme of dimensionality reduction [4, 36] can be applied. For example, it can be done if the constrained problem (1) has been transformed to the unconstrained one in the framework of the penalty function method [7, 20, 37]. According to this method, instead of the problem (1)–(2), the problem

$$\begin{aligned} F(x) \rightarrow \min , \; x \in X \subseteq \mathbb {R}^N, \end{aligned}$$
(5)

is considered with the “penalized” objective function

$$\begin{aligned} F(x) = f(x) + P H(x), \end{aligned}$$
(6)

where \(P > 0\) is the penalty constant and H(x) is the penalty function such that \(H(x) = 0\), if \(x \in D\), and \(H(x) > 0\), if \(x \notin D\). If to choose the penalty function as

$$\begin{aligned} H(x) = \max \{ 0, h_1(x), \dots , h_q(x) \}, \end{aligned}$$
(7)

then F(x) meets the Lipschitz condition under requirements (4).

In its original classical form the nested optimization scheme was oriented at unconstrained optimization, or more detailed, at solving problems (1) when constraints of the type (2) are absent, i.e., \(D = X\). In this situation there takes place [4] the relation

$$\begin{aligned} \min _{x \in X} f(x) = \min _{x_1 \in X_1} \min _{x_2 \in X_2} \cdots \min _{x_N \in X_N} f(x_1, \dots , x_N). \end{aligned}$$
(8)

where \(X_i\) is a line segment \([ a_i, b_i ]\), \(1 \le i \le N\).

This approach can be generalized (see, for example, [16]) to the case with continuous constraints (2) that allows one to present (8) for the domain D in the form

$$\begin{aligned} \min _{x \in D} f(x) = \min _{x_1 \in \varLambda _1} \min _{x_2 \in \varLambda _2(\xi _1)} \cdots \min _{x_N \in \varLambda _N(\xi _{N-1})} f(x_1, \dots , x_N), \end{aligned}$$
(9)

where \(\xi _s =(x_1, \dots , x_s)\), \(1 \le s \le N\), and the region \(\varLambda _s(\xi _{s-1})\) is the projection of the set

$$\begin{aligned} \varOmega _s(\xi _s) = \{ \xi _s \in \mathbb {R}^s : (\xi _s, x_{s+1}, \dots , x_N ) \in D\}, \end{aligned}$$
(10)

onto the coordinate axis \(x_s\).

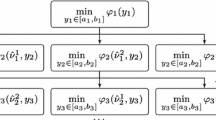
Now the nested optimization scheme applied for the case (9) can be described as follows.

Let us introduce a family of reduced function \(f^s(\xi _s)\), \(1 \le s \le N\), in the following manner:

$$\begin{aligned} f^{s-1}(\xi _{s-1}) = \min _{x_s \in \varLambda _s(\xi _{s-1})} f^s(\xi ), \; 2 \le s \le N, \end{aligned}$$
(11)
$$\begin{aligned} f^N(x) \equiv f(x). \end{aligned}$$
(12)

Then, the solving the multidimensional problem (1) can be substituted with searching for the global minimum of the univariate function \(f^1(x_1)\) in the domain \(\varLambda _1\), as according to (9)–(11)

$$\begin{aligned} \min _{x \in D} f(x) = \min _{x_1 \in \varLambda _1} f^1(x_1). \end{aligned}$$
(13)

But any evaluation of the function \(f^1(x_1)\) at a chosen point \(x_1\) requires solving the problem

$$\begin{aligned} f^2(x_1, x_2) \rightarrow \min , \; x_2 \in \varLambda _2(x_1), \end{aligned}$$
(14)

which is one-dimensional because the coordinate \(x_1\) is fixed.

The necessity of evaluation of the function \(f^2(x_1, x_2)\) generates solving the problem of minimization of the function \(f^3(\xi _2, x_3)\) in the domain \(\varLambda _3(\xi _2)\), and this problem is univariate as well, because the vector \(\xi _2\) is fixed.

This recursive procedure is in progress until we reach the level N where it is required to solve problem

$$\begin{aligned} f^N(\xi _{N-1}, x_N) \rightarrow \min , \; x_N \in \varLambda _N(\xi _{N-1}) \end{aligned}$$
(15)

This problem is univariate too because the vector \(\xi _{N-1}\) has been given at previous levels and is fixed for the problem (15). Moreover, in this problem an evaluation of the objective function consists in computation of the value \(f (\xi _{N-1}, x_N)\) of the function f(x) from the original problem (1).

The approach of reducing the multidimensional problem (1) to solving the family of one-dimensional subproblems

$$\begin{aligned} f^s(\xi _{s-1}, x_s) \rightarrow \min , \; x_s \in \varLambda _s(\xi _{s-1}), \; 1 \le s \le N, \end{aligned}$$
(16)

in accordance of the above procedure is called the nested scheme of dimensionality reduction or the nested scheme of optimization.

The structure of domains \(\varLambda _s(\xi _{s-1})\) depends on the properties and complexity of the constraints \(h_s(x)\) from (2). For example, if all the functions \(h_s(x)\) are convex, then the domain is a convex set, and any projection \(\varLambda _s(\xi _{s-1})\) is a single interval of the axis \(x_s\). In general case, when the constraints \(h_s(x)\) are continuous, the domain \(\varLambda _s(\xi _{s-1})\) is a union of closed intervals, i.e.,

$$\begin{aligned} \varLambda _s(\xi _{s-1}) = \cup _{m=1}^{M} [a_s^m, b_s^m], \; 1 \le s \le N, \end{aligned}$$
(17)

where the end points \(a_s^m\), \(b_s^m\) of intervals and even the number of interval M can depend on the vector \(\xi _{s-1}\).

If all the end points \(a_s^m\), \(b_s^m\) and all numbers M can be given explicitly (for example, as analytical expressions or by means of a computational procedure) in all the subtasks (16) then the domain D is called as the domain with computable boundaries. These domains can have very complicated structure, in particular, can be non-convex and even disconnected.

As an example, let us consider a 2-dimensional domain (2) determined by the following constraints:

$$\begin{aligned} h_1(x_1, x_2)&= 1 - \frac{(x_2 - 0.5 (u_1(x_1) + u_2(x_1)))^2}{0.25 (u_1(x_1) - u_2(x_1))^2}, \end{aligned}$$
(18)
$$\begin{aligned} h_2(x_1, x_2)&= 0.04 - (x_1 - 0.6)^2 - (x_2 - 0.59)^2, \end{aligned}$$
(19)
$$\begin{aligned} h_3(x_1, x_2)&= x_2 - u_3(x_1), \end{aligned}$$
(20)

where

$$\begin{aligned} u_1(x_1)&= -0.05 \cos (40 x_1) - 0.1 x_1 + 0.15, \\ u_2(x_1)&= -0.05 \cos (45 x_1) + 0.1 x_1 - 0.22, \\ u_3(x_1)&= 0.1 \sin (50x_1) + 0.5x_1 + 0.6, \end{aligned}$$

and coordinate constraints (3), \(0 \le x_1, x_2 \le 1\). For this domain

$$\begin{aligned} \varLambda _1 = [0, 1], \end{aligned}$$
(21)
$$\begin{aligned} \varLambda _2(x_1) = {\left\{ \begin{array}{ll} \cup _{m=1}^3 \, [a_2^m, \; b_2^m], &{} |x_1 - 0.6| \le 0.2, \\ \cup _{m=1}^2 \, [\alpha _2^m, \; \beta _2^m], &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$
(22)

where

$$\begin{aligned} \begin{aligned} a_2^1&= \alpha _2^1 = 0, \\ a_2^2&= \alpha _2^2 = u_2(x_1), \\ a_2^3&= 0.59 + \sqrt{0.04 - (x_1 - 0.6)^2}, \end{aligned}\qquad \begin{aligned} b_2^1&= \beta _2^1 = u_1(x_1), \\ b_2^2&= 0.59 - \sqrt{0.04 - (x_1 - 0.6)^2}, \\ b_2^3&= \beta _2^2 = \min \{ u_3(x_1), 1 \}. \end{aligned} \end{aligned}$$

The domain D corresponding to these constraints is shown in Fig. 1, where inaccessible part is dark. The domain consists of two disconnected parts and inside the upper part there is a removed circle. Moreover, the boundaries have complicated “oscillating” structure.

The nested optimization scheme in combination with univariate global search methods providing optimization on several intervals like characteristical algorithms [19] allows one to execute trials in the feasible domain only and not to spend resources to evaluate the objective function at inaccessible points as opposed to penalty function or index methods.

In present paper we propose to apply the adaptive nested scheme to solving problems with computable boundaries in combination with information-statistical univariate algorithm of global search [36] adapted to optimization in the domain of type (17). In the adaptive scheme all one-dimensional subproblems (16) are considered in dynamics simultaneously and to each of them a numerical value called the characteristic of the subproblem is assigned. The characteristic depends on the domain (17) and values of the subproblem objective function. The iteration of the multidimensional search consists in the choice of the subproblem with the best characteristic and executing a new trial in it. Such organization allows one to take into account the full information about the multidimensional problem obtained in the course of optimization and to focus on the most perspective subproblems. The effectiveness of the new proposed adaptive nested technique is demonstrated in the next section on the base of representative experiment on test classes of multiextremal problems in domains with computable boundaries of complicated structure.

3 Numerical Experiments

The efficiency estimation of different approaches to solving constrained global optimization problems was executed experimentally on two test classes of multiextremal functions which are often used for testing the global search algorithms [9, 10, 18, 32, 36]. The first class GLOB2 included 2-dimensional functions

$$\begin{aligned} f(x_1, x_2) = - \Bigg \{ \bigg ( \sum _{i=1}^7 \sum _{j=1}^7 u_{ij}(x_1, x_2) \bigg )^2 + \bigg ( \sum _{i=1}^7 \sum _{j=1}^7 v_{ij}(x_1, x_2) \bigg )^2 \Bigg \} ^ \frac{1}{2} \end{aligned}$$
(23)

where

$$\begin{aligned}&u_{ij}(x_1, x_2) = \alpha _{ij} \sin (\pi i x_1) \sin (\pi j x_2) + \beta _{ij} \cos (\pi i x_2) \cos (\pi j x_2), \\&v_{ij}(x_1, x_2) = \gamma _{ij} \sin (\pi i x_1) \sin (\pi j x_2) - \delta _{ij} \cos (\pi i x_2) \cos (\pi j x_2), \end{aligned}$$

and the parameters \(a_{ij}\), \(\beta _{ij}\), \(\gamma _{ij}\), \(\delta _{ij}\), \(1 \le i, j \le 7\), are the independent random numbers, distributed uniformly over the interval \([-1, 1]\). The functions (23) were considered in the box \(X = \{ x \in \mathbb {R}^2 : 0 \le x_1, x_2 \le 1 \}\).

The multiextremal class GKLS [8] was chosen as the second class of objective functions in the problem (1). The functions were taken from the hard GKLS subclass of the dimension 3 and for them \(X = \{ x \in \mathbb {R}^3 : -1 \le x_1, x_2, x_3 \le 1 \}\).

For building constraints (2) for both GLOB2 and GKLS the idea close to making constraints in the EMMENTAL GKLS [31] was used. Namely, in the domain X several random points were generated which are considered as centers of spheres with random radii. The hyperparallelepiped X without internal parts of the generated spheres was considered as the feasible domain D. Such way allows one to form complicated domains with computable boundaries because the information about centers and radii of spheres enables to build explicitly the regions (17) in univariate subproblems of the nested scheme.

Three methods were compared in experiments:

  • CNS-CB Classical nested scheme with computable boundaries;

  • ANS-CB Adaptive nested scheme with computable boundaries;

  • ANS-PF Adaptive nested scheme combined with penalty function method.

In all three methods for solving univariate problems (16) the information-statistical Global Search Algorithm (GSA) was used.

An example of comparative behavior of the methods taking computable boundaries into account (ANS-CB) and applying penalty function approach (5), (6) (ANS-PF) is presented in Fig. 1 for a function from class GLOB2 and constraints (18)–(20). The pictures contain level curves of the function, points of trials, and the infeasible part \(X \setminus D\) is dark.

Fig. 1.
figure 1

Distribution of trials by ANS-CB (the left panel) and by ANS-PF (the right panel).

Full size image

Comparison of the algorithms on the test classes was carried out according to the method of operational characteristics introduced in [15]. In the framework of this method a set of test problems is taken, the problems of the set are solved by an optimization algorithm with different parameters and two criteria are used for evaluating the algorithm’s quality: average number K of trials executed (search spending) and number \( {\Delta }\) of problems solved successfully (search reliability). For launches of the algorithm with different parameters we obtain several pairs \((\tilde{K}, {\tilde{\Delta }})\). The set of these pairs on the plane \((K, {\Delta })\) is called the operational characteristic of the algorithm.

Figure 2 shows the operational characteristics (from left to right) of ANS-CB, CNS-CB and 3 operational characteristics of ANS-PF for different values of penalty factor P from (6) on the class (23) with 100 test problems. The axis K is presented in the logarithmic scale.

Fig. 2.
figure 2

Operational characteristics on 2-dimensional class GLOB2

Full size image

As it follows from the results presented in Fig. 2 the adaptive and classical schemes using the computable boundaries approach excel significantly the version with the penalty function method. With the value of penalty constant \(P = 100\) the algorithm with transformation to the penalized function (6) did not provide solving all test problems and spent considerably more trials.

Fig. 3.
figure 3

Operational characteristics on 3-dimensional class GKLS

Full size image

As the functions of the test class are very complicated, attempts to enlarge the penalty constant have demonstrated one of the drawbacks of the penalty function method for Lipschitzian optimization problems, namely, such the enlargement leads to increasing the Lipschitz constant for the function (6) and, as a consequence, to the growth of the trial number. Moreover, the adaptive nested scheme is better than its classical prototype CNS-CB.

The experiment with 100 3-dimensional functions from the class GKLS has shown even more advantage of the computable boundaries approach over the penalty function technique. Figure 3 presents the operational characteristic for ANS-CB (the left plot) and the operational characteristic for ANS-PF (the right plot) with the penalty constant \(P = 100\).

The algorithm ANS-CB has solved all the test problems for about 12000 objective function evaluations and its rival ANS-PF having spent 30000 trials could not find all the global minima.

4 Conclusion

In the paper the multidimensional global optimization problems with non-linear and multiextremal objective functions and constraints generating domains with computable boundaries have been considered. The domains of this type can have a complicated structure, in particular, can be non-convex and disconnected. For solving the problems under consideration a new global optimization algorithm based on the adaptive nested scheme has been proposed. The algorithm reduces the initial multidimensional problem to a family of univariate subproblems in which the domains of one-dimensional optimization can be presented as systems of closed intervals with explicitly given boundary points. For solving univariate subproblems a modification of the information-statistic algorithm of global search is used which execute iteration within the feasible intervals only. It provides evaluation of multidimensional objective function in the accessible domain only and distinguishes the proposed method from known approaches to solving global constrained optimization such as penalty function and index methods which can carry out iterations at infeasible points.

The more economical behavior of the new method has been confirmed in the experiment where the proposed adaptive nested algorithm was compared with the classical nested scheme and adaptive scheme combined with penalty function method. The results of the experiment have demonstrated the significant advantage of the suggested adaptive scheme over its opponents.

As continuation of the research it is interesting to evaluate the efficiency of the new adaptive scheme via comparison with the global optimization methods of different nature, for example, with some component methods of DIRECT-type. Moreover, it would be perspective to develop a parallel version of the algorithm and to study its effectiveness of parallelizing on various computational architectures.