Abstract
In his seminal work, Robert McNaughton (see [1] and [7]) developed a model of infinite games played on finite graphs. This paper presents a new model of infinite games played on finite graphs using the Grossone paradigm. The new Grossone model provides certain advantages such as allowing for draws, which are common in board games, and a more accurate and decisive method for determining the winner when a game is played to infinite duration.
This research was supported by the following grant: PSC-CUNY Research Award: TRADA-47-445.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
This paper applies the theory of grossone (see [10, 13, 15,16,17,18,19,20]) to investigate games of infinite duration with finitely many configurations. The games investigated occur on finite graphs and are those with perfect information. That is, and typically, a perfect information game is played on a board where a player moves pieces subject to a given set of rules and each player knows everything important to the game that has previously occurred.
We are all very familiar with finite board games such as tic-tac-toe, chess, checkers, and go, to provide four examples. These are games of strategy, once the specific positions are known. Of course we must exclude all games of chance and card games where players do not reveal their hands, since these are not games with perfect information. A board game will have a configuration (a state or a state of play) and it must be made precise to include all information about any situation in the game. The configuration describes the current state or standing of the game. Of significant importance, the configuration will dictate which player is to move next. Hence, in board games, the play moves go from one player to the other. A board game such as tic-tac-toe has only a very small number of configurations. Here we can easily compute (via computer search techniques) all the configurations and hence this game is not very interesting. However, and on the other hand, games of checkers, chess and go have an extremely large number of configurations and command a lot of attention from computer scientists and mathematicians.
Finite board games that are played to infinity may sound like science or mathematical fiction. Indeed, following the traditional Turing machine model, a computation is complete when it halts and produces some type of result. However when a game is played to infinity, it is implied that the game continues for an indefinite period (play continues without bound). For instance, a typical application that can be considered an infinite game is the operating system of a computer (a multiprogramming machine). The operating system has to manage multiple processes (or users on a server) without termination. When one process (or user) is satisfied, there are others waiting for system resources to be processed. Hence process-oriented theory is an application of infinite games to computer science (see [1]).
2 The Infinite Unit Axiom and Grossone
Applying the following new paradigm facilitates us to better understand the notion of infinite games on graphs. The problem of better understanding the notion of computing with infinity was approached beginning in 2003 by Yaroslav Sergeyev (see [15,16,17,18]). In these works, a new unit of measure on the set of natural numbers, \(\mathbb {N}\) is defined. Thus, the following axiom evolves the idea of the infinite unit.
Axiom 1
Infinite Unit Axiom. The number of elements in the set \(\mathbb {N}\) of natural numbers is equal to the infinite unit denoted as
 and called grossone.
and called grossone.
The following properties are part of the Infinite Unit Axiom:
-
1.
Infinity: For any finite natural number n,
 .
. -
2.
Identity: The following relationships hold and are extended from the usual identity relationships of the natural numbers:

-
3.
Divisibility: For any finite natural number n, the numbers

are defined as the number of elements in the \(n^{th}\) part of \(\mathbb {N}\)Footnote 1
The divisibility property will be of significant importance in determining a winner of an infinite game. Indeed, determining a winner will result by counting the number of elements in a sequence. It is important to mention, with the introduction of the Infinite Unit Axiom and grossone,  , we list the natural numbers as
, we list the natural numbers as

and as a consequence of this new paradigm, we have the following important theorem.
Theorem 1
The number of elements of any infinite sequence is less or equal to  .
.
Proof
Recently there has been a large amount of research activity on the logical theory and applications of grossone. To name a few, see [2,3,4,5,6, 8, 10,11,12,13,14, 20, 21]. This next section will describe a new application of grossone to infinite games.
3 Infinite Games
Formally, an infinite graph game is defined on a finite bipartite directed graph whose set, Q, of vertices are partitioned into two sets: R, the set of vertices from which player Red moves, and B, the set of vertices from which player Blue moves. The game has a place marker which is moved from vertex to vertex along the directed edges. The place marker signifies the progress of the play. When the marker is on a vertex of R, it is Red’s move to move to a vertex in B. When the marker is on a vertex of B, it is Blue’s turn to move to a vertex of set R and the play continues in this fashion.
Definition 1
An infinite game, G, is a 6-tuple
where,
-
1.
Q is the finite set of positions (vertices).
-
2.
B and R are subsets of Q, such that \(B\cup R =Q\) and \(B \cap R = \emptyset \)
-
3.
E is a set of directed edges between B and R such that:
-
(a)
for each \(b \in B\) there exists \(r \in R\) such that \((b,r) \in E\).
-
(b)
for each \(r \in R\) there exists \(b \in B\) such that \((r,b) \in E\).
-
(a)
-
4.
W(B) is called the winning set for Blue.
-
5.
W(R) is called the winning set for Red.
-
6.
\(W(B)\cap W(R)=\emptyset \).
At this time it should be noted that the winning sets for each player are not limited to vertices of the player’s color.
Definition 2
A play that begins from position q is a completeFootnote 2 infinite sequence  such that \(q=q_1\) and \((q_i , q_{i+1}) \in E, \; \forall i \in \mathbb {N}\), E is the edge relation.
such that \(q=q_1\) and \((q_i , q_{i+1}) \in E, \; \forall i \in \mathbb {N}\), E is the edge relation.
Hence a play is a sequence of states of the game. That is,
To determine how a player can win, let p be a play and consider the set of all vertices that occur infinitely often. We now have the following definition.
Definition 3
In(p) is the set of vertices, in play p, that occur infinitely often, called the infinity set of p.
We now have the following cases to determine a win:
-
1.
\(W(B) \subset In(p)\) and \(W(R) \not \subset In(p)\), then Blue wins.
-
2.
\(W(B) \not \subset In(p)\) and \(W(R) \subset In(p)\), then Red wins.
-
3.
\(W(B) \not \subset In(p)\) and \(W(R) \not \subset In(p)\), then Draw.
-
4.
\(W(B) \subset In(p)\) and \(W(R) \subset In(p)\), then the frequencies of occurrence of the elements in each set must be considered; the player with the higher frequency wins.
Cases 1 and 2 above are the result that whatever winning set a player chooses, all vertices must occur infinitely often for a player to have a chance of winning (this concept is consistent with the ideology presented in [19]). All vertices must occur infinitely often also prevents a player from choosing too many vertices for their winning setFootnote 3. Next we look at a simple example to analyze the situation when a player chooses the empty set.
Example 1
Suppose Blue chooses \(\emptyset \) as their winning set (this is consistent with the premise that no choice is also a choice). That is, \(W(B) = \emptyset \). The reason for Blue’s choice is clear. \(\emptyset \subset In(p)\), hence Blue is hoping that \(W(R) \not \subset In(p)\) and Blue wins the game (the same can be true for Red, if Red chooses the empty set). Of course the situation can arise if both players choose \(\emptyset \). In that case, the game will result in a draw. However, to show this we first need to define more machinery.
It is necessary to define a frequency function to count the number of occurrences of a given vertex in a play sequence. This gives rise to the next two definitions.
Definition 4
Given \(Q=\{q_1,q_2,...,q_n\}\) is the finite set of states and let D be a subset of Q. Let p be an infinite sequence of states, from a play, define a new sequence by the function
where,
Definition 5
Define the frequency function, \(freq_p\), as

These definitions are in general, however here they are applied to the winning sets for Blue and Red, respectively W(B) and W(R).
With the previous definitions, if both winning sets are subsets of the infinity set (the elements of both player’s winning sets occur infinitely often) a winner can be determined. If the frequency of the elements in W(B) is greater than the frequency of the elements in W(R), then Blue is the winner. If the frequency of the elements in W(R) is greater than the frequency of the elements in W(B), then Red is the winner. If the frequencies are equal, then a draw results. This is a key advancement as a result of the grossone theory. As an immediate consequence from the above definitions, the following propositions are true.
Proposition 1
For any sequence p, \(freq_p(\emptyset ) = 0\).
Proof
\(p(i) \not \in \emptyset \;\forall i \in \mathbb {N}\). Hence \(\psi _{\emptyset ,p}(i) = 0 \;\forall i \in \mathbb {N}\) and \(freq_p(\emptyset )=0\).
Proposition 2
If both players choose the empty set as their winning set, then the game is a draw.
Proof
By Proposition 1, \(freq_p(W(B)) = freq_p(W(R)) =freq_p(\emptyset )=0\).
4 Examples and Results
Example 2
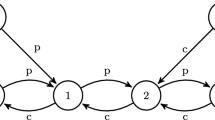
Referring to the game in Fig. 1. Assume that \(W(B)=\{b1\}\) and \(W(R) =\{r1\}\). Then Blue is always the winner, no matter where the game begins. If \(W(B)=\{b1\}\) and if \(W(R)=\{r1,r2\}\), then Blue’s winning strategy would be to move to either r1 or r2 finitely many times and the other infinitely times. Therefore \(W(R) \not \subset In(p)\).
For instance, if the following sequence is played
then \(In(p)=\{b1,r1\}\) and \(W(R)\not \subset In(p)\), however \(W(B) \subset In(p)\), which implies Blue wins the game.
The following theorem and corollaries provide a better understanding of the frequency function.
Theorem 2
For any set A and play p,  .
.
Proof
This follows directly from the properties of  and Theorem 1.
and Theorem 1.
Corollary 1
For any game, the frequency of occurrence of any single vertex is  .
.
Proof
Follows from Theorem 2 and the definition of a game, since there are two players.
Corollary 2
For any game where Q is the set of vertices,  .
.
Proof
Using the premise of a complete sequence, the corollary directly follows from Theorems 1 and 2.
Example 3
Again, referring to Fig. 1, if \(W(B) =\{r1\}\) and \(W(R)=\{r2\}\) (as mentioned previously, a player does not have to choose their color as their winning set) then Blue wins the game. The winning strategy for Blue consists of moving to r2 finitely many times. Actually Blue can move to r2 infinitely many times, however it must be less than  times.
times.
This next example will illustrate this new application of the grossone paradigm to infinite games.
Example 4
Referring to the game in Fig. 1, suppose the play goes as follows:
Here the \(In(p) = \{b1,r1,r2\}\). Hence, the frequency of occurrence for each vertex in the In(p) is:

Using the same winning sets for Red and Blue as in Example 3, namely \(W(B) =\{r1\}\) and \(W(R)=\{r2\}\), Blue wins the game.
Example 5
In Fig. 2, if Blue chooses b4, that is \(W(B)=\{b4\}\), a strategy for Red would be to choose \(\emptyset \). Then from r3, Red can always move to b3 an infinite number of times or move to b4 a finite number of times.
Example 6
Referring again to Fig. 2, if each node is visited once in the 6 node outside cycle, that is via edges (r1, b3), (b3, r3), (r3, b4), (b4, r2), (r2, b1), (b1, r1), then the frequency of each vertex occurrence is  . The sequence that will ensure this is:
. The sequence that will ensure this is:
If player Blue chooses their winning sets \(W(B)=\{b1,b3\}\), then Red can choose \(W(R)=\{r2,r3\}\) and Red has a winning strategy. When Blue lands on vertex b1, Blue must move to r1 to get to b3 (part of Blue’s winning set). The play continues and can follow the outside cycle. However, at some point, Red moves from r2 back to b4 a finite number of times. For instance, a play can follow:
hence

and Red wins the game.
5 Conclusion
This paper has presented a new model of infinite games played on finite graphs by applying the theory of grossone and the Infinite Unit Axiom. In his original work, McNaughton (see [1]) presented and developed a model of infinite games played on finite graphs using traditional methods of dealing with infinity. This paper has extended that work to count the number of times vertices in a board game are visited, although vertices can5 be visited an infinite number of times. Indeed, two players choose their winning sets and the player whose winning set is visited more frequently wins the game. With this new paradigm, as is common in the usual finite duration board games (chess, checkers, go), a draw can result. This was not the case in McNaughton’s original work. Hence a more finer decision process is used in determining the winner or draw.
Notes
- 1.
In [15], Sergeyev formally presents the divisibility axiom as saying for any finite natural number n sets \(\mathbb {N}_{k,n}, \; 1\le k\le n\), being the nth parts of the set \(\mathbb {N}\), have the same number of elements indicated by the numeral
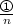 where$$\begin{aligned} \mathbb {N}_{k,n}=\{k,k+n,k+2n,k+3n,...\}, \; 1\le k \le n,\; \bigcup ^n_{k=1}\mathbb {N}_{k,n}=\mathbb {N}. \end{aligned}$$
where$$\begin{aligned} \mathbb {N}_{k,n}=\{k,k+n,k+2n,k+3n,...\}, \; 1\le k \le n,\; \bigcup ^n_{k=1}\mathbb {N}_{k,n}=\mathbb {N}. \end{aligned}$$.
- 2.
Here we use the notion of complete taken from [15], that is the sequence containing
 elements is complete.
elements is complete. - 3.
It is noted here that, as is usual, the \(\subset \) symbol can also imply equality.
References
McNaughton, R.: Infinite games played on finite graphs. Ann. Pure Appl. Logic 65, 149–184 (1993)
Caldarola, F.: The exact measures of the Sierpiński d-dimensional tetrahedron in connection with a Diophantine nonlinear system. Commun. Nonlinear Sci. Numer. Simul. 63, 228–238 (2018)
De Leone, R., Fasano, G., Sergeyev, Ya.D.: Planar methods and grossone for the Conjugate Gradient breakdown in nonlinear programming. Comput. Optim. Appl. 71(1), 73–93 (2018)
De Leone, R.: Nonlinear programming and grossone: quadratic programming and the role of constraint qualifications. Appl. Math. Comput. 318, 290–297 (2018)
D’Alotto, L.: A classification of one-dimensional cellular automata using infinite computations. Appl. Math. Comput. 255, 15–24 (2015)
Fiaschi, L., Cococcioni, M.: Numerical asymptotic results in Game Theory using Sergeyev’s Infinity Computing. Int. J. Unconv. Comput. 14(1), 1–25 (2018)
Khoussainov, B., Nerode, A.: Automata Theory and Its Applications. Birkhauser, Basel (2001)
Iudin, D.I., Sergeyev, Ya.D., Hayakawa, M.: Infinity computations in cellular automaton forest-fire model. Commun. Nonlinear Sci. Numer. Simul. 20(3), 861–870 (2015)
Lolli, G.: Infinitesimals and infinites in the history of mathematics: a brief survey. Appl. Math. Comput. 218(16), 7979–7988 (2012)
Lolli, G.: Metamathematical investigations on the theory of Grossone. Appl. Math. Comput. 255, 3–14 (2015)
Margenstern, M.: Using Grossone to count the number of elements of infinite sets and the connection with bijections. p-Adic Numbers Ultrametric Anal. Appl. 3(3), 196–204 (2011)
Montagna, F., Simi, G., Sorbi, A.: Taking the Pirahá seriously. Commun. Nonlinear Sci. Numer. Simul. 21(1–3), 52–69 (2015)
Rizza, D.: Numerical methods for infinite decision-making processes. Int. J. Unconv. Comput. 14(2), 139–158 (2019)
Rizza, D.: How to make an infinite decision. Bull. Symb. Logic 24(2), 227 (2018)
Sergeyev, Y.D.: Arithmetic of Infinity. Edizioni Orizzonti Meridionali, Cosenza (2003)
Sergeyev, Y.D.: A new applied approach for executing computations with infinite and infinitesimal quantities. Informatica 19(4), 567–596 (2008)
Cococcioni, M., Pappalardo, M., Sergeyev, Y.D.: Lexicographic multiobjective linear programming using grossone methodology: theory and algorithm. Appl. Math. Comput. 318, 298–311 (2018)
Sergeyev, Y.D.: Computations with grossone-based infinities. In: Calude, C.S., Dinneen, M.J. (eds.) UCNC 2015. LNCS, vol. 9252, pp. 89–106. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-21819-9_6
Sergeyev, Ya.D.: The Olympic medals ranks, lexicographic ordering and numerical infinities. Math. Intelligencer 37(2), 4–8 (2015)
Sergeyev, Ya.D.: Numerical infinities and infinitesimals: methodology, applications, and repercussions on two Hilbert problems. EMS Surv. Math. Sci. 4(2), 219–320 (2017)
Sergeyev, Ya.D., Garro, A.: Observability of Turing Machines: a refinement of the theory of computation. Informatica 21(3), 425–454 (2010)
Zhigljavsky, A.: Computing sums of conditionally convergent and divergent series using the concept of grossone. Appl. Math. Comput. 218, 8064–8076 (2012)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
D’Alotto, L. (2020). Infinite Games on Finite Graphs Using Grossone. In: Sergeyev, Y., Kvasov, D. (eds) Numerical Computations: Theory and Algorithms. NUMTA 2019. Lecture Notes in Computer Science(), vol 11974. Springer, Cham. https://doi.org/10.1007/978-3-030-40616-5_29
Download citation
DOI: https://doi.org/10.1007/978-3-030-40616-5_29
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-40615-8
Online ISBN: 978-3-030-40616-5
eBook Packages: Computer ScienceComputer Science (R0)




 .
.



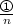 where
where elements is complete.
elements is complete.