Abstract
This paper studies information changes in default justification logic with argumentation semantics. We introduce dynamic operators that combine belief revision and default theory tools to define both prioritized and non-prioritized operations of contraction, expansion and revision for justification logic-based default theories. This combination enriches both default logics and belief revision techniques. We argue that the kind of attack called “undermining” amounts to those operations that contract a knowledge base by an attacked formula.
I wish to thank Allard Tamminga, Barteld Kooi and Rineke Verbrugge for their useful advice on this project. My research is supported by Ammodo KNAW award Rational Dynamics and Reasoning.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
This paper investigates the dynamics of default theories with justification logic formulas. Our logic has been presented in [28] as a theory of structured arguments where justification formulas of the form t : F are interpreted as arguments that can defeat other formulas by means of undercut or rebuttal. Technically, the workings of undercut and rebuttal rely on defining default theories with default rules based on justification logic formulas. In such rules, justification terms codify defeasible inferences in their structure. In this paper, we will take a step further to add reasoning about changes to default theories.
The existing work about dynamics in formal argumentation [9, 11,12,13, 33] almost entirely focuses on abstract argumentation frameworks in the style of [14]. The literature on the dynamics of structured argumentation is limited to the DeLP framework [2], where the dynamics is understood as adding or removing strict and defeasible rules, and ASPIC+ [26], where the dynamic component is meant to resolve symmetric attacks by updating preferences. The current paper advances this line of research by specifying a variety of dynamic operators for modeling changes of argument systems based on justification logic.
We will show that introducing dynamic operators for justification logic default theories enables us to model an additional kind of defeat: undermining. According to [16], an argument is undermined if its premises or assumptions are attacked. Defeating an argument by attacking its premise or its assumption is not new to structured argumentation. In assumption-based argumentation (ABA) [15], all attacks are reduced to this type of attacks and in ASPIC+ [30], ordinary premises of an argument are susceptible to undermining. However, these systems do not provide an insight into the logical workings of undermining, because they neither specify a concrete logical language nor inference rules.Footnote 1
In our default theories, undermining can be given a precise logical interpretation. While undercut and rebuttal rely on the uncertainty of defeasible arguments, undermining changes the context from which agents make further inferences. For a specific default theory, this context is determined by the set of starting premises, sometimes also called “axioms”. Our idea is that, since undermining targets axioms that are considered as a given, it should be modeled as a result of non-inferential information inputs that require contracting the set of axioms of a default theory. This means that we will define undermining by “climbing up” the definitions of more fundamental operations of default theory changes. To elicit the reasoning process behind undermining, we specify four different logical operations that model undermining: prioritized and non-prioritized contraction and prioritized and non-prioritized revision.
The paper is organized as follows. Section 2 introduces the basics of the logic of default justifications first introduced in [27, 29] and developed as a theory of structured arguments in [28]. This logic already models non-monotonic behavior with the use of undercut and rebuttal. Section 3 is the main technical contribution of this paper, where we define dynamic operations for default theories with justification formulas. The operations we introduce combine base revision operations as defined in, e.g., [20] with a specific kind of standard Reiter default rules. Our approach to defining the dynamic operators for default theory revision has most in common with the approach of [4], which deals with the dynamics of Reiter’s default theories. It turns out by the end of the paper that undermining attacks on premises correspond to those dynamic operations that involve either contraction or a variant of non-prioritized contraction defined in Sect. 3.
2 Logic of Default Reasons
The logic of default justifications was first defined in [27] and our definitions in this section follow those given in [29]. We start by outlining the underlying justification logic on which we base default theories. Before we formally introduce syntax, several preliminary remarks on how to build justification assertions of the type t : F are in order.
One of the basic operations of standard justification logics is Application (‘\(\cdot \)’) exemplified by the following formula \({u:(F \rightarrow G) \rightarrow (t:F \rightarrow (u \cdot t):G)}\). By focusing only on the propositional content of the formula, one may notice the familiar structure of a modus ponens inference from \(F \rightarrow G\) and F to G. The added machinery of reason terms syntactically captures the dependence of the consequent G on the propositions \(F \rightarrow G\) and F. This dependence is witnessed by the structure of the reason term \((u \cdot t)\) which shows that the reason u has been applied to the reason t.
In addition to application, all standard justification logics include the operation known as Sum ‘\(+\)’. Sum admits of merging two reason terms into a single term as done, for example, in the formula \(t:F \rightarrow (t+u):F\). The intuition behind Sum is that, if evidence t justifies some formula F, then adding new evidence u to t will not invalidate t being a reason for F. Thus, standard justifications are inherently non-defeasible.
The underlying logic for our default theories is a standard justification logic with non-defeasible and truth-inducing reasons.Footnote 2 We assume both Application and Sum operations for this logic. Moreover, to ensure that all reasons in this logic are truth-inducing, the logic contains the axiom \(t:F \rightarrow F\) called Factivity. This axiom corresponds to the modal logic truth axiom: \(\Box F \rightarrow F\) read as “If F is known, then F”. Our choice of basing default theories on a logic of non-defeasible and truth-inducing reasons is in line with the strategy of standard default logics [3], where defeasible conclusions are based on certain information.
2.1 Logic of Factive Reasons \({\mathbf {J}}\mathbf {T}_{\mathbf {C}\mathbf {S}}\)
Syntax, Axioms and Rules. The basic format of justification assertions is “t : F”, where a justification term “t” is informally interpreted as a reason or justification for “F”. The set Tm consists of all justification terms, constructed from variables \(x_1, \dots , x_n, \dots \) and proof constants \(c_1, \dots , c_n, \dots \) by means of operations \(\cdot \) and \(+\). The following BNF gives the grammar of justification terms:

where x is a variable denoting an unspecified justification and c is a proof constant, taken as atomic within the system. A set of subterms Sub(t) is defined by induction on the construction of a term t. The set Fm consists of exactly all \({\mathbf {J}\mathbf {T}}_{\mathbf {C}\mathbf {S}}\) formulas based on the countable set of propositional atoms \(\mathcal {P}\) and defined by the following BNF:

where \(P \in \mathcal {P}\) and \(t \in Tm\).
We can now define the logic \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\), which is the weakest logic with non-defeasible reasons containing axiom schemes for the two basic operations \(\cdot \) and \(+\). These are the axioms and rules of \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\):
-
A0. All the instances of propositional logic tautologies from Fm
-
A1. \(t:(F \rightarrow G) \rightarrow (u:F \rightarrow (t \cdot u):G)\) (Application)
-
A2. \(t:F \rightarrow (t+u):F; u:F \rightarrow (t+u): F \) (Sum)
-
A3. \(t:F \rightarrow F\) (Factivity)
-
R0. From F and \(F \rightarrow G\) infer G (Modus ponens)
-
R1. If F is an axiom instance of A0–A3 and \(c_n, c_{n-1}, \dots , c_1\) proof constants, then infer \({c_n: c_{n-1}: \dots :c_1:F}\) (Iterated axiom necessitation)
The set of all justified formulas produced by the use of R1 is called a Constant Specification (\({\mathcal {C}}{\mathcal {S}}\)) set:
Definition 1
(Constant specification). \({\mathcal {C}}{\mathcal {S}} = \{c_n: c_{n-1}:\dots :c_1:F \mid F \text{ is } \text{ an } \text{ instance } \text{ of } \text{ A0-A3, } c_n, c_{n-1},\dots , c_1 \text{ are } \text{ proof } \text{ constants } \text{ and } n \in \mathbb {N} \}\).
The intuition behind the set of formulas \({\mathcal {C}}{\mathcal {S}}\) in R1 is that the basic logical axioms are taken to be justified by proof constants and so are the formulas likewise produced. In the set of formulas \({\mathcal {C}}{\mathcal {S}}\) from Definition 1, any axiom instance can be labelled with any sequence of proof constants. A constant specification of this type is thus appropriately called Total Constant Specification (\(\mathcal {TCS}\)) and the logic we defined with the use of \(\mathcal {TCS}\) is called \(\mathbf {JT_{TCS}}\).
Following the idea that each logical axiom is justified by exactly one constant, we require that the use of proof constants respects the following two conditions and we say that \({\mathcal {C}}{\mathcal {S}}\) is:Footnote 3
-
Axiomatically appropriate: for each axiom instance A, there is a constant c such that \(c:A \in {\mathcal {C}}{\mathcal {S}}\) and for each formula \(c_n: c_{n-1}: \dots :c_1:A \in {\mathcal {C}}{\mathcal {S}}\) such that \(n \ge 1\), there is a constant \(c_{n+1}\) such that \(c_{n+1}: c_n: c_{n-1}: \dots :c_1:A \in {\mathcal {C}}{\mathcal {S}}\);
-
Injective: each proof constant c justifies at most one formula.
According to the restrictions on an axiomatically appropriate and injective \({\mathcal {C}}{\mathcal {S}}\), we replace R1 of \(\mathbf {JT_{TCS}}\) with the following rule to obtain the logic \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\):
- R1*:
-
If F is an axiom instance of A0–A3 and \(c_n, c_{n-1}, \dots , c_1\) proof constants such that \(c_n: c_{n-1}: \dots :c_1:F \in {\mathcal {C}}{\mathcal {S}}\), then infer \(c_n: c_{n-1}: \dots :c_1:F\)
We say that the formula F is \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\)-provable (\({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}} \vdash F\)) if F can be derived using the axioms A0–A3 and rules R0 and R1.
Semantics. The semantics for \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) is an adapted version of the semantics for the logic of proofs (\({\mathbf {L}}{\mathbf {P}}\)) given by [25].
Definition 2
(\({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) model). We define a function reason assignment based on \({\mathcal {C}}{\mathcal {S}}\), \(*(\cdot ):Tm \rightarrow 2^{Fm}\), a function mapping each term to a set of formulas from Fm. We assume that it satisfies the following conditions:
-
(1)
If \(F \rightarrow G \in *(t)\) and \(F \in *(u)\), then \(G \in *(t \cdot u)\),
-
(2)
\(*(t) \cup *(u) \subseteq *(t + u)\) and
-
(3)
If \(c:F \in {\mathcal {C}}{\mathcal {S}}\), then \(F \in *(c)\).
A truth assignment \(v: \mathcal {P} \rightarrow \{ True, False \}\) is a function assigning truth values to propositional atoms in \(\mathcal {P}\). We define the interpretation \(\mathcal {I}\) as a pair \((v, *)\). For an interpretation \(\mathcal {I}\), \(\models \) is a truth relation on the set of formulas of \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\). We say that, for any formula \(t:F\in Fm\), \(\mathcal {I}\,\models \,t:F\) iff \(F \in *(t)\). Truth conditions for atomic propositions, \(\lnot \), \(\rightarrow \), \(\wedge \) and \(\vee \) are defined as usual. An interpretation \(\mathcal {I}\) is reflexive iff the truth relation for \(\mathcal {I}\) fulfills the following condition:
-
For any term t and any formula F, if \(F \in *(t)\), then \(\mathcal {I} \,\models \, F\).
The consequence relation of the logic of factive reasons \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) is defined on reflexive interpretations:
Definition 3
(\({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) consequence relation). \(\varSigma \models F\) iff for all reflexive interpretations \(\mathcal {I}\), if \(\mathcal {I} \models B\) for all \(B \in \varSigma \), then \(\mathcal {I} \models F\).
For a set of formulas \(\varGamma \subseteq Fm\) and the \(JT_{CS}\) consequence relation \(\models \) defined above, a \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) closure of \(\varGamma \) is given by \(Th^{JT_{CS}}(\varGamma ) = \{F | \varGamma \models F\}\). For a closure \(Th^{JT_{CS}}(\varGamma )\), it holds that \({\mathcal {C}}{\mathcal {S}} \subseteq Th^{JT_{CS}}(\varGamma )\).
2.2 Logic of Default Reasons
Building on the \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) syntax, we introduce the definition of the default theory:
Definition 4
(Default Theory). A default theory T is a pair (W, D), where W is a finite set of \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) formulas and D is a countable set of default rules.
Each default rule is of the following form:
The informal reading of the default \(\delta \) is: “If t is a reason justifying F, and it is consistent to assume that \((u \cdot t)\) is a reason justifying G, then \((u \cdot t)\) is a defeasible reason justifying G”. The default rule \(\delta \) introduces a unique reason term u, which means that, for a default theory T, the following three conditions are required:
-
(1)
For any formula v : H such that \(v:H \in Th^{JT_{CS}}(W)\), it holds that \(u \ne v\);
-
(2)
For any formula \(H \in W\), \(u: (F \rightarrow G)\) is not a subformula of H and
-
(3)
For any default rule \(\delta ' \in D\) such that \({\delta ' = \frac{t':F' \,{:}{:}\, (u'\cdot t'):G'}{(u'\cdot t'):G'}}\), if \(u = u'\), then \(F = F'\) and \(G = G'\).
In the rule \(\delta \), the formula t : F is called the prerequisite, \((u \cdot t):G\) above the line is called the consistency requirement and \((u \cdot t):G\) below the line is called the consequent of \(\delta \). We refer to each of these formulas by \( pre (\delta )\), \( req (\delta )\) and \( cons (\delta )\) respectively.
Every default rule produces a reason term whose structure codifies an application operation step. Notice that in \(\delta \) above, in contrast to axiom A1, we do not require the formula \(u: (F \rightarrow G)\) to be a part of the knowledge base. Instead, \(u: (F \rightarrow G)\) is the underlying assumption of \(\delta \) on the basis of which we are able to extend an incomplete knowledge base. The propositions of this kind are important in the system since they function as rules allowing for default steps, but they are also specific \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) formulas. They will be referred to as “warrants”, because their twofold role mirrors that of Toulmin’s argument warrants ([34], p. 91). Warrants extend the interpretation of the application operation “\(\cdot \)” and each warrant is made explicit by means of a function warrant assignment: \(\#(\cdot ): D \rightarrow Fm\). The function maps each default rule to a specific justified conditional as follows: \(\#(\delta _i) = u:(F \rightarrow G)\), where \(\delta _i \in D\) and \(\delta _i = \frac{t:F \,{:}{:}\, (u\cdot t):G}{(u\cdot t):G}\), for some reason term t, a unique reason term u and some formulas F and G. It is important that uniqueness of u does not prevent two default rules to share a warrant formula. This reflects also the informal idea of warrants as general rules that are, in principle, applicable to different starting data.Footnote 4
A set of all such underlying warrants of default rules is called Warrant Specification (\({\mathcal {W}}{\mathcal {S}}\)) set.
Definition 5
(Warrant specification). For a default theory \(T = (W, D)\), justified defeasible conditionals are given by the Warrant Specification set:
The basis of operational semantics for a default theory \(T = (W, D)\) is the procedure of collecting new, reason-based information from the available defaults. This procedure is defined following Antoniou’s [3] operational semantics for Reiter’s default theories. A sequence of default rules \(\varPi =(\delta _0,\delta _1, \ldots )\) is a possible order in which a list of default rules without multiple occurrences from D is applied (\(\varPi \) is possibly empty). Applicability of defaults is determined in the following way: for a set of \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\)-closed formulas \(\varGamma \) we say that a default rule \(\delta = \frac{t:F \,{:}{:}\, (u\cdot t):G}{(u\cdot t):G}\) is applicable to \(\varGamma \) iff \(t:F \in \varGamma \) and \(\lnot (u\cdot t):G \notin \varGamma \). Default consequents are brought together in the set of \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) formulas that represents the current evidence base: \( In (\varPi ) = Th^{JT_{CS}}(W \cup \{ cons (\delta ) \mid \delta \text{ occurs } \text{ in } \varPi \})\). The set \( In (\varPi )\) pools reason-based formulas whose acceptability depends on the acceptability of other available (counter-)reasons.
We need to further specify those sequences of defaults that are significant for a theory T namely, default processes. For a sequence \(\varPi \), the initial segment of the sequence is denoted as \(\varPi [k]\), where k indicates the number of elements contained in that segment of the sequence and a minimal number of defaults for the sequence \(\varPi \). Any segment \(\varPi [k]\) is also a sequence. We can now define default processes:
Definition 6
(Process). A sequence of default rules \(\varPi \) is a process of a default theory \(T = (W, D)\) iff every k such that \(\delta _k \in \varPi \) is applicable to the set \( In (\varPi [k])\), where \(\varPi [k] = (\delta _0,\ldots \delta _{k-1})\).
The kind of process that we are focusing on is called closed process: a process \(\varPi \) is said to be closed iff every \(\delta \in D\) that is applicable to \( In (\varPi )\) is already in \(\varPi \).
The possibility to refer to warrants within the language enables us to model undercutting defeaters. They defeat other reasons by denying that their warrant provides support for the conclusion in an undercutting circumstance.
Definition 7
(Undercut). A reason u undercuts reason t being a reason for F in a set of \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) formulas \(\varGamma \subseteq In (\varPi [k])\) iff \({\bigvee _{(v) \in Sub(t)} u: \lnot [v:(G \rightarrow H)]} \in Th^{JT_{CS}}(\varGamma )\) and \(v:(G \rightarrow H) \in {\mathcal {W}}{\mathcal {S}}^{\varPi '}\) for a process \(\varPi '\) of T.
We say that a set \(\varGamma \subseteq In (\varPi [k])\) undercuts reason t being a reason for F iff, for a subterm v of t, \(\lnot [v:(G \rightarrow H)] \in Th^{JT_{CS}}(\varGamma )\) and \(v:(G \rightarrow H) \in {\mathcal {W}}{\mathcal {S}}^{\varPi '}\) for a process \(\varPi '\) of T.
For any default theory \(T = (W, D)\), an agent always considers potential extension sets of \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) formulas that meet the following conditions:
-
1.
\(W \subseteq \varGamma \) and
-
2.
\(\varGamma \subseteq \{ W \cup cons (\varPi ) \mid \varPi \text{ is } \text{ some } \text{ process } \text{ of } T \}\).
Besides undercut, reasons may conflict each other due to the fact that they cannot be both added to a same consistent process. For example, if a knowledge base contains a reason for a statement F, then any default introducing a reason for \(\lnot F\) will be inapplicable. This enables us to obtain a formal representation of rebuttal among reasons for free. Formally, every rebuttal will imply an undercut for formulas that cannot possibly extend a knowledge base together. Thus, we exclusively rely on the definition of undercut to characterize all the standard argumentation extension notions [14] in justification logic. For any potentially acceptable set \(\varGamma \) we say that \(\varGamma \) is conflict-free if its closure is undercut-free and we define the notion of acceptability of a justified formula t : F:
Definition 8
(Acceptability). For a process \(\varPi \) of a default theory \(T = (W, D)\), a formula \(t:F \in cons (\varPi )\) is acceptable w.r.t. a set of \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) formulas \(\varGamma \subseteq In (\varPi )\) iff for each undercutting reason u for t being a reason for F such that \(u:G \in In (\varPi )\), \(Th^{JT_{CS}}(\varGamma )\) undercuts u being a reason for G.
Definition 9
(\({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) Extensions). We define multiple argumentation theory extensions for any default theory \(T = (W, D)\) based on the \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) language:
-
\({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) Admissible Extension. A potential extension set of \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) formulas \(\varGamma \subset In (\varPi )\) is a \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) admissible extension of a default theory \(T = (W, D)\) iff \(Th^{JT_{CS}}(\varGamma )\) is conflict-free, each formula \(t:F \in \varGamma \) is acceptable w.r.t. \(\varGamma \) and \(\varPi \) is closed.
-
\({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) Preferred Extension. A closure \(Th^{JT_{CS}}(\varGamma )\) of a \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) admissible extension \(\varGamma \) is a \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) preferred extension of T iff for any other \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) admissible extension \(\varGamma '\), \(\varGamma \not \subset \varGamma '\).
-
\({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) Complete Extension. A closure \(Th^{JT_{CS}}(\varGamma )\) of a \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) admissible extension \(\varGamma \) is a \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) complete extension of T iff for each closed process \(\varPi \) for which \(\varGamma \subset In (\varPi )\) is \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) admissible it holds that, if a formula \(t:F \in cons (\varPi )\) is acceptable w.r.t., then t : F belongs to \(\varGamma \).
-
\({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) Grounded Extension. A \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) complete extension \(Th^{JT_{CS}}(\varGamma )\) is the unique \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) grounded extension of T if \(\varGamma \) is the smallest potential extension with respect to set inclusion such that \(Th^{JT_{CS}}(\varGamma )\) is a \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) complete extension of T.
-
\({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) Stable Extension. A conflict-free closure \(Th^{JT_{CS}}(\varGamma )\) of a potential extension \(\varGamma \) is a \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) stable extension iff \(\varGamma \) undercuts all the formulas \(t:F \in cons (\varPi )\) outside \(Th^{JT_{CS}}(\varGamma )\), for any process \(\varPi \) of T.
It turns out that a large subclass of Dung’s frameworks, excluding only some kinds of attack cycles, can be proven to be a special case of our logic via establishing the correspondences of extensions. This result is shown in [28].
The above presented account of default reasons suffices to represent reasoning from an incomplete knowledge base, but it does not represent reasoning with information changes that alter the facts from which an agent starts to reason. Still, the basic account can already model one type of non-monotonic behavior induced by the definition of undercut. We will refer to this way of revising as “inferential” revision. The workings of undercut can be illustrated with Toulmin’s famous example ([34], p. 92) of arguing for the claim that Harry is a British subject. This claim “can be defended by appeal to the information that he was born in Bermuda, for this datum lends support to our conclusion on account of the warrants implicit in the British Nationality Acts...”. The example is translated into a justification logic default as follows. Given the fact that Harry was born in Bermuda (B), an agent can conclude that Harry is a British subject (S):
The default can be read as follows: “If r is a reason justifying that Harry was born in Bermuda and it is consistent to assume that \((s\cdot r)\) is a reason justifying that Harry is a British subject, then \((s\cdot r)\) is a defeasible reason justifying that Harry is a British subject”.
However, if the agent were in possession of the additional information saying that both Harry’s parents are aliens (P), the “general authority of the warrant” \(s:(B \rightarrow S)\) for the claim S would have to be set aside. This is modeled with the following rule that introduces an undercutting reason:
The consequent can be read as follows: “\((u\cdot t)\) is a defeasible reason denying that the reason s justifies that if Harry was born in Bermuda, then Harry is a British subject”. This is a classical argumentation theory example of a defeater that leads to the suspension of the conclusion supported by the reason \((s\cdot r)\). For a default theory \(T_1 = (W, D)\) with \(W = \{ r:B, t:P \}\) and \(D = \{ \delta _1, \delta _2 \}\), the process \((\delta _1, \delta _2)\) corresponds to such course of reasoning with revised \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extensions. Notice that the warrant underlying \(\delta _2\) can also be questioned in a further course of reasoning. For example, one could find out that one of Harry’s parents was settled in Bermuda at the time when he was born, thus reinstating the authority of the warrant used in \(\delta _1\).
Notice that in the logic above, the argument \((s\cdot r): S\) is susceptible to attack due to the fallibility of inference \(\delta _1\) that is characteristic for defeasible reasoning. For the argument \((s\cdot r): S\) to be undermined, we consider a wider Toulminian interpretation of the argument that includes the formula r : B as the data for the argument. Since r : B is in the set W, the only possibility to attack r : B is to remove it from W and to thereby undermine \((s\cdot r): S\). This kind of attack on arguments is studied under the paradigm of plausible reasoning (see [31], pp. 59–61 for details on this distinction). In this paradigm, arguments are taken to be susceptible to attack due to the uncertainty of their premises. The aim of the current work is to unify the two paradigms in a single logical formalism.
3 Dynamic Operations for Default Theories: Introducing Undermining Attack
As mentioned above, undermining can be interpreted as an attack on the formulas that are considered to be facts. In our view, undermining is essentially non-inferential because introducing conflicting information that undermines facts cannot be done with the use of warrants.Footnote 5 For a default theory, these facts are represented by the set of justification logic formulas W and, in constructing a defeasible argument, such formulas can be prerequisites of default rules. A plausible interpretation of undermining defeaters would be that they propose alternative states of facts which ground further reasoning steps. To be able to incorporate factual changes, we need methods based on belief revision methods. Our selection of the belief-revision operations follows the way in which default theories are defined—since the set of facts W is typically finite, it is natural to use operators for sets that do not require closure. Therefore, our choice is to make use of base revision operators [20] instead of the AGM operators [1].
To model changes to default theories, we will use the capacity of default logic to represent two levels of information certainty. The top-level of information certainty is represented by formulas that are included in all extensions. Typical examples of such formulas are those contained in a set of facts W. The lower-level of information certainty is represented by formulas whose status is contingent on whether it becomes defeated by other available information. Such formulas are typically consequents of default rules. Our goal is to use the two levels and to define dynamic operators that can bring about the changes that fix whether a formula is included in or excluded from all extensions, but also to define non-prioritizing operations that leave the status of a formula undecided.
To be able to model the dynamics at the two levels of information certainty, we extend the above defined default theories with defaults without warrants, which correspond to Reiter’s supernormal defaults, but (possibly) containing justification assertions:
Standard default rules with justification assertions encode inferential steps supported by warrants. In contrast to inferential steps, supernormal defaults will be used to represent non-inferential, information-changing actions in which an agent accepts that a formula can be included in (at least) one extension. We will extend sets of defaults with supernormal defaults whenever we represent introducing uncertain information to a theory T or relegate information from W to the status of uncertain information.
Why would we want to make changes only to the lower-level of information certainty or alter a default theory at the level of some, instead of all extensions? Sometimes, an agent has doubts with respect to whether it is safe to include some information or not and, analogously, whether it is safe to remove some information or not. In the standard base revision approach to modeling information change, incoming information is always prioritized over the existing one, which is ensured by the success postulate. Consider again the example of the agent reasoning about Harry’s eligibility for British nationality. It is possible that, according to the census record, Harry was born in Bermuda and, according to the military record, he was born outside Bermuda. The fact that the agent first collected the census record data and then collected the military record data cannot justify the prioritization of the newly acquired information. If the agent does not know which information source is reliable, the order of data input is irrelevant. In these cases, default logic can avoid the “naive” priority ascription by the use of multiple extensions. The rest of this section gives a solution to the problem of non-prioritized change of default theories, along with the more standard prioritized change. In a case of non-prioritized change, the corresponding dynamic operator uses supernormal defaults with an aim to alter the lower-level of information certainty of a default theory. On our interpretation of undermining attacks, whether undermining fully or partially realizes its defeating potential depends on whether the new information is prioritized or not.
3.1 Default Theory Expansion
The first kind of change we want to consider corresponds to learning new information. For example, adding a formula F to a set of facts W can be based on the information provided by some information channel. The formal operation that naively adds new information without checking the joint consistency of the resulting set of beliefs is called “expansion”:
Definition 10
(Expansion). For a default theory \(T = (W, D)\) and a formula F, \(T^+_F = (W^+_F, D)\) is the expansion of the default theory T, where \(W^+_F\) is the base expansion of the set W such that \(W^+_F = W \cup \{F\}\).
If the added information results in an inconsistent set \(W^+_F\), any definable \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extension will be inconsistent. Notice that default theory expansion can already cause non-monotonic behaviour on the level of default theory extensions. For example, if the added formula is a prerequisite for a default rule with an undercutter for some other default consequent, the new information can result in removing elements from \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extensions of T.
An agent can approach accepting incoming information more cautiously. If the agent accepts new information as a plausible premise, but hesitates to consider it a fact, the change is made to the set of default rules:
Definition 11
(Conservative Expansion). For a default theory \(T = (W, D)\) and a formula F, \(T^{\times }_F = (W, D\ \cup \ \{\delta _F\})\) is the conservative expansion of the default theory T with F, where \(\delta _F = \frac{\top \,{:}{:}\, F}{F}\).
Notice that the operation \(\times \) opens up a possibility that the formula F is included in all extensions, but it can also be excluded from all extensions. For example, if \(\lnot F\) is contained in \(Th^{JT_{CS}}(W)\), then \(\delta _F\) is not applicable. The following statements characterize the introduced operators.Footnote 6
Proposition 12
For a default theory \(T = (W, D)\) with unwarranted default rules and a \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) formula F it holds that
-
(a)
If F is not a contradiction, then F is contained in each \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extension of the theory \(T^+_F\).
-
(b)
If F is not a contradiction and if \(\lnot F\) is not contained in any \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extension of T, then F is contained in each \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extension of the theory \(T^{\times }_F\).
-
(c)
If W is not inconsistent and if \(\lnot F\) is contained in \(Th^{JT_{CS}}(W)\), then F is not contained in any \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extension of the theory \(T^{\times }_F\).
3.2 Default Theory Contraction
How does an agent give up on some information, if the information is proven to be unreliable? We will again differentiate between two strategies of giving up on information or contracting default theories: one of them aims to remove a formula from all extensions and another leaves the possibility that extensions still contain the formula. One problem we face in removing a formula from all theory extensions is that the base contraction of a set of facts is necessary, but not sufficient to secure that the formula will not be reintroduced by the application of a default rule. To illustrate the need for such operation, consider that changes in information may cause that a certain source of justification t is denied its reliability as a reason for some formula F.
To deal with this problem, we propose to put constraints on the application of default rules. The aim of constraints on application is to prevent an unwanted formula F to become a part of any default theory extension. Such “application-constrained” default theories can be defined for any default theory for which the closure of a set of facts W does not entail F:
Definition 13
(Application-Constrained Default Theory). For a finite set of \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) formulas W such that \(\lnot F \notin Th^{JT_{CS}}(W)\), a countable set of default rules D and a finite set of \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) formulas \(C = W \cup \{ F \}\), an application-constrained default theory \(_{[F]}T\) is defined as a triple (W, D, C) such that:
For any application-constrained default theory, the expansion operation \((_{[F]}T)^+_G\) and the conservative expansion operation \((_{[F]}T)^{\times }_G\) are both defined analogously to the corresponding default theory operations, with the following two convention in effect. Firstly, if a formula \(F \in Th^{JT_{CS}}(W \cup \{ G \})\), then \((_{[F]}T)^+_G = (_{[\emptyset ]}T)^+_G = T^+_G\), where \((_{[\emptyset ]}T)^+_G\) is an application-constrained default theory for which \(C=W\). Secondly, if a formula \(\lnot F \in Th^{JT_{CS}}(W \cup \{ G \})\), then \((_{[F]}T)^+_G = T^+_G\).
We first define a contraction operation that aims at removing a formula at the level of a whole default theory. The operation corresponds to the action of removing information when an agent is confident that the information is not reliable. To achieve this in a default theory, a formula has to be removed from the set of facts by a base contraction and its reintroduction should be prevented. In the definition of contraction, remainder sets will be used: for any set of \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) formulas \(\varGamma \) and a formula F, the remainder set \(\varGamma \,\bot \,F\) is defined as the set of maximal subsets of \(\varGamma \) that do not entail F.
Definition 14
(Contraction). For a default theory \(T = (W, D)\) and a formula F, the application-constrained theory \(_{[\lnot F]}T^-_F = (W^-_F, D \cup D_{!F}, C)\) is the contraction of the default theory T by F, where
-
1.
\(W^-_F\) is the (full) meet contraction of the set W such that \(W^-_F = \bigcap (W\, \bot \, F)\),
-
2.
\(D_{!F} = \{ \delta _G \mid \delta _G = \frac{\top \,{:}{:}\, G}{G} \text{ for } \text{ every } G \in W \setminus \bigcap (W\, \bot \,F) \}\) and
-
3.
\(C = W^-_F \cup \{ \lnot F \}\).
Notice that an application-constrained default theory \(_{[\lnot F]}T^-_F\) is definable for any theory T since, due to condition 1, the formula F cannot be an element of the set \(Th^{JT_{CS}}(W^-_F)\).
The combination of the constraint set C and the set of default rules \(D_{!F}\) provides a balanced solution for avoiding extremely cautious and extremely incautious behavior. Since the set of formulas \(W\,\bot \, F\) usually contains many elements, theory contraction operations need to include a procedure of selecting the formulas that can be kept after contracting by F. It is difficult to define such procedures in a principled and intuitively plausible way. In default theory contraction, we do not need to force selection by a function. Instead, the choice of formulas selected upon contraction depends on the type of extension that is being computed. For example, a \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) preferred extension corresponds to the idea of maxichoice contraction, while \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extension corresponds to the idea of full meet contraction ([20], pp. 12–13).
Using again the two-leveled perspective on changing default theories, we can define a more conservative way of giving up a belief. In conservative contraction, agents are reluctant to entirely give up on some information, but the information is no longer considered to be a fact. To relegate the status of a formula in such a way within a default theory, the formula is removed from the set of facts and then reintroduced through application of a supernormal default rule.
Definition 15
(Conservative Contraction). For a default theory \(T = (W, D)\) and a formula F, \(T^{\div }_F = (W^-_F, D \cup D_{!F})\) is the conservative contraction of the default theory T by F, where
-
1.
\(W^-_F\) is the (full) meet contraction of the set W such that \(W^-_F = \bigcap (W\, \bot \, F)\) and
-
2.
\(D_{!F} = \{ \delta _G \mid \delta _G = \frac{\top \,{:}{:}\, G}{G} \text{ for } \text{ every } G \in W \setminus \bigcap (W \,\bot \, F) \}\).
Clearly, \(_{[\lnot F]}T^{\div }_F\) and \(_{[\lnot F]}T^-_F\) are defining the same application-constrained default theory.
Conservative contraction is an open-ended operation in the sense that it does not preclude the possibility of reintroducing a formula F in an extension through a default rule application. Furthermore, it leaves open the possibility that F occurs in all extensions of the resulting default theory.Footnote 7 In ([4], p. 1149), a different approach has been taken. Namely, that of securing that there is at least one extension added that does not contain the formula removed from the set of facts. In our view, it is unnecessary to have such an operation. If some formula is not regarded to be a fact, but it is still plausible that the formula is true, accepting it as the only available information might be the only reasonable action. Instead of “forcing” an extension without the formula, conservative contraction enables the possibility of an extension without the formula. If there is no support for the contrary statement whatsoever, an agent might still need to hold on to the only available information. The following statement immediately follows from conditions 1 and 3 of Definition 14.
Proposition 16
For a default theory \(T = (W, D)\) with unwarranted default rules and a non-tautological \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) formula F, it holds that F is not contained in any \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extension of the theory \(_{[\lnot F]}T^-_F\).
3.3 Default Theory Revision
The task of adding new information to the set of facts by the expansion operation (Definition 10) can lead to an inconsistent set of facts. A more realistic dynamic operator for adding information needs to specify a process by which an agent adds information inconsistent with W without being committed to an inconsistent set of facts. One possible way is to only add information via the conservative expansion operation (Definition 11), but this comes with an obvious flaw: an agent is not able to confidently replace an old, unreliable piece of information with a new, reliable one. This is one of the motivations to define a default theory revision operator that not only adds a formula, but also removes inconsistent formulas at one of the two levels of the default theory.
A revision operation can be defined from a combination of the expansion and contraction operations.Footnote 8 In our approach, we will follow the traditional arrangement of the operations ([20], p. 203), namely, removing formulas will precede adding a formula. This kind of revision operations in which contraction is followed by expansion are called “internal revision” operators and we define the following four internal revision operators for each combination of the operations.
Definition 17
(Revision Operators). For a default theory \(T = (W, D)\) and a formula F, (internal) revision operators for T are defined as follows:
-
1.
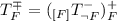
-
2.

-
3.

-
4.

The variety of possible revision operators raises the question about what kinds of revision strategies they represent.Footnote 9
We can show that the four operations amount to two strategies. Again, as in the cases of expansion and contraction, one strategy is meant to revise confidently and the other strategy more conservatively. The key to show this is to prove that the operations  ,
,  and
and  give equivalent extensions in revising a default theory with some formula F. This is the result stated in the (a) clause of Proposition 18.
give equivalent extensions in revising a default theory with some formula F. This is the result stated in the (a) clause of Proposition 18.
Proposition 18
For a default theory \(T = (W, D)\) with unwarranted default rules and a \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) formula F, it holds that
-
(a)
If F is not a contradiction, then F is contained in all \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extensions of the theories
 and
and  .
. -
(b)
If F is not a contradiction, then F is contained in at least one \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extension of the theory
 .
. -
(c)
If F is not a contradiction, then \(\lnot F\) is not contained in all \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extensions of
 .
.
Proof
To prove that (a) holds, consider the three revision operators  and
and  and the resulting theories
and the resulting theories  ,
,  and
and  . For the case of the default theory
. For the case of the default theory  , it follows from Proposition 16 that \(\lnot F\) is not contained in any \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extension of \({}_{[F]}T^-_{\lnot F}\). By Proposition 12 (a), F is contained in each \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extensions of \(({}_{[F]}T^-_{\lnot F})^+_F\).
, it follows from Proposition 16 that \(\lnot F\) is not contained in any \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extension of \({}_{[F]}T^-_{\lnot F}\). By Proposition 12 (a), F is contained in each \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extensions of \(({}_{[F]}T^-_{\lnot F})^+_F\).
For the case of the default theory  , it follows from Proposition 16 that \(\lnot F\) is not contained in any \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extension of \(_{[F]}T^-_{\lnot F}\). Moreover, the constraint set C contains the formula F, which means that the default rule \(\frac{\top \,{:}{:}\, F}{F}\) is applicable to any \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extension of the conservative expansion \((_{[F]}T^-_{\lnot F})^{\times }_F\) of the theory \(_{[F]}T^-_{\lnot F}\). Therefore, F is contained in each \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extensions of \((_{[F]}T^-_{\lnot F})^{\times }_F\).
, it follows from Proposition 16 that \(\lnot F\) is not contained in any \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extension of \(_{[F]}T^-_{\lnot F}\). Moreover, the constraint set C contains the formula F, which means that the default rule \(\frac{\top \,{:}{:}\, F}{F}\) is applicable to any \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extension of the conservative expansion \((_{[F]}T^-_{\lnot F})^{\times }_F\) of the theory \(_{[F]}T^-_{\lnot F}\). Therefore, F is contained in each \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extensions of \((_{[F]}T^-_{\lnot F})^{\times }_F\).
For the case of the default theory  , consider that the base contraction of W ensures that \(\lnot F\) cannot be contained in the set of facts \(W^-_{\lnot F}\) of the default theory \(T^{\div }_{\lnot F}\), but \(\lnot F\) can still be reintroduced by applying the defaults from \(D_{!\lnot F}\). However, after expanding the theory \(T^{\div }_{\lnot F}\) by F, the inclusion of the formula \(\lnot F\) into any \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extension of the theory
, consider that the base contraction of W ensures that \(\lnot F\) cannot be contained in the set of facts \(W^-_{\lnot F}\) of the default theory \(T^{\div }_{\lnot F}\), but \(\lnot F\) can still be reintroduced by applying the defaults from \(D_{!\lnot F}\). However, after expanding the theory \(T^{\div }_{\lnot F}\) by F, the inclusion of the formula \(\lnot F\) into any \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extension of the theory  is blocked and, by Proposition 12(a), F is in contained each \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extensions of
is blocked and, by Proposition 12(a), F is in contained each \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extensions of  .
.
To prove that (b) holds, consider that the base contraction of W ensures that \(\lnot F\) cannot be contained in the set of facts \(W^-_{\lnot F}\) for the conservative contraction \(T^{\div }_{\lnot F}\). This means that, for the conservative expansion \((T^{\div }_{\lnot F})^{\times }_F\), it holds that the default rule \(\frac{\top \,{:}{:}\, F}{F}\) is applicable to \(Th^{JT_{CS}}(W)\) and, therefore, contained in at least one \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extension of  .
.
To prove (c), consider that after the base contraction of W by \(\lnot F\), \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) extensions of \(T^{\div }_{\lnot F}\) are \({{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}\) consistent. Since we also know that, after the conservative expansion \((T^{\div }_{\lnot F})^{\times }_F\), (b) holds, then (c) holds.
To show the equivalence of the operators  and
and  , we first say that for any \(\sigma \)-extension, where
, we first say that for any \(\sigma \)-extension, where

\(\sigma (T)\) is the set of all \(\sigma \)-extensions for a theory T. Then we prove that for any default theory T, the default theories  and
and  realize the same set of extensions under any \(\mathbf {J} \mathbf {T}_{\mathbf {C}\mathbf {S}}\) extension-based semantics for default theories. The following result is obtainable from Proposition 18(a) together with the fact that none of the three operators
realize the same set of extensions under any \(\mathbf {J} \mathbf {T}_{\mathbf {C}\mathbf {S}}\) extension-based semantics for default theories. The following result is obtainable from Proposition 18(a) together with the fact that none of the three operators  ,
,  and
and  change the status of formulas that do not take part in F-implying sets:
change the status of formulas that do not take part in F-implying sets:
Theorem 19
For any default theory \(T = (W, D)\), a \({\mathbf {J}\mathbf {T}}_{\mathbf {C}\mathbf {S}}\) formula F and the (internal) revision operators  ,
,  and
and  , it holds that
, it holds that  .
.
Intuitively, the three operations represent a type of revision in which an agent confidently includes new and possibly inconsistent information into all \({\mathbf {J}\mathbf {T}}_{{\mathbf {CS}}}\) extensions. Another option specified by the operator  is to accept the new information in some extensions while maintaining the old information in other extensions. The revision operators comply to the two-leveled view of default semantics: the first three revision operators of Definition 17 fix the status of a revision at the level of a default theory as a whole, while the last revision operator targets at modifying only some extensions. Any of the three operations
is to accept the new information in some extensions while maintaining the old information in other extensions. The revision operators comply to the two-leveled view of default semantics: the first three revision operators of Definition 17 fix the status of a revision at the level of a default theory as a whole, while the last revision operator targets at modifying only some extensions. Any of the three operations  and
and  will be referred to as the Revision of T with F and the operation
will be referred to as the Revision of T with F and the operation  will be referred to as the Conservative Revision of T with F.
will be referred to as the Conservative Revision of T with F.
3.4 The Notion of Undermining
Finally, we are now able to say in what way the dynamic operations connect to the notion of undermining defeat. It was mentioned in the Introduction that by undermining we understand the attack whereby argument premises are being questioned. This intuition can now be cashed out by using those dynamic operators for default theories that involve contracting a default theory.
Definition 20
(Undermining). For a default theory \(T = (W, D)\) and a \({{{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}}\) formula F such that \(F \in W\) and \({F = pre (\delta )}\) for some \(\delta \in D, F\) is undermined iff W is contracted by F by applying any of the following operations to T:
-
1.
\({}_{[\lnot F]}T^-_F\) (Contraction)
-
2.
\(T^{\div }_F\) (Conservative Contraction)
-
3.
 or
or  for \({{{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}}\) inconsistent formulas F and G (Revision)
for \({{{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}}\) inconsistent formulas F and G (Revision) -
4.
 for \({{{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}}\) inconsistent formulas F and G (Conservative Revision).
for \({{{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}}\) inconsistent formulas F and G (Conservative Revision).
Notice that there is no requirement on the structure of F. However, each meaningful undermining targets justification assertions because W cannot be successfully contracted by a tautology and justification assertions are the only other type of formula occurring as a default prerequisite. Not every attack on the premises results in confidently revising the set of facts. It is possible that undermining leaves an agent undecided as to whether newly acquired information or older information should be prioritized.
Starting from the theory \({T_1}\) defined in Sect. 2, we can give a formalized undermining example from the beginning of this section to show the difference between inferential and non-inferential ways of information acquisition. Recall that the agent started to reason from the information that Harry was born in Bermuda. This piece of information is represented in the set of facts W with the formula r : B, where r can now be taken to reflect the source of information as, e.g., data from census records. However, if the information based on military records says that Harry was born outside Bermuda, and having no means to resolve this conflict of information, the theory \({T_1}\) needs to be conservatively revised. The theory  is the revision of \({T_1}\) with the formula \(v:\lnot B\), where v reflects the new source of information for the claim that Harry was not born in Bermuda.
is the revision of \({T_1}\) with the formula \(v:\lnot B\), where v reflects the new source of information for the claim that Harry was not born in Bermuda.
To see this revision in more detail, recall that the theory \({T_1 = (W, D)}\) consisted of the set of facts \({W = \{ r:B, t: P \}}\) and the set of defaults \({D = \{ \delta _1, \delta _2 \}}\). The first dynamic operation in revising with \({v:\lnot B}\) is contracting the theory by \({\lnot v: \lnot B}\). The resulting theory \({T^{\div }_{1_{\lnot v:\lnot B}} = (W^-_{\lnot v:\lnot B}, D \cup D_{!\lnot v:\lnot B})}\) consists of the set of facts \({W^-_{\lnot v:\lnot B} = \{ t:P \}}\) and the set of defaults D extended with the default \({\delta _{r:B} = \frac{\top \,{:}{:}\, r:B}{r:B}}\).
Finally, the agent conservatively expands the theory  with the information that Harry was not born in Bermuda. The new default theory is defined as
with the information that Harry was not born in Bermuda. The new default theory is defined as  . The change of the theory after conservative expansion with \({v:\lnot B}\) amounts to adding the new default rule \({\delta _{v:\lnot B} = \frac{\top \,{:}{:}\, v:\lnot B}{v:\lnot B}}\), which means that the new set of defaults is
. The change of the theory after conservative expansion with \({v:\lnot B}\) amounts to adding the new default rule \({\delta _{v:\lnot B} = \frac{\top \,{:}{:}\, v:\lnot B}{v:\lnot B}}\), which means that the new set of defaults is
 . The revised theory
. The revised theory
 changes the default processes in which the agent reasons about Harry’s nationality and, eventually, changes the structure of acceptable reasons by changing the way in which \({{{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}}\) extensions are computed.
changes the default processes in which the agent reasons about Harry’s nationality and, eventually, changes the structure of acceptable reasons by changing the way in which \({{{\mathbf {J}}{\mathbf {T}}}_{{{\mathbf {C}}{\mathbf {S}}}}}\) extensions are computed.
4 Related Work and Conclusions
As mentioned in the Introduction, our approach to structured argumentation dynamics builds on similar ideas as the approach to the dynamics of standard default theories from [4]. Antoniou’s approach significantly differs from ours in the way he treats those changes that add or remove a formula at the level of some, but not necessarily all extensions. Unlike our conservative expansion and conservative contraction, none of Antoniou’s operations leaves the inclusion status of a formula undecided. For instance, to secure that a formula is not contained in at least one extension, Antoniou ([4], p. 1149) adds a new extension where introducing the formula is blocked by adding either a new atom or its negation to any default, dependent on whether they are allowed to be in a same extension or not.
Some approaches to default reasoning such as [23] and [24] represent the idea of defaults in dynamic epistemic logic. The main focus of [23] is to embed supernormal defaults in a multi-agent modal logic with knowledge, belief and update modalities. The authors show that Reiter’s extensions can be represented as a result of consecutive jump actions to default conclusions, but they do not focus on how such extensions are revised due to information changes. In [24], a preference modality is introduced to differ between known and (provisionally) preferred information. A non-monotonic belief revision component consists in changing preferences as a result of obtaining knowledge.
Baltag, Renne and Smets [7, 8] and Renne [32] define extensions of justification logic in which agents may acquire new information that defeats the reasons they accepted. The logics combine belief revision and dynamic epistemic logic techniques to model a kind of defeat that seems to correspond to undermining. However, each of the logics assumes prioritizing new information and none of these logics is able to model undercut and rebuttal. Even so, approaches based on dynamic epistemic logic are attractive because they open up a possibility of developing a multi-agent justification logic with defeaters.
We indicated in the Introduction that the work in the area of the dynamics of argumentation frameworks without argument structures is already well-developed. Among the approaches, it is worth mentioning those that follow the belief revision methods applied to Dung’s frameworks such as [9] and [12]. In [9], the authors start from a labelling approach to Dung’s frameworks and constraints on a framework’s output. Their focus is on finding the best way to recover a rational output given a framework and a constraint on its output. For this, they use ordering of conflict-free labellings in a way that the most rational conflict-free labelling is chosen when none of complete labellings respects the constraint. In the work by [12], we find two kinds of revision operators. One of them revises a Dung framework by taking a propositional formula as a means to represent the new information, while the other operation revises an input framework by information in the form of another framework. Both operations give a single output framework respecting a particular type of rankings on extensions.
Finally, our paper contributes to the study of non-prioritized belief revision operations, that is, such operations for which the new information has no special priority due to its novelty [19]. The way in which our operators are defined meaningfully combines resources from both belief revision and default logic. The relation between belief revision and non-monotonic reasoning has long been a matter of discussion [18] among AI researchers. Although it was not our aim to discuss the relation between modeling reasoning with incomplete information in default theories and modeling reasoning with changing information in belief revision, we showed that our justification logic creates a useful junction for the two approaches.
As a result of connecting the two reasoning paradigms, the logic presented here, we can model both plausible and defeasible reasoning. According to [31], “argumentation models of plausible reasoning locate all fallibility of an argument in its premises, while argumentation models of defeasible reasoning locate all fallibility in its defeasible inferences”. To the best of our knowledge, the system presented here is the first logic to combine the two approaches by modeling all the standard notions of defeat in AI: rebuttal, undercut and undermining.
Notes
- 1.
In fact, ABA does not distinguish between different kinds of attacks and models each attack as that on premises or what we call here undermining. In ASPIC+, undermining is taken as a primitive notion of attack, which is different from rebuttal or undercut only by virtue of targeting “ordinary” premises of an argument.
- 2.
The first variant of justification logic, the logic of proofs (LP), was developed in [5]. The logic of non-defeasible and factive reasons that we use here was first defined in [10]. For more basic information on its relation to other justification logics see [17]. For recent overviews of justification logic systems, see [6] and [22].
- 3.
For example, one such constant specification set could be generated by assigning a Gödel number to each axiom instance and to each instance of R1.
- 4.
Formally, we also do not require that \(t = t'\) holds in the antecedent of condition (3) for the general definition of defaults above. This reflects the independence of the warrant \((u\cdot t):G\) from the data t : F to which we apply the warrant.
- 5.
The non-inferential view of information change is also relevant for human interaction. As Hlobil [21] argues, we can believe by accepting testimonies, but we cannot make inferences by merely accepting testimony. Two testimonies that contradict each other are to be, ceteris paribus, equally treated and the acceptance of new information is not the same process as inferentially extending the existing (incomplete) information.
- 6.
Proving Proposition 12 is straightforward. Details are omitted due to space limitations.
- 7.
Analogously, conservative expansion might not guarantee that there will be any extension containing a formula F, after a default theory has been conservatively expanded with F.
- 8.
If we were to exhaust all possible combinations, eight revision operators could be defined. Note that the revision operation symbols we use below reflect the composition of the introduced revision operations that are defined in terms of contraction and expansion variants. The symbols are not intended to be in continuity with the standard usage of revision operation symbols.
- 9.
Note that the second output theory \((_{[F]}T^-_{\lnot F})^{\times }_F\) of Definition 17 is an application-constrained default theory (\((_{[F]}T^-_{\lnot F})^+_F\) is, by our convention, a default theory after F has been added to the set of facts). The fact that \((_{[F]}T^-_{\lnot F})^{\times }_F\) is an application-constrained theory might cause problems if we want to make our operators global, rather than local, and enable iterated revision. A solution to this problem would be to allow for iterated contraction and generalize the contraction operation to application-constrained theories. This could be done if we allow that an application-constrained theory \(_{[F]}T\) can be further constrained by a formula G. We leave the details of developing iterated variants of the present operators for the future work.
References
Alchourrón, C.E., Gärdenfors, P., Makinson, D.: On the logic of theory change: partial meet contraction and revision functions. J. Symbolic Log. 50(2), 510–530 (1985)
Alfano, G., Greco, S., Parisi, F., Simari, G.I., Simari, G.R.: An incremental approach to structured argumentation over dynamic knowledge bases. In: Thielscher, M., Toni, F., Wolter, F. (eds.) Sixteenth International Conference on Principles of Knowledge Representation and Reasoning, KR 2018 (2018)
Antoniou, G.: Nonmonotonic Reasoning. MIT Press, Cambridge (1997)
Antoniou, G.: On the dynamics of default reasoning. Int. J. Intell. Syst. 17(12), 1143–1155 (2002)
Artemov, S.N.: Explicit provability and constructive semantics. Bull. Symbolic Log. 7, 1–36 (2001)
Artemov, S.N., Fitting, M.: Justification Logic: Reasoning with Reasons, Cambridge Tracts in Mathematics, vol. 216. Cambridge University Press, Cambridge (2019)
Baltag, A., Renne, B., Smets, S.: The logic of justified belief change, soft evidence and defeasible knowledge. In: Ong, L., de Queiroz, R. (eds.) WoLLIC 2012. LNCS, vol. 7456, pp. 168–190. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-32621-9_13
Baltag, A., Renne, B., Smets, S.: The logic of justified belief, explicit knowledge, and conclusive evidence. Ann. Pure Appl. Log. 165(1), 49–81 (2014)
Booth, R., Kaci, S., Rienstra, T., van der Torre, L.: A logical theory about dynamics in abstract argumentation. In: Liu, W., Subrahmanian, V.S., Wijsen, J. (eds.) SUM 2013. LNCS (LNAI), vol. 8078, pp. 148–161. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40381-1_12
Brezhnev, V.: On the logic of proofs. In: Striegnitz, K. (ed.) Proceedings of the Sixth ESSLLI Student Session, Helsinki, pp. 35–46 (2001)
Coste-Marquis, S., Konieczny, S., Mailly, J.G., Marquis, P.: On the revision of argumentation systems: minimal change of arguments statuses. In: Baral, C., De Giacomo, G., Eiter, T. (eds.) Fourteenth International Conference on the Principles of Knowledge Representation and Reasoning, KR 2014 (2014)
Diller, M., Haret, A., Linsbichler, T., Rümmele, S., Woltran, S.: An extension-based approach to belief revision in abstract argumentation. In: Yang, Q., Wooldridge, M. (eds.) Twenty-Fourth International Joint Conference on Artificial Intelligence, IJCAI 2015 (2015)
Doutre, S., Herzig, A., Perrussel, L.: A dynamic logic framework for abstract argumentation. In: Baral, C., De Giacomo, G., Eiter, T. (eds.) Fourteenth International Conference on the Principles of Knowledge Representation and Reasoning, KR 2014 (2014)
Dung, P.M.: On the acceptability of arguments and its fundamental role in nonmonotonic reasoning, logic programming and n-person games. Artif. Intell. 77(2), 321–357 (1995)
Dung, P.M., Kowalski, R.A., Toni, F.: Assumption-based argumentation. In: Rahwan, I., Simari, G.R. (eds.) Argumentation in Artificial Intelligence, pp. 199–218. Springer, Boston (2009). https://doi.org/10.1007/978-0-387-98197-0_10
van Eemeren, F.H., Garssen, B., Krabbe, E.C.W., Henkemans, A.F.S., Verheij, H.B., Wagemans, J.H.M.: Argumentation and artificial intelligence. In: Handbook of Argumentation Theory, pp. 615–675. Springer, Boston (2014). https://doi.org/10.1007/978-0-387-98197-0
Fitting, M.: Justification logics, logics of knowledge, and conservativity. Ann. Math. Artif. Intell. 53(1–4), 153–167 (2008)
Gärdenfors, P.: Belief revision and nonmonotonic logic: two sides of the same coin? In: van Eijck, J. (ed.) JELIA 1990. LNCS, vol. 478, pp. 52–54. Springer, Heidelberg (1991). https://doi.org/10.1007/BFb0018432
Hansson, S.O.: A survey of non-prioritized belief revision. Erkenntnis 50(2–3), 413–427 (1999)
Hansson, S.O.: A Textbook of Belief Dynamics: Theory Change and Database Updating. Kluwer Academic Publishers, Dordrecht (1999)
Hlobil, U.: We cannot infer by accepting testimony. Philos. Stud. 1–10 (2018). https://doi.org/10.1007/s11098-018-1142-3
Kuznets, R., Studer, T.: Logics of Proofs and Justifications. College Publications, Wenham (2019)
van Linder, B., van der Hoek, W., Meyer, J.J.C.: The dynamics of default reasoning. Data Knowl. Eng. 3(21), 317–346 (1997)
Meyer, J.-J.C., van der Hoek, W.: Non-monotonic reasoning by monotonic means. In: van Eijck, J. (ed.) JELIA 1990. LNCS, vol. 478, pp. 399–411. Springer, Heidelberg (1991). https://doi.org/10.1007/BFb0018455
Mkrtychev, A.: Models for the logic of proofs. In: Adian, S., Nerode, A. (eds.) LFCS 1997. LNCS, vol. 1234, pp. 266–275. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-63045-7_27
Modgil, S., Prakken, H.: Resolutions in structured argumentation. In: Verheij, B.H., Szeider, S., Woltran, S. (eds.) Computational Models of Argument: Proceedings of COMMA 2012, pp. 310–321. IOS Press (2012)
Pandžić, S.: A logic of default justifications. In: Fermé, E., Villata, S. (eds.) 17th International Workshop on Nonmonotonic Reasoning, NMR 2018, pp. 126–135 (2018)
Pandžić, S.: Logic of defeasible argumentation: constructing arguments in justification logic. Unpublished manuscript (2019)
Pandžić, S.: Reifying default reasons in justification logic. In: Beierle, C., Ragni, M., Stolzenburg, F., Thimm, M. (eds.) Proceedings of the KI 2019 Workshop on Formal and Cognitive Reasoning, DKB-KIK 2019, CEUR Workshop Proceedings, vol. 2445, pp. 59–70 (2019)
Prakken, H.: An abstract framework for argumentation with structured arguments. Argument Comput. 1(2), 93–124 (2010)
Prakken, H.: Historical overview of formal argumentation. IfCoLog J. Log. Their Appl. 4(8), 2183–2262 (2017)
Renne, B.: Multi-agent justification logic: communication and evidence elimination. Synthese 185(1), 43–82 (2012)
de Saint-Cyr, F.D., Bisquert, P., Cayrol, C., Lagasquie-Schiex, M.C.: Argumentation update in YALLA (yet another logic language for argumentation). Int. J. Approximate Reasoning 75, 57–92 (2016)
Toulmin, S.E.: The Uses of Argument. Cambridge University Press, Cambridge (2003)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Pandžić, S. (2020). On the Dynamics of Structured Argumentation: Modeling Changes in Default Justification Logic. In: Herzig, A., Kontinen, J. (eds) Foundations of Information and Knowledge Systems. FoIKS 2020. Lecture Notes in Computer Science(), vol 12012. Springer, Cham. https://doi.org/10.1007/978-3-030-39951-1_14
Download citation
DOI: https://doi.org/10.1007/978-3-030-39951-1_14
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-39950-4
Online ISBN: 978-3-030-39951-1
eBook Packages: Computer ScienceComputer Science (R0)




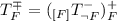



 and
and  .
. .
. .
. or
or  for
for  for
for