New Approach for Fast Residual Strain Estimation Through Rational 2D Diffraction Pattern Processing

Abstract

Highly brilliant synchrotron X-ray beams enable fast non-destructive evaluation of residual strains even in large and thick engineering objects under operando conditions. Large datasets of 2D patterns are acquired at high rate, meaning that near real time evaluation demands fast data processing and mapping of residual strain. The somewhat time-consuming traditional data processing algorithms involve the conversion of each 2D X-ray diffraction pattern within a substantial stack to 1D intensity plots by radial-azimuth sectoral binning (“caking”), followed by peak fitting to determine peak center positions. A new approach was realized and programmed as the open-source code to perform residual strain evaluation by direct ‘polar transformation’ of 2D X-ray diffraction patterns. We compare residual strain calculations by ‘polar transformation’ and ‘caking’ respectively for an Aluminum alloy bar containing a Friction Stir Weld and subjected to ex-situ three-point bending. ‘Polar transformation’ method shows good agreement with the traditional ‘caking’ technique, but also exhibits excellent speed, and robustness.

1 Introduction

In the last two decades, various approaches were developed connecting the conventional mechanical methods with modern microscopy techniques for experimental evaluation of residual stress and strain at the micro-scale. Diffraction of micro-focused high-energy synchrotron X-ray beams (µSXRD) proved to be one of the fastest and most convenient techniques for residual strain estimation [1]. For the empirical evaluation of residual stress, the µSXRD method offers unique benefits [2]. Firstly, µSXRD is a non-destructive technique which preserves material integrity during the test, unlike other destructive or semi-destructive methods which cannot be directly checked by repeat measurements. Secondly, different approaches require stress-free reference samples, which are usually challenging to construct and prepare. Furthermore, their spatial resolution and depth penetration are typically orders of magnitude worse than those of µSXRD [3]. An additional benefit of the synchrotron-based method is that it can provide information about the average bulk strain over the depth of the sample, and not just from the surface as for other techniques [4, 5].

The term residual stress refers to the presence of internal forces in a body in the absence of external fields [6]. They play a crucial role in the deformation behavior of processed engineering materials [7]. The knowledge of residual stress distribution allows optimizing the durability of engineering components and assemblies [8]. The stress is a derived extrinsic property that is defined as force per unit cross-sectional area, and is not directly measurable. Consequently, the approaches to stress evaluation rely on the measurement of some intrinsic property, such as strain, or indirect deduction of force.

The use of high energy synchrotron X-ray diffraction provides the possibility of measuring residual elastic lattice strain and then deducing stress by using the material’s elastic properties in the generalized Hooke’s law expression.

Thus, the emphasis of synchrotron diffraction data interpretation falls on strain determination from µSXRD scattering patterns. To streamline and speed up the analysis of many data files, a ‘polar transformation’ approach has been proposed that obviates the need for the traditional radial binning technique.

2 Methods and Materials

2.1 Sample Preparation

A 4 mm-thick rolled plate of Aluminum alloy AA6082-T6 plate was used for the manufacturing of a Friction Stir Welded joint. The welded plate was subjected to wire Electro Discharge Machining to cut out a sample with parallel sides. The sample was then subjected to four-point bending to induce permanent plastic deformation associated with specific bending strain profile. The resulting residual stress state within the sample represents a combination (superposition) of welding-induced and bending-induced effects.

2.2 SXRD Experiment

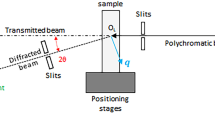
The experiment was conducted at Diamond Light Source on the Test Beamline B16. The beam energy was defined at 18 keV using multi-layer monochromator. The variation of strain across the bent bar was investigated by scanning the sample across the beam (collimated to 0.1 mm square beam spot) as shown in Fig. 1.

Fig. 1.

Illustration of the investigated Aluminium alloy bar with the scan area.

2.3 Center Estimation of Calibration Pattern

In this study calibration test was performed using silicon powder that enables to define the exact center position of the diffraction pattern and use this for all subsequent analyses. The analysis of the 2D diffraction pattern of the reference specimen is demonstrated in Fig. 2.

Fig. 2.

The scheme of the center estimation for calibration pattern (3056 pixel = 15 cm).

The correct center of the calibration diffraction pattern was found by several simple operations, as follows:

• (a) select the specific circle and make markers in four directions ($0^{\circ}$, $90^{\circ}$, $180^{\circ}$ and $360^{\circ}$, respectively) for the initial center estimation;

• (b) set indent from the circle and create a region of the interest (ROI);

• (c) choose a circle and perform a numerically stable direct Least Squares fit [9] using an ellipse, to account for various sources of distortion, namely, the combination of detector misalignment (tilt of the detector normal direction with respect to the incident beam), and non-equibiaxial residual strain.

2.4 ‘Caking’

Defining precise residual strain values requires careful interpretation of 2D µSXRD patterns so that the radial peak position reaches the accuracy approaching 10⁻⁴ or even better. Currently, there is a reliable and efficient approach for 2D µSXRD data interpretation in use based on radial-azimuthal binning (colloquially referred to as ‘caking’) which allows obtaining strains with high accuracy. However, this method has some drawbacks in terms of the large processing time and a large number of steps required. ‘Caking’ is a multi-stage process that involves the following stages: calibration, conversion of the 2D pattern into a 1D profile, and Gaussian fitting for peak center determination to calculate strain values.

The first experimental step is the assembly of ancillary equipment for positioning (and possibly loading) the sample, placing the detector and beam stop, calibrating the sample-detector distance, obtaining exact information regarding the image center of diffraction patterns, and calibrating the geometrical distortion related to detector’s orientation angle. Next, it is essential to collect scattering patterns from reference sample(s) and processing them via ‘caking’ to reduce 2D diffraction pattern to 1D radial functions of the azimuthal angle $\varphi$ that can be visualized as line plots of scattered beam intensity against radial position $R$ as shown in Fig. 3.

Fig. 3.

2D diffraction pattern of calibration with selected azimuthal angle φ in $20^{\circ}$ increments to produce 1D intensity distributions (3056 pixel = 15 cm).

These operations were then applied to each 1D profile for azimuthal angles around values of $0^{\circ}$, $45^{\circ}$, $90^{\circ}$, $135^{\circ}$, $180^{\circ}$, $225^{\circ}$, $270^{\circ}$, $315^{\circ}$, and $360^{\circ}$.

Step three is fitting of most intense peak positions $\left( {R_{i} } \right)$ as a function of the azimuthal angle $\left( {\varphi_{i} } \right)$ by a sine function, namely,

$$ R_{i} = a + b\,\sin \left( {2\left( {\phi_{i} + c} \right)} \right) $$

(1)

where $a$, $b$ and $c$ are offset, amplitude and phase shift, respectively.

The relationship between residual strain and d-spacing is defined as

$$ \varepsilon = \frac{{d - d_{0} }}{{d_{0} }} = \frac{d}{{d_{0} }} - 1 = \frac{a + b}{{a_{0} + b_{0} }} - 1 $$

(2)

where $\varepsilon$ is an elastic residual strain, $d = a + b$ is $d$-spacing of a strained sample, and $d_{0} = a_{0} + b_{0}$ is the value of $d$-spacing when the sample is strain free (from calibration image).

Nevertheless, conventional ‘caking’ approach has drawbacks, as it requires defining regions, selecting directions, splitting into sectors and averaging them that are imprecise for a textured sample whose ring intensity is nonuniform or spread on ring region. This should be considered in the context of the processing time of this analysis increasing manifold for large amounts of images.

2.5 ‘Polar Transformation’

In this investigation, we consider a new technique of determining residual strain based on the geometric transformation [10] of the 2D diffraction pattern from a Cartesian to a polar coordinate system with respect to the pattern center as shown in Fig. 4, namely,

Fig. 4.

The typical 2D diffraction pattern (a) and its polar transformation (b) (3056 pixel = 15 cm).

$$ \begin{array}{*{20}c} {R = \frac{{X_{i} - X_{0} }}{height\,of\,image} \cdot magnitude\left( I \right);} \\ {\phi = \frac{{\left( {Y_{i} - Y_{0} } \right)}}{{360^{\circ} }} \cdot angle\left( I \right)} \\ \end{array} $$

(3)

Following this cartesian-to-polar transformation, Debye–Scherrer rings can be displayed as lines on the radial-azimuthal contour plot. Following this, the entire transformed intensity pattern can be fitted with a sine function (1) to determine the residual strain variation (2).

3 Results and Discussions

In this study, the accuracy of a new technique based on the polar transformation of 2D µSXRD patterns was validated by comparison with the conventional ‘caking’ method. The programming language Python 3.7 with set standard libraries (os, numpy, scipy, matplotlib, lmfit, opencv and skimage) was used for obtaining 1D profiles from 2D patterns, Gaussian and polar transformation fitting respectively.

The approaches described above were applied to the series of summed diffraction patterns as a function of vertical position. Figure 5 shows the dependence of peak center positions on the azimuthal angle. The set of experimental data of ‘caking’ significantly less than in case ‘polar transformation’. It influences essential difficulties related with comparison two methods: the lack of experimental points for ‘caking’ approach is connected with a particular small angle range by contrast with ‘polar transformation’ where fitting the entire 360˚. At the result, the errors are reduced in determining the fitting parameters, and hence strain.

Fig. 5.

The dependence of peak center position against azimuth angle range on ($0^{\circ}$, $360^{\circ}$, step $15^{\circ}$) for ‘caking’ (a) and the complete revolution for ‘polar transformation’ (b): the blue ‘o’ markers are experimental data, the red solid lines are sine fitting (with black error bars). (Color figure online)

Figure 6 demonstrates the correlation between data of residual elastic strains at the azimuth angles from $0^{\circ}$ to $360^{\circ}$ with a step equals $15^{\circ}$ respectively.

Fig. 6.

Comparison of residual elastic strains obtained from ‘caking’ (red line) and ‘polar transformation’ (blue line) techniques. (Color figure online)

The presented Cartesian-to-polar transformation technique allows determining the strain and subsequently stress values for various in plane directions. The results of this approach show good agreement with ‘caking’ microstrain results.

In this study, a technique for the processing of 2D X-ray diffraction patterns from synchrotron experiments is presented that is referred to as the ‘polar transformation’ interpretation approach. The advantage of ‘polar transformation’ lies in the ability to perform fast processing of large numbers of 2D diffraction patterns without repeated binning conversions, with the specific purpose of extracting strain information.

The key benefits of the new method are:

• (a) reduction of computational effort and processing time (the library time was imported from Python for time process measurement; the results showed 41 vs 1011 s for ‘polar transformation’ and ‘caking’, respectively);

• (b) simplification of the analysis by omitting the conversion of 2D patterns to 1D profiles followed by Gaussian peak fitting;

• (c) minimizing possible error sources associated with radial-azimuthal binning.

The new technique for the processing of 2D X-ray diffraction patterns collected at synchrotrons in large volumes conforms to these requirements. Furthermore, the efficiency of the original method may additionally facilitate online strain mapping in engineering objects during data collection. Cartesian-to-polar transformation of 2D synchrotron X-ray diffraction patterns allows separating Debye-Scherrer rings distortions into the contributions from detector misalignment and strain, respectively.