Precedence-Constrained Scheduling and Min-Sum Set Cover

Abstract

We consider a single-machine scheduling problem with bipartite AND/OR-constraints that is a natural generalization of (precedence-constrained) min-sum set cover. For min-sum set cover, Feige, Lovàsz and Tetali [15] showed that the greedy algorithm has an approximation guarantee of 4, and obtaining a better approximation ratio is NP-hard. For precedence-constrained min-sum set cover, McClintock, Mestre and Wirth [30] proposed an $O(\sqrt{m})$-approximation algorithm, where m is the number of sets. They also showed that obtaining an algorithm with performance $O(m^{1/12-\varepsilon })$ is impossible, assuming the hardness of the planted dense subgraph problem.

The more general problem examined here is itself a special case of scheduling AND/OR-networks on a single machine, which was studied by Erlebach, Kääb and Möhring [13]. Erlebach et al. proposed an approximation algorithm whose performance guarantee grows linearly with the number of jobs, which is close to best possible, unless P = NP.

For the problem considered here, we give a new LP-based approximation algorithm. Its performance ratio depends only on the maximum number of OR-predecessors of any one job. In particular, in many relevant instances, it has a better worst-case guarantee than the algorithm by McClintock et al., and it also improves upon the algorithm by Erlebach et al. (for the special case considered here).

Yet another important generalization of min-sum set cover is generalized min-sum set cover, for which a 12.4-approximation was derived by Im, Sviridenko and Zwaan [23]. Im et al. conjecture that generalized min-sum set cover admits a 4-approximation, as does min-sum set cover. In support of this conjecture, we present a 4-approximation algorithm for another interesting special case, namely when each job requires that no less than all but one of its predecessors are completed before it can be processed.

This work has been supported by the Alexander von Humboldt Foundation with funds from the German Federal Ministry of Education and Research (BMBF).

1 Introduction

In this paper, we consider the problem of scheduling jobs subject to AND/OR-precedence constraints on a single machine. These scheduling problems are closely related to (precedence-constrained) min-sum set cover [14, 15, 30] and generalized min-sum set cover [3, 4, 23, 37]. Let $N = A \dot{\cup } B$ be the set of n jobs with processing times $p_j \ge 0$ and weights $w_j \ge 0$ for all $j \in N$. The precedence constraints are given by a directed graph $G=(N,E_{\wedge }\,\dot{\cup }\,E_{\vee })$, where $(i,j) \in E_{\wedge } \cup E_{\vee }$ means that job i is a predecessor of job j. The arcs in $E_{\wedge } \subseteq (A \times A)\,\cup \,(B \times B)$ and $E_{\vee } \subseteq A \times B$ represent AND- and OR-precedence constraints, respectively. That is, a job in N requires that all its predecessors w.r.t. $E_{\wedge }$ are completed before it can start. A job in B, however, requires that at least one of its predecessors w.r.t. $E_{\vee }$ is completed beforehand. The set of OR-predecessors of job $b \in B$ is $\mathcal {P}(b) := \{a \in A \, | \, (a,b) \in E_{\vee } \}$. Note that $\mathcal {P}(b)$ might be empty for some $b \in B$.

A schedule C is an ordering of the jobs on a single machine such that each job j is processed non-preemptively for $p_j$ units of time, and no jobs overlap. The completion time of $j \in N$ in the schedule C is denoted by $C_j$. A schedule C is feasible if (i) $C_j \ge \max \{C_i\ | \ (i,j) \in E_{\wedge } \} + p_j$ for all $j \in N$ (AND-constraints), and (ii) $C_b \ge \min \{C_a \ | \ a \in \mathcal {P}(b) \} + p_b$ for all $b \in B$ with $\mathcal {P}(b) \not = \emptyset$ (OR-constraints). The goal is to determine a feasible schedule C that minimizes the sum of weighted completion times, $\sum _{j \in N} w_j C_j$. We denote this problem by $1 \, | \, ao\text {-}prec=A\,\dot{\vee }\,B \, | \, \sum w_j C_j$, in an extension of the notation of Erlebach, Kääb and Möhring [13] and the three-field notation of Graham et al. [18]. This scheduling problem is NP-hard. In fact, it generalizes a number of NP-hard problems, as discussed below. Therefore, we focus on approximation algorithms. Let $\varPi$ be a minimization problem, and $\rho \ge 1$. Recall that a $\rho$-approximation algorithm for $\varPi$ is a polynomial-time algorithm that returns, for every instance of $\varPi$, a feasible solution with objective value at most $\rho$ times the optimal objective value. If $\rho$ does not depend on the input parameters, we call the algorithm a constant-factor approximation.

Due to space limitations, we defer all proofs to the journal version of this paper. As already indicated, the scheduling problem we consider is motivated by its close connection to min-sum covering problems. Figure 1 gives an overview of the related problems, which we describe briefly in the following paragraphs.

(Min-Sum) Set Cover. The most basic problem is min-sum set cover (MSSC), where the input consists of a hypergraph with vertices V and hyperedges $\mathcal {E}$. Given a linear ordering of the vertices $f: V \rightarrow \vert V \vert$, the covering time of hyperedge $e \in \mathcal {E}$ is defined as $f(e) := \min _{v \in e} f(v)$. The goal is to find a linear ordering of the vertices that minimizes the sum of covering times, $\sum _{e \in \mathcal {E}} f(e)$. MSSC is indeed a special case of $1 \, | \, ao\text {-}prec=A\,\dot{\vee }\,B \, | \, \sum w_j C_j$: we introduce a job in A for every vertex of V and a job in B for every hyperedge in $\mathcal {E}$, and we set $p_a = w_b = 1$ and $p_b = w_a = 0$ for all jobs $a \in A$ and $b \in B$. Further, we let $E_{\wedge } = \emptyset$ and introduce an arc $(a,b) \in E_{\vee }$ in the precedence graph, if the vertex corresponding to a is contained in the hyperedge corresponding to b.

MSSC was first introduced by Feige, Lovàsz and Tetali [14], who observed that a simple greedy heuristic due to Bar-Noy et al. [6] yields an approximation factor of 4. Feige et al. [14] simplified the analysis via a primal/dual approach based on a time-indexed linear program. In the journal version of their paper, Feige et al. [15] also proved that it is NP-hard to obtain an approximation factor strictly better than 4. The special case of MSSC where the hypergraph is an ordinary graph is called min-sum vertex cover (MSVC), and is APX-hard [15]. It admits a 2-approximation that is also based on a time-indexed linear program, and uses randomized rounding [14, 15].

Munagala et al. [31] generalized MSSC by introducing non-negative costs $c_v$ for each vertex $v \in V$ and non-negative weights $w_e$ for each hyperedge $e \in \mathcal {E}$. Here, the goal is to minimize the sum of weighted covering costs, $\sum _{e \in \mathcal {E}} w_e f(e)$, where the covering cost of $e \in \mathcal {E}$ is defined as $f(e):= \min _{v \in e} \sum _{w: f(w) \le f(v)} c_w$. The authors called this problem pipelined set cover, and proved, among other things, that the natural extension of the greedy algorithm of Feige et al. for MSSC still yields a 4-approximation. Similar to MSSC, we can model pipelined set cover as an instance of $1 \, | \, ao\text {-}prec=A\,\dot{\vee }\,B \, | \, \sum w_j C_j$.

Munagala et al. [31] asked whether there is still a constant-factor approximation for pipelined set cover if there are AND-precedence constraints in form of a partial order $\prec$ on the vertices of the hypergraph. That is, any feasible linear ordering $f: V \rightarrow \vert V \vert$ must satisfy $f(v) < f(w)$, if $v \prec w$. This question was partly settled by McClintock, Mestre and Wirth [30]. They presented a $4\sqrt{\vert V \vert }$-approximation algorithm for precedence-constrained MSSC, which is the extension of MSSC where $E_{\wedge } = \{(a',a) \in A \times A \, | \, a' \prec a\}$. The algorithm uses a $\sqrt{\vert V \vert }$-approximative greedy algorithm on a problem called max-density precedence-closed subfamily. The authors also propose a reduction from the so-called planted dense subgraph conjecture [7] to precedence-constrained MSSC. Roughly speaking, the conjecture says that for all $\varepsilon > 0$ there is no polynomial-time algorithm that can decide with advantage $> \varepsilon$ whether a random graph on m vertices is drawn from $(m,m^{\alpha -1})$ or contains a subgraph drawn from $(\sqrt{m},\sqrt{m}^{\beta -1})$ for certain $0< \alpha , \beta < 1$.¹ If the conjecture holds true, then this implies that there is no $\mathcal {O}(\vert V \vert ^{1/12-\varepsilon })$-approximation for precedence-constrained MSSC [30].

The ordinary set cover problem is also a special case of $1 \, | \, ao\text {-}prec=A\,\dot{\vee }\,B \, | \, \sum w_j C_j$: we introduce a job in A with $p_a = 1$ and $w_a = 0$ for every set, a job in B with $p_b = w_b = 0$ for every element, and an arc $(a,b) \in E_{\vee }$ in the precedence graph, if the set corresponding to a contains the element corresponding to b. Further, we include an additional job x in B with $p_x = 0$ and $w_x = 1$, and introduce an arc $(b,x) \in E_{\wedge }$ for every job $b \in B \setminus \{x\}$. If the set cover instance admits a cover of cardinality k, we first schedule the corresponding set-jobs in A, so all element-jobs are available for processing at time k. Then job x can complete at time k, which gives an overall objective value of k. Similarly, any schedule with objective value equal to k implies that all element-jobs are completed before time k, so there exists a cover of size at most k. Recall that set cover admits an $\ln (m)$-approximation [25, 28], where m is the number of elements, and this is best possible, unless P = NP [12].

A New Approximation Algorithm. W.l.o.g., suppose that $E_{\wedge }$ is transitively closed, i.e. $(i,j) \in E_{\wedge }$ and $(j,k) \in E_{\wedge }$ implies $(i,k) \in E_{\wedge }$. We may further assume that there are no redundant OR-precedence constraints, i.e. if $(a,b) \in E_{\vee }$ and $(a',a) \in E_{\wedge }$, then $(a',b) \notin E_{\vee }$. Otherwise we could remove the arc (a, b) from $E_{\vee }$, since any feasible schedule has to schedule $a'$ before a. Let $\varDelta := \max _{b \in B} \vert \mathcal {P}(b) \vert$ be the maximum number of OR-predecessors of a job in B. One can see that $\varDelta$ is bounded from above by the cardinality of a maximum independent set in the induced subgraph on $E_{\wedge } \cap (A \times A)$. Note that $\varDelta$ is often relatively small compared to the total number of jobs. For instance, if the precedence constraints are derived from an underlying graph, where the predecessors of each edge are its incident vertices (as in MSVC), then $\varDelta = 2$. Our first result is the following.

Theorem 1

There is a $2\varDelta$-approximation algorithm for $1 \, | \, ao\text {-}prec=A\,\dot{\vee }\,B, \, p_j \in \{0,1\} \, | \, \sum w_j C_j$. Moreover, for any $\varepsilon > 0$, there is a $(2\varDelta \,+\,\varepsilon )$-approximation algorithm for $1 \, | \, ao\text {-}prec=A\,\dot{\vee }\,B \, | \, \sum w_j C_j$.

In Sect. 2, we first exhibit a randomized approximation algorithm for $1\, | \, ao\text {-}prec=A\,\dot{\vee }\,B, \, p_j \in \{0,1\} \, | \, \sum w_j C_j$, i.e. if all processing times are 0/1, and then we show how to derandomize it. This proves the first part of Theorem 1. A natural question that arises in the context of real-world scheduling problems is whether approximation guarantees for 0/1-problems still hold for arbitrary processing times. As observed by Munagala et al. [31], the natural extension of the greedy algorithm for MSSC still works, if the processing times of jobs in A are arbitrary, but all jobs in B have zero processing time, and there are no AND-precedence constraints. Once jobs in B have non-zero processing times, the analysis of the greedy algorithm fails. In fact, it is not clear whether there are constant-factor approximations. Our algorithm can be extended to arbitrary processing times (which proves the second part of Theorem 1) and, additionally, release dates.

Note that the result of Theorem 1 improves on the algorithm of [30] for precedence-constrained MSSC in two ways. First, the approximation factor of $2\varDelta$ does not depend on the total number of jobs, but on the maximum number of OR-predecessors of a job in B. In particular, we immediately obtain a 4-approximation for the special case of precedence-constrained MSVC. Secondly, the algorithm works for arbitrary processing times, additional AND-precedence constraints on $B \times B$, and it can be extended to non-trivial release dates of the jobs. Note that, in general, $\varDelta$ and $\sqrt{\vert V \vert }$ are incomparable. In most practically relevant instances, $\varDelta$ should be considerably smaller than $\sqrt{\vert V \vert }$.

It is important to highlight that the approximation factor of $2 \varDelta$ in Theorem 1 does not contradict the conjectured hardness of precedence-constrained MSSC stated in [30]. The set A in the reduction of [30] from the planted dense subgraph problem contains a job for every vertex and every edge of the random graph on m vertices. Each vertex-job consists of the singleton $\{0\}$ whereas each edge-job is a (random) subset of $[q] := \{1,\dots ,q\}$, for some non-negative integer q. Every element in [q] appears in expectation in $mp^2$ many edge-jobs, where p is a carefully chosen probability. If we interpret this as a scheduling problem, we can remove the dummy element 0 from the instance. So the maximum indegree of a job in $B =[q]$ (maximum number of appearances of the element) is $\varDelta ~\approx ~m p^2 \ge ~m^{\frac{1}{4}}$, see [30]. Hence the gap $\varOmega (m^{\frac{1}{8}})$ in the reduction translates to a gap of $\varOmega (\sqrt{\varDelta })$ in our setting. Therefore, if the planted dense subgraph conjecture [7] holds true, then there is no $\mathcal {O}(\varDelta ^{1/3 - \varepsilon })$-approximation algorithm for $1 \, | \, ao\text {-}prec=A\,\dot{\vee }\,B \, | \, \sum w_j C_j$ for any $\varepsilon > 0$.

Note that in the reduction from set cover to $1 \, | \, ao\text {-}prec=A\,\dot{\vee }\,B \, | \, \sum w_j C_j$ the parameter $\varDelta$ equals the maximum number of appearances of an element in the set cover instance. Hochbaum [22] presented an approximation algorithm for set cover with a guarantee of $\varDelta$. Hence the $2\varDelta$-approximation of Theorem 1 does not contradict the hardness of obtaining a $(1-\varepsilon )\ln (m)$-approximation for set cover [12]. If the planted dense subgraph conjecture [7] is false, then constant-factor approximations for $1 \, | \, ao\text {-}prec=A\,\dot{\vee }\,B \, | \, \sum w_j C_j$ with $E_{\wedge } \subseteq A \times A$ may be possible. However, the reduction from set cover shows that, in general, we cannot get a constant-factor approximation if $E_{\wedge } \cap (B \times B) \not = \emptyset$.

Fig. 1.

Overview of related problems and results. An arrow from problem $\varPi _1$ to $\varPi _2$ indicates that $\varPi _2$ generalizes $\varPi _1$. Problems in rectangular frames are explicitly considered in this paper, and our results are depicted in bold. Lower bounds indicated with “??” are assuming hardness of the planted dense subgraph problem [7].

Generalized Min-Sum Set Cover. A different generalization of MSSC, called generalized min-sum set cover (GMSSC), was introduced by Azar, Gamzu and Yin [3]. The input of GMSSC is similar to MSSC, but, in addition, each hyperedge $e \in \mathcal {E}$ is associated with a covering requirement $\kappa (e) \in [\vert e \vert ]$. Given a linear ordering of the vertices, the covering time of $e \in \mathcal {E}$ is now the first point in time when $\kappa (e)$ of its incident vertices appear in the linear ordering. The goal is again to minimize the sum of covering times over all hyperedges.

In our notation, this means that $E_{\wedge } = \emptyset$ and each job $b \in B$ requires at least $\kappa (b) \in [\vert \mathcal {P}(b) \vert ]$ of its OR-predecessors to be completed before it can start. The extreme cases $\kappa (b) = 1$ and $\kappa (b) = \vert \mathcal {P}(b) \vert$ are MSSC and the minimum latency set cover problem. The latter is, in fact, equivalent to single-machine scheduling with AND-precedence constraints [40]. Over time, several constant-factor approximations for GMSSC were proposed. Bansal, Gupta and Krishnaswamy [4] presented an algorithm with an approximation guarantee of 485, which was improved to 28 by Skutella and Williamson [37]. Both algorithms are based on the same time-indexed linear program, but use different rounding techniques, namely standard randomized rounding [4] and $\alpha$-points [37], respectively.

The currently best-known approximation ratio for GMSSC is 12.4, due to Im, Sviridenko and Zwaan [23]. However, Im et al. [23] conjecture that GMSSC admits a 4-approximation. By adapting the proof of Theorem 1, we obtain a 4-approximation for GMSSC if $\kappa (b) = \max \{\vert \mathcal {P}(b) \vert - 1,1\}$ for all $b \in B$. To the best of the authors’ knowledge, this case, which we call all-but-one MSSC, was not considered before. Here, each job (with more than one predecessor) needs at least all but one of them to be completed before it can start. This is a natural special case inbetween MSSC and AND-precedence constrained scheduling (where $\kappa (b)= 1$ and $\kappa (b) = \vert \mathcal {P}(b) \vert$, respectively). Note that all-but-one MSSC generalizes MSVC. The algorithm of Theorem 2 is described in Sect. 3.

Theorem 2

There is a 4-approximation algorithm for all-but-one MSSC.

Related Work on Scheduling Problems. The first polynomial-time algorithm for scheduling jobs on a single machine to minimize the sum of weighted completion times is due to Smith [38]. Once there are AND-precedence constraints, the problem becomes strongly NP-hard [27]. The first constant-factor approximation for AND-precedence constraints was proposed by Hall, Shmoys and Wein [20] with an approximation factor of $4 + \varepsilon$. Their algorithm is based on a time-indexed linear program and $\alpha$-point scheduling with a fixed value of $\alpha$. Subsequently, various 2-approximations based on linear programs [10, 19, 34] as well as purely combinatorial algorithms [8, 29] were derived. Assuming a variant of the Unique Games Conjecture of Khot [26], Bansal and Khot [5] showed that the approximation ratio of 2 is essentially best possible.

If the precedence constraints are of AND/OR-structure, then the problem does not admit constant-factor approximations anymore. Let $0< c < \frac{1}{2}$ and $\gamma = (\log \log n )^{-c}$. It is NP-hard to approximate the sum of weighted completion times of unit processing time jobs on a single machine within a factor of $2^{\log ^{1-\gamma } n}$, if AND/OR-precedence constraints are involved [13]. The precedence graph in the reduction consists of four layers with an OR/AND/OR/AND-structure. Erlebach, Kääb and Möhring [13] also showed that scheduling the jobs in order of non-decreasing processing times (among the available jobs) yields an n-approximation for general weights and a $\sqrt{n}$-approximation for unit weights, respectively. It can easily be verified that $1 \, | \, ao\text {-}prec=A\,\dot{\vee }\,B \, | \, \sum w_j C_j$ is a special case of the problem considered in [13].

Scheduling unit processing time jobs with OR-precedence constraints only on parallel machines to minimize the sum of completion times can be solved in polynomial time [24]. However, once we want to minimize the sum of weighted completion times, already the single-machine problem with unit processing times becomes strongly NP-hard [24]. We strengthen this result and show that even more restricted special cases are strongly NP-hard already.

Theorem 3

$1 \, | \, ao\text {-}prec=A\,\dot{\vee }\,B, \, p_j \in \{0,1\} \, | \, \sum C_j$ and $1 \, | \, ao\text {-}prec=A\,\dot{\vee }\,B, \, p_j = 1 \, | \, \sum w_j C_j$ with $w_j \in \{0,1\}$ are NP-hard, even if $E_{\wedge } = \emptyset$.

Note that the latter problem is a special case of the problem considered in [24], where it was denoted by $1 \, | \, or\text {-}prec, \, p_j = 1 \, | \, \sum w_j C_j$, and that $1 \, | \, ao\text {-}prec=A\,\dot{\vee }\,B, \, p_j = 1 \, | \, \sum C_j$ is trivial.

Our Techniques and LP Relaxations. The algorithms that lead to Theorems 1 and 2 are based on time-indexed linear programs and the concept of random $\alpha$-point scheduling, similar to, e.g., [9, 16, 17, 19, 20, 35]. One new element here is to not use a global value for $\alpha$, but to use different values of $\alpha$ for the jobs in A and B, respectively. This is crucial in order to obtain feasible schedules. We focus on time-indexed linear programs, since other standard LP formulations fail in the presence of OR-precedence constraints; see Sect. 4.

More specifically, we show that these relaxations have an integrality gap that is linear in the number of jobs, even on instances with $\varDelta = 2$ and $E_{\wedge } = \emptyset$. In Sect. 4.1, we discuss a formulation in linear ordering variables that was introduced by Potts [32]. We present a class of constraints that is facet-defining for the integer hull (Theorem 4), and show that the integrality gap remains linear, even if we add these inequalities. In Sect. 4.2, we consider an LP relaxation in completion time variables, which was proposed by Wolsey [41] and Queyranne [33]. We first generalize the well-known parallel inequalities [33, 41], that fully describe the polytope in the absence of precedence constraints, to OR-precedence constraints (Theorem 5). Then we show that, even though we add an exponential number of tight valid inequalities, the corresponding LP relaxation still exhibits a linear integrality gap.

2 A New Generalization of Min-Sum Set Cover

Consider an instance of $1\, | \, ao\text {-}prec=A\,\dot{\vee }\,B \, | \, \sum w_j C_j$. W.l.o.g., we may assume that $w_a = 0$ for all $a \in A$. Otherwise, we can shift a positive weight of a job in A to an additional successor in B with zero processing time. Further, we may assume that all data is integer and $p_j \ge 1$ for every job $j \in N$ that has no predecessors (otherwise such a job can be disregarded). So no job can complete at time 0 in a feasible schedule.

Suppose that $p_j \in \{0,1\}$ for all $j \in N$, and let $T = \sum _{j \in N} p_j$ be the time horizon. We consider the time-indexed linear programming formulation of Sousa and Wolsey [39] with AND-precedence constraints [20]. The binary variable $x_{jt}$ indicates whether job $j \in N$ completes at time $t \in [T]$ or not. Additionally, we introduce constraints corresponding to $E_{\vee }$. The resulting linear relaxation is

$$\begin{aligned}&\min&\sum \limits _{b \in B} \sum \limits _{t = 1}^{T} w_b \cdot t \cdot x_{bt}&\end{aligned}$$

(1a)

$$\begin{aligned}&\text {s.t.}&\sum \limits _{t=1}^T x_{jt}&= 1 \quad \forall \,j \in N, \end{aligned}$$

(1b)

$$\begin{aligned}&\sum \limits _{j \in N} \sum \limits _{s=t -p_j + 1}^{t} x_{js}&\le 1 \quad \forall \, t \in [T], \end{aligned}$$

(1c)

$$\begin{aligned}&\sum \limits _{s=1}^{t + p_b} x_{bs} - \sum \limits _{a \in \mathcal {P}(b)} \sum \limits _{s=1}^{t} x_{as}&\le 0 \quad \forall \, b \in B: \, \mathcal {P}(b) \not = \emptyset , \ \forall \, t \in [T -p_b], \end{aligned}$$

(1d)

$$\begin{aligned}&\sum \limits _{s =1}^{t+p_j} x_{js} - \sum \limits _{s=1}^t x_{is}&\le 0 \quad \forall \, (i,j) \in E_{\wedge }, \ \forall \, t \in [T - p_j], \end{aligned}$$

(1e)

$$\begin{aligned}&x_{jt}&\ge 0 \quad \forall \, j \in N, \ \forall \, t \in [T] . \end{aligned}$$

(1f)

Constraints (1b) and (1c) ensure that each job is executed and no jobs overlap, respectively. Note that only jobs with $p_j = 1$ appear in (1c). Constraints (1d) and (1e) ensure OR- and AND-precedence constraints, respectively. Note that we can solve LP (1) in polynomial time, since $T \le n$.

Let $\overline{x}$ be an optimal fractional solution of LP (1). For $j \in N$, we call $\overline{C}_j = \sum _t t \cdot \overline{x}_{jt}$ its fractional completion time. Note that $\sum _j w_j \overline{C}_j$ is a lower bound on the objective value of an optimal integer solution, which corresponds to an optimal schedule. For $0 < \alpha \le 1$ and $j \in N$, we define its $\alpha$-point, $t^\alpha _j := \min \{t \, | \, \sum _{s=1}^t \overline{x}_{js} \ge \alpha \}$, to be the first integer point in time when an $\alpha$-fraction of j is completed [20].

The algorithm, hereafter called Algorithm 1, works as follows. First, solve LP (1) to optimality, and let $\overline{x}$ be an optimal fractional solution. Then, draw $\beta$ at random from the interval (0, 1] with density function $f(\beta ) = 2\beta$, and set $\alpha = \frac{\beta }{\varDelta }$. (Choosing $\alpha$ as a function of $\beta$ is crucial in order to obtain a feasible schedule in the end. This together with (1d) ensures that at least one OR-predecessor of a job $b \in B$ completes early enough in the constructed schedule. The density function $f(\beta ) = 2\beta$ is chosen to cancel out an unbounded term of $\frac{1}{\beta }$ in the expected value of the completion time of job b, as in [16, 35].) Now, compute $t^\alpha _a$ and $t^\beta _b$ for all jobs $a \in A$ and $b \in B$, respectively. Sort the jobs in order of non-decreasing values $t^\alpha _a$ ($a \in A$) and $t^\beta _b$ ($b \in B$), and denote this total order by $\prec$. If there is $b \in B$ and $a \in \mathcal {P}(b)$ with $t^\alpha _a = t^\beta _b$, then set $a \prec b$. Similarly, set $i \prec j$, if $(i,j) \in E_{\wedge }$ and $t^\alpha _{i} = t^\alpha _j$ (for $i,j \in A$) or $t^\beta _{i} = t^\beta _j$ (for $i,j \in B$). (Recall that $E_{\wedge } \subseteq (A \times A) \cup (B \times B)$, so $(i,j) \in E_{\wedge }$ implies $i,j \in A$ or $i,j \in B$.) Break all other ties arbitrarily. Our main result shows that ordering jobs according to $\prec$ yields a feasible schedule and that the expected objective value of this schedule is at most $2\varDelta$ times the optimum.

Lemma 1

Algorithm 1 is a randomized $2 \varDelta$-approximation for $1 \, | \, ao\text {-}prec=A\,\dot{\vee }\,B, \, p_j \in \{0,1\} \, | \, \sum w_j C_j$.

For fixed $\overline{x}$ and $0 < \beta \le 1$ we call the schedule that orders the jobs according to $\prec$ the $\beta$-schedule of $\overline{x}$. Given $\overline{x}$ and $0 < \beta \le 1$, we can construct the $\beta$-schedule in time $\mathcal {O}(n)$. We derandomize Algorithm 1 by a simple observation similar to [9, 17]. List all possible schedules that occur as $\beta$ goes from 0 to 1, and pick the best one. The next lemma shows that the number of different $\beta$-schedules is not too large.

Lemma 2

For every $\overline{x}$ there are $\mathcal {O}(n^2)$ different $\beta$-schedules.

Lemmas 1 and 2 together prove the first part of Theorem 1. Note that for scheduling instances that are equivalent to MSVC, $\varDelta = 2$. Hence, we immediately obtain a 4-approximation for these instances.

Corollary 1

There is a 4-approximation algorithm for precedence-constrained MSVC.

If we use an interval-indexed LP instead of a time-indexed LP, see e.g. [19, 20], then Algorithm 1 can be generalized to arbitrary processing times. This will prove the second part of Theorem 1. Let $\varepsilon ' > 0$, and recall that all processing times are non-negative integers. Let $T = \sum _{j \in N} p_j$ be the time horizon and L be minimal such that $(1+\varepsilon ')^{L-1} \ge T$. Set $\tau _{0} := 1$, and let $\tau _l = (1+ \varepsilon ')^{l-1}$ for every $l \in [L]$. We call $(\tau _{l-1},\tau _l]$ the l-th interval for $l \in [L]$. (The first interval is the singleton $(1,1]:=\{1\}$.) We introduce a binary variable $x_{jl}$ for every $j \in N$ and for every $l \in [L]$ that indicates whether or not job j completes in the l-th interval. If we relax the integrality constraints on the variables we obtain the following relaxation:

$$\begin{aligned}&\min&\sum \limits _{b \in B} \sum \limits _{l = 1}^{L} w_b \cdot \tau _{l-1} \cdot x_{bl}&\end{aligned}$$

(2a)

$$\begin{aligned}&\text {s.t.}&\sum \limits _{l=1}^L x_{jl}&= 1 \quad \forall \,j \in N, \end{aligned}$$

(2b)

$$\begin{aligned}&\sum \limits _{j \in N} \sum \limits _{k=1}^l p_j \, x_{jk}&\le \tau _l \quad \forall \, l \in [L], \end{aligned}$$

(2c)

$$\begin{aligned}&\sum \limits _{k=1}^l x_{bk} - \sum \limits _{a \in \mathcal {P}(b)} \sum \limits _{k=1}^l x_{ak}&\le 0 \quad \forall \, b \in B: \, \mathcal {P}(b) \not = \emptyset , \ \forall \, l \in [L], \end{aligned}$$

(2d)

$$\begin{aligned}&\sum \limits _{k =1}^{l} x_{jk} - \sum \limits _{k=1}^l x_{ik}&\le 0 \quad \forall \, (i,j) \in E_{\wedge }, \ \forall \, l \in [L], \end{aligned}$$

(2e)

$$\begin{aligned}&x_{jl}&\ge 0 \quad \forall \, j \in N, \ \forall \, l \in [L]: \, \tau _{l-1} \ge p_j . \end{aligned}$$

(2f)

Given $\varepsilon '$, the size of LP (2) is polynomial, so we can solve it in polynomial time. Again (2b) ensures that every job is executed. Constraints (2c) are valid for any feasible schedule, since the total processing time of all jobs that complete within the first l intervals cannot exceed $\tau _l$. Constraints (2d) and (2e) model OR- and AND-precedence constraints, respectively.

Let $\overline{x}$ be an optimal fractional solution of LP (2), and let $\overline{C}_j = \sum _l \tau _{l-1} \, \overline{x}_{jl}$. Note that $\sum _j w_j \, \overline{C}_j$ is a lower bound on the optimal objective value of an integer solution, which is a lower bound on the optimal value of a feasible schedule. Let $l^\alpha _j = \min \{l \, | \, \sum _{k=1}^l \overline{x}_{jk} \ge \alpha \}$ be the $\alpha$-interval of job $j \in N$. This generalizes the notion of $\alpha$-points from before.

The algorithm for arbitrary processing times is similar to Algorithm 1. We call it Algorithm 2 and it works as follows. In order to achieve a $(2 \varDelta + \varepsilon )$-approximation, solve LP (2) with $\varepsilon ' = \frac{\varepsilon }{2\varDelta }$ and let $\overline{x}$ be an optimal solution. Then, draw $\beta$ at random from the interval (0, 1] with density function $f(\beta ) = 2\beta$, and set $\alpha = \frac{\beta }{\varDelta }$. Compute $l^\alpha _a$ and $l^\beta _b$ for all jobs $a \in A$ and $b \in B$, respectively. Sort the jobs in order of non-decreasing values $l^\alpha _a$ ($a \in A$) and $l^\beta _b$ ($b \in B$) and denote this total order by $\prec$. If $l^\alpha _a = l^\beta _b$ for some $b \in B$ and $a \in \mathcal {P}(b)$, set $a \prec b$. Similarly, set $i \prec j$, if $(i,j) \in E_{\wedge }$ and $l^\alpha _{i} = l^\alpha _j$ (for $i,j \in A$) or $l^\beta _{i} = l^\beta _j$ (for $i,j \in B$). Break all other ties arbitrarily. Finally, schedule the jobs in the order of $\prec$. Note that $\prec$ extends the order for $\alpha$-points from Algorithm 1 to $\alpha$-intervals.

Lemma 3

For any $\varepsilon > 0$, Algorithm 2 is a randomized $(2 \varDelta + \varepsilon )$-approximation for $1 \, | \, ao\text {-}prec=A\,\dot{\vee }\,B \, | \, \sum w_j C_j$.

We can derandomize Algorithm 2 similar to Lemma 2. Algorithms 1 and 2 can be further extended to release dates. To do so, we need to add constraints to LP (1) and LP (2) that ensure that no job completes too early. More precisely, fix $x_{jt} = 0$ for all $j \in N$ and $t < r_j + p_j$ in LP (1) and $x_{jl} = 0$ for all $j \in N$ and $\tau _{l-1} < r_j + p_j$ in LP (2), respectively. When scheduling the jobs according to $\prec$, we might have to add idle time in order to respect the release dates. This increases the approximation factor slightly.

Lemma 4

There is a $(2\varDelta + 2)$- and $(2\varDelta + 2 + \varepsilon )$-approximation algorithm for $1 \, | \, r_j, \, ao\text {-}prec=A\,\dot{\vee }\,B, \, p_j \in \{0,1\} \, | \, \sum w_j C_j$ and $1 \, | \, r_j, \, ao\text {-}prec=A\,\dot{\vee }\,B \, | \, \sum w_j C_j$, respectively.

3 The Generalized Min-Sum Set Cover Problem

Recall that we can model GMSSC as a single-machine scheduling problem to minimize the sum of weighted completion times with job set $N = A\,\dot{\cup }\,B$, processing times $p_j \in \{0,1\}$, and certain precedence requirements $\kappa (b)$ for each job $b \in B$.

In this section, we prove Theorem 2. That is, we give a 4-approximation algorithm for the special case of GMSSC where $\kappa (b) = \max \{d(b) - 1,1\}$ with $d(b) := \vert \mathcal {P}(b) \vert$ for all $b \in B$. So each job in B requires all but one of its predecessors to be completed before it can start, unless it has only one predecessor (all-but-one MSSC). Suppose we want to schedule a job $b \in B$ with $d(b) \ge 2$ at time $t \ge 0$. Then we need at least $d(b) - 1$ of its predecessors to be completed before t. Equivalently, for each pair of distinct $i,j \in \mathcal {P}(b)$ at most one of the two jobs i, j may complete after t. This gives the following linear relaxation with the same time-indexed variables as before and time horizon $T =\sum _{j \in N} p_j \le n$.

$$\begin{aligned}&\min&\sum \limits _{b \in B} \sum \limits _{t = 1}^{T} w_b \cdot t \cdot x_{bt} \end{aligned}$$

(3a)

$$\begin{aligned}&\text {s.t.}&\sum \limits _{t=1}^T x_{jt}&= 1 \quad \forall \,j \in N, \end{aligned}$$

(3b)

$$\begin{aligned}&\sum \limits _{j \in N} \sum \limits _{s=t -p_j +1}^{t} x_{js}&\le 1 \quad \forall \, t \in [T], \end{aligned}$$

(3c)

$$\begin{aligned}&\sum \limits _{s=1}^{t+p_b} x_{bs} - \sum \limits _{s=1}^{t} ( x_{is} + x_{js})&\le 0 \quad \forall \, b \in B, \, \forall i,j \in \mathcal {P}(b), \, \forall \, t \in [T -p_b], \end{aligned}$$

(3d)

$$\begin{aligned}&\sum \limits _{s=1}^{t+p_b} x_{bs} - \sum \limits _{s=1}^{t} x_{is}&\le 0 \quad \forall \, b \in B: \, \mathcal {P}(b) = \{i\}, \ \forall \, t \in [T -p_b], \end{aligned}$$

(3e)

$$\begin{aligned}&x_{jt}&\ge 0 \quad \forall \, j \in N, \ \forall \, t \in [T] . \end{aligned}$$

(3f)

Constraints (3b) and (3c) again ensure that each job is processed and no jobs overlap, respectively. Note that only jobs with non-zero processing time contribute to (3c). If $d(b) = 1$, then (3e) dominates (3d). It ensures that the unique predecessor of $b \in B$ is completed before b starts. Note that this is a classical AND-precedence constraint which will not affect the approximation factor.

If $d(b) \ge 2$, then (3d) models the above observation. Suppose at most ${d(b) - 2}$ predecessors of b complete before time t. Then there are $i,j \in \mathcal {P}(b)$ such that $\sum _{s=1}^t (x_{is} + x_{js}) = 0 \ge \sum _{s=1}^{t} x_{bs}$, so b cannot complete by time t.

Note that we can solve LP (3) in polynomial time. Similar to the algorithms of Sect. 2, we first solve LP (3) and let $\bar{x}$ be an optimal fractional solution. We then draw $\beta$ randomly from (0, 1] with density function $f(\beta ) = 2\beta$, and schedule the jobs in A and B in order of non-decreasing $\frac{\beta }{2}$-points and $\beta$-points, respectively. Again, we break ties consistently with precedence constraints. (Choosing $\frac{\beta }{2}$ for the jobs in A ensures that at most one of the predecessors of a job $b \in B$ is scheduled after b in the constructed schedule.) This algorithm is called Algorithm 3.

Lemma 5

Algorithm 3 is a randomized 4-approximation for all-but-one MSSC.

One can derandomize Algorithm 3 similar to Lemma 2, which proves Theorem 2. Note that Algorithm 3 also works if jobs in B have unit processing time. It can be generalized to release dates and arbitrary processing times, if we use an interval-indexed formulation similar to LP (2). If we choose $\varepsilon ' = \frac{\varepsilon }{4}$ and solve the corresponding interval-indexed formulation instead of LP (3), then Algorithm 3 is a $(4 +\varepsilon )$-approximation for any $\varepsilon > 0$. Again, AND-precedence constraints do not affect the approximation factor, similar to Lemmas 1 and 3.

4 Integrality Gaps for Other LP Relaxations

In this section, we analyze other standard linear programming relaxations that have been useful for various scheduling problems, and show that they fail in the presence of OR-precedence constraints. More precisely, we show that the natural LPs in linear ordering variables (Sect. 4.1) and completion time variables (Sect. 4.2) both exhibit integrality gaps that are linear in the number of jobs, even on instances where $E_{\wedge } = \emptyset$ and $\varDelta = 2$.

4.1 Linear Ordering Formulation

The following relaxation for single-machine scheduling problems was proposed by Potts [32]. It is based on linear ordering variables $\delta _{ij}$, which indicate whether job i precedes job j ($\delta _{ij} = 1$) or not ($\delta _{ij} = 0$). This LP has played an important role in better understanding Sidney’s decomposition [11, 36], and in uncovering the connection between AND-scheduling and vertex cover [1, 2, 10, 11]. A nice feature of this formulation is that we can model OR-precedence constraints in a very intuitive way with constraints $\sum _{a \in \mathcal {P}(b)} \delta _{ab} \ge 1$ for all $b \in B$. Together with the total ordering constraints ($\delta _{ij} + \delta _{ji} = 1$), standard transitivity constraints ($\delta _{ij} + \delta _{jk} + \delta _{ki} \ge 1$) and AND-precedence constraints ($\delta _{ij} = 1$) we thus obtain a polynomial size integer program for $1 \, | \, ao\text {-}prec=A\,\dot{\vee }\,B \, | \, \sum w_j C_j$. The LP-relaxation is obtained by relaxing the integrality constraints to $\delta _{ij} \ge 0$.

$$\begin{aligned}&\min&\sum \limits _{j \in N} \sum \limits _{i \in N} w_j p_i \delta _{ij}&\end{aligned}$$

(4a)

$$\begin{aligned}&\text {s.t.}&\delta _{ij} + \delta _{ji}&= 1 \quad \forall \, i,j \in N: \, i \not = j \end{aligned}$$

(4b)

$$\begin{aligned}&\delta _{ij} + \delta _{jk} + \delta _{ki}&\ge 1 \quad \forall \, i,j,k \in N \end{aligned}$$

(4c)

$$\begin{aligned}&\sum \limits _{a \in \mathcal {P}(b)} \delta _{ab}&\ge 1 \quad \forall \, b \in B: \, \mathcal {P}(b) \not = \emptyset , \end{aligned}$$

(4d)

$$\begin{aligned}&\delta _{ij}&= 1 \quad \forall \, (i,j) \in E_{\wedge }, \end{aligned}$$

(4e)

$$\begin{aligned}&\delta _{ii}&= 1 \quad \forall \, i \in N, \end{aligned}$$

(4f)

$$\begin{aligned}&\delta _{ij}&\ge 0 \quad \forall \, i,j \in N. \end{aligned}$$

(4g)

We set $\delta _{ii} = 1$ in (4f) so the completion time of job j is $C_j = \sum _i p_i \delta _{ij}$. Note that every feasible single-machine schedule without idle time corresponds to a feasible integer solution of LP (4), and vice versa. If $E_{\vee } = \emptyset$, i.e., $\mathcal {P}(b) = \emptyset$ for all $b \in B$, then this relaxation has an integrality gap of 2 (lower and upper bound of 2 due to [8] and [34], respectively). However, in the presence of OR-precedence constraints, the gap of LP (4) grows linearly in the number of jobs, even if $E_{\wedge } = \emptyset$ and $\varDelta = 2$.

Lemma 6

There is a family of instances such that the integrality gap of LP (4) is $\varOmega (n)$.

Fig. 2.

Instance for which LP (4) exhibits an integrality gap that is linear in the number of jobs. The processing times and weights are $p_{j_q} = 0$, $p_{i_q} = p_{k_q} = 1$ and $w_{j_q} = 1$, $w_{i_q} = w_{k_q} = 0$ for all $q \in [m]$.

The instances of Lemma 6 consist of copies of an instance on three jobs, as illustrated in Fig. 2. Note that these satisfy $\vert \mathcal {P}(b) \vert \le 2$ for all $b \in B$. For this special case, we present facet-defining inequalities. If $\vert \mathcal {P}(b) \vert \le 2$ for all $b \in B$, then LP (4) can be reformulated as

$$\begin{aligned}&\min&\sum \limits _{j \in N} \sum \limits _{i \in N} w_j p_i \delta _{ij}&\end{aligned}$$

(5a)

$$\begin{aligned}&\text {s.t.}&\delta _{ij} + \delta _{ji}&= 1 \quad \forall \, i,j \in N: \, i \not = j ,\end{aligned}$$

(5b)

$$\begin{aligned}&\delta _{ij} + \delta _{jk} + \delta _{ki}&\ge 1 \quad \forall \, i,j,k \in N, \end{aligned}$$

(5c)

$$\begin{aligned}&\delta _{ab} + \delta _{a'b}&\ge 1 \quad \forall \, b \in B: \, \mathcal {P}(b)=\{a,a'\}, \end{aligned}$$

(5d)

$$\begin{aligned}&\delta _{ij}&= 1 \quad \forall \, (i,j) \in E_{\wedge }, \text { or } \mathcal {P}(j) = \{i\}, \end{aligned}$$

(5e)

$$\begin{aligned}&\delta _{ii}&= 1 \quad \forall \, i \in N, \end{aligned}$$

(5f)

$$\begin{aligned}&\delta _{ij}&\ge 0 \quad \forall \, i,j \in N. \end{aligned}$$

(5g)

Note that constraints (5b), (5c), and (5f) coincide with the corresponding constraints in LP (4). Constraints (5d) model the OR-precedence constraints for jobs $b \in B$ with $\vert \mathcal {P}(b) \vert = 2$. For $b \in B$ with $\vert \mathcal {P}(b) \vert = 1$, the corresponding OR-precedence constraint is equivalent to an AND-constraint and is included in (5e).

Theorem 4

For all $b \in B$ and $\mathcal {P}(b) = \{a,a'\}$, the constraints

$$\begin{aligned} \delta _{aa'} + \delta _{a'b} \ge 1 \end{aligned}$$

(6)

are valid for the integer hull of LP (5). Moreover, if they are tight, then they are either facet-defining or equality holds for all feasible integer solutions of LP (5).

One can verify that the integrality gap of LP (5) remains linear for the example in Fig. 2, even if we add constraints (6). Recall that in GMSSC each job $b \in B$ requires at least $\kappa (b) \in [\vert \mathcal {P}(b) \vert ]$ of its predecessors to be completed before it can start. This can also be easily modeled with linear ordering variables by introducing a constraint $\sum _{a \in \mathcal {P}(b)} \delta _{ab} \ge \kappa (b)$. However, note that the instance in Fig. 2 is an instance of MSVC (which is a special case of MSSC and all-but-one MSSC). So already for $\kappa (b) = 1$ or $\kappa (b) = \max \{\vert \mathcal {P}(b) \vert -1,1\}$ and $\varDelta = 2$ this formulation has an unbounded integrality gap.

4.2 Completion Time Formulation

The LP relaxation examined in this section contains one variable $C_j$ for every job $j \in N$ that indicates the completion time of this job. In the absence of precedence constraints, the convex hull of all feasible completion time vectors can be fully described by the set of vectors $\{C \in \mathbb {R}^n \, | \, \sum _{j \in S} p_j C_j \ge f(S) \ \forall \, S \subseteq N\}$, where $f(S) := \frac{1}{2}\left( \sum _{j \in S} p_j \right) ^2 + \frac{1}{2} \sum _{j \in S} p_j^2$ is a supermodular function [33, 41]. One should note that, although there is an exponential number of constraints, one can separate them efficiently [33]. That is, one can solve $\min \sum _{j \in N} w_j C_j$ subject to $\sum _{j \in S} p_j C_j \ge f(S)$ for all $S \subseteq N$ in polynomial time. In the presence of AND-precedence constraints, Schulz [34] proposed the first 2-approximation algorithm. The algorithm solves the corresponding linear program with additional constraints $C_j \ge C_i + p_j$ for $(i,j) \in E_{\wedge }$ and schedules the jobs in non-decreasing order of their LP-values.

For OR-precedence constraints, we use the concept of minimal chains, see e.g. [21], to generalize the parallel inequalities of [33, 41]. More specifically, we present a class of inequalities that are valid for all feasible completion time vectors of an instance of $1 \, | \, ao\text {-}prec=A\,\dot{\vee }\,B \, | \, \sum w_j C_j$, and that, in the absence of precedence constraints, coincide with the parallel inequalities. We add inequalities for AND-precedence constraints in the obvious way, $C_j \ge C_i + p_j$ for $(i,j) \in E_{\wedge }$, so we assume $E_{\wedge } = \emptyset$ for the moment.

We call $S \subseteq N$ a feasible starting set, if we can schedule the jobs in S without violating any OR-precedence constraints. The set of feasible starting sets is denoted by $\mathcal {S}$. That is, $S \in \mathcal {S}$, if $j \in B \cap S$ implies that $\mathcal {P}(j) \cap S \not = \emptyset$. The length of a minimal chain of a job k w.r.t. a set $S \subseteq N$ is defined as

$$\begin{aligned} mc(S,k) := \min \{ \sum _{j \in T} p_j \ | \ T \subseteq N: \exists \, U \subseteq S \cup T \text { with } k \in U \in \mathcal {S}\}. \end{aligned}$$

(7)

Intuitively, the value mc(S, k) is the minimal amount of time that we need to schedule job k in a feasible way, if we can schedule the jobs in S for free, i.e. if we assume all jobs in S have zero processing time. Let $2^N$ be the power set of N. For all $k \in N$, we define a set function $f_k(S): 2^N \rightarrow \mathbb {R}_{\ge 0}$ via

$$\begin{aligned} f_k(S) := \frac{1}{2} \left( \sum _{j \in S} p_j + mc(S,k)\right) ^2 + \frac{1}{2} \left( \sum _{j \in S} p_j^2 + mc(S,k)^2\right) . \end{aligned}$$

(8)

Note that if $k \in S \in \mathcal {S}$, then $mc(S,k) = 0$, so $f_k(S) = f(S)$. In particular, (8) generalizes the function $f: 2^N \rightarrow \mathbb {R}_{\ge 0}$ of [33, 41] to OR-precedence constraints.²

Theorem 5

For any $k \in N$ and $S \subseteq N$ the inequality

$$\begin{aligned} \sum \limits _{j \in S} p_j C_j + mc(S,k) \, C_k \ge f_k(S) \end{aligned}$$

(9)

is valid for all feasible completion time vectors. If there is $T \in {\text {argmin}}(mc(S,k))$ such that $S \cup T \in \mathcal {S}$ is a feasible starting set, then (9) is tight.

Theorem 5 suggests the following natural LP-relaxation for $1 \, | \, ao\text {-}prec=A\,\dot{\vee }\,B \, | \, \sum w_j C_j$:

$$\begin{aligned}&\min&\sum _{j \in N} w_j C_j&\end{aligned}$$

(10a)

$$\begin{aligned}&\text {s.t.}&\sum _{j \in S} p_j C_j + mc(S,k) \, C_k&\ge f_k(S)&\forall \, k \in N, \ \forall \, S \subseteq N, \end{aligned}$$

(10b)

$$\begin{aligned}&C_j - C_i&\ge p_j \quad&\forall \, (i,j) \in E_{\wedge } . \end{aligned}$$

(10c)

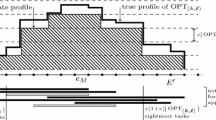
Note that it is not clear how to separate constraints (10b). The gap of LP (10) can grow linearly in the number of jobs, even for instances of $1 \, | \, ao\text {-}prec=A\,\dot{\vee }\,B \, | \, \sum w_j C_j$ with $E_{\wedge } = \emptyset$ and $\varDelta = 2$, see Fig. 3.

Lemma 7

There is a family of instances such that the gap between an optimal solution for LP (10) and an optimal schedule is $\varOmega (n)$.

Fig. 3.

Sketch of instance for which LP (10) exhibits a gap that is linear in the number of jobs. The processing times and weights are $p_k = \frac{m}{2}$, $w_k = w_{i_q} = p_{j_q} = 0$, and $w_{j_q} = p_{i_q} = 1$ for all $q \in [m]$.

5 Conclusion

In this extended abstract, we analyze single-machine scheduling problems with certain AND/OR-precedence constraints that are extensions of min-sum set cover, precedence-constrained min-sum set cover, pipelined set cover, minimum latency set cover, and set cover. Using machinery from the scheduling context, we derive new approximation algorithms that rely on solving time-indexed linear programming relaxations and scheduling jobs according to random $\alpha$-points. In a nutshell, one may say that the new key technique is to choose the value of $\alpha$ for jobs in A dependent on the corresponding $\beta$-value of jobs in B. This observation allows us also to derive the best constant-factor approximation algorithm for an interesting special case of the generalized min-sum set cover problem—the all-but-one MSSC problem—which in itself is a generalization of min-sum vertex cover. This 4-approximation algorithm may further support the conjecture of Im et al. [23], namely that GMSSC is 4-approximable.

It is easy to see that one can also include AND-precedence constraints between jobs in A and B, i.e., allow $E_{\wedge } \subseteq (A \times N) \cup (B \times B)$. This does not affect the approximation guarantees or feasibility of the constructed schedules, since $\alpha \le \beta$ and constraints (1e) imply $t^\alpha _a \le t^\beta _b$ for $(a,b) \in E_{\wedge }$. Similarly, $l^\alpha _a \le l^\beta _b$ for $(a,b) \in E_{\wedge }$ follows from (2e). Note that it is not clear whether the analysis of the algorithms in Sects. 2 and 3 are tight.

Besides deriving approximation algorithms based on time-indexed LPs, we analyze other standard LP relaxations, namely linear ordering and completion time formulations. These relaxations facilitated research on scheduling with AND-precedence constraints, see e.g. [1, 2, 10, 11, 19, 32,33,34]. For the integer hull of the linear ordering relaxation we present a class of facet-defining valid inequalities and we generalize the well-known inequalities of [33, 41] for the completion time relaxation. We show that, despite these additional constraints, both relaxations exhibit linear integrality gaps, even if $\varDelta = 2$ and $E_{\wedge } = \emptyset$. Thus, unless one identifies stronger valid inequalities, these formulations seem to fail as soon as OR-precedence constraints are incorporated. In view of the integrality gaps in Sect. 4, it would be interesting to obtain stronger bounds on the integrality gap of the time-indexed formulation considered in Sects. 2 and 3.