An Experimental Study of Univariate Global Optimization Algorithms for Finding the Shape Parameter in Radial Basis Functions

Abstract

In this contribution, an interpolation problem using radial basis functions is considered. A recently proposed approach for the search of the optimal value of the shape parameter is studied. The approach consists of using global optimization algorithms to minimize the error function obtained using a leave-one-out cross validation (LOOCV) technique, which is commonly used for solving machine learning problems. In this paper, the proposed approach is studied experimentally on classes of randomly generated test problems using the GKLS-generator, which is widely used for testing global optimization algorithms. The experimental study on classes of randomly generated test problems is very important from the practical point of view, since results show the behavior of the algorithms for solving not a single test problem, but the whole class with controllable difficulty, which is the main property of the GKLS-generator. The obtained results are relevant, since the experiments have been carried out on 200 randomized test problems, and show that the algorithms are efficient for solving difficult real-life problems demonstrating a promising behavior.

The work of M. S. Mukhametzhanov was supported by the project “Smart Electronic Invoices Accounting” - SELINA CUP: J28C17000160006 (POR CALABRIA FESR-FSE 2014–2020) and by the INdAM-GNCS funding “Giovani Ricercatori 2018–2019”. The work of R. Cavoretto and A. De Rossi was partially supported by the Department of Mathematics “Giuseppe Peano” of the University of Torino via Project 2019 “Mathematics for applications” and by the INdAM–GNCS Project 2019 “Kernel-based approximation, multiresolution and subdivision methods and related applications”.

1 Introduction

Finding an optimal value of the shape parameter is a very important problem in the Radial Basis Functions (RBF) community. As it has been shown in [5], the choice of the shape parameter influences both the accuracy and stability in interpolation using RBFs. Traditionally, there are several ways to choose the value of the shape parameter in RBF interpolation: ad hoc choices, pre-fixed constant values (see, e.g., [6, 12]), using local optimization methods (see, e.g., [34]), etc. In the recent paper [4], it has been proposed to use global optimization algorithms for finding a good value of the shape parameter. A well-known Leave-One-Out Cross Validation technique has been used in order to introduce the error function, which is the objective function for the optimization problem. Well-known geometric and information univariate global optimization algorithms have been modified in order to increase their efficiency while solving this type of problems. Numerical experiments on several single benchmark test problems have shown the advantages of the proposed techniques.

In this paper, the algorithms proposed in [4] are studied experimentally on the classes of randomly generated test problems. The widely used in testing global optimization algorithms GKLS-generator of randomized test functions is used for this purpose. It can generate classes of 100 test functions with the same properties and controllable difficulty, allowing one to perform a more efficient experimental analysis of numerical algorithms. In this paper, the generator is used for constructing the objective functions for the interpolation problems, which are then used for constructing the respective optimization problems. It should be also noted that the use of classes of randomized test problems allows one not only to perform more reliable and homogeneous numerical experiments, but to visualize the results in a more clear way with respect to numerical tables, using, e.g., graphical representations or statistical notations.

The rest of the paper is organized as follows. In Sect. 2, RBF interpolation and the respective optimization problems are stated briefly. In Sect. 3, numerical algorithms used in this paper and performed experiments are described briefly. Section 4 presents the obtained results. Finally, Sect. 5 concludes the paper.

2 Problem Statement

2.1 Statement of the Interpolation Problem

Let us consider the following interpolation problem. Let the set $X_n= \{x_1,...,$ $x_n\},$ $x_i \in \mathbb {R}^s,~i=1,...,n,$ $x_i \ne x_j,~i,j = 1,...,n$ of n interpolation nodes and the corresponding set $F_n=\{f(x_1),\ldots ,f(x_n)\}$ of values of the function $f: \mathbb {R}^s \rightarrow \mathbb {R}$ be given. Let $\mathcal{I}_f: \mathbb {R}^s \rightarrow \mathbb {R}$ be the radial basis function (RBF) interpolant given as the linear combination of RBFs of the form

$$\begin{aligned} \mathcal{I}_f(x)= \sum _{i=1}^{n} c_i \phi _{\varepsilon } (||x - x_i ||_2), \quad x \in \mathbb {R}^s, \end{aligned}$$

(1)

where $c_i,~i = 1,...,n,$ are unknown real coefficients that can be found from the interpolation conditions $\mathcal{I}_f(x_i) = f(x_i),~i=1,...,n$, $||\cdot ||_2$ denotes the Euclidean norm, and $\phi : \mathbb {R}_{\ge 0}\rightarrow \mathbb {R}$ is a strictly positive definite RBF depending on a shape parameter $\varepsilon > 0$. In this paper, the Gaussian (GA) RBF is used:

$$\begin{aligned} \phi _{\varepsilon }(r) = \mathrm{e}^{-\varepsilon ^2 r^2}. \end{aligned}$$

(2)

The Leave-one-out cross validation technique for the search of the optimal value of the shape parameter $\varepsilon$ can be briefly described as follows. First, for any fixed $\varepsilon$ and each $k = 1,...,n,$ the point $x_k$ and the respective value $f(x_k)$ are excluded from the sets $X_n$ and $F_n$, respectively. Then, the partial RBF interpolant is constructed using only $n-1$ remaining nodes and the error of interpolation at the point $x_k$ is calculated. It has been proved in several works (see, e.g., [24]) that this error can be also calculated without solving n interpolation problems of dimension $n-1$ as follows:

$$\begin{aligned} e_k(\varepsilon ) = f(x_k) - \mathcal{I}_f^{[k]}( x_k) = \frac{c_k}{A_{kk}^{-1}}, \end{aligned}$$

(3)

where $c_k$ is the $k-$th coefficient of the full RBF interpolant $\mathcal{I}_f(x)$ from (1), $\mathcal{I}_f^{[k]}(x)$ is the partial RBF interpolant calculated using only $n-1$ remaining nodes, and $A_{kk}^{-1}$ is the inverse diagonal element of the matrix A:

$$\begin{aligned} A_{ij} = \phi _{\varepsilon }(|| x_i - x_j ||_2), i,j=1,..., n.\end{aligned}$$

(4)

As a consequence, the value of the shape parameter $\varepsilon$ can be fixed in order to minimize the error function $Er(\varepsilon )$ that can be defined, e.g., as follows:

$$\begin{aligned} Er(\varepsilon ) = \max _{k=1,...,n} \left| \frac{c_k}{A_{kk}^{-1}}\right| . \end{aligned}$$

(5)

2.2 Statement of the Optimization Problem

In this paper, the value of the shape parameter $\varepsilon$ is fixed by solving the following optimization problem (see [4] for a detailed discussion): it is required to find the point $\varepsilon ^*$ and the corresponding value $Er^*$ such that

$$\begin{aligned} Er^* = Er(\varepsilon ^*) = \min Er(\varepsilon ),~\varepsilon \in [0,\varepsilon _{max}], \end{aligned}$$

(6)

where $\varepsilon _{max}$ is large enough (in our experiments $\varepsilon _{max}$ was set equal to 20).

The function $Er(\varepsilon )$ can be multiextremal, non-differentiable and hard to evaluate even at one value of $\varepsilon$, since each its computation requires to reconstruct the interpolant (1). It is supposed that $Er(\varepsilon )$ satisfies the Lipschitz condition over the interval $[0, \varepsilon _{max}]$:

$$\begin{aligned} |Er(\varepsilon _1) - Er(\varepsilon _2)| \le L|\varepsilon _1-\varepsilon _2|, \varepsilon _1, \varepsilon _2 \in [0, \varepsilon _{max}], \end{aligned}$$

(7)

where $L,~0<L<\infty ,$ is the Lipschitz constant. Since the function $Er(\varepsilon )$ can be ill-conditioned for small $\varepsilon$ (see, e.g., [3, 5, 7]), then the Lipcshitz constant L can be very large.

There exist a lot of algorithms for solving global optimization problems (see, e.g., [1, 2, 14] for parallel optimization, [9, 13] for dimensionality reduction schemes, [10, 11, 25] for numerical solution of real-life optimization problems, [21] for simplicial optimization methods, [15, 35, 36] for stochastic optimization methods, [16, 17, 22, 32] for univariate Lipschitz global optimization, [23] for interval branch-and-bound methods, etc. Among them, there can be distinguished two groups of algorithms: nature-inspired metaheuristic algorithms (as, for instance, genetic algorithm, firefly algorithm, particle swarm optimization, etc. (see, e.g., [31])) and deterministic mathematical programming algorithms (as, for instance, geometric or information algorithms from [20, 30, 33]). Even though metaheuristic algorithms are used often in practice for solving difficult multidimensional problems, it has been shown in [18, 19, 29] that for solving ill-conditioned univariate problems (6), (7), deterministic algorithms are more efficient. In particular, in [4], it has been shown on a class of benchmarks and two real-world problems that information global optimization algorithms can be successfully used for this purpose. In this paper, these algorithms are studied experimentally on classes of test problems generated by the GKLS-generator of test problems (see [8] for its description).

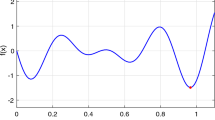
The GKLS-generator of test problems is widely used in practice for testing global optimization algorithms (see, e.g., [1, 21, 31]). It generates classes of 100 randomized multidimensional test problems with the controllable difficulty and a full knowledge about all local and global minimizers (including their positions and their regions of attraction). In this paper, the GKLS-generator is used to generate two-dimensional test functions $f_i(x),~x \in \mathbb {R}^2,$ for the interpolation problem (1). Then, the generated test functions are evaluated at a uniform grid in order to generate n interpolation nodes. Two classes of test functions were used: the “simple” and “difficult”¹ two-dimensional test classes from [26], since they are used frequently for testing global optimization algorithms. In Fig. 1, an example of the GKLS-type test function is presented. The behavior of this function is typical for the functions from both the classes generated by the GKLS-generator.

Fig. 1.

An example of the GKLS-type test function.

3 Algorithms and Organization of Experiments

For each test problem, 128 interpolation nodes are generated on a uniform grid in the square $[-1, 1]\times [-1, 1]$. Hereinafter, the Information global optimization algorithm with Optimistic Local Improvement LOOCV-GOOI from [4] is used for solving (6) as one of the best global optimization algorithms. This algorithm is a locally-biased version of the information global optimization algorithm with “Maximum-Additive” local tuning and optimistic local improvement from [4]. In particular, the main advantage of this method with respect to the original information global optimization algorithm from [32] consists of the ill-conditioned region refinement and restriction of the search interval. Since it is well known that for small values of the parameter $\varepsilon$, the function $Er(\varepsilon )$ becomes ill-conditioned (see, e.g., [3]), then it could be reasonable to study better the region with the small values of $\varepsilon$. For this purpose, the algorithm is launched first on the whole search interval (the Preliminary Search step). Then, the global search is performed on the first subinterval (the Ill-Conditioned Region Refinement step). Finally, after the preliminary search and the ill-conditioned region refinement, the search interval is restricted in a neighborhood of the best obtained values of $\varepsilon$. After that, the search is continued over the restricted interval (the Main Search step). The standard exhaustive LOOCV method using uniform grids of the values of $\varepsilon$ as well as the local minimization algorithm LOOCV-min implemented as MATLAB’s procedure fminbnd from [4] are compared with the LOOCV-GOOI algorithm.

Parameters of the algorithms were set following [4]. In particular, the value $\delta = 10^{-3}$ was used for the stopping condition in LOOCV-GOOI, the reliability parameter r was set to $r = 12$ for the preliminary search, $r = 8$ for the ill-conditioned region refinement, and $r = 4$ for the main search. The local optimization algorithm LOOCV-min uses only the parameter tolX, which was set to $10^{-15}$ in our experiments in order to achieve the machine precision, for the stopping condition. Since, in [4] the LOOCV method using a uniform grid with 500 nodes has been used, but both the local and global optimization algorithms LOOCV-min and LOOCV-GOOI have not generated more than 100 trials, then it can be reasonable to study the LOOCV method with a larger stepsize. Thus, the LOOCV method with the stepsizes $h_1 = \varepsilon _{max}/99$ and $h_2 = \varepsilon _{max}/499$ (called LOOCV-100 and LOOCV-500, respectively) are compared with the LOOCV-min and LOOCV-GOOI algorithms (the algorithm LOOCV-500 corresponds to the standard LOOCV method in [4]).

The algorithms have been coded and compiled in MATLAB (version R2016b) on a DELL Inspiron 17 5000 Series machine with 8 GB RAM and Processor Intel Core i7-8550U under the MS Windows 10 operating system.

Each algorithm has been launched on each test problem from both the classes. First, the execution times have been calculated for each algorithm on each test class as follows. The execution time $T_{total}^{i},~i=1,...,100,$ of each algorithm has been measured for each test problem of the class. Then, the average execution time $T_{total}^{avg}$ over 100 test problems has been calculated:

$$\begin{aligned} T_{total}^{avg} = \frac{1}{100} \sum _{i=1}^{100} T_{total}^{i}, \end{aligned}$$

(8)

as well as its standard deviation $StDev(T_{total})$:

$$\begin{aligned} StDev(T_{total}) = \sqrt{\frac{1}{99}\sum _{i=1}^{100} (T_{total}^i - T_{total}^{avg})^2},\end{aligned}$$

(9)

the smallest and the largest values $T_{total}^{min}$ and $T_{total}^{max}$:

$$\begin{aligned} T_{total}^{min} = \min \{T_{total}^{i},~i=1,...,100\},~~T_{total}^{max} = \max \{T_{total}^{i},~i=1,...,100\}.\end{aligned}$$

(10)

Then, for each test problem, the average execution time per trial $T_{trial}^i$ has been calculated by division of the total execution time $T_{total}^{i}$ by the number of trials $N_{it}^i$ executed by the algorithm for finding the shape parameter: $T_{trial}^i = T_{total}^i/N_{it}^i$. Finally, the average value, the standard deviation, the smallest and the largest values have been calculated for $T_{trial}^i$, as well.

Then, the average value, the standard deviation, the smallest and the largest values have been calculated in the same way for the best found values $\varepsilon ^*$ and $Er(\varepsilon ^*)$ from (6) and for the number of performed trials (i.e., the executed evaluations of the function $Er(\varepsilon )$ ad different values of $\varepsilon$) for each algorithm for each test class.

Finally, since all test problems of the same GKLS-class differ only in parameters fixed randomly (see [8, 28]), then the error obtained by each algorithm on different test problems from the same class can be considered as a random variable $Er^*$. So, for each algorithm on each class of test problems, the linear regression model has been constructed for the best obtained error:

$$\begin{aligned} Er = \beta _0 + \beta _1 \times X, \end{aligned}$$

(11)

where X is the number of the function from the class and Er is the obtained error using the value $\varepsilon ^*$ found by each algorithm for the test problem number X. The coefficients $\beta _0$ and $\beta _1$ have been estimated using the standard Ordinary Least Squares estimator:

$$\begin{aligned} \beta _1 = \frac{\sum _{i=1}^{100} (X_i - \overline{X})(Er_i^* - \overline{Er^*})}{\sum _{i=1}^{100} (X_i - \overline{X})^2}, \end{aligned}$$

(12)

$$\begin{aligned} \beta _0 = \overline{Er^*} - \beta _1 \overline{X}, \end{aligned}$$

(13)

where $\overline{Er^*}$ is the average error from the Tables 3 and 4:

$$\begin{aligned} \overline{Er^*} = \frac{1}{100} \sum _{i=1}^{100} Er_i^*,~\text{ and }~\overline{X} = \frac{1}{100} \sum _{i=1}^{100} X_i = \frac{1 + 100}{2} = 50.5.\end{aligned}$$

(14)

4 Results of Numerical Experiments

Results of the experiments are presented in Tables 1, 2, 3 and 4. Tables 1 and 2 show the execution times for all the methods over both the classes of test problems. For each method, the average value, the standard deviation, the smallest and the largest values over 100 test problems calculated following (8)–(10) are shown for the total execution time $T_{total}$ and for the average execution time per trial $T_{trial}$ (i.e., the total execution time divided by the number of trials, which is equal to 100 and 500 for the methods LOOCV-100 and LOOCV-500). As it can be seen from Tables 1 and 2, the execution times for the standard LOOCV method both using 100 and 500 trials is larger, than the execution times of the local and global optimization methods LOOCV-min and LOOCV-GOOI. Moreover, the average execution time is quite similar for the LOOCV-min and LOOCV-GOOI methods.

Table 1. Execution times for “simple” class. For each method, the average, the standard deviation, the smallest and the largest values over 100 test problems are shown.

Table 2. Execution times for “Difficult” class. For each method, the average, the standard deviation, the smallest and the largest values over 100 test problems are shown.

Table 3. Results on the “simple” class. For each method, the average value, the standard deviation, the smallest and the largest values over 100 functions are shown.

Table 4. Results on the “difficult” class. For each method, the average value, the standard deviation, the smallest and the largest values over 100 functions are shown.

Then, Tables 3 and 4 show the results obtained by each optimization algorithm on both the classes of test problems. In each table, the rows $\varepsilon ^*$ show the average best obtained value of the shape parameter $\varepsilon$ by each method over all 100 test functions, its standard deviation over 100 test functions, its smallest and largest values, respectively. The rows $Er^*$ show the average error using the best obtained values of the shape parameter $\varepsilon$, its standard deviation, the smallest and the largest values, respectively, over all 100 test functions. Finally, the rows $N_{it}$ show the average number of executed trials (or evaluations of the error at different values of $\varepsilon$), its standard deviation, the smallest and the largest values over all 100 test functions for the methods LOOCV-min and LOOCV-GOOI.

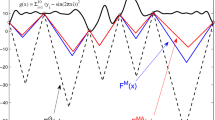
As it can be seen from Tables 3 and 4, the best average error was obtained by the method LOOCV-500 for both the classes of test problems, while the average error obtained by the method LOOCV-GOOI is better, than the average error obtained by the methods LOOCV-100 and LOOCV-min. However, the method LOOCV-500 has executed 500 trials in order to obtain better error, while the method LOOCV-GOOI has executed less than 65 trials for both the classes (see the column “Max” and the rows “$N_{it}$”). In average, the algorithm LOOCV-GOOI executed almost 55 trials for both the classes, which is almost 9 times smaller, than the number of trials of the method LOOCV-500. Moreover, the average and minimum values of $\varepsilon$ for LOOCV-min are larger than those for LOOCV-100, LOOCV-500 and LOOCV-GOOI, while its standard deviation is smaller, which means that the local optimization algorithm is not able to study the ill-conditioned region with small values of $\varepsilon$. It stops very frequently on the locally optimal values of $\varepsilon$, while the smallest obtained value of $\varepsilon$ for LOOCV-GOOI is smaller, than the value for LOOCV-100, which means that the algorithm LOOCV-GOOI studies the ill-conditioned region even better, than the “greedy” method LOOCV-100. In Fig. 2, an example of the error functions (6) is presented for the first test problem from both the “Simple” and “Difficult” classes.

Fig. 2.

The error functions for the first test problem from the “Simple” (top) and “Difficult” (bottom) classes used in the experiments. The best found values by LOOCV-100, LOOCV-500, LOOCV-min, and LOOCV-GOOI are indicated as “o”, “x”, “*”, and “+”, respectively.

Fig. 3.

Interpolation errors for test problems from the “simple” class (top) and from the “difficult” class (bottom). The regression lines for each algorithm are also indicated as blue dashed line for the method LOOCV-min, green and black solid lines - for the methods LOOCV-100 and LOOCV-500, respectively, and red dash-and-dot line for the method LOOCV-GOOI. (Color figure online)

Finally, Fig. 3 shows the distribution of the best obtained values $Er(\varepsilon ^*)$ and the regression lines (11) for each test problem by each algorithm. As it can be seen from Fig. 3, the lowest regression line corresponds to the method LOOCV-500 for both the classes, while the regression lines of the methods LOOCV-100 and LOOCV-min are higher than the regression function of the method LOOCV-GOOI. It can be also seen from Fig. 3 that the error obtained by the LOOCV-GOOI method is the best one in several cases (see, e.g., the obtained errors for the functions number 79 and 100 of the “simple” class). The error obtained by the global optimization method LOOCV-GOOI is always not worse than the error obtained by the local optimization method, but it is better in a lot of cases.

5 Conclusion

It has been shown that global optimization methods can be successfully used for finding a good value of the shape parameter in radial basis functions. The obtained error in this case is better in average, than the error obtained by the standard LOOCV method using a uniform grid with a small size of the grid (using, e.g., 100 evaluations). It has been also shown that even a grid with 500 nodes can be not sufficient for guaranteeing the best value of $\varepsilon$, since in several cases the global optimization method has found a better value executing in average always no more than 55 evaluations. Finally, it has been shown that the traditionally used local optimization algorithm LOOCV-min is not able to study the ill-conditioned region with small values of the shape parameter, giving a locally optimal solution, which is worse than the globally optimal one found by the other methods. It should be also noted that the number of trials executed by the global optimization method is larger than the number of trials executed by the local optimization method, but the difference is small (almost 15 trials in average for both the classes) and not meaningful since it is related to the study of the ill-conditioned region and, in practice, the number of trials for solving ill-conditioned optimization problems is always much higher (see, e.g., [27]).

To conclude, the presented global optimization algorithm has shown a promising performance and can be successfully used in practice for finding good values of the shape parameter in radial basis functions interpolation.