Analysis of Active Suspension Performance Improvement Based on Introducing Front/Rear LQ Control Coupling

Abstract

The paper investigates the potential of improving vehicle ride comfort based on introducing control design coupling between front- and rear-axle active suspensions. The considered linear quadratic regulator (LQR) cost function includes conflicting criteria related to ride comfort, vehicle handling, and suspension stroke. A covariance analysis related to standard deviations of cost function criteria with respect to stochastic road profile input is carried out for half-car models with two and four degrees of freedom. The presented results show that the control-design coupling can considerably improve the ride comfort in terms of reduced sprung mass pitch or heave acceleration with a relatively small sacrifice of vehicle handling and suspension stroke. The performance improvement is explained by the fact that the rear suspension controller uses state information from the front axle (and vice versa), which may be considered as a kind of preview action.

1 Introduction

Half-car model introduces several effects which are not present in the basic quarter-car model, such as wheel-base filtering and sprung mass pitch dynamics. When designing an active suspension control system, decoupled controllers targeted to each axle are typically considered (see e.g. [1]). Such design relies on decoupling the half-car model into two separate quarter-car models based on satisfying specific mechanical- and control-design conditions, where the latter defines the ratio of pitch and heave acceleration penalization [2]. In this paper, it is investigated if further ride comfort improvement can be achieved through coupling the control actions of front and rear suspensions, i.e. by separating the tuning of heave and pitch acceleration penalizations.

The remaining part of the paper is organized in three sections. Section 2 contains details on the vehicle models and related controls, and introduces mechanical and control decoupling conditions. Section 3 details the methodology for evaluation of performance metrics based on standard deviations of system outputs (so-called covariance analysis). The covariance analysis results are discussed in the same section, with emphasis on improvements obtained by front/rear axle control coupling. Concluding remarks are given in Sect. 4.

2 Active Suspension Modeling and Control

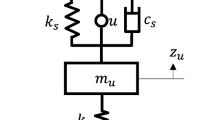
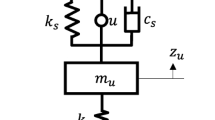
Two typical representations of half-car model are depicted in Fig. 1, and they include a two degree of freedom (DOF) model (Fig. 1a) and a four DOF model (Fig. 1b) [1]. The chosen state variables are front and rear suspension deflections and front and rear sprung mass velocities for the 2DOF model, and additional two state variables per axle corresponding to the tire deflections for the 4DOF model. The 2DOF model is described in the state-space form as [1]:

Fig. 1.

Half-car model with two degrees-of-freedom (2DOF) (a) and four degrees of freedom (4DOF) (b)

$$ \underbrace {{\left[ {\begin{array}{*{20}c} {\dot{z}_{sf} } \\ {\ddot{z}_{f} } \\ {\dot{z}_{sr} } \\ {\ddot{z}_{r} } \\ \end{array} } \right]}}_{{{\dot{\mathbf{x}}}}} = \underbrace {{\left[ {\begin{array}{*{20}c} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right]}}_{{\mathbf{A}}}\underbrace {{\left[ {\begin{array}{*{20}c} {z_{sf} } \\ {\dot{z}_{f} } \\ {z_{sr} } \\ {\dot{z}_{r} } \\ \end{array} } \right]}}_{{\mathbf{x}}} + \underbrace {{\left[ {\begin{array}{*{20}c} 0 & 0 \\ {\frac{{J_{p} + M_{s} l_{f}^{2} }}{{J_{p} M_{s} }}} & {\frac{{J_{p} - M_{s} l_{f} l_{r} }}{{J_{p} M_{s} }}} \\ 0 & 0 \\ {\frac{{J_{p} - M_{s} l_{f} l_{r} }}{{J_{p} M_{s} }}} & {\frac{{J_{p} + M_{s} l_{r}^{2} }}{{J_{p} M_{s} }}} \\ \end{array} } \right]}}_{{\mathbf{B}}}\underbrace {{\left[ {\begin{array}{*{20}c} {U_{f} } \\ {U_{r} } \\ \end{array} } \right]}}_{{\mathbf{u}}} + \underbrace {{\left[ {\begin{array}{*{20}c} { - 1} & 0 \\ 0 & 0 \\ 0 & { - 1} \\ 0 & 0 \\ \end{array} } \right]}}_{{\mathbf{G}}}\underbrace {{\left[ {\begin{array}{*{20}c} {w_{f} } \\ {w_{r} } \\ \end{array} } \right]}}_{{\mathbf{w}}}, $$

(1)

where x is the state vector, A, B, and G are the system, control input, and disturbance input matrices, respectively, u is the control input vector corresponding to front and rear active suspension actuator forces, and w is the ground velocity vector. The model parameters used throughout this paper are given at the end of Appendix.

Note that the matrix B contains two elements (b₂₂ and b₄₁) which mechanically couple rear actuator force and front suspension dynamics, and vice versa, thus meaning that the control action at the rear axle affects front suspension states, and vice versa. In order to mechanically decouple front and rear suspension dynamics, these two terms have to be equal to zero, which gives the mechanical decoupling condition [1, 2]:

$$ J_{p} = M_{s} l_{f} l_{r} , $$

(2)

where J_p is the pitch moment of inertia, M_s is the sprung mass, and l_f and l_r are distances between the center of gravity (CoG) and the front and rear axle, respectively (Fig. 1a). The mechanical decoupling condition is rarely fully satisfied, but the ratio J_p/(M_sl_fl_r) is close to 1 for most of vehicles. According to the vehicle data available in CarSim, this ratio is between 0.73 and 0.89 for all vehicle types considered therein. Thus, it is reasonable to assume that the mechanical decoupling condition is satisfied, which is confirmed by the analysis presented in Sect. 3 (along results presented in Fig. 2). Note that the decoupling condition (2) holds for the 4DOF model, as well [1, 2].

Fig. 2.

Performance plot of 2DOF model for varying mechanical coupling ratio and heave penalization (r₁), with fixed suspension stroke penalization ($r_{ 4f} = 1$ and $r_{ 4r} = l_{f} /l_{r}$) and satisfied control decoupling condition (r₂ = r₁J ²_p /(M ²_s l_fl_r)).

The active suspension is considered to be controlled by a linear quadratic regulator (LQR). The LQR-design cost function for 4DOF model includes penalization of root-mean-square (RMS) sprung mass heave $\left( {\ddot{z}} \right)$ and pitch $\left( {\ddot{\theta }} \right)$ accelerations, RMS front and rear tire deflections (z_tf and z_tr), and RMS front and rear suspension deflections (z_sf and z_sr) [1]:

$$ J = {\text{E}}\left( {r_{1} \ddot{z}^{2} + r_{2} \ddot{\theta }^{2} + r_{ 3f} z_{tf}^{2} + r_{3r} z_{tr}^{2} + r_{ 4f} z_{sf}^{2} + r_{4r} z_{sr}^{2} } \right). $$

(3)

In the case of 2DOF model, the penalization terms corresponding to tire deflection are omitted: $r_{ 3f} = r_{ 3r} = 0$. Penalization coefficients of front and rear suspension deflection may be fixed (e.g. $r_{ 4f} = r_{ 4r} = 1$), while the ones related to front and rear tire deflections may be set to be proportional to those of corresponding suspension deflections (e.g. $r_{ 3f} = 10\;r_{ 4f} = 10$). In this way we eliminate the solutions which do not result in practical designs, in a similar fashion as done in the quarter-car model [3] (see Appendix).

The cost function Eq. (3) can be rewritten into the LQ matrix form:

$$ J = {\text{ E}}\left( {{\mathbf{x}}^{T} {\mathbf{Qx}} + {\mathbf{u}}^{T} {\mathbf{Ru}}} \right), $$

(4)

where the state vector equals $\left[ {z_{sf} \dot{z}_{f} z_{sr} \dot{z}_{r} } \right]^{\text{T}}$ and $\left[ {z_{tf} \dot{z}_{usf} z_{sf} \dot{z}_{f} z_{tr} \dot{z}_{usr} z_{sr} \dot{z}_{r} } \right]^{\text{T}}$ for the 2DOF and 4DOF models, respectively, while the matrices Q (for 2DOF model) and R (for both models) read:

$$ {\mathbf{Q}} = \left[ {\begin{array}{*{20}c} {r_{4f} } & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & {r_{4r} } & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} } \right],\quad {\mathbf{R}} = \left[ {\begin{array}{*{20}c} {\frac{{r_{1} }}{{M_{s}^{2} }} + r_{2} \frac{{l_{f}^{2} }}{{J_{p}^{2} }}} & {\frac{{r_{1} }}{{M_{s}^{2} }} - r_{2} \frac{{l_{f} l_{r} }}{{J_{p}^{2} }}} \\ {\frac{{r_{1} }}{{M_{s}^{2} }} - r_{2} \frac{{l_{f} l_{r} }}{{J_{p}^{2} }}} & {\frac{{r_{1} }}{{M_{s}^{2} }} + r_{2} \frac{{l_{r}^{2} }}{{J_{p}^{2} }}} \\ \end{array} } \right]. $$

(5)

The optimal state-feedback control law that minimizes the cost function Eq. (4) is defined for the 2DOF model as:

$$ \left[ {\begin{array}{*{20}c} {U_{\text{f}} } & {U_{\text{r}} } \\ \end{array} } \right]^{T} = - {\mathbf{Kx}} = \left[ {\begin{array}{*{20}c} {k_{11} } & {k_{12} } & {k_{13} } & {k_{14} } \\ {k_{21} } & {k_{22} } & {k_{23} } & {k_{24} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {z_{sf} } & {\dot{z}_{f} } & {z_{sr} } & {\dot{z}_{r} } \\ \end{array} } \right]^{T} , $$

(6)

The control decoupling condition follows from setting the cross-diagonal terms of control input penalization matrix R to zero, and it is given by [2]:

$$ r_{2} = \frac{{J_{p}^{2} }}{{M_{s}^{2} l_{\text{f}} l_{\text{r}} }}r_{1} . $$

(7)

The same control decoupling condition is valid for 4DOF model, as well [1, 2]. Equation (7) when related to Eq. (3) implies the loss of a control degree of freedom, i.e. the pitch and heave criteria become coupled when the ratio r₂/r₁ is set to J ²_p /(M ²_s l_fl_r). Note that in case when the mechanical decoupling condition (2) is satisfied, the control design decoupling condition (7) reduces to r₂ = l_fl_rr₁.

3 Performance Analysis of Control-Design Coupling

Performance analysis of the considered active suspension control system is based on covariance analysis [4], which results in normalized RMS values of state variables with respect to zero-mean Gaussian white noise ground velocity w, which is a typical approximation of stochastic road profile [3]. Assuming that the active suspension closed-loop system is stable, standard deviations of state variables can be numerically obtained by solving variance equation, which is similar to Lyapunov equation [4]:

$$ {\mathbf{A}}_{cl} {\mathbf{X}} + {\mathbf{XA}}_{cl}^{T} + {\mathbf{GQ}}_{{\mathbf{w}}} {\mathbf{G}}^{T} = 0, $$

(8)

where A_cl is the closed-loop system matrix A_cl = A − BK, X is the state covariance matrix, and Q_w is the power spectral density matrix of ground velocity. The term GQ_wG^T should take into account the time delay between front and rear ground velocity inputs because of introduced control coupling. This is an extension of the decoupled control approach considered in [1], where the time delay is not taken into account. For the considered 2D case, the ground velocity input is represented by [5]:

$$ {\mathbf{w}} = \left[ {\begin{array}{*{20}c} {w_{f} } \\ {w_{r} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {w\left( t \right)} \\ {w\left( {t - t_{wb} } \right)} \\ \end{array} } \right] $$

(9)

where t_wb = (l_f + l_r)/v_x is time delay between axles, with v_x denoting the vehicle longitudinal velocity. Such white noise input is represented by its power spectral density matrix [5, Chap. 29]:

$$ {\mathbf{Q}}_{{\mathbf{w}}} = \frac{2}{\pi }\int\limits_{0}^{\infty } {R_{{\mathbf{w}}} \left( \tau \right)\cos } \left(\Omega \right)\tau d\tau = \frac{2}{\pi }\int\limits_{0}^{\infty } {q_{w} \left[ {\begin{array}{*{20}c} {\delta \left( \tau \right)} & {\delta \left( {\tau + t_{\text{wb}} } \right)} \\ {\delta \left( {\tau - t_{\text{wb}} } \right)} & {\delta \left( \tau \right)} \\ \end{array} } \right]\cos } \left(\Omega \right)\tau d\tau $$

(10)

where δ is Dirac function. Q_w is now 2 × 2 matrix with power spectral densities of ground velocities. If we partition the matrix G from Eq. (1) such that ${\mathbf{G}} = \left[ {\begin{array}{*{20}c} {{\mathbf{G}}_{1}^{4 \times 1} } & {{\mathbf{G}}_{2}^{4 \times 1} } \\ \end{array} } \right]$, i.e. such that each axle has its own input matrix, and insert it into GQ_wG^T of Eq. (8), while taking into account Eq. (10) we get [5, chap. 29]:

$$ {\mathbf{Q}}_{wn} = {\mathbf{GQ}}_{{\mathbf{w}}} {\mathbf{G}}^{T} = q_{w} \left[ {{\mathbf{G}}_{1}^{{}} {\mathbf{G}}_{1}^{T} + {\mathbf{G}}_{2}^{{}} {\mathbf{G}}_{2}^{T} + e^{{{\mathbf{A}}t_{wb} }} {\mathbf{G}}_{1}^{{}} {\mathbf{G}}_{2}^{T} + {\mathbf{G}}_{2}^{{}} {\mathbf{G}}_{1}^{T} e^{{{\mathbf{A}}^{T} t_{wb} }} } \right], $$

(11)

where e^Atwb is matrix exponential of At_wb. If we set q_w = 2πAV, where A is the road roughness coefficient [1], insert Q_wn given by Eq. (11) into Eq. (8), and divide the obtained results with square root of q_w we get normalized RMS values of state variables. The normalized RMS values of output variables can be obtained from Y = C_clXC ^T_cl , where C_cl = C − DK is the closed-loop output matrix, and C and D are the matrices of model output equation (y = Cx + Du). The reason for why the covariance equation cannot be normalized before being solved lies in Eq. (11), where v_x is implicitly present through t_wb = (l_f + l_r)/v_x.

Figure 2 shows the performance plot of 2DOF model, obtained by varying the mechanical decoupling ratio J_p/(M_sl_fl_r) between 0.5 and 1.5, with the control-design decoupling condition (7) satisfied, i.e. r₂ = r₁J ²_p /(M ²_s l_fl_r) held, and suspension stroke penalization coefficients in Eq. (3) set to $r_{ 4f} = 1$ and r_4r = l_f/l_r (it can be readily shown that this particular choice of ratio $r_{ 4f} /r_{ 4r}$ ensures same front and rear suspension strokes), and varying penalization of heave acceleration r₁. It can be observed from the plot that by increasing the pitch inertia J_p (higher mechanical coupling ratio), the RMS heave acceleration is somewhat increased while the RMS pitch acceleration (shown in color) is somewhat decreased for the same value of suspension stroke. This trend is more pronounced for the case of lower heave acceleration penalization coefficient r₁. Note that the front and rear suspension strokes are condensed in Fig. 2 into the mean suspension stroke, in order to present the results in a compact manner, with no loss of generality since the front and rear suspension stroke are equally penalized.

If the system is mechanically decoupled (J_p/(M_sl_fl_r) = 1), the front suspension actuator force will not affect the rear suspension states, and vice versa. If along with the mechanical decoupling condition, the control decoupling condition is satisfied, i.e. r₂/r₁ = l_fl_r (1.875 for the particular vehicle data listed in Appendix), the state controller gain matrix K and the matrix R are equal to:

$$ {\mathbf{K}} = \left[ {\begin{array}{*{20}c} {812.4} & {987.3625} & 0 & 0 \\ 0 & 0 & {677} & {822.8} \\ \end{array} } \right],\quad {\mathbf{R}} = 10^{ - 5} \cdot \left[ {\begin{array}{*{20}c} {0.1515} & 0 \\ 0 & {0.1818} \\ \end{array} } \right] $$

This means that the front actuator (U_f) does not use rear suspension states $(z_{sr} \dot{z}_{r} )$, as feedback gains corresponding to the rear suspension states, i.e. cross-coupling gains, are equal to zero. The same conclusion holds for rear actuator and front suspension states.

The control coupling is reflected in appearance of non-zero cross-coupling terms in the state controller gain matrix K, where there are two characteristic cases. The first case is defined by the inequality r₂/r₁ > l_fl_r, which results in the following matrices K and R (given for r₂/r₁ = 10):

$$ {\mathbf{K}} = \left[ {\begin{array}{*{20}c} {559.9} & {790.94} & {252.5} & {196.42} \\ {252.5} & {196.42} & {424.5} & {626.38} \\ \end{array} } \right],\quad {\mathbf{R}} = 10^{ - 4} \cdot \left[ {\begin{array}{*{20}c} {0.0771} & { - 0.0744} \\ { - 0.0744} & {0.1074} \\ \end{array} } \right] $$

The second case, in which the ratio r₂/r₁ < l_fl_r, here r₂/r₁ = 0.1, results in:

$$ {\mathbf{K}} = 10^{3} \cdot \left[ {\begin{array}{*{20}c} {1.6109} & {1.3367} & { - 0.7985} & { - 0.3493} \\ { - 0.7985} & { - 0.3493} & {1.4755} & {1.1721} \\ \end{array} } \right],\quad {\mathbf{R}} = 10^{ - 6} \cdot \left[ {\begin{array}{*{20}c} {0.8953} & {0.7438} \\ {0.7438} & {0.9256} \\ \end{array} } \right] $$

The above LQR parameter results for the two characteristic cases point out that positive cross-diagonal elements of matrix R cause negative LQR cross-gains (elements k₁₃, k₁₄ and k₂₁, k₂₂), and negative cross-diagonal elements of matrix R cause positive LQR cross-gains. In both cases this means that, even for mechanically decoupled suspension model, the rear suspension controller gets information from front axle, which could be viewed as some sort of preview. Also, in the case when cross-gains are positive, front and rear suspension forces will be in the same direction with respect to same state variable, thus attempting to reduce pitch motion (note that in this case r₂ > r₁ holds), but from this we cannot determine at what cost.

Figure 3 shows the obtained performance plot of 2DOF model from Fig. 1a, which indicates the trade-off between ride comfort and suspension stroke. For the case of control-design decoupling (i.e. when the condition (7) is satisfied), the pitch acceleration has the same trend as heave acceleration (see dark orange line in Fig. 3 and cf. the results from Fig. 2 for the decoupled case), and it decreases as the suspension stroke increases. Thus, there are two conflicting criteria: heave/pitch acceleration and suspension stroke.

Fig. 3.

Performance plot for control design coupling case of mechanically decoupled 2DOF model (J_p/(M_sl_fl_r) = 1), obtained for fixed suspension stroke penalizations $\left( {r_{ 4f} = 1,r_{ 4r} = l_{f} /l_{r} } \right)$ and varying heave (r₁) and pitch (r₂) penalizations.

In the control-design coupling case, the weighting factors r₁ and r₂ can be set independently, thus resulting in one control degree-of-freedom more and 3D performance plot in Fig. 3 (the three performance criteria become conflicting to each other), compared to the control decoupling case represented by 2D plot. One may increase r₂ while keeping r₁ constant to come below the decoupled-case performance line, i.e. to reduce pitch acceleration without significantly affecting heave acceleration and suspension strokes. More specifically, when considering point E_c in comparison with the decoupled-case point E, the RMS pitch acceleration is reduced by 86% with no change in RMS heave acceleration and with RMS mean suspension stroke increase of 1% (note that front suspension stroke is increased by 4% and rear suspension stroke decreased by 3%). It should be noted that while the pitch acceleration can be reduced without significant increase of suspension strokes, the heave acceleration cannot be reduced without affecting the suspension stroke.

Figure 4 shows the trade-off between ride comfort, vehicle handling and suspension stroke for the 4DOF model. Here, the ratio of tire deflection and suspension stroke penalizations is set to r₃/r₄ = 10, as this results in a good trade-off between tire deflection and suspension stroke (see [3] and Appendix), and both front and rear states are equally penalized (r_3f = r_3r = r₃, r_4f = r_4r = r₄ = 1). The front and rear RMS tire deflections and RMS suspension deflections are represented by their mean values, similarly as in the case of 2DOF model. The control decoupling case (magenta line; r₂/r₁ = l_fl_r) results in qualitatively similar trade-off between heave/pitch acceleration and suspension stroke as observed in the 2DOF model case (cf. Figure 3 and note that the RMS values of suspension and tire deflection are related to each other for fixed ratio r₃/r₄ selected).

Fig. 4.

Performance plot for control-design coupling case of mechanically decoupled 4DOF model (J_p/(M_sl_fl_r) = 1), obtained for fixed tire deflection penalizations $\left( {r_{ 3f} = r_{ 3r} = 10} \right)$ and fixed suspension deflection penalization $(r_{ 4f} = r_{ 4r} = 1)$, and varying heave (r₁) and pitch (r₂) penalization.

However, when control-design coupling is exploited $(r_{2} /r_{1} \ne l_{f} l_{r} )$, pitch acceleration or heave acceleration can be additionally decreased with mostly minor sacrifices in tire deflection and/or suspension stroke (generally, there are four conflicting criteria, i.e. three in the particular case of fixed ratio r₃/r₄). For instance, when considering points E₁ and E_1c in Fig. 4, the RMS pitch acceleration is reduced by 26% at the cost of RMS mean suspension stroke increase of 2% and RMS mean tire deflection increase of 6%, without impact on heave acceleration.

Furthermore, when considering points E₂ and E_2c in Fig. 4, the RMS heave acceleration can be reduced by 21% with unchanged level of RMS pitch acceleration, and with only 3% increase in RMS mean tire deflection and less than 9% increase in RMS mean suspension stroke. The control coupling benefits are generally lower than for the 2DOF model, as a consequence of introduction of unsprung mass dynamics and tire deflection criteria.

4 Conclusion

The benchmark performance of half-car model equipped with LQR-controlled active suspension, expressed in terms of trade-off of normalized RMS heave and pitch accelerations, tire deflections and suspension strokes, has been evaluated in the cases of front/rear axle mechanical coupling and control-design coupling. The control-design coupling, in which the heave and pitch accelerations penalizations can be set separately, results in improvements of ride comfort without significant deterioration of handling and suspension stroke criteria when compared to the decoupled case. Unlike in the decoupled case, the rear-axle suspension controller acts on the front-axle state measurements (and vice versa), thus providing a kind of preview action that improves the performance. However, from the implementation point of view, exploiting front/rear axle control coupling may result in more complex design of realistic control system (including observers) and eventually less robust behavior when compared to decoupled, quarter car model-based controllers.

Apart from designing and analyzing more realistic control system, the future work can be directed to expanding the knowledge gained from the presented analysis on a full-car model, which has additional degree of freedom related to roll dynamics, and/or on the case of added road preview control. Furthermore, adaptive control schemes could be derived, which would, for instance, emphasize either heave suppression or pitch suppression depending on the driving conditions or driver’s preferences.

Appendix

Applying the covariance analysis to the quarter-car model (a half of the model shown in Fig. 1b) and the cost function (cf. Eq. (3)):

$$ J = {\text{ E}}\left( {r_{0} \ddot{z}^{2} + r_{1} z_{t}^{2} + r_{2} z_{s}^{2} } \right), $$

(12)

gives the performance plot shown in Fig. 5, which indicates the trade-off between the three conflicting criteria in a similar (but more illustrative way) than the carpet plots given in [1]. Although the three criteria are conflicting, it can be observed from the plot in Fig. 5 that there exists an area bounded roughly by lines corresponding to r₁ = 0.01 and (r₁/r₂)_max = 1000 in which both RMS tire deflection and RMS suspension deflection monotonically fall with increasing sprung mass acceleration. Thus, this practical design area can be associated with tire deflection penalization (r₁) being stronger than suspension deflection penalization (r₂). Satisfying trade-off between RMS tire deflection and suspension deflection is obtained for r₁/r₂ = 10 (cf. intersections between equally colored solid and dashed lines in Fig. 5), which is used as design setting related to 4DOF model in the main body of this paper (r₃/r₄ = 10, therein).

Fig. 5.

Performance plot of quarter-car model obtained with sprung mass penalization r₀ set to 1, and varying tire deflection penalization (r₁) and suspension stroke penalization (r₂).

The half-car model parameters used in the main body of this paper are [1]: J_p= 2475 kgm², M_s = 1100 kg, $l_{f} = 1. 2 5\;{\text{m}}$, l_r = 1.75 m, $m_{usf} = m_{usr} = 40 \;{\text{kg}},k_{tf} = k_{tr} = 1 60000 \;{\text{N}}/{\text{m}},b_{tf} = b_{tr} = 0\;{\text{Ns}}/{\text{m}}$. The quarter-car model parameters used to obtain the plot in Fig. 5 are [3]: m_s = 400 kg, m_us= 40 kg, $k_{t} = 1 60000\;{\text{N}}/{\text{m}}$, $b_{t} = 0\;{\text{Ns}}/{\text{m}}$.