Abstract
We can define the traditional trigonometric functions in several different ways: via differential equations, via an arclength definition on the unit circle x 2 + y 2 = 1, or via an analytic approach. In this project, we adapt these approaches to define analogous functions for a unit squircle |x|p + |y|p = 1, p ≥ 1. As we develop these functions using only elementary calculus, we will ponder the importance and role of π, and glimpse some very deep ideas in elliptic integrals, special functions, non-Euclidean geometry, number theory, and complex analysis.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Knowledge of basic trigonometric functions, differential and integral calculus are a must. Some knowledge of differential equations is helpful, but not essential.
1 Introduction
The circle is a “perfect” object, and our familiarity with it can cause us to lose sight of just how remarkable it is. It is one of the first geometric shapes we encounter in school; children can identify it easily. The unit circle can be described as the set of points (x, y) in the plane satisfying the equation x 2 + y 2 = 1. The sine and cosine functions emerge as natural functions with which to describe it.
In this project, we look to enhance appreciation of the circle’s perfection by introducing some imperfection, by developing an analog of trigonometry for something that is not quite a circle.
Our primary model is the unit p-circle, or “squircle,” a superellipse defined as the set of points (x, y) in the plane satisfying the equation |x|p + |y|p = 1 for some real p ≥ 1. This generalizes the Euclidean circle which emerges as the case p = 2 (note that we can drop the absolute values when p is a rational number whose reduced fraction has an even numerator). We will examine the p = 4 case quite closely for examples.
2 Defining Trigonometric Functions
We often define the sine and cosine functions in one of three ways:
-
via differential equations,
-
geometrically, as coordinates of points on the unit circle x 2 + y 2 = 1,
-
analytically, via the use of definite integrals.
Conveniently, all three definitions yield the same functions. Let us examine these three methods separately, as these will be the directions for our generalizations to squigonometric functions.
2.1 Differential Equations Approach
This approach is inspired by methods discussed in [6] and [7] of using initial value problems (IVP’s) to develop transcendental functions in a first-year calculus course.
Recall from calculus that \(\frac {d}{dt}\cos t = -\sin t\) and \(\frac {d}{dt}\sin t = \cos t\). We view these as defining properties for the cosine and sine functions. By choosing to start the parameterization on the x-axis, we further adopt the initial conditions \(\cos 0 = 1\) and \(\sin 0 = 0\). Thus we can say that cosine and sine are the functions satisfying
where x corresponds to cosine and y to sine. This is an example of a coupled initial value problem (or CIVP). It turns out problems like these always have unique solutions [5]. Therefore, we may define cosine and sine to be the unique solution to (1).
Exercise 1
Consider the function f(t) = u(t)2 + v(t)2, where \(u(t) = \cos {}(t)\) and \(v(t)=\sin {}(t)\). Use the properties (1) to show that f′(t) is identically 0 and that f(0) = 1. Conclude that f(t) is identically 1 and thus \(\cos ^2 t + \sin ^2 t = 1\) for all t.
Exercise 2
Use similar techniques to show that cosine is even and sine is odd.
2.2 Unit Circle Approach
The unit circle is the set of points (x, y) that are exactly 1 unit from the origin. Such points satisfy the equation x 2 + y 2 = 1.
Any line through the origin intersects the unit circle at a point t units away from (1, 0) as measured along the arc of the circle. We define the radian as a measure of angle such that one radian subtends an arc of the unit circle of length 1. Thus the line passing through our point subtends an angle of t radians, and we define the cosine and sine of t to be the x- and y-coordinates, respectively of our intersection point (Fig. 1). Thus we have that \(\cos ^2 t + \sin ^2 t = 1\) for all \(t\in \mathbb {R}\).
As a full circuit of the unit circle subtends 2π radians, each point on the unit circle is associated with infinitely many angles, all multiples of 2π radians apart. In particular, this means that the cosine and sine functions are periodic—they repeat their values every 2π radians:
for all \(k\in \mathbb {Z}\).
The parameter t in cosine and sine thus simultaneously specifies both the arclength and the angle. It also determines the area of the sector. We see that a sector traced out by t radians has an area of \(\frac {t}{2\pi }\) times the area of the whole circle, or \(\frac {t}{2\pi }\times \pi = \frac {t}{2}\). Thus the angular, arclength, and areal parameterizations all lead to the same functions. We will come to appreciate this remarkable feature of Euclidean geometry when we lose it in the geometries we will soon explore.
2.3 Analytic Approach
We can also define the sine and cosine functions as solutions to integral equations. The sine function is the function S(t) such that
In a similar manner, we can define the cosine function to be the function C(t) such that
Suppose that (1) holds. The result of Exercise 1 shows that \(\cos ^2 t + \sin ^2 t = 1\) and we have the sine and cosine functions from our unit circle approach.
Now let S(t) and C(t) be, respectively, the sine and cosine functions defined in Eqs. (2) and (3). We first claim that \(C(t) = \sqrt {1-S^2(t)}\) (and thus \(S(t) =\sqrt {1-C^2(t)}\) and C 2(t) + S 2(t) = 1). If we substitute \(s=\sqrt {1-u^2}\) into Eq. (2), then \(u=\sqrt {1-s^2}\), \(du =-\frac {s}{\sqrt {1-s^2}}\,ds\) and
Comparing this last integral to (3), we see that \(C(t)=\sqrt {1-S^2(t)}\). Furthermore, Eqs. (2) and (3) show that S(0) = 0 and C(0) = 1.
Taking the derivatives across Eqs. (2) and (3), we obtain
and so \(S'(t) = \sqrt {1-S^2(t)} = C(t)\) and \(C'(t) = -\sqrt {1-C^2(t)} = -S(t)\). Thus S and C fulfill the CIVP (1) and must be the same cosine and sine functions found there.
Once again, we see these three approaches inevitably yield the same cosine and sine functions.
Exercise 3
3 Squigonometric Functions
We will now develop an analog of trigonometry for the unit p-circle , the set of points (x, y) in the plane satisfying |x|p + |y|p = 1, p ≥ 1, depicted in Fig. 2. The absolute values are necessary in the defining equation, as our next exercise shows.
Exercise 4
Use a computer algebra system to implicitly plot the equation x 3 + y 3 = 1 where x ranges from − 2 to 2. Do the same for x 5 + y 5 = 1.
3.1 Differential Equations Approach
We first generalize our differential equations approach in order to define our squigonometric functions. Consider the function g(t) = u(t)p + v(t)p for some p ≥ 1. We will design a CIVP whose solutions u(t) and v(t) will make g(t) constant. To wit:
Thus if u(t) and v(t) are the solutions to (4) then
so g(t) must be constant. Since g(0) = 1, we then have that g(t) ≡ 1, as desired.
We denote cosp(t) = x(t) and sinp(t) = y(t) to be the unique pair of functions that solve (4). (The cosquine and squine functions, if we prefer.) Note that \(\cos _p^p(t)+ \sin _p^p(t) = 1\). For p = 2 or any other positive even integer, we get the entire unit squircle from this equation. Otherwise, we can either take absolute values (as Exercise 4 showed, |cosp(t)|p + |sinp(t)|p = 1 works), or we can deftly restrict the interval of solution for Eqs. (4) and then extend the solutions by symmetry. We will see how to do this shortly.
We can define the other squigonometric functions through the usual definitions using ratios of the squine and cosquine functions:
It is here that we abandon whimsy for practicality and refer to these functions by referencing p, so, for example, tanp is simply the p-tangent.
Exercise 5
Prove that \(1+\tan _p^p(t) = \sec _p^p(t)\) and \(1+\cot _p^p(t) = \csc _p^p(t)\).
Exercise 6
Use the quotient rule along with our initial derivative formulas for sinp(t) and cosp(t)to obtain
(see [9]).
3.2 The Many Values of π
If we look at a graph of, say, sin4(t) and cos4(t), we notice that, much like the squircle, the graphs resemble those of our usual sine and cosine functions, but flattened out a bit (Fig. 3).
We also notice that the period of these sine and cosine functions is longer than the usual 2π, and that the first vertical asymptote in the tangent graph is far beyond the classical t = π∕2 ≈ 1.57. We can find this new value of π by first defining inverse functions for our squine and cosquine functions.
Let x =sinp(y). Then \(dx/dy =\cos _p^{p-1}(y) = (1-x^p)^{(p-1)/p}\). This is a separable differential equation and we can solve for y to obtain
In a similar way, since cosp(0) = 1, we have
This leads organically to being able to define π as a function of p (see Fig. 4):
In particular,
Exercise 7
Use a computer algebra system to find an approximate value for π 4.
Though not expressible in terms of elementary functions, π p can be expressed in terms of the beta and gamma functions [2]. The beta function is a function of two variables defined in terms of an integral:
The gamma function is defined as \(\varGamma (z) = \int _0^\infty t^{z-1}e^{-t}\,dt\). If n is a positive integer, then Γ(n) = (n − 1)!. Thus the gamma function is a generalization of the factorial. Its relationship to the gamma function is via the identity \(\operatorname {B}(x,y)=\frac {\varGamma (x)\varGamma (y)}{\varGamma (x+y)}\).
Exercise 8
Verify these properties of the beta and gamma functions.
If we make the change of variable u = t p in Eq. (6), we get
We can use the well-known gamma function identities
to derive some facts and, in particular, values for the gamma function and for some π p’s.
Exercise 9
Show that \(\varGamma (\frac 12) = \sqrt {\pi }\).
Challenge Problem 1 (Legendre Duplication Formula)
We will use the identity \(\operatorname {B}(x,y)=\frac {\varGamma (x)\varGamma (y)}{\varGamma (x+y)}\) to derive the Legendre duplication formula, which gets the value of Γ(2z) from the value of Γ(z) and \(\varGamma (z+\frac 12)\).
-
(a)
Use the above identity with x = y = z to show
$$\displaystyle \begin{aligned} \frac{\varGamma^2(z)}{\varGamma(2z)} = \int_0^1 u^{z-1}(1-u)^{z-1}\,du. \end{aligned}$$ -
(b)
Substitute u = (1 + x)∕2 in the previous integral and show that
$$\displaystyle \begin{aligned} \frac{\varGamma^2(z)}{\varGamma(2z)} = 2^{2-2z}\int_0^1 (1-x^2)^{z-1}\,dx. \end{aligned}$$ -
(c)
Show that
$$\displaystyle \begin{aligned} \operatorname{B}(m,n) = 2\int_0^1 x^{2m-1}(1-x^2)^{n-1}\,dx. \end{aligned}$$(Hint: Set u = x 2 in formula (7).)
-
(d)
Use the result of the previous problem to show
$$\displaystyle \begin{aligned} \frac{\varGamma^2(z)}{\varGamma(2z)} = 2^{1-2z}\operatorname{B}(\tfrac12, z) =2^{1-2z} \frac{\varGamma(\frac 12)\varGamma(z)}{\varGamma(z+\frac 12)}. \end{aligned}$$ -
(e)
Use the result of part (d) above and Exercise 9 to conclude
$$\displaystyle \begin{aligned} \varGamma(2z) = \frac{\varGamma(z)\varGamma(z+\frac 12)}{2^{1-2z}\sqrt{\pi}}. \end{aligned} $$(10)
Exercise 10
Use the Legendre duplication formula (10) and the first identity from (9) to show that \(\lim \limits _{p\to \infty } \pi _p = 4\).
Using the formulas (9) leads to
This leads to the formulas
Since these are considered to be “unknown” values of the gamma function, a good source of classroom discussion could encompass whether these are now solved. (Both values have been proved to be transcendental [4].)
Exercise 11
Use either formula (9) or (10) to find exact values of \(\varGamma (\frac 34)\) and \(\varGamma (\frac 23)\) in terms of π 4 and π 3, respectively. Then use formula (8) to find formulas for \(\varGamma (\frac 1{2^n})\) (see [19]) and \(\varGamma (\frac 1{3\cdot 2^n})\) for \(n\in \mathbb {N}\).
Research Project 1
The integral that defines π 4 is elliptic in nature, and several relationships exist between gamma function values and elliptic integral singular values, or between various gamma function values. Consult with [16, 21] and [22], and rewrite some of the listed relationships in terms of various π p’s.
The solutions for the coupled initial value problem (4) can be restricted to hold for 0 ≤ t ≤ π p∕2. We can then extend the function definitions via symmetry, first to 0 ≤ t ≤ π p, then to 0 ≤ t < 2π p, and finally, via periodicity, to the entire real line. To wit:
We finish by setting sinp(t + 2π pk) = sinp(t) for \(k\in \mathbb {Z}\) and do the same for our cosquine function.
Exercise 12
Show that the squine functions are odd and the cosquine functions are even for all p. (cf. Exercise 2).
Exercise 13
Previously, we were able to find an integral definition for arcsinp(x). Use a similar technique along with formula (5) and the result of Exercise 5 to derive an integral formula for arctanp(x). Use that formula to state another integral definition for π p. Then consult [18].
4 The Geometry of p-Circles
We generalize the unit circle approach by studying a geometry in which the squircles really are circles, i.e., they represent the set of points whose distance from a center point is a constant. To do that we will need to rethink what distance means.
4.1 The Planar p-Norm
A metric on \(\mathbb {R}^2\) is a function \(d:\mathbb {R}^2\to \mathbb {R}\) for which the following properties hold for any x, y, z in \(\mathbb {R}^2\).
- Positive Definite::
-
d(x, y) ≥ 0 with equality if and only if x = y
- Symmetric::
-
d(x, y) = d(y, x)
- Triangle Inequality::
-
d(x, y) ≤ d(x, z) + d(z, y)
The metrics we will study are translation-invariant, meaning for any \(b\in \mathbb {R}^2\), d(x, y) = d(x + b, y + b). In this case, we can understand the metric by the norm, ∥x∥d = d(x, 0). The Euclidean metric d 2(x, y) = ((x 1 − y 1)2 + (x 2 − y 2)2)1∕2 satisfies these properties and is of course the most familiar. We will study a generalization of this metric called the p-metric, wherein we turn the 2’s into p’s and add absolute values as before, giving, d p(x, y) = (|x 1 − y 1|p + |x 2 − y 2|p)1∕p with norm ∥x∥p = |x 1|p + |x 2|p. We also refer to this metric as the p-norm, a reference to the fact that because it is translation-invariant, the geometry can be fully explored by assuming one point is the origin.
Theorem 1
The p-metric is a translation-invariant metric on \(\mathbb {R}^2\).
Exercise 14
Verify that the p-metric is positive definite, symmetric, and translation-invariant.
Exercise 15
Show that if p ≠ 2 then the p-metric is not rotation-invariant, meaning that if points A and B are rotated about the origin, the distance between the points may change.
The triangle inequality for the p-metric is a consequence of Minkowski’s inequality, a discussion of which would take us a bit astray (see, e.g., [10]).
Of course, p = 2 is the usual Euclidean metric. The special case of p = 1 is also well-studied. It is often called taxicab geometry or the Manhattan metric because it models the distance a car would travel through a gridded street. See [12] for a full exploration of this geometry. It is useful to study as the extreme case of the p-metric satisfying the triangle inequality. The other extreme is p = ∞, which is defined as \(d(\boldsymbol {x}, \boldsymbol {y})=\max (|\boldsymbol {x}|,|\boldsymbol {y}|)\). This is the limiting case of the definition for finite p. In explorations, we find p = 4 to be a good case study because the 4-squircle is not extremal but still asymmetric, and p = 4 has some features that simplify some calculations.
4.2 Sines Everywhere
There are plenty of reasonable ways to parameterize a p-circle. We saw in the p = 2 case that all of these reasonable ways turn out to be the same, making the classical definitions of the trigonometric functions extremely natural. The choice is much less obvious for other values of p, and we will explore some of this variation.
We started with \(\arcsin _p(x) = \int _0^x \frac {1}{(1-t^p)^{(p-1)/p}} \ dt\) which we will now show corresponds to an areal parameterization of the p-circle, one in which the area of the unit p-circle is π p square units. This argument is due to Levin [14].
To mimic the classical case, we want the parameter α to be twice the area of the sector from the positive x-axis to the segment connecting the origin to (cosp(α), sinp(α)). See Fig. 5. For example, if p = 2 then α = π gives the semicircle with area \(\frac {\pi }{2}\). This sector splits into a triangle and half of a p-circular segment whose combined area is
By expressing the area in terms of y, we have found an expression for the inverse of the areal version of sine. A more explicit formula is found by differentiating and integrating:
Then \(\alpha (y) = \int _0^y (1-t^p)^{\frac {1}{p}-1}\ dt = \arcsin _p(y)\). In particular, when y = 1, α returns a value of π p∕2, twice the area of the first quadrant portion of the p-circle. Thus the area of the unit p-circle is π p square units.
Exercise 16
Repeat this calculation in terms of x to show α(x) =arccosp(x).
Exercise 17
Use polar coordinates to find explicit formulas in terms of classical trigonometric functions for the p-squigonometric functions parameterized by angle.
Note on Exercise 17
The polar formulas can be useful for numerical estimates and drawing pictures because they are expressed in terms of well-known and well-implemented functions. However, the non-Euclidean p-norms do not have a natural notion of angle so this parameterization is not as useful intrinsically. The next exercise illustrates this.
Exercise 18
Show that the areal 1-squine function is piecewise linear but the angular version of the 1-squine from Exercise 17 is not. See Fig. 6
4.3 Transcendental Functions
With our generalized trigonometric functions in place, we may now use them to build new p-norm versions of other transcendental functions. We start by adapting the defining differential equations (4) to define the hyperbolic p-trigonometric functions.
This CIVP has a unique solution x(t) =coshp(t) and y(t) =sinhp(t) which we define to be the hyperbolic p-cosine and p-sine, respectively. Just as (cosp(t), sinp(t)) parameterize the p-circle, (coshp(t), sinhp(t)) parameterize a p-hyperbola. See Fig. 7.
Exercise 19
Find integral expressions for the inverse hyperbolic p-sine and p-cosine functions.
Exercise 20
Show that if ω p = −1, then ωsinhp(t) =sinp(ω t) and coshp(t) =cosp(ω t).
Exercise 21
Show that |coshp(t)|p −|sinhp(t)|p = 1 for all t.
Exercise 21 brings us back to the geometry. It seems reasonable to define the curve |x|p −|y|p = 1 to be a rectangular p-hyperbola, and it is clearly parameterized by (coshp(t), sinhp(t)).
Exercise 22
Continuing with the methods of Exercises 2 and 12, prove the symmetries of the hyperbolic p-sine and p-cosine functions.
Exercise 23
Try to replicate Fig. 7 in your favorite computer algebra system. More generally, try to implement and graph as many of our special functions as you can.
Exercise 24
How might we define more general p-hyperbolas and p-ellipses?
Exercise 25
Use a computer algebra system to plot families of p-ellipses and p-hyperbolas and describe how they change shape as p varies from 1 to ∞.
Research Project 2 ( p-Conics)
Conic sections have a few different analytic and geometric definitions that are equivalent in Euclidean geometry but not in the p-metric. Explore p-conics in general. To what extent do classical geometric properties of these curves carry over to the p-norm? (See [12] for a delightful exploration of conics when p = 1).
Research Project 3 (Geometric Curves)
There are plenty of other interesting geometric curves besides conics. For example, a lemniscate is the set of points such that the product of the distances to two foci is constant (as opposed to the sum or difference in conics). Levin shows in [14] that the circumference of a standard Euclidean lemniscate is equal to the area of the 4-squircle. Can this relationship be generalized in any way? More broadly, explore geometric properties of curves and how they generalize to different p.
Taking a cue from the identity \(e^t = \sinh t+\cosh t\), our generalized hyperbolic functions offer a candidate for the p-exponential function expp(t) =sinhp(t) +coshp(t).
Exercise 26
Show that exp1(t) = { 1 t ≤ 02t + 1 t > 0
Research Project 4 (p-Exponential Growth)
Exercise 26 shows that expp(t) grows linearly in t if p = 1. It is obviously exponential if p = 2. What is the growth rate for general p?
Research Project 5 (General Transcendentals)
Keep going. We have generalized trigonometric and exponential functions, and other functions can be expressed in terms of those. Explore how such functions as a p-logarithm mirror their classical counterparts.
4.4 π Redux
We have defined \(\pi _p = 2\int _0^1 \frac {1}{(1-t^p)^{(p-1)/p}} \ dt\). It is the half-period of sinp and also represents the area of the unit p-circle. Another definition could be expressed in terms of p-arclength. Recall that the Euclidean arclength of a parameterized curve (x(t), y(t)) is obtained by considering a small arc of the curve to be the hypotenuse of an infinitesimal Euclidean triangle with side lengths dx and dy. We integrate over some interval a ≤ t ≤ b to obtain \(L= \int _a^b \sqrt {(dx)^2+(dy)^2}\ dt\). If we want to change to the p-arclength, we simply adjust our measure of the length of this hypotenuse to obtain \(L= \int _a^b \sqrt [p]{|dx|{ }^p+|dy|{ }^p}\ dt\).
Exercise 27
Show that if f(x) is a continuous function on a ≤ x ≤ b, then the p-arclength of the graph of y = f(x) over the interval a ≤ x ≤ b is \(\int _a^b \sqrt [p]{1+|f'(x)|{ }^p} \ dx\). Experiment with some of your favorite familiar functions to get a sense of how their “lengths” change with p, and which such integrals can be calculated exactly.
Exercise 28
Calculate the p-arclength of the segment connecting the origin to the point (1, 0). Compare with the p-arclength of the segment connecting the origin to the point (1, 1).
Define
Notice that \(\pi ^{arc}_p\) has different dynamics from π p. It takes a minimum value at p = 2, where \(\pi _2^{arc}=\pi _2=\pi \) [1].
Another candidate for defining π is to simply use the Euclidean arclength, \(\pi ^{euc}_p = 4 \int _0^1 \sqrt {1+(t^{p-1}(1-t^p))^2}\ dt\). Although this does not consider arclength in the circle’s natural geometry unless p = 2, it offers some insight into the geometry of the p-circle. The isoperimetric ratio of simple closed curve is the square of the length of the curve divided by its area. For the unit p-circle, this is \(I_p = \frac {\mathrm {length}^2}{\mathrm {area}} = \frac {(2\pi ^{euc}_p)^2}{\pi _p} = \frac {4(\pi ^{euc}_p)^2}{\pi _p}\). (See Figs. 8 and 9.) For p = 2, where all of our definitions of π are equivalent, this is 4π. The circle is the solution to the isoperimetric problem, meaning that 4π is the minimum possible value of the isoperimetric ratio. That is, the circle is the most efficient shape to enclose the most area with the smallest perimeter [3].
Exercise 29
Calculate directly the values of \(\pi ^{arc}_p\) and \(\pi ^{euc}_p\) for p = 1 and p = ∞.
Research Project 6 (Flavors of π)
Analyze \(\pi ^{euc}_p\) and \(\pi ^{arc}_p\) as functions of p. Is there any significance to the inflection point of \(\pi ^{arc}_p\) near p = 2.9?
Research Project 7 ( p-Isoperimetric Ratios)
Explore the isoperimetric properties of p-circles. What can be said about the isoperimetric ratio if we use p-arclength instead of Euclidean? We may define \(\hat {I}_p = \frac {4(\pi ^{arc}_p)^2}{\pi _p}\) and we see that the minimum is not attained at p = 2. I p and \(\hat I_p\) also have inflection points perhaps worth exploring.
5 Widening the Scope
We are seeing that for p ≠ 2, we get different definitions of π depending not just on the value of p, but on what geometric features we wish to capture. We will look closer at this variety and offer some tools to try to find connections among them.
5.1 Duality
Two real numbers p, p′ > 0 are conjugate if \(\frac {1}{p}+\frac {1}{p'}=1\). There are well-documented connections between the p-norm and p′-norm when p and p′ are conjugate, in which case the metric spaces are called dual . We explore how these connections are reflected in the squigonometric functions, beginning with an observation of Lindqvist and Peetre [15].
Exercise 30
Confirm the following notable relationships for conjugate numbers p, p′ > 1.
-
pp′ = p + p′
-
p = p′(p − 1)
-
\( p = \frac {p'}{p'-1}\)
-
p = p′ if and only if p = p′ = 2
Note that these expressions are all valid if p and p′ are exchanged. We also extend the definition to p = 1 by defining its conjugate to be p′ = ∞.
Theorem 2
Let p and p′ be conjugate. Then the p′-circumference of the unit p-circle is 2π p.
Proof
By symmetry, we may take the circumference to be four times the arclength of the quarter-circle. We use our p-trigonometric parameterization and calculate the circumference C directly to be
One phenomenon to watch for is seeing a “nice” property of Euclidean geometry as an artifact of the self-conjugacy of p = 2. For example, consider a particle moving according to the standard Euclidean circle parameterization \((\cos t, \sin t)\). The velocity of the particle \((-\sin t, \cos t)\) also parameterizes a unit circle. When we look at the generalized setting, we find that the velocity is actually parameterizing the conjugate circle, which is obscured in Euclidean geometry where the circle and its dual are indistinguishable.
Exercise 31
The graph of \(\pi ^{arc}_p\) in Fig. 8 suggests a symmetry related to conjugacy. Explore \(\pi ^{arc}_p\) and \(\pi ^{arc}_{p'}\) for conjugate p′, p and make a conjecture. Then see [11].
Exercise 32
Parameterize the unit p-circle by r(t) = (cosp(t), sinp(t)). Show that r′(t) parameterizes the unit p′-circle, where p and p′ are conjugate. Find a related result for a p-hyperbola.
Research Project 8 (Duality Relationships)
Theorem 2 suggests we might look for other relationships among geometric quantities in dual p-norms. Compare quantifiable features of various geometric objects in conjugate norms and try to establish some new connections.
5.2 Arclength Trigonometric Functions
We can use the definition of \(\pi _p^{arc}\) to analytically present an arclength parameterization of the unit squircle. Define our new sine function S(t) to be the function such that
and our new cosine function C(t) to be the function such that
with \(0\le t\le \pi _p^{arc}/2\). We first claim that S p(t) + C p(t) = 1. In Eq. (13), set s = (1 − u p)1∕p. Then u = (1 − s p)1∕p and \(du = -\frac {s^{p-1}}{(1-s^p)^{(p-1)/p}}\,ds\). Thus Eq. (13) becomes
which is (14) if C(t) = (1 − S p(t))1∕p, and the claim follows.
If we differentiate (13) with respect to t, we get
Through similar means, we can derive
From (13) and (14), we have that S(0) = 0, and C(0) = 1. We will call S and C the arclength sine and arclength cosine functions, respectively, notate them as \(\sin _p^{arc}\) and \(\cos _p^{arc}\), and note that they are the unique solutions on \(0\le t\le \pi _p^{arc}/2\) of the CIVP
with x corresponding to the arclength cosine and y corresponding to the arclength sine. We can then extend the functions to the entire real line in the usual manner via symmetry. A graph of \(y=\sin _4^{arc}(t)\) and its intimidating derivative
can be seen in Fig. 10.
This graph was rendered in Mathematica by first defining arclength p-sine and p-cosine functions in terms of the Euclidean angle t, then another for the “p-angle” φ. We then produced a parametric plot of the sine function and the cosine function against φ. (Try this in your favorite computer algebra system.)
5.3 Other Parameterizations
We have seen two different parameterizations of the unit p-circle leading to quite different versions of trigonometric functions, as well as different versions of π p. With (4), π p gave the correct area of the unit p-circle. With (15), \(2\pi _p^{arc}\) gave the correct arclength. This points to a key difference between the circle and the p-circle, which relates to the existence of π. The trigonometric functions are arranged so that their periods reflect the arclength and the areal and the angular parameterizations of the circle. No parameterization of the p-circle can do all three at the same time. We have values that play some of the roles of π, but none that can do it all.
We can, in fact, choose any CIVP of the form
to parameterize the unit p-circle, where ζ(x(t), y(t), t) is any appropriate differentiable function [23], and the solutions are taken over a suitable interval. In general, each such parameterization will occasion a new definition of π p, which may or may not correspond to a geometric trait of the p-circle, and result in generalized trigonometric functions which may not do much beyond parameterizing the unit p-circle.
Exercise 33
Find a function ζ(x(t), y(t), t) so that (16) results in the angular parameterization; that is, one in which the angle function \(\theta (t) = \arctan (\frac {y(t)}{x(t)})\) is the identity map. Compare with Exercise 17.
Exercise 34
We saw why the solution curves to a CIVP of the form (4) must lie on the unit p-circle, but we want to get the whole p-circle. What goes wrong if we let ζ(x, y, t) = x? How can we fix it?
Returning to the integral expression (2), we notice that we are seeing integrals of similar forms. This invites a more general two-parameter definition
and define \(\sin ^*_{p,q}\) as the inverse function of \(\arcsin ^*_{p,q}\).
Exercise 35
Verify that \(\sin ^*_{p,p'}(x) = \sin _p(x)\) where p and p′ are conjugate. We may then define an alternate version of our generalized trigonometric functions by \(\sin _p^*(x) = \sin ^*_{p,p}(x)\) and \(\cos _p^*(x)= \frac {d}{dx}\sin ^*_p(x)\). Show that \((\cos _p^*(x), \sin _p^*(x))\) parameterizes the unit p-circle. Define yet another version of π in this context.
Exercise 35 illustrates an expository inconvenience in this topic. Depending on your point of view, there are multiple definitions of generalized trigonometric functions that may seem natural, and they are all related by duality or other geometric properties. The definition in Exercise 35 is used in [13], which details many of the properties and applications of generalized trigonometry. That definition sets cosine as the derivative of sine, which is certainly convenient, but the parameter is no longer the area. It is mostly a matter of preference but one must take care to keep straight which versions have which properties. Unless p = 2, you will have multiple reasonable options.
Challenge Problem 2 (General Parameterizations)
Revisit the previous exercises in this chapter using different parameterizations, such as \(\sin _p^*\) and \(\sin ^{arc}_p\). For example, how would the derivative and integral tables change?
Research Project 9 (Unification)
We have cut across the different types of squigonometric functions both by varying p and varying what geometric information they encode. The previous Challenge Problem is not so challenging if p = 2 because the same functions encode everything. These lead to different functions for each p, but they are related by geometric properties and duality. In practice this makes for a somewhat disorganized theory. Are there any unifying principles we might establish to more generally work with the various versions of squigonometric functions?
6 Onward
In addition to the specific projects we suggested, we should also observe a variety of projects available by exploring ways the study of generalized trigonometric functions cuts across other fields.
For example, consider the following algebraic property of p-circles [24].
Theorem 3
For any integer p > 2, the unit p-circle passes through no rational points except on the axes. That is, if (x, y) is on the unit p-circle and \(x,y\in \mathbb {Q}\), then either x = 0 or y = 0.
Proof
Suppose \((\frac {m_1}{n_1},\frac {m_2}{n_2})\) is a rational point on the unit p-circle, where m 1, m 2, n 1, n 2, p are positive integers and p > 2. Then \(\left (\frac {m_1}{n_1}\right )^p+\left (\frac {m_2}{n_2}\right )^p=1\), or (m 1n 2)p + (m 2n 1)p = (n 1n 2)p. But this contradicts Fermat’s Last Theorem, a storied result [20] that says x p + y p = z p has no solutions in integers for p > 2.
This suggests looking at curves defined geometrically in the planar p-norm as algebraic curves, bringing in a new set of tools to understand their properties.
In the case p = 4, the integrals defining the inverse trigonometric functions are elliptic. Elliptic integrals have a wealth of special properties that can lead to special identities in the 4-norm, including a (messy) formula for sin4(t + u) [14]. Could this be pushed further?
The squigonometric functions offer a generalization of Fourier analysis, the foundations of which are laid out in [13]. The geometries we are studying are special cases of Minkowski geometry, which offers a more general lens through which to see these problems. Also, duality is a cornerstone of the function-analytic view in that the space of linear functionals on a vector space with the p-norm is isometric to the conjugate p′-norm. This offers yet another set of tools. Studies of higher dimensions may also open new territory.
Overall, this is a subject with a long but fractured history (cf. [1, 8, 17,18,19, 23] and the references therein) and there are many connections among the special functions associated with p-norm geometry yet to explore.
References
Adler, C.L., Tanton, J.: π is the minimum value of Pi. College Mathematics Journal 31(2), 102–106 (2000)
Andrews, G., Askey, R., Roy, R.: Special Functions (Encyclopedia of Mathematics and its Applications). Cambridge University Press (1999). https://doi.org/10.1017/CBO9781107325937
Blåjö, V.: The Isoperimetric Problem. The American Mathematical Monthly 112 (6), 526–566 (2005)
Borwein, J., Bailey, D.: Mathematics by Experiment: Plausible Reasoning in the 21st Century. A K Peters (2003)
Boyce, W., DiPrima, R.: Elementary Differential Equations, 9th edition. Wiley (2008)
Callahan, J., Cox, D., Hoffman, K., O’Shea, D., Pollatsek, H., Senechal, L.: Calculus in Context: The Five College Calculus Project. W.H. Freeman (1995)
Cha, B.: Transcendental Functions and Initial Value Problems: A Different Approach to Calculus II. College Mathematics Journal 38(4), 288–296 (2007)
Euler, R., Sadek, J.: The π’s go full circle, Mathematics Magazine 72, 59–63 (1999)
R. Grammel: Eine Verallgemeinerung der Kreis- und Hyperbelfunktionen, (German) Ing.-Arch. 16, 188–200 (1948)
Hardy, G., Littlewood, J., Pólya, G., Inequalities, Cambridge Univ. Press (1934)
Keller, J., Vakil, R.:
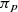 , the Value of π in
, the Value of π in 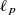 . The American Mathematical Monthly, 116(10), 931–935 (2009). https://doi.org/10.4169/000298909X477069
. The American Mathematical Monthly, 116(10), 931–935 (2009). https://doi.org/10.4169/000298909X477069
Krause, E.: Taxicab Geometry: Adventures in Non-Euclidean Geometry. Dover (1987)
Lang, J., Edmunds, D.: Eigenvalues, Embeddings and Generalised Trigonometric Functions, Springer Lecture Notes in Mathematics (2016)
Levin, A.: A Geometric Interpretation of an Infinite Product for the Lemniscate Constant. The American Mathematical Monthly, 113(6), 510–520 (2006). https://doi.org/10.2307/27641976
Lindqvist, P., Peetre, J.: p-arclength of the q-circle, Math. Student 72 (1–4) 139–145(2003)
Maican, C.C: Integral Evaluations Using the Gamma and Beta Functions and Elliptic Integrals in Engineering: A Self-Study Approach, International Press, 2005.
Markushevich, A.I.: The Remarkable Sine Functions, Elsevier (1966)
Poodiack, R.: Squigonometry, Hyperellipses, and Supereggs, Mathematics Magazine, 89(2) 92–102 (2016)
Shelupsky, D.: A Generalization of the Trigonometric Functions, The American Mathematical Monthly, 66(10), 879-884 (1959). https://doi.org/10.1080/00029890.1959.11989425
Singh, S.: Fermat’s last theorem: the story of a riddle that confounded the world’s greatest minds for 358 years. Harper Perennial (2007)
Weisstein, E.W.: Gamma Function. From Mathworld – A Wolfram Web Resource. http://mathworld.wolfram.com/GammaFunction.html
Weisstein, E.W.: Elliptic Integral Singular Value. From Mathworld – A Wolfram Web Resource. http://mathworld.wolfram.com/EllipticIntegralSingularValue.html
Wood, W.: Squigonometry, Mathematics Magazine, 84(4): 257–265 (2011)
Young, R.M. Excursions in Calculus: An Interplay of the Continuous and the Discrete, Cambridge Univ. Press (1992)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Wood, W.E., Poodiack, R.D. (2020). Squigonometry: Trigonometry in the p-Norm. In: Harris, P., Insko, E., Wootton, A. (eds) A Project-Based Guide to Undergraduate Research in Mathematics. Foundations for Undergraduate Research in Mathematics. Birkhäuser, Cham. https://doi.org/10.1007/978-3-030-37853-0_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-37853-0_9
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-030-37852-3
Online ISBN: 978-3-030-37853-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)













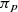 , the Value of π in
, the Value of π in 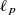 . The American Mathematical Monthly, 116(10), 931–935 (2009).
. The American Mathematical Monthly, 116(10), 931–935 (2009).