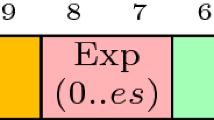Keywords

1 Introduction

The use of deep neural networks (DNN) as a general tool for signal and data processing is increasing both in industry and academia. One of the key challenge is the cost-effective computation of DNNs in order to ensure that these techniques can be implemented at low-cost, low-power and in real-time for embedded applications in IoT devices, robots, autonomous cars and so on. To this aim, an open research field is devoted to the cost-effective implementation of the main operators used in DNN, among them the activation function. The basic node of a DNN implements the sum of products of inputs (X) and their corresponding Weights (W) and then applies an activation function \(f(\, \cdot \,)\) to it to get the output of that layer and feed it as an input to the next layer. If we do not apply an activation function then the output signal would simply be a simple linear function, which has a low complexity but is not power enough to learn complex mappings (typically non-linear) from data. This is why the most used activation functions like Sigmoid, Tanh (Hyperbolic tangent) and ReLu (Rectified linear units) introduce non-linear properties to DNN [1, 2]. Choosing the activation function for a DNN model must take into account various aspects of both the considered data distribution and the underlying information representation. Moreover, for decision critical applications like machine perception for robotic and autonomous cars, also the implementation accuracy is important.

Indeed, one of the main trend in industry to keep low the complexity of DNN computation is avoiding complex arithmetic like double-precision floating point (64-bit), but relying on much more compact formats like BFLOAT or Flexpoint [3, 4] (i.e. a revised version of the 16-bit IEEE-754 floating point format adopted by Google Tensor Processing Units and Intel AI processors) or transprecision computing [5, 6] (e.g. the last Turing GPU from NVIDIA sustains INT32, INT8, INT4 and fp32 and fp16 computation [5]). To this aim, this paper presents a fast approximation of the hyperbolic tangent activation function combined with a new hardware-friendly information representation based on Posit numerical format.

Hereafter, Sect. 25.2 introduces the Posit format and the CppPosit library implemented at University of Pisa for the computation of the new numerical format. Section 25.3 introduces the hyperbolic tangent and its approximation. Implementation results when the proposed technique is applied to DNN with known benchmark dataset are reported in Sect. 25.4, where also a comparison with other known activation functions, like sigmoid, is discussed. Conclusions are drawn in Sect. 25.5.

2 Posit Arithmetic and the CppPosit Library

The Posit format as proposed in [7,8,9] is a fixed-length representation composed by at most 4 fields as shown in Fig. 25.1.: 1-bit sign field, variable-length regime field, variable-length (up to es-bits) exponent field and a variable-length fraction field. The overall length and the maximum exponent lengths are decided a-priori. Regime length and bit-content is determined as by the number of consecutive zeroes or ones terminated, respectively, by a single one (negative regime) or zero (positive regime) (see Fig. 25.2).

Fig. 25.1
figure 1

An example of Posit data type

Full size image
Fig. 25.2
figure 2

Two examples of 16-bit Posit with 3 bits for exponent (es = 3). In the upper the numerical value is: (221/256 is the value of the fraction, 1 + 221/256 is the mantissa). The final value is therefore 1.907348 × 10−6 · (1 + 221/256) = 3.55393 × 10−6. In the lower the numerical value is: (40/512 is the value of the fraction, 1 + 40/512 is the value of mantissa). The final value is therefore 2048 · (1 + 40/512) = 2208

Full size image

In this work we are going to use the cppPosit library, a modern C++ 14 implementation of the original Posit number system. The library identifies four different operational levels (L1–L4):

  • L1 operations are the ones involving bit-manipulation of the posit, without decoding it, considering it as an integer. L1 operations are thus performed on ALU and are fast.

  • L2 operations involve unpacking the Posit into its four different fields, with no exponent computation.

  • L3 operations instead involve full exponent unpacking, but without the need to perform arithmetic operations on the unpacked fields (examples are converting to/from float, posit or fixed point).

  • L4 operations require the unpacked version to perform software/hardware floating point computation using unpacked fields.

L1 operations are the most interesting, since they are the most efficient ones. L1 operations include inversion, negation, comparisons and absolute value. Moreover, when esbits = 0, L1 operations also include doubling/halving, 1’s complement when the specific Posit representation falls within the range [0, 1] and an approximation of the sigmoid function, called here fast Sigmoid, and described in [9]. Table 25.1 reports some implemented L1 operations stating whether the formula is exact or an approximation and the operation requirements in terms of Posit configuration and value. It is important to underline that every effort put in finding an L1 expression for some functions or operations has two advantages: a faster execution when using a software emulated PPU (Posit Processing Units), and a lower area required (i.e. less transistors) when the PPU is implemented in hardware.

Table 25.1 L1 operations summary
Full size table

3 The Hyperbolic Tangent and Its Approximation FastTanh

The hyperbolic tangent is a non-linear activation function typically adopted as a replacement to the sigmoid activation function. The advantage of the hyperbolic tangent over the sigmoid is the higher enhancement given to the negative values. In fact, the output of the hyperbolic tangent spans in [−1, 1] while the sigmoid outputs are only half of the previous, lying in [0, 1]. Furthermore, this difference in output range heavily impacts performances when using small-sized number representation, such as Posits with 10 or 8 bits. If we consider the sigmoid function applied to a Posit with x bits, we are actually using, as output, a Posit with x − 1 bits, since we are discarding the range [−1, 0], which is significantly dense when using the Posit format (see Fig. 25.3).

Fig. 25.3
figure 3

The posit circle when the total number of bits is 5. The hyperbolic tangent uses all the numbers in [−1, 1], while the sigmoid function only the ones in [0, 1]

Full size image

However, as already mentioned before, the sigmoid function

$$ {\text{sigmoid}}(x) = 1/\left( {e^{x} - 1} \right) $$

has a fast and efficient L1 approximation when using Posits with 0 exponent bits [9] (FastSigmoid). In order to exploit a similar trick for the hyperbolic tangent, we first introduced the scaled sigmoid function:

$$ {\text{sSigmoid}}_{k} (x) = k \cdot {\text{sigmoid}}(k \cdot x) - k/2 $$
(25.1)

Particularly interesting is the case k = 2, when the scaled sigmoid coincides with the hyperbolic tangent:

$$ {\text{sSigmoid}}_{2} (x) = \left( {e^{2 \cdot x} - 1} \right)/\left( {e^{2 \cdot x} + 1} \right) = \tanh (x) $$
(25.2)

Now that we can express the hyperbolic tangent as a linear function of the sigmoid one, we must rework the expression in order to provide a fast and efficient approximation to be used with Posits.

We know that Posit properties guarantee that, when using 0 exponent bits format, doubling the Posit value and computing its sigmoid approximation is just a matter of bit manipulations, so they can be efficiently obtained. The subtraction in Eq. (25.1) does not come with an efficient bit manipulation implementation as-is. In order to transform it into an L1 operation we have to rewrite it as:

$$ {\text{FastTanh}}(x) = 2 \cdot {\text{FastSigmoid}}(2 \cdot x) - 1 $$
(25.3)

Then let us focus on negative values for x only. For these values, the expression \(2 \cdot {\text{FastSigmoid}}(2 \cdot x)\) is inside the unitary region [0, 1]. Therefore, the L1 1’s complement can be applied. Finally, the negation is always an L1 operation, thus for all negative values of x the hyperbolic tangent approximation can be computed as an L1 operation. Moreover, thanks to the anti-symmetry of the hyperbolic tangent, this approach can also be extended to positive values. The following is a possible pseudo-code implementation:

  • FastTanh(x) → y

  •       x_n = x > 0? -x:x

  •       s = x > 0

  •       y_n = neg(compl1(twice(FastSigmoid(twice(x_n)))))

  •       y = s > 0? -y_n:y_n

where twice is an L1 operation which computes \({2} \cdot x\) and compl1 is the L1 function that computes the 1’s complement, again as an L1 operation.

Since we are also interested in training neural networks, we also need an efficient implementation of the hyperbolic tangent derivative:

$$ d\left( {\tanh (x)} \right)/d(x) = 1 - \tanh (x)^{2} $$

Let y = tanh(x)2, we know that 1 − y is always a L1 operation when esbits = 0, since tanh(x)2 is always in [0, 1].

4 Experimental Results

We compared the approximated hyperbolic tangent to the original version in terms of execution time and precision. Figure 25.4 shows the precision comparison, reporting also for Posit8 and Posit16 the mean squared error between the approximated and the original form (for both types, we used 0 bits of exponent). Figure 25.5 shows execution time comparison for several repetitions. Each repetition consists in computing about 60,000 hyperbolic tangents with the approximated formula and the exact one. As reported, the precision degradation is in the order of 10–3 while the gain in speed is around a factor 6 (six time faster). In Figs. 25.4 and 25.5 fast appr tanh is the Posit-based implementation, using L1 operations, of the Tanh function, by using the FastTanh formula in Eq. 25.3. This corresponds to the column labeled has FastTanh in Table 25.2.

Fig. 25.4
figure 4

Comparison between exact hyperbolic tangent (True tanh, in blue) and FastTanh (fast appr. tanh, in black), for Posit<8,0> (top) and Posit<16,0> (bottom). For Posit<8,0> the mean squared error is 2.816 × 10–3, while for Posit<16,0> it is 2.947 × 10–3

Full size image
Fig. 25.5
figure 5

Comparison of execution time of multiple consecutive executions between exact hyperbolic tangent (True tanh, in blue) and FastTanh (fast appr tanh, in black)

Full size image
Table 25.2 Accuracy (%) and inference time (ms) comparison between different activation functions and different Posit configurations (MNIST and Fashion-MNIST data set)
Full size table

Then we tested the approximated hyperbolic tangent as activation function for the LeNet-5 convolutional neural network, replacing the exact hyperbolic tangent used in the original implementation proposed in [10, 11] and comparing results against the original activation. The network model has been trained on MNIST [11] and Fashion-MNIST datasets [12].

Table 25.2 shows performance comparison between the two activation functions (FastTanh and Tanh) on the two datasets. Moreover, also the results obtained with Sigmoid and ReLu are reported, since they are widely adopted in literature as activation functions for DNN. The results in Table 25.2 in terms of accuracy show that the FastTanh outperforms both the ReLu and the FastSigmoid (a well-known approximation of the sigmoid function) which are widely used in state-of-art to implement activation functions in DNN.

5 Conclusions

In this work we have introduced FastTanh, a fast approximation of the hyperbolic tangent for numbers represented in Posit format which uses only L1 operations. We have used this approximation to speed up the training phase of deep neural networks. The proposed approximation has been tested on common deep neural network benchmarks. The use of this approximation resulted in a slightly less accurate neural network, with respect to the use of the slower true hyperbolic tangent, but with better performance in terms of inference time of the network. In our experiment, the FastTanh also outperforms both the ReLu and the FastSigmoid, which is a well-known approximation of the sigmoid function, a de facto standard activation function in neural networks.