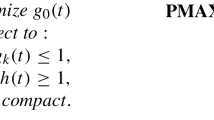Numerical Solution of Generalized Minimax Problems

Abstract

This contribution contains the description and investigation of three numerical methods for solving generalized minimax problems. These problems consists in the minimization of nonsmooth functions which are compositions of special smooth convex functions with maxima of smooth functions. The most important functions of this type are the sums of maxima of smooth functions. Section 11.2 is devoted to primal interior point methods which use solutions of nonlinear equations for obtaining minimax vectors. Section 11.3 contains investigation of smoothing methods, based on using exponential smoothing terms. Section 11.4 contains short description of primal-dual interior point methods based on transformation of generalized minimax problems to general nonlinear programming problems. Finally the last section contains results of numerical experiments.

1 Generalized Minimax Problems

In many practical problems we need to minimize functions that contain absolute values or pointwise maxima of smooth functions. Such functions are nonsmooth but they often have a special structure enabling the use of special methods that are more efficient than methods for minimization of general nonsmooth functions. The classical minimax problem, where F(x) =max_1≤k≤mf _k(x), or problems where the function to be minimized is a nonsmooth norm, e.g. F(x) = ∥f(x)∥_∞, F(x) = ∥f ₊(x)∥_∞, F(x) = ∥f(x)∥₁, F(x) = ∥f ₊(x)∥₁ with f(x) = [f ₁(x), …, f _m(x)]^T and $f_+({\boldsymbol x}) = [\max \{f_1({\boldsymbol x}),0\}, \dots , \max \{f_m({\boldsymbol x}),0\}]^T$, are typical examples. Such functions can be considered as special cases of more general functions, so it is possible to formulate more general theories and construct more general numerical methods. One possibility for generalization of the classical minimax problem consists in the use of the function

$$\displaystyle \begin{aligned} F({\boldsymbol x}) = \max_{1 \leq k \leq \overline{k}} {\boldsymbol p}_k^T {{\boldsymbol f}}({\boldsymbol x}), \end{aligned} $$

(11.1)

where ${\boldsymbol p}_k \in \mathbb {R}^m$, $1 \leq k \leq \overline {k}$, and ${{\boldsymbol f}}: \mathbb {R}^n \to \mathbb {R}^m$ is a smooth mapping. This function is a special case of composite nonsmooth functions of the form $F({\boldsymbol x}) = f_0({\boldsymbol x}) + \max _{1 \leq k \leq \overline {k}} ({\boldsymbol p}_k^T {{\boldsymbol f}}({\boldsymbol x}) + b_k)$, where $f_0:\mathbb {R}^n \to \mathbb {R}$ is a continuously differentiable function [8, Section 14.1].

Remark 11.1

We can express all above mentioned minimax problems and nonsmooth norms in form (11.1).

• (a) Setting p _k = e _k, where e _k is the k-th column of an identity matrix and $\overline {k} = m$, we obtain F(x) =max_1≤k≤mf _k(x) (the classical minimax).

• (b) Setting p _k = e _k, p _m+k = −e _k and $\overline {k} = 2m$, we obtain $F({\boldsymbol x}) = \max _{1 \leq k \leq m} \max \{f_k({\boldsymbol x}), -f_k({\boldsymbol x})\} = \|f({\boldsymbol x})\|{ }_{\infty }$.

• (c) Setting p _k = e _k, p _m+1 = 0 and $\overline {k} = m+1$, we obtain $F({\boldsymbol x}) = \max \{\max _{1 \leq k \leq m} f_k({\boldsymbol x}), 0\} = \|f({\boldsymbol x})_+\|{ }_{\infty }$.

• (d) If $\overline {k} = 2^m$ and p _k, 1 ≤ k ≤ 2^m, are mutually different vectors whose elements are either 1 or − 1, we obtain $F({\boldsymbol x}) = \sum _{k=1}^m \max \{f_k({\boldsymbol x}), -f_k({\boldsymbol x})\} = \|f({\boldsymbol x})\|{ }_1$.

• (e) If $\overline {k} = 2^m$ and p _k, 1 ≤ k ≤ 2^m, are mutually different vectors whose elements are either 1 or 0, we obtain $F({\boldsymbol x}) = \sum _{k=1}^m \max \{f_k({\boldsymbol x}), 0\} = \|f_+({\boldsymbol x})\|{ }_1$.

Remark 11.2

Since the mapping f(x) is continuously differentiable, the function (11.1) is Lipschitz. Thus, if the point ${\boldsymbol x} \in \mathbb {R}^n$ is a local minimum of F(x), then 0 ∈ ∂F(x) [25, Theorem 3.2.5] holds. According to [25, Theorem 3.2.13], one has

$$\displaystyle \begin{aligned}\partial F({\boldsymbol x}) = (\nabla {{\boldsymbol f}}({\boldsymbol x}))^T \operatorname{\mathrm{conv}} \left\{{\boldsymbol p}_k: k \in \bar{\mathcal{I}}({\boldsymbol x}) \right\},\end{aligned}$$

where $\bar {\mathcal {I}}({\boldsymbol x}) = \{k \in \{1, \dots , \overline {k}\} : {\boldsymbol p}_k^T {{\boldsymbol f}}({\boldsymbol x}) = F({\boldsymbol x})\}$. Thus, if the point ${\boldsymbol x} \in \mathbb {R}^n$ is a local minimum of F(x), then multipliers λ _k ≥ 0, $1 \leq k \leq \overline {k}$, exist, such that $\lambda _k ({\boldsymbol p}_k^T {{\boldsymbol f}}({\boldsymbol x}) - F({\boldsymbol x})) = 0$, $1 \leq k \leq \overline {k}$,

$$\displaystyle \begin{aligned}\sum_{k=1}^{\overline{k}} \lambda_k = 1 \quad \mathrm{and} \quad \sum_{k=1}^{\overline{k}} \lambda_k J^T({\boldsymbol x}) {\boldsymbol p}_k = {\mathbf{0}},\end{aligned}$$

where J(x) is a Jacobian matrix of the mapping f(x).

Remark 11.3

It is clear that a minimum of function (11.1) is a solution of a nonlinear programming problem consisting in minimization of a function $\tilde {F}: \mathbb {R}^{n+1} \to \mathbb {R}$, where $\tilde {F}({\boldsymbol x},z) = z$, on the set

$$\displaystyle \begin{aligned}{\mathcal{C}} = \{({\boldsymbol x},z) \in \mathbb{R}^{n+1}: {\boldsymbol p}_k^T {{\boldsymbol f}}({\boldsymbol x}) \leq z, \; 1 \leq k \leq \overline{k}\}.\end{aligned}$$

Denoting $c_k({\boldsymbol x},z) = {\boldsymbol p}_k^T {{\boldsymbol f}}({\boldsymbol x}) - z$ and a _k = ∇c _k(x, z), $1 \leq k \leq \overline {k}$, we obtain ${\boldsymbol a}_k = [{\boldsymbol p}_k^T J({\boldsymbol x}), -1]^T$ and ${\boldsymbol g} = \nabla \tilde {F}({\boldsymbol x},z) = [{\mathbf {0}}^T,1]^T$, so the necessary KKT conditions can be written in the form

$$\displaystyle \begin{aligned}\left[\begin{array}{c} {\mathbf{0}} \\ 1 \end{array}\right] + \sum_{k=1}^{\overline{k}} \left[\begin{array}{c} J^T({\boldsymbol x}) {\boldsymbol p}_k \\ -1 \end{array}\right] \lambda_k = {\mathbf{0}},\end{aligned}$$

$\lambda _k ({\boldsymbol p}_k^T {{\boldsymbol f}}({\boldsymbol x}) - z) = 0$, where λ _k ≥ 0, $1 \leq k \leq \overline {k}$, are the Lagrange multipliers and z = F(x). Thus, we obtain the same necessary conditions for an extremum as in Remark 11.2.

From the examples given in Remark 11.1 it follows that composite nondifferentiable functions are not suitable for representation of the functions F(x) = ∥f(x)∥₁ and F(x) = ∥f ₊(x)∥₁ because in this case the expression on the right-hand side of (11.1) contains 2^m elements with vectors p _k, 1 ≤ k ≤ 2^m. In the subsequent considerations, we will choose a somewhat different approach. We will consider generalized minimax functions established in [5] and [23].

Definition 11.1

We say that $F:\mathbb {R}^n \to \mathbb {R}$ is a generalized minimax function if

$$\displaystyle \begin{aligned} F({\boldsymbol x}) = h(F_1({\boldsymbol x}), \dots, F_m({\boldsymbol x})), \quad F_k({\boldsymbol x}) = \max_{1 \leq l \leq m_k}f_{kl}({\boldsymbol x}), \quad 1 \leq k \leq m, \end{aligned} $$

(11.2)

where $h: \mathbb {R}^m \to \mathbb {R}$ and $f_{kl}: \mathbb {R}^n \to \mathbb {R}$, 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, are smooth functions satisfying the following assumptions.

Assumption 11.1

Functions f _kl, 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, are bounded from below on $\mathbb {R}^n$, so that there exists a constant $\underline {F} \in \mathbb {R}$such that $f_{kl}({\boldsymbol x}) \geq \underline {F}$, 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, for all ${\boldsymbol x} \in \mathbb {R}^n$.

Assumption 11.2

Functions F _k, 1 ≤ k ≤ m, are bounded from below on $\mathbb {R}^n$, so that there exist constants $\underline {F}_k \in \mathbb {R}$such that $F_k({\boldsymbol x}) \geq \underline {F}_k$, 1 ≤ k ≤ m, for all ${\boldsymbol x} \in \mathbb {R}^n$.

Assumption 11.3

The function h is twice continuously differentiable and convex satisfying

$$\displaystyle \begin{aligned} 0 < \underline{h}_k \leq \frac{\partial}{\partial z_k} h({\boldsymbol z}) \leq \overline{h}_k, \quad 1 \leq k \leq m, \end{aligned} $$

(11.3)

for every ${\boldsymbol z} \in {\mathcal {Z}} = \{{\boldsymbol z} \in \mathbb {R}^m: z_k \geq \underline {F}_k, \; 1 \leq k \leq m\}$ (vector ${\boldsymbol z} \in \mathbb {R}^m$ is called the minimax vector).

Assumption 11.4

Functions f _kl(x), 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, are twice continuously differentiable on the convex hull of the level set

$$\displaystyle \begin{aligned}{\mathcal{D}}_F(\overline{F}) = \{{\boldsymbol x} \in \mathbb{R}^n: F_k({\boldsymbol x}) \leq \overline{F}, \; 1 \leq k \leq m\}\end{aligned}$$

for a sufficiently large upper bound $\overline {F}$and subsequently, constants $\overline {g}$and $\overline {G}$exist such that $\|{\boldsymbol g}_{kl}({\boldsymbol x})\| \leq \overline {g}$and $\|G_{kl}({\boldsymbol x})\| \leq \overline {G}$for all 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, and ${\boldsymbol x} \in \operatorname {\mathrm {conv}} {\mathcal {D}}_F(\overline {F})$, whereg _kl(x) = ∇f _kl(x) and G _kl(x) = ∇²f _kl(x).

Remark 11.4

The conditions imposed on the function h(z) are relatively strong but many important nonsmooth functions satisfy them.

• (1) Let $h: \mathbb {R} \to \mathbb {R}$ be an identity mapping, so h(z) = z and h′(z) = 1 > 0. Then setting $\overline {k} = 1$, $m_1 = \overline {l}$ and

  $$\displaystyle \begin{aligned}F({\boldsymbol x}) = h(F_1({\boldsymbol x})) = F_1({\boldsymbol x}) = \max_{1 \leq l \leq \overline{l}} {\boldsymbol p}_l^T {{\boldsymbol f}}({\boldsymbol x})\end{aligned}$$

  (since $f_{1l} = {\boldsymbol p}_l^T {{\boldsymbol f}}({\boldsymbol x})$), we obtain the composite nonsmooth function (11.1) and therefore the functions F(x) =max_1≤k≤mf _k(x), F(x) = ∥f(x)∥_∞, F(x) = ∥f ₊(x)∥_∞.

• (2) Let $h: \mathbb {R}^m \to \mathbb {R}$, where h(z) = z ₁ + ⋯ + z _m, so $\frac {\partial }{\partial z_k} h({\boldsymbol z}) = 1 > 0$, 1 ≤ k ≤ m. Then function (11.2) has the form

  $$\displaystyle \begin{aligned} F({\boldsymbol x}) = \sum_{k=1}^m F_k({\boldsymbol x}) = \sum_{k=1}^m \max_{1 \leq l \leq m_k}f_{kl}({\boldsymbol x}) \end{aligned} $$

  (11.4)

  (the sum of maxima). If m _k = 2 and $F_k({\boldsymbol x}) = \max \{f_k({\boldsymbol x}), -f_k({\boldsymbol x})\}$, we obtain the function F(x) = ∥f(x)∥₁. If m _k = 2 and $F_k({\boldsymbol x}) = \max \{f_k({\boldsymbol x}), 0\}$, we obtain the function F(x) = ∥f ₊(x)∥₁. It follows that the expression of functions F(x) = ∥f(x)∥₁ and F(x) = ∥f ₊(x)∥₁ by (11.2) contains only m summands and each summand is a maximum of two function values. Thus, this approach is much more economic than the use of formulas stated in Remark 11.1(d)–(e).

Remark 11.5

Since the functions F _k(x), 1 ≤ k ≤ m, are regular [25, Theorem 3.2.13], the function h(z) is continuously differentiable, and $h_k = \frac {\partial }{\partial z_k} h({\boldsymbol z}) > 0$, one can write [25, Theorem 3.2.9]

$$\displaystyle \begin{aligned} \begin{array}{rcl} \partial F({\boldsymbol x}) &\displaystyle =&\displaystyle \operatorname{\mathrm{conv}} \sum_{k=1}^m h_k \partial F_k({\boldsymbol x}) = \sum_{k=1}^m h_k \partial F_k({\boldsymbol x}) \\ &\displaystyle =&\displaystyle \sum_{k=1}^m h_k \operatorname{\mathrm{conv}} \{{\boldsymbol g}_{kl}({\boldsymbol x}): l \in \bar{\mathcal{I}}_k({\boldsymbol x})\}, \end{array} \end{aligned} $$

where $\bar {\mathcal {I}}_k({\boldsymbol x}) = \{l: 1 \leq l \leq m_k, f_{kl}({\boldsymbol x}) = F_k({\boldsymbol x})\}$. Thus, one has

$$\displaystyle \begin{aligned}\partial F({\boldsymbol x}) = \sum_{k=1}^m h_k \sum_{l=1}^{m_k} \lambda_{kl} {\boldsymbol g}_{kl}({\boldsymbol x}),\end{aligned}$$

where for 1 ≤ k ≤ m it holds λ _kl ≥ 0, λ _kl(F _k(x) − f _kl(x)) = 0, 1 ≤ l ≤ m _k, and $\sum _{l=1}^{m_k} \lambda _{kl}=1$. Setting u _kl = h _kλ _kl, 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, we can write

$$\displaystyle \begin{aligned}\partial F({\boldsymbol x}) = \sum_{k=1}^m \sum_{l=1}^{m_k} u_{kl} {\boldsymbol g}_{kl}({\boldsymbol x}),\end{aligned}$$

where for 1 ≤ k ≤ m it holds u _kl ≥ 0, u _kl(F _k(x) − f _kl(x)) = 0, 1 ≤ l ≤ m _k, and $\sum _{l=1}^{m_k} u_{kl} = h_k$. If a point ${\boldsymbol x} \in \mathbb {R}^n$ is a minimum of a function F(x), then 0 ∈ ∂F(x), so there exist multipliers u _kl, 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, such that

$$\displaystyle \begin{aligned} &\sum_{k=1}^m \sum_{l=1}^{m_k} {\boldsymbol g}_{kl}({\boldsymbol x}) u_{kl} = {\mathbf{0}}, \quad \sum_{l=1}^{m_k} u_{kl} = h_k, \quad h_k = \frac{\partial}{\partial z_k} h({\boldsymbol z}),{} \end{aligned} $$

(11.5)

$$\displaystyle \begin{aligned} &u_{kl} \geq 0, \quad F_k({\boldsymbol x}) - f_{kl}({\boldsymbol x}) \geq 0, \quad u_{kl} (F_k({\boldsymbol x}) - f_{kl}({\boldsymbol x})) = 0.{} \end{aligned} $$

(11.6)

Remark 11.6

Unconstrained minimization of function (11.2) is equivalent to the nonlinear programming problem

$$\displaystyle \begin{aligned} \begin{cases} \text{minimize}\quad & \tilde{F}({\boldsymbol x},{\boldsymbol z}) = h({\boldsymbol z}) \\ \text{subject to} & f_{kl}({\boldsymbol x}) \leq z_k, \quad 1 \leq k \leq m, \quad 1 \leq l \leq m_k. \end{cases} \end{aligned} $$

(11.7)

The condition (11.3) is sufficient for satisfying equalities z _k = F _k(x), 1 ≤ k ≤ m, at the minimum point. Denoting c _kl(x, z) = f _kl(x) − z _k and a _kl(x, z) = ∇c _kl(x, z), 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, we obtain ${\boldsymbol a}_{kl}({\boldsymbol x},{\boldsymbol z}) = [{\boldsymbol g}_{kl}^T({\boldsymbol x}), -{\boldsymbol e}_k^T]^T$, where g _kl(x) is a gradient of f _kl(x) in x and e _k is the k-th column of the unit matrix of order m. Thus, the necessary first-order (KKT) conditions have the form

$$\displaystyle \begin{aligned} &{\boldsymbol g}({\boldsymbol x},{\boldsymbol u}) = \sum_{k=1}^m \sum_{l=1}^{m_k} {\boldsymbol g}_{kl}({\boldsymbol x}) u_{kl} = {\mathbf{0}}, \quad \sum_{l=1}^{m_k} u_{kl} = h_k, \quad h_k = \frac{\partial}{\partial z_k} h({\boldsymbol z}),{} \end{aligned} $$

(11.8)

$$\displaystyle \begin{aligned} &u_{kl} \geq 0, \quad z_k - f_{kl}({\boldsymbol x}) \geq 0, \quad u_{kl} (z_k - f_{kl}({\boldsymbol x})) = 0,{} \end{aligned} $$

(11.9)

where u _kl, 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, are Lagrange multipliers and z _k = F _k(x). So we obtain the same necessary conditions for an extremum as in Remark 11.5.

Remark 11.7

A classical minimax problem

$$\displaystyle \begin{aligned} F({\boldsymbol x}) = \max_{1 \leq k \leq m} f_k({\boldsymbol x}) {} \end{aligned} $$

(11.10)

can be replaced with an equivalent nonlinear programming problem

$$\displaystyle \begin{aligned} \begin{cases} \text{minimize}\quad & \tilde{F}({\boldsymbol x},z) = z \\ \text{subject to} & f_k({\boldsymbol x}) \leq z, \quad 1 \leq k \leq m, \end{cases} \end{aligned} $$

(11.11)

and the necessary KKT conditions have the form

$$\displaystyle \begin{aligned} &\sum_{k=1}^m {\boldsymbol g}_{k}({\boldsymbol x}) u_k = {\mathbf{0}}, \quad \sum_{k=1}^{m} u_k = 1, {} \end{aligned} $$

(11.12)

$$\displaystyle \begin{aligned} &u_k \geq 0, \quad z - f_{k}({\boldsymbol x}) \geq 0, \quad u_k (z - f_{k}({\boldsymbol x})) = 0, \quad 1 \leq k \leq m. {} \end{aligned} $$

(11.13)

Remark 11.8

Minimization of the sum of absolute values

$$\displaystyle \begin{aligned} F({\boldsymbol x}) = \sum_{k=1}^m |f_k({\boldsymbol x})| = \sum_{k=1}^m \max\{f_k^+({\boldsymbol x}), f_k^-({\boldsymbol x})\}, \end{aligned} $$

(11.14)

where

$$\displaystyle \begin{aligned}f_k^+({\boldsymbol x}) = f_k({\boldsymbol x}), \quad f_k^-({\boldsymbol x}) = -f_k({\boldsymbol x})\end{aligned}$$

can be replaced with an equivalent nonlinear programming problem

$$\displaystyle \begin{aligned} \begin{cases} \text{minimize}\quad & \tilde{F}({\boldsymbol x},{\boldsymbol z}) = \sum_{k=1}^m z_k \\ \text{subject to} & -z_k \leq f_k({\boldsymbol x}) \leq z_k, \end{cases} \end{aligned} $$

(11.15)

(there are two constraints $c_k^-({\boldsymbol x}) = z_k - f_k({\boldsymbol x}) \geq 0$ and $c_k^+({\boldsymbol x}) = z_k + f_k({\boldsymbol x}) \geq 0$ for each index 1 ≤ k ≤ m) and the necessary KKT conditions have the form

$$\displaystyle \begin{aligned} &\sum_{k=1}^m {\boldsymbol g}_k({\boldsymbol x}) (u_k^+ - u_k^-) = {\mathbf{0}}, ~\quad u_k^+ + u_k^- = 1, {} \end{aligned} $$

(11.16)

$$\displaystyle \begin{aligned} &u_k^+ \geq 0, \quad z_k - f_k({\boldsymbol x}) \geq 0, \quad u_k^+ (z_k - f_k({\boldsymbol x})) = 0,{} \end{aligned} $$

(11.17)

$$\displaystyle \begin{aligned} &u_k^- \geq 0, \quad z_k + f_k({\boldsymbol x}) \geq 0, \quad u_k^- (z_k + f_k({\boldsymbol x})) = 0,{} \end{aligned} $$

(11.18)

where 1 ≤ k ≤ m. If we set $u_k = u_k^+ - u_k^-$ and use the equality $u_k^+ + u_k^- = 1$, we obtain $u_k^+ = (1 + u_k)/2$, $u_k^- = (1 - u_k)/2$. From conditions $u_k^+ \geq 0$, $u_k^- \geq 0$ the inequalities − 1 ≤ u _k ≤ 1, or |u _k|≤ 1, follow. The condition $u_k^+ + u_k^- = 1$ implies that the numbers $u_k^+$, $u_k^-$ cannot be simultaneously zero, so either z _k = f _k(x) or z _k = −f _k(x), that is z _k = |f _k(x)|. If f _k(x) ≠ 0, it cannot simultaneously hold z _k = f _k(x) and z _k = −f _k(x), so the numbers $u_k^+$, $u_k^-$ cannot be simultaneously nonzero. Then either $u_k = u_k^+ = 1$ and z _k = f _k(x) or $u_k = -u_k^- = -1$ and z _k = −f _k(x), that is u _k = f _k(x)∕|f _k(x)|. Thus, the necessary KKT conditions have the form

$$\displaystyle \begin{aligned} &\sum_{k=1}^m {\boldsymbol g}_k({\boldsymbol x}) u_k = {\mathbf{0}}, \quad z_k = |f_k({\boldsymbol x})|, \\ &|u_k| \leq 1, \quad u_k = \frac{f_k({\boldsymbol x})}{|f_k({\boldsymbol x})|}, \quad \mathrm{if} \quad |f_k({\boldsymbol x})| > 0. {} \end{aligned} $$

(11.19)

Remark 11.9

Minimization of the sum of absolute values can also be reformulated so that more slack variables are used. We obtain the problem

$$\displaystyle \begin{aligned} \begin{cases} \text{minimize}\quad & \tilde{F}({\boldsymbol x},{\boldsymbol z}) = \sum_{k=1}^m (z_k^+ + z_k^-) \\ \text{subject to} & f_k({\boldsymbol x}) = z_k^+ - z_k^-, \quad z_k^+ \geq 0, \quad z_k^- \geq 0, \end{cases} \end{aligned} $$

(11.20)

where 1 ≤ k ≤ m. This problem contains m general equality constraints and 2m simple bounds for 2m slack variables.

In the subsequent considerations, we will restrict ourselves to functions of the form (11.4), the sums of maxima that include most cases important for applications. In this case, it holds

$$\displaystyle \begin{aligned} h({\boldsymbol z}) = \sum_{k=1}^m z_k, \quad \nabla h({\boldsymbol z}) = \tilde{{\boldsymbol e}}, \quad \nabla^2 h({\boldsymbol z}) = 0, {} \end{aligned} $$

(11.21)

where $\tilde {{\boldsymbol e}} \in \mathbb {R}^m$ is a vector with unit elements. The case when h(z) is a general function satisfying Assumption 11.3 is studied in [23].

2 Primal Interior Point Methods

2.1 Barriers and Barrier Functions

Primal interior point methods for equality constraint minimization problems are based on adding a barrier term containing constraint functions to the minimized function. A resulting barrier function, depending on a barrier parameter $0 < \mu \leq \overline {\mu } < \infty$, is successively minimized on $\mathbb {R}^n$ (without any constraints), where μ ↓ 0. Applying this approach on the problem (11.7), we obtain a barrier function

$$\displaystyle \begin{aligned} B_{\mu}({\boldsymbol x},{\boldsymbol z}) = h({\boldsymbol z}) + \mu \sum_{k=1}^m \sum_{l=1}^{m_k} \varphi(z_k - f_{kl}({\boldsymbol x})), \quad 0 < \mu \leq \overline{\mu}, {} \end{aligned} $$

(11.22)

where $\varphi : (0,\infty ) \to \mathbb {R}$ is a barrier which satisfies the following assumption.

Assumption 11.5

Function φ(t), t ∈ (0, ∞), is twice continuously differentiable, decreasing, and strictly convex, with lim_t↓0φ(t) = ∞. Function φ′(t) is increasing and strictly concave such that lim_t↑∞φ′(t) = 0. For t ∈ (0, ∞) it holds − tφ′(t) ≤ 1, t ²φ″(t) ≤ 1. There exist numbers τ > 0 and $\underline {c} > 0$such that for t < τ it holds

$$\displaystyle \begin{aligned} -t \varphi'(t) \geq \underline{c} {} \end{aligned} $$

(11.23)

and

$$\displaystyle \begin{aligned} \varphi'(t) \varphi'''(t) - \varphi''(t)^2 > 0. {} \end{aligned} $$

(11.24)

Remark 11.10

A logarithmic barrier function

$$\displaystyle \begin{aligned} \varphi(t) = \log t^{-1} = -\log t, {} \end{aligned} $$

(11.25)

is most frequently used. It satisfies Assumption 11.5 with $\underline {c} = 1$ and τ = ∞ but it is not bounded from below since $\log t \uparrow \infty$ for t ↑∞. For that reason, barriers bounded from below are sometimes used, e.g. a function

$$\displaystyle \begin{aligned} \varphi(t) = \log(t^{-1}+\tau^{-1}) = -\log\frac{t \tau}{t + \tau}, {} \end{aligned} $$

(11.26)

which is bounded from below by number $\underline {\varphi } = -\log \tau$, or a function

$$\displaystyle \begin{aligned} \varphi(t) = -\log t, \quad 0 < t \leq \tau, \qquad \varphi(t) = a t^{-2}+b t^{-1} + c, \quad t \geq \tau, {} \end{aligned} $$

(11.27)

which is bounded from below by number $\underline {\varphi } = c = -\log \tau -3/2$, or a function

$$\displaystyle \begin{aligned} \varphi(t) = -\log t, \quad 0 < t \leq \tau, \qquad \varphi(t) = a t^{-1}+b t^{-1/2} + c, \quad t \geq \tau, {} \end{aligned} $$

(11.28)

which is bounded from below by number $\underline {\varphi } = c = -\log {\tau }-3$. Coefficients a, b, c are chosen so that function φ(t) as well as its first and second derivatives are continuous in t = τ. All these barriers satisfy Assumption 11.5 [23] (the proof of this statement is trivial for logarithmic barrier (11.25)).

Even if bounded from below barriers (11.26)–(11.28) have more advantageous theoretical properties (Assumption 11.1 can be replaced with a weaker Assumption 11.2 and the proof of Lemma 11.2 below is much simpler, see [23]), algorithms using logarithmic barrier (11.26) are usually more efficient. Therefore, we will only deal with methods using the logarithmic barrier $\varphi (t) = -\log t$ in the subsequent considerations.

2.2 Iterative Determination of a Minimax Vector

Suppose the function h(z) is of form (11.21). Using the logarithmic barrier $\varphi (t) = -\log t$, function (11.22) can be written as

$$\displaystyle \begin{aligned} B_{\mu}({\boldsymbol x},{\boldsymbol z}) = \sum_{k=1}^m z_k - \mu \sum_{k=1}^m \sum_{l=1}^{m_k} \log(z_k - f_{kl}({\boldsymbol x})), \quad 0 < \mu \leq \overline{\mu}. {} \end{aligned} $$

(11.29)

Further, we will denote g _kl(x) and G _kl(x) gradients and Hessian matrices of functions f _kl(x), 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, and set

$$\displaystyle \begin{aligned} u_{kl}({\boldsymbol x},{\boldsymbol z}) &= \frac{\mu}{z_k - f_{kl}({\boldsymbol x})} \geq 0, \\ v_{kl}({\boldsymbol x},{\boldsymbol z}) &= \frac{\mu}{(z_k - f_{kl}({\boldsymbol x}))^2} = \frac{1}{\mu} u_{kl}^2({\boldsymbol x},{\boldsymbol z}) \geq 0, {} \end{aligned} $$

(11.30)

and

Denoting by g(x, z) the gradient of the function B _μ(x, z) and $\gamma _k({\boldsymbol x},{\boldsymbol z}) = \frac {\partial }{\partial z_k} B_{\mu }({\boldsymbol x},{\boldsymbol z})$, the necessary conditions for an extremum of the barrier function (11.22) can be written in the form

$$\displaystyle \begin{aligned} {\boldsymbol g}({\boldsymbol x},{\boldsymbol z}) &= \sum_{k=1}^m \sum_{l=1}^{m_k} {\boldsymbol g}_{kl}({\boldsymbol x}) u_{kl}({\boldsymbol x},{\boldsymbol z}) = \sum_{k=1}^m A_k({\boldsymbol x}) {\boldsymbol u}_k({\boldsymbol x},{\boldsymbol z}) = {\mathbf{0}}, {} \end{aligned} $$

(11.31)

$$\displaystyle \begin{aligned} \gamma_k({\boldsymbol x},{\boldsymbol z}) &= 1 - \sum_{l=1}^{m_k} u_{kl}({\boldsymbol x},{\boldsymbol z}) =1 - \tilde{{\boldsymbol e}}_k^T {\boldsymbol u}_k({\boldsymbol x},{\boldsymbol z}) = 0, \quad 1 \leq k \leq m, {} \end{aligned} $$

(11.32)

where $A_k({\boldsymbol x}) = [{\boldsymbol g}_{k1}({\boldsymbol x}), \ldots , {\boldsymbol g}_{km_k}({\boldsymbol x})]$, which is a system of n + m nonlinear equations for unknown vectors x and z. These equations can be solved by the Newton method. In this case, the second derivatives of the Lagrange function (which are the first derivatives of expressions (11.31) and (11.32)) are computed. Denoting

$$\displaystyle \begin{aligned} G({\boldsymbol x},{\boldsymbol z}) = \sum_{k=1}^m \sum_{l=1}^{m_k} G_{kl}({\boldsymbol x}) u_{kl}({\boldsymbol x},{\boldsymbol z}), {} \end{aligned} $$

(11.33)

the Hessian matrix of the Lagrange function and setting

$$\displaystyle \begin{aligned} \begin{array}{rcl} U_k({\boldsymbol x},{\boldsymbol z}) &\displaystyle = &\displaystyle \operatorname{\mathrm{diag}}[u_{k1}({\boldsymbol x},{\boldsymbol z}), \dots, u_{km_k}({\boldsymbol x},{\boldsymbol z})], \\ V_k({\boldsymbol x},{\boldsymbol z}) &\displaystyle = &\displaystyle \operatorname{\mathrm{diag}}[v_{k1}({\boldsymbol x},{\boldsymbol z}), \dots, v_{km_k}({\boldsymbol x},{\boldsymbol z})] = \frac{1}{\mu} U_k^2({\boldsymbol x},{\boldsymbol z}), \end{array} \end{aligned} $$

we can write

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{\partial}{\partial {\boldsymbol x}} {\boldsymbol g}({\boldsymbol x},{\boldsymbol z}) &\displaystyle = &\displaystyle \sum_{k=1}^m \sum_{l=1}^{m_k} G_{kl}({\boldsymbol x}) u_{kl}({\boldsymbol x},{\boldsymbol z}) + \sum_{k=1}^m \sum_{l=1}^{m_k} {\boldsymbol g}_{kl}({\boldsymbol x})v_{kl}({\boldsymbol x},{\boldsymbol z}) {\boldsymbol g}_{kl}^T({\boldsymbol x}) \\ &\displaystyle = &\displaystyle G({\boldsymbol x},{\boldsymbol z}) + \sum_{k=1}^m A_k({\boldsymbol x}) V_k({\boldsymbol x},{\boldsymbol z}) A_k^T({\boldsymbol x}), \end{array} \end{aligned} $$

(11.34)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \frac{\partial}{\partial z_k} {\boldsymbol g}({\boldsymbol x},{\boldsymbol z}) &\displaystyle = &\displaystyle -\sum_{l=1}^{m_k} {\boldsymbol g}_{kl}({\boldsymbol x}) v_{kl}({\boldsymbol x},{\boldsymbol z}) = -A_k({\boldsymbol x}) {\boldsymbol v}_k({\boldsymbol x},{\boldsymbol z}), \end{array} \end{aligned} $$

(11.35)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \frac{\partial}{\partial {\boldsymbol x}} \gamma_k({\boldsymbol x},{\boldsymbol z}) &\displaystyle = &\displaystyle -\sum_{l=1}^{m_k} v_{kl}({\boldsymbol x},{\boldsymbol z}) {\boldsymbol g}_{kl}^T({\boldsymbol x}) = -{\boldsymbol v}_k^T({\boldsymbol x},{\boldsymbol z}) A_k^T({\boldsymbol x}), \end{array} \end{aligned} $$

(11.36)

$$\displaystyle \begin{aligned} \begin{array}{rcl} {} \frac{\partial}{\partial z_k} \gamma_k({\boldsymbol x},{\boldsymbol z}) &\displaystyle = &\displaystyle \sum_{l=1}^{m_k} v_{kl}({\boldsymbol x},{\boldsymbol z}) = \tilde{{\boldsymbol e}}_k^T {\boldsymbol v}_k({\boldsymbol x},{\boldsymbol z}). \end{array} \end{aligned} $$

(11.37)

Using these formulas we obtain a system of linear equations describing a step of the Newton method

(11.38)

where

$$\displaystyle \begin{aligned} W({\boldsymbol x},{\boldsymbol z}) = G({\boldsymbol x},{\boldsymbol z}) + \sum_{k=1}^m A_k({\boldsymbol x}) V_k({\boldsymbol x},{\boldsymbol z}) A_k^T({\boldsymbol x}). {} \end{aligned} $$

(11.39)

Setting

$$\displaystyle \begin{aligned} \begin{array}{rcl} C({\boldsymbol x},{\boldsymbol z}) &\displaystyle = &\displaystyle [A_1({\boldsymbol x}) {\boldsymbol v}_1({\boldsymbol x},{\boldsymbol z}), \dots, A_m({\boldsymbol x}) {\boldsymbol v}_m({\boldsymbol x},{\boldsymbol z})], \\ D({\boldsymbol x},{\boldsymbol z}) &\displaystyle = &\displaystyle \operatorname{\mathrm{diag}}[\tilde{{\boldsymbol e}}_1^T {\boldsymbol v}_1({\boldsymbol x},{\boldsymbol z}), \dots, \tilde{{\boldsymbol e}}_m^T {\boldsymbol v}_m({\boldsymbol x},{\boldsymbol z})] \end{array} \end{aligned} $$

and γ(x, z) = [γ ₁(x, z), …, γ _m(x, z)]^T, a step of the Newton method can be written in the form

(11.40)

The diagonal matrix D(x, z) is positive definite since it has positive diagonal elements.

During iterative determination of a minimax vector we know a value of the parameter μ and vectors ${\boldsymbol x} \in \mathbb {R}^n$, ${\boldsymbol z} \in \mathbb {R}^m$ such that z _k > F _k(x), 1 ≤ k ≤ m. Using formula (11.40) we determine direction vectors Δx, Δz. Then, we choose a step length α so that

$$\displaystyle \begin{aligned} B_{\mu}({\boldsymbol x} + \alpha \varDelta {\boldsymbol x}, {\boldsymbol z} + \alpha \varDelta {\boldsymbol z}) < B_{\mu}({\boldsymbol x}, {\boldsymbol z}) {} \end{aligned} $$

(11.41)

and z _k + αΔz _k > F _k(x + αΔx), 1 ≤ k ≤ m. Finally, we set x ₊ = x + αΔx, z ₊ = z + αΔz and determine a new value μ ₊ < μ. If the matrix of system of equations (11.40) is positive definite, inequality (11.41) is satisfied for a sufficiently small value of the step length α.

Theorem 11.1

Let the matrix G(x, z) given by (11.33) be positive definite. Then the matrix of system of equations (11.40) is positive definite.

Proof

The matrix of system of equations (11.40) is positive definite if and only if the matrix D and its Schur complement W − CD ⁻¹C ^T are positive definite [7, Theorem 2.5.6]. The matrix D is positive definite since it has positive diagonal elements. Further, it holds

$$\displaystyle \begin{aligned}W - C D^{-1} C^T = G + \sum_{k=1}^m \left(A_k V_k A_k^T - A_k V_k \tilde{{\boldsymbol e}}_k (\tilde{{\boldsymbol e}}_k^T V_k \tilde{{\boldsymbol e}}_k)^{-1} (A_k V_k \tilde{{\boldsymbol e}}_k)^T\right),\end{aligned}$$

matrices $A_k V_k A_k^T - A_k V_k \tilde {{\boldsymbol e}}_k (\tilde {{\boldsymbol e}}_k^T V_k \tilde {{\boldsymbol e}}_k)^{-1} (A_k V_k \tilde {{\boldsymbol e}}_k)^T$, 1 ≤ k ≤ m, are positive semidefinite due to the Schwarz inequality and the matrix G is positive definite by the assumption. □

2.3 Direct Determination of a Minimax Vector

Now we will show how to solve system of equations (11.31)–(11.32) by direct determination of a minimax vector using two-level optimization

$$\displaystyle \begin{aligned} {\boldsymbol z}({\boldsymbol x};\mu) = \mathop{\operatorname{\mathrm{argmin}} }\limits_{{\boldsymbol z} \in \mathbb{R}^m} B_{\mu}({\boldsymbol x},{\boldsymbol z}), {} \end{aligned} $$

(11.42)

and

$$\displaystyle \begin{aligned} {\boldsymbol x}^* = \mathop{\operatorname{\mathrm{argmin}} }\limits_{{\boldsymbol x} \in \mathbb{R}^n} \hat{B}({\boldsymbol x};\mu), \quad \hat{B}({\boldsymbol x};\mu) \stackrel{\varDelta}{=} B_{\mu}({\boldsymbol x},{\boldsymbol z}({\boldsymbol x};\mu)). {} \end{aligned} $$

(11.43)

The problem (11.42) serves for determination of an optimal vector ${\boldsymbol z}({\boldsymbol x};\mu ) \in \mathbb {R}^m$. Let $\tilde {B}_{\mu }({\boldsymbol z}) = B_{\mu }({\boldsymbol x},{\boldsymbol z})$ for a fixed chosen vector ${\boldsymbol x} \in \mathbb {R}^n$. The function $\tilde {B}_{\mu }({\boldsymbol z})$ is strictly convex (as a function of a vector z), since it is a sum of convex function (11.21) and strictly convex functions $-\mu \log (z_k - f_{kl}({\boldsymbol x}))$, 1 ≤ k ≤ m, 1 ≤ l ≤ m _k. A minimum of the function $\tilde {B}_{\mu }({\boldsymbol z})$ is its stationary point, so it is a solution of system of equations (11.32) with Lagrange multipliers (11.30). The following theorem shows that this solution exists and is unique.

Theorem 11.2

The function $\tilde {B}_{\mu }({\boldsymbol z}): (F({\boldsymbol x}),\infty ) \to \mathbb {R}$has a unique stationary point which is its global minimum. This stationary point is characterized by a system of equationsγ(x, z) = 0, or

$$\displaystyle \begin{aligned} 1 - \tilde{{\boldsymbol e}}_k^T {\boldsymbol u}_k = 1 - \sum_{l=1}^{m_k} \frac{\mu}{z_k - f_{kl}({\boldsymbol x})} = 0, \quad 1 \leq k \leq m, {} \end{aligned} $$

(11.44)

which has a unique solution ${\boldsymbol z}({\boldsymbol x};\mu ) \in \mathbb {Z} \subset \mathbb {R}^m$ such that

$$\displaystyle \begin{aligned} F_k({\boldsymbol x}) < F_k({\boldsymbol x}) + \mu < z_k({\boldsymbol x};\mu) < F_k({\boldsymbol x}) + m_k \mu {} \end{aligned} $$

(11.45)

for 1 ≤ k ≤ m.

Proof

Definition 11.1 implies f _kl(x) ≤ F _k(x), 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, where the equality occurs for at least one index l.

• (a) If (11.44) holds, then we can write

  $$\displaystyle \begin{aligned} \begin{array}{rcl} 1 = \sum_{l=1}^{m_k} \frac{\mu}{z_k - f_{kl}({\boldsymbol x})} > \frac{\mu}{z_k - F_k({\boldsymbol x})} \; &\displaystyle \Leftrightarrow &\displaystyle \; z_k - F_k({\boldsymbol x}) > \mu, \\ 1 = \sum_{l=1}^{m_k} \frac{\mu}{z_k - f_{kl}({\boldsymbol x})} < \frac{m_k \mu}{z_k - F_k({\boldsymbol x})} \; &\displaystyle \Leftrightarrow &\displaystyle \; z_k - F_k({\boldsymbol x}) < m_k \mu, \end{array} \end{aligned} $$

  which proves inequalities (11.45).

• (b) Since

  

  and the function γ _k(x, z _k) is continuous and decreasing in F _k(x) + μ < z _k(x;μ) < F _k(x) + m _k by (11.37), the equation γ _k(x, z _k) = 0 has a unique solution in this interval. Since the function $\tilde {B}_{\mu }({\boldsymbol z})$ is convex this solution corresponds to its global minimum.

□

System (11.44) is a system of m scalar equations with localization inequalities (11.45). These scalar equations can be efficiently solved by robust methods described e.g. in [14] and [15] (details are stated in [22]). Suppose that z = z(x;μ) and denote

$$\displaystyle \begin{aligned} \hat{B}({\boldsymbol x};\mu) = \sum_{k=1}^m z_k({\boldsymbol x};\mu) - \mu \sum_{k=1}^m \sum_{l=1}^{m_k} \log(z_k({\boldsymbol x};\mu) - f_{kl}({\boldsymbol x})). {} \end{aligned} $$

(11.46)

To find a minimum of B _μ(x, z) in $\mathbb {R}^{n+m}$, it suffices to minimize $\hat {B}({\boldsymbol x};\mu )$ in $\mathbb {R}^n$.

Theorem 11.3

Consider the barrier function (11.46). Then

$$\displaystyle \begin{aligned} \nabla \hat{B}({\boldsymbol x};\mu) = \sum_{k=1}^m A_k({\boldsymbol x}) {\boldsymbol u}_k({\boldsymbol x};\mu), {}\end{aligned} $$

(11.47)

$$\displaystyle \begin{aligned} \begin{array}{rcl} \nabla^2 \hat{B}({\boldsymbol x};\mu) &\displaystyle = &\displaystyle W({\boldsymbol x};\mu) - C({\boldsymbol x};\mu) D^{-1}({\boldsymbol x};\mu) C^T({\boldsymbol x};\mu) \\ &\displaystyle = &\displaystyle G({\boldsymbol x};\mu) + \sum_{k=1}^m A_k({\boldsymbol x}) V_k({\boldsymbol x};\mu) A_k^T({\boldsymbol x}) \\ &\displaystyle &\displaystyle \qquad \quad \; -\sum_{k=1}^m \frac{A_k({\boldsymbol x}) V_k({\boldsymbol x};\mu) \tilde{{\boldsymbol e}}_k \tilde{{\boldsymbol e}}_k^T V_k({\boldsymbol x};\mu) A_k^T({\boldsymbol x})} {\tilde{{\boldsymbol e}}_k^T V_k({\boldsymbol x};\mu) \tilde{{\boldsymbol e}}_k}, {} \end{array} \end{aligned} $$

(11.48)

where G(x;μ) = G(x, z(x;μ)) and W(x;μ), C(x;μ), D(x;μ), U _k(x;μ), $V_k({\boldsymbol x};\mu ) = U_k^2({\boldsymbol x};\mu ) / \mu$, 1 ≤ k ≤ m, are obtained by the same substitution. A solution of equation

$$\displaystyle \begin{aligned} \nabla^2 \hat{B}({\boldsymbol x};\mu) \varDelta {\boldsymbol x} = -\nabla \hat{B}({\boldsymbol x};\mu) \end{aligned} $$

(11.49)

is identical with Δxgiven by (11.40), wherez = z(x;μ) (soγ(x, z(x;μ)) = 0).

Proof

Differentiating the barrier function (11.46) and using (11.32) we obtain

where

$$\displaystyle \begin{aligned} u_{kl}({\boldsymbol x};\mu) = \frac{\mu}{z_k({\boldsymbol x};\mu)-f_{kl}({\boldsymbol x})}, \quad 1 \leq k \leq m, \quad 1 \leq l \leq m_k. {} \end{aligned} $$

(11.50)

Formula (11.48) can be obtained by additional differentiation of relations (11.32) and (11.47) using (11.50). A simpler way is based on using (11.40). Since (11.32) implies γ(x, z(x;μ)) = 0, we can substitute γ = 0 into (11.40), which yields the equation

$$\displaystyle \begin{aligned}\left(W({\boldsymbol x},{\boldsymbol z}) - C({\boldsymbol x},{\boldsymbol z}) D^{-1}({\boldsymbol x},{\boldsymbol z}) C^T({\boldsymbol x},{\boldsymbol z})\right) \varDelta {\boldsymbol x} = -{\boldsymbol g}({\boldsymbol x},{\boldsymbol z}),\end{aligned}$$

where z = z(x;μ), that confirms validity of formulas (11.48) and (11.49) (details can be found in [22]). □

Remark 11.11

To determine an inverse of the Hessian matrix, one can use a Woodbury formula [7, Theorem 12.1.4] which gives

$$\displaystyle \begin{aligned} \begin{array}{rcl} (\nabla^2 \hat{B}({\boldsymbol x};\mu))^{-1} &\displaystyle = &\displaystyle W^{-1}({\boldsymbol x};\mu) - W^{-1}({\boldsymbol x};\mu) C({\boldsymbol x};\mu) \\ &\displaystyle &\displaystyle \left(C^T({\boldsymbol x};\mu) W^{-1}({\boldsymbol x};\mu) C({\boldsymbol x};\mu) - D({\boldsymbol x};\mu)\right)^{-1} \\ &\displaystyle &\displaystyle C^T({\boldsymbol x};\mu) W^{-1}({\boldsymbol x};\mu). {} \end{array} \end{aligned} $$

(11.51)

If the matrix $\nabla ^2 \hat {B}({\boldsymbol x};\mu )$ is not positive definite, it can be replaced by a matrix $L L^T = \nabla ^2 \hat {B}({\boldsymbol x};\mu ) + E$, obtained by the Gill–Murray decomposition [10]. Note that it is more advantageous to use system of linear equations (11.40) instead of (11.49) for determination of a direction vector Δx because the system of nonlinear equations (11.44) is solved with prescribed finite precision, and thus a vector γ(x, z), defined by (11.32), need not be zero.

From

$$\displaystyle \begin{aligned}V_k({\boldsymbol x};\mu) = \frac{1}{\mu} U_k^2({\boldsymbol x};\mu), \quad {\boldsymbol u}_k({\boldsymbol x};\mu) \geq 0, \quad \tilde{{\boldsymbol e}}_k^T {\boldsymbol u}_k({\boldsymbol x};\mu) = 1, \quad 1 \leq k \leq m,\end{aligned}$$

it follows that ∥V _k(x;μ)∥↑∞ if μ ↓ 0, so Hessian matrix (11.48) may be ill-conditioned if the value μ is very small. From this reason, we use a lower bound $\underline {\mu } > 0$ for μ.

Theorem 11.4

Let Assumption 11.4be satisfied and $\mu \geq \underline {\mu } > 0$. If G(x;μ) is uniformly positive definite (if a constant $\underline {G}$exists such that ${\boldsymbol v}^T G({\boldsymbol x}; \mu ) {\boldsymbol v} \geq \underline {G} \|{\boldsymbol v}\|{ }^2$), then there is a number $\overline {\kappa } \geq 1$such that $\kappa (\nabla ^2 \hat {B}({\boldsymbol x};\mu )) \leq \overline {\kappa }$.

Proof

• (a) Using (11.30), (11.48), and Assumption 11.4, we obtain

  $$\displaystyle \begin{aligned} \|\nabla^2 \hat{B}({\boldsymbol x};\mu)\| & \leq \left\|G({\boldsymbol x};\mu) + \sum_{k=1}^m A_k({\boldsymbol x}) V_k({\boldsymbol x};\mu) A_k^T({\boldsymbol x})\right\| \\ & \leq \sum_{k=1}^m \sum_{l=1}^{m_k} \left(\left|G_{kl}({\boldsymbol x}) u_{kl}({\boldsymbol x},\mu)\right| +\frac{1}{\mu} \left|u^2_{kl}({\boldsymbol x};\mu) {\boldsymbol g}_{kl}({\boldsymbol x}) {\boldsymbol g}_{kl}^T({\boldsymbol x}) \right|\right) \\ & \leq \frac{\overline{m}}{\mu} \left(\overline{\mu} \, \overline{G} + \overline{g}^2\right)\stackrel{\varDelta}{=} \frac{\overline{c}}{\mu} \leq \frac{\overline{c}}{\underline{\mu}}, {} \end{aligned} $$

  (11.52)

  because $0 \leq u_{kl}({\boldsymbol x}; \mu ) \leq \tilde {{\boldsymbol e}}_k^T {\boldsymbol u}_k({\boldsymbol x}; \mu ) =1$, 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, by (11.44).

• (b) From the proof of Theorem 11.1 it follows that the matrix $\nabla ^2 \hat {B}({\boldsymbol x};\mu ) - G({\boldsymbol x};\mu )$ is positive semidefinite. Therefore,

  $$\displaystyle \begin{aligned}\underline{\lambda}(\nabla^2 \hat{B}({\boldsymbol x};\mu)) \geq \underline{\lambda}(G({\boldsymbol x};\mu)) \geq \underline{G}.\end{aligned}$$

• (c) Since (a) implies $\overline {\lambda }(\nabla ^2 \hat {B}({\boldsymbol x};\mu )) = \|\nabla ^2 \hat {B}({\boldsymbol x};\mu )\| \leq \overline {c} / \underline {\mu }$, using (b) we can write

  $$\displaystyle \begin{aligned} \kappa(\nabla^2 \hat{B}({\boldsymbol x};\mu)) = \frac{\overline{\lambda}(\nabla^2 \hat{B}({\boldsymbol x};\mu))}{\underline{\lambda}(\nabla^2 \hat{B}({\boldsymbol x};\mu))} \leq \frac{\overline{c}}{\underline{\mu} \, \underline{G}} \stackrel{\varDelta}{=}\overline{\kappa}. {} \end{aligned} $$

  (11.53)

□

Remark 11.12

If there exists a number $\overline {\kappa } > 0$ such that $\kappa (\nabla ^2 \hat {B}({\boldsymbol x}_i;\mu _i)) \leq \overline {\kappa }$, $i \in \mathbb {N}$, the direction vector Δx _i, given by solving a system of equations $\nabla ^2\hat {B}({\boldsymbol x}_i;\mu _i)\varDelta {\boldsymbol x}_i = -\nabla \hat {B}({\boldsymbol x}_i;\mu _i)$, satisfies the condition

$$\displaystyle \begin{aligned} (\varDelta {\boldsymbol x}_i)^T {\boldsymbol g}({\boldsymbol x}_i; \mu_i) \leq -\varepsilon_0 \|\varDelta {\boldsymbol x}_i\| \|{\boldsymbol g}({\boldsymbol x}_i; \mu_i)\|, \quad i \in \mathbb{N}, {} \end{aligned} $$

(11.54)

where $\varepsilon _0 = 1 / \sqrt {\overline {\kappa }}$ and ${\boldsymbol g}({\boldsymbol x};\mu ) = \nabla \hat {B}({\boldsymbol x};\mu )$. Then, for arbitrary numbers 0 < ε ₁ ≤ ε ₂ < 1 one can find a step length parameter α _i > 0 such that for x _i+1 = x _i + α _iΔx _i it holds

$$\displaystyle \begin{aligned} \varepsilon_1 \leq \frac{\hat{B}({\boldsymbol x}_{i+1};\mu_i) - \hat{B}({\boldsymbol x}_i;\mu_i)}{\alpha_i (\varDelta {\boldsymbol x}_i)^T {\boldsymbol g}({\boldsymbol x}_i; \mu_i)} \leq \varepsilon_2, {} \end{aligned} $$

(11.55)

so there exists a number c > 0 such that (see [26, Section 3.2])

$$\displaystyle \begin{aligned} \hat{B}({\boldsymbol x}_{i+1};\mu_i) - \hat{B}({\boldsymbol x}_i;\mu_i) \leq - c \|{\boldsymbol g}({\boldsymbol x}_i;\mu_i)\|{}^2, \quad i \in \mathbb{N}. \end{aligned} $$

(11.56)

If Assumption 11.4 is not satisfied, then only (Δx _i)^Tg(x _i;μ _i) < 0 holds (because the matrix $\nabla ^2 \hat {B}({\boldsymbol x};\mu )$ is positive definite by Theorem 11.1) and

$$\displaystyle \begin{aligned} \hat{B}({\boldsymbol x}_{i+1};\mu_i) - \hat{B}({\boldsymbol x}_i;\mu_i) \leq 0, \quad i \in \mathbb{N}. \end{aligned} $$

(11.57)

2.4 Implementation

Remark 11.13

In (11.39), it is assumed that G(x, z) is the Hessian matrix of the Lagrange function. Direct computation of the matrix G(x;μ) = G(x, z(x;μ)) is usually difficult (one can use automatic differentiation as described in [13]). Thus, various approximations G ≈ G(x;μ) are mostly used.

• The matrix G ≈ G(x;μ) can be determined using differences

  $$\displaystyle \begin{aligned}G {\boldsymbol w}_j = \frac 1{\delta} \left( \sum_{k=1}^m A_k({\boldsymbol x} + \delta {\boldsymbol w}_j) {\boldsymbol u}_k({\boldsymbol x}; \mu) - \sum_{k=1}^m A({\boldsymbol x}) {\boldsymbol u}_k({\boldsymbol x}; \mu) \right).\end{aligned}$$

  The vectors w _j, $1 \leq j \leq \overline {k}$, are chosen so that the number of them is as small as possible [4, 27].

• The matrix G ≈ G(x;μ) can be determined using the variable metric methods [17]. The vectors

  $$\displaystyle \begin{aligned}{\boldsymbol d} = {\boldsymbol x}_+ - {\boldsymbol x}, \quad {\boldsymbol y} = \sum_{k=1}^m A_k({\boldsymbol x}_+) {\boldsymbol u}_k({\boldsymbol x}_+; \mu) - \sum_{k=1}^m A_k({\boldsymbol x}) {\boldsymbol u}_k({\boldsymbol x}_+; \mu)\end{aligned}$$

  are used for an update of G.

• If the problem is separable (i.e. f _kl(x), 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, are functions of a small number n _kl = O(1) of variables), one can set as in [12]

  $$\displaystyle \begin{aligned}G = \sum_{k=1}^m \sum_{l=1}^{m_k} Z_{kl} \hat{G}_{kl} Z_{kl}^T u_{kl}({\boldsymbol x}, {\boldsymbol z}),\end{aligned}$$

  where the reduced Hessian matrices $\hat {G}_{kl}$ are updated using the reduced vectors $\hat {{\boldsymbol d}}_{kl} = Z_{kl}^T ({\boldsymbol x}_+ - {\boldsymbol x})$ and $\hat {{\boldsymbol y}}_{kl} = Z_{kl} ({\boldsymbol g}_{kl}({\boldsymbol x}_+) - {\boldsymbol g}_{kl}({\boldsymbol x}))$.

Remark 11.14

The matrix G ≈ G(x;μ) obtained by the approach stated in Remark 11.13 can be ill-conditioned so condition (11.54) (with a chosen value ε ₀ > 0) may not be satisfied. In this case it is possible to restart the iteration process and set G = I. Then $\overline {G} = 1$ and $\underline {G} = 1$ in (11.52) and (11.53), so it is a higher probability of fulfilment of condition (11.54). If the choice G = I does not satisfy (11.54), we set Δx = −g(x;μ) (a steepest descent direction).

An update of μ is an important part of interior point methods. Above all, μ ↓ 0 must hold, which is a main property of interior point methods. Moreover, rounding errors may cause that z _k(x;μ) = F _k(x) when the value μ is small (because F _k(x) < z _k(x;μ) ≤ F _k(x) + m _kμ and F _k(x) + m _kμ → F _k(x) if μ ↓ 0), which leads to a breakdown (division by z _k(x;μ) − F _k(x) = 0) when computing 1∕(z _k(x;μ) − F _k(x)). Therefore, we need to use a lower bound $\underline {\mu }$ for a barrier parameter (e.g. $\underline {\mu } = 10^{-8}$ when computing in double precision).

The efficiency of interior point methods also depends on the way of decreasing the value of a barrier parameter. The following heuristic procedures proved successful in practice, where $\underline {g}$ is a suitable constant.

Procedure A

Phase 1.:

If $\|{\boldsymbol g}({\boldsymbol x}_i;\mu _i)\| \geq \underline {g}$, then μ _i+1 = μ _i (the value of a barrier parameter is unchanged).

Phase 2.:

If $\|{\boldsymbol g}({\boldsymbol x}_i;\mu _i)\| < \underline {g}$, then

$$\displaystyle \begin{aligned} \mu_{i+1} = \max\left\{\tilde{\mu}_{i+1}, \, \underline{\mu}, \, 10 \, \varepsilon_M |F({\boldsymbol x}_{i+1})|\right\}, {} \end{aligned} $$

(11.58)

where F(x _i+1) = F ₁(x _i+1) + ⋯ + F _m(x _i+1), ε _M is a machine precision, and

(11.59)

The values $\underline {\mu } = 10^{-8}$, λ = 0.85, and σ = 100 are usually used.

Procedure B

Phase 1.:

If ∥g(x _i;μ _i)∥² ≥ 𝜗μ _i, then μ _i+1 = μ _i (the value of a barrier parameter is unchanged).

Phase 2.:

If ∥g(x _i;μ _i)∥² < 𝜗μ _i, then

$$\displaystyle \begin{aligned} \mu_{i+1} = \max\{\underline{\mu},\|{\boldsymbol g}_i({\boldsymbol x}_i;\mu_i)\|{}^2\}. {} \end{aligned} $$

(11.60)

The values $\underline {\mu } = 10^{-8}$ and 𝜗 = 0.1 are usually used.

The choice of $\underline {g}$ in Procedure A is not critical. We can set $\underline {g} = \infty$ but a lower value is sometimes more advantageous. Formula (11.59) requires several comments. The first argument of the minimum controls the decreasing speed of the value of a barrier parameter which is linear (a geometric sequence) for small i (the term λμ _i) and sublinear (a harmonic sequence) for large i (the term μ _i∕(σμ _i + 1)). Thus, the second argument ensuring that the value μ is small in a neighborhood of a desired solution is mainly important for large i. This situation may appear if the gradient norm ∥g(x _i;μ _i)∥ is small even if x _i is far from a solution. The idea of Procedure B proceeds from the fact that a barrier function $\hat {B}({\boldsymbol x};\mu )$ should be minimized with a sufficient precision for a given value of a parameter μ.

The considerations up to now are summarized in Algorithm 11.1 introduced in the Appendix. This algorithm supposes that the matrix A(x) is sparse. If it is dense, the algorithm is simplified because there is no symbolic decomposition.

2.5 Global Convergence

Now we prove the global convergence of the method realized by Algorithm 11.1.

Lemma 11.1

Let numbers z _k(x;μ), 1 ≤ k ≤ m, be solutions of Eq.(11.44). Then

$$\displaystyle \begin{aligned}\frac{\partial}{\partial \mu} z_k({\boldsymbol x};\mu) > 0, \ 1 \leq k \leq m, \,\,\, \frac{\partial}{\partial \mu} \hat{B}({\boldsymbol x};\mu) = - \sum_{k=1}^m \sum_{l=1}^{m_k} \log(z_k({\boldsymbol x};\mu) - f_{kl}({\boldsymbol x})).\end{aligned}$$

Proof

Differentiating (11.44) with respect to μ, one can write for 1 ≤ k ≤ m

$$\displaystyle \begin{aligned}-\sum_{l=1}^{m_k} \frac{1}{z_k({\boldsymbol x};\mu) - f_{kl}({\boldsymbol x})} + \sum_{l=1}^{m_k} \frac{\mu}{(z_k({\boldsymbol x};\mu) - f_{kl}({\boldsymbol x}))^2} \frac{\partial}{\partial \mu} z_k({\boldsymbol x};\mu) = 0,\end{aligned}$$

which after multiplication of μ together with (11.30) and (11.44) gives

$$\displaystyle \begin{aligned}\frac{\partial}{\partial \mu} z_k({\boldsymbol x};\mu) = \left(\sum_{l=1}^{m_k} \frac{\mu^2}{(z_k({\boldsymbol x};\mu) - f_{kl}({\boldsymbol x}))^2}\right)^{-1} = \left(\sum_{l=1}^{m_k} u_{kl}^2({\boldsymbol x};\mu) \right)^{-1}> 0.\end{aligned}$$

Differentiating the function

$$\displaystyle \begin{aligned} \hat{B}({\boldsymbol x};\mu) = \sum_{k=1}^m z_k({\boldsymbol x};\mu) - \mu \sum_{k=1}^m \sum_{l=1}^{m_k} \log (z_k({\boldsymbol x};\mu) - f_{kl}({\boldsymbol x})) {} \end{aligned} $$

(11.61)

and using (11.44) we obtain

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{\partial}{\partial \mu} \hat{B}({\boldsymbol x};\mu) &\displaystyle = &\displaystyle \sum_{k=1}^m \frac{\partial}{\partial \mu} z_k({\boldsymbol x};\mu) - \sum_{k=1}^m \sum_{l=1}^{m_k} \log(z_k({\boldsymbol x};\mu) - f_{kl}({\boldsymbol x})) \\ &\displaystyle &\displaystyle \quad -\sum_{k=1}^m \sum_{l=1}^{m_k} \frac{\mu}{z_k({\boldsymbol x};\mu) - f_{kl}({\boldsymbol x})} \frac{\partial}{\partial \mu} z_k({\boldsymbol x};\mu) \\ &\displaystyle = &\displaystyle \frac{\partial}{\partial \mu} z_k({\boldsymbol x};\mu) \sum_{k=1}^m \left(1 - \sum_{l=1}^{m_k} \frac{\mu}{z_k({\boldsymbol x};\mu) - f_{kl}({\boldsymbol x})}\right) \\ &\displaystyle &\displaystyle \quad -\sum_{k=1}^m \sum_{l=1}^{m_k} \log(z_k({\boldsymbol x};\mu) - f_{kl}({\boldsymbol x})) \\ &\displaystyle = &\displaystyle -\sum_{k=1}^m \sum_{l=1}^{m_k} \log(z_k({\boldsymbol x};\mu) - f_{kl}({\boldsymbol x})). \end{array} \end{aligned} $$

□

Lemma 11.2

Let Assumption 11.1be satisfied. Let {x _i} and {μ _i}, $i \in \mathbb {N}$, be the sequences generated by Algorithm 11.1. Then the sequences $\{\hat {B}({\boldsymbol x}_i;\mu _i)\}$, {z(x _i;μ _i)}, and {F(x _i)}, $i \in \mathbb {N}$, are bounded. Moreover, there exists a constant L ≥ 0 such that for $i \in \mathbb {N}$it holds

$$\displaystyle \begin{aligned} \hat{B}({\boldsymbol x}_{i+1};\mu_{i+1}) \leq \hat{B}({\boldsymbol x}_{i+1};\mu_i) + L (\mu_i - \mu_{i+1}). {} \end{aligned} $$

(11.62)

Proof

• (a) We first prove boundedness from below. Using (11.61) and Assumption 11.1, one can write

  $$\displaystyle \begin{aligned} \begin{array}{rcl} \hat{B}({\boldsymbol x};\mu) - \underline{F} &\displaystyle = &\displaystyle \sum_{k=1}^m z_k({\boldsymbol x};\mu) - \underline{F} - \mu \sum_{k=1}^m \sum_{l=1}^{m_k} \log(z_k({\boldsymbol x};\mu) - f_{kl}({\boldsymbol x})) \\ &\displaystyle \geq &\displaystyle \sum_{k=1}^m \left(z_k ({\boldsymbol x};\mu) - \underline{F} - m_k \mu \log(z_k({\boldsymbol x};\mu) - \underline{F})\right). \end{array} \end{aligned} $$

  A convex function $\psi (t) = t - m \mu \log (t)$ has a unique minimum at the point t = mμ because ψ′(mμ) = 1 − mμ∕mμ = 0. Thus, it holds

  $$\displaystyle \begin{aligned} \hat{B}({\boldsymbol x};\mu) & \geq \underline{F} + \sum_{k=1}^m (m_k \mu - m_k \mu \log(m_k \mu))\\ & \geq \underline{F} +\sum_{k=1}^m \min \{0, \, m_k \overline{\mu} (1 - \log(m_k \overline{\mu})\} \\ & \geq \underline{F} + \sum_{k=1}^m \min \{0, \, m_k \overline{\mu}(1 - \log(2 m_k \overline{\mu})\} \stackrel{\varDelta}{=} \underline{B}. \end{aligned} $$

  Boundedness from below of sequences {z(x _i;μ _i)} and {F(x _i)}, $i \in \mathbb {N}$, follows from inequalities (11.45) and Assumption 11.1.

• (b) Now we prove boundedness from above. Similarly as in (a) we can write

  $$\displaystyle \begin{aligned} \begin{array}{rcl} \hat{B}({\boldsymbol x};\mu) - \underline{F} &\displaystyle \geq &\displaystyle \sum_{k=1}^m \frac{z_k({\boldsymbol x};\mu) - \underline{F}}{2} \\ &\displaystyle &\displaystyle + \sum_{k=1}^m \left(\frac{z_k({\boldsymbol x};\mu) - \underline{F}}{2} - m_k \mu \log(z_k({\boldsymbol x};\mu) - \underline{F})\right). \end{array} \end{aligned} $$

  A convex function $t/2 - m \mu \log (t)$ has a unique minimum at the point t = 2mμ. Thus, it holds

  $$\displaystyle \begin{aligned} \begin{array}{rcl} \hat{B}({\boldsymbol x};\mu) &\displaystyle \geq &\displaystyle \sum_{k=1}^m \frac{z_k({\boldsymbol x};\mu) - \underline{F}}{2} + \underline{F} + \sum_{k=1}^m \min \{0, \, m \overline{\mu} (1 - \log(2 m_k \overline{\mu}))\} \\ &\displaystyle = &\displaystyle \sum_{k=1}^m \frac{z_k({\boldsymbol x};\mu) - \underline{F}}{2} + \underline{B} \end{array} \end{aligned} $$

  or

  $$\displaystyle \begin{aligned} \sum_{k=1}^m (z_k({\boldsymbol x};\mu) - \underline{F}) \leq 2(\hat{B}({\boldsymbol x};\mu) - \underline{B}). {} \end{aligned} $$

  (11.63)

  Using the mean value theorem and Lemma 11.1, we obtain

  $$\displaystyle \begin{aligned} \hat{B}({\boldsymbol x}_{i+1}; \mu_{i+1}&) - \hat{B}({\boldsymbol x}_{i+1}; \mu_i) \\ &= \sum_{k=1}^m \sum_{l=1}^{m_k} \log(z_k({\boldsymbol x}_{i+1}; \tilde{\mu}_i) - f_{kl}({\boldsymbol x}_{i+1}))(\mu_i - \mu_{i+1}) \\ & \leq \sum_{k=1}^m \sum_{l=1}^{m_k} \log(z_k({\boldsymbol x}_{i+1};\mu_i) - f_{kl}({\boldsymbol x}_{i+1}))(\mu_i - \mu_{i+1}) \\ & \leq \sum_{k=1}^m m_k \log(z_k({\boldsymbol x}_{i+1};\mu_i) - \underline{F}) (\mu_i - \mu_{i+1}), {} \end{aligned} $$

  (11.64)

  where $0 < \mu _{i+1} \leq \tilde {\mu }_i \leq \mu _i$. Since $\log (t) \leq t/e$ (where $e = \exp (1)$) for t > 0, we can write using inequalities (11.63), (11.64), and (11.45)

  $$\displaystyle \begin{aligned} \hat{B}({\boldsymbol x}_{i+1}; \mu_{i+1}) - \underline{B} &\leq \hat{B}({\boldsymbol x}_{i+1}; \mu_i) - \underline{B} \\ &~~+ \sum_{k=1}^{m} m_k \log(z_k({\boldsymbol x}_{i+1};\mu_i) - \underline{F}) (\mu_i - \mu_{i+1}) \\ & \leq \hat{B}({\boldsymbol x}_{i+1}; \mu_i) - \underline{B} \\ &~~ + e^{-1} \sum_{k=1}^{m} m_k (z_k({\boldsymbol x}_{i+1};\mu_i) - \underline{F})(\mu_i - \mu_{i+1}) \\ & \leq \hat{B}({\boldsymbol x}_{i+1}; \mu_i) - \underline{B} \\ &~~ + 2 e^{-1} \overline{m} (\hat{B}({\boldsymbol x}_{i+1};\mu_i) - \underline{B})(\mu_i - \mu_{i+1}) \\ & = (1 + \lambda \delta_i)(\hat{B}({\boldsymbol x}_{i+1};\mu_i) - \underline{B})\\ &\leq (1 + \lambda \delta_i)(\hat{B}({\boldsymbol x}_i;\mu_i) - \underline{B}), \end{aligned} $$

  where $\lambda =2 \overline {m} / e$ and δ _i = μ _i − μ _i+1. Therefore,

  $$\displaystyle \begin{aligned} \begin{array}{rcl} \hat{B}({\boldsymbol x}_{i+1}; \mu_{i+1}) - \underline{B} &\displaystyle \leq &\displaystyle \prod_{j=1}^i (1 + \lambda \delta_j) (\hat{B}({\boldsymbol x}_1; \mu_1) - \underline{B}) \\ &\displaystyle \leq &\displaystyle \prod_{i=1}^\infty (1 + \lambda \delta_i) (\hat{B}({\boldsymbol x}_1; \mu_1) - \underline{B}) {} \end{array} \end{aligned} $$

  (11.65)

  and since

  $$\displaystyle \begin{aligned}\sum_{i=1}^{\infty} \lambda \delta_i = \lambda \sum_{i=1}^{\infty} (\mu_i - \mu_{i+1}) = \lambda (\overline{\mu} - \lim_{i \uparrow \infty} \mu_i) \leq \lambda \overline{\mu}\end{aligned}$$

  the expression on the right-hand side of (11.65) is finite. Thus, the sequence $\{\hat {B}({\boldsymbol x}_i;\mu _i)\}$, $i \in \mathbb {N}$, is bounded from above and the sequences {z(x _i;μ _i)} and {F(x _i)}, $i \in \mathbb {N}$, are bounded from above as well by (11.63) and (11.45).

• (c) Finally, we prove formula (11.62). Using (11.64) and (11.45) we obtain

  $$\displaystyle \begin{aligned} \hat{B}({\boldsymbol x}_{i+1}; \mu_{i+1}) - \hat{B}(&{\boldsymbol x}_{i+1}; \mu_i) \\ &\leq \sum_{k=1}^m m_k \log(z_k({\boldsymbol x}_{i+1};\mu_i) - \underline{F})(\mu_i - \mu_{i+1}) \\ & \leq \sum_{k=1}^m m_k \log(F_k({\boldsymbol x}_{i+1}) + m_k \mu_i - \underline{F})(\mu_i - \mu_{i+1}) \\ & \leq \sum_{k=1}^m m_k \log(\overline{F} + m_k \overline{\mu} - \underline{F})(\mu_i - \mu_{i+1})\\ & \stackrel{\varDelta}{=} L (\mu_i - \mu_{i+1}) \end{aligned} $$

  (the existence of a constant $\overline {F}$ follows from boundedness of a sequence {F(x _i)}, $i \in \mathbb {N}$), which together with (11.57) gives $\hat {B}({\boldsymbol x}_{i+1};\mu _{i+1}) \leq \hat {B}({\boldsymbol x}_i;\mu _i) + L (\mu _i - \mu _{i+1})$, $i \in \mathbb {N}$. Thus, it holds

  $$\displaystyle \begin{aligned} \hat{B}({\boldsymbol x}_i;\mu_i) \leq \hat{B}({\boldsymbol x}_1;\mu_1) + L (\mu_1 - \mu_i) \leq \hat{B}({\boldsymbol x}_1;\mu_1) + L \overline{\mu} \stackrel{\varDelta}{=} \overline{B}, \quad i \in N. {} \end{aligned} $$

  (11.66)

□

The upper bounds $\overline {g}$ and $\overline {G}$ are not used in Lemma 11.2, so Assumption 11.4 may not be satisfied. Thus, there exists an upper bound $\overline {F}$ (independent of $\overline {g}$ and $\overline {G}$) such that $F({\boldsymbol x}_i) \leq \overline {F}$ for all $i \in \mathbb {N}$. This upper bound can be used in definition of a set ${\mathcal {D}}_F(\overline {F})$ in Assumption 11.4.

Lemma 11.3

Let Assumption 11.4and the assumptions of Lemma 11.2be satisfied. Then, if we use Procedure Aor Procedure Bfor an update of parameter μ, the values {μ _i}, $i \in \mathbb {N}$, form a non-decreasing sequence such that μ _i ↓ 0.

Proof

The value of parameter μ is unchanged in the first phase of Procedure A or Procedure B. Since a function $\hat {B}({\boldsymbol x};\mu )$ is continuous, bounded from below by Lemma 11.2, and since inequality (11.56) is satisfied (with μ _i = μ), it holds ∥g(x _i;μ)∥↓ 0 if phase 1 contains an infinite number of subsequent iterative steps [26, Section 3.2]. Thus, there exists a step (with index i) belonging to the first phase such that either $\|{\boldsymbol g}({\boldsymbol x}_i;\mu )\| < \underline {g}$ in Procedure A or ∥g(x _i;μ)∥² < 𝜗μ in Procedure B. However, this is in contradiction with the definition of the first phase. Thus, there exists an infinite number of steps belonging to the second phase, where the value of parameter μ is decreased so that μ _i ↓ 0. □

Theorem 11.5

Let assumptions of Lemma 11.3be satisfied. Consider a sequence {x _i}, $i \in \mathbb {N}$, generated by Algorithm 11.1, where $\underline {\delta } = \underline {\varepsilon } = \underline {\mu } = 0$. Then

$$\displaystyle \begin{aligned} &\lim_{i \uparrow \infty} \sum_{k=1}^m \sum_{l=1}^{m_k} {\boldsymbol g}_{kl}({\boldsymbol x}_i) u_{kl}({\boldsymbol x}_i;\mu_i) = {\mathbf{0}}, \quad \sum_{l=1}^{m_k} u_{kl}({\boldsymbol x}_i;\mu_i) = 1,\\ &z_k({\boldsymbol x}_i;\mu_i) - f_{kl}({\boldsymbol x}_i) \geq 0, \quad u_{kl}({\boldsymbol x}_i;\mu_i) \geq 0,\\ &\lim_{i \uparrow \infty} u_{kl}({\boldsymbol x}_i;\mu_i) (z_k({\boldsymbol x}_i;\mu_i) - f_{kl}({\boldsymbol x}_i)) = 0 \end{aligned} $$

for 1 ≤ k ≤ m and 1 ≤ l ≤ m _k.

Proof

• (a) Equalities $\tilde {{\boldsymbol e}}_k^T {\boldsymbol u}_k({\boldsymbol x}_i;\mu _i) = 1$, 1 ≤ k ≤ m, are satisfied by (11.44) because $\underline {\delta }=0$. Inequalities z _k(x _i;μ _i) − f _kl(x _i) ≥ 0 and u _kl(x _i;μ _i) ≥ 0 follow from formulas (11.45) and statement (11.50).

• (b) Relations (11.56) and (11.62) yield

  $$\displaystyle \begin{aligned} \begin{array}{rcl} \hat{B}({\boldsymbol x}_{i+1};\mu_{i+1}) - \hat{B}({\boldsymbol x}_i;\mu_i) &\displaystyle = &\displaystyle (\hat{B}({\boldsymbol x}_{i+1};\mu_{i+1}) - \hat{B}({\boldsymbol x}_{i+1};\mu_i)) \\ &\displaystyle &\displaystyle + (\hat{B}({\boldsymbol x}_{i+1};\mu_i) - \hat{B}({\boldsymbol x}_i;\mu_i)) \\ &\displaystyle \leq &\displaystyle L \, (\mu_i - \mu_{i+1}) - c \, \|{\boldsymbol g}({\boldsymbol x}_i;\mu_i)\|{}^2 \end{array} \end{aligned} $$

  and since lim_i↑∞μ _i = 0 (Lemma 11.3), we can write by (11.66) that

  $$\displaystyle \begin{aligned} \begin{array}{rcl} \underline{B} &\displaystyle \leq &\displaystyle \lim_{i \uparrow \infty} \hat{B}({\boldsymbol x}_{i+1};\mu_{i+1}) \\ &\displaystyle \leq &\displaystyle \hat{B}({\boldsymbol x}_1;\mu_1) + L \sum_{i=1}^{\infty} (\mu_i - \mu_{i+1}) - c \sum_{i=1}^{\infty} \|{\boldsymbol g}({\boldsymbol x}_i;\mu_i)\|{}^2 \\ &\displaystyle \leq &\displaystyle \hat{B}({\boldsymbol x}_1;\mu_1) + L \overline{\mu} - c \sum_{i=1}^{\infty} \|{\boldsymbol g}({\boldsymbol x}_i;\mu_i)\|{}^2 = \overline{B} - c \sum_{i=1}^{\infty} \|{\boldsymbol g}({\boldsymbol x}_i;\mu_i)\|{}^2. \end{array} \end{aligned} $$

  Thus, it holds

  $$\displaystyle \begin{aligned}\sum_{i=1}^{\infty} \|{\boldsymbol g}({\boldsymbol x}_i;\mu_i)\|{}^2 \leq \frac{1}{c}(\overline{B} - \underline{B}) < \infty,\end{aligned}$$

  which gives ${\boldsymbol g}({\boldsymbol x}_i;\mu _i) = \sum _{k=1}^m \sum _{l=1}^{m_k} {\boldsymbol g}_{kl}({\boldsymbol x}_i) u_{kl}({\boldsymbol x}_i;\mu _i) \downarrow {\mathbf {0}}$.

• (c) Let indices 1 ≤ k ≤ m and 1 ≤ l ≤ m _k are chosen arbitrarily. Using (11.50) and Lemma 11.3 we obtain

  $$\displaystyle \begin{aligned}u_{kl}({\boldsymbol x}_i;\mu_i) (z_k({\boldsymbol x}_i;\mu_i) - f_{kl}({\boldsymbol x}_i)) = \frac{\mu_i(z_k({\boldsymbol x}_i;\mu_i) - f_{kl}({\boldsymbol x}_i))}{z_k({\boldsymbol x}_i;\mu_i) - f_{kl}({\boldsymbol x}_i)} = \mu_i \downarrow 0.\end{aligned}$$

□

Corollary 11.1

Let the assumptions of Theorem 11.5be satisfied. Then, every cluster point ${\boldsymbol x} \in \mathbb {R}^n$of a sequence {x _i}, $i \in \mathbb {N}$, satisfies necessary KKT conditions (11.8)–(11.9) wherezandu(with elements z _kand u _kl, 1 ≤ k ≤ m, 1 ≤ l ≤ m _k) are cluster points of sequences {z(x _i;μ _i)} and {u(x _i;μ _i)}, $i \in \mathbb {N}$.

Now we will suppose that the values $\underline {\delta }$, $\underline {\varepsilon }$, and $\underline {\mu }$ are nonzero and show how a precise solution of the system of KKT equations will be after termination of computation.

Theorem 11.6

Let the assumptions of Lemma 11.3be satisfied. Consider a sequence {x _i}, $i \in \mathbb {N}$, generated by Algorithm 11.1. Then, if the values $\underline {\delta } > 0$, $\underline {\varepsilon } > 0$, and $\underline {\mu } > 0$are chosen arbitrarily, there exists an index i ≥ 1 such that

$$\displaystyle \begin{aligned} &\|{\boldsymbol g}({\boldsymbol x}_i;\mu_i)\| \leq \underline{\varepsilon}, \quad \left|1 - \sum_{l=1}^{m_k} u_{kl}({\boldsymbol x}_i;\mu_i)\right| \leq \underline{\delta},\\ &z_k({\boldsymbol x}_i;\mu_i) - f_{kl}({\boldsymbol x}_i) \geq 0, \quad u_{kl}({\boldsymbol x}_i;\mu_i) \geq 0,\\ &u_{kl}({\boldsymbol x}_i;\mu_i) (z_k({\boldsymbol x}_i;\mu_i) - f_{kl}({\boldsymbol x}_i)) \leq \underline{\mu}, \end{aligned} $$

for 1 ≤ k ≤ m and 1 ≤ l ≤ m _k.

Proof

Inequality $|1 - \tilde {{\boldsymbol e}}_k^T {\boldsymbol u}_k({\boldsymbol x}_i;\mu _i)| \leq \underline {\delta }$ follows immediately from the fact that the equation $\tilde {{\boldsymbol e}}_k^T {\boldsymbol u}_k({\boldsymbol x}_i;\mu _i) = 1$, 1 ≤ k ≤ m, is solved with precision $\underline {\delta }$. Inequalities z _k(x _i;μ _i) − f _kl(x _i) ≥ 0, u _kl(x _i;μ _i) ≥ 0 follow from formulas (11.45) and statement (11.50) as in the proof of Theorem 11.5. Since μ _i ↓ 0 and g(x _i;μ _i) ↓0 by Lemma 11.3 and Theorem 11.5, there exists an index i ≥ 1 such that $\mu _i \leq \underline {\mu }$ and $\|{\boldsymbol g}({\boldsymbol x}_i;\mu _i)\| \leq \underline {\varepsilon }$. Using (11.50) we obtain

$$\displaystyle \begin{aligned}u_{kl}({\boldsymbol x}_i;\mu_i) (z_k({\boldsymbol x}_i;\mu_i) - f_{kl}({\boldsymbol x}_i)) = \frac{\mu_i(z_k({\boldsymbol x}_i;\mu_i) - f_{kl}({\boldsymbol x}_i))}{z_k({\boldsymbol x}_i;\mu_i) - f_{kl}({\boldsymbol x}_i)} = \mu_i \leq \underline{\mu}.\end{aligned}$$

□

Theorem 11.5 is a standard global convergence result. If the stopping parameters $\underline {\delta }, \underline {\varepsilon }, \underline {\mu }$ are zero, the sequence of generated points converges to the point satisfying the KKT conditions for the equivalent nonlinear programming problem. Theorem 11.6 determines a precision of the obtained solution if the stopping parameters are nonzero.

2.6 Special Cases

Both the simplest and most widely considered generalized minimax problem is the classical minimax problem (11.10), when m = 1 in (11.4) (in this case we write m, z, u, v, U, V , A instead of m ₁, z ₁, u ₁, v ₁, U ₁, V ₁, A ₁). For solving a classical minimax problem one can use Algorithm 11.1, where a major part of computation is very simplified. System of equations (11.38) is of order n + 1 and has the form

(11.67)

where g(x, z) = A(x)u(x, z), $\gamma ({\boldsymbol x},z) = 1 - \tilde {{\boldsymbol e}}^T {\boldsymbol u}({\boldsymbol x},z)$, $V({\boldsymbol x},z) = U^2({\boldsymbol x},z) / \mu = \operatorname {\mathrm {diag}} [u_1^2({\boldsymbol x},z), \dots , u_m^2({\boldsymbol x},z)] / \mu$, and u _k(x, z) = μ∕(z − f _k(x)), 1 ≤ k ≤ m. System of equations (11.44) is reduced to one nonlinear equation

$$\displaystyle \begin{aligned} 1 - \tilde{{\boldsymbol e}}^T {\boldsymbol u}({\boldsymbol x},z) = 1 - \sum_{k=1}^m \frac{\mu}{z - f_k({\boldsymbol x})} = 0, {} \end{aligned} $$

(11.68)

whose solution z(x;μ) lies in the interval F(x) + μ ≤ z(x;μ) ≤ F(x) + mμ. To find this solution by robust methods from [14, 15] is not difficult. A barrier function has the form

$$\displaystyle \begin{aligned} \hat{B}({\boldsymbol x};\mu) = z({\boldsymbol x};\mu) - \mu \sum_{k=1}^m \log(z({\boldsymbol x};\mu) - f_k({\boldsymbol x})) {} \end{aligned} $$

(11.69)

with $\nabla \hat {B}({\boldsymbol x};\mu ) = A({\boldsymbol x}) {\boldsymbol u}({\boldsymbol x};\mu )$ and

$$\displaystyle \begin{aligned}\nabla^2 \hat{B}({\boldsymbol x};\mu) = G({\boldsymbol x};\mu) + A({\boldsymbol x}) V({\boldsymbol x};\mu) A^T({\boldsymbol x}) - \frac{A({\boldsymbol x}) V({\boldsymbol x};\mu) \tilde{{\boldsymbol e}} \tilde{{\boldsymbol e}}^T V({\boldsymbol x};\mu) A^T({\boldsymbol x})}{\tilde{{\boldsymbol e}}^T V({\boldsymbol x};\mu) \tilde{{\boldsymbol e}}}.\end{aligned}$$

If we write system (11.67) in the form

where W(x, z) = G(x, z) + A(x)V (x, z)A ^T(x), ${\boldsymbol c}({\boldsymbol x},z) = A({\boldsymbol x}) V({\boldsymbol x},z) \tilde {{\boldsymbol e}}$ and $\delta ({\boldsymbol x},z) = \tilde {{\boldsymbol e}}^T V({\boldsymbol x},z) \tilde {{\boldsymbol e}}$, then

$$\displaystyle \begin{aligned}\nabla^2 \hat{B}({\boldsymbol x};\mu) = W({\boldsymbol x}; \mu) - \frac{{\boldsymbol c}({\boldsymbol x}; \mu) {\boldsymbol c}^T({\boldsymbol x}; \mu)}{\delta({\boldsymbol x}; \mu)}.\end{aligned}$$

Since

where ω = c ^TW ⁻¹c − δ, we can write

where

$$\displaystyle \begin{aligned}\varDelta z = \omega^{-1}({\boldsymbol c}^T W^{-1} {\boldsymbol g} + \gamma).\end{aligned}$$

The matrix W is sparse if the matrix A(x) has sparse columns. If the matrix W is not positive definite, we can use the Gill–Murray decomposition

$$\displaystyle \begin{aligned} W + E = L L^T, {} \end{aligned} $$

(11.70)

where E is a positive semidefinite diagonal matrix. Then we solve equations

$$\displaystyle \begin{aligned} L L^T {\boldsymbol p} = {\boldsymbol g}, \quad L L^T {\boldsymbol q} = {\boldsymbol c} {} \end{aligned} $$

(11.71)

and set

$$\displaystyle \begin{aligned} \varDelta z = \frac{{\boldsymbol c}^T {\boldsymbol p} + \gamma}{{\boldsymbol c}^T {\boldsymbol q} - \delta}, \quad \varDelta {\boldsymbol x} = {\boldsymbol q} \, \varDelta z - {\boldsymbol p}. {} \end{aligned} $$

(11.72)

If we solve the classical minimax problem, Algorithm 11.1 must be somewhat modified. In Step 2, we solve only Eq. (11.68) instead of the system of equations (11.44). In Step 4, we determine a vector Δx by solving Eq. (11.71) and using relations (11.72). In Step 4, we use the barrier function (11.69) (the nonlinear equation (11.68) must be solved at the point x + αΔx).

Minimization of a sum of absolute values, i.e., minimization of the function (11.14) is another important generalized minimax problem. In this case, a barrier function has the form

$$\displaystyle \begin{aligned} \begin{array}{rcl} B_{\mu}({\boldsymbol x},{\boldsymbol z}) &\displaystyle = &\displaystyle \sum_{k=1}^m z_k - \mu \sum_{k=1}^m \log(z_k - f_k({\boldsymbol x})) - \mu \sum_{k=1}^m \log(z_k + f_k({\boldsymbol x})) \\ &\displaystyle = &\displaystyle \sum_{k=1}^m z_k - \mu \sum_{k=1}^m \log(z_k^2 - f_k^2({\boldsymbol x})), {} \end{array} \end{aligned} $$

(11.73)

where z _k > |f _k(x)|, 1 ≤ k ≤ m. Differentiating B _μ(x, z) with respect to x and z we obtain the necessary conditions for an extremum

$$\displaystyle \begin{aligned} \begin{aligned} &\sum_{k=1}^m \frac{2 \mu f_k({\boldsymbol x})}{z_k^2 - f_k^2({\boldsymbol x})} \, {\boldsymbol g}_k({\boldsymbol x}) = \sum_{k=1}^m u_k({\boldsymbol x},z_k) \, {\boldsymbol g}_k({\boldsymbol x}) = {\mathbf{0}}, \\ &u_k({\boldsymbol x},z_k) = \frac{2 \mu f_k({\boldsymbol x})}{z_k^2 - f_k^2({\boldsymbol x})} {} \end{aligned} \end{aligned} $$

(11.74)

and

$$\displaystyle \begin{aligned} 1 - \frac{2 \mu z_k}{z_k^2 - f_k^2({\boldsymbol x})} = 1 - u_k({\boldsymbol x},z_k) \frac{z_k}{f_k({\boldsymbol x})} = 0 \quad \Rightarrow \quad u_k({\boldsymbol x},z_k) = \frac{f_k({\boldsymbol x})}{z_k}, {} \end{aligned} $$

(11.75)

where g _k(x) = ∇f _k(x), 1 ≤ k ≤ m, which corresponds to (11.31)–(11.32). Equations in (11.44) are quadratic of the form

$$\displaystyle \begin{aligned} \frac{2 \mu z_k({\boldsymbol x};\mu)}{z_k^2({\boldsymbol x};\mu) - f_k^2({\boldsymbol x})} = 1 \quad \Leftrightarrow \quad z_k^2({\boldsymbol x};\mu) - f_k^2({\boldsymbol x}) = 2 \mu z_k({\boldsymbol x};\mu), {} \end{aligned} $$

(11.76)

where 1 ≤ k ≤ m, and their solutions is given by

$$\displaystyle \begin{aligned} z_k({\boldsymbol x};\mu) = \mu + \sqrt{\mu^2 + f_k^2({\boldsymbol x})}, \quad 1 \leq k \leq m, {} \end{aligned} $$

(11.77)

(the second solutions of quadratic equations (11.76) do not satisfy the condition z _k > |f _k(x)|, so the obtained vector z does not belong to a domain of $\tilde {B}_{\mu }({\boldsymbol z})$). Using (11.75) and (11.77) we obtain

$$\displaystyle \begin{aligned} u_k({\boldsymbol x};\mu) = u_k({\boldsymbol x},z_k({\boldsymbol x};\mu)) = \frac{f_k({\boldsymbol x})}{z_k({\boldsymbol x};\mu)} = \frac{f_k({\boldsymbol x})}{\mu + \sqrt{\mu^2 + f_k^2({\boldsymbol x})}} {} \end{aligned} $$

(11.78)

for 1 ≤ k ≤ m and

$$\displaystyle \begin{aligned} \begin{array}{rcl} \hat{B}({\boldsymbol x};\mu) &\displaystyle = &\displaystyle B({\boldsymbol x},{\boldsymbol z}({\boldsymbol x};\mu)) = \sum_{k=1}^m z_k({\boldsymbol x};\mu) - \mu \sum_{k=1}^m \log(z_k^2({\boldsymbol x};\mu) - f_k^2({\boldsymbol x})) \quad \\ &\displaystyle = &\displaystyle \sum_{k=1}^m z_k({\boldsymbol x};\mu) - \mu \sum_{k=1}^m \log(2 \mu z_k({\boldsymbol x};\mu)) \\ &\displaystyle = &\displaystyle \sum_{k=1}^m \left[z_k({\boldsymbol x};\mu) - \mu \log(z_k({\boldsymbol x};\mu))\right] -\mu m \log(2\mu). {} \end{array} \end{aligned} $$

(11.79)

Using these expressions, we can write formulas (11.47) and (11.48) in the form

$$\displaystyle \begin{aligned} \nabla \hat{B}({\boldsymbol x};\mu) = \sum_{k=1}^m {\boldsymbol g}_k({\boldsymbol x}) u_k({\boldsymbol x};\mu) \end{aligned} $$

(11.80)

and

$$\displaystyle \begin{aligned} \nabla^2 \hat{B}({\boldsymbol x};\mu) = W({\boldsymbol x};\mu) = \sum_{k=1}^m G_k({\boldsymbol x}) u_k({\boldsymbol x};\mu) + \sum_{k=1}^m {\boldsymbol g}_k({\boldsymbol x}) v_k({\boldsymbol x};\mu) {\boldsymbol g}_k^T({\boldsymbol x}), \end{aligned} $$

(11.81)

where

$$\displaystyle \begin{aligned} G_k({\boldsymbol x}) = \nabla^2 f_k({\boldsymbol x}), \quad v_k({\boldsymbol x};\mu) = \frac{2 \mu}{z_k^2({\boldsymbol x};\mu) + f_k^2({\boldsymbol x})}, \quad 1 \leq k \leq m. \end{aligned} $$

(11.82)

A vector $\varDelta {\boldsymbol x} \in \mathbb {R}^n$ is determined by solving the equation

$$\displaystyle \begin{aligned} \nabla^2 \hat{B}({\boldsymbol x};\mu) \varDelta {\boldsymbol x} = - {\boldsymbol g}({\boldsymbol x};\mu), \end{aligned} $$

(11.83)

where ${\boldsymbol g}({\boldsymbol x};\mu ) = \nabla \hat {B}({\boldsymbol x};\mu ) \neq 0$. From (11.83) and (11.81) it follows

$$\displaystyle \begin{aligned}(\varDelta {\boldsymbol x})^T {\boldsymbol g}({\boldsymbol x};\mu) = -(\varDelta {\boldsymbol x})^T \nabla^2 \hat{B}({\boldsymbol x};\mu) \varDelta {\boldsymbol x} \leq -(\varDelta {\boldsymbol x})^T G({\boldsymbol x};\mu) \varDelta {\boldsymbol x},\end{aligned}$$

so if a matrix G(x;μ) is positive definite, a matrix $\nabla \hat {B}({\boldsymbol x};\mu )$ is positive definite as well (since a diagonal matrix V (x;μ) is positive definite by (11.82)) and (Δx)^Tg(x;μ) < 0 holds (a direction vector Δx is descent for a function $\hat {B}({\boldsymbol x};\mu )$).

If we minimize a sum of absolute values, Algorithm 11.1 needs to be somewhat modified. In Step 2, we solve quadratic equations (11.76) whose solutions are given by (11.77). In Step 4, we determine a vector Δx by solving Eq. (11.83), where matrix $\nabla ^2 \hat {B}({\boldsymbol x};\mu )$ is given by (11.83). In Step 4, we use the barrier function (11.79).

3 Smoothing Methods

3.1 Basic Properties

Similarly as in Sect. 11.2.1 we will restrict ourselves to sums of maxima, where a mapping ${\boldsymbol h}: \mathbb {R}^n \to \mathbb {R}^m$ is a sum of its arguments, so (11.4) holds. Smoothing methods for minimization of sums of maxima replace function (11.4) by a smoothing function

$$\displaystyle \begin{aligned} S({\boldsymbol x};\mu) = \sum_{k=1}^m S_k({\boldsymbol x};\mu), {} \end{aligned} $$

(11.84)

where

$$\displaystyle \begin{aligned} \begin{array}{rcl} S_k({\boldsymbol x};\mu) &\displaystyle = &\displaystyle \mu \log \sum_{l=1}^{m_k} \exp \left(\frac{f_{kl}({\boldsymbol x})}{\mu}\right) \\ &\displaystyle = &\displaystyle F_k({\boldsymbol x}) + \mu \log \sum_{l=1}^{m_k} \exp \left(\frac{f_{kl}({\boldsymbol x}) - F_k({\boldsymbol x})}{\mu}\right), {} \end{array} \end{aligned} $$

(11.85)

depending on a smoothing parameter $0 < \mu \leq \overline {\mu }$, which is successively minimized on $\mathbb {R}^n$ with μ ↓ 0. Since f _kl(x) ≤ F _k(x), 1 ≤ l ≤ m _k, and the equality arises for at least one index, at least one exponential function on the right-hand side of (11.85) has the value 1, so the logarithm is positive. Thus $F_k({\boldsymbol x}) \leq S_k({\boldsymbol x};\mu ) \leq F_k({\boldsymbol x}) + \mu \, \log \, m_k$, 1 ≤ k ≤ m, hold. Therefore

$$\displaystyle \begin{aligned} F({\boldsymbol x}) \leq S({\boldsymbol x};\mu) \leq F({\boldsymbol x}) + \mu \, \sum_{k=1}^m \log \, m_k, {} \end{aligned} $$

(11.86)

so S(x;μ) → F(x) if μ ↓ 0.

Remark 11.15

Similarly as in Sect. 11.2.2 we will denote g _kl(x) and G _kl(x) the gradients and Hessian matrices of functions f _kl(x), 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, and

where

$$\displaystyle \begin{aligned} u_{kl}({\boldsymbol x};\mu) = \frac{\exp(f_{kl}({\boldsymbol x})/\mu)}{\sum_{l=1}^{m_k} \exp(f_{kl}({\boldsymbol x})/\mu)} = \frac{\exp((f_{kl}({\boldsymbol x}) - F_k({\boldsymbol x}))/\mu)} {\sum_{l=1}^{m_k} \exp((f_{kl}({\boldsymbol x}) - F_k({\boldsymbol x}))/\mu)}. {} \end{aligned} $$

(11.87)

Thus, it holds u _kl(x;μ) ≥ 0, 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, and

$$\displaystyle \begin{aligned} \tilde{{\boldsymbol e}}_k^T {\boldsymbol u}_k({\boldsymbol x};\mu) = \sum_{l=1}^{m_k} u_{kl}({\boldsymbol x};\mu) = 1. {} \end{aligned} $$

(11.88)

Further, we denote $A_k({\boldsymbol x}) = J_k^T({\boldsymbol x}) = [{\boldsymbol g}_{k1}({\boldsymbol x}), \dots , {\boldsymbol g}_{km_k}({\boldsymbol x})]$ and $U_k({\boldsymbol x};\mu ) = \operatorname {\mathrm {diag}} [u_{k1}({\boldsymbol x};\mu ), \dots , u_{km_k}({\boldsymbol x};\mu )]$ for 1 ≤ k ≤ m.

Theorem 11.7

Consider the smoothing function (11.84). Then

$$\displaystyle \begin{aligned} \nabla S({\boldsymbol x};\mu) = {\boldsymbol g}({\boldsymbol x};\mu) \end{aligned} $$

(11.89)

and

$$\displaystyle \begin{aligned} \nabla^2 S({\boldsymbol x};\mu) & = G({\boldsymbol x};\mu) + \frac{1}{\mu} \sum_{k=1}^m A_k({\boldsymbol x}) U_k({\boldsymbol x};\mu) A_k^T({\boldsymbol x}) \\ & \qquad \quad \quad ~ -\frac{1}{\mu} \sum_{k=1}^m A_k({\boldsymbol x}) {\boldsymbol u}_k({\boldsymbol x};\mu) (A_k({\boldsymbol x}) {\boldsymbol u}_k({\boldsymbol x};\mu))^T \\ & = G({\boldsymbol x};\mu) + \frac{1}{\mu} A({\boldsymbol x}) U({\boldsymbol x};\mu) A^T({\boldsymbol x}) - \frac{1}{\mu} C({\boldsymbol x};\mu) C({\boldsymbol x};\mu)^T {} \end{aligned} $$

(11.90)

where ${\boldsymbol g}({\boldsymbol x};\mu ) = \sum _{k=1}^m A_k({\boldsymbol x}) {\boldsymbol u}_k({\boldsymbol x};\mu ) = A({\boldsymbol x}) {\boldsymbol u}({\boldsymbol x})$ and

$$\displaystyle \begin{aligned} G({\boldsymbol x};\mu) &= \sum_{k=1}^m G_k({\boldsymbol x}) {\boldsymbol u}_k({\boldsymbol x};\mu),\quad A({\boldsymbol x}) = [A_1({\boldsymbol x}), \dots, A_m({\boldsymbol x})],\\ U({\boldsymbol x};\mu) &= \operatorname{\mathrm{diag}} [U_1({\boldsymbol x};\mu), \dots, U_m({\boldsymbol x};\mu)],\\ C({\boldsymbol x};\mu) &= [A_1({\boldsymbol x}) {\boldsymbol u}_1({\boldsymbol x};\mu), \dots, A_m({\boldsymbol x}) {\boldsymbol u}_m({\boldsymbol x};\mu)]. \end{aligned} $$

Proof

Obviously,

$$\displaystyle \begin{aligned}\nabla S({\boldsymbol x};\mu) = \sum_{k=1}^m \nabla S_k({\boldsymbol x};\mu), \quad \nabla^2 S({\boldsymbol x};\mu) = \sum_{k=1}^m \nabla^2 S_k({\boldsymbol x};\mu).\end{aligned}$$

Differentiating functions (11.85) and using (11.87) we obtain

$$\displaystyle \begin{aligned} \begin{array}{rcl} \nabla S_k({\boldsymbol x}; \mu) &\displaystyle = &\displaystyle \frac{\mu}{\sum_{l=1}^{m_k} \exp(f_{kl}({\boldsymbol x})/\mu)} \sum_{l=1}^{m_k} \frac{1}{\mu}\exp(f_{kl}({\boldsymbol x})/\mu) {\boldsymbol g}_{kl}({\boldsymbol x}) \\ &\displaystyle = &\displaystyle \sum_{l=1}^{m_k} {\boldsymbol g}_{kl}({\boldsymbol x}) u_{kl}({\boldsymbol x};\mu) = A_k({\boldsymbol x}) {\boldsymbol u}_k({\boldsymbol x};\mu). {} \end{array} \end{aligned} $$

(11.91)

Adding up these expressions yields (11.89). Further, it holds

$$\displaystyle \begin{aligned} \nabla u_{kl}({\boldsymbol x}; \mu) & = \frac{1}{\mu} \frac{\exp(f_{kl}({\boldsymbol x})/\mu)}{\sum_{l=1}^{m_k} \exp(f_{kl}({\boldsymbol x})/\mu)} {\boldsymbol g}_{kl}({\boldsymbol x}) \\ & ~~-\frac{\exp(f_{kl}({\boldsymbol x})/\mu)}{\left(\sum_{l=1}^{m_k} \exp(f_{kl}({\boldsymbol x})/\mu)\right)^2} \sum_{l=1}^{m_k} \frac{1}{\mu} \exp(f_{kl}({\boldsymbol x})/\mu) {\boldsymbol g}_{kl}({\boldsymbol x}) \\ & = \frac{1}{\mu} u_{kl}({\boldsymbol x}; \mu) {\boldsymbol g}_{kl}({\boldsymbol x}) - \frac{1}{\mu} u_{kl}({\boldsymbol x}; \mu) \sum_{l=1}^{m_k} u_{kl}({\boldsymbol x}; \mu) {\boldsymbol g}_{kl}({\boldsymbol x}). {} \end{aligned} $$

(11.92)

Differentiating (11.91) and using (11.92) we obtain

$$\displaystyle \begin{aligned} \nabla ^2 S_k({\boldsymbol x}; \mu) & = \sum_{l=1}^{m_k} G_{kl}({\boldsymbol x}) u_{kl}({\boldsymbol x}; \mu) + \sum_{l=1}^{m_k} {\boldsymbol g}_{kl}({\boldsymbol x}) \nabla u_{kl}({\boldsymbol x}; \mu) \\ & = G_k({\boldsymbol x};\mu) + \frac{1}{\mu} \sum_{l=1}^{m_k} {\boldsymbol g}_{kl}({\boldsymbol x}) u_{kl}({\boldsymbol x}; \mu) {\boldsymbol g}_{kl}^T({\boldsymbol x}) \\ & \qquad \qquad ~~~ -\frac{1}{\mu} \sum_{l=1}^{m_k} {\boldsymbol g}_{kl}({\boldsymbol x}) u_{kl}({\boldsymbol x}; \mu) \left(\sum_{l=1}^{m_k} {\boldsymbol g}_{kl}({\boldsymbol x}) u_{kl}({\boldsymbol x}; \mu)\right)^T \\ & = G_k({\boldsymbol x};\mu) + \frac{1}{\mu} A_k({\boldsymbol x}) U_k({\boldsymbol x};\mu) A_k^T({\boldsymbol x}) \\ & \qquad \qquad ~~~ -\frac{1}{\mu} A_k({\boldsymbol x}) {\boldsymbol u}_k({\boldsymbol x};\mu) (A_k({\boldsymbol x}) {\boldsymbol u}_k({\boldsymbol x};\mu))^T, \end{aligned} $$

where $G_k({\boldsymbol x};\mu ) = \sum _{l=1}^{m_k} G_{kl}({\boldsymbol x}) u_{kl}({\boldsymbol x}; \mu )$. Adding up these expressions yields (11.90). □

Remark 11.16

Note that using (11.90) and the Schwarz inequality we obtain

$$\displaystyle \begin{aligned} \begin{array}{rcl} {\boldsymbol v}^T \nabla^2 S({\boldsymbol x};\mu) {\boldsymbol v} &\displaystyle = &\displaystyle {\boldsymbol v}^T G({\boldsymbol x};\mu){\boldsymbol v} \\ &\displaystyle + &\displaystyle \frac{1}{\mu} \sum_{k=1}^m \left({\boldsymbol v}^T A_k({\boldsymbol x}) U_k({\boldsymbol x};\mu) A_k^T({\boldsymbol x}) {\boldsymbol v} - \frac{({\boldsymbol v}^T A_k({\boldsymbol x}) U_k({\boldsymbol x};\mu) \tilde{{\boldsymbol e}}_k)^2}{\tilde{{\boldsymbol e}}_k^T U_k({\boldsymbol x};\mu) \tilde{{\boldsymbol e}}_k}\right) \\ &\displaystyle \geq &\displaystyle {\boldsymbol v}^T G({\boldsymbol x};\mu) {\boldsymbol v}, \end{array} \end{aligned} $$

because $\tilde {{\boldsymbol e}}_k^T U_k({\boldsymbol x};\mu ) \tilde {{\boldsymbol e}}_k = \tilde {{\boldsymbol e}}_k^T {\boldsymbol u}_k({\boldsymbol x};\mu ) = 1$, so the Hessian matrix ∇²S(x;μ) is positive definite if the matrix G(x;μ) is positive definite.

Using Theorem 11.7, a step of the Newton method can be written in the form x ₊ = x + αΔx where

$$\displaystyle \begin{aligned} \nabla^2 S({\boldsymbol x};\mu) \varDelta {\boldsymbol x} = - \nabla S({\boldsymbol x};\mu), \end{aligned} $$

or

$$\displaystyle \begin{aligned} \left(W({\boldsymbol x};\mu) - \frac{1}{\mu} C({\boldsymbol x};\mu) C^T({\boldsymbol x};\mu) \right) \varDelta {\boldsymbol x} = - {\boldsymbol g}({\boldsymbol x};\mu), {} \end{aligned} $$

(11.93)

where

$$\displaystyle \begin{aligned} W({\boldsymbol x};\mu) = G({\boldsymbol x};\mu) + \frac{1}{\mu} A({\boldsymbol x}) U({\boldsymbol x};\mu) A^T({\boldsymbol x}), \quad {\boldsymbol g}({\boldsymbol x};\mu) = A({\boldsymbol x}) {\boldsymbol u}({\boldsymbol x};\mu). {} \end{aligned} $$

(11.94)

A matrix W in (11.94) has the same structure as a matrix W in (11.48) and, by Theorem 11.7, smoothing function (11.84) has similar properties as the barrier function (11.46). Thus, one can use an algorithm that is analogous to Algorithm 11.1 and considerations stated in Remark 11.12, where S(x;μ) and ∇²S(x;μ) are used instead of $\hat {B}({\boldsymbol x}; \mu )$ and $\nabla ^2 \hat {B}({\boldsymbol x}; \mu )$. It means that

$$\displaystyle \begin{aligned} S({\boldsymbol x}_{i+1};\mu_i) - S({\boldsymbol x}_i;\mu_i) \leq - c \|{\boldsymbol g}({\boldsymbol x}_i;\mu_i)\|{}^2 \quad \mbox{for all} ~ i \in \mathbb{N}, \end{aligned} $$

(11.95)

if Assumption 11.4 is satisfied and

$$\displaystyle \begin{aligned} S({\boldsymbol x}_{i+1};\mu_i) - S({\boldsymbol x}_i;\mu_i) \leq 0 \quad \mbox{for all} ~ i \in \mathbb{N} \end{aligned} $$

(11.96)

in remaining cases.

The considerations up to now are summarized in Algorithm 11.2 introduced in the Appendix. This algorithm differs from Algorithm 11.1 in that a nonlinear equation $\tilde {{\boldsymbol e}}^T {\boldsymbol u}({\boldsymbol x}; \mu ) = 1$ need not be solved in Step 2 (because (11.88) follows from (11.87)), Eq. (11.93)–(11.94) instead of (11.71)–(11.72) are used in Step 4, and a barrier function $\hat {B}({\boldsymbol x}; \mu )$ is replaced with a smoothing function S(x;μ) in Step 6. Note that the parameter μ in (11.84) has different meaning than the same parameter in (11.46), so we could use another procedure for its update in Step 7. However, it is becoming apparent that using Procedure A or Procedure B is very efficient. On the other hand, it must be noted that using exponential functions in Algorithm 11.2 has certain disadvantages. Computation of the values of exponential functions is more time consuming than performing standard arithmetic operations and underflow may also happen (i.e. replacing nonzero values by zero values) if the value of a parameter μ is very small.

3.2 Global Convergence

Now we prove the global convergence of the smoothing method realized by Algorithm 11.2.

Lemma 11.4

Choose a fixed vector ${\boldsymbol x} \in \mathbb {R}^n$. Then $S_k({\boldsymbol x}; \mu ): (0, \infty ) \to \mathbb {R}$, 1 ≤ k ≤ m, are nondecreasing convex functions of μ > 0 and

$$\displaystyle \begin{aligned} 0 \leq \log \underline{m}_k \leq \frac{\partial}{\partial \mu} S_k({\boldsymbol x}; \mu) \leq \log m_k, {} \end{aligned} $$

(11.97)

where $\underline {m}_k$is a number of active functions (for which f _kl(x) = F _k(x)) and

$$\displaystyle \begin{aligned} \frac{\partial}{\partial \mu} S_k({\boldsymbol x}; \mu) = \log \sum_{l=1}^{m_k} \exp \left(\frac{f_{kl}({\boldsymbol x}) - F_k({\boldsymbol x})}{\mu}\right) - \sum_{l=1}^{m_k} \left(\frac{f_{kl}({\boldsymbol x}) - F_k({\boldsymbol x})}{\mu}\right) u_{kl}({\boldsymbol x}; \mu). {} \end{aligned} $$

(11.98)

Proof

Denoting φ _kl(x;μ) = (f _kl(x) − F _k(x))∕μ ≤ 0, 1 ≤ k ≤ m, so

$$\displaystyle \begin{aligned}\varphi^{\prime}_{kl}({\boldsymbol x}; \mu) \stackrel{\varDelta}{=} \frac{\partial}{\partial \mu} \varphi_{kl}({\boldsymbol x}; \mu) = -\frac{\varphi_{kl}({\boldsymbol x}; \mu)}{\mu} \geq 0,\end{aligned}$$

we can write by (11.85) that

$$\displaystyle \begin{aligned} S_k({\boldsymbol x}; \mu) = F_k({\boldsymbol x}) + \mu \log \sum_{l=1}^{m_k} \exp \varphi_{kl}({\boldsymbol x}; \mu) \end{aligned} $$

and

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{\partial}{\partial \mu} S_k({\boldsymbol x}; \mu) &\displaystyle = &\displaystyle \log \sum_{l=1}^{m_k} \exp \varphi_{kl}({\boldsymbol x}; \mu) + \mu \frac{\sum_{l=1}^{m_k} \varphi^{\prime}_{kl}({\boldsymbol x}; \mu) \exp \varphi_{kl}({\boldsymbol x}; \mu) }{\sum_{l=1}^{m_k} \exp \varphi_{kl}({\boldsymbol x}; \mu)} \\ &\displaystyle = &\displaystyle \log \sum_{l=1}^{m_k} \exp \varphi_{kl}({\boldsymbol x}; \mu) - \sum_{l=1}^{m_k} \varphi_{kl}({\boldsymbol x}; \mu) u_{kl}({\boldsymbol x}; \mu) \geq 0, {} \end{array} \end{aligned} $$

(11.99)

because φ _kl(x;μ) ≤ 0, u _kl(x;μ) ≥ 0, 1 ≤ k ≤ m, and φ _kl(x;μ) = 0 holds for at least one index. Thus, functions S _k(x;μ), 1 ≤ k ≤ m, are nondecreasing. Differentiating (11.87) with respect to μ we obtain

$$\displaystyle \begin{aligned} \frac{\partial}{\partial \mu} u_{kl}({\boldsymbol x}; \mu) &= -\frac{1}{\mu} \frac{\varphi_{kl}({\boldsymbol x}; \mu) \exp \varphi_{kl}({\boldsymbol x}; \mu)}{\sum_{l=1}^{m_k} \exp \varphi_{kl}({\boldsymbol x}; \mu)} \\ & ~~ +\frac{1}{\mu} \frac{\exp \varphi_{kl}({\boldsymbol x}; \mu)}{\sum_{l=1}^{{}_k}m \exp \varphi_{kl}({\boldsymbol x}; \mu)} \frac{\sum_{l=1}^{m_k} \varphi_{kl}({\boldsymbol x}; \mu) \exp \varphi_{kl}({\boldsymbol x}; \mu)}{\sum_{l=1}^{m_k} \exp \varphi_{kl}({\boldsymbol x}; \mu)} \\ &= \frac{1}{\mu} u_{kl}({\boldsymbol x}; \mu) \left( -\varphi_{kl}({\boldsymbol x}; \mu) + \sum_{l=1}^{m_k} \varphi_{kl}({\boldsymbol x}; \mu) u_{kl}({\boldsymbol x}; \mu)\right). {} \end{aligned} $$

(11.100)

Differentiating (11.99) with respect to μ and using Eqs. (11.88) and (11.100) we can write

$$\displaystyle \begin{aligned} \begin{array}{rcl} \frac{\partial^2}{\partial \mu^2} S_k({\boldsymbol x}; \mu) &\displaystyle = &\displaystyle -\frac{1}{\mu} \sum_{l=1}^{m_k} \varphi_{kl}({\boldsymbol x}; \mu) u_{kl}({\boldsymbol x}; \mu) \\ &\displaystyle &\displaystyle + \frac{1}{\mu} \sum_{l=1}^{m_k} \varphi_{kl}({\boldsymbol x}; \mu) u_{kl}({\boldsymbol x}; \mu) - \frac{1}{\mu} \sum_{l=1}^{m_k} \varphi_{kl}({\boldsymbol x}; \mu) \frac{\partial}{\partial \mu} u_{kl}({\boldsymbol x}; \mu) \\ &\displaystyle = &\displaystyle - \frac{1}{\mu} \sum_{l=1}^{m_k} \varphi_{kl}({\boldsymbol x}; \mu) \frac{\partial}{\partial \mu} u_{kl}({\boldsymbol x}; \mu) \\ &\displaystyle = &\displaystyle \frac{1}{\mu^2} \left(\sum_{l=1}^{m_k} \varphi_{kl}^2({\boldsymbol x}; \mu) u_{kl}({\boldsymbol x}; \mu)\right) \left(\sum_{l=1}^{m_k} u_{kl}({\boldsymbol x}; \mu)\right) \\ &\displaystyle &\displaystyle -\frac{1}{\mu^2} \left(\sum_{l=1}^{m_k} \varphi_{kl}({\boldsymbol x}; \mu) u_{kl}({\boldsymbol x}; \mu)\right)^2 \geq 0, \end{array} \end{aligned} $$

because

$$\displaystyle \begin{aligned} \begin{array}{rcl} \left(\sum_{l=1}^{m_k} \varphi_{kl}({\boldsymbol x}; \mu) u_{kl}({\boldsymbol x}; \mu)\right)^2 &\displaystyle = &\displaystyle \left(\sum_{l=1}^{m_k} \varphi_{kl}({\boldsymbol x}; \mu) \sqrt{u_{kl}({\boldsymbol x}; \mu)} \sqrt{u_{kl}({\boldsymbol x}; \mu)}\right)^2 \\ &\displaystyle \leq &\displaystyle \sum_{l=1}^{m_k} \varphi_{kl}^2({\boldsymbol x}; \mu) u_{kl}({\boldsymbol x}; \mu) \sum_{l=1}^{m_k} u_{kl}({\boldsymbol x}; \mu) \end{array} \end{aligned} $$

holds by the Schwarz inequality. Thus, functions S _k(x;μ), 1 ≤ k ≤ m, are convex, so their derivatives $\frac {\partial }{\partial \mu } S_k({\boldsymbol x}; \mu )$ are nondecreasing. Obviously, it holds

$$\displaystyle \begin{aligned} \begin{array}{rcl} \lim_{\mu \downarrow 0} \frac{\partial}{\partial \mu} S_k({\boldsymbol x}; \mu) &\displaystyle = &\displaystyle \lim_{\mu \downarrow 0} \log \sum_{l=1}^{m_k} \exp \varphi_{kl}({\boldsymbol x}; \mu) - \lim_{\mu \downarrow 0} \sum_{l=1}^{m_k} \varphi_{kl}({\boldsymbol x}; \mu) u_{kl}({\boldsymbol x}; \mu) \\ &\displaystyle = &\displaystyle \log \underline{m}_k - \frac{1}{\underline{m}_k} \lim_{\mu \downarrow 0} \sum_{l=1}^{m_k} \varphi_{kl}({\boldsymbol x}; \mu) \exp \varphi_{kl}({\boldsymbol x}; \mu) = \log \underline{m}_k, \end{array} \end{aligned} $$

because φ _kl(x;μ) = 0 if f _kl(x) = F _k(x) and lim_μ↓0φ _kl(x;μ) = −∞, $\lim _{\mu \downarrow 0} \varphi _{kl}({\boldsymbol x}; \mu ) \exp \varphi _{kl}({\boldsymbol x}; \mu ) = 0$ if f _kl(x) < F _k(x). Similarly, it holds

$$\displaystyle \begin{aligned} \begin{array}{rcl} \lim_{\mu \uparrow \infty} \frac{\partial}{\partial \mu} S_k({\boldsymbol x}; \mu) &\displaystyle = &\displaystyle \lim_{\mu \uparrow \infty} \log \sum_{l=1}^{m_k} \exp \varphi_{kl}({\boldsymbol x}; \mu) - \lim_{\mu \uparrow \infty} \sum_{l=1}^{m_k} \varphi_{kl}({\boldsymbol x}; \mu) u_{kl}({\boldsymbol x}; \mu) \\ &\displaystyle = &\displaystyle \log m, \end{array} \end{aligned} $$

because lim_μ↑∞φ _kl(x;μ) = 0 and lim_μ↑∞|u _kl(x;μ)|≤ 1 for 1 ≤ k ≤ m. □

Lemma 11.5

Let Assumptions 11.2and 11.4be satisfied. Then the values μ _i, $i \in \mathbb {N}$, generated by Algorithm 11.2, create a nonincreasing sequence such that μ _i ↓ 0.

Proof

Lemma 11.5 is a direct consequence of Lemma 11.3 because the same procedures for an update of a parameter μ are used and (11.95) holds. □

Theorem 11.8

Let the assumptions of Lemma 11.5be satisfied. Consider a sequence {x _i} $i \in \mathbb {N}$, generated by Algorithm 11.2, where $\underline {\varepsilon } = \underline {\mu } = 0$. Then

$$\displaystyle \begin{aligned}\lim_{i \uparrow \infty} \sum_{k=1}^m \sum_{l=1}^{m_k} u_{kl}({\boldsymbol x}_i;\mu_i) {\boldsymbol g}_{kl}({\boldsymbol x}_i) = {\mathbf{0}}, \quad \sum_{l=1}^{m_k} u_{kl}({\boldsymbol x}_i;\mu_i) = 1\end{aligned}$$

and

$$\displaystyle \begin{aligned}F_k({\boldsymbol x}_i) - f_{kl}({\boldsymbol x}_i) \geq 0, \,\,\, u_{kl}({\boldsymbol x}_i;\mu_i) \geq 0, \,\,\, \lim_{i \uparrow \infty} u_{kl}({\boldsymbol x}_i;\mu_i) (F_k({\boldsymbol x}_i) - f_{kl}({\boldsymbol x}_i)) = 0\end{aligned}$$

for 1 ≤ k ≤ m and 1 ≤ l ≤ m _k.

Proof

• (a) Equations $\tilde {{\boldsymbol e}}_k^T {\boldsymbol u}_k({\boldsymbol x}_i; \mu _i) = 1$ for 1 ≤ k ≤ m follow from (11.88). Inequalities F _k(x _i) − f _kl(x _i) ≥ 0 and u _kl(x _i;μ _i) ≥ 0 for 1 ≤ k ≤ m and 1 ≤ l ≤ m _k follow from (11.4) and (11.87).

• (b) Since S _k(x;μ) are nondecreasing functions of the parameter μ by Lemma 11.4 and (11.95) holds, we can write

  $$\displaystyle \begin{aligned} \begin{array}{rcl} \underline{F} &\displaystyle \leq &\displaystyle \sum_{k=1}^m F_k({\boldsymbol x}_{i+1}) \leq S({\boldsymbol x}_{i+1};\mu_{i+1}) \leq S({\boldsymbol x}_{i+1};\mu_i) \\ &\displaystyle \leq &\displaystyle S({\boldsymbol x}_i;\mu_i) - c \|{\boldsymbol g}({\boldsymbol x}_i;\mu_i)\|{}^2 \leq S({\boldsymbol x}_1;\mu_1) - c \sum_{j=1}^i \|{\boldsymbol g}({\boldsymbol x}_j;\mu_j)\|{}^2, \end{array} \end{aligned} $$

  where $\underline {F} = \sum _{k=1}^m \underline {F}_k$ and $\underline {F}_k$, 1 ≤ k ≤ m, are lower bounds from Assumption 11.2. Thus, it holds

  $$\displaystyle \begin{aligned}\underline{F} \leq \lim_{i \uparrow \infty} S({\boldsymbol x}_{i+1};\mu_{i+1}) \leq S({\boldsymbol x}_1;\mu_1) - c \sum_{i=1}^{\infty} \|{\boldsymbol g}({\boldsymbol x}_i;\mu_i)\|{}^2,\end{aligned}$$

  or

  $$\displaystyle \begin{aligned}\sum_{i=1}^{\infty} \|{\boldsymbol g}({\boldsymbol x}_i;\mu_i)\|{}^2 \leq \frac{1}{c}(S({\boldsymbol x}_1;\mu_1) - \underline{F}),\end{aligned}$$

  so ∥g(x _i;μ _i)∥↓ 0, which together with inequalities 0 ≤ u _kl(x _i;μ _i) ≤ 1, 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, gives lim_i↑∞u _kl(x _i;μ _i)g _kl(x _i) = 0.

• (c) Let indices 1 ≤ k ≤ m and 1 ≤ l ≤ m _k be chosen arbitrarily. Using (11.87) we get

  $$\displaystyle \begin{aligned} \begin{array}{rcl} 0 &\displaystyle \leq &\displaystyle u_{kl}({\boldsymbol x}_i;\mu_i) (F_k({\boldsymbol x}_i) - f_{kl}({\boldsymbol x}_i)) = -\mu_i \frac{\varphi_{kl}({\boldsymbol x}_i; \mu_i) \exp \varphi_{kl}({\boldsymbol x}_i; \mu_i)}{\sum_{l=1}^{m_k} \exp \varphi_{kl}({\boldsymbol x}_i; \mu_i)} \\ &\displaystyle \leq &\displaystyle -\mu_i \varphi_{kl}({\boldsymbol x}_i; \mu_i) \exp \varphi_{kl}({\boldsymbol x}_i; \mu_i) \leq \frac{\mu_i}{e}, \end{array} \end{aligned} $$

  where φ _kl(x _i;μ _i), 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, are functions used in the proof of Lemma 11.4, because

  $$\displaystyle \begin{aligned}\sum_{l=1}^{m_k} \exp \varphi_{kl}({\boldsymbol x}_i; \mu_i) \geq 1\end{aligned}$$

  and the function $t \exp t$ attains its minimal value − 1∕e at the point t = −1. Since μ _i ↓ 0, we obtain u _kl(x _i;μ _i)(F _k(x _i) − f _kl(x _i)) ↓ 0.

□

Corollary 11.2

Let the assumptions of Theorem 11.8be satisfied. Then every cluster point ${\boldsymbol x} \in \mathbb {R}^n$of a sequence {x _i}, $i \in \mathbb {N}$, satisfies the necessary KKT conditions (11.5) and (11.6), whereu(with elementsu _k, 1 ≤ k ≤ m) is a cluster point of a sequence {u(x _i;μ _i)}, $i \in \mathbb {N}$.

Now we will suppose that the values $\underline {\varepsilon }$ and $\underline {\mu }$ are nonzero and show how a precise solution of the system of KKT equations will be after termination of computation of Algorithm 11.2.

Theorem 11.9

Let the assumptions of Theorem 11.5be satisfied and let {x _i}, $i \in \mathbb {N}$, be a sequence generated by Algorithm 11.2. Then, if the values $\underline {\varepsilon } > 0$and $\underline {\mu } > 0$are chosen arbitrarily, there exists an index i ≥ 1 such that

$$\displaystyle \begin{aligned}\|{\boldsymbol g}({\boldsymbol x}_i;\mu_i)\| \leq \underline{\varepsilon}, \quad \tilde{{\boldsymbol e}}_k^T {\boldsymbol u}_k({\boldsymbol x}_i;\mu_i) = 1, \quad 1 \leq k \leq m,\end{aligned}$$

and

$$\displaystyle \begin{aligned}F_k({\boldsymbol x}_i) - f_{kl}({\boldsymbol x}_i) \geq 0, \quad u_{kl}({\boldsymbol x}_i;\mu_i) \geq 0, \quad u_{kl}({\boldsymbol x}_i;\mu_i) (F_k({\boldsymbol x}_i) - f_{kl}({\boldsymbol x}_i)) \leq \frac{\underline{\mu}}{e}\end{aligned}$$

for all 1 ≤ k ≤ m and 1 ≤ l ≤ m _k.

Proof

Equalities $\tilde {{\boldsymbol e}}_k^T {\boldsymbol u}_k({\boldsymbol x}_i; \mu _i) = 1$, 1 ≤ k ≤ m, follow from (11.88). Inequalities F _k(x _i) − f _kl(x _i) ≥ 0 and u _kl(x _i;μ _i) ≥ 0, 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, follow from (11.10) and (11.87). Since μ _i ↓ 0 holds by Lemma 11.5 and ∥g(x _i;μ _i)∥↓ 0 holds by Theorem 11.8, there exists an index i ≥ 1 such that $\mu _i \leq \underline {\mu }$ and $\|{\boldsymbol g}({\boldsymbol x}_i;\mu _i)\| \leq \underline {\varepsilon }$. By (11.87), as in the proof of Theorem 11.8, one can write

$$\displaystyle \begin{aligned}u_{kl}({\boldsymbol x}_i;\mu_i) (F_k({\boldsymbol x}_i) - f_{kl}({\boldsymbol x}_i)) \leq -\mu_i \varphi_{kl}({\boldsymbol x}_i; \mu_i) \exp \varphi_{kl}({\boldsymbol x}_i; \mu_i) \leq \frac{\mu_i}{e} \leq \frac{\underline{\mu}}{e}\end{aligned}$$

for 1 ≤ k ≤ m and 1 ≤ l ≤ m _k. □

Theorems 11.8 and 11.9 have the same meaning as Theorems 11.5 and 11.6 introduced in Sect. 11.2.5.

3.3 Special Cases

Both the simplest and most widely considered generalized minimax problem is the classical minimax problem (11.10), when m = 1 in (11.4) (in this case we write m and z instead of m ₁ and z ₁). For solving a classical minimax problem one can use Algorithm 11.2, where a major part of computation is very simplified. A step of the Newton method can be written in the form x ₊ = x + αΔx where

$$\displaystyle \begin{aligned}\nabla^2 S({\boldsymbol x};\mu) \varDelta {\boldsymbol x} = - \nabla S({\boldsymbol x};\mu),\end{aligned} $$

or

$$\displaystyle \begin{aligned} \left(W({\boldsymbol x};\mu) - \frac{1}{\mu} {\boldsymbol g}({\boldsymbol x};\mu) {\boldsymbol g}^T({\boldsymbol x};\mu) \right) \varDelta {\boldsymbol x} = - {\boldsymbol g}({\boldsymbol x};\mu), {} \end{aligned} $$

(11.101)

where

$$\displaystyle \begin{aligned} W({\boldsymbol x};\mu) = G({\boldsymbol x};\mu) + \frac{1}{\mu} A({\boldsymbol x}) U({\boldsymbol x};\mu) A^T({\boldsymbol x}), \quad {\boldsymbol g}({\boldsymbol x};\mu) = A({\boldsymbol x}) {\boldsymbol u}({\boldsymbol x};\mu). {} \end{aligned} $$

(11.102)

Since

$$\displaystyle \begin{aligned}\left(W - \frac{1}{\mu} {\boldsymbol g} {\boldsymbol g}^T\right)^{-1} = W^{-1} + \frac{W^{-1} {\boldsymbol g} {\boldsymbol g}^T W^{-1}} {\mu - {\boldsymbol g}^T W^{-1} {\boldsymbol g}}\end{aligned} $$

holds by the Sherman–Morrison formula, the solution of system of equations (11.101) can be written in the form

$$\displaystyle \begin{aligned} \varDelta {\boldsymbol x} = \frac{\mu}{{\boldsymbol g}^T W^{-1} {\boldsymbol g} - \mu} W^{-1} {\boldsymbol g}. {} \end{aligned} $$

(11.103)

If a matrix W is not positive definite, it may be replaced with a matrix LL ^T = W + E obtained by the Gill–Murray decomposition described in [10]. Then, we solve an equation

$$\displaystyle \begin{aligned} L L^T {\boldsymbol p} = {\boldsymbol g}, {} \end{aligned} $$

(11.104)

and set

$$\displaystyle \begin{aligned} \varDelta {\boldsymbol x} = \frac{\mu}{{\boldsymbol g}^T {\boldsymbol p} - \mu} {\boldsymbol p}. {} \end{aligned} $$

(11.105)

Minimization of a sum of absolute values, i.e., minimization of the function (11.14) is another important generalized minimax problem. In this case, a smoothing function has the form

$$\displaystyle \begin{aligned} S({\boldsymbol x};\mu) & = F({\boldsymbol x}) \\ & ~~ + \mu \sum_{k=1}^m \log \left(\exp \left(-\frac{|f_k({\boldsymbol x})| - f_k^+({\boldsymbol x})}{\mu}\right) + \exp \left(-\frac{|f_k({\boldsymbol x})| - f_k^-({\boldsymbol x})}{\mu}\right)\right) \\ & = \sum_{k=1}^m |f_k({\boldsymbol x})| + \mu \sum_{k=1}^m \log \left(1 + \exp \left(-\frac{2 |f_k({\boldsymbol x})|}{\mu}\right)\right), \end{aligned} $$

because $f_k^+({\boldsymbol x}) = |f_k({\boldsymbol x})|$ if f _k(x) ≥ 0 and $f_k^-({\boldsymbol x}) = |f_k({\boldsymbol x})|$ if f _k(x) ≤ 0, and by Theorem 11.7 we have

$$\displaystyle \begin{aligned} \nabla S({\boldsymbol x};\mu) &= \sum_{k=1}^m ({\boldsymbol g}_k^+ u_k^+ + {\boldsymbol g}_k^- u_k^-) = \sum_{k=1}^m {\boldsymbol g}_k (u_k^+ - u_k^-) = \sum_{k=1}^m {\boldsymbol g}_k u_k = {\boldsymbol g}({\boldsymbol x};\mu),\\ \nabla^2 S({\boldsymbol x};\mu) & = \sum_{k=1}^m G_k (u_k^+ - u_k^-) +\frac{1}{\mu} \sum_{k=1}^m {\boldsymbol g}_k {\boldsymbol g}_k^T (u_k^+ + u_k^-) \\ & ~~ - \frac{1}{\mu} \sum_{k=1}^m {\boldsymbol g}_k {\boldsymbol g}_k^T (u_k^+ - u_k^-)^2 = G({\boldsymbol x};\mu) + \frac{1}{\mu} \sum_{k=1}^m {\boldsymbol g}_k {\boldsymbol g}_k^T (1 - u_k^2), \end{aligned} $$

(because $u_k^+ + u_k^- = 1$), where g _k = g _k(x),

$$\displaystyle \begin{aligned} \begin{array}{rcl} u_k &\displaystyle = &\displaystyle u_k^+ - u_k^- = \frac{\exp \left(-\frac{|f_k({\boldsymbol x})| - f_k^+({\boldsymbol x})}{\mu}\right) - \exp \left(-\frac{|f_k({\boldsymbol x})| - f_k^-({\boldsymbol x})}{\mu}\right)} {\exp \left(-\frac{|f_k({\boldsymbol x})| - f_k^+({\boldsymbol x})}{\mu}\right) + \exp \left(-\frac{|f_k({\boldsymbol x})| - f_k^-({\boldsymbol x})}{\mu}\right)} \\ &\displaystyle = &\displaystyle \frac{1 - \exp \left(-\frac{2 |f_k({\boldsymbol x})|}{\mu}\right)} {1 + \exp \left(-\frac{2 |f_k({\boldsymbol x})|}{\mu}\right)} \mathrm{sign}(f_k({\boldsymbol x})), \end{array} \end{aligned} $$

and

$$\displaystyle \begin{aligned} \begin{array}{rcl} 1 - u_k^2 = \frac{4 \exp \left(-\frac{2 |f_k({\boldsymbol x})|}{\mu}\right)}{\left(1 + \exp \left(-\frac{2 |f_k({\boldsymbol x})|}{\mu}\right)\right)^2}, \end{array} \end{aligned} $$

and where sign(f _k(x)) is a sign of a function f _k(x).

4 Primal-Dual Interior Point Methods

4.1 Basic Properties

Primal interior point methods for solving nonlinear programming problems profit from the simplicity of obtaining and keeping a point in the interior of the feasible set (for generalized minimax problems, it suffices to set z _k > F _k(x), 1 ≤ k ≤ m). Minimization of a barrier function without constraints and a direct computation of multipliers u _kl, 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, are basic features of these methods. Primal-dual interior point methods are intended for solving general nonlinear programming problems, where it is usually impossible to assure validity of constraints. These methods guarantee feasibility of points by adding slack variables, which appear in a barrier term added to the objective function. Positivity of the slack variables is assured algorithmically (by a step length selection). Minimization of a barrier function with equality constraints and an iterative computation of the Lagrange multipliers (dual variables) are the main features of primal-dual interior point methods.

Consider function (11.4). As is mentioned in the introduction, minimization of this function is equivalent to the nonlinear programming problem

$$\displaystyle \begin{aligned} \begin{cases} \text{minimize}\quad & \sum_{k=1}^m z_k \\ \text{subject to} & f_{kl}({\boldsymbol x}) \leq z_k, \quad 1 \leq k \leq m, \quad 1 \leq l \leq m_k. \end{cases} \end{aligned} $$

(11.106)

Using slack variables s _kl > 0, 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, and a barrier function

$$\displaystyle \begin{aligned} B_{\mu}({\boldsymbol x},{\boldsymbol z},{\boldsymbol s}) = \sum_{k=1}^m z_k - \mu \sum_{k=1}^m \sum_{l=1}^{m_k} \log(s_{kl}), {} \end{aligned} $$

(11.107)

a solving of the problem (11.106) can be transformed to a successive solving of problems

$$\displaystyle \begin{aligned} \begin{cases} \text{minimize}\quad & B_{\mu}({\boldsymbol x},{\boldsymbol z},{\boldsymbol s}) \\ \text{subject to} & f_{kl}({\boldsymbol x}) + s_{kl}- z_k = 0, \quad 1 \leq k \leq m, \quad 1 \leq l \leq m_k, \end{cases} \end{aligned} $$

(11.108)

where μ ↓ 0. Necessary conditions for an extremum of the problem (11.108) have the form

$$\displaystyle \begin{aligned} &{\boldsymbol g}({\boldsymbol x},{\boldsymbol u}) = \sum_{k=1}^m \sum_{l=1}^{m_k} {\boldsymbol g}_{kl}({\boldsymbol x}) u_{kl} = {\mathbf{0}}, \\ &1 - \sum_{l=1}^{m_k} u_{kl} = 0, \quad 1 \leq k \leq m,\\ &u_{kl} s_{kl} - \mu = 0, \quad 1 \leq k \leq m, \quad 1 \leq l \leq m_k,\\ &f_{kl}({\boldsymbol x}) + s_{kl}- z_k = 0, \quad 1 \leq k \leq m, \quad 1 \leq l \leq m_k, \end{aligned} $$

which is $n + m + 2 \bar {m}$ equations for $n + m + 2 \bar {m}$ unknowns (vectors x, z = [z _k], s = [s _kl], u = [u _kl], 1 ≤ k ≤ m, 1 ≤ l ≤ m _k), where $\bar {m} = m_1 + \dots + m_m$. Denote A(x) = [A ₁(x), …, A _m(x)], f = [f _kl], $S = \operatorname {\mathrm {diag}}[s_{kl}]$, $U = \operatorname {\mathrm {diag}}[u_{kl}]$, 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, and

(matrices A _k(x), vectors $\tilde {{\boldsymbol e}}_k$, and numbers z _k, 1 ≤ k ≤ m, are defined in Sect. 11.2.2). Applying the Newton method to this system of nonlinear equations, we obtain a system of linear equations for increments (direction vectors) Δx, Δz, Δs, Δu. After arrangement and elimination

$$\displaystyle \begin{aligned} \varDelta {\boldsymbol s} = - U^{-1} S ({\boldsymbol u} + \varDelta {\boldsymbol u}) + \mu S^{-1} \tilde{{\boldsymbol e}}, {} \end{aligned} $$

(11.109)

this system has the form

(11.110)

where $G({\boldsymbol x},{\boldsymbol u}) = \sum _{k=1}^m \sum _{l=1}^{m_k} G_{kl}({\boldsymbol x}) u_{kl}$. Vector $\tilde {{\boldsymbol e}}$ in the equation $\tilde {{\boldsymbol e}} - E^T {\boldsymbol u} = {\mathbf {0}}$ has unit elements, but its dimension is different from the dimension of a vector $\tilde {{\boldsymbol e}}$ in (11.109).

For solving this linear system, we cannot advantageously use the structure of a generalized minimax problem (because substituting $z_k = F_k({\boldsymbol x}) = \max _{1 \leq l \leq m_k} f_{kl}({\boldsymbol x})$ we would obtain a nonsmooth problem whose solution is much more difficult). Therefore, we need to deal with a general nonlinear programming problem. To simplify subsequent considerations, we use the notation $\tilde {{\boldsymbol x}} = [{\boldsymbol x}^T,{\boldsymbol z}^T]^T$,

(11.111)

and write (11.110) in the form

(11.112)

where ${\boldsymbol c}(\tilde {{\boldsymbol x}}) = {{\boldsymbol f}}({\boldsymbol x}) - E {\boldsymbol z}$. This system of equations is more advantageous against systems (11.49) and (11.93) in that its matrix does not depend on the barrier parameter μ, so it is not necessary to use a lower bound $\underline {\mu }$. On the other hand, system (11.112) has a dimension $n + m + \bar {m}$, while systems (11.49) and (11.93) have dimensions n. It would be possible to eliminate the vector Δu, so the resulting system

$$\displaystyle \begin{aligned} (\tilde{G}(\tilde{{\boldsymbol x}},{\boldsymbol u}) + \tilde{A}(\tilde{{\boldsymbol x}}) M^{-1} \tilde{A}^T(\tilde{{\boldsymbol x}})) \varDelta \tilde{{\boldsymbol x}} = -\tilde{{\boldsymbol g}}(\tilde{{\boldsymbol x}},{\boldsymbol u}) - \tilde{A}(\tilde{{\boldsymbol x}}) (M^{-1}{\boldsymbol c}(\tilde{{\boldsymbol x}}) + \mu S^{-1} \tilde{{\boldsymbol e}}), {} \end{aligned} $$

(11.113)

where M = U ⁻¹S, would have dimension n + m (i.e., n + 1 for classical minimax problems). Nevertheless, as follows from the equation u _kls _kl = μ, either u _kl ↓ 0 or s _kl ↓ 0 if μ ↓ 0, so some elements of a matrix M ⁻¹ may tend to infinity, which increases the condition number of system (11.113). Conversely, the solution of Eq. (11.112) is easier if the elements of a matrix M are small (if M = 0, we obtain the saddle point system, which can be solved by efficient iterative methods [1, 18]). Therefore, it is advantageous to split the constraints to active with $s_{kl} \leq \tilde {\varepsilon } u_{kl}$ (we denote active quantities by $\hat {{\boldsymbol c}}(\tilde {{\boldsymbol x}})$, $\hat {A}(\tilde {{\boldsymbol x}})$, $\hat {{\boldsymbol s}}$, $\varDelta \hat {{\boldsymbol s}}$, $\hat {S}$, $\hat {{\boldsymbol u}}$, $\varDelta \hat {{\boldsymbol u}}$, $\hat {U}$, $\hat {M} = \hat {U}^{-1} \hat {S}$) and inactive with $s_{kl} > \tilde {\varepsilon } u_{kl}$ (we denote inactive quantities by $\check {{\boldsymbol c}}(\tilde {{\boldsymbol x}})$, $\check {A}(\tilde {{\boldsymbol x}})$, $\check {{\boldsymbol s}}$, $\varDelta \check {{\boldsymbol s}}$, $\check {S}$, $\check {{\boldsymbol u}}$, $\varDelta \check {{\boldsymbol u}}$, $\check {U}$, $\check {M} = \check {U}^{-1} \check {S}$). Eliminating inactive equations from (11.112) we obtain

$$\displaystyle \begin{aligned} \varDelta \check{{\boldsymbol u}} = \check{M}^{-1} (\check{{\boldsymbol c}}(\tilde{{\boldsymbol x}}) + \check{A}(\tilde{{\boldsymbol x}})^T \varDelta \tilde{{\boldsymbol x}}) + \mu\check{S}^{-1} \tilde{{\boldsymbol e}} {} \end{aligned} $$

(11.114)

and

(11.115)

where

$$\displaystyle \begin{aligned} \begin{array}{rcl} \hat{G}(\tilde{{\boldsymbol x}},{\boldsymbol u}) &\displaystyle = &\displaystyle G(\tilde{{\boldsymbol x}},{\boldsymbol u}) + \check{A}(\tilde{{\boldsymbol x}}) \check{M}^{-1} \check{A}^T(\tilde{{\boldsymbol x}}), \\ \hat{{\boldsymbol g}}(\tilde{{\boldsymbol x}},{\boldsymbol u}) &\displaystyle = &\displaystyle {\boldsymbol g}(\tilde{{\boldsymbol x}},{\boldsymbol u}) + \check{A}(\tilde{{\boldsymbol x}}) (\check{M}^{-1} \check{{\boldsymbol c}}(\tilde{{\boldsymbol x}}) + \mu \check{S}^{-1} \tilde{{\boldsymbol e}}), \end{array} \end{aligned} $$

and $\hat {M} = \hat {U}^{-1} \hat {S}$ is a diagonal matrix of order $\hat {m}$, where $0 \leq \hat {m} \leq \bar {m}$ is the number of active constraints. Substituting (11.114) into (11.109) we can write

$$\displaystyle \begin{aligned} \varDelta \hat{{\boldsymbol s}} = -\hat{M} (\hat{{\boldsymbol u}} + \varDelta \hat{{\boldsymbol u}}) + \mu \hat{U}^{-1} \tilde{{\boldsymbol e}}, \quad \varDelta \check{{\boldsymbol s}} = -(\check{{\boldsymbol c}} + \check{A}^T \varDelta \tilde{{\boldsymbol x}} + \check{{\boldsymbol s}}). {} \end{aligned} $$

(11.116)

The matrix of the linear system (11.115) is symmetric, but indefinite, so its Choleski decomposition cannot be determined. In this case, we use either dense [3] or sparse [6] Bunch–Parlett decomposition for solving this system. System (11.115) (especially if it is large and sparse) can be efficiently solved by iterative conjugate gradient method with indefinite preconditioner [20]. If the vectors $\varDelta \tilde {{\boldsymbol x}}$ and $\varDelta \hat {{\boldsymbol u}}$ are solutions of system (11.115), we determine vector $\varDelta \check {{\boldsymbol u}}$ by (11.114) and vectors $\varDelta \hat {{\boldsymbol s}}$, $\varDelta \check {{\boldsymbol s}}$ by (11.116).

Having vectors $\varDelta \tilde {{\boldsymbol x}}$, Δs, Δu, we need to determine a step length α > 0 and set

$$\displaystyle \begin{aligned} \tilde{{\boldsymbol x}}_+ = \tilde{{\boldsymbol x}} + \alpha \varDelta \tilde{{\boldsymbol x}}, \quad {\boldsymbol s}_+ = {\boldsymbol s}(\alpha), \quad {\boldsymbol u}_+ = {\boldsymbol u}(\alpha), {} \end{aligned} $$

(11.117)

where s(α) and u(α) are vector functions such that s(α) > 0, s′(0) = Δs and u(α) > 0, u′(0) = Δu. This step is not trivial, because we need to decrease both the value of the barrier function $\tilde {B}_{\mu }(\tilde {{\boldsymbol x}},{\boldsymbol s}) = B_{\mu }({\boldsymbol x},{\boldsymbol z},{\boldsymbol s})$ and the norm of constraints $\|{\boldsymbol c}(\tilde {{\boldsymbol x}})\|$, and also to assure positivity of vectors s and u. We can do this in several different ways: using either the augmented Lagrange function [20, 21] or a bi-criterial filter [9, 29] or a special algorithm [11, 16]. In this section, we confine our attention to the augmented Lagrange function which has (for the problem (11.106)) the form

$$\displaystyle \begin{aligned} \begin{array}{rcl} P(\alpha) = \tilde{B}_{\mu}(\tilde{{\boldsymbol x}} + \alpha \varDelta \tilde{{\boldsymbol x}}, {\boldsymbol s}(\alpha)) &\displaystyle + &\displaystyle ({\boldsymbol u} + \varDelta {\boldsymbol u})^T ({\boldsymbol c}(\tilde{{\boldsymbol x}} + \alpha \varDelta \tilde{{\boldsymbol x}}) + {\boldsymbol s}(\alpha)) \\ &\displaystyle + &\displaystyle \frac{\sigma}{2} \|{\boldsymbol c}(\tilde{{\boldsymbol x}} + \alpha \varDelta \tilde{{\boldsymbol x}}) + {\boldsymbol s}(\alpha)\|{}^2, {} \end{array} \end{aligned} $$

(11.118)

where σ ≥ 0 is a penalty parameter. The following theorem, whose proof is given in [20], holds.

Theorem 11.10

Lets > 0,u > 0 and let vectors $\varDelta \tilde {{\boldsymbol x}}$, $\varDelta \hat {{\boldsymbol u}}$be solutions of the linear system

(11.119)

whererand $\hat {{\boldsymbol r}}$are residual vectors, and let vectors $\varDelta \check {{\boldsymbol u}}$and Δsbe determined by (11.114) and (11.116). Then

$$\displaystyle \begin{aligned} \begin{array}{rcl} P'(0) = -(\varDelta \tilde{{\boldsymbol x}})^T \tilde{G}(\tilde{{\boldsymbol x}},{\boldsymbol u}) \varDelta \tilde{{\boldsymbol x}} &\displaystyle - &\displaystyle (\varDelta {\boldsymbol s})^T M^{-1} \varDelta {\boldsymbol s} - \sigma \|{\boldsymbol c}(\tilde{{\boldsymbol x}}) + {\boldsymbol s}\|{}^2 \\ &\displaystyle + &\displaystyle (\varDelta \tilde{{\boldsymbol x}})^T {\boldsymbol r} + \sigma (\hat{{\boldsymbol c}}(\tilde{{\boldsymbol x}}) + \hat{{\boldsymbol s}})^T \hat{{\boldsymbol r}}. {} \end{array} \end{aligned} $$

(11.120)

If

$$\displaystyle \begin{aligned} \sigma > - \frac{(\varDelta \tilde{{\boldsymbol x}})^T \tilde{G}(\tilde{{\boldsymbol x}},{\boldsymbol u}) \varDelta \tilde{{\boldsymbol x}} + (\varDelta {\boldsymbol s})^T M^{-1} \varDelta {\boldsymbol s}} {\|{\boldsymbol c}(\tilde{{\boldsymbol x}}) + {\boldsymbol s}\|{}^2} {} \end{aligned} $$

(11.121)

and if system (11.115) is solved in such a way that

$$\displaystyle \begin{aligned} (\varDelta \tilde{{\boldsymbol x}})^T {\boldsymbol r} {+}\, \sigma (\hat{{\boldsymbol c}}(\tilde{{\boldsymbol x}}) {+}\, \hat{{\boldsymbol s}})^T \hat{{\boldsymbol r}} < (\varDelta \tilde{{\boldsymbol x}})^T \tilde{G}(\tilde{{\boldsymbol x}},{\boldsymbol u}) \varDelta \tilde{{\boldsymbol x}} + (\varDelta {\boldsymbol s})^T M^{-1} \varDelta {\boldsymbol s} {+}\, \sigma (\|{\boldsymbol c}(\tilde{{\boldsymbol x}}) {+} {\boldsymbol s}\|{}^2), {} \end{aligned} $$

(11.122)

then P′(0) < 0.

Inequality (11.122) is significant only if linear system (11.115) is solved iteratively and residual vectors r and $\hat {{\boldsymbol r}}$ are nonzero. If these vectors are zero, then (11.122) follows immediately from (11.121). Inequality (11.121) serves for determination of a penalty parameter, which should be as small as possible. If the matrix $\tilde {G}(\tilde {{\boldsymbol x}},{\boldsymbol u})$ is positive semidefinite, then the right-hand side of (11.121) is negative and we can choose σ = 0.

4.2 Implementation

The algorithm of the primal-dual interior point method consists of four basic parts: determination of the matrix G(x, u) or its approximation, solving linear system (11.115), a step length selection, and an update of the barrier parameter μ. The matrix G(x, u) has form (11.33), so its approximation can be determined in the one of the ways introduced in Remark 11.13.

The linear system (11.115), obtained by determination and subsequent elimination of inactive constraints in the way described in the previous subsection, is solved either directly using the Bunch–Parlett decomposition or iteratively by the conjugate gradient method with the indefinite preconditioner

(11.123)

where $\hat {D}$ is a positive definite diagonal matrix that approximates matrix $\hat {G}(\tilde {{\boldsymbol x}},{\boldsymbol u})$. An iterative process is terminated if residual vectors satisfy conditions (11.122) and

$$\displaystyle \begin{aligned}\|{\boldsymbol r}\| \leq \omega \|\tilde{{\boldsymbol g}}(\tilde{{\boldsymbol x}},{\boldsymbol u})\|, \quad \|\hat{{\boldsymbol r}}\| \leq \omega \min\{\|\hat{{\boldsymbol c}}(\tilde{{\boldsymbol x}}) + \mu \hat{U}^{-1} \tilde{{\boldsymbol e}}\|, \|\hat{{\boldsymbol c}}(\tilde{{\boldsymbol x}}) + \hat{{\boldsymbol s}}\|\},\end{aligned} $$

where 0 < ω < 1 is a prescribed precision. The directional derivative P′(0) given by (11.118) should be negative. There are two possibilities how this requirement can be achieved. We either determine the value σ ≥ 0 satisfying inequality (11.121), which implies P′(0) < 0 if (11.122) holds (Theorem 11.10), or set σ = 0 and ignore inequality (11.122). If P′(0) ≥ 0, we determine a diagonal matrix $\tilde {D}$ with elements

$$\displaystyle \begin{aligned} \begin{cases} \tilde{D}_{jj} = \underline{\varGamma}, & \quad \mbox{if} \quad \frac{\| \tilde{{\boldsymbol g}} \|}{10} | \tilde{G}_{jj} | < \underline{\varGamma}, \\ \tilde{D}_{jj} = \frac{\| \tilde{{\boldsymbol g}} \|}{10} | \tilde{G}_{jj} |, & \quad \mbox{if} \quad \underline{\varGamma} \leq \frac{\| \tilde{{\boldsymbol g}} \|}{10} | \tilde{G}_{jj} | \leq \overline{\varGamma}, \\ \tilde{D}_{jj} = \overline{\varGamma}, & \quad \mbox{if} \quad \overline{\varGamma} < \frac{\| \tilde{{\boldsymbol g}} \|}{10} | \tilde{G}_{jj} |, \end{cases}\end{aligned} $$

(11.124)

for 1 ≤ j ≤ n + m, where $\tilde {{\boldsymbol g}} = \tilde {{\boldsymbol g}}(\tilde {{\boldsymbol x}},{\boldsymbol u})$ and $0 < \underline {\varGamma } < \overline {\varGamma }$, set $\tilde {G}(\tilde {{\boldsymbol x}},{\boldsymbol u}) = \tilde {D}$ and restart the iterative process by solving new linear system (11.115).

We use functions s(α) = [s _kl(α)], u(α) = [u _kl(α)], where $s_{kl}(\alpha ) = s_{kl} + \alpha _{s_{kl}} \varDelta s_{kl}$, $u_{kl}(\alpha ) = u_{kl} + \alpha _{u_{kl}} \varDelta u_{kl}$ and

$$\displaystyle \begin{aligned} \begin{cases} \alpha_{s_{kl}} = \alpha, & \quad \mbox{if} \quad \varDelta s_{kl} \geq 0, \\ \alpha_{s{kl}} = \min \{\alpha, -\gamma \frac{s_{kl}}{\varDelta s_{kl}}\}, & \quad \mbox{if} \quad \varDelta s_{kl} < 0, \\ \alpha_{u_{kl}} = \alpha, & \quad \mbox{if} \quad \varDelta u_{kl} \geq 0,\\ \alpha_{u_{kl}} = \min \{\alpha, -\gamma \frac{u_{kl}}{\varDelta u_{kl}}\}, & \quad \mbox{if} \quad \varDelta u_{kl} < 0 \end{cases}\end{aligned} $$

when choosing a step length using the augmented Lagrange function. A parameter 0 < γ < 1 (usually γ = 0.99) assures the positivity of vectors s ₊ and u ₊ in (11.117). A parameter α > 0 is chosen to satisfy the inequality P(α) − P(0) ≤ ε ₁αP′(0), which is possible because P′(0) < 0 and a function P(α) is continuous.

After finishing the iterative step, a barrier parameter μ should be updated. There exist several heuristic procedures for this purpose. The following procedure proposed in [28] seems to be very efficient.

Procedure C

• Compute the centrality measure

  $$\displaystyle \begin{aligned}\varrho = \frac{\bar{m} \, \min_{kl}\{s_{kl} u_{kl}\}}{{\boldsymbol s}^T {\boldsymbol u}},\end{aligned}$$

  where $\bar {m} = m_1 + \dots + m_m$ and 1 ≤ k ≤ m, 1 ≤ l ≤ m _k. Compute the value

  $$\displaystyle \begin{aligned}\lambda = 0.1 \min\left\{0.05 \frac{1 - \varrho}{\varrho}, 2\right\}^3\end{aligned}$$

  and set $\mu = \lambda {\boldsymbol s}^T {\boldsymbol u} / \bar {m}$.

The considerations up to now are summarized in Algorithm 11.3 introduced in the Appendix.

5 Numerical Experiments

The methods studied in this contribution were tested by using two collections of test problems TEST14 and TEST15 described in [19], which are the parts of the UFO system [24] and can be downloaded from the web-page www.cs.cas.cz/luksan/test.html. Both these collections contain 22 problems with functions f _k(x), 1 ≤ k ≤ m, ${\boldsymbol x} \in \mathbb {R}^n$, where n is an input parameter and m ≥ n depends on n (we have used the values n = 100 and n = 1000 for numerical experiments). Functions f _k(x), 1 ≤ k ≤ m, have a sparse structure (the Jacobian matrix of a mapping f(x) is sparse), so sparse matrix decompositions can be used for solving linear equation systems.

The tested methods, whose results are reported in Tables 11.1, 11.2, 11.3, 11.4, and 11.5 introduced in the Appendix, are denoted by five letters. The first pair of letters gives the problem type: either a classical minimax MX (when a function F(x) has form (11.10) or F(x) = ∥f(x)∥_∞ holds) or a sum of absolute values SA (when F(x) = ∥f(x)∥₁ holds). Further two letters specify the method used:

PI :

–the primal interior point method (Sect. 11.2),

Table 11.1 TEST14 (minimization of maxima) — 22 problems

Table 11.2 TEST14 (L _∞-approximation) — 22 problems

Table 11.3 TEST15 (L _∞-approximation) — 22 problems

Table 11.4 TEST14 (L ₁-approximation) — 22 problems

Table 11.5 TEST15 (L ₁-approximation) — 22 problems

SM :

–the smoothing method (Sect. 11.3),

DI :

–the primal-dual interior point method (Sect. 11.4).

The last letter denotes the procedure for updating a barrier parameter μ (procedures A and B are described in Sect. 11.2.4 and procedure C is described in Sect. 11.4.2).

The columns of all tables correspond to two classes of methods. The Newton methods use approximations of the Hessian matrices of the Lagrange function obtained by gradient differences [4] and variable metric methods update approximations of the Hessian matrices of the partial functions by the methods belonging to the Broyden family [12] (Remark 11.13).

The tables contain total numbers of iterations NIT, function evaluations NFV, gradient evaluations NFG, and also the total computational time, the number of problems with the value $\overline {\varDelta }$ decreased and the number of failures (the number of unsolved problems). The decrease of the maximum step length $\overline {\varDelta }$ is used for three reasons. First, too large steps may lead to overflows if arguments of functions (roots, logarithms, exponentials) lie outside of their definition domain. Second, the change of $\overline {\varDelta }$ can affect the finding of a suitable (usually global) minimum. Finally, it can prevent from achieving a domain in which the objective function has bad behavior leading to a loss of convergence. The number of times the step length has decreased is in some sense a symptom of robustness (a lower number corresponds to higher robustness).

Several conclusions can be done from the results stated in these tables.

• The smoothing methods are less efficient than the primal interior point methods. For testing the smoothing methods, we had to use the value $\underline {\mu } = 10^{-6}$, while the primal interior methods work well with the smaller value $\underline {\mu } = 10^{-8}$, which gives more precise results.

• The primal-dual interior point methods are slower than the primal interior point methods, especially for the reason that system of equations (11.115) is indefinite, so we cannot use the Choleski (or the Gill–Murray [10]) decomposition. If the matrix of linear system (11.115) is large and sparse, we can use the Bunch–Parlett decomposition [6]. In this case, a large fill-in of new nonzero elements (and thus to overflow of the operational memory or large extension of the computational time) may appear. In this case, we can also use the iterative conjugate gradient method with an indefinite preconditioner [18], however, the ill-conditioned systems can require a large number of iterations and thus a large computational time.

• It cannot be uniquely decided whether Procedure A is better than Procedure B. The Newton methods usually work better with Procedure A while the variable metric methods are more efficient with Procedure B.

• The variable metric methods are usually faster because it is not necessary to determine the elements of the Hessian matrix of the Lagrange function by gradient differences. The Newton methods seem to be more robust (especially in case of L ₁-approximation).

Appendix

Algorithm 11.1: Primal interior point method

________________________

 

Data::

A tolerance for the gradient norm of the Lagrange function $\underline {\varepsilon } > 0$. A precision for determination of a minimax vector $\underline {\delta } > 0$. Bounds for a barrier parameter $0 < \underline {\mu } < \overline {\mu }$. Coefficients for decrease of a barrier parameter 0 < λ < 1, σ > 1 (or 0 < 𝜗 < 1). A tolerance for a uniform descent ε ₀ > 0. A tolerance for a step length selection ε ₁ > 0. A maximum step length $\overline {\varDelta } > 0$.

Input.:

A sparsity pattern of the matrix A(x) = [A ₁(x), …, A _m(x)]. A starting point ${\boldsymbol x} \in \mathbb {R}^n$.

Step 1.:

(Initiation) Choose $\mu \leq \overline {\mu }$. Determine a sparse structure of the matrix W = W(x;μ) from the sparse structure of the matrix A(x) and perform a symbolic decomposition of the matrix W (described in [2, Section 1.7.4]). Compute values f _kl(x), 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, values $F_k({\boldsymbol x}) = \max _{1 \leq l \leq m_k} f_{kl}({\boldsymbol x})$, 1 ≤ k ≤ m, and the value of objective function (11.4). Set r = 0 (restart indicator).

Step 2.:

(Termination) Solve nonlinear equations (11.44) with precision $\underline {\delta }$ to obtain a minimax vector z(x;μ) and a vector of Lagrange multipliers u(x;μ). Determine a matrix A = A(x) and a vector g = g(x;μ) = A(x)u(x;μ). If $\mu \leq \underline {\mu }$ and $\|{\boldsymbol g}\| \leq \underline {\varepsilon }$, terminate the computation.

Step 3.:

(Hessian matrix approximation) Set G = G(x;μ) or compute an approximation G of the Hessian matrix G(x;μ) using gradient differences or using quasi-Newton updates (Remark 11.13).

Step 4.:

(Direction determination) Determine a matrix $\nabla ^2 \hat {B}({\boldsymbol x}; \mu )$ by (11.48) and a vector Δx by solving Eq. (11.49) with the right-hand side defined by (11.47).

Step 5.:

(Restart) If r = 0 and (11.54) does not hold, set G = I, r = 1 and go to Step 4. If r = 1 and (11.54) does not hold, set Δx = −g. Set r = 0.

Step 6.:

(Step length selection) Determine a step length α > 0 satisfying inequalities (11.55) (for a barrier function $\hat {B}({\boldsymbol x}; \mu )$ defined by (11.46)) and $\alpha \leq \overline {\varDelta }/\|\varDelta {\boldsymbol x}\|$. Note that nonlinear equations (11.44) are solved at the point x + αΔx. Set x := x + αΔx. Compute values f _kl(x), 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, values $F_k({\boldsymbol x}) = \max _{1 \leq l \leq m_k} f_{kl}({\boldsymbol x})$, 1 ≤ k ≤ m, and the value of objective function (11.4).

Step 7.:

(Barrier parameter update) Determine a new value of a barrier parameter $\mu \geq \underline {\mu }$ using Procedure A or Procedure B. Go to Step 2.

The values $\underline {\varepsilon } = 10^{-6}$, $\underline {\delta } = 10^{-6}$, $\underline {\mu } = 10^{-8}$, $\overline {\mu } = 1$, λ = 0.85, σ = 100, 𝜗 = 0.1, ε ₀ = 10⁻⁸, ε ₁ = 10⁻⁴, and $\overline {\varDelta } = 1000$ were used in our numerical experiments.

Algorithm 11.2: Smoothing method

________________________________

 

Data::

A tolerance for the gradient norm of the smoothing function $\underline {\varepsilon } > 0$. Bounds for a smoothing parameter $0 < \underline {\mu } < \overline {\mu }$. Coefficients for decrease of a smoothing parameter 0 < λ < 1, σ > 1 (or 0 < 𝜗 < 1). A tolerance for a uniform descent ε ₀ > 0. A tolerance for a step length selection ε ₁ > 0. A maximum step length $\overline {\varDelta } > 0$.

Input.:

A sparsity pattern of the matrix A(x) = [A ₁(x), …, A _m(x)]. A starting point ${\boldsymbol x} \in \mathbb {R}^n$.

Step 1.:

(Initiation) Choose $\mu \leq \overline {\mu }$. Determine a sparse structure of the matrix W = W(x;μ) from the sparse structure of the matrix A(x) and perform a symbolic decomposition of the matrix W (described in [2, Section 1.7.4]). Compute values f _kl(x), 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, values $F_k({\boldsymbol x}) = \max _{1 \leq l \leq m_k} f_{kl}({\boldsymbol x})$, 1 ≤ k ≤ m, and the value of objective function (11.4). Set r = 0 (restart indicator).

Step 2.:

(Termination) Determine a vector of smoothing multipliers u(x;μ) by (11.87). Determine a matrix A = A(x) and a vector g = g(x;μ) = A(x)u(x;μ). If $\mu \leq \underline {\mu }$ and $\|{\boldsymbol g}\| \leq \underline {\varepsilon }$, terminate the computation.

Step 3.:

(Hessian matrix approximation) Set G = G(x;μ) or compute an approximation G of the Hessian matrix G(x;μ) using gradient differences or using quasi-Newton updates (Remark 11.13).

Step 4.:

(Direction determination) Determine the matrix W by (11.94) and the vector Δx by (11.93) using the Gill–Murray decomposition of the matrix W.

Step 5.:

(Restart) If r = 0 and (11.54) does not hold, set G = I, r = 1 and go to Step 4. If r = 1 and (11.54) does not hold, set Δx = −g. Set r = 0.

Step 6.:

(Step length selection) Determine a step length α > 0 satisfying inequalities (11.55) (for a smoothing function S(x;μ)) and $\alpha = \overline {\varDelta }/\|\varDelta {\boldsymbol x}\|$. Set x := x + αΔx. Compute values f _kl(x), 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, values $F_k({\boldsymbol x}) = \max _{1 \leq l \leq m_k} f_{kl}({\boldsymbol x})$, 1 ≤ k ≤ m, and the value of the objective function (11.4).

Step 7.:

(Smoothing parameter update) Determine a new value of the smoothing parameter $\mu \geq \underline {\mu }$ using Procedure A or Procedure B. Go to Step 2.

The values $\underline {\varepsilon } = 10^{-6}$, $\underline {\mu } = 10^{-6}$, $\overline {\mu } = 1$, λ = 0.85, σ = 100, 𝜗 = 0.1, ε ₀ = 10⁻⁸, ε ₁ = 10⁻⁴, and $\overline {\varDelta } = 1000$ were used in our numerical experiments.

Algorithm 11.3: Primal-dual interior point method

___________________

Data::

A tolerance for the gradient norm $\underline {\varepsilon } > 0$. A parameter for determination of active constraints $\tilde {\varepsilon } > 0$. A parameter for initiation of slack variables and Lagrange multipliers δ > 0. An initial value of the barrier parameter $\overline {\mu } > 0$. A precision for the direction determination 0 ≤ ω < 1. A parameter for the step length selection 0 < γ < 1. A tolerance for the step length selection ε ₁ > 0. Maximum step length $\overline {\varDelta } > 0$.

Input.:

A sparsity pattern of the matrix A(x) = [A ₁(x), …, A _m(x)]. A starting point ${\boldsymbol x} \in \mathbb {R}^n$.

Step 1.:

(Initialization) Compute values f _kl(x), 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, and set $F_k({\boldsymbol x}) = \max _{1 \leq l \leq m_k} f_{kl}({\boldsymbol x})$, z _k = F _k(x) + δ, 1 ≤ k ≤ m. Compute values $c_{kl}(\tilde {{\boldsymbol x}}) = f_{kl}({\boldsymbol x}) - z_k$, and set $s_{kl} = -c_{kl}(\tilde {{\boldsymbol x}})$, u _kl = δ. Set $\mu = \overline {\mu }$ and compute the value of the barrier function $\tilde {B}_{\mu }(\tilde {{\boldsymbol x}},{\boldsymbol s})$.

Step 2.:

(Termination) Determine a matrix $\tilde {A}(\tilde {{\boldsymbol x}})$ and a vector $\tilde {{\boldsymbol g}}(\tilde {{\boldsymbol x}},{\boldsymbol u}) = \tilde {A}(\tilde {{\boldsymbol x}}) {\boldsymbol u}$ by (11.111). If the KKT conditions $\|\tilde {{\boldsymbol g}}(\tilde {{\boldsymbol x}},{\boldsymbol u})\| \leq \underline {\varepsilon }$, $\|{\boldsymbol c}(\tilde {{\boldsymbol x}}) + {\boldsymbol s}\| \leq \underline {\varepsilon }$, and ${\boldsymbol s}^T {\boldsymbol u} \leq \underline {\varepsilon }$ are satisfied, terminate the computation.

Step 3.:

(Hessian matrix approximation) Set G = G(x, u) or compute an approximation G of the Hessian matrix G(x, u) using gradient differences or utilizing quasi-Newton updates (Remark 11.13). Determine a parameter σ ≥ 0 by (11.121) or set σ = 0. Split the constraints into active if $\hat {s}_{kl} \leq \tilde {\varepsilon } \hat {u}_{kl}$ and inactive if $\check {s}_{kl} > \tilde {\varepsilon } \check {u}_{kl}$.

Step 4.:

(Direction determination) Determine the matrix $\tilde {G} = \tilde {G}(\tilde {{\boldsymbol x}},{\boldsymbol u})$ by (11.111) (where the Hessian matrix G(x, u) is replaced with its approximation G). Determine vectors $\varDelta \tilde {{\boldsymbol x}}$ and $\varDelta \hat {{\boldsymbol u}}$ by solving linear system (11.115), a vector $\varDelta \check {{\boldsymbol u}}$ by (11.114), and a vector Δs by (11.116). Linear system (11.115) is solved either directly using the Bunch–Parlett decomposition (we carry out both the symbolic and the numeric decompositions in this step) or iteratively by the conjugate gradient method with indefinite preconditioner (11.123). Compute the derivative of the augmented Lagrange function by formula (11.120).

Step 5.:

(Restart) If P′(0) ≥ 0, determine a diagonal matrix $\tilde {D}$ by (11.124), set $\tilde {G} = \tilde {D}$, σ = 0, and go to Step 4.

Step 6.:

(Step length selection) Determine a step length parameter α > 0 satisfying inequalities P(α) − P(0) ≤ ε ₁αP′(0) and $\alpha \leq \overline {\varDelta }/\|\varDelta {\boldsymbol x}\|$. Determine new vectors $\tilde {{\boldsymbol x}} := \tilde {{\boldsymbol x}} + \alpha \varDelta \tilde {{\boldsymbol x}}$, s := s(α), u := u(α) by (11.117). Compute values f _kl(x), 1 ≤ k ≤ m, 1 ≤ l ≤ m _k, and set $c_{kl}(\tilde {{\boldsymbol x}}) = f_{kl}({\boldsymbol x}) - z_k$, 1 ≤ k ≤ m, 1 ≤ l ≤ m _k. Compute the value of the barrier function $\tilde {B}_{\mu }(\tilde {{\boldsymbol x}},{\boldsymbol s})$.

Step 7.:

(Barrier parameter update) Determine a new value of the barrier parameter $\mu \geq \underline {\mu }$ using Procedure C. Go to Step 2.

The values $\underline {\varepsilon } = 10^{-6}$, $\tilde {\varepsilon } = 0.1$, δ = 0.1, ω = 0.9, γ = 0.99, $\overline {\mu } = 1$, ε ₁ = 10⁻⁴, and $\overline {\varDelta } = 1000$ were used in our numerical experiments.