Patterning as a Mathematical Activity: An Analysis of Young Children’s Strategies When Working with Repeating Patterns

Abstract

In both educational and research settings on repeating patterns, the focus seems to be put more on the product (i.e., the correct solution) than on the process (i.e., the strategies children employ in solving a patterning task). This chapter explores different patterning strategies and strategy use in early childhood and reflects on selected patterning tasks from a strategy point of view. One hundred and fifty-nine 3- to 5-year-old children were interviewed while working on various patterning tasks, and their strategies were coded into five strategy categories and quantified. Results show that young children use a variety of different patterning strategies, with the older children using more advanced strategies more often. When considering the mathematical structure of repeating patterns, it becomes apparent that most young children approach patterning activities without referring to or using the unit of repeat.

1 Introduction

It is at the heart of mathematics education that it is not all about the right solution but about the way a solution is found. We clearly differentiate strategies in arithmetic and look at HOW children solve a task (CCSSI, 2010; Houlihan & Ginsburg, 1981). It is part of a sound mathematical diagnostic to not only survey if a child can solve a task like 8 + 6 correctly, but also to analyze if the child solves it by counting or maybe by using the law of constancy as 7 + 7 (DEET, 2001). In general, we try to guide children’s learning from their informal (counting-)strategies to more advanced, formal strategies (Sarama & Clements, 2009).

For repeating patterning activities, which are part of preschool and primary school curricula in many countries, strategies do not seem to be considered as relevant, yet (NCTM, 2013; Sekretariat der Ständigen Konferenz der Kultusminister der Länder in der Bundesrepublik Deutschland, 2005). Recent psychology-based research on young children’s patterning competencies mainly focuses on correct solution frequencies or error types (Rittle-Johnson, Fyfe, McLean, & McEldoon, 2013). The relation between patterning skills (measured by correct performance) and early mathematic knowledge/arithmetic achievement is measured and quantified (Lee, Ng, Bull, Pe, & Ho, 2011; Ngyen et al., 2016; Warren & Miller, 2013), and patterning skills are related to both working memory and relational knowledge (Fyfe, Evans, Eisenband Matz, Hunt, & Alibali, 2017; Miller, Rittle-Johnson, Loehr, & Fyfe, 2016). Intervention studies show effects of teaching patterning on children’s arithmetic skills (Kidd et al., 2013, 2014; Pasnak et al., 2015). In summary, pattern knowledge seems to be significant for children’s mathematical development. But why? Specifically: What is the mathematics in a repeating pattern? How are patterning activities mathematically important? And why is looking at children’s patterning strategies worthwhile?

To address these questions, the chapter first considers the mathematical foundation of repeating patterns and how it relates to other mathematical contents in primary and secondary school. Second, research studies on young children’s patterning strategies are reviewed, and five strategy categories which are the basis of this chapter’s data analysis are introduced. The empirical study that is the subject of this chapter, then, explores how young children address patterning activities in different mathematical and nonmathematical approaches and how these strategies develop with age. Finally, selected activities are evaluated with regard to their potential to elicit strategies that address the pattern’s mathematical structure.

2 Repeating Patterns and Mathematics

A repeating pattern is a periodic sequence of elements that can be reduced to a smallest subset—the unit of repeat—which is repeated in the form of a geometric translation and, thus, creates the repeating pattern. Repeating patterns, therefore, have a cyclic structure (Liljedahl, 2004). Based on this definition, a mathematical approach to a patterning activity would be the recognition and use of the pattern’s structure, i.e., the unit of repeat and its cyclic repetition.

A lot of mathematical topics in primary and secondary school are based on this same or a very similar structure. To show this, I will take three different perspectives on the repeating pattern’s structure.

First, from a geometric mapping point of view, I interpret the unit of repeat as a basic figure. Every congruence mapping then shares the same idea: a basic figure is multiplied by a mapping with certain specifications. Frieze patterns and tessellations contain a basic figure that is repeated (like in the simpler repeating patterns) by a geometric translation. Furthermore, in axially symmetrical and rotationally symmetrical figures, a basic figure can be found; only the mapping specifications are different.

As a second approach, the unit of repeat is interpreted cardinally as a unit of the same size. This structure forms the basis of every base ten number representation, like the ten- or twenty-frame or the hundred-abacus. Other examples of this structure are multiplication as addition of equal parts, or analog, division as partitioning in equal units. Furthermore, understanding the repetition of a unit is the basic idea of measuring, and even the concept of fraction as part whole is based on the comprehension of partitioning a whole into equal parts.

My third perspective focuses on the periodicity of repeating patterns. The experience of a regularly recurring sequence can be made in the sequence of unit digits of any arithmetic sequence; for example, when counting in steps by fives (5, 10, 15, 20, 25 …) the ones digit alternates. The simplest and in daily life most often used example might be the sequence of digits in our decimal system that recur from 0 to 9 through every place. The decimal expansion of rational numbers is nothing else than a repeating pattern, in which the unit of repeat is even explicitly marked (e.g., 11/37 = 0,297297297297… = 0,$\overline{297}$). Finally, one might consider the periodicity of trigonometric functions (sin(x), cos(x)).

Although the examples given above are only exemplary illustrations, they clearly show that the basic concept of repeating patterns underlies a lot of other mathematical contents up to secondary school. Therefore, activities that help children recognize a repeating pattern’s structure may support laying a foundation for an understanding of other mathematical topics.

3 Patterning Strategies

There are few studies that specifically look at the process of solving patterning tasks, the way children think about repeating patterns, and the strategies they employ. Three of these studies are described in the following; all three interviewed children aged 3–5 on various patterning tasks.

Rustigian (1976) might have been the first who—under a problem-solving approach—described “response techniques” (p. 189) which children employed in the course of working on the three patterning tasks reproduction (copy with the model pattern in view while child responds), identification (select a structurally identical pattern), and extension (continue the pattern to one side). Her techniques are specific to the task and describe in detail the children’s approach to finding a solution. Six different techniques are listed for both the activities reproduce and extend. Both category lists start with a random and end with a correct placement technique. In the categories in between, children’s responses, on the one hand, focus only on relationships of similarity, for example, repeating a single element of the given sequence. On the other hand, children’s responses focus on relationships of similarity and difference. Developmental hierarchies are suggested for the reproduction and the extension techniques.

Papic, Mulligan, and Mitchelmore (2011) in their study used similar and additional patterning tasks (copy with and without the model pattern being in view, create, explain, extend). They did not only describe task-specific strategies but formulated five main categories in which the children’s solution strategies fell into. Papic et al. (2011) suggested that their strategy categories have an increasing order of sophistication, starting, similar to Rustigian (1976), with strategies where children choose and place elements randomly (random arrangement). Strategies that match items one-by-one were frequently observed and make up the category direct comparison. The most common strategy in this study was alternation, where children focus on the sequence of individual colors. For strategies in the fourth category, children are able to identify and use the unit of repeat (basic unit of repeat). Strategies where children demonstrate and express simple generalizations about the unit of repeat were sorted into the most sophisticated category advanced unit of repeat.

In the most recent study on patterning strategies, Collins and Laski (2015) suggested that patterning tasks can be solved using either a one-to-one appearance matching strategy or a relational similarity strategy. For a one-to-one appearance matching strategy, children match superficial features without considering the pattern’s underlying structure, e.g., copy a pattern by matching the color or shape of each item in the pattern, one at a time. In order to mentally represent, abstract, and manipulate the unit of repeat, relational similarity strategies are required. The children in Collins and Laski’s (2015) study also used strategies where elements are placed randomly, sorted by color or shape, or used for building. This third strategy category is called off-task errors.

In an effort to bring the findings of the different studies together and systematically investigate patterning strategies for a variety of patterning tasks, I conducted a longitudinal study describing the development of six children’s repeating patterning strategies during their three years of Kindergarten (see Lüken, 2018). The observed patterning strategies could be assigned to five superordinate categories. As these strategy categories form the basis for this chapter’s analyses, they are further explicated:

• 1. The first, most basic strategy category is called no reference to pattern besides reproduction of the pattern’s gestalt. All strategies where children choose elements based on guessing, personal preference, or random selection belong to this category. A common example is using different colors or shapes than those represented in the pattern while copying or extending a pattern. General characteristics of this category’s strategies are that they refer neither to the specific features of the elements nor to the regularity of the pattern. Still, most children will arrange the pattern’s objects in a line, thus recognizing the linear arrangement. Their general perception seems to focus on the external shape. Put simply, two patterns are the same if they have the same shape or form (i.e., gestalt).

• 2. In the second strategy category, attention to singular characteristics, children’s strategies show an understanding of singular aspects of the pattern. For example, they use either the same colors or the same shapes as in the pattern, or they purposely recreate the same length. However, they do not recreate the pattern’s structure. Little regularity can be found in the children’s patterns altogether. The general view on patterns seems to be: Two patterns are the same if they consist of the same elements (e.g., colors).

• 3. The idea of regularity initially becomes visible in the third strategy category comparison & classification. Children compare the pattern’s elements and highlight sameness within and between patterns on a basic, very concrete level (e.g., “The yellows are the same.”; “Three purples and six blacks here. Three yellows and six oranges here.”). A common strategy for extending a pattern is to look at the pattern’s beginning, and to compare and match the extension step by step with the beginning. This procedure shows an emerging sense for some kind of regularity within the pattern, although the specific regularity is not yet graspable for the child.

• 4. The growing awareness of regularity within the pattern can be observed in the strategies that belong to the fourth strategy category focus on sequence. The strategies focus on the relations between successive elements of the pattern, e.g., “Next to green is purple, next to purple is orange, next to orange is green, next to green is purple, next to purple ….” Other typical strategies for this category are alternating colors or cycling through the elements of the pattern over and over again, even chanting them rhythmically. The children are aware that the elements are ordered in a regular way, without explicitly grasping the structure. The elements of the pattern are rather seen as strung together. Children are not yet able to break the pattern down into the units of repeat.

• 5. In the last, most advanced strategy category, view ofunit of repeat, the strategies show the children’s understanding of the pattern’s structure. The children know that there is a smallest part that produces the sequence—they are able to identify this unit of repeat and use it during the tasks.

When we now look at these strategies which children employ when solving a patterning task, not all of them refer to the repeating pattern’s structure. Only the strategies in the fifth category make use of the pattern’s mathematical structure, the unit of repeat, and its repetition. Still, other mathematical approaches become visible in some of the other strategy categories. In category 3, children compare and classify, some even enumerate the number of different objects. These are basic mathematical activities. The strategies in the fourth category show the use and understanding of regularity and succession. Children use the relationship between consecutive elements when predicting an unknown element. In this way, it is only possible to predict the next element in the sequence, and then the next, one element after the other, starting from the last known element (i.e., a_n + 1 = f (a_n)). This type of thinking is called recursivethinking (McGarvey, 2012; Wijns, Torbeyns, De Smedt, & Verschaffel, 2019). In contrast, functionalthinking in a repeating pattern context would be to identify the unit of repeat and to use the pattern’s structure to predict any element of the sequence (i.e., a_n = f(n); Wijns et al., 2019). This mathematical approach can be seen with the strategies of the fifth category.

Threlfall (1999) is an expert on the topic of repeating patterns in the early primary years. Among his reasons for working with these structures, is his belief that they develop a sense of sequencing and regularity. He has found that one way in which children can succeed in creating or extending a repeating pattern is through a rhythmic approach. As shown above, strategies based on the rhythmic approach would be categorized as a focus on the sequence or recursive thinking, and, therefore, belong to the fourth category. However, in line with my considerations on the mathematics in repeating patterns, Threlfall (1999) claimed that in order to generalize the pattern, a rhythmic approach is not sufficient. It is essential that the child develops a perception of the pattern’s unit of repeat. This argument results in my question, how far do children develop this perception in early childhood (without instruction). As Threlfall (1999) already suggested, we cannot infer a perception of the repeating unit from a correct solution but need to consider the child’s way to get to her correct (or wrong) solution—the child’s strategy.

Therefore, this chapter addresses the following research questions: What strategies are employed by children aged 3, 4, and 5 when solving repeating patterning tasks? What differences in the distribution of frequencies for the various strategies are found between the age groups? And, in particular, to what extent do children use strategies from the fifth category (view of unit of repeat)?

For informing early childhood education settings, it might also be worthwhile to investigate if some tasks are more helpful than others for challenging children to use or refer to the unit of repeat. I am, therefore, going to exemplarily analyze the distribution of strategies for selected tasks and discuss some issues I found with these tasks.

4 Method

4.1 Setting and Participants

Consent was obtained for 159 children attending 14 kindergartens¹ in a metropolitan area in Germany. The sample consisted of 54 children of age 3 (30 girls, M_age = 3;6, SD = 2.7 months, range = 2;11–3;11, 76% speaking German as family language), 65 children of age 4 (33 girls, M_age = 4;5, SD = 3.2 months, range = 4;0–4;11, 82% speaking German as family language), and 40 children of age 5 (15 girls, M_age = 5;4, SD = 3.9 months, range = 5;0–5;11, 80% speaking German as family language).

None of the participating kindergartens were using a specialized curriculum focused on patterning, and teachers reported doing no repeating patterning activities at all (which I consider representative of German kindergartens). Therefore, it might be suggested that the findings of this study shed light on children’s informal patterning knowledge and its organic development.

4.2 Tasks and Materials

Eight patterning tasks were designed to test children’s strategy use in working with repeating patterns. They were based on items that are long known in mathematics education (Burton, 1982; Sarama & Clements, 2010) and are also published in research studies (e.g., Papic et al., 2011). In several prestudies, the tasks were adapted and tested. The eight patterning tasks are listed in Table 5.1, organized by the order in which they were administered.

Table 5.1 Description of patterning tasks

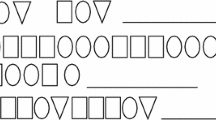
All tasks were conducted consecutively with three repeating patterns that differed according to the length of their unit of repeat. The pattern units contained two (AB), three (ABC), and four elements (ABCC), with only three elements being different in the last, four-element pattern. As shown in Fig. 5.1, the patterns were presented with three (AB) and two (ABC and ABCC) instances of the repeating unit. Whereas the ABCC pattern ended with an additional partial unit, the first two ended with a complete unit. All patterns were constructed with colored wooden cubes, choosing the dimension of color over the dimension of shape. Since 3-year-olds were interviewed, I assumed it easier to communicate about color than relying on children’s knowledge of names for different shapes. A brief color-matching test was administered to each child in order to screen for color blindness. If the child did not specify the colors by herself/himself during the explanation task, the interviewer pointed to each colored cube, one at a time, and asked the child to name the color. No children were excluded for color blindness. Numerous cubes in six different colors were available for the children to choose from during all tasks. For the translation task, counters were offered in four colors that differed from the cubes’ colors. For the identification tasks, all three patterns were presented with three full units of repeat. In this way, it was not possible for the child to identify two equal units that were nonminimal.

Fig. 5.1

AB pattern (green, yellow), ABC pattern (green, purple, orange) (top), and ABCC pattern (yellow, red, blue, blue) (bottom)

4.3 Data Collection and Analysis

The children worked one on one with a researcher in a quiet room in their kindergarten. The session took 45 min on average, and it was split over two days if the child showed signs of fatigue. The interviews were video-recorded so that the interviewer was released from taking any notes, giving her the freedom to completely engage with the child. In addition, observations of all actions, gestures, and the exact wording were available for the analyses.

The answers to every task with all three patterns (i.e., 24 answers for each child) were coded by strategy and correctness. To establish interrater reliability, a second rater coded 20% of the answers; agreement was high (95%).

5 Results

As Table 5.2 displays, all age groups used patterning strategies from the complete range of strategy categories. However, the proportion of categories differed largely according to the age groups. The 3-year-olds mainly used strategies from category 1. Half of the strategies used by the 4-year-olds also belonged to category 1; the other half was distributed nearly evenly among categories 2–4. The majority (63%) of the strategies employed by the 5-year-old children were divided into the categories 3 and 4. Therefore, the older children used more sophisticated strategies than the younger children. Strategies from category 5 were almost never used by the 3- and 4-year-olds; the proportion of category 5 strategies for the 5-year-old children was under 10%. I conclude that with the vast majority of children who started formal schooling 4–10 months later, an understanding of the unit of repeat was not developed yet.

Table 5.2 Distribution of frequencies (%) of strategy categories (all tasks) for 3-/4-/5-year-olds

If we explicitly look at the distribution of frequencies for each of the patterns individually, it becomes apparent that for the easiest AB pattern all age groups used more advanced strategies more frequently (see Table 5.2). That is to say, the more complex the pattern was, the less sophisticated were the strategies.

The following results show the finely fanned out distribution of frequencies for three selected tasks (copy with the model pattern in view, translate, identify) for each pattern (see Table 5.3). The tasks are selected for their common inclusion in research studies (copy) or are suggested to help children focus on the unit of repeat (translate, identify). The findings are described and interpreted in turn using the example of the 5-year-olds.

Table 5.3 Distribution of frequencies (%) of strategy categories (selected tasks) for 5-year-olds

Copy with the model pattern in view: The distribution of frequencies for this task is striking and exceptional compared to all other tasks. Seventy to ninety percent of all strategies employed while copying a visible pattern belonged to category 3 comparison & classification. Looking closer at the kind of strategy, it quickly became apparent during the analysis that the majority of 5-year-olds used a compare and match strategy, meaning they executed a one-to-one correspondence. They did this—contrary to the finding of the overall strategy use—although they showed more advanced strategies for other tasks.

Translate: During the analysis, I found it remarkable that 14% of the 5-year-olds were able to correctly translate an AB pattern, but also created an AB pattern when translating an ABC pattern. Looking at their strategy use, it became apparent that the successful children mainly used two strategies. Some of the children argued about similarities in color intensity and matched, in a one-to-one manner, a dark color with another dark and a light color with another light (category 3). The others very confidently created a repeating AB pattern step by step, some even arguing about alternation of color (category 4). A large proportion of the children who were using an alternation strategy with the AB pattern kept the strategy of alternating two colors for translating the ABC pattern (now coded category 2).

Identify: The task identify was the only task where it was difficult to fit the strategies into the five strategy categories. It rather became a classification of children’s solutions than of strategies. Category 1 comprised solutions where children cut the pattern into parts which were of different length, and no regularity could be found whatsoever. In category 2, the patterns were cut into equal parts (mostly single cubes) without regularity regarding the color. The most common strategy made up category 3: cutting the patterns into single cubes and sorting them by color. There were no strategies or solutions that involved the succession of elements (category 4). In category 5, all children cut the patterns into units of repeat immediately after they had been asked to do so. As this task seemed difficult to explain verbally, all interviewers offered help to every child that produced a wrong solution during the first try. We contrasted two different parts that the child had produced previously and asked if the child thought the parts were really the same. If the child negated, the child was encouraged to try again. If the child cut the pattern correctly into units of repeats during the second try, the solution was then coded category 4. Hence, only the categories 4 and 5 contained correct solutions. This means that a child either had an understanding of the unit of repeat, i.e., the structure of the pattern and consequently was able to cut the pattern correctly or did not have an understanding of the unit of repeat and, therefore, was not able to solve the task identify correctly. This finding is different from the other tasks where children could produce very well a correct solution without having perceived the pattern’s structure.

6 Discussion

This study considers strategies that children employ while working on repeating pattern tasks as an important diagnostic tool for assessing their understanding of the pattern and its structure. The results show that the 3-year-olds’ strategies are mainly based on an understanding of the pattern’s shape and, to a lesser extent, on the perception of singular, external characteristics of the pattern, like color. Regarding an AB pattern, half of the 4-year-olds show those same strategies. The other half of the 4-year-olds’ strategies refer to basic regularities in the pattern (e.g., “The greens are the same, the yellows are the same.”) or regard the succession of the specific colors (e.g., “Next to green is yellow, next to yellow is green, next to green is yellow, …”). It is interesting that the 4-year-olds’ strategies are distributed nearly evenly among the first four strategy categories for the AB pattern, thus showing a broad developmental range. The 5-year-olds’ main strategies belong to categories 3 (comparison & classification) and 4 (focus on sequence) and are thus displaying an emergent understanding of regularity, order, and succession. These findings go in line with Papic et al.’s (2011) categories direct comparison and alternation, which were observed most frequently for their overall sample, too.

Hence, the data show huge differences regarding the use of patterning strategies between the 3-, 4-, and 5-year-olds. The tendency is that older children use strategies focused on regularity and structure more often than younger children. It has to be said, though, that the strategy categories do not constitute a developmental stage model. One limitation of the study is that it is a cross-sectional study, and only trends between groups (not a development on an individual level) can be stated. Hence, it cannot be accounted for that every child’s strategies will progress through all five categories. Furthermore, by sorting the participants into age groups for an easy comparison, some information gets lost. Children are possibly born only days apart but belong to different age groups. This is a limitation of working in a quantitative way.

What developmental mechanisms might underlie the improving understanding of repeating patterns? As the children did not receive any instruction on repeating patterning other than what they might have experienced at home or observed on television, the development is presumably not due to instruction. A possible explanation could be the general cognitive development in early childhood. Previous studies have shown that working memory is particularly important for helping preschoolers identify, re-create, and learn about patterns (Miller et al., 2016; Rittle-Johnson et al., 2013). Increases in working memory capacity are thought to allow young children to transition from focusing on singular aspects of a task to coordinating attention to two dimensions (Case & Okatomo, 1996). Furthermore, children between 3 and 5 years undergo significant development in their language ability. Children’s explanations form the basis of categorization, and with more elaborate language, it is more likely that the interpretation of a child’s strategy reflects her true thinking.

Another main finding is the variability of strategy regarding the difficulty of pattern: The more complex the pattern was, the less sophisticated were the strategies which the children employed. This goes in line with findings suggesting that children use more basic strategies in calculating when asked to solve unknown, complex tasks (Siegler, 1988).

Radford (2012) argued that the ability to discern and generalize patterns and mathematical structure in general does not develop spontaneously; rather it depends on cultural influence or some kind of education. Sarama and Clements (2009) noted that being able to recognize the unit of repeat may not develop until the age of 6 years. However, this study found that, in single cases, children as young as 3-year-olds are capable of recognizing structure. Still, only 8% of all strategies used by the 5-year-olds hint at a recognition of the unit of repeat. Since formal schooling in Germany starts when children are 6 years old, and patterns are part of the curriculum, it would be interesting to see the extent to which school education on patterning fosters the understanding of the pattern’s structure. It would also be interesting to compare 3- to 5-year-old children’s strategy use in countries where formal schooling starts earlier and/or patterning is part of the preschool curriculum.

This chapter also specifically reflects on some selected patterning tasks and how these tasks challenge children to use the pattern’s underlying structure. A very common task with children of various ages is to copy a pattern while the model pattern is still displayed in front of the child. It is interesting to see that children who are otherwise showing advanced strategies, even referring to the repeating unit, regress to doing a one-to-one correspondence for this task. From this finding, I conclude that this kind of copying task is not challenging the children to use the repeating unit in finding a solution and, consequently, it might be an inappropriate task in an educational setting for older children, i.e., most 5-year-olds.

The task translate, where a model pattern is recreated with different materials, is often considered a helpful task for children to shift their attention from the superficially different characteristics of two patterns (e.g., color, shape) to the underlying identical structure (e.g., unit of repeat consists of two different elements) (Hoenisch & Niggemeyer, 2004; Warren & Cooper, 2006). Being able to translate patterns into new media is considered a more advanced stage by Sarama and Clements (2009, p. 331) than being able to copy, extend, or repair a pattern. Rittle-Johnson et al. (2013) even interpret a correct solution in a translation task as the child’s ability to abstract the pattern’s structure. Hence, this task is called an “abstraction task” (p. 381). Looking at the strategies, it becomes obvious that children are able to correctly translate a pattern into different material without having an understanding of the unit of repeat. This goes especially in line with the findings of Collins and Laski (2015), which highlight the one-to-one matching strategy also for the translation tasks. Furthermore, it seems that some 5-year-olds have developed an understanding of “pattern” as an alternation of two colors, a succession of colors with a certain regularity. Or, put differently, the AB pattern has become the prototype example for a repeating pattern. If asked to produce a pattern, this prototype is reproduced, regardless of its particular structure. In the work on patterning with children, it is, therefore, important to ask for the children’s view of similarities and differences between the two patterns and what strategy they used to create the same pattern in the different medium.

The only task children gain a correct solution exclusively with an understanding of the unit of repeat is identify, i.e., breaking the pattern down into the repeating units. Although children show many different ideas for breaking a pattern down into parts, there are no differing strategies that lead to the correct solution. As it is the specific aim of the task to put the repeating part and with it the pattern’s structure into focus, it might be a valuable task in teaching children the pattern’s structure. Similar tasks would be, for example, to circle the unit of repeat, place a string around it (Papic et al., 2011), or build a tower with a repeating pattern and request the child to build the smallest tower that still keeps the same pattern as the one already built (Rittle-Johnson et al., 2013).

This argument leads to learning environments that teachers create around patterning activities in school. What kind of patterning tasks do teachers choose? What explanations do they give, and which strategies do they (sub-)consciously foster? Do they link repeating pattern’s structure to other mathematical content with a similar structure?

My hope is that the findings of this study convince teachers to ask more questions like “How do you do it? How do you know?” and to look closer at the process of patterning instead of the correct solution. The goal is to make patterning more of a mathematical activity.