Keywords

1 Introduction

Wire ropes are commonly employed to sustain large axial loads. At the same time, they can be successfully exploited for applications in the field of structural vibration control. The first patented device based on steel wire ropes dates to the beginning of the last century and its scope consisted in the mitigation of galloping oscillations in cable electric transmission lines [1]. In recent years, several devices based on the hysteresis provided by wire rope assemblies have been proposed [2,3,4,5,6,7].

In this work, a nonlinear isolation system for reducing vertical vibrations is identified and experimentally investigated. The isolator is a so-called wire rope spring while the structure to be controlled is represented by two cantilevers with a tip mass undergoing bending motion. The nonlinear hysteretic behavior of the isolator is first characterized evaluating the equivalent stiffness and hysteretic damping at various displacement amplitudes and then identified through a suitable nonsymmetric hysteresis model. Subsequently, the test and the structure to be controlled are designed. Experimental FRCs of the isolated and non-isolated structures are finally obtained in order to estimate the transmissibility in the frequency bandwidth of interest.

2 The Isolator Response

The isolation system consists of a compact wire rope isolator (see Fig. 1). It is made of two metal plates joined by a stainless steel wire rope having a diameter of 4 mm (7 × 7 wire of 0.4 mm) [8]. The geometric nonlinearities of the cables induce an asymmetric hysteretic behavior. Hardening or softening is manifested under tension or compression, respectively. The device high deformability together with its high damping capacity makes it ideal for vibration control of machinery and other kinds of structures. Antonelli et al. investigated the hysteretic behavior of the device via quasi-static testing (Fig. 2) applying cyclic time histories with increasing amplitudes, namely (0, ±2.5, ±5, ±7.5, ±10, ±12.5, ±15) mm.

Fig. 1
figure 1

The compact wire rope isolator

Full size image
Fig. 2
figure 2

Hysteretic loops under cyclic tests

Full size image

The equivalent stiffness and damping versus displacement are obtained at each quasi-static cyclic amplitude proving the softening behavior under compression and the softening-hardening behavior under tension with a decreasing trend in equivalent hysteretic damping (Fig. 3).

Fig. 3
figure 3

(Left) Stiffness vs. displacement (tension and compression stiffness represented by the dotted line, the average stiffness is indicated by the solid line) and (right) equivalent hysteretic damping vs. displacement

Full size image

Starting from the modified asymmetric Bouc–Wen model of hysteresis proposed by Carboni et al. [9], a further generalization of the asymmetric constitutive response is proposed and implemented in this study. By employing the differential evolution algorithm [10], the model parameters that best fit the experimental quasi-static force–displacement cycles at different amplitudes are found (see Fig. 4).

Fig. 4
figure 4

(Left) Numerical (red) vs. experimental (black) force–displacement cycles and (right) numerically obtained FRCs for the device with a mass of 1 kg for different base accelerations (i.e., 0.25, red, 0.5, 0.75, 1.0, 1.25 g, blue)

Full size image

3 Experimental Setup

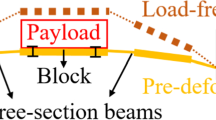
The structure to control during the tests was designed starting with the stiffness of the device in order to obtain a frequency shift, between the non-isolated and the isolated structure, of about five times. The designed structure consists of two symmetric cantilever steel beams (b = 30 mm, h = 2 mm, l = 7.5 cm) with a tip mass of 0.24 kg for both beams. In order to evaluate the FRCs and the transmissibility over the investigated frequency range, for both the non-isolated and the isolated systems, shaker tests were carried out in frequency sweeps (i.e., sinusoidal input with constant amplitude and varying frequency) (Fig. 5).

Fig. 5
figure 5

Test setup for (left) the non-isolated structure and (right) the isolated structure

Full size image

The range of investigated frequencies was between 5 and 100 Hz with a logarithmic sweep of 0.5 oct/min. The test was repeated four times for both systems with different acceleration amplitudes. The accelerations of the masses (0.24 kg × 2) at the beam tips, of the mass mounted on the support (0.45 kg) and of the shaker head were acquired through four PCB piezotronic accelerometers.

4 Dynamic Behavior of the Uncontrolled Structure

For the considered range of base motions, the non-isolated structure responds linearly, so the theoretical FRC curves can be obtained with acceptable approximation in closed form. The steady-state response in displacement, x ss(Ω), and acceleration, \( {\ddot{x}}_{\mathrm{ss}}\left(\Omega \right) \), and the linear transfer function H(Ω) are given by: \( {x}_{\mathrm{ss}}\left(\Omega \right)=H\left(\Omega \right)\ {\ddot{x}}_g,\kern0.5em {\ddot{x}}_{\mathrm{ss}}\left(\Omega \right)={\Omega}^2H\left(\Omega \right)\ {\ddot{x}}_g,H\left(\Omega\right)=\left(\mathrm{m}/\mathrm{k}\right)/\sqrt{{\left[1-{\left(\Omega /{\omega}_n\right)}^2\right]}^2+{\left(2\xi \Omega /{\omega}_n\right)}^2}, \) where Ω is the excitation frequency and ω n the frequency of the nth mode of the structure. The structural stiffness is that of a cantilever beam with a point load at the tip. By knowing the mass, the governing parameters are the elastic constant and the damping ratio, namely k = a · EI/l 3 where the constant a = 3 for a perfect clamp; ξ = c/(2mω n) is the damping ratio expressed in terms of the viscous damping coefficient c which embodies the beam material damping and the boundary friction.

The frequency sweep tests were repeated for four different amplitudes, and for each amplitude, the stiffness and damping constant which better fit the experimental FRCs were found (see Table 1). The accelerations registered by the accelerometers were first filtered through the Savitzky–Golay filter [11] and then doubly integrated to obtain velocities and displacements. The results of the integration were filtered again by a high-pass filter to remove the integration drift. In the subsequent figures, the experimental FRCs (Fig. 6) and the trend of the transmissibility function (Fig. 7) are reported.

Table 1 Base accelerations, stiffness constant
Full size table
Fig. 6
figure 6

Experimental FRCs in terms of (left) displacement and (right) acceleration for base accelerations of 0.1, 0.15, 0.2, 0.25 g

Full size image
Fig. 7
figure 7

Displacement (dotted) and acceleration and damping ratio for each test (cont.) transmissibility peak vs. acceleration amplitude

Full size image

5 Experimental Response of the Isolated Structure

The same frequency sweep tests were repeated for four different excitation levels for the isolated structure. As in the previous tests, displacements of each mass can be obtained by double integration and filtering of the acquired accelerations. Figure 8 shows the comparison between the experimental FRCs in displacement and acceleration for the isolated (red) and non-isolated structures (black) for an input acceleration of 0.25 g.

Fig. 8
figure 8

Experimental FRCs of the uncontrolled structure (black line) vs. controlled structure (the red solid lines represent the response of the mass at the beam tip, while the red dashed lines indicate the response of the lumped mass on the isolator): (left) displacement and (right) acceleration

Full size image

A strong reduction of the maximum acceleration of the isolated system can be observed due to the high compliance (hence, low frequency) of the device. As expected, at low frequencies the displacement of the isolated structure is larger than that of the non-isolated structure. At the same time, the maximum displacement of the isolated structure (elongation of the isolator) is indeed much smaller than the maximum displacement of the non-isolated structure (flexural beam vibration), thanks to the energy dissipation provided by the device built-in hysteresis. Figure 9 represents the displacement and acceleration FRCs for the isolated structure for different excitation amplitudes (i.e., 0.25, 0.5, 0.75, 1 g). The first and the second resonance frequencies, about 14 and 24 Hz, are relative at the elongation modes of the isolator. The third mode, near 74 Hz, is the flexural mode of the beam. Furthermore, please note that the mass on the beam functions as a vibration absorber for the constraint mass at the frequency of 70 Hz, making its relative acceleration vanish.

Fig. 9
figure 9

(Left) Displacement FRC and (right) acceleration FRC of the isolated structure for different excitation amplitudes (i.e., 0.25, 0.5, 0.75, 1 g). The solid lines represent the response of the mass at the beam tip, while the black dashed lines indicate the response of the lumped mass on the isolator

Full size image

By focusing on the frequency range of the two last modes, we can observe a softening trend on both (24 and 74 Hz) due to the softening geometric nonlinearities of the device (see Fig. 10).

Fig. 10
figure 10

Acceleration FRC near (left) the second mode and (right) the third mode of the isolated structure. Solid lines indicate the response of the mass on the beam and dotted lines denote the response of the mass on the isolator

Full size image

The transmissibility is reduced by an order of magnitude over the entire frequency range examined (see Fig. 11). In fact, it goes from an average value of about 75 for both the acceleration and displacement factors to an average value of about 6. The transmissibility factor is evaluated for the third mode (74 Hz), which exhibits the maximum acceleration and the maximum displacement. The transmissibility factor shows a decreasing trend due to the softening behavior which causes a more pronounced decoupling between the structure and the ground for larger excitation amplitudes (see Fig. 12 left). By making use of considerations of balance of linear momentum, the restoring force of the isolator during the test is also estimated. Figure 12 (right) shows the force–displacement cycles at the resonance frequency of the isolator for four amplitudes. The agreement with the hysteretic loops provided by the quasi-static cyclic tests confirms the hardening-softening asymmetric behavior. There is also a drift because of the system weight during the dynamic tests, differently from the static tests.

Fig. 11
figure 11

(Left) Displacement transmissibility and (right) acceleration transmissibility vs. frequency of isolated structure for an excitation amplitude of 0.25 (red), 0.5, 0.75, 1.0 g (blue)

Full size image
Fig. 12
figure 12

(Left) Displacement (dotted line) and acceleration (solid line) transmissibility vs. acceleration amplitude and (right) force–displacement cycle of the device for the four test amplitudes

Full size image

6 Conclusions

The performance of the investigated hysteretic, nonsymmetric wire rope isolator shows a strong reduction of the transmissibility in terms of both acceleration and displacement over a wide frequency range. The hysteretic restoring force provided by the wire ropes under compressional and tensile cyclic loads was identified, and it was shown to be suitable for vibration damping applications because of the large dissipation rate. This can mitigate the well-known drawback of isolation systems arising from the large compliance at low frequencies. However, the main problem with this type of devices for large-scale structural isolation is the relative size between the device and the structure to be controlled. The present chapter sets the initial steps of a wider experimental and theoretical work aimed at validating a reduced order nonlinear model capable of reproducing accurately the dynamic behavior of the device and the structure in order to achieve a wide nonlinear isolation system optimization.