Abstract
Non-committing encryption (NCE) was introduced by Canetti et al. (STOC ’96). Informally, an encryption scheme is non-committing if it can generate a dummy ciphertext that is indistinguishable from a real one. The dummy ciphertext can be opened to any message later by producing a secret key and an encryption random coin which “explain” the ciphertext as an encryption of the message. Canetti et al. showed that NCE is a central tool to achieve multi-party computation protocols secure in the adaptive setting. An important measure of the efficiently of NCE is the ciphertext rate, that is the ciphertext length divided by the message length, and previous works studying NCE have focused on constructing NCE schemes with better ciphertext rates.
We propose an NCE scheme satisfying the ciphertext rate  based on the decisional Diffie-Hellman (DDH) problem, where
based on the decisional Diffie-Hellman (DDH) problem, where  is the security parameter. The proposed construction achieves the best ciphertext rate among existing constructions proposed in the plain model, that is, the model without using common reference strings. Previously to our work, an NCE scheme with the best ciphertext rate based on the DDH problem was the one proposed by Choi et al. (ASIACRYPT ’09) that has ciphertext rate
is the security parameter. The proposed construction achieves the best ciphertext rate among existing constructions proposed in the plain model, that is, the model without using common reference strings. Previously to our work, an NCE scheme with the best ciphertext rate based on the DDH problem was the one proposed by Choi et al. (ASIACRYPT ’09) that has ciphertext rate  . Our construction of NCE is similar in spirit to that of the recent construction of the trapdoor function proposed by Garg and Hajiabadi (CRYPTO ’18).
. Our construction of NCE is similar in spirit to that of the recent construction of the trapdoor function proposed by Garg and Hajiabadi (CRYPTO ’18).
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
1.1 Background
Secure multi-party computation (MPC) allows a set of parties to compute a function of their inputs while maintaining the privacy of each party’s input. Depending on when corrupted parties are determined, two types of adversarial settings called static and adaptive have been considered for MPC. In the static setting, an adversary is required to declare which parties it corrupts before the protocol starts. On the other hand, in the adaptive setting, an adversary can choose which parties to corrupt on the fly, and thus the corruption pattern can depend on the messages exchanged during the protocol. Security guarantee in the adaptive setting is more desirable than that in the static setting since the former naturally captures adversarial behaviors in the real world while the latter is somewhat artificial.
In this work, we study non-committing encryption (NCE) which is introduced by Canetti, Feige, Goldreich, and Naor [4] and known as a central tool to achieve MPC protocols secure in the adaptive setting. NCE is an encryption scheme that has a special property called non-committing property. Informally, an encryption scheme is said to be non-committing if it can generate a dummy ciphertext that is indistinguishable from real ones, but can later be opened to any message by producing a secret key and an encryption random coin that “explain” the ciphertext as an encryption of the message. Cannetti et al. [4] showed how to create adaptively secure MPC protocols by instantiating the private channels in a statically secure MPC protocol with NCE.
Previous Constructions of NCE and their Ciphertext Rate. The ability to open a dummy ciphertext to any message is generally achieved at the price of efficiency. This is in contrast to ordinary public-key encryption for which we can easily obtain schemes the size of whose ciphertext is  by using hybrid encryption methodology, where n is the length of an encrypted message and
by using hybrid encryption methodology, where n is the length of an encrypted message and  is the security parameter. The first NCE scheme proposed by Canetti et al. [4] only needs the optimal number of rounds (that is, two rounds), but it has ciphertexts of
is the security parameter. The first NCE scheme proposed by Canetti et al. [4] only needs the optimal number of rounds (that is, two rounds), but it has ciphertexts of  -bits for every bit of an encrypted message. In other words, the ciphertext rate of their scheme is
-bits for every bit of an encrypted message. In other words, the ciphertext rate of their scheme is  , which is far from that of ordinary public-key encryption schemes. Subsequent works have focused on building NCE schemes with better efficiency.
, which is far from that of ordinary public-key encryption schemes. Subsequent works have focused on building NCE schemes with better efficiency.
Beaver [1] proposed a three-round NCE scheme with the ciphertext rate  based on the decisional Diffie-Hellman (DDH) problem. Damgård and Nielsen [8] generalized Beaver’s scheme and achieved a three-round NCE scheme with ciphertext rate
based on the decisional Diffie-Hellman (DDH) problem. Damgård and Nielsen [8] generalized Beaver’s scheme and achieved a three-round NCE scheme with ciphertext rate  based on a primitive called simulatable PKE which in turn can be based on concrete problems such as the DDH, computational Diffie-Hellman (CDH), and learning with errors (LWE) problems. Choi, Dachman-Soled, Malkin, and Wee [7] further improved these results and constructed a two-round NCE scheme with ciphertext rate
based on a primitive called simulatable PKE which in turn can be based on concrete problems such as the DDH, computational Diffie-Hellman (CDH), and learning with errors (LWE) problems. Choi, Dachman-Soled, Malkin, and Wee [7] further improved these results and constructed a two-round NCE scheme with ciphertext rate  based on a weaker variant of simulatable PKE called trapdoor simulatable PKE which can be constructed the factoring problem.
based on a weaker variant of simulatable PKE called trapdoor simulatable PKE which can be constructed the factoring problem.
The first NCE scheme achieving a sub-linear ciphertext rate was proposed by Hemenway, Ostrovsky, and Rosen [20]. Their scheme needs only two rounds and achieves the ciphertext rate \(\mathcal {O}\left( \log n \right) \) based on the \(\phi \)-hiding problem which is related to (and generally believed to be easier than) the RSA problem, where n is the length of messages. Subsequently, Hemenway, Ostrovsky, Richelson, and Rosen [19] proposed a two-round NCE scheme with the ciphertext rate  based on the LWE problem. Canetti, Poburinnaya, and Raykova [5] showed that by using indistinguishability obfuscation, an NCE scheme with the asymptotically optimal ciphertext rate (that is, \(1+o(1)\)) can be constructed. Their scheme needs only two rounds but was proposed in the common reference string model.
based on the LWE problem. Canetti, Poburinnaya, and Raykova [5] showed that by using indistinguishability obfuscation, an NCE scheme with the asymptotically optimal ciphertext rate (that is, \(1+o(1)\)) can be constructed. Their scheme needs only two rounds but was proposed in the common reference string model.
Despite the many previous efforts, as far as we know, we have only a single NCE scheme satisfying a sub-linear ciphertext rate based on widely and classically used problems, that is, the scheme proposed by Hemenway et al. [19] based on the LWE problem. Since NCE is an important cryptographic tool in constructing MPC protocols secure in the adaptive setting, it is desirable to have more constructions of NCE satisfying a better ciphertext rate.
1.2 Our Contribution
We propose an NCE scheme satisfying the ciphertext rate  based on the DDH problem. The proposed construction achieves the best ciphertext rate among existing constructions proposed in the plain model, that is, the model without using common reference strings. The proposed construction needs only two rounds, which is the optimal number of rounds for NCE. Previously to our work, an NCE scheme with the best ciphertext rate based on the DDH problem was the one proposed by Choi et al. [7] that satisfies the ciphertext rate
based on the DDH problem. The proposed construction achieves the best ciphertext rate among existing constructions proposed in the plain model, that is, the model without using common reference strings. The proposed construction needs only two rounds, which is the optimal number of rounds for NCE. Previously to our work, an NCE scheme with the best ciphertext rate based on the DDH problem was the one proposed by Choi et al. [7] that satisfies the ciphertext rate  . We summarize previous results on NCE and our result in Table 1.
. We summarize previous results on NCE and our result in Table 1.
We first show an NCE scheme that we call basic construction, which satisfies the ciphertext rate  . Then, we give our full construction satisfying the ciphertext rate
. Then, we give our full construction satisfying the ciphertext rate  by extending the basic construction using error-correcting codes. Especially, in the full construction, we use a linear-rate error-correcting code which can correct errors of weight up to a certain constant proportion of the codeword length.
by extending the basic construction using error-correcting codes. Especially, in the full construction, we use a linear-rate error-correcting code which can correct errors of weight up to a certain constant proportion of the codeword length.
 , and the message length n. Common-domain TDP can be instantiated based on the CDH and RSA problems. Simulatable and trapdoor simulatable PKE can be instantiated based on many computational problems realizing ordinary PKE. \(^{(*)}\) This scheme uses common reference strings.
, and the message length n. Common-domain TDP can be instantiated based on the CDH and RSA problems. Simulatable and trapdoor simulatable PKE can be instantiated based on many computational problems realizing ordinary PKE. \(^{(*)}\) This scheme uses common reference strings.Our construction of NCE utilizes a variant of chameleon encryption. Chameleon encryption was originally introduced by Döttling and Garg [10] as an intermediate tool for constructing an identity-based encryption scheme based on the CDH problem. Roughly speaking, chameleon encryption is public-key encryption in which we can use a hash value of a chameleon hash function and its pre-image as a public key and a secret key, respectively. We show a variant of chameleon encryption satisfying oblivious samplability can be used to construct an NCE scheme with a sub-linear ciphertext rate. Informally, oblivious samplability of chameleon encryption requires that a scheme can generate a dummy hash key obliviously to the corresponding trapdoor, and sample a dummy ciphertext that is indistinguishable from a real one, without using any randomness except the dummy ciphertext itself.
Need for the DDH Assumption. A key and a ciphertext of the CDH based chameleon encryption proposed by Döttling and Garg [10] together form multiple Diffie-Hellman tuples. Thus, it seems difficult to sample them obliviously unless we prove that the knowledge of exponent assumption [2, 18] is false. In order to solve this issue, we rely on the DDH assumption instead of the CDH assumption. Under the DDH assumption, a hash key and a ciphertext of our chameleon encryption are indistinguishable from independent random group elements, and thus we can perform oblivious sampling of them by sampling random group elements directly from the underlying group.
Public Key Size. As noted above, we first give the basic construction satisfying the ciphertext rate  , and then extend it to the full construction satisfying the ciphertext rate
, and then extend it to the full construction satisfying the ciphertext rate  . In addition to satisfying only the ciphertext rate
. In addition to satisfying only the ciphertext rate  , the basic construction also has a drawback that its public key size depends on the length of a message quadratically.
, the basic construction also has a drawback that its public key size depends on the length of a message quadratically.
A public key of the basic construction contains ciphertexts of our obliviously samplable chameleon encryption. The size of those ciphertexts is quadratic in the length of an input to the associated chameleon hash function similarly to the construction by Döttling and Garg [10]. Since the input length of the chameleon hash function is linear in the message length of the basic construction, the public key size of the basic construction depends on the message length quadratically.
Fortunately, we can remove this quadratic dependence by a simple block-wise encryption technique. Thus, in the full construction, we utilize such a block-wise encryption technique in addition to the error-correcting code. By doing so, we reduce not only the ciphertext rate to  , but also the public key size to linear in the length of a message as in the previous constructions of NCE.
, but also the public key size to linear in the length of a message as in the previous constructions of NCE.
Relation with Trapdoor Function by Garg and Hajiabadi [14]. There has been a line of remarkable results shown by using variants of chameleon encryption, starting from the one by Cho, Döttling, Garg, Gupta, Miao, and Polychroniadou [6]. This includes results on identity-based encryption [3, 9,10,11], secure MPC [6, 16], adaptive garbling schemes [15, 17], and so on. Garg and Hajiabadi [14] showed how to realize trapdoor function (TDF) based on the CDH problem using a variant of chameleon encryption called one-way function with encryption.Footnote 1
Our construction of NCE can be seen as an extension of that of TDF by Garg and Hajiabadi. Our formulation of chameleon encryption is based on that of one-way function with encryption. Concretely, we define chameleon encryption so that it has recyclability introduced by Garg and Hajiabadi as a key property in their work.
1.3 Paper Organization
Hereafter, in Sect. 2, we first review the definition of NCE. Then, in Sect. 3, we provide high-level ideas behind our construction of NCE. In Sect. 4, we formally define and construct obliviously samplable chameleon encryption. In Sect. 5, using obliviously samplable chameleon encryption, we construct an NCE scheme that we call the basic construction satisfying the ciphertext rate  . Finally, in Sect. 6, we improve the basic construction and provide the full construction that achieves the ciphertext rate
. Finally, in Sect. 6, we improve the basic construction and provide the full construction that achieves the ciphertext rate  .
.
2 Preliminaries
Let PPT denote probabilistic polynomial time. In this paper,  always denotes the security parameter. For a finite set X, we denote the uniform sampling of x from X by \(x\overset{\$}{\leftarrow }X\). \(y{\leftarrow }\mathsf {A}(x;r)\) denotes that given an input x, a PPT algorithm \(\mathsf {A}\) runs with internal randomness r, and outputs y. A function f is said to be negligible if
always denotes the security parameter. For a finite set X, we denote the uniform sampling of x from X by \(x\overset{\$}{\leftarrow }X\). \(y{\leftarrow }\mathsf {A}(x;r)\) denotes that given an input x, a PPT algorithm \(\mathsf {A}\) runs with internal randomness r, and outputs y. A function f is said to be negligible if  , and we write
, and we write  to denote that f is negligible. Let
to denote that f is negligible. Let  denotes the Hamming weight of
denotes the Hamming weight of  . \(\mathbb {E}\left[ X \right] \) denotes expected value of X. [n] denotes \(\left\{ 1,\dots ,n \right\} \).
. \(\mathbb {E}\left[ X \right] \) denotes expected value of X. [n] denotes \(\left\{ 1,\dots ,n \right\} \).
Lemma 1 (Chernoff bound)
For a binomial random variable X. If \(\mathbb {E}\left[ X \right] \le \mu \), then for all \(\delta >0\), \( \Pr \left[ X\ge (1+\delta )\mu ) \right] \le e^{-\frac{\delta ^2}{2+\delta }\mu } \) holds.
We provide the definition of the DDH assumption and its variants used in the proof of Theorem 1. We first introduce the leftover hash lemma.
Lemma 2 (Leftover hash lemma)
Let X and Y are sets. Let \(\mathcal {H}:=\{\mathsf {H}:X\rightarrow Y\}\) be a universal hash family. Then, the distributions \((\mathsf {H}, \mathsf {H}(x))\) and \((\mathsf {H}, y)\) are \(\sqrt{\frac{\left|Y\right|}{4\left|X\right|}}\)-close, where \(\mathsf {H}\overset{\$}{\leftarrow }\mathcal {H}\), \(x\overset{\$}{\leftarrow }X\), and \(y\overset{\$}{\leftarrow }Y\).
We review some computational assumptions. Below, we let \(\mathbb {G}\) be a cyclic group of order \(p\) with a generator \(g\). We also define the function \(\mathsf {dh}\left( \cdot ,\cdot \right) \) as \(\mathsf {dh}\left( g^a,g^b \right) \,{:=}\,g^{ab}\) for every \(a,b\in \mathbb {Z}_p\). We start with the decisional Diffie-Hellman (DDH) assumption.
Definition 1 (Decisional Diffie-Hellman Assumption)
We say that the DDH assumption holds if for any PPT adversary \(\mathcal {A}\),

holds, where  .
.
We introduce a lemma that is useful for the proof of oblivious samplability of our chameleon encryption. We can prove this lemma by using the self reducibility of the DDH problem.
Lemma 3
Let n be a polynomial of \(\lambda \). Let \(g_{i,b}\overset{\$}{\leftarrow }\mathbb {G}\) for every \(i\in [n]\) and \(b\in \{0,1\}\). We set \(M:=(g_{i,b})_{i\in [n],b\in \{0,1\}}\in \mathbb {G}^{2\times n}\).
Then, if the DDH assumption holds, for any PPT adversary \(\mathcal {A}\), we have

where \(M^\rho =(g_{i,b}^\rho )_{i\in [n],b\in \{0,1\}}\in \mathbb {G}^{2\times n}\) and \(R\leftarrow \mathbb {G}^{2\times n}\).
We next define the hashed DDH assumption which is a variant of the DDH assumption.
Definition 2 (Hashed DDH Assumption)
Let \(\mathcal {H}=\{\mathsf {H_{\mathbb {G}}}:\mathbb {G}\rightarrow \{0,1\}^\ell \}\) be a family of hash functions. We say that the hashed DDH assumption holds with respect to \(\mathcal {H}\) if for any PPT adversary \(\mathcal {A}\),

holds, where  ,
,  , and
, and  .
.
In this work, we use the hashed DDH assumption with respect to a hash family \(\mathcal {H}\) whose output length \(\ell \) is small enough such as  or
or  . In this case, by using a family of universal hash functions \(\mathcal {H}\), we can reduce the hardness of the hashed DDH problem to that of the DDH problem by relying on the leftover hash lemma. Formally, we have the following lemma.
. In this case, by using a family of universal hash functions \(\mathcal {H}\), we can reduce the hardness of the hashed DDH problem to that of the DDH problem by relying on the leftover hash lemma. Formally, we have the following lemma.
Lemma 4
Let \(\mathcal {H}=\{\mathsf {H_{\mathbb {G}}}:\mathbb {G}\rightarrow \{0,1\}^\ell \}\) be a family of universal hash functions, where  . Then, if the DDH assumption holds, the hashed DDH assumption with respect to \(\mathcal {H}\) also holds by the leftover hash lemma.
. Then, if the DDH assumption holds, the hashed DDH assumption with respect to \(\mathcal {H}\) also holds by the leftover hash lemma.
Non-Committing Encryption. A non-committing encryption (NCE) scheme is a public-key encryption scheme that has efficient simulator algorithms  satisfying the following properties. The simulator
satisfying the following properties. The simulator  can generate a simulated public key \(pk\) and a simulated ciphertext \(CT\). Later
can generate a simulated public key \(pk\) and a simulated ciphertext \(CT\). Later  can explain the ciphertext
can explain the ciphertext  as encryption of any plaintext. Concretely, given a plaintext
as encryption of any plaintext. Concretely, given a plaintext  can output a pair of random coins for key generation
can output a pair of random coins for key generation  and encryption
and encryption  , as if \(pk\) was generated by the key generation algorithm with the random coin
, as if \(pk\) was generated by the key generation algorithm with the random coin  , and \(CT\) is encryption of
, and \(CT\) is encryption of  with the random coin
with the random coin  .
.
Some previous works proposed NCE schemes that are three-round protocols. In this work, we focus on NCE that needs only two rounds, which is also called non-committing public-key encryption, and we use the term NCE to indicate it unless stated otherwise. Below, we introduce the definition of NCE according to Hemenway et al. [19].
Definition 3 (Non-Committing Encryption)
A non-committing encryption scheme \(\mathtt {NCE}\) consists of the following PPT algorithms  .
.
-
 : Given the security parameter
: Given the security parameter  , using a random coin
, using a random coin  , it outputs a public key
, it outputs a public key  and a secret key
and a secret key 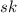 .
. -
 : Given a public key
: Given a public key  and a plaintext
and a plaintext  , using a random coin
, using a random coin  , it outputs a ciphertext
, it outputs a ciphertext 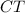 .
. -
 : Given a secret key
: Given a secret key  and a ciphertext
and a ciphertext  , it outputs
, it outputs  or \(\bot \).
or \(\bot \). -
 : Given the security parameter
: Given the security parameter  , it outputs a simulated public key \(pk\), a simulated ciphertext \(CT\), and an internal state
, it outputs a simulated public key \(pk\), a simulated ciphertext \(CT\), and an internal state  .
. -
 : Given a plaintext
: Given a plaintext  and a state
and a state  , it outputs random coins for key generation
, it outputs random coins for key generation  and encryption
and encryption  .
.
We require \(\mathtt {NCE}\) to satisfy the following correctness and security.
-
Correctness. \(\mathtt {NCE}\) is called \(\gamma \)-correct, if for any plaintext
 ,
, 
When
 , we call it correct. Note that \(\gamma \) cannot be equal to 1 in the plain model (i.e., the model without using common reference strings).
, we call it correct. Note that \(\gamma \) cannot be equal to 1 in the plain model (i.e., the model without using common reference strings). -
Security. For any stateful PPT adversary \(\mathcal {A}\), we define two experiments as follows.

We say that \(\mathtt {NCE}\) is secure if

holds for every PPT adversary \(\mathcal {A}\).
3 Ideas of Our Construction
In this section, we provide high-level ideas behind our construction of NCE.
As a starting point, we review the three-round NCE protocol proposed by Beaver [1], which contains a fundamental idea to build NCE from the DDH problem. Next, we show how to extend it and construct a two-round NCE scheme whose ciphertext rate is  . Then, we show how to reduce the ciphertext rate to
. Then, we show how to reduce the ciphertext rate to  , and obtain our main result. Finally, we state that our resulting construction can be described by using a variant of chameleon encryption, and it can be seen as an extension of trapdoor function proposed by Garg and Hajiabadi [14].
, and obtain our main result. Finally, we state that our resulting construction can be described by using a variant of chameleon encryption, and it can be seen as an extension of trapdoor function proposed by Garg and Hajiabadi [14].
3.1 Starting Point: Beaver’s Protocol
Beaver’s NCE protocol essentiality executes two Diffie-Hellman key exchange protocols in parallel. This protocol can send a 1-bit message. The ciphertext rate is  . We describe the protocol below and in Fig. 1.
. We describe the protocol below and in Fig. 1.
-
Step1. Let \(\mathbb {G}\) be a group of order p with a generator g. The sender picks a random bit
 and an exponent
and an exponent  , and then sets
, and then sets  . The sender also generates a random group element
. The sender also generates a random group element  obliviously, i.e., without knowing the discrete log of
obliviously, i.e., without knowing the discrete log of  . The sender sends
. The sender sends  to the receiver and stores the secret
to the receiver and stores the secret  . The random coin used in this step is
. The random coin used in this step is  .
. -
Step2. The receiver picks a random bit
 and an exponent
and an exponent  , and then sets
, and then sets  . The receiver also obliviously generates
. The receiver also obliviously generates  . Moreover, the receiver computes
. Moreover, the receiver computes  and obliviously samples
and obliviously samples  . The receiver sends
. The receiver sends  to the sender. The random coin used in this step is
to the sender. The random coin used in this step is  .
. -
Step3. The sender checks whether
 holds or not, by checking if
holds or not, by checking if  holds. With overwhelming probability, this equation holds if and only if
holds. With overwhelming probability, this equation holds if and only if  . If
. If  , the sender sends
, the sender sends  , and otherwise quits the protocol.
, and otherwise quits the protocol. -
Step4. The receiver recovers the message by
 .
.
The description of Beaver’s protocol [1].
We next describe the simulator for this protocol.
-
Simulator. The simulator simulates a transcript
 , and
, and  as follows. It generates
as follows. It generates  and sets
and sets 
The simulator also generates
 .
.The simulator can later open this transcript to both messages 0 and 1. In other words, for both messages, the simulator can generate consistent sender and receiver random coins. For example, when opening it to
 , the simulator sets
, the simulator sets  , and outputs
, and outputs  and
and  as the sender’s and receiver’s opened random coins, respectively.
as the sender’s and receiver’s opened random coins, respectively. -
Security. Under the DDH assumption on \(\mathbb {G}\), we can prove that any PPT adversary \(\mathcal {A}\) cannot distinguish the pair of transcript and opened random coins generated in the real protocol from that generated by the simulator. The only difference of them is that
 is generated as a random group element in the real protocol, but it is generated as
is generated as a random group element in the real protocol, but it is generated as  in the simulation. When the real protocol proceeds to Step. 4, we have
in the simulation. When the real protocol proceeds to Step. 4, we have  with overwhelming probability. Then, the random coins used by the sender and receiver (and thus given to \(\mathcal {A}\)) does not contain exponents of
with overwhelming probability. Then, the random coins used by the sender and receiver (and thus given to \(\mathcal {A}\)) does not contain exponents of  and
and  , that is,
, that is,  and
and  . Thus, under the DDH assumption, \(\mathcal {A}\) cannot distinguish randomly generated
. Thus, under the DDH assumption, \(\mathcal {A}\) cannot distinguish randomly generated  from
from  . Thus, this protocol is a secure NCE protocol.
. Thus, this protocol is a secure NCE protocol.
This protocol succeeds in transmitting a message only when  , and otherwise it fails. Note that even when
, and otherwise it fails. Note that even when  , the protocol can transmit a message because in Step. 3, the sender knows the receiver’s secret
, the protocol can transmit a message because in Step. 3, the sender knows the receiver’s secret  . However, in that case, we cannot construct a successful simulator. In order to argue the security based on the DDH assumption, we have to ensure that either one pair of exponents
. However, in that case, we cannot construct a successful simulator. In order to argue the security based on the DDH assumption, we have to ensure that either one pair of exponents  or
or  is not known to the adversary, but when
is not known to the adversary, but when  , we cannot ensure this.
, we cannot ensure this.
Next, we show how to extend this protocol into a (two-round) NCE scheme and obtain an NCE scheme with the ciphertext rate  .
.
3.2 Extension to Two-Round NCE Scheme
As a first attempt, we consider an NCE scheme \(\mathtt {NCE}_{\mathtt {lin}}^1\) that is a natural extension of Beaver’s three-round NCE protocol. Intuitively, \(\mathtt {NCE}_{\mathtt {lin}}^1\) is Beaver’s protocol in which the role of the sender and receiver is reversed, and the sender sends a message even when  and
and  are different. Specifically, the receiver generates the public key
are different. Specifically, the receiver generates the public key  and secret key
and secret key  , and the sender generates the ciphertext
, and the sender generates the ciphertext  , where
, where  , and
, and  are generated in the same way as those in Beaver’s protocol. When decrypting the
are generated in the same way as those in Beaver’s protocol. When decrypting the  , the receiver first recovers the value of
, the receiver first recovers the value of  by checking whether
by checking whether  holds or not, and then computes
holds or not, and then computes  .
.
Of course, \(\mathtt {NCE}_{\mathtt {lin}}^1\) is not a secure NCE scheme in the sense that we cannot construct a successful simulator when  for a similar reason stated above. However, we can fix this problem and construct a secure NCE scheme by running multiple instances of \(\mathtt {NCE}_{\mathtt {lin}}^1\).
for a similar reason stated above. However, we can fix this problem and construct a secure NCE scheme by running multiple instances of \(\mathtt {NCE}_{\mathtt {lin}}^1\).
In \(\mathtt {NCE}_{\mathtt {lin}}^1\), if  coincides with
coincides with  , we can construct a simulator similarly to Beaver’s protocol, which happens with probability \(\frac{1}{2}\). Thus, if we run multiple instances of it, we can construct simulators successfully for some fraction of them. Based on this observation, we construct an NCE scheme \(\mathtt {NCE}_{\mathtt {lin}}\) as follows. We also describe \(\mathtt {NCE}_{\mathtt {lin}}\) in Fig. 2.
, we can construct a simulator similarly to Beaver’s protocol, which happens with probability \(\frac{1}{2}\). Thus, if we run multiple instances of it, we can construct simulators successfully for some fraction of them. Based on this observation, we construct an NCE scheme \(\mathtt {NCE}_{\mathtt {lin}}\) as follows. We also describe \(\mathtt {NCE}_{\mathtt {lin}}\) in Fig. 2.
Let the length of messages be \(\mu \) and \(n=\mathcal {O}\left( \mu \right) \). We later specify the concrete relation of \(\mu \) and n. The receiver first generates  . Then, for every \(i\in [n]\), the receiver generates a pubic key of \(\mathtt {NCE}_{\mathtt {lin}}^1\),
. Then, for every \(i\in [n]\), the receiver generates a pubic key of \(\mathtt {NCE}_{\mathtt {lin}}^1\),  in which the single bit randomness is
in which the single bit randomness is  . We let the exponent of
. We let the exponent of  be \(\rho _i\), that is,
be \(\rho _i\), that is,  . The receiver sends these n public keys of \(\mathtt {NCE}_{\mathtt {lin}}^1\) as the public key of \(\mathtt {NCE}_{\mathtt {lin}}\) to the sender. The secret key is
. The receiver sends these n public keys of \(\mathtt {NCE}_{\mathtt {lin}}^1\) as the public key of \(\mathtt {NCE}_{\mathtt {lin}}\) to the sender. The secret key is  .
.
When encrypting a message m, the sender first generates  . Then, for every \(i\in [n]\), the sender generates
. Then, for every \(i\in [n]\), the sender generates  in the same way as \(\mathtt {NCE}_{\mathtt {lin}}^1\) (and thus Beaver’s protocol) “encapsulates”
in the same way as \(\mathtt {NCE}_{\mathtt {lin}}^1\) (and thus Beaver’s protocol) “encapsulates”  by using the i-th public key
by using the i-th public key  . We call it i-th encapsulation. Finally, the sender generates \(w=m\oplus H(x)\), where H is a hash function explained later in more detail.
. We call it i-th encapsulation. Finally, the sender generates \(w=m\oplus H(x)\), where H is a hash function explained later in more detail.
The resulting ciphertext is

Decryption is done by recovering each  in the same way as \(\mathtt {NCE}_{\mathtt {lin}}^1\) and computing
in the same way as \(\mathtt {NCE}_{\mathtt {lin}}^1\) and computing  .
.
The simulator for this scheme runs as follows. It first generates  and
and  . Then, for every index \(i\in [n]\) such that
. Then, for every index \(i\in [n]\) such that  , it simulates the i-th public key and encapsulation in the same way as the simulator for \(\mathtt {NCE}_{\mathtt {lin}}^1\) (and thus Beaver’s protocol). For every index \(i\in [n]\) such that
, it simulates the i-th public key and encapsulation in the same way as the simulator for \(\mathtt {NCE}_{\mathtt {lin}}^1\) (and thus Beaver’s protocol). For every index \(i\in [n]\) such that  , it simply generates i-th public key and encapsulation in the same way as \(\mathtt {NCE}_{\mathtt {lin}}\) does in the real execution. Finally, it generates
, it simply generates i-th public key and encapsulation in the same way as \(\mathtt {NCE}_{\mathtt {lin}}\) does in the real execution. Finally, it generates  .
.
Although the ciphertext generated by the simulator is not “fully non-committing” about  , it loses the information of bits of
, it loses the information of bits of  such that
such that  . Thus, if we can program the output value of the hash function H freely by programming only those bits of
. Thus, if we can program the output value of the hash function H freely by programming only those bits of  , the simulator can later open the ciphertext to any message, and we see that \(\mathtt {NCE}_{\mathtt {lin}}\) is a secure NCE scheme.
, the simulator can later open the ciphertext to any message, and we see that \(\mathtt {NCE}_{\mathtt {lin}}\) is a secure NCE scheme.
To realize this idea, we first set  in order to ensure that the simulated ciphertext loses the information of at least \(\mu \)-bits of
in order to ensure that the simulated ciphertext loses the information of at least \(\mu \)-bits of  with overwhelming probability. This is guaranteed by the Chernoff bound. Moreover, as the hash function H, we use a matrix \({R}\in \{0,1\}^{\mu \times {n}}\), such that randomly picked \(\mu \) out of
with overwhelming probability. This is guaranteed by the Chernoff bound. Moreover, as the hash function H, we use a matrix \({R}\in \{0,1\}^{\mu \times {n}}\), such that randomly picked \(\mu \) out of  column vectors of length \(\mu \) are linearly independent. The ciphertext rate of \(\mathtt {NCE}_{\mathtt {lin}}\) is
column vectors of length \(\mu \) are linearly independent. The ciphertext rate of \(\mathtt {NCE}_{\mathtt {lin}}\) is  , that is already the same as the best rate based on the DDH problem achieved by the construction of Choi et al. [7].
, that is already the same as the best rate based on the DDH problem achieved by the construction of Choi et al. [7].
3.3 Reduce the Ciphertext Rate
Finally, we show how to achieve the ciphertext rate  by compressing the ciphertext of \(\mathtt {NCE}_{\mathtt {lin}}\). This is done by two steps. In the first step, we reduce the size of the first part of a ciphertext of \(\mathtt {NCE}_{\mathtt {lin}}\), that is,
by compressing the ciphertext of \(\mathtt {NCE}_{\mathtt {lin}}\). This is done by two steps. In the first step, we reduce the size of the first part of a ciphertext of \(\mathtt {NCE}_{\mathtt {lin}}\), that is,  . By this step, we compress it into just a single group element. Then, in the second step, we reduce the size of the second part of a ciphertext of \(\mathtt {NCE}_{\mathtt {lin}}\), that is,
. By this step, we compress it into just a single group element. Then, in the second step, we reduce the size of the second part of a ciphertext of \(\mathtt {NCE}_{\mathtt {lin}}\), that is,  . In this step, we compress each
. In this step, we compress each  into a
into a  -bit string. By applying these two steps, we can achieve the ciphertext rate
-bit string. By applying these two steps, we can achieve the ciphertext rate  .
.
The second step is done by replacing each group element  with a hash value of it. In \(\mathtt {NCE}_{\mathtt {lin}}\), they are used to recover the value of
with a hash value of it. In \(\mathtt {NCE}_{\mathtt {lin}}\), they are used to recover the value of  by checking
by checking  . We can successfully perform this recovery process with overwhelming probability even if
. We can successfully perform this recovery process with overwhelming probability even if  is hashed to a
is hashed to a  -bit string. Furthermore, with the help of an error-correcting code, we can reduce the length of the hash value to
-bit string. Furthermore, with the help of an error-correcting code, we can reduce the length of the hash value to  -bit.
-bit.
In the remaining part, we explain how to perform the first step.
Compressing a Matrix of Group Elements into a Single Group Element. We realize that we do not need all of the elements  to decrypt the ciphertext. Although the receiver gets both
to decrypt the ciphertext. Although the receiver gets both  and
and  for every \(i\in [n]\), the receiver uses only
for every \(i\in [n]\), the receiver uses only  . Recall that the receiver recovers the value of
. Recall that the receiver recovers the value of  by checking whether
by checking whether  holds. This recovery of
holds. This recovery of  can be done even if the sender sends only
can be done even if the sender sends only  , and not
, and not  .
.
This is because, similarly to the equation  , with overwhelming probability, the equation
, with overwhelming probability, the equation  holds if and only if
holds if and only if  . For this reason, we can compress the first part of the ciphertext on \(\mathtt {NCE}_{\mathtt {lin}}\) into
. For this reason, we can compress the first part of the ciphertext on \(\mathtt {NCE}_{\mathtt {lin}}\) into  .
.
We further compress  into a single group element generated by multiplying them, that is,
into a single group element generated by multiplying them, that is,  . In order to do so, we modify the scheme so that the receiver can recover
. In order to do so, we modify the scheme so that the receiver can recover  for every \(i\in [n]\) using \(\mathsf {y}\) instead of
for every \(i\in [n]\) using \(\mathsf {y}\) instead of  . Concretely, for every \(i\in [n]\), the sender computes
. Concretely, for every \(i\in [n]\), the sender computes  as
as

where \(\alpha _j\) is the exponent of  for every \(j\in [n]\) generated by the sender. The sender still generates
for every \(j\in [n]\) generated by the sender. The sender still generates  as a random group element for every \(i\in [n]\). In this case, with overwhelming probability, the receiver can recover
as a random group element for every \(i\in [n]\). In this case, with overwhelming probability, the receiver can recover  by checking whether
by checking whether  holds.
holds.
However, unfortunately, it seems difficult to prove the security of this construction. In order to delete the information of  for indices \(i\in [n]\) such that
for indices \(i\in [n]\) such that  as in the proof of \(\mathtt {NCE}_{\mathtt {lin}}\), we have to change the distribution of
as in the proof of \(\mathtt {NCE}_{\mathtt {lin}}\), we have to change the distribution of  from a random group element to
from a random group element to  so that
so that  and
and  are symmetrically generated. However, we cannot make this change by relying on the DDH assumption since all \(\alpha _j\) are given to the adversary as a part of the sender random coin. Thus, in order to solve this problem, we further modify the scheme and construct an NCE scheme \(\mathtt {NCE}\) as follows.
are symmetrically generated. However, we cannot make this change by relying on the DDH assumption since all \(\alpha _j\) are given to the adversary as a part of the sender random coin. Thus, in order to solve this problem, we further modify the scheme and construct an NCE scheme \(\mathtt {NCE}\) as follows.
The Resulting NCE Scheme \(\mathtt {NCE}\). In \(\mathtt {NCE}\), the receiver first generates  and \(\{A_{i,b}\}_{i\in [n],b\in \{0,1\}}\) in the same way as \(\mathtt {NCE}_{\mathtt {lin}}\). Moreover, instead of the sender, the receiver obliviously generates
and \(\{A_{i,b}\}_{i\in [n],b\in \{0,1\}}\) in the same way as \(\mathtt {NCE}_{\mathtt {lin}}\). Moreover, instead of the sender, the receiver obliviously generates  for every \(i\in [n]\) and \(b\in \{0,1\}\), and adds them into the public key. Moreover, for every \(i\in [n]\), the receiver adds
for every \(i\in [n]\) and \(b\in \{0,1\}\), and adds them into the public key. Moreover, for every \(i\in [n]\), the receiver adds

to the public key. In order to avoid the leakage of the information of  from the public key, for every \(i\in [n]\), we have to add
from the public key, for every \(i\in [n]\), we have to add

to the public key. However, the receiver cannot do it since the receiver generates  obliviously. Thus, instead, the receiver adds the same number of random group elements into the public key. At the beginning of the security proof, we can replace them with
obliviously. Thus, instead, the receiver adds the same number of random group elements into the public key. At the beginning of the security proof, we can replace them with  by relying on the DDH assumption, and eliminate the information of
by relying on the DDH assumption, and eliminate the information of  from the public key. For simplicity, below, we suppose that the public key includes
from the public key. For simplicity, below, we suppose that the public key includes  instead of random group elements.
instead of random group elements.
When encrypting a message m by \(\mathtt {NCE}\), the sender first generates  and computes
and computes  . Then, for every \(i\in [n]\), the sender computes
. Then, for every \(i\in [n]\), the sender computes  as
as

just multiplying  included in the pubic key. Recall that
included in the pubic key. Recall that  . Note that
. Note that  is not included in the public key, but we do not need it to compute
is not included in the public key, but we do not need it to compute  . The sender generates
. The sender generates  as a random group element for every \(i\in [n]\) as before. The resulting ciphertext is
as a random group element for every \(i\in [n]\) as before. The resulting ciphertext is

The receiver can recover  by checking whether
by checking whether  holds, and decrypt the ciphertext.
holds, and decrypt the ciphertext.
By defining the simulator appropriately, the security proof of \(\mathtt {NCE}\) proceeds in a similar way to that of \(\mathtt {NCE}_{\mathtt {lin}}\). In \(\mathtt {NCE}\), for indices \(i\in [n]\) such that  , we can eliminate the information of
, we can eliminate the information of  . We can change
. We can change  from a random group element to
from a random group element to  by relying on the fact that
by relying on the fact that  is indistinguishable from a random group element by the DDH assumption. By this change,
is indistinguishable from a random group element by the DDH assumption. By this change,  and
and  become symmetric and the ciphertext loses the information of
become symmetric and the ciphertext loses the information of  . Then, the remaining part of the proof goes through in a similar way as that of \(\mathtt {NCE}_{\mathtt {lin}}\) except the following point. In \(\mathtt {NCE}\), the first component of the ciphertext, that is,
. Then, the remaining part of the proof goes through in a similar way as that of \(\mathtt {NCE}_{\mathtt {lin}}\) except the following point. In \(\mathtt {NCE}\), the first component of the ciphertext, that is,  has the information of
has the information of  . In order to deal with the issue, in our real construction, we replace \(\mathsf {y}\) with
. In order to deal with the issue, in our real construction, we replace \(\mathsf {y}\) with  , where
, where  . Then, \(\mathsf {y}\) no longer leaks any information of
. Then, \(\mathsf {y}\) no longer leaks any information of  . Moreover, after \(\mathsf {y}\) is fixed, for any
. Moreover, after \(\mathsf {y}\) is fixed, for any  , we can efficiently find
, we can efficiently find  such that
such that  . This is important to ensure that the simulator of \(\mathtt {NCE}\) runs in polynomial time.
. This is important to ensure that the simulator of \(\mathtt {NCE}\) runs in polynomial time.
3.4 Abstraction by Chameleon Encryption
We can describe \(\mathtt {NCE}\) by using obliviously samplable chameleon encryption. If we consider  as a hash key
as a hash key  of chameleon hash function, the first element of the ciphertext
of chameleon hash function, the first element of the ciphertext  can be seen as the output of the hash
can be seen as the output of the hash  . Moreover, group elements contained in the public key are considered as ciphertexts of an chameleon encryption scheme. Oblivious samplability of chameleon encryption makes it possible to deal with the above stated issue of sampling random group elements instead of
. Moreover, group elements contained in the public key are considered as ciphertexts of an chameleon encryption scheme. Oblivious samplability of chameleon encryption makes it possible to deal with the above stated issue of sampling random group elements instead of  for every \(i\in [n]\).
for every \(i\in [n]\).
Relation with Trapdoor Function of Garg and Hajiabadi. We finally remark that the construction of \(\mathtt {NCE}\) can be seen as an extension of that of trapdoor function (TDF) proposed by Garg and Hajiabadi [14].
If we do not add the random mask  to
to  , the key encapsulation part of a ciphertext of \(\mathtt {NCE}\), that is,
, the key encapsulation part of a ciphertext of \(\mathtt {NCE}\), that is,

is the same as an output of the TDF constructed by Garg and Hajiabadi. The major difference between our NCE scheme and their TDF is the secret key. A secret key of their TDF contains all discrete logs of  , that is,
, that is,  . On the other hand, a secret key of our NCE scheme contains half of them corresponding to the bit representation of
. On the other hand, a secret key of our NCE scheme contains half of them corresponding to the bit representation of  , that is,
, that is,  . Garg and Hajiabadi already stated that their TDF can be inverted with
. Garg and Hajiabadi already stated that their TDF can be inverted with  for any
for any  , and use this fact in the security proof of a chosen ciphertext security of a public-key encryption scheme based on their TDF. By explicitly using this technique in the construction, we achieve non-committing property.
, and use this fact in the security proof of a chosen ciphertext security of a public-key encryption scheme based on their TDF. By explicitly using this technique in the construction, we achieve non-committing property.
We observe that construction techniques for TDF seem to be useful for achieving NCE. Encryption schemes that can recover an encryption random coin with a message in the decryption process, such as those based on TDFs, is said to be randomness recoverable. For randomness recoverable schemes, receiver non-committing property is sufficient to achieve full (that is, both sender and receiver) non-committing property. This is because an encryption random coin can be recovered from a ciphertext by using a key generation random coin.
4 Obliviously Samplable Chameleon Encryption
Chameleon encryption was originally introduced by Döttling and Garg [10]. In this work, we introduce a variant of chameleon encryption satisfying oblivious samplability.
4.1 Definiton
We start with the definition of the chameleon hash function.
Definition 4 (Chameleon Hash Function)
A chameleon hash function consists of the following PPT algorithms  . Below, we let the input space and randomness space of
. Below, we let the input space and randomness space of  and
and  , respectively, where
, respectively, where  .
.
-
 : Given the security parameter
: Given the security parameter  , it outputs a hash key
, it outputs a hash key  and a trapdoor \(\mathsf {t}\).
and a trapdoor \(\mathsf {t}\). -
 : Given a hash key
: Given a hash key  and input
and input  , using randomness
, using randomness  , it outputs a hash value \(\mathsf {y}\).
, it outputs a hash value \(\mathsf {y}\). -
 : Given a trapdoor \(\mathsf {t}\), an input to the hash
: Given a trapdoor \(\mathsf {t}\), an input to the hash  , randomness for the hash
, randomness for the hash  and another input to the hash
and another input to the hash 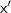 , it outputs randomness
, it outputs randomness  .
.
A chameleon hash function is required to satisfy the following trapdoor collision property.Footnote 2
-
Trapdoor Collision. For all
 and hash randomness
and hash randomness  ,
,  holds, where
holds, where  . Moreover, if
. Moreover, if  is sampled uniformly at random, then so is
is sampled uniformly at random, then so is  .
.
Next, we define the chameleon encryption.
Definition 5 (Chameleon Encryption)
Chameleon encryption (CE) consists of a chameleon hash function  and the following PPT algorithms
and the following PPT algorithms  . Below, we let the input space and randomness space of
. Below, we let the input space and randomness space of  are \(\{0,1\}^n\) and
are \(\{0,1\}^n\) and  , respectively, where
, respectively, where  . We also let the randomness space of
. We also let the randomness space of  and
and  be \(\mathcal {R}_{\mathsf {E}}\). Moreover, we let the output space of
be \(\mathcal {R}_{\mathsf {E}}\). Moreover, we let the output space of  be \(\{0,1\}^\ell \), where \(\ell \) be a polynomial of
be \(\{0,1\}^\ell \), where \(\ell \) be a polynomial of  .
.
-
 : Given a hash key
: Given a hash key 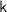 and index
and index  and
and  , using a random coin
, using a random coin  , it outputs a ciphertext \(\mathsf {ct}\).
, it outputs a ciphertext \(\mathsf {ct}\). -
 : Given a hash key
: Given a hash key  and a hash value \(\mathsf {y}\), using a random coin
and a hash value \(\mathsf {y}\), using a random coin  , it outputs
, it outputs  .
. -
 : Given a hash key
: Given a hash key  , a pre-image of the hash
, a pre-image of the hash  and a ciphertext \(\mathsf {ct}\), it outputs
and a ciphertext \(\mathsf {ct}\), it outputs  or \(\bot \).
or \(\bot \).
Chameleon encryption must satisfy the following correctness and security.
-
Correctness. For all
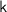 output by
output by  , and
, and  holds, where
holds, where  and
and  .
. -
Security. For any stateful PPT adversary \(\mathcal {A}\), we define the following experiments.

We say \(\mathtt {CE}\) is secure if

holds for every PPT adversary \(\mathcal {A}\).
Remark 1 (On the recyclability)
The above definition of chameleon encryption is slightly different from that of Döttling and Garg [10] since we define it so that it satisfies a property called recyclability introduced by Garg and Hajiabadi [14] when defining a primitive called one-way function with encryption that is similar to chameleon encryption.
More specifically, in our definition, there are two encryption algorithms  and
and  .
.  outputs only a key encapsulation part and
outputs only a key encapsulation part and  outputs only a session key part. In the original definition by Döttling and Garg, there is a single encryption algorithm that outputs the key encapsulation part and a message masked by the session key part at once. Importantly, an output of
outputs only a session key part. In the original definition by Döttling and Garg, there is a single encryption algorithm that outputs the key encapsulation part and a message masked by the session key part at once. Importantly, an output of  does not depend on a hash value \(\mathsf {y}\). This makes possible to relate a single output of
does not depend on a hash value \(\mathsf {y}\). This makes possible to relate a single output of  with multiple hash values. (In other words, a single output of
with multiple hash values. (In other words, a single output of  can be recycled for multiple hash values.) We need this property in the construction of NCE and thus adopt the above definition.
can be recycled for multiple hash values.) We need this property in the construction of NCE and thus adopt the above definition.
We then introduce our main tool, that is, obliviously samplable chameleon encryption (obliviously samplable CE).
Definition 6 (Obliviously Samplable Chameleon Encryption)
Let  be a chameleon encryption scheme. We define two associated PPT algorithms
be a chameleon encryption scheme. We define two associated PPT algorithms  and
and  as follows.
as follows.
-
 : Given the security parameter
: Given the security parameter  , it outputs only a hash key
, it outputs only a hash key 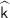 without using any randomness other than
without using any randomness other than  itself.
itself. -
 : Given a hash key
: Given a hash key  and index
and index 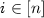 and
and  , it outputs a ciphertext
, it outputs a ciphertext  without using any randomness except
without using any randomness except 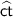 itself.
itself.
For any PPT adversary \(\mathcal {A}\), we also define the following experiments.

The oracles \(O(\cdot ,\cdot )\) and  are defined as follows.
are defined as follows.
-
O(i, b): Given an index
 and
and  , it returns
, it returns  using uniformly random
using uniformly random  .
. -
 : Given an index
: Given an index 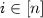 and
and  , it returns
, it returns  .
.
We say that \(\mathtt {CE}\) is obliviously samplable if

holds for every PPT adversary \(\mathcal {A}\).
We define another correctness of obliviously samplable CE necessary to assure the correctness of our NCE.
Definition 7 (Correctness under Obliviously Sampled Keys)
An obliviously samplable CE  is correct under obliviously sampled keys if for all
is correct under obliviously sampled keys if for all  output by
output by  , and
, and  holds, where
holds, where  and
and  .
.
4.2 Construction
We construct an obliviously samplable CE  based on the hardness of the DDH problem.
based on the hardness of the DDH problem.
Let \(\mathbb {G}\) be a cyclic group of order \(p\) with a generator \(g\). In the construction, we use a universal hash family \(\mathcal {H}=\{\mathsf {H_{\mathbb {G}}}:\mathbb {G}\rightarrow \{0,1\}^\ell \}\). Below, let \(\mathsf {H_{\mathbb {G}}}\) be a hash function sampled from \(\mathcal {H}\) uniformly at random, and it is given to all the algorithms implicitly.
-
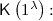
-
For all
 , sample
, sample  and set
and set  .
. -
Output
 (1)
(1)
-
-

-
Sample
 and output
and output  .
.
-
-

-
Parse \(\mathsf {t}\) as in Eq. 1.
-
Output
 .
.
-
-

-
Parse
 as in Eq. 1.
as in Eq. 1. -
Sample
 and compute
and compute  .
. -
Compute
 and
and  .
. -
For all \(j\in [n]\) such that
 , compute
, compute  and
and 
-
Output
 (2)
(2)
-
-
 :
:
-
Output
 .
.
-
-

-
Parse \(\mathsf {ct}\) as in Eq. 2.
-
Output
 .
.
-
-

-
For all
 and
and  , sample
, sample  .
. -
Output
 .
.
-
-

-
Set
 , and sample
, and sample  and
and  .
. -
For all \(j\in [n]\) such that
 , sample
, sample  and
and  .
. -
Output
 .
.
-
Theorem 1
\(\mathtt {CE}\) is an obliviously samplable CE scheme assuming the hardness of the DDH problem.
The trapdoor collision property, correctness, and correctness under obliviously sampled keys of \(\mathtt {CE}\) directly follow from the construction of \(\mathtt {CE}\). Below, we first prove the security of \(\mathtt {CE}\) under the hashed DDH assumption with respect to \(\mathcal {H}\). We then prove the oblivious samplability of \(\mathtt {CE}\) under the DDH assumption.
Security. Let \(\mathcal {A}\) be an adversary against the security of \(\mathtt {CE}\). We construct a reduction algorithm \(\mathcal {A}^{\prime }\) which solves the hashed DDH problem using \(\mathcal {A}\).
Given  , \(\mathcal {A}^{\prime }\) first runs
, \(\mathcal {A}^{\prime }\) first runs  , and generates
, and generates  as follows. For all
as follows. For all  such that
such that  , \(\mathcal {A}^{\prime }\) samples
, \(\mathcal {A}^{\prime }\) samples  and sets
and sets  ,
,  and
and

Next, \(\mathcal {A}^{\prime }\) generates \(\mathsf {ct}\) as follows. \(\mathcal {A}^{\prime }\) first sets \(c\,{:=}\,g_{2}\) and  . Then for all
. Then for all  such that
such that  , \(\mathcal {A}^{\prime }\) sets
, \(\mathcal {A}^{\prime }\) sets  . \(\mathcal {A}^{\prime }\) sets the ciphertext to
. \(\mathcal {A}^{\prime }\) sets the ciphertext to

Finally, \(\mathcal {A}^{\prime }\) outputs what  does.
does.
 and \(\mathsf {ct}\) generated by \(\mathcal {A}^{\prime }\) distribute identically to those output by
and \(\mathsf {ct}\) generated by \(\mathcal {A}^{\prime }\) distribute identically to those output by  and
and  , respectively. \(\mathcal {A}^{\prime }\) perfectly simulates
, respectively. \(\mathcal {A}^{\prime }\) perfectly simulates  to \(\mathcal {A}\) if
to \(\mathcal {A}\) if  because we have
because we have

On the other hand, if  , \(\mathcal {A}^{\prime }\) perfectly simulates
, \(\mathcal {A}^{\prime }\) perfectly simulates  to the adversary. Thus, it holds that
to the adversary. Thus, it holds that  under the hash DDH assumption with respect to \(\mathcal {H}\).
under the hash DDH assumption with respect to \(\mathcal {H}\).
This completes the security proof of \(\mathtt {CE}\).
Oblivious Samplability. Let \(\mathcal {A}\) be an PPT adversary that attacks oblivious samplability of \(\mathtt {CE}\) and makes q queries to its oracle. We prove that the probability that \(\mathcal {A}\) outputs 1 in  is negligibly close to that in
is negligibly close to that in  . The detailed description of these experiments is as follows.
. The detailed description of these experiments is as follows.
-
 : \(\mathcal {A}\) is given a hash key
: \(\mathcal {A}\) is given a hash key  output by
output by  and can access to the oracle
and can access to the oracle  , where \(i\in [n]\), \(b\in \{0,1\}\), and
, where \(i\in [n]\), \(b\in \{0,1\}\), and  . Concretely, O(i, b) behaves as follows.
. Concretely, O(i, b) behaves as follows. - –:
-
Sample
 uniformly from \(\mathbb {Z}_{p}\), and let
uniformly from \(\mathbb {Z}_{p}\), and let  . For all
. For all  , let
, let  and
and  , and let
, and let 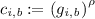 and
and  . Return
. Return  .
.
-
\(\mathsf {Exp}^{\mathrm{os}\text {-}1}_{{\mathtt CE},\mathcal {A}}\): \(\mathcal {A}\) is given a hash key
 output by
output by  and can access to the oracle
and can access to the oracle  , where \(i\in [n]\) and \(b\in \{0,1\}\). Concretely,
, where \(i\in [n]\) and \(b\in \{0,1\}\). Concretely,  behaves as follows.
behaves as follows. - –:
-
Let
 , and sample
, and sample  , and
, and  and
and  for all
for all  uniformly from \(\mathbb {G}\). Return
uniformly from \(\mathbb {G}\). Return  .
.
We define  for every \(j\in \{0,\ldots ,q\}\) that are intermediate experiments between
for every \(j\in \{0,\ldots ,q\}\) that are intermediate experiments between  and
and  as follows. Below, for two experiments
as follows. Below, for two experiments  and
and  , we write
, we write  to denote that the probability that \(\mathcal {A}\) outputs 1 in
to denote that the probability that \(\mathcal {A}\) outputs 1 in  is negligibly close to that in
is negligibly close to that in  .
.
-
 : This experiment is exactly the same as
: This experiment is exactly the same as  except how queries made by \(\mathcal {A}\) are answered. For the \(j'\)-th query \((i,b)\in [n]\times \{0,1\}\) made by \(\mathcal {A}\), the experiment returns
except how queries made by \(\mathcal {A}\) are answered. For the \(j'\)-th query \((i,b)\in [n]\times \{0,1\}\) made by \(\mathcal {A}\), the experiment returns  if \(j < j'\), and
if \(j < j'\), and  otherwise.
otherwise.
We see that  and
and  are exactly the same experiment as
are exactly the same experiment as  and
and  , respectively. Note that \(\mathcal {A}\) is given
, respectively. Note that \(\mathcal {A}\) is given  output by
output by  and can access to the oracle
and can access to the oracle  in
in  , but on the other hand, \(\mathcal {A}\) is given
, but on the other hand, \(\mathcal {A}\) is given  output by
output by  and can access to the oracle
and can access to the oracle  in
in  . However, this is not a problem since
. However, this is not a problem since  output by
output by  and
and  output by
output by  distribute identically in our construction. For every \(j\in [q]\),
distribute identically in our construction. For every \(j\in [q]\),  directly follows from Lemma 3. Therefore, we have
directly follows from Lemma 3. Therefore, we have  under the DDH assumption. From the above arguments, \(\mathtt {CE}\) satisfies oblivious samplability under the DDH assumption.
under the DDH assumption. From the above arguments, \(\mathtt {CE}\) satisfies oblivious samplability under the DDH assumption.
This completes the proof of Theorem 1.
5 Basic Construction of Proposed NCE
In this section, we present our NCE scheme with ciphertext rate  from an obliviously samplable CE. We call this construction basic construction. In Sect. 6, improving the basic construction, we describe our full construction of NCE which achieves ciphertext rate
from an obliviously samplable CE. We call this construction basic construction. In Sect. 6, improving the basic construction, we describe our full construction of NCE which achieves ciphertext rate  .
.
5.1 Construction
We use three parameters \(\mu \), \({n}\), and \(\ell \), all of which are polynomials of  and concretely determined later.
and concretely determined later.
Let  be an obliviously samplable CE scheme. We let the input length of
be an obliviously samplable CE scheme. We let the input length of  be n and let the output length of
be n and let the output length of  (and thus
(and thus  ) be \(\ell \). We also let the randomness spaces of
) be \(\ell \). We also let the randomness spaces of  and
and  be
be  and \(\mathcal {R}_{\mathsf {E}}\), respectively. Below, using \(\mathtt {CE}\), we construct an NCE scheme
and \(\mathcal {R}_{\mathsf {E}}\), respectively. Below, using \(\mathtt {CE}\), we construct an NCE scheme  whose message space is \(\{0,1\}^\mu \).
whose message space is \(\{0,1\}^\mu \).
In the construction, we use a matrix \({R}\in \{0,1\}^{\mu \times {n}}\), such that randomly picked \(\mu \) out of \({n}\) column vectors of length \(\mu \) are linearly independent. A random matrix satisfies such property except for negligible probability [21].
We first describe  and show the correctness of \(\mathtt {NCE}\) below. We also describe a protocol when using \(\mathtt {NCE}\) in Fig. 3.
and show the correctness of \(\mathtt {NCE}\) below. We also describe a protocol when using \(\mathtt {NCE}\) in Fig. 3.
-
 :
:
-
Sample
 and
and  .
. -
For all
 , sample
, sample  .
. -
For all
 and
and  , compute
, compute 
-
Output
 (3)
(3)The random coin
 used in
used in  is
is 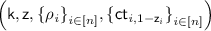 .
.
-
-
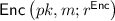 :
:
-
Sample
 and
and  .
. -
Compute
 .
. -
For all
 and
and 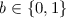 , compute
, compute 
-
Compute
 .
. -
Output
 (4)
(4)The random coin
 used in
used in  is
is 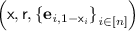 .
.
-
-
 :
:
By setting \(\ell =\mathsf {poly}(\log \lambda )\), \(\mathtt {NCE}\) is correct. Formally, we have the following theorem.
Theorem 2
Let \(\ell =\mathsf {poly}(\log \lambda )\). If \(\mathtt {CE}\) is correct under obliviously sampled keys, then \(\mathtt {NCE}\) is correct.
Proof
Due to the correctness under obliviously sampled keys of \(\mathtt {CE}\), the recovery of  fails only when
fails only when  happens and
happens and  coincides with
coincides with  . Thus, the probability of decryption failure is bounded by
. Thus, the probability of decryption failure is bounded by

Note that at the last step, we used the union bound. Since  , the probability is negligible by setting
, the probability is negligible by setting  . Therefore \(\mathtt {NCE}\) is correct.
. Therefore \(\mathtt {NCE}\) is correct.
Intuition for the Simulators and Security Proof. The description of the simulators  of \(\mathtt {NCE}\) is somewhat complex. Thus, we give an overview of the security proof for \(\mathtt {NCE}\) before describing them. We think this will help readers understand the construction of simulators.
of \(\mathtt {NCE}\) is somewhat complex. Thus, we give an overview of the security proof for \(\mathtt {NCE}\) before describing them. We think this will help readers understand the construction of simulators.
In the proof, we start from the real experiment  , where \(\mathcal {A}\) is an PPT adversary attacking the security of \(\mathtt {NCE}\). We then change the experiment step by step so that, in the final experiment, we can generate the ciphertext
, where \(\mathcal {A}\) is an PPT adversary attacking the security of \(\mathtt {NCE}\). We then change the experiment step by step so that, in the final experiment, we can generate the ciphertext  given to \(\mathcal {A}\) without the message m chosen by \(\mathcal {A}\), which can later be opened to any message. The simulators
given to \(\mathcal {A}\) without the message m chosen by \(\mathcal {A}\), which can later be opened to any message. The simulators  are defined so that they simulate the final experiment.
are defined so that they simulate the final experiment.
In  is of the form
is of the form

Informally,  encapsulates
encapsulates  , and
, and  is a one-time encryption of \(m\in \{0,1\}^\mu \) by
is a one-time encryption of \(m\in \{0,1\}^\mu \) by  . If we can eliminate the information of
. If we can eliminate the information of  from the encapsulation part,
from the encapsulation part,  becomes statistically independent of m. Thus, if we can do that, the security proof is almost complete since in that case,
becomes statistically independent of m. Thus, if we can do that, the security proof is almost complete since in that case,  can be simulated without m and later be opened to any message. While we cannot eliminate the entire information of
can be simulated without m and later be opened to any message. While we cannot eliminate the entire information of  from the encapsulation part, we can eliminate the information of \(\mu \) out of n bits of
from the encapsulation part, we can eliminate the information of \(\mu \) out of n bits of  from the encapsulation part, and it is enough to make
from the encapsulation part, and it is enough to make  statistically independent of m. Below, we briefly explain how to do it.
statistically independent of m. Below, we briefly explain how to do it.
We first change  contained in
contained in  so that every \(\mathsf {ct}_{i,b}\) is generated as
so that every \(\mathsf {ct}_{i,b}\) is generated as  , and set
, and set  , where
, where  is a random string generated in
is a random string generated in  . We can make this change by the oblivious samplability of \(\mathtt {CE}\).
. We can make this change by the oblivious samplability of \(\mathtt {CE}\).
Next, by using the security of \(\mathtt {CE}\), we try to change the experiment so that for every \(i\in [n]\),  and
and  contained in
contained in  are symmetrically generated in order to eliminate the information of
are symmetrically generated in order to eliminate the information of  from the encapsulation part. Concretely, for every \(i\in [n]\), we try to change
from the encapsulation part. Concretely, for every \(i\in [n]\), we try to change  from a random string to
from a random string to

Unfortunately, we cannot change the distribution of every  because some of
because some of  is given to \(\mathcal {A}\) as a part of
is given to \(\mathcal {A}\) as a part of  . Concretely, for \(i\in [n]\) such that
. Concretely, for \(i\in [n]\) such that  ,
,  is given to \(\mathcal {A}\) and we cannot change the distribution of
is given to \(\mathcal {A}\) and we cannot change the distribution of  . On the other hand, for \(i\in [n]\) such that
. On the other hand, for \(i\in [n]\) such that  , we can change the distribution of
, we can change the distribution of  .
.
In order to make clear which index \(i\in [n]\) we can change the distribution of  , in the proof, we replace
, in the proof, we replace  with
with  . Then, we can say that for \(i\in [n]\) such that
. Then, we can say that for \(i\in [n]\) such that  , we can change the distribution of
, we can change the distribution of  . Since
. Since  is chosen uniformly at random, due to the Chernoff bound, we can ensure that the number of such indices is greater than \(\mu \) with overwhelming probability by setting n and \(\mu \) appropriately. Namely, we can eliminate the information of \(\mu \) out of n bits of
is chosen uniformly at random, due to the Chernoff bound, we can ensure that the number of such indices is greater than \(\mu \) with overwhelming probability by setting n and \(\mu \) appropriately. Namely, we can eliminate the information of \(\mu \) out of n bits of  from
from  . At this point,
. At this point,  becomes statistically independent of m, and we almost complete the security proof. Note that \(\mathsf {y}\) itself does not have any information of
becomes statistically independent of m, and we almost complete the security proof. Note that \(\mathsf {y}\) itself does not have any information of  . To make this fact clear, in the proof, we add another step using the trapdoor collision property of \(\mathtt {CE}\) after using the security of \(\mathtt {CE}\).
. To make this fact clear, in the proof, we add another step using the trapdoor collision property of \(\mathtt {CE}\) after using the security of \(\mathtt {CE}\).
To complete the proof formally, we have to ensure that  can later be opened to any message efficiently (i.e., in polynomial time). This is possible by using a matrix \({R}\in \{0,1\}^{\mu \times {n}}\), such that randomly picked \(\mu \) out of \({n}\) column vectors of length \(\mu \) are linearly independent. For more details, see the formal security proof in Sect. 5.2.
can later be opened to any message efficiently (i.e., in polynomial time). This is possible by using a matrix \({R}\in \{0,1\}^{\mu \times {n}}\), such that randomly picked \(\mu \) out of \({n}\) column vectors of length \(\mu \) are linearly independent. For more details, see the formal security proof in Sect. 5.2.
We now show the simulators  .
.
-
\(\mathsf {Sim}_{\mathsf{1}}\,(1^{\lambda })\):
-
Sample
 .
. -
For all
 and
and  , sample
, sample  and compute
and compute  .
. -
Sample
 Footnote 3, and
Footnote 3, and  .
. -
Compute
 and sample
and sample  .
. -
For all
 and
and  , compute
, compute 
-
Output

and
 .
.
-
-
\(\mathsf {Sim}_{\mathsf{2}}\,(m, st )\):
-
Sample
 at random from \(\{0,1\}^n\) under the condition that
at random from \(\{0,1\}^n\) under the condition that  and
and  hold for every \(i\in [n]\) such that
hold for every \(i\in [n]\) such that  .
. -
Compute
 and
and  .
. -
Output
-

5.2 Security Proof
In this section, we prove the security of \(\mathtt {NCE}\). Formally, we prove the following theorem.
Theorem 3
Let  and \({n}=8\mu \). If \(\mathtt {CE}\) is an obliviously samplable CE, then \(\mathtt {NCE}\) is secure.
and \({n}=8\mu \). If \(\mathtt {CE}\) is an obliviously samplable CE, then \(\mathtt {NCE}\) is secure.
Proof
Let \(\mathcal {A}\) is a PPT adversary attacking the security of \(\mathtt {NCE}\). We define a sequence of experiments  . Below, for two experiments
. Below, for two experiments  and
and  , we write
, we write  (resp.
(resp.  ) to denote that the probability that \(\mathcal {A}\) outputs 1 in
) to denote that the probability that \(\mathcal {A}\) outputs 1 in  is negligibly close to (resp. the same as) that in
is negligibly close to (resp. the same as) that in  .
.
-
 : This experiment is exactly the same as
: This experiment is exactly the same as  . The detailed description is as follows. 1. The experiment first samples
. The detailed description is as follows. 1. The experiment first samples  and
and  . Then, for all
. Then, for all  , it samples
, it samples  . Next, for all
. Next, for all  and
and  , it computes
, it computes 
It sets

Finally, it runs
 . Note that
. Note that  is used in the next step.
is used in the next step.2. The experiment samples
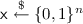 and
and  . It then computes
. It then computes  . For all
. For all  and
and  , it also computes
, it also computes 
It sets

Finally, it outputs
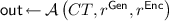 .
. -
 : This experiment is the same as
: This experiment is the same as  except the followings. First,
except the followings. First, 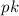 is generated together with a trapdoor of the chameleon hash function \(\mathsf {t}\) as
is generated together with a trapdoor of the chameleon hash function \(\mathsf {t}\) as  instead of
instead of  . Moreover, all ciphertexts of chameleon encryption
. Moreover, all ciphertexts of chameleon encryption  are computed by
are computed by  , instead of
, instead of  . Specifically, for every
. Specifically, for every  and
and  , the experiment samples
, the experiment samples  and compute
and compute  . Also, it sets
. Also, it sets  .
.
Lemma 5
Assuming the oblivious samplability of \(\mathtt {CE}\),  holds.
holds.
Proof
Using \(\mathcal {A}\), we construct a reduction algorithm \({\mathcal {A}^{\prime }}^{{O}^*(\cdot ,\cdot )}\) that attacks the oblivious samplability of \(\mathtt {CE}\) and makes \({n}\) oracle queries.
-
1.
On receiving a hash key
 , \(\mathcal {A}^{\prime }\) generates
, \(\mathcal {A}^{\prime }\) generates  for every \(i\in [n]\) and sets the public key as
for every \(i\in [n]\) and sets the public key as  , where
, where 
\({\mathcal {A}^{\prime }}^{{O}^*(\cdot ,\cdot )}\) also sets
 . Then, \({\mathcal {A}^{\prime }}^{{O}^*(\cdot ,\cdot )}\) runs
. Then, \({\mathcal {A}^{\prime }}^{{O}^*(\cdot ,\cdot )}\) runs  and obtains m.
and obtains m. -
2.
\({\mathcal {A}^{\prime }}^{{O}^*(\cdot ,\cdot )}\) simulates the step 2. of
 and
and  , and outputs what \(\mathcal {A}\) does. Note that the step 2. of
, and outputs what \(\mathcal {A}\) does. Note that the step 2. of  is exactly the same as that of
is exactly the same as that of  .
.
When playing  and
and  , \(\mathcal {A}^{\prime }\) perfectly simulates
, \(\mathcal {A}^{\prime }\) perfectly simulates  and
and  for \(\mathcal {A}\), respectively. By the oblivious samplability of \(\mathtt {CE}\),
for \(\mathcal {A}\), respectively. By the oblivious samplability of \(\mathtt {CE}\),

holds. This proves  .
.
-
 : This experiment is the same as
: This experiment is the same as  , except that we replace
, except that we replace  contained in
contained in  by
by  .
.
Because  distributes uniformly at random, so does
distributes uniformly at random, so does  . Therefore, the distribution of the inputs to \(\mathcal {A}\) does not change between
. Therefore, the distribution of the inputs to \(\mathcal {A}\) does not change between  and
and  , and thus
, and thus  holds.
holds.
-
 : The essential difference from
: The essential difference from  in this experiment is that when
in this experiment is that when  is computed by
is computed by  instead of uniformly sampled from \(\{0,1\}^\ell \).
instead of uniformly sampled from \(\{0,1\}^\ell \).Additionally, each
 is replaced to
is replaced to  from
from  , though this does not change the distribution due to the correctness of \(\mathtt {CE}\). After all, for every
, though this does not change the distribution due to the correctness of \(\mathtt {CE}\). After all, for every  and
and  , the experiment computes
, the experiment computes 
Lemma 6
If \(\mathtt {CE}\) is correct and secure,  holds.
holds.
Proof
This proof is done by hybrid arguments. We define  for every \(j\in \{0,\ldots ,n\}\) that are intermediate experiments between
for every \(j\in \{0,\ldots ,n\}\) that are intermediate experiments between  and
and  as follows.
as follows.
-
 : This experiment is exactly the same as
: This experiment is exactly the same as  except how
except how  is generated for every \(i\in [n]\). For
is generated for every \(i\in [n]\). For  is generated as in
is generated as in  . For
. For  is generated as in
is generated as in  .
.
 is equal to
is equal to  , and
, and  is equal to
is equal to  . In the following, we show
. In the following, we show  for all \(j\in [n]\).
for all \(j\in [n]\).
In the case of  , except negligible probability,
, except negligible probability,  distributes identically in
distributes identically in  and
and  because
because  holds with overwhelming probability due to the correctness of \(\mathtt {CE}\). Moreover,
holds with overwhelming probability due to the correctness of \(\mathtt {CE}\). Moreover,  is generated in the same way in both experiments. Thus
is generated in the same way in both experiments. Thus  holds.
holds.
In the case of  , we show
, we show  by constructing a reduction algorithm \(\mathcal {A}^{\prime }\) that uses \(\mathcal {A}\) and attacks the security of \(\mathtt {CE}\). The description of \(\mathcal {A}^{\prime }\) is as follows.
by constructing a reduction algorithm \(\mathcal {A}^{\prime }\) that uses \(\mathcal {A}\) and attacks the security of \(\mathtt {CE}\). The description of \(\mathcal {A}^{\prime }\) is as follows.
-
1.
\(\mathcal {A}^{\prime }\) samples
 and
and 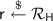 , outputs
, outputs  , and receives
, and receives  . Then, \(\mathcal {A}^{\prime }\) generates
. Then, \(\mathcal {A}^{\prime }\) generates  as follows. \(\mathcal {A}^{\prime }\) first samples
as follows. \(\mathcal {A}^{\prime }\) first samples  and sets
and sets  . For every \((i,b)\in [n]\times \{0,1\}\) such that
. For every \((i,b)\in [n]\times \{0,1\}\) such that  , \(\mathcal {A}^{\prime }\) samples
, \(\mathcal {A}^{\prime }\) samples  and computes
and computes 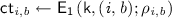 . \(\mathcal {A}^{\prime }\) sets
. \(\mathcal {A}^{\prime }\) sets  ,
, 
Finally, \(\mathcal {A}^{\prime }\) runs
 . Note that
. Note that  since we consider the case of
since we consider the case of  , and thus \(\mathcal {A}^{\prime }\) generates
, and thus \(\mathcal {A}^{\prime }\) generates  by itself for every \(i\in [n]\).
by itself for every \(i\in [n]\). -
2.
\(\mathcal {A}^{\prime }\) computes
 . For
. For  , \(\mathcal {A}^{\prime }\) computes
, \(\mathcal {A}^{\prime }\) computes  as in
as in  , and for
, and for  , it does as in
, it does as in  . For
. For  , \(\mathcal {A}^{\prime }\) computes
, \(\mathcal {A}^{\prime }\) computes  and sets
and sets  . Finally, \(\mathcal {A}^{\prime }\) sets
. Finally, \(\mathcal {A}^{\prime }\) sets 
and outputs
 .
.
When playing  , \(\mathcal {A}^{\prime }\) simulates
, \(\mathcal {A}^{\prime }\) simulates  for \(\mathcal {A}\). Also, when playing
for \(\mathcal {A}\). Also, when playing  , \(\mathcal {A}^{\prime }\) simulates
, \(\mathcal {A}^{\prime }\) simulates  for \(\mathcal {A}\). By the security of \(\mathtt {CE}\),
for \(\mathcal {A}\). By the security of \(\mathtt {CE}\),

holds. From the above, we have

We can conclude  .
.
-
 : This experiment is the same as
: This experiment is the same as  except how \(\mathsf {y}\) and
except how \(\mathsf {y}\) and  are computed. In this experiment, \(\mathsf {y}\) is computed as
are computed. In this experiment, \(\mathsf {y}\) is computed as  . Moreover, the randomness
. Moreover, the randomness  contained in
contained in  is replaced with
is replaced with  .
.
Due to the trapdoor collision property of \(\mathtt {CE}\), the view of \(\mathcal {A}\) does not change between  and
and  . Thus,
. Thus,  holds.
holds.
-
 : This experiment is the same as
: This experiment is the same as  , except that
, except that  is replaced with
is replaced with  . Moreover, the experiment computes
. Moreover, the experiment computes  as
as  , and replaces
, and replaces  in
in  with
with  , where
, where  is a uniformly random string sampled from \(\{0,1\}^n\) under the following two conditions:
is a uniformly random string sampled from \(\{0,1\}^n\) under the following two conditions:–
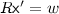 holds.
holds.–
 holds for every \(i\in [n]\) such that
holds for every \(i\in [n]\) such that  .
.
Before showing  , we review a basic lemma on inversion sampling.
, we review a basic lemma on inversion sampling.
Lemma 7
For a function \(f:\mathcal {X}\rightarrow \mathcal {Y}\), we define two distributions \(\mathcal {D}_1\) and \(\mathcal {D}_2\) as  and
and 
 , where \(f^{-1}(y)\) denotes the set of pre-images of y. Then, \(\mathcal {D}_1\) and \(\mathcal {D}_2\) are identical.
, where \(f^{-1}(y)\) denotes the set of pre-images of y. Then, \(\mathcal {D}_1\) and \(\mathcal {D}_2\) are identical.
Furthermore, we define a distribution \(\mathcal {D}_3\) as 
 . If f has a property that f(x) distributes uniformly at random over \(\mathcal {Y}\) if the input x distributes uniformly at random over \(\mathcal {X}\), \(\mathcal {D}_1\) and \(\mathcal {D}_3\) are identical.
. If f has a property that f(x) distributes uniformly at random over \(\mathcal {Y}\) if the input x distributes uniformly at random over \(\mathcal {X}\), \(\mathcal {D}_1\) and \(\mathcal {D}_3\) are identical.
Lemma 8
 holds.
holds.
Proof
According to the Chernoff bound on  ,
,

holds for any \(\delta >0\). By taking \(\delta =1-\frac{2\mu }{{n}}\), we have

Below, we show that  in
in  has the same distribution as
has the same distribution as  in
in  in the case of
in the case of  , and complete the proof of this lemma.
, and complete the proof of this lemma.
We first introduce some notations. For an integer ordered set \(\mathcal {I}\subset [n]\), we define \(R_{\mathcal {I}}\) as the restriction of R to \(\mathcal {I}\), that is \(R_{\mathcal {I}}=(\mathbf {r}_1|\cdots |\mathbf {r}_{\left|\mathcal {I}\right|})\), where \(R=(\mathbf {r}_1|\cdots |\mathbf {r}_n)\). We define  in a similar way.
in a similar way.
Fix any  which satisfies
which satisfies  and set
and set  . Because \(\left|\mathcal {I}\right|\ge \mu \), \({R}_{\mathcal {I}}\) is full rank due to the choice of \({R}\). Hence, \({R}_{\mathcal {I}}\cdot u\) is uniformly random over \(\{0,1\}^\mu \) if u is uniformly random over \(\{0,1\}^{\left|\mathcal {I}\right|}\).
. Because \(\left|\mathcal {I}\right|\ge \mu \), \({R}_{\mathcal {I}}\) is full rank due to the choice of \({R}\). Hence, \({R}_{\mathcal {I}}\cdot u\) is uniformly random over \(\{0,1\}^\mu \) if u is uniformly random over \(\{0,1\}^{\left|\mathcal {I}\right|}\).
Then, from Lemma 7 when setting  , and
, and  , the distribution of
, the distribution of  and \((u,{w})\) are the same, where
and \((u,{w})\) are the same, where  , and
, and  . Moreover, we have
. Moreover, we have  . Since
. Since  sampled in
sampled in  is a bit string generated by replacing \(i_k\)-th bit of
is a bit string generated by replacing \(i_k\)-th bit of  with k-th bit of u for every \(k\in [\left|\mathcal {I}\right|]\), we see that
with k-th bit of u for every \(k\in [\left|\mathcal {I}\right|]\), we see that  has the same distribution as
has the same distribution as  .
.  also has the same distribution as
also has the same distribution as  because \({w}\) is sampled uniformly at random, and thus
because \({w}\) is sampled uniformly at random, and thus  has the same distribution as
has the same distribution as  . This completes the proof of Lemma 8.
. This completes the proof of Lemma 8.
Note that we can sample the above u in polynomial time, by computing a particular solution \(v\in \{0,1\}^{\left|\mathcal {I}\right|}\) of \({R}_{\mathcal {I}}\cdot v ={w}\), and add a vector sampled uniformly at random from the kernel of \({R}_{\mathcal {I}}\).
-
 : This experiment is the same as
: This experiment is the same as  except that \({w}\) is replaced with
except that \({w}\) is replaced with  . By this change,
. By this change,  is of the form
is of the form 
Moreover,
 contained in
contained in  is sampled so that
is sampled so that  holds.
holds.
Since \({w}\) is uniformly at random, so is  . Thus,
. Thus,  holds.
holds.
We see that  is the same as
is the same as  . Put all the above arguments together, we have
. Put all the above arguments together, we have

Hence \(\mathtt {NCE}\) is secure. This completes the proof of Theorem 3.
5.3 Ciphertext Rate
Finally, we evaluate the ciphertext rate of \(\mathtt {NCE}\). From Theorem 2, in order to make \(\mathtt {NCE}\) correct, it is sufficient to set  . Moreover, from Theorem 3, in order to make \(\mathtt {NCE}\) secure, it is sufficient to set
. Moreover, from Theorem 3, in order to make \(\mathtt {NCE}\) secure, it is sufficient to set  and \({n}=8\mu \). In this setting, the ciphertext length of \(\mathtt {NCE}\) is
and \({n}=8\mu \). In this setting, the ciphertext length of \(\mathtt {NCE}\) is  . Note that we assume a group element of \(\mathbb {G}\) is described as a
. Note that we assume a group element of \(\mathbb {G}\) is described as a  -bit string. Then, the ciphertext rate of \(\mathtt {NCE}\) is evaluated as
-bit string. Then, the ciphertext rate of \(\mathtt {NCE}\) is evaluated as

6 Full Construction of Proposed NCE
In the basic construction, we construct an NCE scheme with correctness  , by setting
, by setting  which is the output length of
which is the output length of  (and thus
(and thus  ) of the underlying \(\mathtt {CE}\). Of course, if we set \(\ell \) to
) of the underlying \(\mathtt {CE}\). Of course, if we set \(\ell \) to  , we can make the ciphertext rate of the resulting NCE scheme
, we can make the ciphertext rate of the resulting NCE scheme  . However, this modification also affects the correctness of the resulting NCE scheme. \(\gamma \) is no longer
. However, this modification also affects the correctness of the resulting NCE scheme. \(\gamma \) is no longer  , and is at most
, and is at most  .
.
Fortunately, we can amplify the correctness of the scheme to  from enough large constant without changing the ciphertext rate. For that purpose, we use a constant-rate error-correcting code which can correct errors up to some constant fraction. Concretely, we modify the scheme as follows. In the encryption, we first encode the plaintext by the error-correcting code and parse it into
from enough large constant without changing the ciphertext rate. For that purpose, we use a constant-rate error-correcting code which can correct errors up to some constant fraction. Concretely, we modify the scheme as follows. In the encryption, we first encode the plaintext by the error-correcting code and parse it into  blocks of length \(\mu \). Then, we encrypt each block by the \(\gamma \)-correct NCE scheme for a constant \(\gamma \) using different public keys. The decryption is done naturally, i.e., decrypt each ciphertext, concatenate them, and decode it. The ciphertext rate is still
blocks of length \(\mu \). Then, we encrypt each block by the \(\gamma \)-correct NCE scheme for a constant \(\gamma \) using different public keys. The decryption is done naturally, i.e., decrypt each ciphertext, concatenate them, and decode it. The ciphertext rate is still  because the rate of error-correcting code is constant.
because the rate of error-correcting code is constant.
This block-wise encryption technique not only amplifies the correctness but also reduces the public key size. In the basic construction, the size of a public key depends on the length of a message quadratically. However, by applying the block-wise encryption technique, it becomes linear in the length of a message.
The description of the full construction is as follows. Let  be a constant-rate error-correcting code which can correct errors up to \(\epsilon \)-fraction of the codeword where \(\epsilon >0\) is some constant.
be a constant-rate error-correcting code which can correct errors up to \(\epsilon \)-fraction of the codeword where \(\epsilon >0\) is some constant.
Specifically, given a message  ,
,  outputs a codeword
outputs a codeword  . If
. If  ,
,  . The rate of \(\mathtt {ECC}\) is some constant N/M.
. The rate of \(\mathtt {ECC}\) is some constant N/M.
Let  be an NCE scheme whose message space is \(\{0,1\}^{\mu }\), ciphertext rate is
be an NCE scheme whose message space is \(\{0,1\}^{\mu }\), ciphertext rate is  , and correctness is \(\gamma =1-\frac{\epsilon }{2}\). We construct
, and correctness is \(\gamma =1-\frac{\epsilon }{2}\). We construct  as follows. The message space of \(\overrightarrow{\mathtt {NCE}}\) is \(\{0,1\}^{\mu M}\).
as follows. The message space of \(\overrightarrow{\mathtt {NCE}}\) is \(\{0,1\}^{\mu M}\).
-
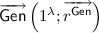 :
:-
Parse the given random coin to
 .
. -
For all
 , generate key pairs
, generate key pairs  .
. -
Output
 and
and  .
.
-
-
 :
:-
Parse
 .
. -
Compute
 and parse
and parse  .
. -
For all
 , compute
, compute  .
. -
Output
 .
.
-
-
 :
: -
For all
 , Compute
, Compute  .
. -
Concatenate them as
 .
. -
Output
 .
.
-
-
 :
:-
For all
 , compute
, compute  ,
, -
Output
 ,
,  , and
, and  .
.
-
-
 :
:-
Compute
 and parse
and parse  .
. -
For all
 , compute
, compute  .
. -
Output
 and
and  .
.
-
Correctness. We can prove the correctness of \(\overrightarrow{\mathtt {NCE}}\) by the Chernoff bound. Formally, we have the following theorem. See the full version for the proof.
Theorem 4
Let \(\mathtt {ECC}\) be an constant-rate error-correcting code which can correct errors up to \(\epsilon \)-fraction of a codeword. Let \(\mathtt {NCE}\) be a \(\gamma \)-correct NCE scheme, where \(\gamma =1-\frac{\epsilon }{2}\). If the number of parsed codeword  , the above \(\overrightarrow{\mathtt {NCE}}\) is correct.
, the above \(\overrightarrow{\mathtt {NCE}}\) is correct.
Security. For the security of  , we have the following theorem. Since we can prove it via a straightforward hybrid argument, we omit it.
, we have the following theorem. Since we can prove it via a straightforward hybrid argument, we omit it.
Theorem 5
If \(\mathtt {NCE}\) is an secure NCE scheme, then \(\overrightarrow{\mathtt {NCE}}\) is also secure.
Ciphertext Rate. Since rate of the error-correcting code  is constant, the ciphertext rate of \(\overrightarrow{\mathtt {NCE}}\) is
is constant, the ciphertext rate of \(\overrightarrow{\mathtt {NCE}}\) is  .
.
Notes
- 1.
- 2.
Usually, a chameleon hash function is required to be collision resistant, but we omit it since it is implied by the security of chameleon encryption defined later.
- 3.
 and
and  do not use
do not use  for
for  such that
such that  , but for simplicity, we generate whole
, but for simplicity, we generate whole  .
.
References
Beaver, D.: Plug and play encryption. In: Kaliski, B.S. (ed.) CRYPTO 1997. LNCS, vol. 1294, pp. 75–89. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0052228
Bellare, M., Palacio, A.: The knowledge-of-exponent assumptions and 3-round zero-knowledge protocols. In: Franklin, M. (ed.) CRYPTO 2004. LNCS, vol. 3152, pp. 273–289. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28628-8_17
Brakerski, Z., Lombardi, A., Segev, G., Vaikuntanathan, V.: Anonymous IBE, leakage resilience and circular security from new assumptions. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part I. LNCS, vol. 10820, pp. 535–564. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78381-9_20
Canetti, R., Feige, U., Goldreich, O., Naor, M.: Adaptively secure multi-party computation. In: 28th ACM STOC, pp. 639–648 (1996)
Canetti, R., Poburinnaya, O., Raykova, M.: Optimal-rate non-committing encryption. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017, Part III. LNCS, vol. 10626, pp. 212–241. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70700-6_8
Cho, C., Döttling, N., Garg, S., Gupta, D., Miao, P., Polychroniadou, A.: Laconic oblivious transfer and its applications. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part II. LNCS, vol. 10402, pp. 33–65. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63715-0_2
Choi, S.G., Dachman-Soled, D., Malkin, T., Wee, H.: Improved non-committing encryption with applications to adaptively secure protocols. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 287–302. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_17
Damgård, I., Nielsen, J.B.: Improved non-committing encryption schemes based on a general complexity assumption. In: Bellare, M. (ed.) CRYPTO 2000. LNCS, vol. 1880, pp. 432–450. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44598-6_27
Döttling, N., Garg, S.: From selective IBE to full IBE and selective HIBE. In: Kalai, Y., Reyzin, L. (eds.) TCC 2017, Part I. LNCS, vol. 10677, pp. 372–408. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70500-2_13
Döttling, N., Garg, S.: Identity-based encryption from the Diffie-Hellman assumption. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017, Part I. LNCS, vol. 10401, pp. 537–569. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63688-7_18
Döttling, N., Garg, S., Hajiabadi, M., Masny, D.: New constructions of identity-based and key-dependent message secure encryption schemes. In: Abdalla, M., Dahab, R. (eds.) PKC 2018, Part I. LNCS, vol. 10769, pp. 3–31. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-76578-5_1
Döttling, N., Garg, S., Ishai, Y., Malavolta, G., Mour, T., Ostrovsky, R.: Trapdoor hash functions and their applications. In: Boldyreva, A., Micciancio, D. (eds.) CRYPTO 2019, Part III. LNCS, vol. 11694, pp. 3–32. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-26954-8_1
Garg, S., Gay, R., Hajiabadi, M.: New techniques for efficient trapdoor functions and applications. In: Ishai, Y., Rijmen, V. (eds.) EUROCRYPT 2019, Part III. LNCS, vol. 11478, pp. 33–63. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-17659-4_2
Garg, S., Hajiabadi, M.: Trapdoor functions from the computational Diffie-Hellman assumption. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part II. LNCS, vol. 10992, pp. 362–391. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96881-0_13
Garg, S., Ostrovsky, R., Srinivasan, A.: Adaptive garbled RAM from laconic oblivious transfer. In: Shacham, H., Boldyreva, A. (eds.) CRYPTO 2018, Part III. LNCS, vol. 10993, pp. 515–544. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-96878-0_18
Garg, S., Srinivasan, A.: Adaptively secure garbling with near optimal online complexity. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part II. LNCS, vol. 10821, pp. 535–565. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_18
Garg, S., Srinivasan, A.: Two-round multiparty secure computation from minimal assumptions. In: Nielsen, J.B., Rijmen, V. (eds.) EUROCRYPT 2018, Part II. LNCS, vol. 10821, pp. 468–499. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-78375-8_16
Hada, S., Tanaka, T.: On the existence of 3-round zero-knowledge protocols. In: Krawczyk, H. (ed.) CRYPTO 1998. LNCS, vol. 1462, pp. 408–423. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0055744
Hemenway, B., Ostrovsky, R., Richelson, S., Rosen, A.: Adaptive security with quasi-optimal rate. In: Kushilevitz, E., Malkin, T. (eds.) TCC 2016, Part I. LNCS, vol. 9562, pp. 525–541. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49096-9_22
Hemenway, B., Ostrovsky, R., Rosen, A.: Non-committing encryption from \(\phi \)-hiding. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015, Part I. LNCS, vol. 9014, pp. 591–608. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-46494-6_24
Tao, T., Vu, V.: On the singularity probability of random Bernoulli matrices. J. Am. Math. Soc. 20(3), 603–628 (2007)
Acknowledgements
A part of this work was supported by NTT Secure Platform Laboratories, JST OPERA JPMJOP1612, JST CREST JPMJCR14D6, JSPS KAKENHI JP16H01705, JP17H01695, JP19J22363.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 International Association for Cryptologic Research
About this paper
Cite this paper
Yoshida, Y., Kitagawa, F., Tanaka, K. (2019). Non-Committing Encryption with Quasi-Optimal Ciphertext-Rate Based on the DDH Problem. In: Galbraith, S., Moriai, S. (eds) Advances in Cryptology – ASIACRYPT 2019. ASIACRYPT 2019. Lecture Notes in Computer Science(), vol 11923. Springer, Cham. https://doi.org/10.1007/978-3-030-34618-8_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-34618-8_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-34617-1
Online ISBN: 978-3-030-34618-8
eBook Packages: Computer ScienceComputer Science (R0)





 : Given the security parameter
: Given the security parameter  , using a random coin
, using a random coin  , it outputs a public key
, it outputs a public key  and a secret key
and a secret key  .
. : Given a public key
: Given a public key  and a plaintext
and a plaintext  , using a random coin
, using a random coin  , it outputs a ciphertext
, it outputs a ciphertext  .
. : Given a secret key
: Given a secret key  and a ciphertext
and a ciphertext  , it outputs
, it outputs  or
or  : Given the security parameter
: Given the security parameter  , it outputs a simulated public key
, it outputs a simulated public key  .
. : Given a plaintext
: Given a plaintext  and a state
and a state  , it outputs random coins for key generation
, it outputs random coins for key generation  and encryption
and encryption  .
. ,
, 
 , we call it correct. Note that
, we call it correct. Note that 

 and an exponent
and an exponent  , and then sets
, and then sets  . The sender also generates a random group element
. The sender also generates a random group element  obliviously, i.e., without knowing the discrete log of
obliviously, i.e., without knowing the discrete log of  . The sender sends
. The sender sends  to the receiver and stores the secret
to the receiver and stores the secret  . The random coin used in this step is
. The random coin used in this step is  .
. and an exponent
and an exponent  , and then sets
, and then sets  . The receiver also obliviously generates
. The receiver also obliviously generates  . Moreover, the receiver computes
. Moreover, the receiver computes  and obliviously samples
and obliviously samples  . The receiver sends
. The receiver sends  to the sender. The random coin used in this step is
to the sender. The random coin used in this step is  .
. holds or not, by checking if
holds or not, by checking if  holds. With overwhelming probability, this equation holds if and only if
holds. With overwhelming probability, this equation holds if and only if  . If
. If  , the sender sends
, the sender sends  , and otherwise quits the protocol.
, and otherwise quits the protocol. .
.
 , and
, and  as follows. It generates
as follows. It generates  and sets
and sets 
 .
. , the simulator sets
, the simulator sets  , and outputs
, and outputs  and
and  as the sender’s and receiver’s opened random coins, respectively.
as the sender’s and receiver’s opened random coins, respectively. is generated as a random group element in the real protocol, but it is generated as
is generated as a random group element in the real protocol, but it is generated as  in the simulation. When the real protocol proceeds to Step. 4, we have
in the simulation. When the real protocol proceeds to Step. 4, we have  with overwhelming probability. Then, the random coins used by the sender and receiver (and thus given to
with overwhelming probability. Then, the random coins used by the sender and receiver (and thus given to  and
and  , that is,
, that is,  and
and  . Thus, under the DDH assumption,
. Thus, under the DDH assumption,  from
from  . Thus, this protocol is a secure NCE protocol.
. Thus, this protocol is a secure NCE protocol.
 : Given the security parameter
: Given the security parameter  , it outputs a hash key
, it outputs a hash key  and a trapdoor
and a trapdoor  : Given a hash key
: Given a hash key  and input
and input  , using randomness
, using randomness  , it outputs a hash value
, it outputs a hash value  : Given a trapdoor
: Given a trapdoor  , randomness for the hash
, randomness for the hash  and another input to the hash
and another input to the hash  , it outputs randomness
, it outputs randomness  .
. and hash randomness
and hash randomness  ,
,  holds, where
holds, where  . Moreover, if
. Moreover, if  is sampled uniformly at random, then so is
is sampled uniformly at random, then so is  .
. : Given a hash key
: Given a hash key 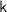 and index
and index  and
and  , using a random coin
, using a random coin  , it outputs a ciphertext
, it outputs a ciphertext  : Given a hash key
: Given a hash key  and a hash value
and a hash value  , it outputs
, it outputs  .
. : Given a hash key
: Given a hash key  , a pre-image of the hash
, a pre-image of the hash  and a ciphertext
and a ciphertext  or
or 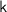 output by
output by  , and
, and  holds, where
holds, where  and
and  .
.

 : Given the security parameter
: Given the security parameter  , it outputs only a hash key
, it outputs only a hash key 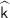 without using any randomness other than
without using any randomness other than  itself.
itself. : Given a hash key
: Given a hash key  and index
and index 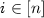 and
and  , it outputs a ciphertext
, it outputs a ciphertext  without using any randomness except
without using any randomness except 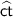 itself.
itself. and
and  , it returns
, it returns  using uniformly random
using uniformly random  .
. : Given an index
: Given an index 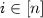 and
and  , it returns
, it returns  .
.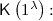
 , sample
, sample  and set
and set  .
.

 and output
and output  .
.
 .
.
 as in Eq.
as in Eq.  and compute
and compute  .
. and
and  .
. , compute
, compute  and
and 

 :
:
 .
.
 .
.
 and
and  , sample
, sample  .
. .
.
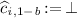 , and sample
, and sample  and
and  .
. , sample
, sample 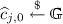 and
and  .
. .
. :
:  output by
output by  and can access to the oracle
and can access to the oracle  , where
, where  . Concretely, O(i, b) behaves as follows.
. Concretely, O(i, b) behaves as follows.  uniformly from
uniformly from  . For all
. For all  , let
, let  and
and  , and let
, and let 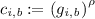 and
and  . Return
. Return  .
. output by
output by  and can access to the oracle
and can access to the oracle  , where
, where 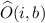 behaves as follows.
behaves as follows.  , and sample
, and sample  , and
, and  and
and  for all
for all  uniformly from
uniformly from  .
. : This experiment is exactly the same as
: This experiment is exactly the same as  except how queries made by
except how queries made by  if
if  otherwise.
otherwise.
 :
:
 and
and  .
. , sample
, sample  .
. and
and  , compute
, compute 

 used in
used in  is
is 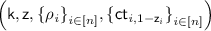 .
.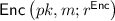 :
:
 and
and  .
. .
. and
and  , compute
, compute 
 .
.
 used in
used in  is
is 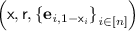 .
. :
:
 and
and  as the Eqs.
as the Eqs.  , set
, set 
 .
. .
. and
and  , sample
, sample  and compute
and compute  .
.
 .
. and sample
and sample  .
. and
and  , compute
, compute 

 .
. at random from
at random from  and
and  hold for every
hold for every  .
. and
and  .
. : This experiment is exactly the same as
: This experiment is exactly the same as  . The detailed description is as follows. 1. The experiment first samples
. The detailed description is as follows. 1. The experiment first samples  and
and  . Then, for all
. Then, for all  , it samples
, it samples  . Next, for all
. Next, for all  and
and  , it computes
, it computes 

 . Note that
. Note that  is used in the next step.
is used in the next step. and
and  . It then computes
. It then computes  . For all
. For all  and
and  , it also computes
, it also computes 

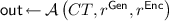 .
. : This experiment is the same as
: This experiment is the same as  except the followings. First,
except the followings. First, 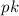 is generated together with a trapdoor of the chameleon hash function
is generated together with a trapdoor of the chameleon hash function  instead of
instead of  . Moreover, all ciphertexts of chameleon encryption
. Moreover, all ciphertexts of chameleon encryption  are computed by
are computed by  , instead of
, instead of  . Specifically, for every
. Specifically, for every  and
and  , the experiment samples
, the experiment samples  and compute
and compute  . Also, it sets
. Also, it sets  .
. ,
,  for every
for every  , where
, where 
 . Then,
. Then,  and obtains m.
and obtains m. and
and  , and outputs what
, and outputs what  is exactly the same as that of
is exactly the same as that of  .
. : This experiment is the same as
: This experiment is the same as  , except that we replace
, except that we replace  contained in
contained in  by
by  .
. : The essential difference from
: The essential difference from  in this experiment is that when
in this experiment is that when  is computed by
is computed by  instead of uniformly sampled from
instead of uniformly sampled from  is replaced to
is replaced to  from
from  , though this does not change the distribution due to the correctness of
, though this does not change the distribution due to the correctness of  and
and  , the experiment computes
, the experiment computes 
 : This experiment is exactly the same as
: This experiment is exactly the same as  except how
except how  is generated for every
is generated for every  is generated as in
is generated as in  . For
. For  is generated as in
is generated as in  .
. and
and 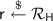 , outputs
, outputs  , and receives
, and receives  . Then,
. Then,  as follows.
as follows.  and sets
and sets  . For every
. For every  ,
,  and computes
and computes 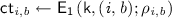 .
.  ,
, 
 . Note that
. Note that  since we consider the case of
since we consider the case of  , and thus
, and thus  by itself for every
by itself for every  . For
. For  ,
,  as in
as in  , and for
, and for  , it does as in
, it does as in  . For
. For  ,
,  and sets
and sets  . Finally,
. Finally, 
 .
. : This experiment is the same as
: This experiment is the same as  except how
except how  are computed. In this experiment,
are computed. In this experiment,  . Moreover, the randomness
. Moreover, the randomness  contained in
contained in  is replaced with
is replaced with  .
. : This experiment is the same as
: This experiment is the same as  , except that
, except that  is replaced with
is replaced with  . Moreover, the experiment computes
. Moreover, the experiment computes  as
as  , and replaces
, and replaces  in
in  with
with  , where
, where  is a uniformly random string sampled from
is a uniformly random string sampled from 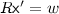 holds.
holds. holds for every
holds for every  .
. : This experiment is the same as
: This experiment is the same as  except that
except that  . By this change,
. By this change,  is of the form
is of the form 
 contained in
contained in  is sampled so that
is sampled so that  holds.
holds.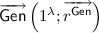 :
: .
. , generate key pairs
, generate key pairs  .
. and
and  .
. :
: .
. and parse
and parse  .
. , compute
, compute  .
. .
. :
:  , Compute
, Compute  .
. .
. .
. :
: , compute
, compute  ,
, ,
,  , and
, and  .
. :
: and parse
and parse  .
. , compute
, compute  .
. and
and  .
. and
and  do not use
do not use  for
for  such that
such that  , but for simplicity, we generate whole
, but for simplicity, we generate whole  .
.