Development of a Constitutive Model for Clays Based on Disturbed State Concept and Its Application to Simulate Pile Installation and Setup

Abstract

In this paper, an elastoplastic model is proposed to describe the behavior of clayey soils subject to disturbance at the soil-structure interaction for application to pile installation and the following setup. The soil remolding that occurs during deep penetration and the following soils thixotropic strength regaining over time were modeled in this study. The disturbed state concept (DSC) was used as a core of the proposed model, and the critical state theory was adopted to define the main components for the DSC model. The Modified Cam-Clay (MCC) model was implemented within the context of DSC to define the intact state response. A novel approach was applied to define the soil shear response for the MCC model to have it applicable in DSC. Furthermore, the soil remolding during shear loading was related to the deviatoric plastic strain developed in the soil body. The proposed model, referred as Critical State and Disturbed State Concept (CSDSC) model, can capture the elastoplastic behavior of both NC and OC soils. The proposed model was implemented in Abaqus software, and it was then validated using the triaxial test results available in the literatures. Very good agreement was obtained between the triaxial test results and the CSDSC model prediction for different stress paths, stress-strain response and the generated excess porewater pressures. Furthermore, pile installation and the following pile setup behavior were modeled using the proposed CSDSC model. The predicted values for pile resistance using CSDSC model were compared with the values measured from field load tests, which indicated that the proposed model is capable of simulating pile installation and predict appropriately the pile capacity as well as the disturbance behavior at the soil body.

1 Introduction

Soils experience variety of load histories during natural deposition, which results in soils to be over-consolidated (OC) or normally consolidated (NC). In engineering application, OC and NC soils experience different behavior under applied external loads; the OC soils exhibit more complicated behavior and have lower void ratio and higher shear strength (Yao et al. 2007). In cases, such as deep penetration, the soil disturbance and particle remolding occur during shear loading and significantly affect the general soil behavior. For engineering problems that involve deep foundations and piles, the soil type usually changes with depth due to difference in the stress history. Therefore, in such a case, incorporating an appropriate constitutive model that can capture the actual behavior for both NC and OC soils is necessary. There are several elastoplastic constitutive model available in the literature attempted to model the soil response under different loading conditions. Most of the developed constitutive models for clays are based on the critical state soil mechanics (CSSM) concept (Pestana and Whittle 1999). The critical state concept models had been formulated based on laboratory test results in axisymmetric condition. The modified Cam-Clay (MCC) model proposed by Roscoe and Burland (1968) is the most well-known critical state model. The MCC model is able to appropriately describe the isotropic NC clay behavior. Since the MCC model indicates elastic response inside the yield surface, its prediction for OC clay is poor (Likitlersuang 2003). Researchers developed series of bounding surface models to overcome this deficiency (e.g., Dafalias and Herman 1986). The bounding surface plasticity concept was used later to develop the MIT-E3 model by Whittle (1993). The bounding surface plasticity has been developed to provide smooth transition from elastic to fully plastic state for soils under general loading. In the bounding surface model, the hardening parameter depends on the distance from the current stress state to an imaginary stress at the bounding surface. The application of the critical sate models for heavily OC clays is limited, and it needs specific consideration. Yao et al. (2007) and (2012) introduced a unified hardening model using Hvorslev envelope to capture the heavily OC clay behavior. Linear and parabolic form of the Hvorslev envelope were adopted to adjust the conventional MCC model for heavily OC clay response under shear loads. Based on CSSM and bounding surface theory, Chakraborty et al. (2013a, b) developed a two surface elastoplastic constitutive model to capture strain rate dependent behavior for clay. Chakraborty et al. (2013a, b) and Basu et al. (2014) used two-surface plasticity constitutive model for the clays, and it was implemented for analysis of shaft resistance in piles. Although, their models were able to describe both NC and OC clay behavior, but they usually include plenty of material parameters that requires performing several lab tests. Furthermore, these models are not able to describe the disturbance occurs in soil body under shear loading in the elastoplastic formulation. Likitlersuang (2003) introduced a rate dependent version for the hyperelasticity model, in which he verified the proposed model by simulating triaxial test results performed on the Bangkok clay. Zhang et al. (2014) introduced a mathematical model to explain the soil shear behavior at the pile interface by using a hyperbolic and bi-linear relation between the skin friction and the relative displacement between pile surface and adjacent soil. They used a different hyperbolic relation to define the softening behavior between the unit skin friction and the pile-soil relative displacement.

Soil disturbance is obvious in the soil body subjected to external shear loading, which causes shear failure in the soil, such as the case in deep penetration problems. Therefore, an appropriate constitutive model should be able to consider the actual soil behavior due to disturbance occurred in the soil-structure interface during shear loading for application to deep penetration problems, such as pile installation. The disturbed state concept (DSC) developed by Desai and Ma (1992) is a powerful technique that is directly formulated based the soil disturbance. In the DSC model, the soil response is obtained using two boundary (reference) state responses, which are the relative intact (RI) state and the fully adjusted (FA) or critical (c) state. The real or observed soil behavior is defined as average combination of RI and FA responses. An appropriate elastoplastic constitutive model usually used to describe the soil behavior of the RI state; while the critical state is used to describe the FA state response of soils. On other words, it is assumed that the soil is in critical state condition when it reaches to FA state. Desai and his coworkers used the elastoplastic hierarchical single surface (HISS) model to define the intact state response (e.g., Desai et al. 1986; Wathugala 1990; Shao 1998; Pal and Wathugala 1999; Katti and Desai 1999; Desai 2005 and Desai 2007; Desai et al. 2011). Hu and Pu (2003) used the conventional hyperbolic model to define the intact reference state, in which they developed an elastoplastic constitutive model for sandy soil response at the soil-structure interface.

For geotechnical cases that deal with extreme shear loading, remolding of soil particles and strength regaining over time after end of soil disturbance due to the soil thixotropic response is common. Fakharian et al. (2013) described a reduction factor to incorporate soil remolding in the numerical simulation. Barnes (1997) introduced a time-dependent exponential function to formulate inks thixotropic response after remolding. In this paper, a new constitutive model is developed based on the combination of the critical state theory and the DSC, which can describe the actual soil behavior of both NC and OC clay soils and the soil disturbance caused by shear loading during deep penetration. In this study, the thixotropic response of clay soils was formulated similar to the inks thixotropy presented in Barnes (1997). The proposed model requires only six model parameters, which is less than the models that have been previously developed based on the DSC. Furthermore, it predicts smooth transition from elastic to plastic state of soil under shear loading, which is usually observed during laboratory tests performed on soil samples.

2 Modified Cam-Clay (MCC) Model

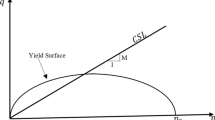
The original Cam-Clay model was developed based on the CSSM concept by Roscoe and Schofield (1963), which was then modified by Roscoe and Burland (1968) to develop the MCC model. This model was developed to study the clayey soil behavior under applied loads. The MCC model has been used widely in past decades to define the soil behavior because, firstly, it is capable in capturing soil realistic behavior than the other conventional models such as Mohr-Coulomb or Von-Misses models. Secondly, it is a simple model with pretty less parameters in comparison with other advanced soil models. The MCC yield locus is assumed to have an elliptical shape, as shown in Fig. 1, and the equation of the yield surface in triaxial stress space is given as:

Fig. 1.

Elliptical yield surface for MCC model in $p^{\prime} - q$ plane.

$$ F = q^{2} - M^{2} \left[ {p^{\prime}\left( {p^{\prime}_{0} - p^{\prime}} \right)} \right]\,{ = }\, 0 { } $$

(1)

where $p^{\prime}$ is the general volumetric stress or hydrostatic stress, which is $p^{\prime} = \left( {\sigma_{1}^{'} + 2\sigma_{3}^{'} } \right)/3$ for triaxial stress state. $q$ is the deviatoric stress, which is $q = \sigma_{1}^{'} - \sigma_{3}^{'}$ for triaxial condition. M is the slope of critical state line on p-q plane, and $p_{0}^{'}$ is the pre-consolidation pressure. The Cam Clay model was developed based on the volumetric behavior of the saturated soil under shear loading, unloading and reloading. For MCC model, the following differential equations define the material behavior:

$$ d\sigma = C^{ep} d\varepsilon $$

(2)

where $d\sigma$ is the incremental stress tensor, $d\varepsilon$ is the incremental strain tensor, $C^{ep}$ is the elastoplastic constitutive matrix, and it can be obtained from Eq. (3).

$$ C_{ijkl}^{ep} = C_{ijkl}^{e} - \frac{{C_{ijtu}^{e} \frac{\partial F}{{\partial \sigma_{tu} }}\frac{\partial F}{{\partial \sigma_{pq} }}C_{pqkl}^{e} }}{{H + \frac{\partial F}{{\partial \sigma_{mn} }}C_{mnrs}^{e} \frac{\partial F}{{\partial \sigma_{rs} }}}} $$

(3)

where $C^{e}$ is the elastic stress-strain matrix and depends on the stress state through the elastic bulk modulus K and the shear modulus G. The term H is the hardening parameter that can be obtained using the following equations:

$$ H = \frac{1 + e}{\lambda - \kappa }p^{\prime}p '_{0} \frac{\partial F}{\partial p '} $$

(4)

where e is the soil void ratio; and $\lambda$ and $\kappa$ represent the slope of the normally consolidated line and the unloading-reloading line, respectively.

3 Disturbed State Concept (DSC)

The disturbed state concept is defined based on the disturbance occurs in the soil body during external loading especially shear loads. The conceptual framework of disturbed state concept is based on the cyclical behavior of materials from its “cosmic state” to the engineering materials state, and then the tendency to return to its initial cosmic state under applied loads (Desai 2001). When the soil deforms under applied loads, its initially intact fabric undergoes microstructural changes, such as sliding, reorientation and cracking of the soil particles (Katti and Desai 1995). By proceeding deformation, part of the soil body become disturbed, which then changes to the fully adjusted (FA) or critical (c) state, while the rest part is still in relative intact (RI) state condition. These two reference states (FA and RI) are used to define observed (averaged) soil behavior under applied loads. Based on this concept, the observed or averaged (a) behavior of the material is an average combination of the RI and FA based on the amount of disturbance occurred in the soil body. An appropriate constitutive model such as linear or nonlinear elastic and elastoplastic model can define the RI response (Desai 2001). The real behavior of a material is a combination of two interacting behaviors in the RI and FA reference states. The stresses at the average state ($\sigma^{a}$) can be obtained from a linear combination of the RI and FA states and by using the disturbance function D according to the following relation:

$$ \sigma_{ij}^{a} = \left( {1 - D} \right)\sigma_{ij}^{i} + D\sigma_{ij}^{c} $$

(5)

where the notations $a$, $i$, and $c$ are representing the observed, intact and fully adjusted (critical state) responses, respectively. At the initial stage of applying load, the RI response has more influence on the overall behavior of a material, and with continuing the applied load, the material particles are displacing and the overall material response gradually approaches to the FA state. The disturbance function D, which is related to the produced plastic strain in the soil body under shear is used to define the averaged response. The following exponential equation was proposed by Desai (2001), which relates soil disturbance D to the developed plastic strain in the soil body under applied load:

$$ D = 1 - e^{{ - A*\varvec{\xi}_{d}^{B} }} $$

(6)

where $\varvec{\xi}_{d}$ is the trajectory of deviatoric plastic strain $dE_{ij}^{p}$, defined as $\varvec{\xi}_{d} = \smallint \left( {dE_{ij}^{p} .dE_{ij}^{p} } \right)^{1/2}$; and A and B are material parameters, which are obtained from results of laboratory soil triaxial tests. At the beginning of loading ($\xi_{d} = 0)$, the function D represents the initial disturbance under natural condition, which is usually assumed to be equal to zero (i.e., soil is undisturbed at initial stage). Then with proceeding at shear loading, plastic strain increases, and hence the soil transform gradually from intact state to fully disturbed state, and therefore, the D function approaches to unity.

For a specific yield surface F and in the case of associated flow rule used for plasticity formulation, the plastic strain increment is related to the deferential of the yield function F with respect to the stress tensor by the following equation:

$$ d\varepsilon_{ij}^{p} = \lambda^{ *} \frac{\partial F}{{\partial \sigma_{ij} }} $$

(7)

where $\lambda^{ *}$ is the plastic multiplier. The star sign in $\lambda^{ *}$ is used here for plastic multiplier to remove confusion. The incremental deviatoric strain $dE_{ij}^{p}$ can be obtained as:

$$ dE_{ij}^{p} = d\varepsilon_{ij}^{p} - \frac{1}{3}d\varepsilon_{kk}^{p} \delta_{ij} = \lambda^{ *} \left( {\frac{\partial F}{{\partial \sigma_{ij} }} - \frac{1}{3}\frac{\partial F}{{\partial \sigma_{kk} }}\delta_{ij} } \right) $$

(8)

The plastic strain increment trajectory $d\varvec{\xi}_{d}$ will be obtained as:

$$ d\varvec{\xi}_{d} = \left( {dE_{ij}^{p} .dE_{ij}^{p} } \right)^{1/2} = \lambda^{ *} \left[ {\frac{\partial F}{{\partial \sigma_{ij} }}\frac{\partial F}{{\partial \sigma_{ij} }} - \frac{1}{3}\frac{\partial F}{{\partial \sigma_{kk} }}\frac{\partial F}{{\partial \sigma_{ll} }}} \right]^{1/2} $$

(9)

By combining Eqs. (6) and (9), the incremental change in the disturbance function is obtained as follows:

$$ dD = AB\varvec{\xi}_{d}^{B - 1} e^{{ - A*\varvec{\xi}_{d}^{B} }} .\lambda^{ *} .\left[ {\frac{\partial F}{{\partial \sigma_{ij} }}\frac{\partial F}{{\partial \sigma_{ij} }} - \frac{1}{3}\frac{\partial F}{{\partial \sigma_{kk} }}\frac{\partial F}{{\partial \sigma_{ll} }}} \right]^{1/2} $$

(10)

In Eq. (10), $\lambda^{ *}$ is obtained from applying equilibrium and consistency conditions for a specific yield surface.

4 Proposed Constitutive Model

In this study, the intact state behavior was modeled using the MCC model. For fully adjusted response, again, the critical state soil mechanics concept was adopted, and it was assumed that the soil is in critical state when it becomes fully adjusted. Adopting the critical state concept for both RI and FA behaviors imposes the model to have two different critical state parameters (M) in order to describe the behaviors of RI and FA reference states: the value for intact material response ($M_{i}$) and the value for the fully adjusted response ($M_{c}$). The former one is not a real soil property, and its value defined based on the proposed model requirement (as will be described in the following sections). The latter one indicates the critical state parameter of soil, and its value is obtained from laboratory test results. Since the proposed model was obtained by combining the DSC and the critical state MCC model, it is called the Critical State and Disturbed State Concept (CSDSC) model. In this model, the disturbance function D is applied to the critical state parameter M as follows:

$$ M_{a} = \left( {1 - D} \right)M_{i} + DM_{c} $$

(11)

where $M_{a}$ is the averaged or observed value for the critical state parameter at each stage of loading process. Figure 2 describes that the evolution of the critical state parameter $M_{a}$ during shear loading. At the initial stage of shear, the soil is assumed to be undisturbed (D =  0 and $\xi_{d} = 0$), which means Eq. 11 yields to $M_{a} = M_{i}$. However, with the proceeding of the applied load, the soil disturbs, the plastic strains develop in the soil body, the values of D and $\xi_{d}$ increase, and eventually the D value approaches to 1. At this point, the soil reaches the critical state (i.e. $M_{a} = M_{c}$) condition.

Fig. 2.

Evolution of critical state parameter M during shear loading

$M_{c}$ and $M_{i}$ were assumed to be constant, so the incremental form for Eq. (11) can be expressed as follows:

$$ dM_{a} = \left( {M_{c} - M_{i} } \right)dD $$

(12)

In case of using the MCC model to represent the intact material response, the plastic multiplier $\lambda^{ *}$ can be defined as follows:

$$ \lambda^{ *} = \frac{{\frac{\partial F}{{\partial \sigma_{ij} }}C_{ijkl}^{e} d\varepsilon_{kl}^{i} }}{{\frac{\partial F}{{\partial \sigma_{mn} }}C_{mnpq}^{e} \frac{\partial F}{{\partial \sigma_{pq} }} - \left[ {\frac{1 + e}{\lambda - \kappa }p^{\prime}p'_{0} \frac{\partial F}{\partial p'}} \right]}} $$

(13)

where $d\varepsilon_{kl}^{i}$ is the incremental intact strain. Replacing Eq. (13) into Eq. (10) yields to the following equation:

$$ dD = \frac{{\left( {AB\varvec{\xi}_{d}^{B - 1} e^{{ - A*\varvec{\xi}_{d}^{B} }} } \right)\frac{\partial F}{{\partial \sigma_{ij} }}.C_{ijkl}^{e} \left[ {\frac{\partial F}{{\partial \sigma_{rs} }}\frac{\partial F}{{\partial \sigma_{rs} }} - \frac{1}{3}\frac{\partial F}{{\partial \sigma_{uu} }}\frac{\partial F}{{\partial \sigma_{vv} }}} \right]^{1/2} }}{{\frac{\partial F}{{\partial \sigma_{mn} }}C_{mnpq}^{e} \frac{\partial F}{{\partial \sigma_{pq} }} - \left[ {\frac{1 + e}{\lambda - \kappa }p^{\prime}p'_{0} \frac{\partial F}{\partial p'}} \right]}}.d\varepsilon_{kl}^{i} $$

(14)

Equation (14) indicates that the incremental change in the disturbance function in related strain increment of the intact material. By combining Eqs. (12) and (14), the incremental change for observed critical state parameter $dM_{a}$, is obtained as follows:

$$ dM_{a} = \left( {M_{c} - M_{i} } \right)\frac{{\left( {AB\varvec{\xi}_{d}^{B - 1} e^{{ - A *\varvec{\xi}_{d}^{B} }} } \right)\frac{\partial F}{{\partial \sigma_{ij} }}.C_{ijkl}^{e} \left[ {\frac{\partial F}{{\partial \sigma_{rs} }}\frac{\partial F}{{\partial \sigma_{rs} }} - \frac{1}{3}\frac{\partial F}{{\partial \sigma_{uu} }}\frac{\partial F}{{\partial \sigma_{vv} }}} \right]^{1/2} }}{{\frac{\partial F}{{\partial \sigma_{mn} }}C_{mnpq}^{e} \frac{\partial F}{{\partial \sigma_{pq} }} - \left[ {\frac{1 + e}{\lambda - \kappa }p^{\prime}p_{0} \frac{\partial F}{\partial p'}} \right]}}.d\varepsilon_{kl}^{i} $$

(15)

The elastic matrix $C^{e}$ is related to the nonlinear elastic bulk and shear modulus K and G. As indicated by Zhang [11] and Sloan [26], the tangent modulus K and G cannot be used directly in numerical analysis of critical state models because of nonlinearity of them within the finite strain increment. Therefore, the secant modulus can be used to replace the tangent modulus as follows:

$$ \bar{K} = \frac{{p^{\prime}}}{{\varDelta \varepsilon_{v}^{e} }}\left( {\exp \left( {\frac{1 + e}{\kappa }\varDelta \varepsilon_{v}^{e} } \right) - 1} \right) $$

(16)

where $p^{\prime}$ is the effective hydrostatic stress at the start of the volumetric elastic strain increment $\varDelta \varepsilon_{v}^{e}$. By assuming that the Poisson’ ratio stays constant during loading; the secant shear modulus can be obtained as:

$$ \bar{G} = \frac{{3\left( {1 - 2\nu } \right)}}{{2\left( {1 + \nu } \right)}}\bar{K} $$

(17)

In the proposed model, MCC model runs in each increment (or sub-increment). However, while the soil shears, the critical state parameter M evolves gradually from $M_{i}$ value and to $M_{c}$ value based on the amount of developed plastic strain in each increment and obeying the DSC theory. Figure 3 presents the formulation of the proposed model in the $p^{\prime} - q$ space. The point A represents the stress state at the beginning of the strain increment $d\varepsilon_{n}$. The MCC model is used to solve the governing equations for $d\varepsilon_{n}$ using $M_{a}^{n}$, and the new stress state is obtained at point B, which is located on the yield surface $a_{n}$. Then, updated value for the averaged critical state parameter $M_{a}^{n + 1}$ is obtained from the incremental value of $dM_{a}$ by using Eq. (15) for use in the next increment. The imaginary yield surface $i_{n + 1}$ will then be defined using the updated critical state parameter $M_{a}^{n + 1}$ and the hardening parameter $p_{c}^{n + 1}$ (the prime index in $p_{c}^{'}$ removed for simplicity). The current stress state (point B) is located inside the imaginary yield surface $i_{n + 1}$, which causes the elastoplastic behavior for the material in the next steps until stress state reaches the critical state. The MCC model is then solved using the new strain increment $d\varepsilon_{n + 1}$ to reach point C and so on. The main advantage of this approach is the possibility of specifying a small value close to zero for $M_{i}$ since the observed behavior is captured by the disturbance parameters regardless of the chosen value for $M_{i}$. By choosing a very small value for $M_{i}$, the plastic behavior inside the yield surface is achieved; leading to a smooth transition between the elastic and plastic behavior. For each strain increment,$d\varepsilon ,$ the elastic and the plastic portions are determined using the yield surface intersection parameter $\alpha_{inter}$ as follows:

Fig. 3.

The proposed (CSDSC) model representation in $p^{\prime} - q$ space

$$ d\varepsilon^{e} = \alpha_{inter} .d\varepsilon $$

(18a)

$$ d\varepsilon^{p} = \left( {1 - \alpha_{inter} } \right).d\varepsilon $$

(18b)

In Eq. (18a, 18b), higher values of $\alpha_{inter}$ indicates dominant elastic response, while lower $\alpha_{inter}$ shows dominant plastic response. A value of $\alpha_{inter} = 0$ indicates that under strain increment $d\varepsilon$ pure plastic deformation occurs, while a value of $\alpha_{inter} = 1$ represents pure elastic deformation. In the proposed model, at the initial stage after loading (D = 0), the elastic behavior is dominant (point B is far from the corresponding yield surface a). By proceeding with loading, the $\alpha_{inter}$ value decreases, the elastic portion reduces, and the plastic behavior become dominant until it reaches the fully plastic response at D = 1 (point B locates on the yield surface). Summary of the required steps to implement the CSDSC model are described as follows:

• 1. For a given strain increment $d\varepsilon$, solve the constitutive equations using the MCC model and implement an appropriate integration scheme to determine the current stress state (Point B in Fig. 3) and corresponding $p_{c} .$

• 2. Calculating the disturbance function increment, dD, based on the induced plastic strain values using the described formulation. Then, calculate $dM_{a}$ using Eq. (15) to update the $M_{a}$ value for use in the next increment.

• 3. An imaginary yield surface is defined based on the updated $M_{a}$ and $p_{c}$ values. This step causes the current stress states (point B in Fig. 3) to stay inside the imaginary yield surface).

• 4. Run the MCC model using the imaginary yield surface and the $M_{a}$ value obtained from step 2, which yields new stress state at point C and new hardening parameter $p_{c} .$

• 5. Repeat Steps 2 to 4 until the stress state reaches the critical state ($M_{a} = M_{c} )$ condition.

5 CSDSC Model Parameters

The proposed CSDSC model has six parameters, including the following four critical state (MCC) model parameters: (1) The Poisson ratio ν, (2) the slope of the critical state line M, (3) slope of the normal compression line ${\varvec{\uplambda}}$, and (4) slope of unloading-reloading line ${\varvec{\upkappa}}$; and two disturbed state parameters for defining the disturbance function D. The first four parameters can be obtained directly from laboratory tests such as consolidation and triaxial tests. Several researchers discussed how to obtain these parameters from conventional laboratory tests (e.g., Yao et al. 2007 and Guan-lin and Bin 2016). There are two parameters in the disturbance function D, namely, A and B parameters, which can be obtained from triaxial test results by some mathematical manipulation. As Desai (2001) has indicated, the D can be obtained from a triaxial test result with the following equation:

$$ D\, = \,\frac{{q_{i} - q_{a} }}{{q_{i} - q_{c} }} $$

(19)

where $q_{i}$, $q_{c }$ and $q_{a}$ are the deviatoric stress for RI, FA and averaged state, respectively. On the other side, by rearranging and taking natural logarithms of the disturbance function, Eq. (6) yields to:

$$ \ln \left( A \right) + Bln\left( {\xi_{d} } \right) = \ln \left( { - ln\left( {1 - D} \right)} \right) $$

(20)

By plotting the value for D obtained from Eq. (19) and using the results of CU triaxial test versus the obtained values for $\xi_{d}$, a best fit straight line as shown in Fig. 4 can be used to determine the A and B parameters.

Fig. 4.

Determination of disturbance function parameters.

6 Soil Thixotropy and the CSDSC Model

Fine-grained cohesive soils show certain degrees of thixotropic response under constant effective stress and constant void ratio. Thixotropy is defined as the “process of softening caused by remolding, followed by a time-dependent return to the original harder state” (Mitchel 1960). Thixotropy is a reversible process, which is mainly related to the rearrangement of the remolded soil particles, and it must be considered in constitutive models that deal with shear failure at the soil-structure interface such as driven piles, and the following increase in pile capacity with time after end of driving (or pile setup). Therefore, for numerical study of pile installation and setup phenomenon, the thixotropic behavior of cohesive soil should be considered in the model. For driven piles, which deal with change in the soil properties during different steps of installation and the following setup, it is necessary to adopt appropriate material properties at each step. Numerical simulation of pile setup using properties obtained from laboratory tests like triaxial or consolidation tests on undisturbed soil samples yields unrealistic results. Therefore, the time-dependent reduction parameter $\upbeta\left( t \right)$ was applied in this study on the critical state parameter M and the soil-structure interface friction coefficient μ to incorporate the effect of soil remolding during pile installation and the following strength regaining with time after that:

$$ \left\{ {\begin{array}{*{20}l} {M\left( t \right) =\upbeta\left( t \right)M} \hfill \\ {\mu \left( t \right) =\upbeta\left( t \right)\mu } \hfill \\ \end{array} } \right. $$

(21)

Based on research performed by Barnes (1997) on the thixotropic strength regaining over time for inks, Abu-Farsakh et al. (2015) proposed the following definition for $\upbeta\left( t \right):$

$$ \upbeta\left( t \right) =\upbeta\left( \infty \right) - \left[ {\upbeta\left( \infty \right) -\upbeta\left( 0 \right)} \right] e^{{ - \left( {\frac{t}{\tau }} \right)}} $$

(22)

Where, the parameter t is time after soil remolding. $\upbeta\left( 0 \right)$ is the initial value for reduction parameter $\upbeta$ immediately after soil shearing (t =  0), which its value depends on the degree of remolding occurs in the soil during shear. $\upbeta\left( \infty \right)$ is the $\upbeta$ value after long time from soil disturbance (t = $\infty$); and τ is a time constant that controls the rate of evolution of $\upbeta$. Abu-Farsakh et al. (2015) related τ to the soil $t_{90}$, which is the time for 90% dissipation of the excess pore water pressure at pile surface.

The initial value of soil disturbance depends on the amount of disturbance has been developed at soil-pile interface during pile installation. The best parameter which can be used to determine the disturbance is deviatoric strain values due to shear force development at the interface. In this study, a similar formulation to the disturbance function D (i.e. Eq. 6) was also proposed, which relates the initial reduction parameter $\upbeta\left( 0 \right)$ to the deviatoric plastic strain trajectory using the following exponential function:

$$ \beta \left( 0 \right) = \beta_{R} + \left( {1 - \beta_{R} } \right)e^{{ - A *\xi_{d}^{B} }} $$

(23)

where $\beta_{R}$ is the $\upbeta$ value for the fully remolded soil, which indicates a maximum reduction of the soil strength during shearing, and its value is related to the soil sensitivity. In order to reduce complexity, the disturbed state parameters A and B were used to introduce a relation between $\upbeta\left( 0 \right)$ and $\xi_{d}$ in Eq. (23). Figures 5a and b present the schematic representations of the variations of D and $\upbeta\left( 0 \right)$ versus the deviatoric plastic strain trajectory, respectively. These Figures show that while the soil disturbs, the D value approaches unity, and the $\upbeta\left( 0 \right)$ yields to $\beta_{R}$ by proceeding the plastic strain. Abu-Farsakh et al. (2015) correlated $\beta_{R}$ to the soil sensitivity, $S_{r}$ using a simple relation as $\beta_{R} = \left( {S_{r} } \right)^{ - 0.3}$.

Fig. 5.

Variation of soil characteristics during shear loading: (a) disturbance function D, and (b) the soil strength reduction factor immediately after remolding, $\upbeta\left( 0 \right)$.

7 Verification of the Proposed Model

To clarify advantages of the proposed CSDSC model, the triaxial compression test for a typical clay was simulated numerically using the Abaqus software. Three-dimensional model with a cubic porous element for soil specimen was used. The coupled porewater pressure analysis was used to define the multi-phase characteristic of the saturated soil. Triaxial stress state was applied using prescribed stresses for confining stress and using the prescribed displacement to apply deviatoric stress. The sample top surface was assumed to be free for drainage. The model was run first using the Abaqus built in MCC model. Then the same model was run using the proposed CSDSC model through implementation via UMAT; and the obtained results were compared with the results of MCC model as shown in Fig. 6. The figure indicates that the MCC model prediction for OC soil is not realistic, which shows mostly elastic response during undrained shearing, especially for heavily OC soils. On the other hand, the proposed CSDSC model provides a rational elastoplastic response with smooth transition from elastic to plastic behavior even for the heavily OC soils.

Fig. 6.

Comparative result for stress path in triaxial compression obtained from numerical simulation using MCC and the proposed model.

The proposed CSDSC model was then verified via numerical simulation of three case studies. Case1: the triaxial tests performed on Kaolin clay were simulated using CSDSC and MCC models. Case 2: the triaxial test conducted on Boston Blue clay was modeled, and the CSDSC model prediction was compared with the test measurments. Case 3: the proposed CSDSC model was used to simulate a full-scale pile installation and the following pile setup case study of a test pile located at Bayou Laccassine Bridge site, Louisiana. The results then were compared with the measured values obtained from the field load tests. It should be noted that the soil thixotropy formulation (i.e., Eqs. 21 to 23) included only in numerical simulation of the third case because this is the only case that the soil strength regain has been measured through field static and/or dynamic load tests performed after pile installation. However, in the first two case studies, the numerical simulation included only triaxial test procedure using the proposed CSDSC model without considering soil strenght gain after shear because there was no thixotropic information available in the original laboratory tests done by other researchers.

Case study 1: Kaolin Clay

To verify the predictive capability of the proposed model, the results of laboratory triaxial tests on Kaolin clay performed by Yao et al. (2012) was simulated using the proposed CSDSC model. The shear responses from underlined triaxial compression test for different stress history (OCR = 1, 1.20, 5,8,12) were simulated. The four model parameters that are related to the MCC model were obtained from Yao et al. (2012). The remained two model parameters that are related to the disturbed state concept (i.e. $A$ and $B$) were obtained from triaxial test results and following the procedure outlined by Desai (2001) and explained with Eqs. 19 and 20. After a simple curve fitting to the data obtained from triaxial test results and adopting straight line shown in Fig. 4, values of A = 14.43 and B = 0.47 were obtained. The calculated parameters are presented in Table 1.

Table 1. Model Parameters for Kaolin clay used for implementation (Yao et al. 2012)

Using the model parameters presented in Table 1, the FE model was run with MCC model and the results for different stress paths in the undrained condition are presented in Fig. 7a. The figure shows that the MCC model is not able to capture appropriately the actual soil response under undrained shear loads, especially for OC clays.. In the proposed model, the strong capability of the CSDSC in modeling the actual behavior of soils was demonstrated, and the results of numerical simulation for different stress paths using the proposed model are presented in Fig. 7b. The figure clearly indicates that the proposed model can predict the actual soil behavior for both the NC and OC soils with good agreement. The model is also able to capture the strain softening behavior of heavily OC soils. Figure 8 shows the results of proposed model for stress-strain relation at different over-consolidation ratios, which represents good agreement. In this figure, the stress values are normalized with respect to the initial pre-consolidation pressure $p'_{0}$.

Fig. 7.

Prediction of numerical simulation of undrained triaxial test on Kaolin clay (Yao et al. 2012) using (a) MCC model, and (b) the proposed CSDSC model.

Fig. 8.

Stress-strain relation for undrained triaxial test on Kaolin clay (Yao et al. 2012) using the proposed CSDSC model.

Figure 9 presents the numerical simulation for porewater pressure generated during undrained triaxial tests using the proposed CSDSC model, which are in good agreement with the test measurements. The figure shows that, for NC soil and lightly OC soil, the generated porewater pressure is positive, which is representation of soil contraction during undrained shearing. On the other hand, for heavily OC soils, the numerical simulation shows the generation of positive porewater pressure at the initial stage of the test followed by negative pore water pressure until failure. This is an indication of soil dilative behavior, which is common in heavily OC soils. Based on the obtained results, the soil dilation in undrained condition increases by increasing OCR values.

Fig. 9.

Prediction of the excess porewater pressure generated in undrained triaxial test on Kaolin clay (Yao et al. 2012) using the proposed CSDSC model.

Case study 2: Boston Blue Clay

The results of undrained triaxial test for normally consolidated Boston Blue Clay, which are available in literature (e.g. Ling et al. 2002), were used to verify the proposed model prediction. The test was simulated using the proposed CSDSC model, and using the soil properties and model parameters as shown in Table 2 (Ling et al. 2002). The required information including stresses, strains and excess porewater pressure were extracted from the numerical model in order to study the variation of these parameters during shearing. Figures 10, 11 and 12 compare the results obtained from the CSDSC model and the corresponding measurements from the triaxial test results. These figures demonstrate very good agreement between the proposed model prediction and the performed triaxial test results, especially in predicting the stress path and the stress-strain relation. However, the CSDSC model prediction for the generated excess pore water pressure during triaxial tests is slightly under estimated, but still within acceptable tolerance.

Table 2. Model Parameters for Boston Blue Clay used for implementation (Ling et al. 2002)

Fig. 10.

Prediction of numerical simulation of undrained triaxial test on Boston Blue clay (Ling et al. 2002) using the proposed CSDSC model.

Fig. 11.

Stress-strain relation for undrained triaxial test on Boston Blue clay (Ling et al. 2002) using the proposed CSDSC model.

Fig. 12.

Prediction of the excess porewater pressure generated in undrained triaxial test on Boston Blue clay (Ling et al. 2002) using the proposed CSDSC model.

Case study 3: Full-Scale Pile Installation

The load test results for a full-scale instrumented test pile that was conducted at Bayou Laccasine Bridge site, Louisiana (Haque et al. 2014) was simulated using the proposed CSDSC model. The test pile was square concrete pile with 0.76 m width and a total length of 22.87 m. A 6.4 m long casing was installed and driven prior to pile installation to represent the scour effect at shallow depth. The test pile was fully instrumented with pressure cells, vibrating wire piezometers and sister bar strain gages that were installed at different depths of pile length, targeting specific soil layers. In addition, the surrounding soils were instrumented with nine multi-level piezometers located at the same depths as the pressure cells and piezometers installed at the pile’s face. Both static load tests (SLTs) and dynamic load tests (DLTs) were conducted to obtain the pile resistance at different times after end of driving.

In this paper, the numerical simulation of the pile installation and following setup were performed using the Abaqus software and adopting the techniques described in Abu-Farsakh et al. (2015). The geometry of the soil and pile, the applied boundary conditions, and finite element mesh are shown in Fig. 13. Numerical simulation of pile installation was achieved by applying prescribed displacement to the soil nodes to create volumetric cavity expansion. The pile was then placed inside the cavity followed by applying a vertical penetration until the steady state condition is reached.

Fig. 13.

Numerical simulation domain: (a) geometry and boundary conditions and (b) FE mesh (Abu-Farsakh et al. 2015).

The subsurface soil condition at the pile site is mainly consists of clay soil, and the natural water table is 2.24 m below the ground surface. The subsurface soil domain was divided into eight layers based on the soil type and properties as presented in Table 3. In the table, w is the soil water content (%), $S_{u}$ is the undrained shear strength (kPa), and $K$ is the soil permeability (m/s).

Table 3. Subsurface soil properties for the test pile site (Abu-Farsakh et al. 2015)

The proposed CSDSC model was used to describe the elastoplastic behavior of the surrounding clay soil. The soil remolding during pile installation was incorporated in the constitutive model using Eq. (23), and relating $\beta_{R}$ to the soil sensitivity $S_{r}$ with $\beta_{R} = \left( {S_{r} } \right)^{ - 0.3} .$ This relation was depicted for Bayou Laccasine Bridge site based on available data for $S_{r}$ and the pile resistance values obtained from field load tests, which yield a value of $\beta_{R} = 0.75$ (Abu Fasakh et al. 2015). The disturbed state parameter values of A = 8.50 and B = 0.25 were calculated using laboratory triaxial test results, and were then adopted in the proposed model.

Figure 14 represents the disturbance occurs in the soil immediately after pile installation for a typical horizontal path (path 1 in Fig. 13), which was obtained from numerical simulation using the CSDSC model. The figure shows that β has its maximum value $\beta_{R} = 0.75$ for soil adjacent to the pile face and approaches unity at a radial distance equal to eight times the pile size. At the same time, the disturbance function has a maximum value (D =  1) at the soil-pile interface, and it approaches to D =  0 at a radial distance equal to eight times the pile size along the same path.

Fig. 14.

Variation of β and D for a typical horizontal path in the soil body immediately after pile installation.

The numerical simulation using CSDSC model was compared with the measured field test results of the pile load tests. Figure 15a shows the comparison between the predictions of unit shaft resistance one hour after end of driving obtained using the CSDSC model and the measured values from the field load tests. The cumulative values of shaft resistance obtained from numerical simulation were also compared with the calculated values obtained from field tests, and the results are shown in Fig. 15b. These figures clearly indicate that the CSDSC model is able to predict the pile resistance appropriately. For more verification, the increase in pile capacity after end of driving (or pile setup) was obtained from numerical modeling using the CSDSC model, and the model predictions were compared with the measured values from field load test results as shown in Fig. 16. The figure demonstrates that the proposed model is able to simulate pile setup with the model predictions of the pile resistance are slightly over-predicted the measured values.

Fig. 15.

Comparison between the proposed CSDSC model prediction with measured values from field test results (a) unit shaft resistance, and (b) total shaft resistance.

Fig. 16.

Comparison between the proposed CSDSC model prediction and field measurement for pile setup.

8 Conclusions

In this paper, an elastoplastic constitutive model for clay soil was developed and evaluated in application of pile installation and the following setup over time. The proposed model is based on the combination of Disturbed State Concept (DSC) and critical state concept of Modified Cam-Clay (MCC) model, which is referred as the CSDSC model. In the CSDSC model, the disturbance function D was applied to the critical state parameter M to adopt disturbed state concept. The soil remolding behavior was related to the state of deviatoric plastic strain developed in the soil body during shear loading for use to simulate deep penetration problems such as pile installation and the corresponding remolding of surrounding soil. The soil thixotropic response was incorporated in the pile setup phenomenon using a time-dependent function, which increases exponentially with time after end of pile driving. The proposed model was implemented in Abaqus software via a user defined subroutine UMAT. The responses of Kaolin and Boston Blue clays under undrained monotonic loads were simulated for verification. The Kaolin clay was evaluated for NC case and OCR values of 1.2, 5, 8 and 12; however, Boston Blue clay was simulated under NC condition. The proposed CSDSC model prediction, which included stress paths, stress-strain curves, and generated excess porewater pressures were compared with the triaxial test results available in the literatures for verification of the model. Furthermore, a full-scale instrumented pile driven in Louisiana clayey soil and the following setup were simulated using the CSDSC model, and the results obtained from FE model and those measured from field test results were compared. Based on the results of this study, the following conclusions can be made for the numerical simulation using the CSDSC model:

• (a) The developed CSDSC model has only six parameters, which is less than the previous elastoplastic models developed based on DSC, which makes it more effective in geotechnical engineering applications. The model parameters include four critical state parameters and two parameters related to DSC. All the model parameters can be simply obtained from consolidation and triaxial laboratory tests.

• (b) The proposed CSDSC model predictions were compared with laboratory triaxial test results, which show that the model was able to appropriately capture the undrained shear responses for NC clays, lightly OC clays and heavily OC clays.

• (c) The comparison between the results of conventional MCC model and the proposed CSDSC model showed that the CSDSC model is able to remove deficiency of the MCC model in simulation the clay soil behavior especially for heavily OC soils. The steep changes in stress paths inside yield surface, which was observed in MCC model, could be vanished in CSDSC model providing a smooth transition from elastic to plastic response. In other word, the CSDSC model is able to capture accurately the smooth transition from elastic to elastoplastic and to fully plastic state, which is usually observed during experimental tests performed on clayey soils.

• (d) The numerical simulation of a full-scale pile installation and following pile load tests after end of driving indicated that the proposed CSDSC model is able to simulate pile installation and capture the soil disturbance, soil thixotropy and pile setup appropriately.

• (e) The results demonstrated good agreement between the prediction of pile resistance and pile setup using CSDSC model and the measured values obtained from full-scale pile loads tests results.