Predictive Analytics in Future Power Systems: A Panorama and State-Of-The-Art of Deep Learning Applications

Abstract

The challenges surrounding the optimal operation of power systems are growing in various dimensions, due in part to increasingly distributed energy resources and a progression towards large-scale transportation electrification. Currently, the increasing uncertainties associated with both renewable energy generation and demand are largely being managed by increasing operational reserves—potentially at the cost of suboptimal economic conditions—in order to maintain the reliability of the system. This chapter looks at the big picture role of forecasting in power systems from generation to consumption and provides a comprehensive review of traditional approaches for forecasting generation and load in various contexts. This chapter then takes a deep dive into the state-of-the-art machine learning and deep learning approaches for power systems forecasting. Furthermore, a case study of multi-time-horizon solar irradiance forecasting using deep learning is discussed in detail. Smart grids form the backbone of the future interdependent networks. For addressing the challenges associated with the operations of smart grid, development and wide adoption of machine learning and deep learning algorithms capable of producing better forecasting accuracies is urgently needed. Along with exploring the implementation and benefits of these approaches, this chapter also considers the strengths and limitations of deep learning algorithms for power systems forecasting applications. This chapter, thus, provides a panoramic view of state-of-the-art of predictive analytics in power systems in the context of future smart grid operations.

1 Introduction

Overview

The challenges surrounding the optimal operation of power systems are growing in various dimensions, due in part to increasingly distributed energy resources and a progression towards large-scale transportation electrification. Currently, the increasing uncertainties associated with both renewable energy generation and demand are largely being managed by increasing operational reserves—potentially at the cost of suboptimal economic conditions—in order to maintain the reliability of the system. This chapter looks at the big picture role of forecasting in power systems from generation to consumption and provides a comprehensive review of traditional approaches for forecasting generation and load in various contexts. This chapter then takes a deep dive into the state-of-the-art machine learning and deep learning approaches for power systems forecasting. Furthermore, a case study of multi-time-horizon solar irradiance forecasting using deep learning is discussed in detail. Smart grids form the backbone of the future interdependent networks. For addressing the challenges associated with the operations of smart grid, development and wide adoption of machine learning and deep learning algorithms capable of producing better forecasting accuracies is urgently needed. Along with exploring the implementation and benefits of these approaches, this chapter also considers the strengths and limitations of deep learning algorithms for power systems forecasting applications. This chapter, thus, provides a panoramic view of state-of-the-art of predictive analytics in power systems in the context of future smart grid operations.

Forecasting has long played an essential role in power systems planning and operations. With the introduction of deregulated markets, forecasting has emerged as a critical component of electricity markets as well. Reliable forecasting models allow electrical utilities and independent systems operations (ISOs) to make optimal capacity building and dispatch decisions by understanding their economic implications while still maintaining a reliable energy supply. Forecasting models are also used by the market participants to place strategic bids. The significance of forecasting has dramatically increased because of the rapidly changing landscape of traditional power systems. Some of the main drivers of this change are (1) increasing penetration of intermittent renewable energy resources on utility scale as well as distributed energy resources (DERs), (2) deployment of various smart grid technologies such as advanced metering infrastructure, (3) deregulation of electricity markets, (4) demand response programs turning static loads into dynamic loads, (5) forthcoming electrification of the transportation fleet, (6) greenhouse gas reduction targets, and (7) declining costs of energy storage technologies, among others.

The forecasted data in power systems include meteorological variables such as solar irradiance, wind speed, and wind direction; energy production from renewable energy sources such as photovoltaic plants, wind farms, and hydroelectric dams; load or demand; price of electricity or locational marginal prices; price of fossil fuels such as coal, oil, and natural gas; electric vehicle (EV) charging loads, and so on. These quantities are forecasted for different timescales as well as different spatial resolutions. Long-term forecasts are useful for power systems infrastructure building decisions while short-term forecasts are utilized to inform optimal decision-making by system operators dispatching energy on the grid and market participants trading energy in the markets.

1.1 Motivation

Traditionally, in the regulated electricity sector, mostly vertically integrated utilities had a monopoly. The reliability of supply was primarily the utilities’ responsibility and was maintained using short-term load forecasts. The fossil fuel-based generation sources were dispatchable so that variability associated with the demand was the primary source of uncertainty in the system. Electricity users were passive consumers; that is, there was neither a bidirectional flow of energy from the distribution grid end nor any provision of demand response. Planning and investment in new capacity were based on long-term demand forecasts and utilities were responsible for building the transmission capacity to serve their customers. Traditional forecasting methodologies served well in this regulated business scenario.

Competitive electricity markets have been introduced since the last decade of the twentieth century as a part of the deregulation of the electricity sector [1]. Consequently, energy is now traded in competitive markets, making electricity price and demand forecasts fundamental inputs to the day-to-day decision-making process of the various energy-selling entities, including the utilities, independent power producers, large industrial customers with significant amounts of distribution generation production, and so on.

Moreover, building new transmission capacity is not a straightforward decision made by a single utility anymore. FERC Order No. 1000 [2] established new rules regarding the transmission planning and cost allocation requirement for public utility transmission providers, which have made capacity expansion a competitive process as well. As a result, accurate long-term load forecasting for different geographic areas has become even more important for maintaining the reliability of the system and economically expanding the network to accommodate future demand growth as well as distributed generation penetration on the grid.

The shift toward a digital and electrified economy is causing increased research and planning for networks of electrified transportation and a smart grid, operating interdependently. Forecasting will play an essential role in the transition to this new system as well. These future interdependent networks require reliable long-term EV growth forecasts for the planning of EV charging infrastructure as well as distribution network enhancements to accommodate the high penetrations of dynamic EV charging loads. In the operations domain, short-term forecasts of EV charging or discharging are required to get accurate load forecasts. Additional complexity is added when daily EV charging profiles are optimized using intelligent controls. The operational schedule of EV charging responds to the market price (even without the initiation of demand response events from the utility), making it even more challenging for traditional forecasting approaches to predict the dynamically changing demand.

The macrogrid in the USA (as well as many other industrialized countries) is a century old. Various components of generation, transmission, and distribution systems are reaching the end of their useful life and need to be refurbished. Though there are significant capital costs necessary to renovate the thousands of miles of distribution infrastructure, the reliability threats are even more dire. Several recent wildfires in California can be attributed to the aging power systems infrastructure of Pacific Gas and Electric [3]. The remaining useful life of the assets can be assessed to strategically plan the renovation of aging power systems infrastructure by leveraging advanced machine learning and deep learning-based predictive analytics. Accurate remaining useful life predictions for distribution grid components can inform economic investment such that the components with the highest risk of failure are replaced first.

Growing uncertainty in energy consumption, increasing penetration of intermittent renewable energy generation sources (at both utility scale and for small DERs), the burgeoning share of microgrid deployment, smart grid technologies enabling the internet of things (IoT), aging grid infrastructure, and the forthcoming revolution of electrified transportation are rapidly changing the landscape of power systems. Advanced and innovative predictive analytics approaches are urgently needed to enable more accurate forecasts to improve decision-making and provide the foundation for a smart, resilient, and sustainable grid of the future.

1.2 Classification of Power Systems Forecasting Models

Power systems forecasts may be done for various timescales based on the application of the predicted data. These forecasts can also be classified based on their application domain and their role in the power systems generation, transmission, distribution, and consumption areas. When a quantity is forecasted for different time horizons, the input variables used for producing the forecast also change. For example, when forecasting load for a long-term horizon in a given geographical area, inputs such as macroeconomic uncertainty, population growth, climate change patterns (for predicting the extreme loads), and distributed generation penetration projections are considered. For short-term load forecasting like day-ahead forecasting, input variables such as day of week, time of day, and past load consumption are relied upon instead. The effectiveness of machine learning and deep learning algorithms varies based on the timescale and type of input variables. The classification of forecasting models is discussed in detail in the following sections.

1.2.1 Classification Based on the Domain of Application in Power Systems

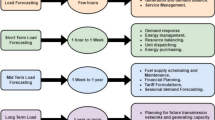
There are three functionally different parts of power systems studies and management, which make it possible to provide reliable and economical electricity to consumers in the present and in the future. These three parts—planning, operations, and market—are described in the following sections. Different types of predictive models are used in these three parts for obtaining forecasts for different quantities, such as load, resource, production, and so on, as shown in Fig. 7.1.

Fig. 7.1

Classification of forecasting models based on domain of applicability

1.2.1.1 Planning

The process of power systems planning is ever evolving and has the largest strategic impact on the future of power systems. Future power systems are planned using a set of forecasts, including load forecasting (which in turn depends onmacroeconomic uncertainty, extreme weather, and climate changes for a given geographic location), distributed generation technologies growth predictions (which depend on the rate of decrease in the cost of these technologies and energy policy that provides incentives), and resource forecasting (which includes short-term production forecasts as well as long-term changes in solar irradiance and wind patterns for a given geographic area).

Smart and clean energy technologies form the foundation of the future smart grid. The key to enabling the adoption of clean energy technologies lies in how well power systems enhancements are planned to accommodate new technologies, enabling their smooth integration with the existing power systems. The goal of planning is to build and modify the generation, transmission, and distribution infrastructure that are needed to meet predicted future needs. Therefore, power systems planning has traditionally been divided into centralized generation planning, transmission planning, and distribution planning. The outcome of planning studies is to address what to build (more generation or transmission/distribution), how much to build, and where to build.

Traditionally, generation planning begins with load forecasting. Reliability evaluation is then conducted to determine if and when additional generation is needed. The remaining useful life of existing base load plants, which are largely powered by fossil fuels, is also accounted for in the next step. This is followed by capacity expansion studies based on economic considerations [4]. Nowadays, however, generation planning is not a solitary process. DER penetration forecasts, including behind-the-meter distributed generation, need to be accounted for in the process. Also, economical siting of utility-scale renewable generation plants depends on availability of solar and wind resources, which may or may not coincide with the demand pockets and existing transmission infrastructure. High penetration of utility-scale renewable energy resources, given their intermittent and variable nature, adds increased complexity to generation planning studies that depend on renewable resource forecasts [5, 6].

Transmission planning is aimed at optimizing the use of a generation portfolio by supplying loads from the most economical sources of power and improving the reliability of overall systems by operating generation stations flexibly [7]. Generation and transmission planning are closely related because the powerflows through the transmission system are a direct result of generation dispatch [8, 9]. Distribution system planning, on the other hand, is optimized for the lowest cost operation that meets the desired reliability of the electricity service. However, the introduction and increased adoption of DERs has changed the process of distribution system planning drastically. This is because components of distribution and transmission systems are not designed to handle the bidirectional flow of power from the DERs, so additional measures must be taken to refurbish the distribution grid with this capability [10, 11].

For generation and transmission planning, load forecasting is done for a long time horizon—often between 2 and 10 years. This is because system capacity expansion projects require a long lead time. Peak annual demand/load (in kilowatts) and total annual energy sales (in kilowatt-hours) are calculated for long-term load forecasts [12]. Peak load is highly correlated with weather. Therefore, peak load forecast is normalized based on extreme weather predictions. Projected EV andDER growth in the future has led to researching and employing methodologies that explicitly consider DERs as well as EV load along with its charging patterns [13, 14]. Load forecasting also needs to be specific to geographical locations, along with maintaining reasonable accuracies of the predicted magnitude.

1.2.1.2 Operations

Power systems operations are associated with making decisions regarding the use of existing equipment and infrastructure to generate, transmit, and deliver energy. It is primarily aimed at doing so safely, reliably, and efficiently. The operations domain deals with three different time horizons: (1) operations planning (a few weeks to months), (2) near real time (a few hours to days), and (3) real time (typically 5–10 min) [15].

Operations planning ensures that sufficient resources are available to meet demand for the next few months. It takes load forecasts (and associated errors), utility-scale renewable generation forecasts, and generation and transmission outages into account. Operations planning also defines the reserve capacity requirements to mitigate the risk imbalances because of forecast errors and unplanned outages of generation or transmission components [16]. The aim of near real-time operations is to select the most economic generation portfolio for the next few days using a process called unit commitment. Real-time operations are aimed at ensuring system reliability and supply sufficiency by revising the near real-time schedule on an as-needed basis.

Load forecasting is the first step of all three time horizons of power systems operations, making it a critical component. For the operations planning and near real-time applications, hourly load forecasts are used. For real-time applications, however, subhourly (minute-level) resolution is typically required. Once the magnitude and geographic location of demand are obtained using load forecasts, least-cost generation is scheduled to meet that demand. The production forecasts of utility-scale renewable generation plants are also considered while scheduling the generation. In the regions with high DER penetration, their production is also considered; behind-the-meter DERs are typically considered negative load.

1.2.1.3 Markets

The landscape of the power sector has substantially changed after the introduction of competitive markets coupled with the deregulation of the industry. This has led to the trading of electricity under market rules using spot and derivative contracts. But the price dynamics of this unique commodity is different from any other commodity because of its unique properties, requirements, and dependencies. For example, energy typically experiences a constant balance between production and consumption because large quantities are not economically storable. Additionally, power demand can depend on weather factors, such as temperature, precipitation, and wind speeds, and on the magnitude of activity in different sectors (i.e., holidays vs. workdays, weekdays vs. weekends, on-peak vs. off-peak hours).

Electricity prices in the wholesale market, therefore, exhibit seasonality at various timescales (daily, weekly, annually) as well as abrupt and brief price spikes. According to [17], “[t]he costs of over-/under-contracting and then selling/buying power in the balancing (or real-time) market are typically so high that they can lead to huge financial losses or even bankruptcy. Extreme price volatility, which can be up to two orders of magnitude higher than that of any other commodity or financial asset, has forced market participants to hedge not only against volume risk but also against price movements.”

Short-term electricity price forecasting is done for the day-ahead market, where the bids are submitted for the delivery of electricity during each load period, which can be hourly or subhourly. Medium-term time horizons are used for risk management and derivative pricing. These forecasts can either be point-forecasts or probability distributions of the prices. Long-term electricity price forecasts are done for planning and economic feasibility analysis of future power plants, establishing long-term power purchase agreements, forward capacity markets, seasonal capacity markets, financial transmission rights auctions, and so on. The time horizon can vary from months to years for such applications.

Renewable generation forecasts in the short term are also required for owners to bid in the market. ISOs need the production forecasts of intermittent energy sources to schedule the generation with sufficient reserves to minimize the risk of underproduction. To avoid financial losses associated with underbidding or overbidding, renewable generation plant owners need reasonably accurate forecasts of solar and wind resources [18].

For each time horizon, the choice of input variables plays a significant role in the effectiveness of the model for both traditional forecasting approaches as well as deep learning methods. For short-term forecasts, the daily and hourly variability must be considered. On the other hand, medium-term forecasting favors annual variations more than weekly ones. For long-term price forecasts, seasonality itself becomes irrelevant. Instead, long-term trends such as load-growth in a certain geographic area, large penetration of cheap renewable energy resources in close proximity, and EV load demand play the major role.

1.2.2 Classification Based on Timescale

In the previous section, various power systems forecasting models were discussed in the context of their applicability to planning, operation, and market domains. Another way of classifying the forecasting models in power systems is based on the timescale for which the quantities are being forecasted. These timescales can mainly be classified into five types, as given in Table 7.1.

Table 7.1 Types of forecasting models based on timescale

1.3 Organization of the Chapter

The introduction section first lays out the motivation behind exploring newer approaches such as deep learning for power systems predictive analytics. The power systems forecasting problems are then classified in broad categories based on timescale of forecasting as well as their application in power systems planning, operations, and market domains. The second section, forecasting power systems using classical approaches, takes a deeper look at the widely used statistical times-series forecasting methods as well as traditional machine learning-based approaches. The third section then introduces state-of-the-art deep learning algorithms and explores their recent applications in the power systems forecasting literature. A solar irradiance forecasting case study is discussed in detail in the fourth section. The fifth section identifies future work areas in this domain and concludes the chapter.

2 Forecasting in Power Systems Using Classical Approaches

The power systems forecasting problems discussed in the previous section most closely align with the mathematical framework of the time series forecasting problem. This section introduces this general mathematical framework and provides a broad overview of several statistical and machine learning approaches to time series forecasting. Note that deep learning methods are left to Sect. 7.3 to be explored in more detail.

2.1 Time Series Data

A general time series dataset can be written as

$$ \left\{{x}_1,{x}_2,{x}_3,\dots \right\}, $$

(7.1)

where each x _t for t = 1, 2, 3, … represents the realization of some random variable. A common additive modeling approach to characterizing Eq. (7.1) is to partition the time series into a trend, seasonality, and stochastic term,

$$ {x}_t={T}_t+{S}_t+{Z}_t. $$

(7.2)

The trend term T _t represents the long-term, nonperiodic changes in the data, the seasonality term S _t describes any periodic behavior of the time series, and the stochastic term Z _t is stationary process (defined later) that models the random noise in the data.

Note that Eq. (7.1) frames the time series data in terms of scalar-valued quantities. This is done to simplify the discussion in this section in order to provide a clear and broad overview of traditional approaches to time series forecasting. The extension of this perspective to the multivariate case is relatively straightforward. One feature of multivariate time series data that is important to power systems modeling is the concept of exogenous variables. In time series forecasting, exogenous variables are causally independent of other factors in the system. In the case of solar irradiance forecasting, examples of exogenous variables may include factors like wind speed and cloud cover. Including exogenous variables in the forecasting process may improve performance.

Recall that each x _t in Eq. (7.1) is a realization of some random variable. The complete time series is then fully characterized by the joint distribution of theserandom variables. However, such a perspective is typically impractical or impossible for real-world applications. A more reasonable approach is to characterize the time series in terms of secondary properties, such as the mean and covariance functions of the series,

$$ {\mu}_t= m{E}\left[{x}_t\right]\; \mathrm{and}\; {\sigma}_{t,s}={C}\mathrm{ov}\left[{x}_t,{x}_s\right]=m{E}\left[\left({x}_t-{\mu}_t\right)\left({x}_s-{\mu}_s\right)\right]. $$

(7.3)

The dependence of the value of x _t on previous terms is characterized by the autocovariance function γ _t(h) = σ _{t, t + h} and the autocorrelation function ρ _t(h) = γ _t(h)/γ _t(0), where h is the lag parameter.

A key property of time series data is the idea of stationarity. A given time series is said to be strictly stationary if any two subseries,

$$ \left\{{\mathrm{x}}_t,{x}_{t+1},{x}_{t+2},\dots, {x}_{t+n}\right\}\kern0.5em \mathrm{and}\kern0.5em \left\{{x}_s,{x}_{s+1},{x}_{s+2},\dots, {x}_{s+n}\right\}\kern1em \mathrm{for}\kern0.75em t,s,n\in {N}, $$

(7.4)

have the same joint distribution. Notice that if each x _t in a given time series is independent and identically distributed (iid), then the time series is strictly stationary. Such a sequence drawn from a distribution with mean 0 and variance σ ² is typically referred to as white noise.

As discussed earlier, characterizing the full joint distribution of a time series is not realistic for most real-world applications, making the identification of a time series as strictly stationary infeasible. Alternatively, a time series is said to be weakly (or wide-sense) stationary if any two subseries have the same mean and covariance functions, μ _t and σ _{t, s}, respectively. Equivalently, a weakly stationary time series has mean and covariance functions that are independent of t. That is, μ _t = μ and σ _{t, s} = σ. Notice that this also implies that the autocovariance and autocorrelation functions only depend on the lag parameter, γ _t(h) = γ(h) and ρ _t(h) = ρ(h). Because this definition is of more practical use, it is common to use the term stationary to refer to weakly stationary and specifically refer to a time series as strictly stationary when the stricter definition is meant.

The next two sections explore various statistical and machine learning approaches to time series forecasting. In general, the goal of forecasting is to predict values of future datapoints $\left\{{\hat{x}}_{n+1},{\hat{x}}_{n+2},\dots \right\}$ given a finite set of observed data {x ₁, x ₂, x ₃, …, x _n}. Generally, time series forecasting is classified according to the horizon out to which the forecast is made, as illustrated in Table 7.1.

The differences between short-, medium-, and long-term forecasts are highly dependent on the problem under consideration. However, short- and medium-term forecasts typically are more dependent on autocorrelation factors and shorter seasonality behaviors. These prediction horizons tend to be more amenable to the types of data-driven methods covered here. Long-term forecasting seeks to model trends in the data and often depends on the additional models of the relevant systems to help predict changes in these trends.

Power systems forecasting is a particularly difficult problem. Figure 7.2 shows an example time series data of total solar irradiance over a 20-year range [19]. It is immediately obvious that this dataset is nonstationary (as is the case of many time series data arising from power systems). The data show seasonal cycles of increased and decreased solar irradiance that have a period of approximately 11 years. In addition to fluctuations in the mean of the data, the seasonality also changes the variance of the data. The time series varies more significantly during periods of high solar irradiance and less significantly during periods of low solar irradiance. Lastly, the example data in Fig. 7.2 highlight the differences in short-, medium-, and long-term forecasting. Short-term forecasts are focused on accurately capturing the high-frequency fluctuations in the data. Medium- and long-term predictions cannot hope to perfectly predict these behaviors and instead focus on the large-scale trends and seasonal characteristics in the time series.

Fig. 7.2

Total solar irradiance measured daily from 1980 to 2000. These data come from the NOAA’s National Centers for Environment Information database [19]

2.2 Statistical Forecasting Approaches

2.2.1 Naïve Model Approach

The naïve model approach to time series forecasting simply predicts that the next value in the sequence is the same as the current value,

$$ {\hat{x}}_{t+1}={x}_t. $$

(7.5)

This approach produces the optimal prediction for random walk data and is therefore also known as the random walk model for time series forecasting. The main purpose of this model is to serve as a simple baseline to compare with moresophisticated models. This naïve model approach is also called the persistence model [20].

2.2.2 Exponential Smoothing

Exponential smoothing is a relatively simple approach to modeling time series that predicts new values in time series using a weighted moving average that more heavily favors recent datapoints [21]. Given time series data {x ₁, x ₂, x ₃, …, x _n}, the simple exponential smoothing model computes the smoothed approximation of ${\hat{x}}_{n+1}$ as

$$ {\hat{x}}_{n+1}=\alpha {\mathrm{x}}_n+\left(1-\alpha \right){\hat{x}}_n, $$

(7.6)

where α ∈ (0, 1) is the smoothing factor. Notice that this method computes a weighted average of the current true value and the current predicted (or smoothed) value. The current smoothed value was computed similarly. Thus, previous terms contribute to the current predict value with exponentially decreasing importance. The rate of this decay is controlled by the smoothing factor α. Extensions to simple exponential smoothing incorporate trends and seasonality [22, 23].

Simple exponential smoothing is among the earliest forecasting techniques applied to load forecasting [24]. In particular, this work explores the application of exponential smoothing to short-term forecasting at hourly intervals. More recently, several studies have explored the application of double seasonality exponential smoothing to short-term load forecasting and found this approach to be robust despite its relative simplicity [25, 26].

2.2.3 Autoregressive Moving Average (ARMA) Models

The autoregressive moving average (ARMA) model and its variations are powerful forecasting tools that are among the most popular statistical methods for power systems analysis. The ARMA model has long been used for power-related problems, such as solar irradiance and load forecasting [27, 28]. More recently, an ARMA variant called ARIMA (covered in the next section) has been applied to short-term solar forecasting [29, 30], next-day electricity pricing [31], and hourly load predictions [32].

As the name suggests, the ARMA model makes two key assumptions on the time series. The first is that the time series data can be modeled by an autoregressive process. An autoregressive process of order p, denoted by AR(p), assumes a linear dependence of the current timestep on the previous p timesteps,

$$ {\hat{x}}_t=\sum \limits_{i=1}^p{\omega}_i{x}_{t-i}+{z}_t, $$

(7.7)

where ω _i are constants and z _t is a white noise term. The second assumption of the ARMA model is that of a moving average model. The moving average model of order q, denoted by MA(q), represents the sequence as a linear relationship of some other white noise sequence,

$$ {\hat{x}}_t=\sum \limits_{i=1}^q{\theta}_i{z}_{t-i}+{z}_t, $$

(7.8)

where θ _i are constants and each z _t is an iid white noise term. The ARMA model of orders p and q, denoted by ARMA(p, q), combines Eqs. (7.7) and (7.8) to form

$$ {\hat{x}}_t=\sum \limits_{i=1}^p{\omega}_i{x}_{t-i}+\sum \limits_{i=1}^q{\theta}_i{z}_{t-i}+{z}_t. $$

(7.9)

The ARMA model is typically solved using the Box-Jenkins method [33]. This is an iterative process of specifying the model, fitting the parameters, and verifying the process. Specifying the model involves the order of the ARMA(p, q) model (i.e., selecting the appropriate values of p and q). Heuristically, this can be accomplished by examining the autocorrelation function ρ _t(h) and the partial autocorrelation function. Recall that the autocorrelation function explains the relationship between two terms with lag h. However, because this relationship can have a recursive structure, it may be difficult to distinguish between a time series that is dependent on the previous n points and one that is highly dependent only on the previous one. The partial autocorrelation addresses this concern by filtering out the influence of the intermediate terms {x _t − 1, x _t − 2, …, x _{t − h + 1}}. This is computed by solving the linear system

$$ \boldsymbol{\Sigma} \boldsymbol{\upalpha} =\boldsymbol{\upgamma}, $$

(7.10)

where (Σ)_{i, j} = γ _t(i − j) and (γ)_i = γ _t(i) for i, j = 1, 2, …, h. The partial autocorrelation with lag h is α _t(h) = (α)_h. Reasonable guesses of p and q for ARMA can be made from examining plots of the autocorrelation and partial autocorrelation functions. If the autocorrelation plot slowly decays to zero and the partial autocorrelation plot abruptly decays to zero after a lag of h, then the model is likely ARMA(h, 0), or equivalently AR(h). Alternatively, if the partial autocorrelation plot slowly decays to zero and the autocorrelation plot abruptly decays to zero after a lag of h, then the model is likely ARMA(0, h) or MA(h). If both values slowly decay to zero, then the model is likely ARMA(p, q) where the orders are taken to be a lag after which the plots have sufficiently decayed. Selecting the appropriate value of p and q can be difficult and take some trial and error.

Once the order of the ARMA model has been determined, the parameters ω _i and θ _i must be fit. This is accomplished using any preferred numerical optimization method to solve for the maximum likelihood estimate of these parameters. Once ω _i and θ _i have been computed, the model is examined for errors and overfitting. If necessary, the process is repeated with a new model selection.

2.2.4 Autoregressive Moving Integrated Average (ARIMA) Models

The success and popularity of the ARMA model have led to multiple variations and extensions of the method. The autoregressive integrated moving average (ARIMA) model was introduced to address the stationarity assumption on the time series data. ARIMA has been used recently for predicting the EV charging demand for stochastic power systems operation [34]. It incorporates differencing of the time series data to attempt to remove any nonstationary behavior. The number of differencing steps d is treated as another modeling parameter so that the model is written ARIMA(p, d, q).

Notice that the discussion of the Box–Jenkins method discussed in the previous section appears to assume that both the autocorrelation and the partial autocorrelation functions will eventually decay to zero (whether slowly or rapidly). If this is not the case, then differencing may be applied to the data to remove the nonstationarity. Differencing is a common approach to producing a stationary time series. One differencing iteration produces a new time series with

$$ {y}_t={x}_{t+1}-{x}_t. $$

(7.11)

The Box–Jenkins method determines d by differencing on the time series until the autocorrelation and partial autocorrelation plots decay appropriately.

2.3 Machine Learning Forecasting Approaches

Supervised machine learning seeks to construct a predictive model f _Θ(x), based on a given training set of data ${\left\{{\mathbf{x}}_i,{y}_i\right\}}_{i=1}^N$, where x _i and y _i represent the feature vector and the target value [35]. For time series forecasting, the feature vectors are typically constructed by a moving window over the given data, x _i = [x _i, x _i + 1, x _i + 2, …, x _i + n]^⊤, and the target value is the first datapoint after this window, y _i = x _{i + n + 1}. The subscript Θ in the model denotes the collection of parameters that are tuned to best fit the data. Machine learning methods fit the model parameters from the data through iterative updates to reduce some loss function, such as the squared-error loss $L={\sum}_{i=1}^N{\left({y}_i-{f}_{\boldsymbol{\Theta}}\left({\mathbf{x}}_i\right)\right)}^2$ or the absolute-error loss $L={\sum}_{i=1}^N\left|{y}_i-{f}_{\boldsymbol{\Theta}}\left({\mathbf{x}}_i\right)\right|$.

This section introduces two popular machine learning methods for time series forecasting: the support vector regression (SVR) and the Gaussian process regression (GPR). There are many more approaches that may be appropriate depending on the specific problem at hand, such as k-nearest neighbor regression or regression trees. A more comprehensive overview of these methods can be found in [20, 36, 37]. Deep learning (or neural network) methods tend to fall within the realm of machine learning as well. However, their discussion is reserved for Sect. 7.3 so that they may be explored more in depth.

2.3.1 Support Vector Regression

Support vector regression (SVR) is a form of the popular machine learning approach known as support vector machine (SVM) [38]. The linear SVR attempts to fit the model

$$ y={\boldsymbol{\uptheta}}^{\top}\mathbf{x}+{\theta}_0 $$

(7.12)

to the data while minimizing ‖θ‖. A linear model may be insufficient to describe the complex relationships underlying real-world datasets. Nonlinear or kernel SVR reformulates the model as

$$ y=\sum \limits_{i=1}^N{\theta}_ik\left({\mathbf{x}}_i,\mathbf{x}\right)+{\theta}_0, $$

(7.13)

where k(·, ·) is a kernel function such as the radial basis function, or squared-exponential kernel k(x _i, x _j) =  exp (−γ(x _i − x _j)²), where γ is a hyperparameter that can be tuned using a grid search with cross-validation. The use of the kernel function implicitly defines a nonlinear mapping of the feature vector to some higher-dimensional space where a linear model is applied. This nonlinear mapping provides greater flexibility than simply applying the linear model directly to the features as in Eq. (7.12). Such a mapping is guaranteed to exist, provided that the kernel satisfies the so-called Mercer condition [39].

As mentioned previously, training any machine learning model requires the formulation of some loss function that informs the optimal set of model parameters. For SVR, it is common to use the ϵ-insensitive loss function. This loss ignores any points within ±ϵ of the model prediction and is equal to the absolute error in the model for datapoints outside this range. Using the ϵ-insensitive loss, the SVR learning problem can be stated as

$$ \underset{\Theta}{\min}\left\Vert \Theta \right\Vert +c\sum \limits_{i=1}^N{\xi}_i\kern0.5em \mathrm{subject}\kern0.5em \mathrm{to}\kern0.5em \left|{y}_i-\sum \limits_{i=1}^N{\theta}_ik\left({\mathbf{x}}_i,\mathbf{x}\right)+{\theta}_0\right|\le \epsilon +{\xi}_i $$

(7.14)

where ξ _i are slack variables that penalize deviation outside the ϵ-insensitive region of the loss function.

SVR is a popular machine learning approach to load forecasting [40,41,42]. SVRs have also been combined with other approaches to enhance performance on the short-term load forecasting problem. For example, an SVR can be combined with a locally weighted regression method that more heavily favors nearby points when making predictions [43]. Another approach combines SVRs with the empirical mode decomposition that separates out the high- and low-frequency components of a time series [44]. Both of these hybrid approaches were found to outperform the classical SVR method.

2.3.2 Gaussian Process Regression

Gaussian process regression (GPR) approaches time series forecasting from a Bayesian perspective by assuming that the underlying model for the data is drawn from prior distribution of functions [45]. For GPR, this prior is assumed to be a mixture of multivariate Gaussian random variables, or a Gaussian process,

$$ f\left(\mathbf{x}\right)\sim \mathcal{GP}\left(m\left(\mathbf{x}\right),k\left(\mathbf{x},{\mathbf{x}}^{\prime}\right)\right), $$

(7.15)

where m(x) and k(x, x ^′) are the mean and variance function, respectively. Often, the problem is formulated with mean zero and the kernel function equal to the squared-exponential from SVR.

Conditioning on the given dataset generates the posterior distribution of f, which is also a Gaussian process with mean and variance

$$ m{E}\left[f\left(\mathbf{x}\right)|{\left\{{\mathbf{x}}_i,{y}_i\right\}}_{i=1}^N\right]=\mathbf{k}{\left(\mathbf{x}\right)}^{\top }{\mathbf{K}}^{-1}\mathbf{y}, $$

$$ m{V}\mathrm{ar}\left[f\left(\mathbf{x}\right)|{\left\{{\mathbf{x}}_i,{y}_i\right\}}_{i=1}^N\right]=k\left(\mathbf{x},\mathbf{x}\right)-\mathbf{k}{\left(\mathbf{x}\right)}^{\top }{\mathbf{K}}^{-1}\mathbf{k}\left(\mathbf{x}\right), $$

(7.16)

where (y)_i = y _i, (K)_{i, j} = k(x _i, x _j) and (k(x))_i = k(x _i, x) for any x. Using the decaying exponential kernel, it can be shown that the model interpolates the data without any variance. By assuming the data are corrupted by Gaussian noise with variance σ ², the posterior distribution then has mean and variance

$$ m{E}\left[f\left(\mathbf{x}\right)|{\left\{{\mathbf{x}}_i,{y}_i\right\}}_{i=1}^N\right]=\mathbf{k}{\left(\mathbf{x}\right)}^{\top }{\left(\mathbf{K}+{\sigma}^2\mathbf{I}\right)}^{-1}\mathbf{y}, $$

$$ m{V}\mathrm{ar}\left[f\left(\mathbf{x}\right)|{\left\{{\mathbf{x}}_i,{y}_i\right\}}_{i=1}^N\right]=k\left(\mathbf{x},\mathbf{x}\right)-\mathbf{k}{\left(\mathbf{x}\right)}^{\top }{\left(\mathbf{K}+{\sigma}^2\mathbf{I}\right)}^{-1}\mathbf{k}\left(\mathbf{x}\right). $$

(7.17)

Gaussian processes have been applied to the load forecasting problem with promising success [46]. Additionally, GPR has been used for renewable energy forecasting relating to solar radiation [47] and wind power [48]. One study used GPRs with time-based composite covariance to handle seasonality in solar radiation data [49].

2.4 Shortcomings of Classical Approaches

Statistical and machine learning approaches to time series forecasting are powerful tools for understanding and modeling power systems forecasts. These methods have been performing reasonably well for short- and medium-term forecasting with traditionally acceptable level of accuracies. However, these methods can require significant data preprocessing that is not explored deeply here. For example, most of the statistical approaches assume stationary time series data with variable-independence and normality assumptions. Extensions to these methods that effectively deal with nonstationary data require manual tuning of various meta-parameters that essentially transform the data to be stationary.

Additionally, with the increasing dynamism in the future power systems, there is a need to obtain forecasts with higher accuracy than what is being achieved with traditional statistical and machine learning methods. The operations of power systems are getting more dynamic in nature with bidirectional flow of power through distributed energy resources, prosumer participation with demand-response, and other smart grid technologies. Increasing renewable energy penetration and decreasing synchronous generation resources are reducing the overall inertia of the grid [50]. This requires a finer temporal resolution of the forecasts in order to maintain reliable real-time operations of the grid. Furthermore, price forecasting for electricity markets can benefit greatly from a small percentage gain in the prediction accuracy, and better renewable energy forecasts are required by ISOs to lower the amount of the costly operational reserves [51].

The next section examines the history and current state-of-the-art in deep learning methods for power systems forecasting. With their ability to represent complex nonlinear behaviors in nonstationary, high-frequency, and high-dimensional time series data, these methods have been shown to be more robust to some of the abovementioned pitfalls of traditional approaches, but at the expense of some new hurdles.

3 Forecasting in Power Systems Using Deep Learning

3.1 Deep Learning

Artificial neural networks (ANN) are universal function approximators [52]; that is, it is possible to represent complex nonlinear behavior in a high-dimensional, high-frequency, and nonstationary time series using ANNs. A deep neural network is an ANN with multiple hidden layers and nodes cascaded between input and output layers. Deep neural networks are sophisticated neural networks that have been successfully applied to analyze data in many disciplines in the past several years such as computer vision, image recognition, automatic speech recognition, bioinformatics, finance, and nature language processing [53].

In general, supervised machine learning algorithms are particularly task specific. However, deep learning networks are capable of learning intricate structures in large datasets, allowing them to generalize better to scenarios not present in the training data. Because of their capability to learn nonlinear relationships between input features, these networks can identify and ignore features that do not impact the target variable by minimizing the appropriate weights. Consequently, deep learning algorithms typically do not require the type of extensive data preprocessing and feature engineering that is required of other traditional machine learning methods. Additionally, deep learning algorithms are also capable of managing high-dimensional datasets better than traditional machine learning algorithms.

Recurrent neural networks (RNN), long short-term memory networks (LSTM), convolutional neural networks (CNN), autoencoders, restricted Boltzmann machines, deep belief networks, and deep Boltzmann machines are all common types of deep learning algorithms. The following sections introduce deep learning algorithms that are often applied to power systems forecasting problems and describe their mathematic framework briefly.

3.1.1 Recurrent Neural Network

Unlike traditional feedforward neural networks in which information flows from each layer to the next, RNNs allow the output from a layer to flow back into itself. This allows RNNs to process sequential data without assuming the independence among the time series samples or the datapoints [54]. Feedforward networks lose any knowledge of the system state after processing each time series sample, thereby failing to account for the relationship between exogenous variables along the temporal dimension. The recurrent edges in an RNN introduce temporal coupling into the model. The internal memory, formed by the feedback connections of the neurons in the hidden-layer nodes, updates the states of each neuron in the network with the previous input. The addition of this temporal coupling, which unfolds over time, allows RNNs to learn and exhibit complex system dynamics, making them efficient at time series forecasting problems.

The input to an RNN is a sequence of real-valued datapoints {x ₁, x ₂, x ₃, …}, where x _t represents the value of time series variables timestep t. Given a finite input subsequence of length n, the target output for the RNN is the next value y _n + 1. Note that the target y values may contain the same variables as the input x values but at future timesteps, or they may be different if the input includes exogenous variables. The network output (i.e., the predictions from the network) is denoted by ${\hat{\mathbf{y}}}_t$. Figure 7.3 shows how the network unfolds the data along the temporal dimension. Mathematically, this unfolding is written as

$$ {\mathbf{h}}_t={f}_h\left({\mathbf{W}}_{hx}{\mathbf{x}}_t+{\mathbf{W}}_{hh}{\mathbf{h}}_{t-1}+{\mathbf{b}}_h\right), $$

$$ {\hat{\mathbf{y}}}_{t+1}={f}_o\left({\mathbf{W}}_{yh}{\mathbf{h}}_t+{\mathbf{b}}_y\right), $$

(7.18)

where the current input datapoint x _t is fed into the network along with the output of the hidden layer from the previous timestep h _t − 1, and the output from the hidden layer is used to generate the prediction ${\hat{\mathbf{y}}}_{t+1}$. The remaining terms in Eq. (7.18) include the activation functions f _o and f _h, the weight matrices W _hx, W _hh, and W _yh, and the biases for each layer b _h and b _y.

Fig. 7.3

Unfolding of an RNN over the temporal dimension

3.1.2 Long Short-Term Memory Network

In theory, RNNs should be capable of handling long-term temporal relationships because of their ability to retain information from previous timesteps. In practice, vanishing gradients make it difficult for them to learn long-term dependencies. Long short-term memory networks (LSTM) are a variation on the traditional RNN that are more effective at learning long-term trends in data, making them efficient at time series forecasting problems.

The key difference between RNNs and LSTMs is that the latter replaces hidden nodes with a more complex memory cell that handles the recurrent transfer of information (see Fig. 7.4). Four layers of neural connections, which exchange information in a particular special way, form the foundation of these memory cells. LSTMs are capable of learning long-term dependencies because the memory cells retain the existing information and append the unit with the new information; in RNNs, the content of the hidden node is replaced with the new value calculated from the current input.

Fig. 7.4

LSTM memory cell diagram (from [55])

The mathematical formulation governing the flow of information in a LSTM cellis

$$ {\mathbf{f}}_t=\sigma \left({\mathbf{W}}_f{\left[\ {\boldsymbol{h}}_{t-1}^{\top}\kern0.75em {\mathbf{x}}_t^{\top}\right]}^{\top }+{\mathbf{b}}_f\right), $$

$$ {\mathbf{i}}_t=\sigma \left({\mathbf{W}}_i{\left[\ {\boldsymbol{h}}_{t-1}^{\top}\kern0.75em {\mathbf{x}}_t^{\top}\right]}^{\top }+{\mathbf{b}}_i\right), $$

$$ {\overset{\sim }{\mathbf{C}}}_t=\tanh \left({\mathbf{W}}_c{\left[\ {\boldsymbol{h}}_{t-1}^{\top}\kern0.75em {\mathbf{x}}_t^{\top}\right]}^{\top }+{\mathbf{b}}_c\right), $$

$$ {\mathbf{C}}_t={\mathbf{f}}_t\circ {\mathbf{C}}_{t-1}+{\mathbf{i}}_t\circ {\overset{\sim }{\mathbf{C}}}_t, $$

$$ {\mathbf{o}}_t=\sigma \left({\mathbf{W}}_o{\left[\ {\boldsymbol{h}}_{t-1}^{\top}\kern0.75em {\mathbf{x}}_t^{\top}\right]}^{\top }+{\mathbf{b}}_o\right), $$

$$ {\mathbf{h}}_t={\mathbf{o}}_t\circ \tanh \left({\mathbf{C}}_t\right). $$

(7.19)

Note that the nodes in the cell operate on the concatenated vector ${\left[\ {\boldsymbol{h}}_{t-1}^{\top}\kern0.75em {\mathbf{x}}_t^{\top}\right]}^{\top }$where x _t is the current input vector and h _t − 1 denotes the output from the cell at the previous timestep. The value C _t is the current state of the cell and is defined by a combination of the information from the forget gate f _t and the input gate i _t (where ∘ denotes the element-wise Hadamard product). The output gate o _t is acted on by the cell state to produce the output of the cell h _t. The various W’s and b’s represent the weights and biases in the cell, while σ and tanh are the sigmoid and hyperbolic tangent activation functions, respectively.

Once the model is chosen, there are two main iterative phases in the learning algorithm: (1) forward propagation and (2) weight update. For an RNN or LSTM, the architecture first unfolds the time series input along the temporal dimension, making the network similar to a traditional feedforward neural network. In the forward propagation phase, the input vector propagates through the hidden layers (using randomly initialized values for the weight matrices and biases) to compute the output vector. The mismatch between the interim prediction output and the actual target is calculated as a loss function (e.g., the mean squared-error loss). Theweights are updated using gradient descent with the gradients with respect to the loss function computed using the backpropagation through time algorithm.

3.1.3 Other Relevant Models

WaveNet deep learning models were recently introduced that apply deep learning techniques from audio signal processing and computer vision models to time series (sequential) data [56]. Convolutional neural networks (CNN) are a type of deep feedforward ANN that have been used to analyze visual imagery on a large scale. A deep convolutional WaveNet architecture, which is variation of CNN, has been successfully used for conditional time series forecasting [57].

3.2 Deep Learning Applications

Deep learning has been applied to a variety of power systems prediction problems recently, including solar forecasting, building load forecasting, system load forecasting, wind forecasting, and electricity price forecasting. RNN and LSTMs are the most popular architectures published in the literature for power systems forecasting problems. The following sections discuss the recent literature of power systems predictive analytics using deep learning.

3.2.1 Load Forecasting

Load forecasting may be done at either a systems level or building level and for different time horizons. Deep neural networks have been used for building energy load forecasting using an LSTM and an LSTM-based sequence to sequence modeling approach [58]. Short-term residential load forecasting is done using an LSTM in [59]. Shi et al. [60] propose a pooling-based RNN architecture, which outperforms traditional RNNs, along with other traditional machine learning algorithms in residential load forecasting. Another variation of RNN, called the gated recurrent unit network, is used in [61] for daily peak load forecasting. CNNs with k-means clustering have also been applied for short-term load forecasting for smart grids [62].

3.2.2 Generation Forecasting

In the field of renewable energy, deep learning has been applied for wind and solar forecasting problems. A short-term wind forecasting problem is addressed using RNNs with a so-called infinite feature selection method in [63] and using CNNs in [64]. A hybrid deep learning approach is proposed for day-ahead wind power forecasting in [65]. Wind and solar irradiance forecasting are done using CNNs with input data obtained from numerical weather prediction in [66].

Solar forecasting methodologies vary widely based on the type of inputs being used for the process. For example, a standard time series forecasting problem may only make use of previous solar irradiance measurement (endogenous variables). Alternatively, one might use ground-based meteorological parameters (exogenous variables) or sky imagery/video for predicting solar irradiance. Siddiqui et al. propose a deep learning-based approach for solar irradiance forecasting using sky videos [67]. LSTMs are used for solar power forecasting by Gensler et al. in [68] and RNNs are used in [69] for solar irradiance forecasting. Section 7.4 in this chapter examines a case study in multi-time-horizon solar irradiance forecasting using RNNs and LSTMs [55, 70].

3.2.3 Electricity Price Forecasting and Electric Vehicle Charging

Electricity price forecasting in competitive energy markets is a challenging prediction problem because of the rare characteristics of electricity. Electricity cannot be treated like other commodities because trading requires a balance between supply and demand at every point in time. The failure to maintain this balance results in blackouts and brownouts that are hugely detrimental to the society as a whole. The research around deep learning-based approaches to electricity price forecasting is growing. There have been a few articles exploring this topic [71,72,73,74,75]. Deep learning has also been applied for demand-side management for smart charging of EVs [76].

3.3 Deep Learning Strengths and Shortcomings

Deep learning has shown promising results in the field of predictive analysis, because of its ability to model complex, nonlinear relationships between various exogenous input variables and the associated output. It is capable of uncovering trends in the historical dataset, providing highly accurate forecasts. For power systems forecasting problems, deep learning algorithms are increasingly outpacing traditional approaches for nowcasting and short-term forecasting. In order to produce such accurate predictions for these time horizons, deep learning algorithms require a relatively significant amount of training data. The next two sections summarize the strengths and weaknesses of deep learning approaches in the context of power systems forecasting problems.

3.3.1 Strengths

Deep learning algorithms with recurrent connections (e.g., RNN and LSTM) are capable of capturing short- and long-term trends in time series data. When trained using exogenous variables, these algorithms are effective at finding and modeling the complex temporal relationships between various input variables. Deep learning also has the rather unique capability of performing in situ feature engineering; that is, extensive manual feature engineering is not required for deep learning algorithms like traditional machine learning algorithms. The data availability in power systems has exploded in recent years, creating a natural environment for the emergence of deep learning algorithms. For this reason, it is reasonable to assume that deep learning has yet to reach its full potential in revolutionizing power systems predictive analytics field.

3.3.2 Shortcomings

Deep learning models have traditionally been difficult to train because of their expensive computational costs. This limitation has been overcome in recent years with technical advances in GPUs, network architectures, and development of performance optimization techniques. While ANNs act as universal function approximators, they are also often a black-box approach to modeling. They lack interpretability and are prone to overfitting because of the high capacity to learn (especially deep neural networks). Also, deep learning algorithms require significant amounts of data for training. For cases where data are limited, deep learning algorithms may not be the optimal method to use. Lastly, for long-term forecasting horizons (5+ years), statistical methods still provide reasonably good predictions, given the limited data availability.

4 Case Study: Multi-Timescale Solar Irradiance Forecasting Using Deep Learning

This section reviews an example of using deep learning for real-time forecasting of solar irradiance [55, 70], where a unified architecture is proposed for predicting multi-time-horizon solar irradiance. This work uses both RNNs and LSTMs to make predictions of global horizontal irradiance (GHI), also referred to as the total solar irradiance. Recall from Sect. 7.3 that these deep learning architectures use data from previous timesteps to inform the current one. This allows the models to learn the underlying dynamics of system in order to enhance their predictive capabilities.

4.1 Data

The data for this study come from the seven Surface Radiation Budget Network (SURFRAD) measurement stations, scattered across the continental USA (see Fig. 7.5) that measure various meteorological parameters, including solar radiation. The distribution of these research stations across various climate zones demonstrates the robustness of the constructed networks in predicting GHI. ¹ Minute-by-minute meteorological data for 2009–2011 from this database is used in this study. The data are averaged over each hour to obtain mean hourly GHI values for forecasting. Data from 2010 and 2011 at each location are used for training while corresponding datafrom 2009 are used for measuring performance.

Fig. 7.5

The seven SURFRAD research stations distributed across the continental USA

4.1.1 Global Horizontal Irradiance

Global horizontal irradiance (GHI) refers to the total solar power per unit area that is incident on some surface (e.g., a photovoltaic solar panel) and is typically measured in W/m ². This value has two main components: (1) direct normal irradiance (DNI) and (2) diffuse horizontal irradiance (DHI). The GHI at a particular time t can be expressed as

$$ {\mathrm{GHI}}_t={\mathrm{DNI}}_t\times \cos \left(\theta \right)+{\mathrm{DHI}}_t,$$

(7.20)

where θ denotes the solar zenith angle, which is the angle between the zenith (overhead) and the sun. This value is important to understanding the availability of solar energy on the grid.

The constructed networks (discussed in Sect. 7.4.2) directly predict a value known as the clear-sky index K _t. This value is a ratio of the true GHI to the expected GHI in a cloud-free scenario,

$$ {K}_t=\raisebox{1ex}{${\mathrm{GHI}}_t$}\!\left/ \!\raisebox{-1ex}{${\mathrm{GHI}}_t^{\mathrm{clear}}$}\right.. $$

(7.21)

The clear-sky index is a dimensionless value that describes the total solar irradiance relative to a theoretical upper limit, which occurs in cloud-free situations. This acts as a type of normalization for the model that can increase robustness to location or seasonality. The clear-sky GHI (${\mathrm{GHI}}_t^{\mathrm{clear}}$) in Eq. (7.21) is calculated using the Bird clear-sky model [77] based on latitude, longitude, elevation, and atmospheric parameters, such as column water vapor, ozone optical thickness, and aerosol optical depth. Based on this calculation and the predicted clear-sky index from the deep learning model, one can easily obtain the predicted GHI.

4.1.2 Exogenous Input Variables

The input to the deep learning model is a vector of 20 exogenous variables for each timestep:

• downwelling global solar (W/m²),

• upwelling global solar (W/m²),

• direct-normal solar (W/m²),

• downwelling diffuse solar (W/m²),

• downwelling thermal infrared (W/m²),

• downwelling infrared case temperature (K),

• downwelling infrared dome temperature (K),

• upwelling thermal infrared (W/m²),

• upwelling infrared case temperature (K),

• upwelling infrared dome temperature (K),

• global UVB (mW/m²),

• photosynthetically active radiation (W/m²),

• net solar (W/m²),

• net infrared (W/m²),

• net radiation (W/m²),

• 10-mean air temperature (C),

• relative humidity (%),

• wind speed (m/s),

• wind direction (^°),

• station pressure (mb).

Not all of the variables listed here are necessarily important to the solar irradiance forecast, but they have been used in this case study. As an extension to this work, further experiments can be conducted to understand the relevance of the individual input variables and accordingly reduce the dimensionality of the dataset.

4.1.3 Data Preprocessing and Postprocessing

The algorithmic approach in this case study begins by preprocessing the data. This includes removing extreme outliers (values which are +/− 4 standard deviation away from the mean) as well as nighttime values, filling in missing data with the mean value of surrounding points, and normalizing the input data vectors. The clear-sky GHI is computed using the Bird model (see Sect. 7.4.1.1) and used to transform target GHI values to the clear-sky index K _t. Postprocessing the data includes recovering the predicted GHI from the clear-sky index and computing the performance of the network using the mean squared error.

4.2 Model Architecture and Training

This case study examines two scenarios: (1) a fixed-time horizon that is similar to other statistical and machine learning forecasting approaches (such as those discussed in Sects. 7.2.2 and 7.2.3) and (2) a multi-time-horizon that is better suited for the flexibility of a deep learning model. In the fixed-time case, separate models are trained for each desired time horizon (1, 2, 3, and 4 h) while a single model is used to predict all of the time horizons in the multi-time case. In both scenarios, separate models are trained for each of the seven SURFRAD locations.

For the fixed-time-horizon problem, this study only considers traditional RNN models and compares the performance of this deep learning method to standard machine learning approaches. The network is constructed using rectified linear units (ReLU) activation functions for all hidden layers and a linear activation on the output layer. The output is scalar-valued because the goal is to predict GHI for a single time horizon.

The multi-time-horizon networks predict GHI at 1-, 2-, 3-, and 4-h time horizons simultaneously, producing a four-dimensional output vector. This work also proposes an extension to the unified architecture for predicting multi-time-scale solar irradiance, which covers 5-min, 15-min, and other such intrahour time horizons. This work compares LSTMs and RNNs; however, no comparison is made to traditional machine learning methods because these approaches are unable to perform multi-time-horizon predictions. The RNNs have similar activation architectures to the fixed-time-horizon case. The LSTM networks use sigmoid and hyperbolic tangent activations within the memory cells.

For training, the deep learning models have access to the target GHI values so that the mean squared loss can be computed. The models are trained using stochastic gradient descent where the gradients with respect to this loss are computed using backpropagation through time. The training minibatch sizes are n = 100, and the networks are trained for 1000 epochs.

4.3 Results

4.3.1 Single Time Horizon Model

Table 7.2 shows the comparison between the RNN performance and the performance of other machine learning forecasting approaches. The values in the ML column are those presented in [78] where the authors perform the same fixed-time-horizon study using several traditional machine learning algorithms (SVRs, random forests, and gradient boosting) as well as a traditional feedforward neural network. The listed performance is the optimal performance across all testing algorithms for each horizon/location combination. In each case, the RNN approach significantly outperforms the others.

Table 7.2 Root mean squared error of predicted GHI (W/m²) for fixed-time-horizon RNNs and machine learning (ML) approaches

4.3.2 Multi-Time-Horizon Model

Table 7.3 contains the results of the RNN/LSTM comparison study for the multi-time-horizon problem.² Recall that for this study, a single RNN or LSTM network is trained for each location that forecasts GHI out to all four time horizons. Neither network architecture outperformed the other across all seven locations. However, within each location there is a significant increase in error from the 3-h to the 4-h forecasting horizon. This could indicate that autocorrelation in the time series data decays after 3 h.

Table 7.3 Root mean squared error of the predicted clear-sky index for multi-time-horizon RNN and LSTM models

5 Summary and Future Work

Given the rapidly occurring technological changes in power systems and their forthcoming transformation into the smart grid, which operates as a part of a complex amalgamation of interdependent transportation, communication, and IoT networks, there is an urgent need for developing and deploying better algorithms for forecasting the various power systems quantities. Moreover, operational uncertainties continue to increase with the burgeoning share of utility-scale as well as DER-scale renewable energy generation on the grid, calling for better short-term forecasts. These play a significant role in the optimization of the operational efficiency of power systems, both economically and in terms of reliability.

Forecasting accuracies for electricity price prediction play a major role in maintaining the economic viability of energy producers’ businesses in the market. Resource and load forecasting also have a major role to play in large-scale deployment of microgrids because these quantities are the main inputs to the optimization algorithms aimed at operating the microgrids intelligently (i.e., maximizing economic benefit while maintaining the reliability of the local supply).

Deep learning algorithms (e.g., RNNs and LSTMs) have been applied to power systems forecasting problems with promising results in the recent literature. They also offer the potential to continue improving as they are trained further on the continuous stream of newly generated data. As with any research area, the goal is to ultimately move these algorithms to the industry deployment phase. Because of their low forward inference time (on the order of milliseconds), these algorithms and architectures can provide forecasts in the near real-time horizon. The performance of the deployed systems can be further improved by implementing sophisticated hyperparameter tuning mechanisms.

The following two sections briefly note some areas where there is plenty of scope as well as a need for further development of deep learning applications for power systems.

5.1 Deterministic Versus Probabilistic Forecasting

The forecasted values from the deep learning models discussed in Sect. 7.3 are deterministic in nature. That is, given the same sequence of inputs, the networks will always produce the same output. Furthermore, there is no measure of confidence related to the predictions. Recall the Gaussian process regression (GPR) from Sect. 7.2.3.2. This probabilistic forecasting approach naturally produces a measure of confidence based on the variance in the GP. As the predicted values get further from any given data, the variance grows and the confidence in the predicted value decreases. Such understanding of uncertainties in power systems forecasting is critical because of the highly variable nature of the data and the large cost of grid blackouts and brownouts. Some work has considered how deep learning can be recast as a probabilistic model [79, 80], but continued research into the topic is critical.

5.2 Other Potential Applications

Anomaly detection in smart grids is a timely and relevant topic as the distribution grid infrastructure in industrialized countries like the USA has aged and needs refurbishment and replacement to maintain the reliability of the supply. There has been relatively less progress in applying deep learning algorithms for anomaly detection in power systems prognostics and fault prediction problems [81,82,83]. The application areas include anomaly detection for predicting the remaining useful life of the components of power systems, predicting impending fault on power systems, and predicting building level faults based on the data from building sensors.