Keywords

1 Introduction

We consider steady water waves in two dimensions, travelling over a flat bottom with speed c and a free surface, under the influence of gravity. This means that in a frame moving along the wave with the same speed c, the velocity field, pressure and shape of the wave does not change over time. This model can be used to study plane waves by considering their cross section perpendicular to the wave crest. For a more detailed derivation of the model equations we refer to [6, 8].

This problem is governed by the Euler equations, find u(x, y, t), v(x, y, t) and P(x, y, t) that solve

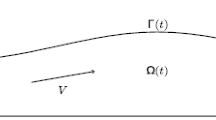
$$\displaystyle \begin{aligned}\begin{array}{r*{20}l}{} u_{x} + v_{y} & = 0 & \quad & \text{in } -d < y < \eta(x,t), \\ u_t + u u_{x} + v u_{y} & = - P_{x} & \quad & \text{in } -d < y < \eta(x,t), \\ v_t + u v_{x} + v v_{y} & = - P_{y} -g & \; & \text{in } -d < y < \eta(x,t) \end{array}\end{aligned} $$
(1)

with the free surface η(x, t) and the depth d. The fluid domain is sketched on the left hand side of Fig. 1. The boundary conditions for the pressure P and the velocity field (u, v) are the dynamic boundary condition

$$\displaystyle \begin{aligned} P = P_{\text{atm}} \quad \text{on } y = \eta(x,t) \end{aligned} $$
(2)

which model the interaction on the free surface where negligible surface tension is assumed. Additionally we have kinematic boundary conditions, those are that the surface of the wave is always made up of the same particles and that the water can not penetrate the flat bottom. These boundary conditions are modelled by

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} v & = \eta_t + u \eta_x & \quad & \text{on } y = \eta(x,t), {} \end{array}\end{aligned} $$
(3)
$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} v & = 0 & \quad & \text{on } y = -d. {} \end{array}\end{aligned} $$
(4)

Since we consider steady periodic waves, we introduce a frame moving at the constant speed c which removes the time variable from our system. The new system is

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l}{} U_{X} + V_{Y} & = 0 & \quad & \text{in } -d < Y < \eta, \\ (U - c) U_{X} + V U_{Y} & = - \tilde{P}_{X} & \quad & \text{in } -d < Y < \eta, \\ (U - c) V_{X} + V V_{Y} & = - \tilde{P}_{Y} -g & \; & \text{in } -d < Y < \eta \end{array}\end{aligned} $$
(5)

where (X, Y ) = (x − ct, y) and \((U,V,\tilde {P})\) are the functions (u, v, P) transformed to the moving frame. The boundary conditions now read

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \tilde{P} & = \tilde{P}_{\text{atm}} & \quad & \text{on } Y = \eta, {} \end{array}\end{aligned} $$
(6)
$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} V & = (U - c) \eta_X & \quad & \text{on } Y = \eta, {} \end{array}\end{aligned} $$
(7)
$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} V & = 0 & \quad & \text{on } Y = -d. {} \end{array}\end{aligned} $$
(8)

Of particular interest are rotational waves, that means that the vorticity γ = v x − u y is not zero. One reason for the importance of vorticity is its influence on the existence and position of stagnation points, these are points in the wave where the velocity of the fluid is equal to the wave speed c. For the effects that stagnation points have on the flow structure of wave see [13, 14, 35]. For example, waves with a non-smooth peak, such as the Stokes wave of maximal height, see [33], have a stagnation point at that peak.

In this work several schemes on how to solve (1)–(4) numerically are discussed. While there exists a large literature concerning this problem, see [10, 16, 29, 30], here some more recent approaches are presented. Section 2 presents two schemes based on a Dubreil-Jacotin transformation, a numerical continuation approach [3, 20, 21, 32] and an asymptotic expansion approach [2, 9, 18]. Section 3 discusses a non-local formulation [1, 4, 11, 15] and a conformal mapping approach [5, 24, 28] is presented in Sect. 4. The schemes have in common that in order to be able to solve their respective systems, they assume all but one of the parameters, like depth, vorticity or velocity, are fixed. The remaining parameter can be varied to continue along the solution branch.

A non-exhaustive list of further numerical schemes not included in this discussion are: in [31] a shape optimisation approach applied to a stream formulation that allows for a non-flat bottom is presented; [17] modifies the nonlinear shallow water equations to allow for constant vorticity and examines wave breaking; the papers [22, 23] study and compute periodic waves based on an integral formulation.

2 Dubreil-Jacotin Transformation

Following the procedure described in [8] we define the stream function ψ by ψ x = −V  and ψ y = U − c. Then the system (5)–(8) can be reformulated as the equivalent system

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \Delta \psi & =\gamma(\psi) & \quad & \text{in } -d < y < \eta, {} \end{array}\end{aligned} $$
(9)
$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \psi & = 0 & \quad & \text{on } y=\eta, {} \end{array}\end{aligned} $$
(10)
$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} |\nabla\psi |{}^2 +2 g (y+d) -Q \psi & = -p_0 & \quad & \text{on } y = -d, {} \end{array}\end{aligned} $$
(11)
$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \psi & = 0 & \quad & \text{on } y=\eta. {} \end{array}\end{aligned} $$
(12)

Here Q is the hydraulic head, p 0 the relative mass flux and γ the vorticity function. In order to ensure that the vorticity is a function of ψ one has to assume

$$\displaystyle \begin{aligned} u < c \end{aligned} $$
(13)

in the whole fluid domain. This condition excludes stagnation points since there it holds u = c.

One major difficulty with the original system as well as the stream formulation is the unknown free surface η. In [8, 32] a fixed domain formulation equivalent to (9)–(12) is discussed. The used coordinate transform known as the Dubreil-Jacotin transform, see [12], is illustrated in Fig. 1. This transform exploits that ψ is constant both on the flat bottom and the free surface as well as strictly increasing inside the domain, note that this again makes use of the assumption (13). Introducing the fixed domain R = {(q, p)|− π < q < π;p 0 < p < 0} and the height function h = y + d where y depends implicitly on q and p, results in a new system of equations.

Hence instead of (9)–(12) the problem is now to find h and Q satisfying

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \mathcal{H}[h] & := & (1+h_q^2) h_{pp} - 2 h_p h_q h_{qp} + h_p^2 h_{qq} - \gamma(-p) h_p^3 & = 0 & \quad & \text{in } R, {} \end{array}\end{aligned} $$
(14)
$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \mathcal{B}_0[h,Q] & := &\qquad \qquad \qquad 1 + h_q^2 + (2gh - Q) h_p^2 & = 0 & \quad & \text{for } p = 0, {} \end{array}\end{aligned} $$
(15)
$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \mathcal{B}_1[h] & := &\qquad \qquad \qquad \qquad h & = 0 & \quad & \text{for } p = p_0 {} \end{array}\end{aligned} $$
(16)

for a given domain R and vorticity function γ. Due to assumption (13), the formulations presented in this chapter and all schemes based on the Dubreil-Jacotin transformation can not be used to compute waves with stagnation point.

A special family of solutions of these equations are the so called laminar waves. These solutions, defined in the fixed domain R, describe parallel shear flows that do not depend on the q variable and are denoted as H. In the case of linear vorticity the laminar waves are given by

$$\displaystyle \begin{aligned} H (p; \lambda) = \frac{2(p-p_0)}{\sqrt{\lambda - 2 \gamma p} + \sqrt{\lambda - 2 \gamma p_0}} \end{aligned} $$
(17)

where the parameter λ > 0 is coupled to Q by the relation D

$$\displaystyle \begin{aligned} Q = \lambda - \frac{4 g p_0}{\sqrt{\lambda} + \sqrt{\lambda - 2 \gamma p_0}}. \end{aligned}$$

In general, there are no non-laminar waves in the neighbourhood of the laminar wave (Q(λ), H(λ)). For certain values of λ and thus Q, determined by the dispersion relation [19], a branch of non-laminar waves bifurcates from the family of laminar flows. These bifurcation points are denoted as λ ∗ and Q ∗ respectively.

While the schemes presented in Sects. 3 and 4 consider different system of equations and computational domains, the concepts of laminar branches and bifurcation of a branch of non-trivial waves remain the same.

2.1 Numerical Continuation Scheme

One straightforward approach is to discretise (14)–(16) with a second order finite difference scheme as was done in [3, 20, 21, 32]. The resulting system is underdetermined since the hydraulic head Q as well as the height function h are unknown. A numerical continuation scheme can be used to compute waves along the solution branch. This means introducing additional conditions to make the system determined and provide initial guesses based on previous solutions, the resulting system of nonlinear equations is solved with a Newton’s method.

Finding the bifurcation point Q ∗ and the initial guess for the first non-trivial wave can be done by either computing eigenvalues of the linearised system, using analytical results [19] or employing other approaches such as the asymptotic expansion, see Sect. 2.2.

For numerical computations, wavelength and the relative mass flux p 0 have to be chosen.Footnote 1 In the standard case of a given vorticity function γ the hydraulic head Q is the only free parameter which makes it the natural choice for the bifurcation parameter.

Note that other choices are valid and may be beneficial. For example consider the case of constant vorticity γ = γ 0, then one can fix Q and consider γ 0 as the bifurcation parameter. Given one solution, new waves can then be computed by varying γ 0 while Q remains fixed. This strategy was used in [3] to compute parts of the solution branch beyond a wave with stagnation points. This branch is not reachable by continuation with Q since there, the part of the branch that violates (13), can not be bypassed.

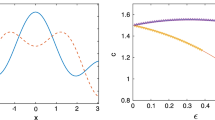
The biggest drawback of this approach is that, due to the assumption (13) of the Dubreil-Jacotin transform, waves with stagnation points are not modelled by (14)–(16). This manifests in an increasingly ill-condition Jacobian of the discretisation near stagnating waves. The advantage of this scheme are its ease of use and the big flexibility it has: no assumptions on the vorticity function γ are made, examples presented in [3, 20, 21] include piecewise constant and cubic vorticity with respect to the stream function; Fig. 2 shows some examples of linear vorticity; The scheme is also flexible with regard to the model equation (1). Extensions, like periodic travelling equatorial waves [7, 27], that add earths rotation to the model, are straightforward to incorporate.

Fig. 1
figure 1

Dubreil-Jacotin transformation

Full size image
Fig. 2
figure 2

Free boundary of the limiting wave with vorticity \(\gamma _\alpha (p) = \alpha (1 - \frac {p}{p_0}) \) for α ∈{−1, 0, 1}

Full size image

2.2 Asymptotic Expansion

In the approach presented in [2] and based on [9, 18], one considers the fixed domain formulation (14)–(16) and finds asymptotic expansion of its solution around a bifurcation point.

Looking for q-independent solutions of (14)–(16) leads to the laminar flows H. Similarly, one can obtain solutions for the linearised problem with the approach

$$\displaystyle \begin{aligned} \hat{h}(q,p; b) = H(p, \lambda) + b m(q,p) \end{aligned}$$

where \(b \in \mathbb {R}\) and m is an even and 2π-periodic function in q. The unknown function m is chosen such that \(\hat {h}\) is the solution of the linearised problem, that is

$$\displaystyle \begin{aligned} \mathcal{H}[\hat{h}] = \mathcal{O}(b^2), \quad \mathcal{B}_0[\hat{h}, Q] = \mathcal{O}(b^2), \quad \mathcal{B}_1[\hat{h}] = 0. \end{aligned}$$

This linearised problem only has non-trivial solutions at bifurcation points, that is (Q ∗, H(λ ∗)). Those are either known analytically [19] for some vorticities or can be approximated numerically. A way to compute a better approximation of h would be to consider higher order approximations. As discussed in [9], adding more terms to \(\hat {h}\) only yields solutions of the system up to second order. There exists no expansion \(\hat {h}_3\) of third order that satisfies the system (14)–(16) up to third order, that is

$$\displaystyle \begin{aligned} \mathcal{H}[\hat{h}_3] = \mathcal{O}(b^4), \quad \mathcal{B}_0[\hat{h}_3, Q] = \mathcal{O}(b^4), \quad \mathcal{B}_1[\hat{h}_3] = 0. \end{aligned}$$

This caveat was remedied in [18] by approximating not just the height function h but Q as well. For this introduce approximations of the pair (Q, h) by the polynomials in \(b \in \mathbb {R}\)

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} Q & \approx Q^{(2N)}(b) & & := Q^* + \sum_{k=1}^N Q_{2k} b^k, \end{array}\end{aligned} $$
(18)
$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} h(q,p;Q) & \approx h^{(2N+1)}(q,p; b) & & := \sum_{k=0}^{2N+1} h_k(q,p) b^k {} \end{array}\end{aligned} $$
(19)

with coefficients \(Q_{2k} \in \mathbb {R}\) and h k defined as

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} h_{2k}(q,p) & := \sum_{m=0}^k \cos{}(2mq) f_{2m}^{2k}(p), {} \end{array}\end{aligned} $$
(20)
$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} h_{2k+1}(q,p) & := \sum_{m=0}^k \cos{}((2m+1)q) f_{2m+1}^{2k+1}(p) {} \end{array}\end{aligned} $$
(21)

where \(f_m^k \in C^\infty ([p_0,0])\) for all m, k. Note that the functions \(f_m^k\) only depend on p introduced by the Dubreil-Jacotin transformation. Let the wavelength, vorticity γ and relative mass flux p 0 be given. What remains to be computed are the constants Q 2k and functions \(f_m^k\) such that (Q (2N), h (2N+1)) satisfies (14)–(16) up to \(\mathcal {O}(b^{2N+2})\). The structure of h (2N+1), given by (19)–(21), can be exploited to considerably simplify this problem, as shown in [2]. Ultimately, what has to be solved is a series of one dimensional systems of differential equations which can be done numerically.

Due to the used Dubreil-Jacotin transformation, restriction (13) must be satisfied what in turn means this approach is limited to non-stagnation waves. The advantage of this scheme is its flexibility with regard to the vorticity, in particular non constant vorticity is possible, see [2]. This, together with the availability of analytical results for the first couple expansion terms [18], allows the use of this expansion as a very good initial guess for other approaches.

3 Non-local Formulations

In [1], a new, non-local formulation of the Euler equations was presented which is based on the unified transform or Fokas method. While this approach allows for rotational waves, we present here the periodic irrotational case as was considered in [11]. In the irrotational case, that is γ = 0, the Euler equations can be formulated in terms of a velocity potential ϕ and become

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \Delta \phi & = 0 & \quad & \text{in } -d < y < \eta {} \end{array}\end{aligned} $$
(22)
$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \phi_y & = 0 &\quad & \text{on } y = -d, \end{array}\end{aligned} $$
(23)
$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \eta_t + \phi_x \eta_x & = \phi_y & \quad & \text{on } y = \eta, \end{array}\end{aligned} $$
(24)
$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \phi_t + \frac{1}{2} \left( \phi_x^2 + \phi_y^2 \right) + g \eta & = \sigma \frac{\eta_{xx}}{(1 + \eta_x^2)^{3/2}} & \quad & \text{on } y = \eta {} \end{array}\end{aligned} $$
(25)

where σ denotes the constant surface tension and ρ is the density.

Introduce the velocity potential evaluated at the surface, see [36], as q(x, t) = ϕ(x, η(x, t), t) which leads to the dynamic boundary condition

$$\displaystyle \begin{aligned} q_t + \frac{1}{2} q_x^2 + g \eta - \frac{1}{2} \frac{(\eta_t + q_x \eta_x)^2}{1 + \eta_x^2} = \sigma \frac{\eta_{xx}}{(1 + \eta_x^2)^{3/2}}. \end{aligned} $$
(26)

Additionally one gets a non-local equation

$$\displaystyle \begin{aligned} \int_{0}^L e^{-ikx} \{ i \eta_t \cosh[k(\eta + d)] + q_x \sinh[k ( \eta + d ) ] \} dx = 0, \quad t > 0 \end{aligned} $$
(27)

where \(k = k_n = \frac {2 k \pi }{L}\) with \(n \in \mathbb {Z}\setminus \{0\}\).

Starting from the set of Eqs. (26)–(27) several modifications and generalisations can be made. Considerations include the constant vorticity case [4, 34], a variable bottom [1] and using a moving frame [11]. A hybrid of the novel formulation and an approach based on conformal mapping is presented in [15], where water waves with variable bottom are studied numerically.

For numerical considerations in the case of steady periodic water waves (26) and (27) can be reformulated as a single non-local equation only containing the unknown η, see [11]. The wave profile η is approximated by truncated Fourier series and the non-local equation discretised using a spectral collocation method. Then the problem to find solutions can be seen as a bifurcation problem for fixed wavelength and depth where the wave velocity c is the bifurcation parameter. To find a bifurcation point for which non-trivial solutions exist, the null space of the linearisation about the trivial wave is studied.

This approach allows for the computation of streamlines and pressure in the whole domain, independent of any grid. This holds true even in the presence of stagnation points when rotational waves are considered. For example, in [34] a wave with interior stagnation and a bottom pressure maxima which is not under the crest is presented.

Such non-local formulations are a very active research area, for some more related formulations see [25, 26, 34]. This, together with the easily available information about streamlines, wave form and pressure, make non-local formulations very effective. The main limitation is that the vorticity function has a larger impact on the formulation and is thus more restricted, in most cases to constant vorticity.

4 Conformal Mapping and Spectral Collocation Method

In the approach presented in [28], the constant vorticity case is considered as a superposition of a linear shear flow and a harmonic velocity potential. This leads to a system of equations similar to (22)–(25) but with an additional vorticity term, which is then non-dimensionalised. The manuscript [28] considers the case of periodic travelling waves with constant speed and introduces a frame moving along with wave speed c. Then the problem is to find the potential ϕ satisfying

$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \Delta \phi & = 0 & \quad & \text{in } -1 < y < \eta {} \end{array}\end{aligned} $$
(28)
$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} \phi_y & = 0 &\quad & \text{on } y = -1, \end{array}\end{aligned} $$
(29)
$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} -c \eta_x + (\phi_x - \gamma(\eta + b)) \eta_x & = \phi_y & \quad & \text{on } y = \eta, \end{array}\end{aligned} $$
(30)
$$\displaystyle \begin{aligned}\begin{array}{r*{20}l} -c \phi_x + \frac{1}{2} \left( \phi_x^2 + \phi_y^2 \right) + \eta - \gamma(\eta + b)\phi_x + \gamma \psi & = B & \quad & \text{on } y = \eta {} \end{array}\end{aligned} $$
(31)

where B is the Bernoulli constant, ψ is the streamfunction associated with ϕ and \(b \in \mathbb {R}\) is a parameter of the background flow.

To solve this system, a conformal mapping such as given in [5, 24], that maps the uniform strip onto the wave domain, is considered. In the uniform strip domain, a flat domain of unknown depth, the solution of the Laplace equation is analytically known. It is ensured that this solution satisfies the dynamic and kinematic boundary conditions using a spectral collocation method. For a sketch of the involved domains see Fig. 1, where reversely the fluid domain was mapped onto a rectangle domain.

To compute a first non-laminar wave the irrotational case of small amplitude, for which good approximations are available, is considered. More waves along the solution branch can be computed using a continuation scheme with previous solution as initial guess. For continuation parameters, [28] studies two cases. In the first case, the depth and wave height H are fixed and the continuation parameter is the wavelength λ. In the second case, the depth and wavelength are fixed and either the vorticity γ or the steepness parameter \(\frac {H}{\lambda }\) are varied.

This approach can be used to compute waves with stagnation points as well as wave characteristics such as streamlines, stagnation points, particle paths and the pressure. The results presented in [28] include waves with up to three interior stagnation points and waves with switched pressure maxima and minima at the bottom opposed to the irrotational case. The various continuation schemes allow for the detailed study of interactions between parameters and wave characteristics. The biggest restriction of this approach is that it is limited to constant vorticity.