Optimum Torsion Axis of Multi-storey Buildings Based on Their Dynamic Properties

Abstract

The objective of the present paper is the determination of the optimum torsion axis of multi-storey asymmetric in plan buildings on the basis of their dynamic properties. For this purpose, a three-storey reinforced concrete diaphragm system is analyzed by means of linear time-history analysis for both uniaxial and biaxial horizontal seismic excitations. The mass centers of the diaphragms are successively transposed and the resulting floor rotation angles for each case are computed. The position of the mass center which leads to the minimization of the sum of the squares of the floor rotation angles designates the location of the optimum torsion axis. The results are verified by means of modal analysis and compared with those resulting from the relevant methodology prescribed by the Greek seismic code. All three methods produce results that do not differ significantly, so the approximate procedure suggested by the Greek seismic code can be rigorously applied in order to determine the optimum torsion axis of asymmetric buildings.

1 Introduction

All the modern seismic codes (e.g. CEN 2004; EPPO 2003) adopt the linear static procedure as an alternative method of analysis appropriate for certain categories of buildings. A critical point of this procedure is the representation of the torsional behaviour of the buildings which is achieved by introducing proper static eccentricities from a suitable reference point.

Anastassiadis et al. (1998) studied this issue using single-storey models and developed analytical formulae which allow the calculation of additional eccentricities, so that the maximum static displacements on both sides of the floor as well as the static rotation of the floor are equal to the respective ones obtained by means of response spectrum analysis. The additional eccentricities are measured with reference to the elastic centre, which always exists in single-storey systems and possesses at the same time all the properties of the centre of rigidity , shear centre and twist centre.

The aforementioned concept can be rigorously extended to special categories of multi-storey diaphragm systems in which the rigidity, shear and twist centres coincide in each floor (elastic centre of the floor), while the elastic centres of all the floors lie in the same vertical axis (elastic axis of the building). These categories include doubly symmetric in plan buildings and isotropic buildings (i.e. buildings having vertical resisting elements with proportional stiffness matrices (Makarios and Anastassiadis 1998a, b)).

However, the vast majority of real buildings do not belong to these categories. In order to overcome this problem, Makarios and Anastassiadis (1998a, b) proposed the concept of ‘optimum torsion axis’ as a reference line for the calculation of structural eccentricity in the general case of multi-storey asymmetric buildings. For a given static load pattern, the optimum torsion axis is defined as the vertical line connecting the points of the floor diaphragms, where the horizontal forces must be applied, so that the sum of the squares of the floor rotations θ _i is minimized (i = 1, 2, … N, where N the number of the building diaphragms):

$$ \varSigma {\theta}_i^2=\mathit{\min} $$

(21.1)

Furthermore, in order to simplify the determination of the optimum torsion axis location, they developed an approximate methodology which has been adopted by the Greek seismic code (EPPO 2003). In particular, based on extensive parametric studies, they suggested that, when the minimum $\varSigma {\theta}_i^2$ is attained, the diaphragm rotation becomes zero at the level z = 0.8H from the base, where H is the height of the building.

Marino and Rossi (2004) examined the same problem from an analytical point of view and proposed mathematical expressions to define the exact location of the optimum torsion axis for buildings having the principal axes of the resisting elements parallel to a given orthogonal coordinate system. Generalizing this approach, Doudoumis and Athanatopoulou (2008) proved that the aforementioned analytical methodology can be applied to all asymmetric buildings without any particular restriction.

All the aforementioned studies aim to determine the optimum torsion axis under horizontal static loads. The objective of the present paper is the determination of the optimum torsion axis on the basis of the dynamic properties of buildings. For this purpose, a three-storey reinforced concrete diaphragm system is analyzed by means of linear time-history analysis for both uniaxial and biaxial horizontal seismic excitations. The mass centers of the diaphragms are successively transposed and the resulting floor rotation angles for each case are computed for the critical orientation of the seismic excitation using a relevant procedure developed by Athanatopoulou (2005). The position of the mass centre which leads to the minimization of the sum of the squares of the floor rotation angles designates the location of the optimum torsion axis. The results are verified by means of modal analysis and compared with those resulting from the relevant methodology prescribed by the Greek seismic code. Hence, interesting conclusions are derived.

2 Structural Models

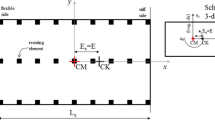
The structural models examined in the framework of the present study are based on an archetype three-storey asymmetric in plan reinforced concrete building. The floor plan of the building as well as the position of the optimum torsion axis (OTA) according to the Greek seismic code is shown in Fig. 21.1. All storey heights are 3 m. The slab thickness is equal to 15 cm. All beams have a height of 60 cm and a thickness of 25 cm. The columns are square shaped with dimension of 40 cm. The length of the walls is equal to 1.5 m (W1), 2 m (W2, W3) or 3 m (W4) and their thickness is equal to 25 cm. All the vertical resisting elements are fixed at base. The mass of each floor is taken equal to 1 t/m². The mass centre of each floor of the building is transposed to 25 different locations (Fig. 21.2). Hence, 25 building models are produced and analyzed by means of linear time-history analysis according to the following section.

Fig. 21.1

Floor plan of the three-storey archetype building

Fig. 21.2

Alternative locations of the mass centre

3 Analysis Process

3.1 Ground Motions

The whole investigation conducted here comprises a number of 7 unscaled accelerograms, which is considered adequate to obtain concrete conclusions. These accelerograms (Table 21.1) are obtained from the PEER strong motion database (2003) and tabulated in table C-3 of Appendix C of FEMA 440 project (ATC 2005).

Table 21.1 Ground motions

3.2 Uniaxial Seismic Excitation

Firstly, the building models are analyzed by means of linear time-history analysis for uniaxial seismic excitation. In particular, each of the recorded accelerograms ${\ddot{u}}_g(t)$is considered to act separately along x (load case ‘0’) and y axis (load case ‘90’) as it is shown in Fig. 21.3. If the values of a scalar response quantity for load cases ‘0’ and ‘90’ are denoted as R _’0′(t) and R _’90′(t) respectively, as it has been demonstrated by Athanatopoulou (2005), the maximum value R _max of the response quantity for the critical orientation of the seismic excitation is:

$$ {R}_{max}=\mathit{\max}\sqrt{R_{\hbox{'} 0\hbox{'}}^2(t)+{R}_{\hbox{'} 90\hbox{'}}^2(t)} $$

(21.2)

Fig. 21.3

Load cases for uniaxial seismic excitation (a) load case ‘0’ and (b) load case ‘90’

The time instant t_cr that R_max occurs as well as the angle θ _cr which defines the critical orientation of the seismic excitation could also be determined applying analytical formulae (Athanatopoulou 2005). However, this is beyond the objective of the present paper.

The sum of the squares of the diaphragm rotations $\varSigma {\theta}_i^2(t)$ is computed for each load case with the aid of the program SAP2000. Then, applying Eq. 21.2 the maximum value $max\varSigma {\theta}_i^2$ is calculated. The resulting values for the 25 analyzed building models are shown in Figs. 21.4, 21.5, 21.6, 21.7, 21.8, 21.9 and 21.10 where each model is characterised by its centre of mass (CM) coordinates in the coordinate system given in Fig. 21.1.

Fig. 21.4

Maximum sum of the squares of diaphragm rotations maxΣθ _i ² – Ground motion 1

Fig. 21.5

Maximum sum of the squares of diaphragm rotations maxΣθ _i ² – Ground motion 2

Fig. 21.6

Maximum sum of the squares of diaphragm rotations maxΣθ _i ² – Ground motion 3

Fig. 21.7

Maximum sum of the squares of diaphragm rotations maxΣθ _i ² – Ground motion 4

Fig. 21.8

Maximum sum of the squares of diaphragm rotations maxΣθ _i ² – Ground motion 5

Fig. 21.9

Maximum sum of the squares of diaphragm rotations maxΣθ _i ² – Ground motion 6

Fig. 21.10

Maximum sum of the squares of diaphragm rotations maxΣθ _i ² – Ground motion 7

The curves given in Figs. 21.4, 21.5, 21.6, 21.7, 21.8, 21.9 and 21.10 are idealized to parabolic curves governed by equations just like Eq. 21.3:

$$ \mathit{\max}\varSigma {\theta_i}^2={ax}^2+ bx+{cy}^2+ dy+e $$

(21.3)

where a, b, c, d, e are constant factors (different for each ground motion ). Applying well known principles of mathematics, the coordinates of the point that leads to the minimization of maxΣθ _i ² are estimated for each ground motion (Table 21.2). The mean values of the coordinates indicate the location of the optimum torsion axis (OTA). It is apparent that the resulting coordinates are much closed to those determined according to the Greek seismic code (see Fig. 21.1).

Table 21.2 Coordinates of the optimum torsion axis – uniaxial excitation

In order to verify the results, the centre of mass of the archetype building is transposed to the location of the optimum torsion axis and a modal analysis is conducted. The resulting mode shape vectors (Table 21.3) resemble those of a doubly symmetric building without coupling between lateral and torsional response . In particular, in modal shape vectors 1, 4 and 7 the terms corresponding to rotations and translations along x axis are negligible and obviously modes 1, 4 and 7 dominate the response under seismic excitation along y axis. On the other hand, in modal shape vectors 2, 5 and 8 the terms corresponding to rotations and translations along y axis are negligible and obviously modes 2, 5 and 8 dominate the response under seismic excitation along x axis. These conclusions are also confirmed by the modal participating mass ratios (Table 21.4). Finally, modes 3, 6 and 9 are mainly rotational.

Table 21.3 Mode shape vectors (CM ≡ OTA for uniaxial excitation)

Table 21.4 Modal participating mass ratios (CM ≡ OTA for uniaxial excitation)

3.3 Biaxial Seismic Excitation

The whole process is identical to that followed for uniaxial seismic excitation. The only difference is the definition of load cases ‘0’ and ‘90’ which comprise concurrent action of each accelerogram along x and y axes (Fig. 21.11).

Fig. 21.11

Load cases for biaxial seismic excitation (a) load case ‘0’ and (b) load case ‘90’

The maximum sum of the squares of the diaphragm rotations maxΣθ _i ² for the 25 analyzed building models is shown in Figs. 21.12, 21.13, 21.14, 21.15, 21.16, 21.17 and 21.18.

Fig. 21.12

Maximum sum of the squares of diaphragm rotations maxΣθ _i ² – Ground motion 1

Fig. 21.13

Maximum sum of the squares of diaphragm rotations maxΣθ _i ² – Ground motion 2

Fig. 21.14

Maximum sum of the squares of diaphragm rotations maxΣθ _i ² – Ground motion 3

Fig. 21.15

Maximum sum of the squares of diaphragm rotations maxΣθ _i ² – Ground motion 4

Fig. 21.16

Maximum sum of the squares of diaphragm rotations maxΣθ _i ² – Ground motion 5

Fig. 21.17

Maximum sum of the squares of diaphragm rotations maxΣθ _i ² – Ground motion 6

Fig. 21.18

Maximum sum of the squares of diaphragm rotations maxΣθ _i ² – Ground motion 7

The coordinates of the point that leads to the minimization of maxΣθ _i ² for each ground motion and the corresponding mean values are shown in Table 21.5. It is apparent that the resulting values are much closed to those calculated for uniaxial excitation as well as to those determined according to the Greek seismic code.

Table 21.5 Coordinates of the optimum torsion axis – biaxial excitation

In order to verify the results, the centre of mass of the archetype building is transposed to the location of the optimum torsion axis and a modal analysis is conducted. The resulting mode shape vectors (Table 21.6) resemble those of a doubly symmetric building without coupling between lateral and torsional response. In particular, in modal shape vectors 1, 4 and 7 the terms corresponding to rotations and translations along x axis are negligible and obviously modes 1, 4 and 7 dominate the response under seismic excitation along y axis. On the other hand, in modal shape vectors 2, 5 and 8 the terms corresponding to rotations and translations along y axis are negligible and obviously modes 2, 5 and 8 dominate the response under seismic excitation along x axis. These conclusions are also confirmed by the modal participating mass ratios (Table 21.7). Finally, modes 3, 6 and 9 are mainly rotational.

Table 21.6 Mode shape vectors (CM ≡ OTA for biaxial excitation)

Table 21.7 Modal participating mass ratios (CM ≡ OTA for biaxial excitation)

4 Conclusions

The objective of the present paper is the determination of the optimum torsion axis on the basis of the dynamic properties of buildings. For this purpose, a three-storey reinforced concrete diaphragm system is analyzed by means of linear time-history analysis . The location of the optimum torsion axis for both uniaxial and biaxial horizontal seismic excitation is very close to the location resulting from the simplified procedure prescribed by the Greek seismic code. The transposition of the mass centre to the determined optimum torsion axis leads to dynamic properties which resemble those of doubly symmetric systems. The method presented herein proves that in asymmetric multistorey buildings there is an optimum torsional axis. This axis can be determined with the aid of real accelerograms or static lateral forces using exact method or approximate method. All three methods produce results that do not differ significantly. So the approximate procedure suggested by the Greek seismic code can be rigorously applied in order to determine the optimum torsion axis of asymmetric buildings. However, the generalization of this conclusion requires further investigations, comprising applications to a large variety of structural systems with more complex configuration.