Lattice Simulations with Chiral Effective Field Theory for Light and Medium-Mass Nuclei

Abstract

In this proceedings we present recent results from lattice simulations with chiral effective field theory up to next-to-next-to-next-to-leading order. We discuss our investigation on the degree of locality of the short-range nucleon-nucleon interactions. We also discuss ground state energies of light and medium-mass nuclei as well as new algorithms for the proton and neutron density distributions and other properties.

Nuclear Lattice Effective Field Theory Collaboration

1 Introduction

Lattice effective field theory is a powerful numerical method formulated in the framework of chiral effective field theory which organizes the nuclear interactions as an expansion in powers of low energy scales, Q, such as the momenta, the pion mass etc. Chiral effective field theory gives a modern description for the nuclear forces in the chiral limit where the light quarks are massless. A relevant recent review can be found in [1]. In the chiral expansion the first term dominates and is called the leading order (LO or $Q^0$) interaction. The first correction to the LO is the next-to-leading order (NLO or $Q^2$) interaction, the second correction is called the next-to-next-to-leading order (NNLO or $Q^{3}$) and so on. These interactions contain sets of coupling constants (or low-energy constants (LECs)) to be determined by fitting to the experimental data.

In lattice effective field theory these interactions are formulated in a periodic cubic lattice, and the LECs on the lattice are determined by fitting to experimental data. Reference [2] discusses the details of lattice interactions and a new lattice formulation of short-range chiral effective field theory interactions with a simpler decomposition into spin channels.

2 Euclidean Time Projection Monte Carlo

In lattice simulations we study the low-lying states of nuclei using the normal ordered transfer-matrix formalism. The transfer matrix is defined in Euclidean time as in the following,

$$\begin{aligned} M_\mathrm{LO} = \ : \ \exp (-\alpha _{t} \ H_\mathrm{LO}): \end{aligned}$$

(94.1)

where H is the lattice Hamiltonian, and $\alpha _{t}$ is the ratio of the temporal lattice spacing $a_{t}$ to the spatial lattice spacing a. The symbol $:\,:$ signifies normal ordering, which moves all annihilation operators to the right and creation operators to the left with the appropriate number of anticommutation minus signs. In our simulation we employ projection Monte Carlo with auxiliary fields for nucleon-nucleon interactions. In auxiliary-field Monte Carlo simulations, the interactions are recast as single particle interacting with fluctuating auxiliary fields. See [3] for a detailed discussion on auxiliary-field Monte Carlo calculations.

Nuclear structure on the lattice: To compute the ground state energies or the properties of nuclei, we consider some initial and final states, respectively $\left| {\varPsi _{i}} \right\rangle$ and $\left| {\varPsi _{f}} \right\rangle$, as Slater determinants of free-particle standing waves on the lattice. These states are projected in Euclidean time using the transfer matrix to form the Euclidean time projection amplitude at LO,

$$\begin{aligned} Z_\mathrm{LO}(L_{t}) = \left\langle {\varPsi _{f}} \right| M_\mathrm{LO}^{L_{t}} \left| {\varPsi _{i}} \right\rangle . \end{aligned}$$

(94.2)

We perform the auxiliary-field Monte Carlo simulations to compute the quantum amplitude $Z_\mathrm{LO}(L_{t})$, and the ground state energy at LO is determined from the ratio $Z_\mathrm{LO}(L_{t}+1)/Z_\mathrm{LO}(L_{t})$ in the limit $L_{t} \rightarrow \infty$. In our simulation the higher order calculations are computed using perturbation theory, and we compute the Euclidean time projection amplitude at higher order,

$$\begin{aligned} Z_\mathrm{ho}(L_{t}+1) = \left\langle {\varPsi _{f}} \right| M_\mathrm{LO}^{(L_{t}-1)/2} \, M_\mathrm{ho} \, M_\mathrm{LO}^{(L_{t}-1)/2} \left| {\varPsi _{i}} \right\rangle , \end{aligned}$$

(94.3)

where

$$\begin{aligned} M_\mathrm{ho} = \ : \ \exp \left[ -\alpha _{t} \left( \ H_\mathrm{LO} + \ H_\mathrm{ho}\right) \right] . \end{aligned}$$

(94.4)

Therefore, the energy correction to the LO energy is computed from the ratio $Z_\mathrm{ho}(L_{t}+1)/Z_\mathrm{LO}(L_{t}+1)$.

Nuclear scattering on the lattice: Scattering and reactions involving clusters can be studied on the lattice using the adiabatic projection method, which is a general framework that constructs a low energy effective field theory for the clusters. See [4,5,6] for the details of the method. The method uses initial states,

$$\begin{aligned} \left| {\mathbf {R}} \right\rangle = \sum _{\mathbf {r}} \left| {\mathbf {r}+\mathbf {R}} \right\rangle _{1} \otimes \left| {\mathbf {r}} \right\rangle _{2}, \end{aligned}$$

(94.5)

which is parameterized by the relative separation between clusters, $\mathbf {R}$. Furthermore, we project these initial states onto spherical harmonics $Y_{\ell ,\ell _z}$ with angular momentum numbers $\ell$, $\ell _z$,

$$\begin{aligned} \left| {R} \right\rangle ^{\ell ,\ell _z} = \sum _{\mathbf {R}^{\prime }} Y_{\ell ,\ell _z}(\hat{R}^{\prime }) \, \delta _{R,|\mathbf {R}^{\prime }|} \, \left| {\mathbf {R}} \right\rangle . \end{aligned}$$

(94.6)

Then we evolve these states using the LO transfer matrix in Euclidean time to form dressed cluster states,

$$\begin{aligned} \left| {R} \right\rangle ^{\ell ,\ell _z}_{n_{t}} = M_\mathrm{LO}^{n_{t}} \, \left| {R} \right\rangle ^{\ell ,\ell _z}. \end{aligned}$$

(94.7)

These dressed cluster states are used to construct the transfer matrix of the cluster-cluster system,

$$\begin{aligned}{}[M_{n_{t}}]^{\ell ,\ell _z}_{R^{\prime },R} = {}^{\ell ,\ell _z}_{\,\,\,\,n_{t}}{ \left\langle {R^{\prime } \left| M_\mathrm{LO}\right| R} \right\rangle }^{\ell ,\ell _z}_{n_{t}}, \end{aligned}$$

(94.8)

and the norm matrix,

$$\begin{aligned}{}[N_{n_{t}}]^{\ell ,\ell _z}_{R^{\prime },R} = {}^{\ell ,\ell _z}_{\,\,\,\,n_{t}}{ \left\langle {R^{\prime } \left| \right. R} \right\rangle }^{\ell ,\ell _z}_{n_{t}}. \end{aligned}$$

(94.9)

The adiabatic projection in Euclidean time gives a systematically improvable description of the low-lying scattering states of clusters, and in the limit of large Euclidean time the description becomes exact. We use the auxiliary-field Monte Carlo simulations to compute the amplitude matrices in (94.8) and (94.9). In addition, we perform metropolis sampling of the cluster positions. Then we use (94.8) and (94.9) to construct the adiabatic transfer matrix,

$$\begin{aligned}{}[M^{a}_{n_{t}}]^{\ell ,\ell _z}_{R^{\prime },R} = \left[ N_{n_{t}}^{-\frac{1}{2}} M_{n_{t}} N_{n_{t}}^{-\frac{1}{2}} \right] , \end{aligned}$$

(94.10)

and by employing the spherical wall method [4, 7] the adiabatic transfer matrix is used to compute the scattering phase shifts for two-cluster systems. The computational scaling of lattice calculations consisting of $A_{1}$-body and $A_{2}$-body clusters is roughly $(A_{1} + A_{2})^{2}$, and this makes ab initio calculations involving a heavier projectile accessible and practical.

3 Results

Alpha-alpha scattering: In this section, we present the recent results from the lattice simulations. We start with the first ab initio calculation of the elastic ${}^4$He$+$ ${}^4$He scattering using the adiabatic projection method. As described above, thanks to mild computational scaling, ab initio calculations involving ${}^4$He cluster as a projectile are possible with the adiabatic projection method. We used the lattice action developed and used in [8], and performed the first ab initio calculation of ${}^4$He$+$ ${}^4$He scattering up to next-to-next-to-leading order in chiral effective field theory [5]. In these calculations the spatial lattice spacing is $a = 1.97$ fm and the temporal lattice spacing is $a_{t} = 1.32$ fm.

Fig. 94.1

Left: S-wave phase shifts up to NNLO and comparison with experimental data [9]. Right: D-wave phase shifts up to NNLO and comparison with experimental data [9]

Figure 94.1 shows the S-wave (left) and the D-wave (right) scattering phase shifts versus laboratory energy up to NNLO in chiral effective field theory comparison with experimental data [9]. We found that for the S-wave the NNLO result is in good agreement with experiment, and we found a fairly good agreement between the D-wave the NNLO result and experiment.

The adiabatic projection method is of significant importance not only because the ${}^4$He nuclei has been the heaviest projectile used in the ab initio calculations of scattering and reactions, but also has opened the door towards using experimental data from collisions of heavier nuclei as input to improve ab initio nuclear structure theory.

Degree of locality of nuclear forces: In [10] we used the ${}^4$He$+$ ${}^4$He scattering as a tool for probing the degree of locality of the short-range nuclear interactions and the nuclear structure of alpha-conjugate nuclei which are nuclei with equal and even numbers of protons and neutrons. We started with two leading order lattice interactions $V_\mathrm{A}(\mathbf {r}^{\prime },\mathbf {r})$ and $V_\mathrm{B}(\mathbf {r}^{\prime },\mathbf {r})$ where $\mathbf {r}$ is the spatial separation between the two incoming nucleons and $\mathbf {r}^{\prime }$ is the spatial separation between the two outgoing nucleons. The interaction $V_\mathrm{A}(\mathbf {r}^{\prime },\mathbf {r})$ includes non-local short-range interactions, while the interaction $V_\mathrm{B}(\mathbf {r}^{\prime },\mathbf {r})$ consists of both non-local and local short-range interactions. We tuned the interactions $V_\mathrm{A}(\mathbf {r}^{\prime },\mathbf {r})$ and $V_\mathrm{B}(\mathbf {r}^{\prime },\mathbf {r})$ to produce the experimental low-energy nucleon-nucleon scattering phase shifts, while the extra parameters of the interaction $V_\mathrm{B}(\mathbf {r}^{\prime },\mathbf {r})$ due to the local terms were tuned to give the alpha-alpha S-wave scattering phase shifts. Figure 94.2 shows the ${}^4$He$+$ ${}^4$He S-wave scattering phase shifts as a function of laboratory energy for interactions $V_\mathrm{A}(\mathbf {r}^{\prime },\mathbf {r})$ and $V_\mathrm{B}(\mathbf {r}^{\prime },\mathbf {r})$. The results from Fig. 94.2 clearly shows that the ${}^4$He$+$ ${}^4$He scattering phase shifts are highly sensitive to the degree of locality of the short-range nuclear interactions. Reference [10] explains these results in detail closely looking at the structure of the ${}^4$He wave function.

Fig. 94.2

${}^4$He$+$ ${}^4$He S-wave scattering. We plot S-wave phase shifts $\delta _{0}$ for alpha-alpha scattering for interactions $V_\mathrm{A}(\mathbf {r}^{\prime },\mathbf {r})$ and $V_\mathrm{B}(\mathbf {r}^{\prime },\mathbf {r})$ versus laboratory energy. We show LO for A (green tiangle), LO + Coulomb for A (orange diamonds), LO for B (blue circles), and LO + Coulomb results for B (red squares) comparison with experimental data [9]

For interactions $V_\mathrm{A}(\mathbf {r}^{\prime },\mathbf {r})$ and $V_\mathrm{B}(\mathbf {r}^{\prime },\mathbf {r})$ we computed the ground state energies of ${}^3$H, ${}^3$He, ${}^4$He as well as alpha-conjugate nuclei ${}^8$Be, ${}^{12}$C, ${}^{16}$O, ${}^{20}$Ne given in Table 94.1. We found that nuclei up to $^8$Be are equally well described by both interactions. For the interaction $V_\mathrm{B}(\mathbf {r}^{\prime },\mathbf {r})$ the results of nuclei heavier than $^8$Be are in agreement with the experimental data, while they are underbound for the interaction $V_\mathrm{A}(\mathbf {r}^{\prime },\mathbf {r})$. Also the ${}^4$He$+$ ${}^4$He scattering phase shifts for interaction $V_\mathrm{A}(\mathbf {r}^{\prime },\mathbf {r})$ is very weak as given in Fig. 94.2. To illuminate what is going on with the interaction $V_\mathrm{A}(\mathbf {r}^{\prime },\mathbf {r})$ we found it useful to look at the ratio of the LO energy for each of the alpha-conjugate nuclei to that of the ${}^4$He particle. The results for the ratios are 1.997(6), 3.00(1), 4.00(2), and 5.03(3) for ${}^8$Be, ${}^{12}$C, ${}^{16}$O, and ${}^{20}$Ne, respectively. The important result revealed here is that in each case the interaction $V_\mathrm{A}(\mathbf {r}^{\prime },\mathbf {r})$ forms a weakly-interacting Bose gas of alpha particles.

In this study we found that the correct description of the ${}^4$He$+$ ${}^4$He scattering phase shifts play a crucial role to describe alpha-conjugate nuclei well. In order to understand the many-body limit in details, we switched off the Coulomb interactions and connect the interaction $V_\mathrm{A}(\mathbf {r}^{\prime },\mathbf {r})$ to the interaction $V_\mathrm{B}(\mathbf {r}^{\prime },\mathbf {r})$ by a simple interpolation, $V_{\lambda } = (1 - \lambda ) V_{A} + \lambda V_{B}$. We did not observe any significant change in the properties of the two-, three-, and four-nucleon systems with $\lambda$, while the many-body ground state of the interpolated interaction $V_{\lambda }$ undergoes a quantum phase transition from a Bose-condensed gas to a nuclear liquid. A schematic view of the zero temperature phase diagram is shown in Fig. 94.3.

Table 94.1 The lattice results for the ground state energies of ${}^3$H, ${}^3$He, ${}^4$He, ${}^8$Be, ${}^{12}$C, ${}^{16}$O, ${}^{20}$Ne from the interactions $V_\mathrm{A}(\mathbf {r}^{\prime },\mathbf {r})$ and $V_\mathrm{B}(\mathbf {r}^{\prime },\mathbf {r})$. All energies are in units of MeV

Fig. 94.3

Zero-temperature phase diagram as a function of the parameter $\lambda$ in the nuclear interaction $V_{\lambda } = (1 - \lambda )V_{A} + \lambda V_{B}$. A first-order quantum phase transition from a Bose gas to nuclear liquid at the point appears where the alpha-alpha scattering length crosses zero. This is very close to the value $\lambda = 0$. Also shown are the alpha-conjugate nuclear ground state energies $E_{A}$ for A nucleons up to $A=20$ relative to the corresponding multi-alpha threshold $E_{\alpha } A/4$. The last alpha-conjugate nucleus to be bound is ${}^8$Be at the unitarity point

Density profiles for nuclei: The simulations with auxiliary-field Monte Carlo methods involve quantum states that are superposition of many different center-of-mass positions. Therefore, the density distrubitions of the nucleons cannot be computed direclty. To solve this problem we developed and introduced a new computational approach called the pinhole algorithm [11], which solves a long-standing deficiency of auxiliary-field Monte Carlo simulations in computing density correlations relative to the center of mass.

Fig. 94.4

A sketch of the pinhole locations and spin-isospin indices at time $\tau /2= L_{t} a_{t}/2$

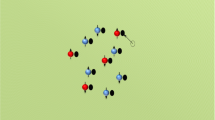
In this algorithm we consider a screen placed at the middle time step having pinholes with spin and isospin labels that allow nucleons with the corresponding spin and isospin to pass. This screen corresponds to the insertion of the normal-ordered A-body density operator at the middle time step,

$$\begin{aligned} \rho _{i_{1},j_{1},\ldots ,i_{A},j_{A}}(\mathbf {n}_{1},\ldots ,\mathbf {n}_{A}) = \, :\rho _{i_{1},j_{1}}(\mathbf {n}_{1}) \, \ldots \, \rho _{i_{A},j_{A}}(\mathbf {n}_{A}): \end{aligned}$$

(94.11)

where $\rho _{i,j}(\mathbf {n}) = a^{\dagger }_{i,j}(\mathbf {n})a^{\,}_{i,j}(\mathbf {n})$ is the density operator for nucleon with spin i and isospin j. Figure 94.4 shows a sketch of the pinhole locations and spin-isospin indices for the operator $\rho _{i_{1},j_{1}, \ldots , i_{A},j_{A}}(\mathbf {n}_{1},\ldots ,\mathbf {n}_{A})$ inserted at time $\tau /2$. The screen has A pinholes for a simulation consist of A nucleons, and we perform Metropolis sampling for the locations as well as the spin and isospin labels of the pinholes. Using the pinhole algorithm, we have computed the proton and neutron densities for the ground states of ${}^{12}$C, ${}^{14}$C, and ${}^{16}$C given in Fig. 94.5.

Fig. 94.5

Plots of the proton and neutron densities as function of radial distance for the ground states of ${}^{12}$C, ${}^{14}$C, and ${}^{16}$C comparison with the experimentally observed proton densities for 12C and 14C [12]. We show data for various $L_{t}$ time steps

Ground state energies for light and medium-mass nuclei: Recently we have constructed a set of short-range chiral effective field theory interactions on the lattice with a simpler decomposition into spin channels. Li et al. [2] presents the full details of these lattice interactions and the results for the neutron-proton scattering on the lattice with various lattice spacings comparision with the empirical phase shifts.

Fig. 94.6

Neutron-proton scattering uncoupled channel phase shifts as function of relative momenta at lattice spacing $a = 1.97$ fm

Fig. 94.7

Neutron-proton scattering coupled channel phase shifts and mixing angles as function of relative momenta at lattice spacing $a = 1.97$ fm

Fig. 94.8

PRELIMINARY RESULTS: Lattice results for ground state energies of light and medium-mass nuclei up to N3LO in chiral effective field theory without the three-body forces

Using the lattice action developed in [2], we have studied the neutron-proton scattering to determine the LECs and computed the ground states energies of light and medium-mass nuclei at lattice spacing $a = 1.97$ fm. Figures. 94.6 and 94.7 show the neutron-proton scattering phase shifts comparision with the empirical phase shifts. Lattice results for ground state energies of light and medium-mass nuclei up to N3LO in chiral effective field theory are given in Fig. 94.8 [13]. We stress that these results are preliminary. Also these results do not include any three-body force, and the relevant work is in progress.

Summary We have reported recent results from lattice simulations with chiral effective field theory up to next-to-next-to-next-to-leading order. We have also discussed our investigation on the degree of locality of the short-range nucleon-nucleon interactions, and algorithm that we developed recently to study the proton and neutron density distributions.