1 Motivation

The nucleon and its excitation spectrum have traditionally been at the heart of strong interaction studies. The proton is the only truly stable hadron and an ubiquitous ingredient in hadron structure experiments: from elastic and deep inelastic ep scattering to pp and \(p\bar{p}\) reactions, \(N\pi \) scattering, pion photo- and electroproduction, nucleon Compton scattering and more; also searches for physics beyond the Standard Model are typically performed on protons and nuclei. In addition, these experiments create meson and baryon resonances too and thereby allow us to extract their properties.

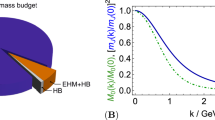
The data collected at Jefferson Lab, CERN and other facilities around the world show that hadrons are more complicated than the naive quark model suggests. For example, ostensibly simple baryon resonances may be mixtures of three-quark and multihadron states, and even our understanding of the nucleon is far from complete. Hadrons are complicated objects made of quarks and gluons, and it is the complexity of their interaction described by Quantum Chromodynamics (QCD) that encodes phenomena such as confinement and spontaneous chiral symmetry breaking. With quarks close to being massless, the dynamics of gluons plays a key role: for all we know today, the major fraction of the mass of the proton and other light hadrons is produced by glue.

Fig. 123.1
figure 1

Top: Some of QCD’s elementary n-point functions. Bottom: Nonperturbative quark DSE together with its perturbative expansion

Full size image

A theoretical description of hadrons is tied to a thorough understanding of nonperturbative QCD, which requires combined efforts from lattice QCD, functional methods, amplitude analyses, phenomenological models and other theoretical approaches. Here we give a brief account of progress with functional methods, in particular the combination of Dyson-Schwinger equations (DSEs) and Bethe-Salpeter equations (BSEs), in calculating hadron spectroscopy and structure properties from QCD. For details we refer to the review [1].

2 From QCD’s Correlation Functions to Hadrons

The basic starting point are QCD’s correlation functions or n-point functions, some of which are collected in Fig. 123.1: the ‘dressed’ quark and gluon propagators, the quark-gluon vertex, three-gluon vertex and so on. In contrast to the few tree-level propagators and interactions that define the classical Lagrangian, the full information on the quantum field theory is encoded in its (infinitely many) correlation functions. These can be calculated from QCD’s partition function, either directly using lattice QCD, or by deriving coupled equations for them, namely the DSEs which are the quantum equations of motion.

The DSEs are nonperturbative, self-consistent, exact equations which form an infinitely coupled system. At large momenta the coupling becomes small and they reproduce perturbation theory, as illustrated in Fig. 123.1 for the quark propagator. At small momenta, on the other hand, they encode effects which cannot happen at any order in perturbation theory, such as the nonperturbative generation of a quark mass scale (a ‘constituent-quark mass’) due to spontaneous chiral symmetry breaking, or the disappearance of the massless gluon pole and thus a gluon ‘mass gap’; see [2,3,4,5] and references therein.

Because the correlation functions are gauge-dependent, one has to choose a gauge and the most convenient one in practice is Landau gauge. Landau-gauge lattice results for some of the elementary two- and three-point functions are available, see e.g. [6,7,8,9,10] and references therein. A different approach is the functional renormalization group (FRG), which leads to a similar tower of equations [11, 12]. To arrive at closed equations which can be systematically improved, the functional methods require truncations, either by neglecting higher n-point functions or higher-order terms in the quantum effective action. For the two- and three-point functions investigated so far [13,14,15,16,17] the three methods—lattice QCD, FRG equations and DSEs—provide qualitatively similar results, which suggests that a quantitative agreement is indeed within reach.

Fig. 123.2
figure 2

Top: Four-point \(q\bar{q}\) correlator, its pole behavior and the corresponding meson Bethe-Salpeter equation. Bottom: Covariant Faddeev equation for a baryon

Full size image

The properties of higher n-point functions become progressively more complicated since they depend on an increasing number of kinematic variables and Lorentz/Dirac tensors. General principles such as Lorentz invariance and gauge invariance pose constraints on them, which should be worked out before calculating their dynamical properties. So far, apart from the two- and three-point correlators, the structure of higher n-point functions is still largely unknown territory but progress is underway [12, 17,18,19,20].

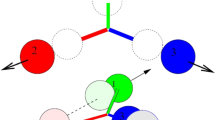
Also the properties of hadrons are encoded in the correlation functions, namely in higher n-point functions which permit a spectral representation in terms of gauge-invariant hadron bound states and multiparticle states. For example, the \(q\bar{q}\) four-point function contains all meson poles, and so does any other n-point function that creates meson quantum numbers (\(q\bar{q}g\), \(q\bar{q}q\bar{q}\) etc.). Likewise, the qqq six-point function contains all baryon poles. The residue at a pole defines the Bethe-Salpeter (BS) wave function \(\varPsi \) shown in Fig. 123.2, which encodes the properties of the respective hadron.

The BS wave function can be calculated from its BSE, which at the same time determines the mass of the state. The BSEs for mesons and baryons are shown in Fig. 123.2. They are homogeneous integral equations in momentum space, which become eigenvalue equations for the respective \(q\bar{q}\) and qqq kernels. The three-body BSE is also known as the covariant Faddeev equation; in this case the kernel is the sum of the irreducible two- and three-quark kernels.

In practice, the general strategy is to keep the full relativistic structure of the BS wave functions intact and make approximations only at the level of the kernels. A popular truncation is the so-called rainbow-ladder interaction, where the two-body kernels are approximated by a vector-vector interaction with a momentum-dependent effective interaction \(\alpha (k^2)\). The quark propagator is solved from its DSE in Fig. 123.1, which dynamically breaks chiral symmetry: if the interaction is strong enough, it produces a running quark mass function which becomes large at small momenta and transforms the current quark into a dynamical ‘constituent quark’. The resulting mass function is what makes hadron masses large even in the chiral limit of massless current quarks, whereas the pseudoscalar mesons remain massless because they are the Goldstone bosons of spontaneous chiral symmetry breaking. Rainbow-ladder has been frequently used in hadron spectrum and structure calculations [21, 22]. It provides a good overall description of heavy mesons but also light mesons in the pseudoscalar and vector channels [23,24,25,26,27,28], their decays, form factors, scattering amplitudes and, as it turns out, also a range of baryon properties including masses, elastic and transition form factors and more [1]. Moreover, the analogous four-quark equation for tetraquarks reproduces the mass pattern of the light scalar mesons [29].

Fig. 123.3
figure 3

Nucleon and \(\varDelta \) spectrum for \(J^P=1/2^\pm \) and \(3/2^\pm \) states. The three-body (open boxes [30, 31]) and quark-diquark results (filled boxes [32]) are compared to the PDG values with their experimental uncertainties [33], see [32] for details

Full size image

To make a step forward to a quantitative understanding of hadron properties, one must improve the description of the underlying n-point functions. For example, in a recent beyond rainbow-ladder calculation all two- and three point functions in the system were solved, so that the BS kernel is no longer an input but a dynamical result [34]. This significantly improves the light meson spectrum: while the pseudoscalar and vector-meson ground states are less sensitive, the scalar and axialvector mesons (which are too strongly bound in rainbow-ladder) acquire large repulsive shifts, which puts them in the ballpark of experimental results, see Fig. 3.21 in [1].

3 Excited Baryons

Most baryon spectroscopy calculations so far have been performed in rainbow-ladder and attempts to go beyond rainbow-ladder are progressing [1, 30, 35]. In fact, already the rainbow-ladder kernels reproduce the masses of the nucleon, the \(\varDelta (1232)\) and the Roper resonance N(1440), cf. Fig. 123.3. The remaining channels, however, come out too low, which is similar to the situation in the meson sector beyond pseudoscalar and vector mesons. The three-body calculations are numerically expensive especially for excited states, because with the full structure of the relativistic Faddeev amplitudes the equations become eigenvalue problems for matrices of the size \(10^6\times 10^6 \dots 10^9\times 10^9\) depending on the numerics.

At this point a quark-diquark interpretation can provide further insight. Instead of solving the three-body Faddeev equation directly, one can approximate it to a quark-diquark BSE where the baryon is treated as a quark-diquark system that interacts by quark exchange. To minimize the model input in such approaches [38,39,40,41], the diquark ingredients in [32] were calculated self-consistently from their DSEs and BSEs, so that also the quark-diquark system can be traced back to the same underlying quark-gluon interaction.

As a result, the three-quark and quark-diquark results essentially agree with each other; the \(N(1/2^+)\) and \(\varDelta (3/2^+)\) channels are described well but the remaining ones show deficiencies. Those are due to the higher-lying diquarks: whereas N and \(\varDelta \) are dominated by scalar and axialvector diquarks, the remaining channels are also sensitive to pseudoscalar and vector diquarks [42] which are ‘too strongly bound’ just like their scalar and axialvector meson partners. By reducing the strength of these diquarks through one parameter, which is fixed by the \(\rho -a_1\) splitting in the meson sector, one arrives at the spectrum in Fig. 123.3 [32]. One observes a 1:1 correspondence between the number of levels with PDG states and the masses are in almost quantitative agreement. An extension of the approach to the hyperon spectrum is underway [43].

The Faddeev amplitudes carry a rich tensorial structure which can be organized into eigenstates of spin and orbital angular momentum (OAM) in the rest frame [1, 38]. The resulting s, p, d and f-wave components (\(L=0, \dots , 3\)) in Fig. 123.4 are different from the nonrelativistic quark model, where each baryon has definite L. Relativistically, these components can mix: the nucleon and \(\varDelta (1232)\) have p-wave components, the N(1535) has s waves, and p waves are even dominant for the Roper. The subleading partial waves have consequences for form factors, for example in the \(N\gamma \rightarrow \varDelta \) transition [44], which demonstrates that relativity is important in the description of light baryons. Although these features should appear in other relativistic approaches as well, they are rarely discussed; exceptions are the covariant spectator theory [45] and light-front holographic QCD [46]. In the relativistic quark model of [47] there is no reference to non-traditional OAM contributions in baryons, but it is conceivable that they can appear after boosting the wave functions, e.g. in form factor calculations [48].

In addition to spectroscopy, more detailed properties of excited baryons can be extracted from their electromagnetic transition form factors \(\gamma ^*N \rightarrow N^*\). Figure 123.5 shows the generic properties of transition form factors. In the spacelike region (\(Q^2>0\)) they are accessible in meson photo- and electroproduction experiments at Jefferson Lab, ELSA and MAMI [49,50,51]. These have been the main experimental sources for the discovery of new nucleon resonances and the combination of precision data with multichannel partial-wave analyses has led to the addition of several new states to the PDG [33]. The timelike region (\(Q^2<0\)) above \(N\bar{N}^*\) threshold is accessible in \(e^+ e^- \leftrightarrow N\bar{N}^*\) reactions, whereas the near timelike region \(Q^2 > -(m^*-m)^2\) can be measured through the Dalitz decays \(N^*\rightarrow N e^+ e^-\) at HADES/GSI [52].

Fig. 123.4
figure 4

Orbital angular-momentum contributions in the Faddeev amplitude of each baryon (in %); all bars sum up to 100% [36]. The rectangular backgrounds are the orbital angular-momentum assignments in the non-relativistic quark model [37]

Full size image
Fig. 123.5
figure 5

Top: Generic behavior of an electromagnetic transition form factor in the spacelike and timelike regions. Bottom: Form factor diagram in the Faddeev approach

Full size image

In the Faddeev approach, whose form factor decomposition is shown in the bottom panel of Fig. 123.5, these different kinematical regions are tightly connected. Spacelike results for elastic and transition form factors are available from both three-body [53,54,55] and quark-diquark calculations [41, 44], see [1] for a review. With the exception of missing meson-cloud effects at low \(Q^2\), they describe the existing data relatively well. The timelike structure, on the other hand, should be dominated by \(\rho , \omega , \dots \) bumps because a photon can fluctuate into vector mesons. The bumps originate in the quark-photon vertex, which is the contraction of the \(q\bar{q}\) four-point function in Fig. 123.2 with \(\gamma ^\mu \) and thus inherits its vector-meson poles. The mesons in rainbow-ladder are stable hadrons and produce poles on the real axis instead of poles in the complex plane on higher Riemann sheets. Thus, to access the timelike properties of form factors one must implement the proper resonance mechanism beyond rainbow-ladder but also develop the necessary numerical tools in terms of residue calculus and contour deformations. Both strategies are currently being explored [56, 57].

4 Nucleon Resonances from Compton Scattering

In the last decade meson photo- and electroproduction experiments have become the main tools for gathering information on the baryon excitation spectrum. Understanding the structure and dynamics of scattering amplitudes is clearly important: dynamical reaction models and amplitude analyses based on general principles such as unitarity, analyticity and crossing symmetry are necessary to organize the experimental data and disentangle the various partial-wave contributions to extract resonance properties. Moreover, scattering amplitudes contain an abundance of information in addition to spectroscopy and thus their study also serves a purpose beyond the extraction of resonances.

An example is nucleon Compton scattering (CS), which encodes a broad range of applications from nucleon polarizabilities, structure functions, two-photon corrections to form factors and the proton radius puzzle to generalized parton distributions, see e.g. [58,59,60,61] for reviews. Our experimental knowledge of the CS amplitude is restricted to a few kinematic limits where direct measurements are possible, such as real and virtual CS and the forward limit.

Here we only focus on the nucleon resonances that appear in CS through the process \(\gamma ^*N \rightarrow N^*\rightarrow \gamma ^*N\). The absence of spurious singularities in the CS amplitude poses constraints on the transition current matrix elements \(\gamma ^*N \rightarrow N^*\), which must satisfy electromagnetic gauge invariance and spin-3/2 gauge invariance [62]. The most general tensors according to these principles can be found in [63], along with a structure analysis of CS including all measured nucleon resonances with \(J^P = 1/2^\pm \) and \(J^P=3/2^\pm \). As a consequence, the corresponding transition form factors are free of kinematic constraints, so their only singularities are physical poles and cuts such as in Fig. 123.5.

Fig. 123.6
figure 6

\(\gamma ^*N \rightarrow N(1440)\) transition form factors and helicity amplitudes. The PDG [33] and CLAS data [50, 64, 65] are shown together with the A1/MAMI point for \(S_{1/2}\) [66] and the MAID parametrization (dashed) [67]. The bands are fits [63]. The form factors are dimensionless and the helicity amplitudes carry units of \(10^{-3}\) GeV\(^{-1/2}\)

Full size image

An example is the Roper resonance, the first excitation of the nucleon. For timelike \(Q^2\) its transition form factors should resemble Fig. 123.5, so that their rise at low spacelike \(Q^2\) is due to the first \(\rho \)-meson pole. However, to see such a behavior one must first cast the experimental data into the constraint-free form factors \(F_1(Q^2)\) and \(F_2(Q^2)\) corresponding to the tensors in [63]. These are shown in the top panels of Fig. 123.6 for spacelike \(Q^2\). The bands are fits to the data and analogous fits for all nucleon resonances with \(J^P = 1/2^\pm \) and \(J^P=3/2^\pm \) can be found in [63].

The existing reaction models usually do not extract the form factors but instead their helicity amplitudes (bottom panels), which are linear combinations of the form factors but not free of kinematic constraints. In particular, in the case of the Roper both \(A_{1/2}\) and \(S_{1/2}\) must vanish at the pseudothreshold \(Q^2 = -(m^*-m)^2\), where m and \(m^*\) are the nucleon and Roper masses. For example, the MAID curve [67] in Fig. 123.6 is compatible with the recent A1/MAMI measurement for \(S_{1/2}\) at very low \(Q^2\) [66] but does not reproduce the behavior at the pseudothreshold. This translates into a turnover of \(F_1(Q^2)\) at very low \(Q^2\), which would be difficult to explain from the analytic structure in the timelike region if the first \(\rho \)-meson pole has a positive residue. While such kinematic constraints must be implemented explicitly in the helicity amplitudes, they follow automatically when using constraint-free form factors.

The \(Q^2\)-dependence of several transition form factors is still poorly known, especially at low \(Q^2\): even the best known resonances such as the N(1440), N(1520) and N(1535) do not have any data below \(Q^2 \lesssim 0.3\) GeV\(^2\). In view of connecting the properties of form factors across the spacelike and timelike regions, this clearly motivates the need for future measurements at low \(Q^2\).