Abstract
Multiphase ranking functions (M\(\varPhi \)RFs) are used to prove termination of loops in which the computation progresses through a number of phases. They consist of linear functions \(\langle f_1,\ldots ,f_d \rangle \) where \(f_i\) decreases during the ith phase. This work provides new insights regarding M\(\varPhi \)RFs for loops described by a conjunction of linear constraints (\( SLC \) loops). In particular, we consider the existence problem (does a given \( SLC \) loop admit a M\(\varPhi \)RF). The decidability and complexity of the problem, in the case that d is restricted by an input parameter, have been settled in recent work, while in this paper we make progress regarding the existence problem without a given depth bound. Our new approach, while falling short of a decision procedure for the general case, reveals some important insights into the structure of these functions. Interestingly, it relates the problem of seeking M\(\varPhi \)RFs to that of seeking recurrent sets (used to prove nontermination). It also helps in identifying classes of loops for which M\(\varPhi \)RFs are sufficient, and thus have linear runtime bounds. For the depth-bounded existence problem, we obtain a new polynomial-time procedure that can provide witnesses for negative answers as well. To obtain this procedure we introduce a new representation for \( SLC \) loops, the difference polyhedron replacing the customary transition polyhedron. We find that this representation yields new insights on M\(\varPhi \)RFs and \( SLC \) loops in general, and some results on termination and nontermination of bounded \( SLC \) loops become straightforward.
This work was funded partially by the Spanish MICINN/FEDER, UE project RTI2018-094403-B-C31, the MINECO project TIN2015-69175-C4-2-R, the CM project S2018/TCS-4314 and by the pre-doctoral UCM grant CT27/16-CT28/16.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Proving that a program will not go into an infinite loop is one of the most fundamental tasks of program verification, and has been the subject of voluminous research. Perhaps the best known, and often used, technique for proving termination is that of ranking functions. This consists of finding a function that maps program states into the elements of a well-founded ordered set, such that its value decreases when applied to consecutive states. This implies termination since infinite descent is impossible in a well-founded order.
Unlike termination of programs in general, which is undecidable, the algorithmic problems of detection (deciding the existence) or generation (synthesis) of a ranking function can well be solvable, given certain choices of the program representation, and the class of ranking function. There is a considerable amount of research in this direction, in which different kinds of ranking functions for different kinds of program representations were considered. In some cases the algorithmic problems have been completely settled, and efficient algorithms provided, while other cases remain open.
The program representation we study is single-path linear-constraint loops (\( SLC \) loops), where a state is described by the values of numerical variables, and the effect of a transition (one iteration) is described by a conjunction of linear constraints. We consider the settings of integer-valued variables and rational-valued (or real-valued) variables. Here is an example of this loop representation; primed variables \(x_1',x_2',\dots \) refer to the state following the transition.
Note that \(x_1'=x_1+x_2\) is an equation, not an assignment. The description of a loop may involve linear inequalities rather than equations, and consequently be nondeterministic. It is a standard procedure to compile sequential code (or approximate it) into such representation using various techniques. We assume the “constraint loop” to be given, and do not concern ourselves with the orthogonal topic of extracting such loops from general programs. The loop is called simple since branching in the loop body is not represented. Despite this restriction, \( SLC \) loops are important, e.g., in approaches that reduce a question about a whole program to questions about simple loops [14,15,16, 21, 27]; see [29] for references that show the importance of such loops in other fields.
Several types of ranking functions have been suggested for \( SLC \) loops; linear ranking functions (\( LRFs \)) are probably the most known. In this case, we seek a function \(\rho (x_1,\dots ,x_n) = a_1x_1+\dots +a_n x_n + a_0\) such that (i) \(\rho (\mathbf {x}) \ge 0\) for any valuation \(\mathbf {x} = \langle x_1,\ldots ,x_n \rangle \) that satisfies the loop constraints (i.e., an enabled state); and (ii) \(\rho (\mathbf {x})-\rho (\mathbf {x}') \ge 1\) for any transition leading from \(\mathbf {x}\) to \(\mathbf {x}' = \langle x_1',\ldots ,x_n' \rangle \). The algorithmic problems of existence and synthesis of \( LRFs \) have been completely settled [5, 12, 18, 31, 33], for both integer-valued and rational-valued variables, not only for \( SLC \) loops but rather for control-flow graphs.
\( LRFs \) do not suffice for all terminating \( SLC \) loops, e.g., Loop (1) does not have a \( LRF \), and in such case, one may resort to an argument that combines several linear functions to capture a more complex behavior. A common such argument is one that uses lexicographic ranking functions, where a tuple of linear functions is required to decrease lexicographically when moving from one state to another. In this paper we are interested in a special case of the lexicographic order argument that is called Multiphase ranking functions (M\(\varPhi \)RF for short). Intuitively, a M\(\varPhi \)RF is a tuple \(\langle f_1,\ldots ,f_d \rangle \) of linear functions that define phases of the loop that are linearly ranked, as follows: \(f_1\) decreases on all transitions, and when it becomes negative \(f_2\) decreases, and when \(f_2\) becomes negative, \(f_3\) will decrease, etc. Loop (1) has the M\(\varPhi \)RF \(\langle x_3+1,x_2+1,x_1 \rangle \). The parameter d is called the depth of the M\(\varPhi \)RF, intuitively the number of phases.
The decision problem Existence of a \(M{\varPhi }RF \) asks to determine whether a \( SLC \) loop has a M\(\varPhi \)RF. The bounded decision problem restricts the search to M\(\varPhi \)RFs of depth d, where d is part of the input. The complexity and algorithmic aspects of the bounded version of the M\(\varPhi \)RF problem were completely settled in [6]. The decision problem is \(\mathtt {PTIME}\) for \( SLC \) loops with rational-valued variables, and \(\mathtt {coNP}\)-complete for \( SLC \) loops with integer-valued variables; synthesizing M\(\varPhi \)RFs, when they exist, can be performed in polynomial and exponential time, respectively. In addition, [6] shows that for \( SLC \) loops M\(\varPhi \)RFs have the same power as general lexicographic-linear ranking functions, and that, surprisingly, M\(\varPhi \)RFs induce linear iteration bounds. The problem of deciding if a given \( SLC \) admits a M\(\varPhi \)RF, without a given bound on the depth, is still open.
In practice, termination analysis tools search for M\(\varPhi \)RFs starting by depth 1 and incrementally increase the depth until they find one, or reach a predefined limit, after which the returned answer is don’t know. Clearly, finding a theoretical upper-bound on the depth of a M\(\varPhi \)RF, given the loop, would also settle this problem. As shown in [6], such bound must depend not only on the number of constraints or variables, but also on the coefficients used in the constraints.
In this paper we make progress towards solving the problem of existence of a \(M{\varPhi }RF \), i.e., seeking a M\(\varPhi \)RF without a given bound on the depth. In particular, we present an algorithm for seeking M\(\varPhi \)RFs that reveals new insights on the structure of these ranking functions. In a nutshell, the algorithm starts from the set of transitions of the given \( SLC \) loop, which is a polyhedron, and iteratively removes transitions \((\mathbf {x},\mathbf {x}')\) such that \(\rho (\mathbf {x})-\rho (\mathbf {x}')>0\) for some function \(\rho (\mathbf {x})=\vec {a}\cdot \mathbf {x}+b\) that is nonnegative on all enabled states. The process continues iteratively, since after removing some transitions, more functions \(\rho \) may satisfy the nonnegativity condition, and they may eliminate additional transitions in the next iteration. When all transitions are eliminated in a finite number of iterations, we can construct a M\(\varPhi \)RF using the \(\rho \) functions; and when reaching a situation in which no transition can be eliminated, we prove that we have actually reached a recurrent set that witnesses nontermination.
The algorithm always finds a M\(\varPhi \)RF if one exists, and in many cases it finds a recurrent set (see experiments in Sect. 5) when the loop is nonterminating, however, it is not a decision procedure as it diverges in some cases. Nonetheless, our algorithm provides important insights on the structure of M\(\varPhi \)RFs. Apart from revealing a relation between seeking M\(\varPhi \)RFs and seeking recurrent sets, these insights are useful for finding classes of \( SLC \) loops for which, when terminating, there is always a M\(\varPhi \)RF and thus have linear runtime bound.
Our research has, in addition, led to a new representation for \( SLC \) loops, that we refer to as the displacement representation, that provides us with new tools for studying termination of \( SLC \) loops in general, and existence of a M\(\varPhi \)RF in particular. In this representation a transition \((\mathbf {x},\mathbf {x}')\) is represented as \((\mathbf {x},\mathbf {y})\) where \(\mathbf {y}=\mathbf {x}'-\mathbf {x}\). Using this representation our algorithm can be formalized in a simple way that avoids computing the \(\rho \) functions mentioned above (which might be expensive), and reduces the existence of a M\(\varPhi \)RF of depth d to unsatisfiability of a certain linear constraint system. Moreover, any satisfying assignment is a witness that explains why the loop has no M\(\varPhi \)RF of depth d. As an evidence on the usefulness of this representation in general, we also show that some nontrivial observations on termination of bounded \( SLC \) loops are made straightforward in this representation, while they are not easy to see in the normal representation.
The article is organized as follows. Section 2 gives precise definitions and necessary background. Section 3 describes our algorithm and its possible outcomes. Section 4 discusses the displacement representation for \( SLC \) loops. Section 5 discusses some experiments. Finally, in Sect. 6 we conclude and discuss related work.
2 Preliminaries
 A rational convex polyhedron \({\mathcal P} \subseteq \mathbb Q ^n\) (polyhedron for short) is the set of solutions of a set of inequalities \(A\mathbf {x} \le \mathbf {b}\), namely \({\mathcal P}=\{ \mathbf {x}\in \mathbb Q ^n \mid A\mathbf {x} \le \mathbf {b} \}\), where \(A \in \mathbb Q ^{m \times n}\) is a rational matrix of n columns and m rows, \(\mathbf {x}\in \mathbb Q ^n\) and \(\mathbf {b} \in \mathbb Q ^m\) are column vectors of n and m rational values respectively. We say that \({\mathcal P}\) is specified by \(A\mathbf {x} \le \mathbf {b}\). If \(\mathbf {b}=\mathbf {0}\), then \({\mathcal P}\) is a cone. The set of recession directions of a polyhedron \({\mathcal P}\) specified by \(A\mathbf {x} \le \mathbf {b}\), also known as its recession cone, is the set \({\mathtt {rec.cone}}({\mathcal P}) = \{ \mathbf {y}\in \mathbb Q ^n \mid A\mathbf {y} \le \mathbf {0}\}\). Polyhedra also have a generator representation in terms of vertices and rays, written as \({\mathcal P} = \mathrm {conv.hull}\{\mathbf {x}_1,\dots ,\mathbf {x}_m\} + \mathrm {cone}\{\mathbf {y}_1,\dots ,\mathbf {y}_t\} \). This means that \(\mathbf {x}\in {\mathcal P}\) iff \(\mathbf {x} = \sum _{i=1}^m a_i\cdot \mathbf {x}_i + \sum _{j=1}^t b_j\cdot \mathbf {y}_j\) for some rationals \(a_i,b_j\ge 0\), where \(\sum _{i=1}^m a_i = 1\). Note that \(\mathbf {y}_1,\dots ,\mathbf {y}_t\) are the recession directions of \({\mathcal P}\), i.e., \(\mathbf {y}\in {\mathtt {rec.cone}}({\mathcal P})\) iff \(\mathbf {y}=\sum _{j=1}^t b_j \cdot \mathbf {y}_j\) for some rationals \(b_j\ge 0\). For a given polyhedron \({\mathcal P} \subseteq \mathbb Q ^n\) we let \(I({{\mathcal P}})\) be \({\mathcal P} \cap \mathbb Z ^n\), i.e., the set of integer points of \({\mathcal P}\). The integer hull of \({\mathcal P}\), commonly denoted by \({{\mathcal P}}_I\), is defined as the convex hull of \(I({{\mathcal P}})\).
A rational convex polyhedron \({\mathcal P} \subseteq \mathbb Q ^n\) (polyhedron for short) is the set of solutions of a set of inequalities \(A\mathbf {x} \le \mathbf {b}\), namely \({\mathcal P}=\{ \mathbf {x}\in \mathbb Q ^n \mid A\mathbf {x} \le \mathbf {b} \}\), where \(A \in \mathbb Q ^{m \times n}\) is a rational matrix of n columns and m rows, \(\mathbf {x}\in \mathbb Q ^n\) and \(\mathbf {b} \in \mathbb Q ^m\) are column vectors of n and m rational values respectively. We say that \({\mathcal P}\) is specified by \(A\mathbf {x} \le \mathbf {b}\). If \(\mathbf {b}=\mathbf {0}\), then \({\mathcal P}\) is a cone. The set of recession directions of a polyhedron \({\mathcal P}\) specified by \(A\mathbf {x} \le \mathbf {b}\), also known as its recession cone, is the set \({\mathtt {rec.cone}}({\mathcal P}) = \{ \mathbf {y}\in \mathbb Q ^n \mid A\mathbf {y} \le \mathbf {0}\}\). Polyhedra also have a generator representation in terms of vertices and rays, written as \({\mathcal P} = \mathrm {conv.hull}\{\mathbf {x}_1,\dots ,\mathbf {x}_m\} + \mathrm {cone}\{\mathbf {y}_1,\dots ,\mathbf {y}_t\} \). This means that \(\mathbf {x}\in {\mathcal P}\) iff \(\mathbf {x} = \sum _{i=1}^m a_i\cdot \mathbf {x}_i + \sum _{j=1}^t b_j\cdot \mathbf {y}_j\) for some rationals \(a_i,b_j\ge 0\), where \(\sum _{i=1}^m a_i = 1\). Note that \(\mathbf {y}_1,\dots ,\mathbf {y}_t\) are the recession directions of \({\mathcal P}\), i.e., \(\mathbf {y}\in {\mathtt {rec.cone}}({\mathcal P})\) iff \(\mathbf {y}=\sum _{j=1}^t b_j \cdot \mathbf {y}_j\) for some rationals \(b_j\ge 0\). For a given polyhedron \({\mathcal P} \subseteq \mathbb Q ^n\) we let \(I({{\mathcal P}})\) be \({\mathcal P} \cap \mathbb Z ^n\), i.e., the set of integer points of \({\mathcal P}\). The integer hull of \({\mathcal P}\), commonly denoted by \({{\mathcal P}}_I\), is defined as the convex hull of \(I({{\mathcal P}})\).
Let \({\mathcal P}\subseteq \mathbb Q ^{n+m}\) be a polyhedron, and let \(\bigl ({\begin{matrix}{\mathbf {x}}\\ {\mathbf {y}}\end{matrix}}\bigr ) \in {\mathcal P}\) be such that \(\mathbf {x}\in \mathbb Q ^{n}\) and \(\mathbf {y}\in \mathbb Q ^{m}\). The projection of \({\mathcal P}\) onto the \(\mathbf {x}\)-space is defined as \({\mathtt {proj}_{\mathbf {x}}{({\mathcal P})}}=\{\mathbf {x}\in \mathbb Q ^n \mid \exists \mathbf {y}\in \mathbb Q ^{m} ~\text{ such } \text{ that }~ \bigl ({\begin{matrix}{\mathbf {x}}\\ {\mathbf {y}}\end{matrix}}\bigr ) \in {\mathcal P}\}\). We will need the following lemmas later.
Lemma 1
\({\mathtt {proj}_{\mathbf {x}}{({\mathtt {rec.cone}}({\mathcal P}))}} = {\mathtt {rec.cone}}({\mathtt {proj}_{\mathbf {x}}{({\mathcal P})}}) \).
Proof
A polyhedron \({\mathcal P}\) whose variables are split into two sets, \(\mathbf {x}\) and \(\mathbf {y}\), can be represented in the form \(A\mathbf {x} + G\mathbf {y} \le \mathbf {b}\) for matrices A, G and a vector \(\mathbf {b}\) of matching dimensions. Then [13, Theorem 11.11] states that \({\mathtt {proj}_{\mathbf {x}}{({\mathcal P})}}\) is specified by the constraints \(V(\mathbf {b} - A\mathbf {x}) \ge \mathbf {0}\) for a certain matrix V determined by G only. From this it follows that \({\mathtt {rec.cone}}({\mathtt {proj}_{\mathbf {x}}{({\mathcal P})}}) = \{ \mathbf {x} \ : \ V\!A\mathbf {x} \le \mathbf {0} \}\). But we can also apply the theorem to \({\mathtt {rec.cone}}({\mathcal P})\), which is specified by \(A\mathbf {x} + G\mathbf {y} \le \mathbf {0}\), and we get the same result \({\mathtt {proj}_{\mathbf {x}}{({\mathtt {rec.cone}}({\mathcal P}))}} = \{ \mathbf {x} \ : \ V\!A\mathbf {x} \le \mathbf {0} \}\). \(\square \)
Lemma 2
(Lemma 1 in [6]). Given a polyhedron \({\mathcal P}\ne \emptyset \), and linear functions \(\rho _1,\ldots ,\rho _k\) such that
-
(i)
\(\mathbf {x}\in {\mathcal P} \rightarrow \rho _1(\mathbf {x})> 0 \vee \cdots \vee \rho _{k-1}(\mathbf {x}) > 0 \vee \rho _k(\mathbf {x}) \ge 0\)
-
(ii)
\(\mathbf {x}\in {\mathcal P} \not \rightarrow \rho _1(\mathbf {x})> 0 \vee \cdots \vee \rho _{k-1}(\mathbf {x}) > 0\)
There exist nonnegative constants \(\mu _1,\ldots ,\mu _{k-1}\) such that \(\mathbf {x}\in {\mathcal P} \rightarrow \mu _1 \rho _1(\mathbf {x})+\cdots + \mu _{k-1} \rho _{k-1}(\mathbf {x})+ \rho _{k}(\mathbf {x}) \ge 0\).
 A single-path linear-constraint loop (\( SLC \) loop) over n variables \(x_1,\ldots ,x_n\) has the form
A single-path linear-constraint loop (\( SLC \) loop) over n variables \(x_1,\ldots ,x_n\) has the form
where  and
and  are column vectors, and for some \(p,q>0\), \(B \in {\mathbb Q}^{p\times n}\), \(A,A'\in {\mathbb Q}^{q\times n}\), \(\mathbf {b}\in {\mathbb Q}^p\), \(\mathbf {c}\in {\mathbb Q}^q\). The constraint \(B\mathbf {x} \le \mathbf {b}\) is called the loop guard and the other constraint is called the update. The update is deterministic if, for any given \(\mathbf {x}\) (satisfying the guard) there is at most one \(\mathbf {x}'\) satisfying the update, and is affine linear if it can be rewritten as \( \mathbf {x}' = U\mathbf {x} + \mathbf {c} \). We say that there is a transition from a state \(\mathbf {x}\in \mathbb Q ^n\) to a state \(\mathbf {x}'\in \mathbb Q ^n\), if \(\mathbf {x}\) satisfies the loop condition and \(\mathbf {x}\) and \(\mathbf {x}'\) satisfy the update constraint. A transition can be seen as a point \(\bigl ({\begin{matrix}{\mathbf {x}}\\ {\mathbf {x}'}\end{matrix}}\bigr ) \in \mathbb Q ^{2n}\), where its first n components correspond to \(\mathbf {x}\) and its last n components to \(\mathbf {x}'\). For ease of notation, we denote \(\bigl ({\begin{matrix}{\mathbf {x}}\\ {\mathbf {x}'}\end{matrix}}\bigr )\) by \(\mathbf {x}''\). The set of all transitions \(\mathbf {x}''\in \mathbb Q ^{2n}\), of a given \( SLC \) loop, will be denoted by \({\mathcal Q}\) and is specified by the set of inequalities \(A'' \mathbf {x}'' \le \mathbf {c}''\) where
are column vectors, and for some \(p,q>0\), \(B \in {\mathbb Q}^{p\times n}\), \(A,A'\in {\mathbb Q}^{q\times n}\), \(\mathbf {b}\in {\mathbb Q}^p\), \(\mathbf {c}\in {\mathbb Q}^q\). The constraint \(B\mathbf {x} \le \mathbf {b}\) is called the loop guard and the other constraint is called the update. The update is deterministic if, for any given \(\mathbf {x}\) (satisfying the guard) there is at most one \(\mathbf {x}'\) satisfying the update, and is affine linear if it can be rewritten as \( \mathbf {x}' = U\mathbf {x} + \mathbf {c} \). We say that there is a transition from a state \(\mathbf {x}\in \mathbb Q ^n\) to a state \(\mathbf {x}'\in \mathbb Q ^n\), if \(\mathbf {x}\) satisfies the loop condition and \(\mathbf {x}\) and \(\mathbf {x}'\) satisfy the update constraint. A transition can be seen as a point \(\bigl ({\begin{matrix}{\mathbf {x}}\\ {\mathbf {x}'}\end{matrix}}\bigr ) \in \mathbb Q ^{2n}\), where its first n components correspond to \(\mathbf {x}\) and its last n components to \(\mathbf {x}'\). For ease of notation, we denote \(\bigl ({\begin{matrix}{\mathbf {x}}\\ {\mathbf {x}'}\end{matrix}}\bigr )\) by \(\mathbf {x}''\). The set of all transitions \(\mathbf {x}''\in \mathbb Q ^{2n}\), of a given \( SLC \) loop, will be denoted by \({\mathcal Q}\) and is specified by the set of inequalities \(A'' \mathbf {x}'' \le \mathbf {c}''\) where
and B, A, \(A'\), \(\mathbf {c}\) and \(\mathbf {b}\) are those of (2). We call \({\mathcal Q}\) the transition polyhedron. An integer loop is a \( SLC \) loop restricted to integer values, i.e., the set of transitions is \(I({{\mathcal Q}})\).
 An affine linear function \(\rho : \mathbb Q ^n \rightarrow \mathbb Q \) is a function of the form \(\rho (\mathbf {x}) = \vec {a}\cdot \mathbf {x} + b\) where \(\vec {a}\in \mathbb Q ^n\) is a row vector and \(b\in \mathbb Q \). For a given function \(\rho \), we define the function \(\varDelta \rho :\mathbb Q ^{2n}\mapsto \mathbb Q \) as \(\varDelta \rho (\mathbf {x}'')=\rho (\mathbf {x})-\rho (\mathbf {x}')\).
An affine linear function \(\rho : \mathbb Q ^n \rightarrow \mathbb Q \) is a function of the form \(\rho (\mathbf {x}) = \vec {a}\cdot \mathbf {x} + b\) where \(\vec {a}\in \mathbb Q ^n\) is a row vector and \(b\in \mathbb Q \). For a given function \(\rho \), we define the function \(\varDelta \rho :\mathbb Q ^{2n}\mapsto \mathbb Q \) as \(\varDelta \rho (\mathbf {x}'')=\rho (\mathbf {x})-\rho (\mathbf {x}')\).
Definition 1
Given a set of transitions \(T\subseteq \mathbb Q ^{2n}\), we say that \(\tau =\langle \rho _1,\dots ,\rho _d \rangle \) is a M\(\varPhi \)RF (of depth d) for T if for every \(\mathbf {x}'' \in T\) there is index i such that:
We say that \(\mathbf {x}''\) is ranked by \(\rho _i\) (for the minimal such i).
It is not hard to see that a M\(\varPhi \)RF \(\langle \rho _1 \rangle \) of depth \(d=1\) is a linear ranking function (\( LRF \)). If the M\(\varPhi \)RF is of depth \(d>1\), it implies that if \(\rho _1(\mathbf {x}) \ge 0\), transition \(\mathbf {x}''\) is ranked by \(\rho _1\), while if \(\rho _1(\mathbf {x}) < 0\), \(\langle \rho _2,\dots ,\rho _d \rangle \) becomes a M\(\varPhi \)RF. This agrees with the intuitive notion of “phases.” We say that \(\tau \) is irredundant if removing any component invalidates the M\(\varPhi \)RF. Finally, it is convenient to allow an empty tuple as a M\(\varPhi \)RF, of depth 0, for the empty set.
The decision problem Existence of a \(M{\varPhi }RF \) asks to determine whether a given \( SLC \) loop admits a M\(\varPhi \)RF. The bounded decision problem restricts the search to M\(\varPhi \)RFs of depth at most d, where d is part of the input.
 A recurrent set is a set of states that witnesses nontermination of a given \( SLC \) loop \({\mathcal Q}\). It is commonly defined as a set of states \(S \subseteq {\mathtt {proj}_{\mathbf {x}}{({\mathcal Q})}}\) where for any \(\mathbf {x}\in S\) there is \(\mathbf {x}'\in S\) such that \((\mathbf {x},\mathbf {x}') \in {\mathcal Q}\). This clearly proves the existence of an infinite run. In this article we use a slightly different notion.
A recurrent set is a set of states that witnesses nontermination of a given \( SLC \) loop \({\mathcal Q}\). It is commonly defined as a set of states \(S \subseteq {\mathtt {proj}_{\mathbf {x}}{({\mathcal Q})}}\) where for any \(\mathbf {x}\in S\) there is \(\mathbf {x}'\in S\) such that \((\mathbf {x},\mathbf {x}') \in {\mathcal Q}\). This clearly proves the existence of an infinite run. In this article we use a slightly different notion.
Definition 2
Give a \( SLC \) loop \({\mathcal Q}\), we say that \(S \subseteq {\mathcal Q}\) is a recurrent set of transitions if \({\mathtt {proj}_{\mathbf {x}'}{(S)}} \subseteq {\mathtt {proj}_{\mathbf {x}}{(S)}}\).
Clearly, both notions are equivalent: if S is a recurrent set of transitions then \({\mathtt {proj}_{\mathbf {x}}{(S)}}\) is a recurrent set of states, and if S is a recurrent set of states then \({\mathcal Q}\cap (S\times S)\) is a recurrent set of transitions. Note that both notions correspond to what is known as existential recurrent sets, i.e., they guarantee the existence of nonterminating runs starting in some initial states, however, due to nondeterminism, these initial states might have terminating runs as well.
3 An Algorithm for Inferring M\(\varPhi \)RFs
In this section we describe our algorithm for deciding the existence of (and constructing) M\(\varPhi \)RFs, which is also able to find recurrent sets for certain nonterminating \( SLC \) loops. In what follows we assume a given \( SLC \) loop \({\mathcal Q}\) where variables range over the rationals (or reals), the case of integer variables is discussed after considering the rational case.
Let us start with an intuitive description of the algorithm and its possible outcomes. Our work started with the following crucial observation: given linear functions \(\rho _1,\ldots ,\rho _l\) such that
-
\(\rho _1,\ldots ,\rho _l\) are nonnegative over \({\mathtt {proj}_{\mathbf {x}}{({\mathcal Q})}}\), i.e., over all enabled states;
-
for some \(\rho _i\), we have \(\varDelta \rho _i(\mathbf {x}'')>0\) for at least one transition \(\mathbf {x}''\in {\mathcal Q}\); and
-
\({\mathcal Q}'={\mathcal Q}\wedge \varDelta \rho _1(\mathbf {x}'')\le 0\wedge \cdots \wedge \varDelta \rho _l(\mathbf {x}'')\le 0\) has a M\(\varPhi \)RF of depth d
then \({\mathcal Q}\) has a M\(\varPhi \)RF of depth at most \(d+1\). The proof of this observation is constructive, i.e., given a M\(\varPhi \)RF \(\tau '\) for \({\mathcal Q}'\), we can construct a M\(\varPhi \)RF \(\tau \) for \({\mathcal Q}\) using conic combinations of the components of \(\tau '\) and \(\rho _1,\ldots ,\rho _l\).
Let us assume that we have a procedure \({F}({\mathcal Q})\) that picks some candidate functions \(\rho _1,\ldots ,\rho _l\), i.e., nonnegative over \({\mathtt {proj}_{\mathbf {x}}{({\mathcal Q})}}\), and computes \({F}({\mathcal Q})={\mathcal Q}\wedge \varDelta \rho _1(\mathbf {x}'')\le 0\wedge \cdots \wedge \varDelta \rho _l(\mathbf {x}'')\le 0\). Clearly, if \({F}^{d}({\mathcal Q})=\emptyset \), for some \(d>0\), then using the above observation we can conclude that \({\mathcal Q}\) has a M\(\varPhi \)RF of depth at most d. Obviously, the difficult part in defining \(F\) is how to pick functions \(\rho _1,\ldots ,\rho _l\), and, moreover, how to ensure that if \({\mathcal Q}\) has a M\(\varPhi \)RF of optimal depth d then \({F}^{d}({\mathcal Q})=\emptyset \), i.e., to find the optimal depth. For this, we observe that the set of all nonnegative functions over \({\mathtt {proj}_{\mathbf {x}}{({\mathcal Q})}}\) is a polyhedral cone, and thus it has generators \(\rho _1,\ldots ,\rho _l\) that can be effectively computed. These \(\rho _1,\ldots ,\rho _l\) turn out to be the right candidates to use. In addition, when using these candidates, we prove that if we cannot make progress, i.e., we get \({F}^{i-1}({\mathcal Q})={F}^{i}({\mathcal Q})\), then we have actually reached a recurrent set that witnesses nontermination.
In Sect. 3.1 we present the algorithm and discuss how it is used to decide existence of M\(\varPhi \)RFs; in Sect. 3.2 we discuss how the algorithm can infer recurrent sets; and in Sect. 3.3 we discuss cases where the algorithm does not terminate and raise some questions on what happens in the limit.
3.1 Deciding Existence of M\(\varPhi \)RFs
Definition 3
The set of all nonnegative functions over a polyhedron \({\mathcal S} \subseteq \mathbb Q ^n\), is defined as \({{\mathcal S}}^{\#}= \{ (\vec {a},b) \in \mathbb Q ^{n+1} \mid \forall \mathbf {x}\in {\mathcal S}.~\vec {a}\cdot \mathbf {x}+b \ge 0 \}.\)
It is known that \({{\mathcal S}}^{\#}\) is a polyhedral cone [32, p. 112]. Equivalently, it is generated by a finite set of rays \((\vec {a}_1,b_1),\ldots ,(\vec {a}_l,b_l)\). The cone generated by \(\vec {a}_1,\ldots ,\vec {a}_l\) is known as the dual of the cone \({\mathtt {rec.cone}}({\mathcal S})\) – we make use of this in Sect. 4. These rays are actually the ones that are important for the algorithm, as can be seen in the definition below, however, in the definition of \({{\mathcal S}}^{\#}\) we included the \(b_i\)’s as they makes some statements smoother. Since \({\mathcal S}\) is a closed convex set, it is known that it is equal to the intersection of all half-spaces defined by the elements of \({{\mathcal S}}^{\#}\), i.e., \({\mathcal S}=\wedge \{ \vec {a}\cdot \mathbf {x}+b \ge 0 \mid (\vec {a},b)\in {{\mathcal S}}^{\#}\}\).
Definition 4
Let \({\mathcal Q}\) be a \( SLC \) loop, and define
where \((\vec {a}_1,b_1),\ldots ,(\vec {a}_l,b_l)\) are the generators of \({{\mathtt {proj}_{\mathbf {x}}{({\mathcal Q})}}}^{\#}\).
It is easy to see that each \(\vec {a}_i\cdot \mathbf {x}-\vec {a}_i\cdot \mathbf {x}'\le 0\) above is actually \(\varDelta \rho _i(\mathbf {x}'')\le 0\) where \(\rho _i=\vec {a}_i\cdot \mathbf {x}+b_i\le 0\). Intuitively, \({F}({\mathcal Q})\) removes from \({\mathcal Q}\) all transitions \(\mathbf {x}''\) for which there is \((\vec {a},b) \in {{\mathtt {proj}_{\mathbf {x}}{({\mathcal Q})}}}^{\#}\) such that \(\vec {a}\cdot \mathbf {x}-\vec {a}\cdot \mathbf {x}' > 0\). This is because any \((\vec {a},b) \in {{\mathtt {proj}_{\mathbf {x}}{({\mathcal Q})}}}^{\#}\) is a conic combination of \((\vec {a}_1,b_1),\ldots ,(\vec {a}_l,b_l)\), and thus for some i we must have \(\vec {a}_i\cdot \mathbf {x}-\vec {a}_i\cdot \mathbf {x}'> 0\), otherwise we would have \(\vec {a}\cdot \mathbf {x}-\vec {a}\cdot \mathbf {x}'=0\).
Example 1
Consider Loop (1), whose transition polyhedron is defined by \({\mathcal Q}= \{ x_1 \ge -x_3, x_1'= x_1 + x_2,\ x_2'=x_2+x_3,\ x_3'=x_3-1\}\). The generators of \({{\mathtt {proj}_{\mathbf {x}}{({\mathcal Q})}}}^{\#}\) are \(\{(1,0,1,0),(0,0,0,1)\}\)—the last component of each generator is the free constant b, and the rest is \(\vec {a}\). The corresponding nonnegative functions are \(\rho _1(x_1,x_2,x_3)=x_1+x_3\) and \(\rho _2(x_1,x_2,x_3)=1\). Computing \({F}({\mathcal Q})\) results in:
This eliminates any transition for which the quantity \(x_1+x_3\) decreases. \(\square \)
In what follows we aim at showing that \({\mathcal Q}\) has a M\(\varPhi \)RF of optimal depth d iff \({F}^{d}({\mathcal Q})=\emptyset \). We first state some auxiliary lemmas.
Lemma 3
If \({\mathcal Q}'={F}({\mathcal Q})\) has a M\(\varPhi \)RF of depth at most d, then \({\mathcal Q}\) has a M\(\varPhi \)RF of depth at most \(d+1\).
Proof
Consider the generators \((\vec {a}_1,b_1),\ldots ,(\vec {a}_l,b_l)\) used in Definition 4, and let \(\rho _i(\mathbf {x})=\vec {a}_i\cdot \mathbf {x}+b_i\). We have \({\mathcal Q}'={\mathcal Q}\wedge \varDelta \rho _1(\mathbf {x}'')\le 0 \wedge \cdots \wedge \varDelta \rho _l(\mathbf {x}'')\le 0\). Let \(\tau =\langle g_1,\ldots ,g_d \rangle \) be a M\(\varPhi \)RF for \({\mathcal Q}'\), and w.l.o.g. assume that it is of optimal depth. Next, we show how to construct a M\(\varPhi \)RF \(\langle g_1'+1,\ldots ,g_d'+1,g_{d+1} \rangle \) for \({\mathcal Q}\). Note that simply appending \(\rho _1,\ldots ,\rho _l\) to \(\tau \) does not always produce a M\(\varPhi \)RF for \({\mathcal Q}\), since the components of \(\tau \) are not guaranteed to decrease over \({\mathcal Q}\setminus {\mathcal Q}'\).
If \(g_1\) is decreasing over \({\mathcal Q}\), we define \(g_1'(\mathbf {x})=g_1(\mathbf {x})\), otherwise we have
and by Lemma 2 there are nonnegative constants \(\mu _1,\ldots ,\mu _l\) such that
Define \(g_1'(\mathbf {x})=g_1(\mathbf {x})+\sum _{i=1}^l \mu _i \rho _i(\mathbf {x})\). Clearly, \(\mathbf {x}''\in {\mathcal Q}\rightarrow \varDelta g_1'(\mathbf {x}'') \ge 1\). Moreover, since \(\rho _1,\ldots ,\rho _l\) are nonnegative on all enabled states, \(g_1'\) is nonnegative on the states on which \(g_1\) is nonnegative. If \(d>1\), we proceed with
If \(g_2\) is decreasing over \({\mathcal Q}^{(1)}\), let \(g_2'=g_2\), otherwise, since transitions in \({\mathcal Q}'\cap {\mathcal Q}^{(1)}\) are ranked by \(\langle g_2,\dots ,g_d \rangle \) we have
and again by Lemma 2 we can construct the desired \(g_2'\) as we did for \(g_1'\). In general, for any \(j\le d\) we construct \(g_{j+1}'\) such that \(\varDelta g_{j+1}'(\mathbf {x}'') \ge 1\) over
and \(\mathbf {x}''\in {\mathcal Q}\wedge g_j(\mathbf {x}) \ge 0 \rightarrow g_j'(\mathbf {x}) \ge 0\). Finally we define
and note that
We assume that no \(\rho _i\) is redundant in (15), otherwise we take an irredundant subset. Now from (15) we get
and since the left-hand side is a polyhedron, there is a constant \(c>0\) such that
W.l.o.g. we may assume that \(c \ge 1\), otherwise we divide \(\rho _l\) by c. Then we have
By Lemma 2 we can construct \(g_{d+1} = \rho _l+\sum _{i=1}^{l-1}\mu _i\rho _i\) such that \(\mathbf {x}''\in {\mathcal Q}^{(d)} \rightarrow \varDelta g_{d+1}(\mathbf {x}'')\ge 1\). Moreover, \(g_{d+1}\) is nonnegative over \({\mathcal Q}^{(d)}\) and thus it ranks all \( {\mathcal Q}^{(d)}\). Now, by construction, \(\tau '=\langle g_1'+1,\dots ,g_d'+1,g_{d+1} \rangle \) is a M\(\varPhi \)RF for \({\mathcal Q}\). \(\square \)
Lemma 4
If \({\mathcal Q}\) has a M\(\varPhi \)RF of depth d then \({\mathcal Q}'={F}({\mathcal Q})\) has a M\(\varPhi \)RF of depth at most \(d-1\).
Proof
Let \(\tau =\langle \rho _1,\ldots ,\rho _k \rangle \) be an M\(\varPhi \)RF for \({\mathcal Q}\), of optimal depth \(k\le d\). As shown in [6], there is no loss of generality in assuming a special form of M\(\varPhi \)RF (nested M\(\varPhi \)RF [25]) in which the last component is nonnegative; so we assume \(\rho _k(\mathbf {x})\ge 0\) over \({\mathtt {proj}_{\mathbf {x}}{({\mathcal Q})}}\). Clearly \(\tau '=\langle \rho _1,\ldots ,\rho _{k-1} \rangle \) is a M\(\varPhi \)RF for \({\mathcal Q}\wedge \varDelta \rho _k(\mathbf {x}'')\le 0\). Now since \(\rho _k\) is a conic combination of the generators of \({{\mathtt {proj}_{\mathbf {x}}{({\mathcal Q})}}}^{\#}\) we have \({\mathcal Q}'={F}({\mathcal Q}) \subseteq {\mathcal Q}\wedge \varDelta \rho _k(\mathbf {x}'')\le 0\) and thus \(\tau '\) is a M\(\varPhi \)RF for \({\mathcal Q}'\) as well. \(\square \)
Lemma 5
\({\mathcal Q}\) has a M\(\varPhi \)RF of depth d iff \({F}^{d}({\mathcal Q})=\emptyset \).
Proof
For the first direction, suppose that \({\mathcal Q}\) has a M\(\varPhi \)RF of depth at most d, then applying Lemma 4 iteratively we must reach \({F}^{k}({\mathcal Q})=\emptyset \) for some \(k \le d\), thus \({F}^{d}({\mathcal Q})=\emptyset \). For the other direction, suppose \({F}^{d}({\mathcal Q})=\emptyset \), then using Lemma 3 we can construct a M\(\varPhi \)RF of depth d. \(\square \)

Procedure  of Algorithm 1 implements the above idea, it basically applies \(F\) (lines 3–4) iteratively until it either reaches an empty set (Line 1) or stabilizes (Line 5). If it returns \(\emptyset \) then \({\mathcal Q}\) has a M\(\varPhi \)RF and we can construct one simply by invoking the polynomial-time procedure for synthesizing nested M\(\varPhi \)RFs as described in [6], or construct one as in the proof of Lemma 3. Note that, by Lemma 5, if we bound the recursion depth by a parameter d, then the algorithm is actually a decision procedure for the existence of M\(\varPhi \)RFs of depth at most d. The case in which it returns a nonempty set is discussed in Sect. 3.2.
of Algorithm 1 implements the above idea, it basically applies \(F\) (lines 3–4) iteratively until it either reaches an empty set (Line 1) or stabilizes (Line 5). If it returns \(\emptyset \) then \({\mathcal Q}\) has a M\(\varPhi \)RF and we can construct one simply by invoking the polynomial-time procedure for synthesizing nested M\(\varPhi \)RFs as described in [6], or construct one as in the proof of Lemma 3. Note that, by Lemma 5, if we bound the recursion depth by a parameter d, then the algorithm is actually a decision procedure for the existence of M\(\varPhi \)RFs of depth at most d. The case in which it returns a nonempty set is discussed in Sect. 3.2.
The complexity of Algorithm 1 is exponential since computing the generators at Line 3 might take exponential time. In Sect. 4 we provide a polynomial-time implementation that avoids computing the generators.
Example 2
Let us apply Algorithm 1 to Loop (1). We start by calling
 with \({\mathcal Q}=\{x_1\ge -x_3, x_1'=x_1+x_2, x_2'=x_2+x_3, x_3'=x_3-1\}\) and proceed as follows (\({\mathcal Q}_i\) represents the polyhedron passed in the i-th call to
with \({\mathcal Q}=\{x_1\ge -x_3, x_1'=x_1+x_2, x_2'=x_2+x_3, x_3'=x_3-1\}\) and proceed as follows (\({\mathcal Q}_i\) represents the polyhedron passed in the i-th call to
 ):
):

Explanation:
-
\({\mathcal Q}_0\) is not empty. We compute the generators of \({{\mathtt {proj}_{\mathbf {x}}{({\mathcal Q}_0)}}}^{\#}\), which define the nonnegative functions \(\rho _1(x_1,x_2,x_3)=x_1+x_3\) and \(\rho _2(x_1,x_2,x_3)=1\), and then compute \({\mathcal Q}_1={\mathcal Q}_0\wedge \varDelta \rho _1(\mathbf {x}'') \le 0 \wedge \varDelta \rho _2(\mathbf {x}'') \le 0\); and since it differs from \({\mathcal Q}_0\) we recursively call
 .
. -
\({\mathcal Q}_1\) is not empty. We compute the generators of \({{\mathtt {proj}_{\mathbf {x}}{({\mathcal Q}_1)}}}^{\#}\), which define the nonnegative function \(\rho _3(x_1,x_2,x_3)=x_2-1\), and then compute \({\mathcal Q}_2={\mathcal Q}_1\wedge \varDelta \rho _3(\mathbf {x}'')\le 0\); and since it differs from \({\mathcal Q}_1\) we recursively call
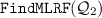 . Note that the only new generator wrt. the previous iteration is the one in bold font, the others are ignored as they have been used for computing \({\mathcal Q}_1\).
. Note that the only new generator wrt. the previous iteration is the one in bold font, the others are ignored as they have been used for computing \({\mathcal Q}_1\). -
\({\mathcal Q}_2\) is not empty. We compute the generators of \({{\mathtt {proj}_{\mathbf {x}}{({\mathcal Q}_2)}}}^{\#}\), which define the nonnegative function \(\rho _4(x_1,x_2,x_3)=x_3\), and then compute \({\mathcal Q}_3={\mathcal Q}_2\wedge \varDelta \rho _4(\mathbf {x}'')\le 0\); and since it differs from \({\mathcal Q}_2\) we recursively call
 .
. -
\({\mathcal Q}_3\) is empty, so we return \(\emptyset \).
Since we have reached an empty set in 3 iterations, we conclude that Loop (1) has a M\(\varPhi \)RF of optimal depth 3, e.g., \(\langle x_3+1,x_2+1,x_1+x_3+1 \rangle \). \(\square \)
For the case of integer-valued variables, i.e., when considering \(I({{\mathcal Q}})\), it is know that \(I({{\mathcal Q}})\) has a M\(\varPhi \)RF iff the integer hull \({{\mathcal Q}}_I\) of \({\mathcal Q}\) has a M\(\varPhi \)RF (over the rationals) [6, Sect. 5]. Thus, \(I({{\mathcal Q}})\) has a M\(\varPhi \)RF of depth d iff \({F}^{d}({{\mathcal Q}}_I)=\emptyset \).
3.2 Inference of Recurrent Sets
Next we discuss the case in which  returns a nonempty set of transition \({\mathcal S} \subseteq {\mathcal Q}\) (Line 5), and show that \({\mathcal S}\) is always a recurrent set, implying that \({\mathcal Q}\) is nonterminating. In Sect. 5 we discuss an experimental evaluation regarding the use of Algorithm 1 for proving nontermination of control-flow graphs.
returns a nonempty set of transition \({\mathcal S} \subseteq {\mathcal Q}\) (Line 5), and show that \({\mathcal S}\) is always a recurrent set, implying that \({\mathcal Q}\) is nonterminating. In Sect. 5 we discuss an experimental evaluation regarding the use of Algorithm 1 for proving nontermination of control-flow graphs.
Lemma 6
Let \({\mathcal S}\subseteq \mathbb Q ^{2n}\) be a polyhedron, if \({\mathcal S}={F}({\mathcal S})\) then \({\mathcal S}\) is a recurrent set.
Proof
According Definition 2, we need to show that \({\mathtt {proj}_{\mathbf {x}'}{({\mathcal S})}} \subseteq {\mathtt {proj}_{\mathbf {x}}{({\mathcal S})}}\). Since \({\mathtt {proj}_{\mathbf {x}}{({\mathcal S})}}\) and \({\mathtt {proj}_{\mathbf {x}'}{({\mathcal S})}}\) are closed convex sets, each is an intersection of half-spaces that are defined by the corresponding sets \({{\mathtt {proj}_{\mathbf {x}}{({\mathcal S})}}}^{\#}\) and \({{\mathtt {proj}_{\mathbf {x}'}{({\mathcal S})}}}^{\#}\), e.g., \({\mathtt {proj}_{\mathbf {x}}{({\mathcal S})}} = \wedge \{ \vec {a}\cdot \mathbf {x}+b \ge 0 \mid (\vec {a},b)\in {{\mathtt {proj}_{\mathbf {x}}{({\mathcal S})}}}^{\#}\}\). Thus, it is enough to show that \({{\mathtt {proj}_{\mathbf {x}}{({\mathcal S})}}}^{\#} \subseteq {{\mathtt {proj}_{\mathbf {x}'}{({\mathcal S})}}}^{\#}\).
Let \((\vec {a},b) \in {{\mathtt {proj}_{\mathbf {x}}{({\mathcal S})}}}^{\#}\), we show that \((\vec {a},b) \in {{\mathtt {proj}_{\mathbf {x}'}{({\mathcal S})}}}^{\#}\) as well. Define \(\rho (\mathbf {x}) = \vec {a}\cdot {\mathbf {x}} + b\). Since \({\mathcal S}={F}({\mathcal S})\), by definition of \(F\) we have
which together with the fact that \(\rho \) is nonnegative over \({\mathtt {proj}_{\mathbf {x}}{({\mathcal S})}}\) implies that \(\rho (\mathbf {x}') \ge 0\) holds for any \(\mathbf {x}'\in {\mathtt {proj}_{\mathbf {x}'}{({\mathcal S})}}\), and thus \((\vec {a},b) \in {\mathtt {proj}_{\mathbf {x}'}{({\mathcal S})}}\). \(\square \)
Corollary 1
If  returns \({\mathcal S} \ne \emptyset \) then \({\mathcal S}\) is a recurrent set, and thus \({\mathcal Q}\) is nonterminating.
returns \({\mathcal S} \ne \emptyset \) then \({\mathcal S}\) is a recurrent set, and thus \({\mathcal Q}\) is nonterminating.
Proof
This follows from Lemma 6, since the algorithm returns a nonempty set \({\mathcal S} \subseteq {\mathcal Q}\) iff it finds one such that \({\mathcal S}={F}({\mathcal S})\) (Line 5 of
 ). \(\square \)
). \(\square \)
Example 3
Let us apply Algorithm 1 to the following loop, from [34]:
This loop does not terminate, e.g., for \(x_1=-1, x_2=-2\). We call
 with \({\mathcal Q}=\{x_1-x_2\ge 1, x_1'=-x_1+x_2,x_2'=x_2\}\), and proceed as in Example 2:
with \({\mathcal Q}=\{x_1-x_2\ge 1, x_1'=-x_1+x_2,x_2'=x_2\}\), and proceed as in Example 2:

Explanation:
-
\({\mathcal Q}_0\) is not empty. We compute the generators of \({{\mathtt {proj}_{\mathbf {x}}{({\mathcal Q}_0)}}}^{\#}\), which define the nonnegative functions \(\rho _1(x_1,x_2,x_3)=x_1-x_2-1\) and \(\rho _2(x_1,x_2,x_3)=1\), and then compute \({\mathcal Q}_1 = {\mathcal Q}_0 \wedge \varDelta \rho _1(\mathbf {x}'')\le 0 \wedge \varDelta \rho _2(\mathbf {x}'')\le 0\); and since it differs from \({\mathcal Q}_0\) we recursively call
 .
. -
\({\mathcal Q}_1\) is not empty. We compute the generators of \({{\mathtt {proj}_{\mathbf {x}}{({\mathcal Q}_1)}}}^{\#}\), which define the nonnegative function \(\rho _3(x_1,x_2,x_3)=-2x_1+x_2\), and then compute \({\mathcal Q}_2 = {\mathcal Q}_1 \wedge \varDelta \rho _3(\mathbf {x}'')\le 0\); and since it differs from \({\mathcal Q}_1\) we invoke
 .
. -
\({\mathcal Q}_2\) is not empty. We compute the generators of \({{\mathtt {proj}_{\mathbf {x}}{({\mathcal Q}_2)}}}^{\#}\), which define the nonnegative functions \(\rho _4(x_1,x_2,x_3)=2x_1-x_2\) and \(\rho _5(x_1,x_2,x_3)=-x_1-1\), and then compute \({\mathcal Q}_3 = {\mathcal Q}_2 \wedge \varDelta \rho _4(\mathbf {x}'')\le 0 \wedge \varDelta \rho _5(\mathbf {x}'') \le 0\); and since it is equal to \({\mathcal Q}_2\) (\(\varDelta \rho _4(\mathbf {x}''){\,\le \,}0\) and \(\varDelta \rho _5(\mathbf {x}'')\,{\le }\, 0\) are implied by \({\mathcal Q}_2\)) we return \({\mathcal Q}_2\).
Thus, \({\mathcal Q}_2\) is a recurrent set of transitions and we conclude that Loop (21) is nonterminating. Projecting \({\mathcal Q}_2\) on \(x_1\) and \(x_2\) we get \(\{x_1 \le -1, 2x_1-x_2=0\}\), which is the corresponding recurrent set of states.
We remark that Loop (21) has a fixed point \((-1,-2)\), i.e., from state \(x_1=-1,x_2=-2\) we have a transition to \(x_1=-1,x_2=-2\). The algorithm also detects nontermination of loops that do not have fixed points. For example, if we change \(x_2'=x_2\) in Loop (21) by \(x_2'=x_2-1\), we obtain a recurrent set of transitions \({\mathcal S}\) such that \({\mathtt {proj}_{\mathbf {x}}{({\mathcal S})}}=\{-2x_2 \ge 3, 4x_1 -2x_2=1\}\). \(\square \)
Now that we have seen the possible outcomes of the algorithm (in case it terminates), we see that this approach reveals an interesting relation between seeking M\(\varPhi \)RFs and seeking recurrent sets. A possible view is that the algorithm seeks a recurrent set (of a particular form) and when it concludes that no such set exists, i.e., reaching \(\emptyset \), we can construct a M\(\varPhi \)RF.
The recurrent sets inferred by Algorithm 1 belong to a narrower class than that of Definition 2. In fact, the condition in Definition 2 is equivalent to requiring that if \(\rho (\mathbf {x}) \ge 0\) over \({\mathtt {proj}_{\mathbf {x}}{({\mathcal S})}}\) then \(\rho (\mathbf {x}) \ge 0\) over \({\mathtt {proj}_{\mathbf {x}'}{({\mathcal S})}}\). In our recurrent sets, we further have \(\rho (\mathbf {x}') \ge \rho (\mathbf {x})\) for any \((\mathbf {x},\mathbf {x}')\in {\mathcal S}\). We call a recurrent set satisfying this stronger condition monotonic.
Example 4
Consider the following \( SLC \) loop:
The largest recurrent set of transitions for this loop is \(\{x \ge 0, x \le 1, x'=1-x\}\), and it is not monotonic. Algorithm 1 infers the largest monotonic recurrent set \(\{x=\frac{1}{2}, x'=\frac{1}{2}\}\), where it first eliminates all transitions for which \(x-x'>0\), i.e., \(x\in (\frac{1}{2},\infty )\), and then those for which \((-x)-(-x')>0\), i.e., \(x\in [0,\frac{1}{2})\). \(\square \)
At this point, it is natural to explore the difference between the two kinds recurrent sets. The most intriguing question is if nonterminating \( SLC \) loops always have monotonic recurrent sets. This is true for loops that have a fixed point, i.e., there is \(\mathbf {x}\) such that \((\mathbf {x},\mathbf {x})\in {\mathcal Q}\), however, this question is left open for the general case. We note that the geometric nontermination argument introduced in [26] is also related to monotonic recurrent sets. Specifically, it is easy to show that in some cases (when the nonnegative coefficients \(\mu _i\) and \(\lambda _i\), in Def. 5 of [26], are either 0 or at least 1), we can construct a monotonic recurrent set.
Let us discuss now the case of integer loops. First, the difference between the two kinds of recurrent sets is clear in the integer case: Loop (22) of Example 4 has a recurrent set of integers \(\{(0,1),(1,0)\}\), but does not have a monotonic recurrent set of integers. Apart from this difference, a natural question is whether the recurrent set \({\mathcal S}\) returned by  , or more precisely \(I({{\mathcal S}})\), witnesses nontermination of \(I({{\mathcal Q}})\). This is not true in general (see Example 5 below), however, there are practical cases for which it is true.
, or more precisely \(I({{\mathcal S}})\), witnesses nontermination of \(I({{\mathcal Q}})\). This is not true in general (see Example 5 below), however, there are practical cases for which it is true.
Lemma 7
Let \({\mathcal Q}\) be a \( SLC \) loop with affine update \(\mathbf {x}'=U\mathbf {x}+\mathbf {c}\), and assume the coefficients of U and \(\mathbf {c}\) are integer. If \({\mathcal S}\) is a recurrent set for \({\mathcal Q}\), and \(I({{\mathcal S}})\) is not empty, then \(I({{\mathcal S}})\) is recurrent for \(I({{\mathcal Q}})\).
Proof
Since the update is affine with integer coefficients, it follows that any state in \({\mathtt {proj}_{\mathbf {x}}{(I({{\mathcal S}}))}}\) has a successor in \({\mathtt {proj}_{\mathbf {x}'}{(I({{\mathcal S}}))}} \subseteq {\mathtt {proj}_{\mathbf {x}}{(I({{\mathcal S}}))}}\), which is the definition of a recurrent set. \(\square \)
In the context of the above lemma, assuming that  , if \({\mathcal S}\ne \emptyset \) and \(I({{\mathcal S}})=\emptyset \) all we can conclude (when the algorithm is applied to \({{\mathcal Q}}_I\)) is that \(I({{\mathcal Q}})\) does not have a M\(\varPhi \)RF, we cannot conclude anything about nontermination as in the rational case. For example, for the loop \({{\mathcal Q}}_I={\mathcal Q}=\{x\ge 0, x'=10-2x\}\) we have \({\mathcal S}=\{(3\frac{1}{3},3\frac{1}{3})\}\) and \(I({{\mathcal S}})=\emptyset \) and the loop is terminating over the integers, and for the loop \({{\mathcal Q}}_I={\mathcal Q}=\{x\ge 0,x'=1-x\}\) we have \({\mathcal S}=\{(\frac{1}{2},\frac{1}{2})\}\) and \(I({{\mathcal S}})=\emptyset \) and the loop is nonterminating over the integers.
, if \({\mathcal S}\ne \emptyset \) and \(I({{\mathcal S}})=\emptyset \) all we can conclude (when the algorithm is applied to \({{\mathcal Q}}_I\)) is that \(I({{\mathcal Q}})\) does not have a M\(\varPhi \)RF, we cannot conclude anything about nontermination as in the rational case. For example, for the loop \({{\mathcal Q}}_I={\mathcal Q}=\{x\ge 0, x'=10-2x\}\) we have \({\mathcal S}=\{(3\frac{1}{3},3\frac{1}{3})\}\) and \(I({{\mathcal S}})=\emptyset \) and the loop is terminating over the integers, and for the loop \({{\mathcal Q}}_I={\mathcal Q}=\{x\ge 0,x'=1-x\}\) we have \({\mathcal S}=\{(\frac{1}{2},\frac{1}{2})\}\) and \(I({{\mathcal S}})=\emptyset \) and the loop is nonterminating over the integers.
The next example demonstrates that the above lemma does not extend to \( SLC \) loops in general, even when the algorithm is applied to the integer hull \({{\mathcal Q}}_I\). This is because it is not guaranteed that any integer state \(\mathbf {x}\in I({{\mathtt {proj}_{\mathbf {x}}{({\mathcal S})}}})\) has an integer successor \(\mathbf {x}'\in I({{\mathtt {proj}_{\mathbf {x}'}{({\mathcal S})}}})\).
Example 5
Consider the following loop
which is nonterminating over the rationals, for any \(x\ge 2\), and is terminating over the integers. For the integer case, the loop stops (or blocks) if for some integer x, there is no integer \(x'\) such that that equality \(x'=\frac{3}{2}x\) holds. The algorithm returns \({\mathcal Q}\) as a recurrent set, but \(I({{\mathcal Q}})\), which is not empty, is not a recurrent set as the loop is terminating over the integers. Note that the transition polyhedron is integral, i.e., \({\mathcal Q}={{\mathcal Q}}_I\). \(\square \)
3.3 Cases in Which Algorithm 1 Does Not Terminate
When Algorithm 1 terminates, it either finds a M\(\varPhi \)RF or proves nontermination of the given loop. This means that if applied to a terminating loop that has no M\(\varPhi \)RF, Algorithm 1 will not terminate, e.g., for the loop \({\mathcal Q}_t=\{x_1\ge x_2, x_2\ge 1, x_1'=2x_1, x_2'=3x_2\}\), which is terminating [25]. Algorithm 1 might also fail to terminate when applied to some nonterminating loops, e.g., the nonterminating loop [26] \({\mathcal Q}_{nt}=\{x_1+x_2 \ge 3, x_1'=3x_1-2,\, x_2'=2x_2\}\).
When the algorithm does not terminate, the iterates \({F}^{i}({\mathcal Q})\) converge to \({\mathcal Q}_\omega =\cap _{i\ge 0}{F}^{i}({\mathcal Q})\). For example, for the terminating loop \({\mathcal Q}_{t}\) above, we have \({\mathcal Q}_\omega =\emptyset \), and for the nonterminating loop \({\mathcal Q}_{nt}\) above, we have \({\mathcal Q}_\omega =\{x_1\ge 1,x_2'=2x_2,\,x_1'=3x_1-2\}\) which is a monotonic recurrent set. Given these examples, we ask: (i) is it true that \({\mathcal Q}_\omega =\emptyset \) iff \({\mathcal Q}\) is terminating? (ii) is it true that if \({\mathcal Q}_\omega \ne \emptyset \) then it is a (monotonic) recurrent set? For deterministic loops, it is easy to show that termination implies \({\mathcal Q}_\omega =\emptyset \), and that if \({\mathcal Q}_\omega \ne \emptyset \) then \({\mathcal Q}_\omega \) is a monotonic recurrent set. The general questions are left open.
4 M\(\varPhi \)RFs and the Displacement Polyhedron
In this section we introduce an alternative representation for \( SLC \) loops, that we refer to as the displacement polyhedron, and show that Algorithm 1, or more precisely the check \({F}^{k}({\mathcal Q})=\emptyset \), has a simple encoding in this representation that can be preformed in polynomial time, specifically, we show that it is equivalent to checking for unsatisfiability of a particular linear constraint system. Note that we already know that deciding the existence of a M\(\varPhi \)RF of depth d can be done in polynomial time [6], so in this sense we do not provide new knowledge. However, apart from the efficient encoding of the check \({F}^{k}({\mathcal Q})=\emptyset \), the new formulation has some importance advantages:
-
Unlike existing algorithms for inferring M\(\varPhi \)RFs [6, 26], it allows synthesizing witnesses for the nonexistence of a M\(\varPhi \)RF of a given depth, see Sect. 4.1.
-
It provides a new tool for addressing the general M\(\varPhi \)RF problem, i.e., without a depth bound, that is still open, see Sect. 4.2.
-
Some nontrivial observations about termination and nontermination \( SLC \) loops are made straightforward through this representation, see Sect. 4.3.
Next, we define the notion of the displacement polyhedron, show how the check \({F}^{d}({\mathcal Q})=\emptyset \) can be encoded in this representation, and then discuss each of the above points.
Definition 5
Given a \( SLC \) loop \({\mathcal Q}\subseteq \mathbb Q ^{2n}\), we define its displacement polyhedron as \({\mathcal R}= {\mathtt {proj}_{\mathbf {x},\mathbf {y}}{({\mathcal Q}\wedge \mathbf {x}'=\mathbf {x}+\mathbf {y})}} \subseteq \mathbb Q ^{2n}\).
Note that the projection drops \(\mathbf {x}'\). Intuitively, an execution step using \({\mathcal Q}\) starts from a state \(\mathbf {x}\), and chooses a state \(\mathbf {x}'\) such that \(\bigl ({\begin{matrix}{\mathbf {x}}\\ {\mathbf {x}'}\end{matrix}}\bigr )\in {\mathcal Q}\). To perform the step using \({\mathcal R}\), select \(\mathbf {y}\) such that \(\bigl ({\begin{matrix}{\mathbf {x}}\\ {\mathbf {y}}\end{matrix}}\bigr )\in {\mathcal R}\) and let the new state be \(\mathbf {x}+\mathbf {y}\). By definition, we obtain the same transitions. The constraint representation of \({\mathcal R}\) can be derived from that of \({\mathcal Q}\) as follows. Let \({\mathcal Q}\equiv [A''\bigl ({\begin{matrix}{\mathbf {x}}\\ {\mathbf {x}'}\end{matrix}}\bigr )\le \mathbf {c}'']\) where \(A''\) is the matrix below on the left (see Sect. 2), then \({\mathcal R}\equiv [R\bigl ({\begin{matrix}{\mathbf {x}}\\ {\mathbf {y}}\end{matrix}}\bigr )\le \mathbf {c}'']\) where \(R\) is the matrix below on the right:
Example 6
Consider Loop (1) which is defined by \({\mathcal Q}=\{x_1\ge -x_3, x_1'=x_1+x_2, x_2'=x_2+x_3, x_3'=x_3-1\}\). The corresponding displacement polyhedron is \({\mathcal R}=\{x_1\ge -x_3, y_1=x_2, y_2=x_3, y_3=-1\}\). \(\square \)
We will show that the displacement polyhedron \({\mathcal R}_k\) of \({\mathcal Q}_k={F}^{k}({\mathcal Q})\) is equivalent to the following polyhedron projected onto \(\mathbf {x}\) and \(\mathbf {y}_0\)
Now since, by Definition 5, \({\mathcal Q}_k\) is empty iff \({\mathcal R}_k\) is empty, the check \({F}^{k}({\mathcal Q})=\emptyset \) is reduced to checking that (25) is empty, which can be done in polynomial time in the bit-size of the constraint representation of \({\mathcal Q}\) and the parameter k. It is important to observe that the first conjunct \(R\bigl ({\begin{matrix}{\mathbf {x}}\\ {\mathbf {y}_0}\end{matrix}}\bigr ) \le \mathbf {c}''\) of (25) is actually \({\mathcal R}\), and that each \(R\bigl ({\begin{matrix}{\mathbf {y}_i}\\ {\mathbf {y}_{i+1}}\end{matrix}}\bigr ) \le \mathbf {0}\) is actually \({\mathtt {rec.cone}}({\mathcal R})\). Observe also how the conjuncts of (25) are connected, i.e., that the lower part of the variables vector of each conjunct is equal to the upper part of the next one.
We first show how \({\mathcal R}_{k+1}\) can be obtained from \({\mathcal R}_{k}\) similarly to \({\mathcal Q}_{k+1}={F}({\mathcal Q}_k)\).
Lemma 8
Let \((\vec {a}_1,b_1),\ldots ,(\vec {a}_l,b_l)\) generate the cone \({{\mathtt {proj}_{\mathbf {x}}{({\mathcal R})}}}^{\#}\). Then \({\mathcal R}_{k+1} = {\mathcal R}_k \wedge -\vec {a}_1\cdot \mathbf {y}\le 0\wedge \cdots \wedge -\vec {a}_l\cdot \mathbf {y}\le 0\).
Proof
Follows from the fact that \({\mathtt {proj}_{\mathbf {x}}{({\mathcal Q}_k)}}={\mathtt {proj}_{\mathbf {x}}{({\mathcal R}_k)}}\), and thus \({{\mathtt {proj}_{\mathbf {x}}{({\mathcal Q}_k)}}}^{\#}\) and \({{\mathtt {proj}_{\mathbf {x}}{({\mathcal R}_k)}}}^{\#}\) are the same, and that for \(\rho (\mathbf {x}) = \vec {a}\cdot \mathbf {x} + b\) we have \(\varDelta \rho (\mathbf {x}'') = \rho (\mathbf {x})-\rho (\mathbf {x}') = -\vec {a}\cdot \mathbf {y}\), by definition of the displacement polyhedron. \(\square \)
Lemma 9
Let \((\vec {a}_1,b_1),\ldots ,(\vec {a}_l,b_l)\) generate the cone \({{\mathtt {proj}_{\mathbf {x}}{({\mathcal R})}}}^{\#}\). Then the condition \(-\vec {a}_1\cdot \mathbf {y}\le 0 \wedge \cdots \wedge -\vec {a}_l\cdot \mathbf {y}\le 0\) of Lemma 8 is equivalent to \(M\mathbf {y}\le 0\), where M is such that \( {\mathtt {proj}_{\mathbf {x}}{({\mathcal R})}} \equiv [M\mathbf {x}\le \mathbf {b}]\).
Proof
Consider \((\vec {a},b) \in {{\mathtt {proj}_{\mathbf {x}}{({\mathcal Q})}}}^{\#}={{\mathtt {proj}_{\mathbf {x}}{({\mathcal R})}}}^{\#}\). By Farkas’ lemma, a function \(f(\mathbf {x})=\vec {a}\cdot \mathbf {x}+b\) is nonnegative over \({\mathtt {proj}_{\mathbf {x}}{({\mathcal R})}}\) iff there are nonnegative \(\vec {\lambda }=(\lambda _1,\ldots ,\lambda _m)\) such that \(\vec {\lambda }\cdot M=-\vec {a}\,\wedge \,\vec {\lambda }\cdot \mathbf {b}\le b\). Note that any (nonnegative) values for \(\vec {\lambda }\) define corresponding values for \(\vec {a}\) and b. Thus the valid values for \(\vec {a}\) are all conic combinations of the rows of \(-M\), i.e., this cone is generated by the rows of \(-M\). Hence \(-\vec {a}_1\cdot \mathbf {y}\le 0 \wedge \cdots \wedge -\vec {a}_l\cdot \mathbf {y}\le 0\) is equivalent to \(M\mathbf {y}\le \mathbf {0}\). \(\square \)
We use the above lemma to show that \({\mathcal R}_k\) can be represented as in (25), without the need to compute M explicitly. We first note that using Lemmas 8 and 9, we have \({\mathcal R}_{k+1} = {\mathcal R}_k \cap {\mathcal D}_k\), where

Lemma 10
\({\mathcal R}_k={\mathtt {proj}_{\mathbf {x},\mathbf {y}_0}{({\widehat{{\mathcal R}}}_k)}}\) where \({\widehat{{\mathcal R}}}_k\) is defined by (25).
Proof
We use induction on k. For \(k=0\) the lemma states that \({\mathcal R}_0\) is specified by \(R\bigl ({\begin{matrix}{\mathbf {x}}\\ {\mathbf {y}_0}\end{matrix}}\bigr ) \le \mathbf {c}'' \), which is correct since by definition \({\mathcal R}_0={\mathcal R}\). Assume the lemma holds for \({\mathcal R}_k\), we prove it for \({\mathcal R}_{k+1} = {\mathcal R}_k \cap {\mathcal D}_k\). By the induction hypothesis,
and

Note that in the last step, we incorporated the recession cone of \({\widehat{{\mathcal R}}}_k\) as in (25), after renaming \(\mathbf {y}_i\) to \(\mathbf {y}_{i+1}\), and \(\mathbf {x}\) to \(\mathbf {y}_0\) just to make it easier to read in the next step. Now, let us compute \({\mathcal R}_{k+1}={\mathcal R}_k\cap {\mathcal D}_k\). Note that any \(\bigl ({\begin{matrix}{\mathbf {x}}\\ {\mathbf {y}_0}\end{matrix}}\bigr ) \in {\mathcal R}_{k+1}\) must satisfy the constraint \(R\bigl ({\begin{matrix}{\mathbf {x}}\\ {\mathbf {y}_0}\end{matrix}}\bigr ) \le \mathbf {c}''\) that comes form \({\mathcal R}_k\). Adding this constraint to \({\mathcal D}_k\) above we clearly obtain a subset of \({\mathcal R}_k\), and thus
which is exactly \({\mathtt {proj}_{\mathbf {x},\mathbf {y}_0}{({\widehat{{\mathcal R}}}_{k+1})}}\), justifying the lemma’s statement for \(k+1\). \(\square \)
Lemma 11
\({\mathcal Q}\) has a M\(\varPhi \)RF of depth d iff \({\widehat{{\mathcal R}}}_{d}\) is empty.
Proof
By Lemma 5, \({\mathcal Q}\) has a M\(\varPhi \)RF of depth d iff \({\mathcal Q}_d={F}^{d}({\mathcal Q})\) is empty, and by Definition 5, \({\mathcal Q}_d\) is empty iff \({\mathcal R}_d\) is empty. Since \({\mathcal R}_d\) is empty iff \({\widehat{{\mathcal R}}}_d\) is empty the lemma follows. \(\square \)
Example 7
Consider Loop (1) and the corresponding displacement polyhedron as in Example 6. As notation, let \(\mathbf {x}_0=(x_1,x_2,x_3)\), \(\mathbf {y}_0=(y_1,y_2,y_3)\), \(\mathbf {y}_1=(w_1,w_2,w_3)\), \(\mathbf {y}_2=(z_1,z_2,z_3)\), and \(\mathbf {y}_3=(v_1,v_2,v_3)\). Then \({\widehat{{\mathcal R}}}_2=\{x_1\ge -x_3, y_1=x_2, y_2=x_3, y_3=-1\} \wedge \{y_1\ge -y_3, w_1=y_2, w_2=y_3, w_3=0\}\wedge \{w_1\ge -w_3, z_1=w_2, z_2=w_3, z_3=0 \}\) is satisfiable, e.g., for \(\mathbf {x}_0 = (0,1,0)\), \(\mathbf {y}_0= (1,0,-1)\), \(\mathbf {y}_1=(0,-1,0)\) and \(\mathbf {y}_2 = (-1,0,0)\), and thus, as expected, the loop does not have a M\(\varPhi \)RF of depth 2. On the other hand, \({\widehat{{\mathcal R}}}_3={\widehat{{\mathcal R}}}_2\wedge \{z_1\ge -z_3, v_1=z_2, v_2=z_3, v_3=0\}\) is not satisfiable, and thus the loop has a M\(\varPhi \)RF of depth 3. \(\square \)
4.1 Witnesses for the Nonexistence of M\(\varPhi \)RFs of a Given Depth
Existing algorithm for deciding whether a given loop has a M\(\varPhi \)RF of depth d [6, 26] synthesize a M\(\varPhi \)RF in the case of success, but in the case of failure they do not provide any further knowledge on why the loop does not have such a M\(\varPhi \)RF. In this section we show that any satisfying assignment for \({\widehat{{\mathcal R}}}_k\) (as defined in (25)) witnesses the nonexistence of M\(\varPhi \)RF of depth k, i.e., it can be used to explains the reason why the loop does not have such M\(\varPhi \)RF.
To gain intuition into the next idea let us start with the case \(k=1\), i.e., the case of \( LRFs \). If \(\mathbf {x}_0,\mathbf {y}_0,\mathbf {y}_1\) is a satisfying assignment for \({\widehat{{\mathcal R}}}_1\), then by construction

Observe that for \(b\ge 0\), \(\bigl ({\begin{matrix}{\mathbf {x}_0}\\ {\mathbf {y}_0}\end{matrix}}\bigr )+b\cdot \bigl ({\begin{matrix}{\mathbf {y}_0}\\ {\mathbf {y}_1}\end{matrix}}\bigr ) \in {\mathcal R}\). If \({\mathcal R}\) has a \( LRF \) \(\rho \), then \(\rho \) ranks \(\bigl ({\begin{matrix}{\mathbf {x}_0}\\ {\mathbf {y}_0}\end{matrix}}\bigr )\) and \(\bigl ({\begin{matrix}{\mathbf {x}_0}\\ {\mathbf {y}_0}\end{matrix}}\bigr )+b\cdot \bigl ({\begin{matrix}{\mathbf {y}_0}\\ {\mathbf {y}_1}\end{matrix}}\bigr ) \in {\mathcal R}\) for any \(b>0\). This requires \(\rho (\mathbf {y}_0) \le -1\) and \(\rho (\mathbf {x}_0)+b\cdot \rho (\mathbf {y_0}) \ge 0\), which contradict for b large enough. Thus the point \(\bigl ({\begin{matrix}{\mathbf {x}_0}\\ {\mathbf {y}_0}\end{matrix}}\bigr )\) and ray \(\bigl ({\begin{matrix}{\mathbf {y}_0}\\ {\mathbf {y}_1}\end{matrix}}\bigr )\) form a witness that explains why the loop does not have a \( LRF \). More precisely, the loop generated by the point and ray of (27), i.e., \(\mathrm {conv.hull}\{\bigl ({\begin{matrix}{\mathbf {x}_0}\\ {\mathbf {y}_0}\end{matrix}}\bigr )\}+\mathrm {cone}\{\bigl ({\begin{matrix}{\mathbf {y}_0}\\ {\mathbf {y}_1}\end{matrix}}\bigr )\} \subseteq {\mathcal R}\), cannot have a \( LRF \).
Let us generalize the above intuition for M\(\varPhi \)RFs. Assume the loop has a M\(\varPhi \)RF \(\langle \rho _1,\ldots ,\rho _k \rangle \), and let \(\mathbf {x_0},\mathbf {y_0},\ldots ,\mathbf {y}_k\) be an assignment satisfying \({\widehat{{\mathcal R}}}_k\), then

We may assume that \(\bigl ({\begin{matrix}{\mathbf {x}_0}\\ {\mathbf {y}_0}\end{matrix}}\bigr )\) is ranked by \(\rho _1\).
Let \({\mathcal R}' = {\mathcal R}\wedge \rho _1(\mathbf {x}) \le -1\). Note that none of the transitions of \({\mathcal R}'\) are ranked by \(\rho _1\). Since \(\rho _1\) is decreasing on all transitions of \({\mathcal R}\), we must have \(\rho _1(\mathbf {y}_0) \le -1\) and \(\rho _1(\mathbf {y}_i) \le 0\) for \(1\le i \le k\). This means that the rays \(\bigl ({\begin{matrix}{\mathbf {y}_0}\\ {\mathbf {y}_1}\end{matrix}}\bigr )\cdots \bigl ({\begin{matrix}{\mathbf {y}_{k-1}}\\ {\mathbf {y}_k}\end{matrix}}\bigr )\) are in \({\mathtt {rec.cone}}({\mathcal R}')\) too. Moreover, for some \(b>0\) large enough, the point \(\bigl ({\begin{matrix}{\mathbf {x}_0+b\cdot \mathbf {y}_0}\\ {\mathbf {y}_0+b\cdot \mathbf {y}_1}\end{matrix}}\bigr )\) is in \({\mathcal R}'\) since \(\rho _1\) can be made arbitrarily negative by increasing b. Now we have
It has the same form as in (28), i.e., the lower part of each point/ray is equal to the upper part of the next one, but the number of rays is reduced by 1, and since \(\langle \rho _2,\ldots ,\rho _k \rangle \) is a M\(\varPhi \)RF for \({\mathcal R}'\) we can apply the same reasoning again and reduce the number of rays to \(k-2\). Repeating this, we arrive to a point and ray as in (27) that are supposed to be ranked by \(\rho _k\), but we know that they cannot have a \( LRF \) so we need at least one more component in the M\(\varPhi \)RF. Thus, we conclude that the solution of (28) is a witness that suffices to prohibit a M\(\varPhi \)RF of depth k. In fact, the loop generated by this witness, i.e., \(\mathrm {conv.hull}\{\bigl ({\begin{matrix}{\mathbf {x}_0}\\ {\mathbf {y}_0}\end{matrix}}\bigr )\}+\mathrm {cone}\{\bigl ({\begin{matrix}{\mathbf {y}_0}\\ {\mathbf {y}_1}\end{matrix}}\bigr ), \ldots ,\bigl ({\begin{matrix}{\mathbf {y}_{k-1}}\\ {\mathbf {y}_k}\end{matrix}}\bigr )\} \subseteq {\mathcal R}\), cannot have a M\(\varPhi \)RF of depth k.
Example 8
The satisfying assignment for \({\widehat{{\mathcal R}}}_2\) in Example 7 is a witness for the nonexistence of \(M{\varPhi }RF \) of depth 2 for Loop (1). The transition polyhedron corresponding to this witness is \(\{ \underline{x_1 = -x_3, x_2 \le 1, x_3 \le 0}, x_1' = x_1+x_2, x_2' = x_2+x_3, x_3' = x_3-1\}\). Note how the guard is strengthened wrt. \(x_1 \ge -x_3\) of Loop (1). \(\square \)
Finally, observe that any polyhedral subset of \({\mathcal R}\) that is disjoint from \({\mathcal R}_k\) has a M\(\varPhi \)RF of depth at most k.
Example 9
Consider Loop (1), for which \({\widehat{{\mathcal R}}}_2\) is satisfiable as we have seen in Example 7. Computing \({\mathcal R}_2={\mathtt {proj}_{\mathbf {x}_0,\mathbf {y}_0}{({\widehat{{\mathcal R}}}_2)}}\) results in \(\{x_3\ge 0, x_2\ge 1, x_1+y_2 \ge 0, y_1=x_2, y_2 = x_3, y_3= -1\}\). For \(\epsilon >0\), any subset of \({\mathcal R}\) that includes \(x_3 \le -\epsilon \) or \(x_2 \le 1-\epsilon \) is disjoint from \({\mathcal R}_2\). Adding either constraint to Loop (1) results in loops that have M\(\varPhi \)RFs of optimal depth 1 and 2 respectively. \(\square \)
4.2 New Directions for Addressing the General M\(\varPhi \)RF Problem
We believe that the displacement polyhedra representation, in particular the check induced by Lemma 10, provides us with new tools that can be used for addressing the problem of deciding whether a given \( SLC \) loop has a \(M{\varPhi }RF \) of any depth, which is still an open problem. Next we discuss some directions.
One direction is to come up with conditions on the matrices \(A''\) (or equivalently \(R\)) and \(\mathbf {c}''\), that define the loop, under which it is guaranteed that if \({\widehat{{\mathcal R}}}_k\) is empty then k must be smaller than some d, i.e., bounding the depth of M\(\varPhi \)RFs for classes of loops that satisfy these conditions.
Let \({\mathcal C} \equiv [R\bigl ({\begin{matrix}{\mathbf {y}}\\ {\mathbf {y}'}\end{matrix}}\bigr ) \le \mathbf {0}]\) and \({\mathcal C}^i\) be the i-fold composition of \({\mathcal C}\). Consider the problem of seeking N, such that \({\mathcal C}^N={\mathcal C}^{N+1}\). This is a sufficient condition for Algorithm 1 to terminate in at most N iterations (either with a recurrent set or with a M\(\varPhi \)RF), since then \({\mathcal R}_N={\mathcal R}_{N+1}\). This is particularly interesting if the loop has an affine update \(\mathbf {x}' = U\mathbf {x} + \mathbf {c}\). In such case \({\mathcal C}\equiv [B\mathbf {y}\le 0\wedge \mathbf {y}'=(U-I)\mathbf {y}]\), where \(I\in \mathbb Q ^{n\times n}\) is the identity matrix, and thus if the matrix \((U-I)\) is nilpotent, for example, then there is N such that \({\mathcal C}^N={\mathcal C}^{N+1}\). This also holds when matrix \((U-I)\) satisfies the finite-monoid property [8].
Another tantalizing observation reduces the existence of d such that \({\widehat{{\mathcal R}}}_d\) is empty to the question whether a related \( SLC \) loop terminates, for a given polyhedron of initial states, in a bounded number of steps. Specifically, the loop:
where B, A and \(A'\) are those used in the definition of \(R\) in (24), and the question whether it terminates in at most d steps for all \(\mathbf {y}\in \{ \mathbf {y}\in \mathbb Q ^n \mid R\bigl ({\begin{matrix}{\mathbf {x}}\\ {\mathbf {y}}\end{matrix}}\bigr )\le \mathbf {c}''\}\). This is because \({\widehat{{\mathcal R}}}_d\) as in (25) is equivalent to unrolling the above loop d times. If the update is affine, i.e., \(\mathbf {x}' = U\mathbf {x} + \mathbf {c}\), then the above loop is equivalent to the following loop: \( \mathtt {while} \,\,\, (B\mathbf {y} \le \mathbf {0})\,\,\, \mathtt {do} \,\,\, \mathbf {y}'=(U-I)\mathbf {y} \).
4.3 Termination and Nontermination of Bounded \( SLC \) Loops
To further demonstrate the usefulness of the displacement polyhedra, in this section we provide some observations, regarding \( SLC \) loops whose set of enabled states are defined by bounded polyhedra, that are easy to see using the displacement polyhedron and are much less obvious using the transition polyhedron. A polyhedron is bounded if its recession cone consists of a single point \(\mathbf {0}\).
Lemma 12
Let \({\mathcal Q}\) be a \( SLC \) loop such that the set of enabled states \({\mathtt {proj}_{\mathbf {x}}{({\mathcal Q})}}\) is a bounded polyhedron, then \({\mathcal Q}\) is nonterminating iff it has a fixpoint \(\bigl ({\begin{matrix}{\mathbf {x}}\\ {\mathbf {x}}\end{matrix}}\bigr )\in {\mathcal Q}\), and it is terminating iff it has a \( LRF \).
Proof
Let \({\mathcal R}\) be the displacement polyhedron of \({\mathcal Q}\). Since \({\mathtt {proj}_{\mathbf {x}}{({\mathcal Q})}}\) is bounded, \({\mathtt {proj}_{\mathbf {x}}{({\mathcal R})}}\) is bounded. This means that its recession cone \(R\bigl ({\begin{matrix}{\mathbf {x}}\\ {\mathbf {y}}\end{matrix}}\bigr )\le \mathbf {0}\) consists of points of the form \(\bigl ({\begin{matrix}{\mathbf {0}}\\ {\mathbf {y}}\end{matrix}}\bigr )\). From the form of \({\widehat{{\mathcal R}}}_k\), which is a conjunction of instances of \(R\bigl ({\begin{matrix}{\mathbf {y}_i}\\ {\mathbf {y}_{i+1}}\end{matrix}}\bigr )\le \mathbf {0}\), it is easy to see that \({\mathcal R}_2={\mathcal R}_1\). This means that the algorithm will terminate in at most two iterations with one of the following outcomes: (i) \({\mathcal R}_0={\mathcal R}_1\); (ii) \({\mathcal R}_2={\mathcal R}_1\); or (iii) \({\mathcal R}_1\) is empty. In the first two cases all transitions of \({\mathcal R}_1\) or \({\mathcal R}_2\) are of the form \(\bigl ({\begin{matrix}{\mathbf {x}}\\ {\mathbf {0}}\end{matrix}}\bigr )\), and thus \(\bigl ({\begin{matrix}{\mathbf {x}}\\ {\mathbf {x}}\end{matrix}}\bigr ) \in {\mathcal Q}\); in the third case we have found a M\(\varPhi \)RF of depth 1, i.e., \( LRF \). Note that the part that relates nontermination to the existence of a fixpoint follows also from [26]. \(\square \)
5 Implementation and Experimental Evaluation
For experimentally evaluating Algorithm 1 for nontermination, we have integrated it in a version of iRankFinder which is available at http://irankfinder.loopkiller.com. It takes as input a control-flow graph, and proves nontermination as follows: when it fails to prove termination, it enumerates closed walks (which are basically \( SLC \) loops) using only transitions whose termination was not proven, and then applies Algorithm 1 to seek recurrent sets. For now it does not check that the recurrent set is reachable, which is an orthogonal problem.
We have analyzed 436 benchmarks that we have taken from TPDB [35] and for which iRankFinder fails to prove termination, and for 412 it finds recurrent sets. These recurrent sets are valid over the rationals, however, at least for 223 benchmarks that satisfy the condition of Lemma 7, they are also valid over the integers. The raw data of the experiments is available at http://irankfinder.loopkiller.com/papers/extra/sas19. Since we do not check reachability, we cannot compare numbers to the other tools, however, in the link above we also provide the results for some other tools when applied to these examples.
We also provide an implementation of Algorithm 1 in a light version of iRankFinder that accepts \( SLC \) loops as input, which is adequate for experimenting with the algorithm both for finding M\(\varPhi \)RFs and recurrent sets – it is available at http://www.loopkiller.com/irankfinder by selecting options \(M{\varPhi }RF (\mathbb Q)\) or \(M{\varPhi }RF (\mathbb Z)\).
6 Conclusion
The purpose of this work has been to improve our understanding of M\(\varPhi \)RFs, in particular of the problem of deciding whether a given \( SLC \) loop has a M\(\varPhi \)RF without a given bound on the depth. The outcomes are important insights that shed light on the structure of these ranking functions.
At the heart of our work is an algorithm that seeks M\(\varPhi \)RFs, which is based on iteratively eliminating transitions, until eliminating them all or stabilizing on a set of transitions that cannot be reduced anymore. In the first case, a M\(\varPhi \)RF can be constructed, and, surprisingly, in the second case the stable set of transitions turns to be a recurrent set that witnesses nontermination. This reveals an equivalence between the problems of seeking M\(\varPhi \)RFs and seeking recurrent sets of a particular form.
Apart from the relation to seeking recurrent sets, the insights of our work are helpful for characterizing classes of loops for which there is always a M\(\varPhi \)RF, when terminating. In addition, our insights led to a new representation for \( SLC \) loops in which our algorithm has a very simple formalization that, unlike previous algorithms, yields witnesses for the nonexistence of M\(\varPhi \)RFs of a given depth. Moreover, this new representation makes some nontrivial observations regarding (bounded) \( SLC \) loop straightforward. We believe that this representation can be useful for other related problems. Our research leaves a number of new open questions, which we hope will trigger the interest of the community.
The problem of seeking M\(\varPhi \)RFs with a given bound on the depth has been considered in several works. The complexity of the problem for \( SLC \) loops was settled in [6]. M\(\varPhi \)RFs for general loops are considered in [25, 28], both using non-linear constraint solving. In [2] the notion of “eventual linear ranking functions,” which are M\(\varPhi \)RFs of depth 2, was studied. The method in [7] can infer M\(\varPhi \)RFs for general loops incrementally, by solving safety problems using Max-SMT. Lexicographic ranking function are closely related. Their algorithmic aspects are considered in [1, 5, 9, 19, 23]. There are other works [17, 36, 37] that address the problem of prove termination by ranking functions, in particular [37] that combines piecewise-linear functions with lexicographic orders. None considers recurrent sets together with ranking-function termination proofs. The combination of piecewise-linear functions with lexicographic orders as in [37] subsumes multiphase ranking functions, however, being more general, and using an approach which is more generic, [37] does not offer any particular insights about multiphase ranking functions and makes no claims of completeness.
Nontermination provers are described in several works. Some techniques are based on finding recurrent sets in one form or another [3, 4, 8, 10, 20, 22, 26, 30]; while others are based on reducing the problem to proving non-reachability of terminating states [11, 24, 38]. The idea of shrinking a set of states until finding a recurrent set can be found in several of these works, the main difference is that they typically remove states that ensure termination while our procedure might remove nonterminating states (so that, when it finds a recurrent set, it is not necessarily the largest one).
References
Alias, C., Darte, A., Feautrier, P., Gonnord, L.: Multi-dimensional rankings, program termination, and complexity bounds of flowchart programs. In: Cousot, R., Martel, M. (eds.) SAS 2010. LNCS, vol. 6337, pp. 117–133. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15769-1_8
Bagnara, R., Mesnard, F.: Eventual linear ranking functions. In: Proceedings of the 15th International Symposium on Principles and Practice of Declarative Programming, PPDP 2013, pp. 229–238. ACM Press (2013)
Bakhirkin, A., Berdine, J., Piterman, N.: A forward analysis for recurrent sets. In: Blazy, S., Jensen, T. (eds.) SAS 2015. LNCS, vol. 9291, pp. 293–311. Springer, Heidelberg (2015). https://doi.org/10.1007/978-3-662-48288-9_17
Bakhirkin, A., Piterman, N.: Finding recurrent sets with backward analysis and trace partitioning. In: Chechik, M., Raskin, J.-F. (eds.) TACAS 2016. LNCS, vol. 9636, pp. 17–35. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49674-9_2
Ben-Amram, A.M., Genaim, S.: Ranking functions for linear-constraint loops. J. ACM 61(4), 26:1–26:55 (2014)
Ben-Amram, A.M., Genaim, S.: On multiphase-linear ranking functions. In: Majumdar, R., Kunčak, V. (eds.) CAV 2017. LNCS, vol. 10427, pp. 601–620. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63390-9_32
Borralleras, C., Brockschmidt, M., Larraz, D., Oliveras, A., Rodríguez-Carbonell, E., Rubio, A.: Proving termination through conditional termination. In: Legay, A., Margaria, T. (eds.) TACAS 2017. LNCS, vol. 10205, pp. 99–117. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-54577-5_6
Bozga, M., Iosif, R., Konečný, F.: Deciding conditional termination. In: Flanagan, C., König, B. (eds.) TACAS 2012. LNCS, vol. 7214, pp. 252–266. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28756-5_18
Bradley, A.R., Manna, Z., Sipma, H.B.: Linear ranking with reachability. In: Etessami, K., Rajamani, S.K. (eds.) CAV 2005. LNCS, vol. 3576, pp. 491–504. Springer, Heidelberg (2005). https://doi.org/10.1007/11513988_48
Brockschmidt, M., Ströder, T., Otto, C., Giesl, J.: Automated detection of non-termination and NullPointerExceptions for Java bytecode. In: Beckert, B., Damiani, F., Gurov, D. (eds.) FoVeOOS 2011. LNCS, vol. 7421, pp. 123–141. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31762-0_9
Chen, H.-Y., Cook, B., Fuhs, C., Nimkar, K., O’Hearn, P.: Proving nontermination via safety. In: Ábrahám, E., Havelund, K. (eds.) TACAS 2014. LNCS, vol. 8413, pp. 156–171. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54862-8_11
Colón, M.A., Sipma, H.B.: Synthesis of linear ranking functions. In: Margaria, T., Yi, W. (eds.) TACAS 2001. LNCS, vol. 2031, pp. 67–81. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45319-9_6
Conforti, M., Cornuéjols, G., Zambelli, G.: Polyhedral approaches to mixed integer linear programming. In: Jünger, M., et al. (eds.) 50 Years of Integer Programming 1958–2008, pp. 343–386. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-540-68279-0_11
Cook, B., Gotsman, A., Podelski, A., Rybalchenko, A., Vardi, M.Y.: Proving that programs eventually do something good. In: Proceedings of the 34th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, POPL 2007, Nice, France, 17–19 January 2007, pp. 265–276 (2007)
Cook, B., Gulwani, S., Lev-Ami, T., Rybalchenko, A., Sagiv, M.: Proving conditional termination. In: Gupta, A., Malik, S. (eds.) CAV 2008. LNCS, vol. 5123, pp. 328–340. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-70545-1_32
Cook, B., Podelski, A., Rybalchenko, A.: Termination proofs for systems code. In: Schwartzbach, M.I., Ball, T. (eds.) Programming Language Design and Implementation, PLDI 2006, pp. 415–426. ACM (2006)
Cousot, P., Cousot, R.: An abstract interpretation framework for termination. In: Field, J., Hicks, M. (eds.) Symposium on Principles of Programming Languages, POPL 2012, pp. 245–258. ACM (2012)
Feautrier, P.: Some efficient solutions to the affine scheduling problem. I. One-dimensional time. Int. J. Parallel Program. 21(5), 313–347 (1992)
Gonnord, L., Monniaux, D., Radanne, G.: Synthesis of ranking functions using extremal counterexamples. In: Grove, D., Blackburn, S. (eds.) Programming Language Design and Implementation, PLDI 2015, pp. 608–618. ACM (2015)
Gupta, A., Henzinger, T.A., Majumdar, R., Rybalchenko, A., Xu, R.-G.: Proving non-termination. In: Necula, G.C., Wadler, P. (eds.) Symposium on Principles of Programming Languages, POPL 2008, pp. 147–158 (2008)
Harrison, M.: Lectures on Sequential Machines. Academic Press, New York (1969)
Larraz, D., Nimkar, K., Oliveras, A., Rodríguez-Carbonell, E., Rubio, A.: Proving non-termination using Max-SMT. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 779–796. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08867-9_52
Larraz, D., Oliveras, A., Rodríguez-Carbonell, E., Rubio, A.: Proving termination of imperative programs using Max-SMT. In: Formal Methods in Computer-Aided Design, FMCAD 2013, pp. 218–225. IEEE (2013)
Le, T.C., Qin, S., Chin, W.-N.: Termination and non-termination specification inference. In: Grove, D., Blackburn, S. (eds.) Programming Language Design and Implementation, PLDI 2015, pp. 489–498. ACM (2015)
Leike, J., Heizmann, M.: Ranking templates for linear loops. Log. Methods Comput. Sci. 11(1), 1–27 (2015)
Leike, J., Heizmann, M.: Geometric nontermination arguments. In: Beyer, D., Huisman, M. (eds.) TACAS 2018. LNCS, vol. 10806, pp. 266–283. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89963-3_16
Leroux, J., Sutre, G.: Flat counter automata almost everywhere!. In: Peled, D.A., Tsay, Y.-K. (eds.) ATVA 2005. LNCS, vol. 3707, pp. 489–503. Springer, Heidelberg (2005). https://doi.org/10.1007/11562948_36
Li, Y., Zhu, G., Feng, Y.: The L-depth eventual linear ranking functions for single-path linear constraint loops. In: 10th International Symposium on Theoretical Aspects of Software Engineering (TASE 2016), pp. 30–37. IEEE (2016)
Ouaknine, J., Worrell, J.: On linear recurrence sequences and loop termination. ACM SIGLOG News 2(2), 4–13 (2015)
Payet, É., Mesnard, F., Spoto, F.: Non-termination analysis of Java bytecode. CoRR, abs/1401.5292 (2014)
Podelski, A., Rybalchenko, A.: A complete method for the synthesis of linear ranking functions. In: Steffen, B., Levi, G. (eds.) VMCAI 2004. LNCS, vol. 2937, pp. 239–251. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24622-0_20
Schrijver, A.: Theory of Linear and Integer Programming. Wiley, New York (1986)
Sohn, K., Van Gelder, A.: Termination detection in logic programs using argument sizes. In: Rosenkrantz, D.J. (ed.) Symposium on Principles of Database Systems, pp. 216–226. ACM Press (1991)
Tiwari, A.: Termination of linear programs. In: Alur, R., Peled, D.A. (eds.) CAV 2004. LNCS, vol. 3114, pp. 70–82. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-27813-9_6
The Termination Problems Data Base. http://termination-portal.org/wiki/TPDB
Urban, C.: The abstract domain of segmented ranking functions. In: Logozzo, F., Fähndrich, M. (eds.) SAS 2013. LNCS, vol. 7935, pp. 43–62. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38856-9_5
Urban, C., Miné, A.: An abstract domain to infer ordinal-valued ranking functions. In: Shao, Z. (ed.) ESOP 2014. LNCS, vol. 8410, pp. 412–431. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-54833-8_22
Velroyen, H., Rümmer, P.: Non-termination checking for imperative programs. In: Beckert, B., Hähnle, R. (eds.) TAP 2008. LNCS, vol. 4966, pp. 154–170. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-79124-9_11
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Ben-Amram, A.M., Doménech, J.J., Genaim, S. (2019). Multiphase-Linear Ranking Functions and Their Relation to Recurrent Sets. In: Chang, BY. (eds) Static Analysis. SAS 2019. Lecture Notes in Computer Science(), vol 11822. Springer, Cham. https://doi.org/10.1007/978-3-030-32304-2_22
Download citation
DOI: https://doi.org/10.1007/978-3-030-32304-2_22
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-32303-5
Online ISBN: 978-3-030-32304-2
eBook Packages: Computer ScienceComputer Science (R0)





 .
.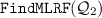 . Note that the only new generator wrt. the previous iteration is the one in bold font, the others are ignored as they have been used for computing
. Note that the only new generator wrt. the previous iteration is the one in bold font, the others are ignored as they have been used for computing  .
. .
. .
.