Keywords

1 Introduction

Throughout the human history, there are diseases that due to their characteristics suddenly affect a large part of the population of a certain region, generating considerable morbidity and mortality [19]. This type of disease is called epidemic and is developed in populations that acquire a certain population density [6]. However, we observe that the term epidemic is also used sometimes in the case of noninfectious diseases that are of population scale, for instance, the dynamic of diabetes. In this work, we will analyze the epidemics due to infectious diseases and within them those that are not transmitted through vectors.

From the historic point of view, we notice that the epidemics caused several health problems on a population scale, jeopardizing the survival of different civilizations. For instance, the bubonic plague [25] and its famous plagues developed in the old Egypt [24], the epidemic of plague in Athens, Typhoid and Syracuse [4] in the old Greece, the black plague that affected the whole of Europe [34], the epidemics due to the meeting between Europeans and Native Americans in America [26], and the outbreaks of cholera due to the contamination of water with fecal matter [26]. We remark that the consequences of the plagues in America are even more important than those occurring in Europe [15].

In the last decades, there are several efforts to understand the dynamics of diseases caused by epidemic. Nowadays, the mathematical epidemiology is one of the most important branches of bio-mathematics [11, 13]. Moreover, we observe that there are several kinds of mathematical models. For instance, there are mathematical models in terms of discrete mathematics, deterministic or even stochastic ordinary differential systems or partial differential equations, and statistical theory.

The mathematical modeling of the population dynamics for infectious diseases is a standard or classical problem in differential equations theory [21, 27]. We observe that the earliest published paper on mathematical modeling of spread of disease was carried out in 1766 by Daniel Bernoulli. Trained as a physician, Bernoulli created a mathematical model to defend the practice of inoculating against smallpox [18]. According to Pesco [26], in 1927 Kermack and Mc Kendrick published an article in which they proposed a mathematical model, implemented in differential equations, that simulates the transmission of an infectious disease. This model divides the population into compartments according to the epidemiological status of the individuals, classifying them as susceptible (S), infected (I), and recovered (R), which is currently known as the SIR model.

On the other hand, related with statistical methods, we notice that inferential methods have also been developed to evaluate the correlation between epidemiological data and possible indicators of risk or health policies [1, 23]. Nowadays, epidemiology is used to describe the clinical spectrum of a disease, to know the transmission mechanisms of the disease, to know the natural history of biological systems, to make population diagnoses, to identify factors that produce the risk of acquiring the disease, and to test the effectiveness of different mitigation strategies. It is mainly used to generate information required by public health professionals to develop, implement, and evaluate health policies [12]. However, in the best of our knowledge, there are no works related with time series theory applied to model calibration in epidemiology. An exception and an advance in this research line is the recent work [9].

In the processes of mathematical modeling by ordinary differential equations, there are at least four phases: abstraction, simplification or mathematical model formulation, solution or analysis, and validation [14]. Particularly, the phase of validation requires the solution of problem well known as the mathematical model calibration.

In a broad sense, parameter calibration means that we want to find (or to calculate) some unknown constants or functions (called model parameters) from some given observations for the solution model. The mathematical concept of calibration or identification is equivalent to that of estimation in statistics. In practice, these problems can be solved by applying the inverse problem methodologies [14]. We remark that, although the estimation (calibration or identification) of unknown parameters has a significant practical importance, there are several problems which are not enough investigated due, for instance, to the lack of results on the uniqueness of the solution of the inverse problem, i.e., while the direct problem may have a unique solution, the inverse problem does not usually have the same property [21, 30]. Moreover, we observe that the inverse problem is crucial for calibrating the model and for controlling the model parameters. Approaches involving inverse problems can be successfully applied to a variety of important biological processes, including the spread of infectious diseases, allowing epidemiologists and public health specialists to predict the time interval between epidemics [5, 21].

The aim of this paper is the identification of certain coefficients (or parameters) in the ordinary differential equations system of SIR type investigated by Bai and Zhou [3] by using the inverse problem methodologies and the time series theory. We start by defining a continuous observation using the time series and an interpolation of discrete data. Then, we define an optimization problem for an appropriate cost function which is equivalent to the inverse problem. To solve the minimization problem, we apply the gradient method where the gradient of the cost function is calculated by the introduction of an adjoint state.

Among some previous and related works with the topic of parameter identification in epidemiological models, we can refer to [16,17,18, 20, 22, 29, 33]. The models considered by the authors are systems of stochastic differential equations and the notion of parameters adopted by them is given by the context of statistics theory. Thus, the methodologies are not comparable with the ones presented in this paper, since the model is a deterministic model and the notion of parameter is used to define the coefficients of the system.

The rest of the paper is organized as follows. In Sect. 2, we present the notation and precise definition of the direct problem. In Sect. 3, we define the inverse problem. In Sect. 4, we present the inverse problem solution methodology. In Sect. 5, we present a numerical experiment. Finally, in Sect. 6, we summarize some conclusions.

2 The Direct Problem

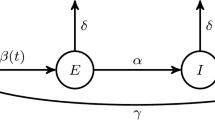
Let S(t) be the number of susceptible individuals, I(t) be the number of infective individuals, and R(t) be the number of recovered individuals at time \(t\in [0,T]\), respectively. According to the writing by Bai and Zou [3], “After studying the cholera epidemic spread in Bari in 1973, Capasso and Serio introduced the saturated incidence rate \(\beta SI(1+kI)^{-1}\) into epidemic model,” where \(\beta I\) measures the infection force of the disease and \((1+kI)^{-1}\) with \(k > 0\) describes the psychological effect or inhibition effect from the behavioral change of the susceptible individuals with the increase of the infective individuals. This incidence rate seems more reasonable than the bilinear incidence rate \(\beta SI\), because it includes the behavioral change and crowding effect of the infective individuals and prevents the unboundedness of the contact rate.

The treatment is an important way to reduce the disease spread, such as measles, tuberculosis, and flu [32]. In classical epidemic models, the treatment rate of infectives is assumed to be proportional to the number of the infectives. The proportional assumption will lead to very fast increase of the treatment resource. In fact, every community has a suitable capacity for treatment. If it is too large, the community pays for unnecessary cost. If it is too small, the community has a higher risk of disease outbreak. It is realistic to maintain a suitable capacity of disease treatment. Wang and Ruan [31] introduced a treatment function h(I), which is a positive constant m for \(I > 0\), and zero for \(I = 0\). This seems more reasonable when we consider the limitation of the treatment resource of a community.

Bai and Zhou [3] formulated a nonautonomous SIR epidemic model with saturated incidence rate and constant removal rate by introducing the periodic transmission rate \(\beta (t)\). The general model is formulated as follows:

$$\begin{aligned} \left. \begin{array}{ll} \displaystyle \frac{d}{dt}S(t)&{}=\varLambda -\mu \,S(t)-\displaystyle \frac{\beta (t) S(t)\,I(t)}{1+kI(t)}, \\ \displaystyle \frac{d}{dt}I(t)&{}=\displaystyle \frac{\beta (t) S(t)\,I(t)}{1+kI(t)}-(\mu +\gamma )\,I(t)-h(I(t)),\quad \\ \displaystyle \frac{d}{dt}R(t)&{}=\gamma I(t)+h(I(t))-\mu \,R(t). \end{array} \right\} \end{aligned}$$
(1)

Here, \(\varLambda \) is the recruitment rate, \(\mu \) is the natural death rate, \(\gamma \) is the recovery rate of the infective population, and \(\beta (t)\) is the transmission rate at time t. Now, noticing that the first two equations in (1) are independent of the third one, and the dynamic behavior of (1) is trivial when \(I(t_0) = 0\) for some \(t_0 > 0\), Bai and Zhou [3] considered only the first two equations with \(I > 0\). Thus, these researchers restricted their study to the model given by

$$\begin{aligned} \left. \begin{array}{ll} \displaystyle \frac{d}{dt}S(t)&{}=\varLambda -\mu \,S(t)-\displaystyle \frac{\beta (t) S(t)\,I(t)}{1+kI(t)}, \\ \displaystyle \frac{d}{dt}I(t)&{}=\displaystyle \frac{\beta (t) S(t)\,I(t)}{1+kI(t)}-(\mu +\gamma )\,I(t)-m.\quad \end{array} \right\} \end{aligned}$$
(2)

In the terminology of inverse problems, we have that the direct problem is given by system (2) with some appropriate initial conditions for S and I. More precisely

Definition 1

The direct problem is formulated as follows: given the constants \(T,\varLambda ,\mu ,k,m,S_0,I_0\) and the function \(\beta \), find the functions S and I satisfying the system (2) on the interval ]0, T] and the initial condition \((S,I)(0)=(S_0,I_0).\)

The direct problem is well-posed since it is the standard Cauchy problem for an ordinary differential system where the right-hand side is a locally Lipschitz function.

3 The Inverse Problem

The inverse problems consist in the determination of \(\mu \) and \(\gamma \) in the system (2) from a distribution of the number of infected individuals \(I^{obs}\) and such that the infected solution of the direct problem for \(\mu \) and \(\gamma \), denoted as \(I_{\mu ,\gamma }\), is “as close as” to \(I^{obs}\). The term “as close as” is numerically precise by considering the \(L_2\)-norm of the distance of \(I_{\mu ,\gamma }\) and \(I^{obs}\). However, we observe that \(I^{obs}\) is not defined on the whole time interval. Then, to extend \(I^{obs}\) continuously we apply time series. Then we precise the definition of the optimization problem.

To precise the application of time series, we consider the numeric values for the parameters used by Bai and Zhou [3] to investigate the stability of the periodic solution of (2) with given parameter values and small degree seasonal fluctuation in transmission rate. We set that \(\varLambda = 400, k = 0.01, \mu = 0.02, \gamma = 0.04, m = 10\), and \(\beta (t) = 0.00006 + \varepsilon \,\sin (\pi t/3)\), where \(0\le \varepsilon < 0.00006\). Then, the system (2) becomes

$$\begin{aligned} \left. \begin{array}{ll} \displaystyle \frac{d}{dt}S(t)&{}=400-0.02\,S(t)- \displaystyle \frac{3\left[ 0.2+\varepsilon \sin (\pi t/3)\right] S(t)\,I(t)}{10000+100\,I(t)},\\ \displaystyle \frac{d}{dt}I(t)&{}= \displaystyle \frac{3\left[ 0.2+\varepsilon \sin (\pi t/3)\right] S(t)\,I(t)}{10000+100\,I(t)}-(0.02+0.04)\,I(t)-10, \\ S(0)&{}=14000,\quad I(0)=600. \end{array} \right\} \end{aligned}$$
(3)

Now, we solve numerically system (3) and obtain the discrete synthetic observed data which is shown on Fig. 1. The next step is to adjust this data by a continuous function. Indeed, due to the structure of the data, we deduced that it would be very useful to use time series to find the best model that fits such data. Figure 2 shows the graph of the time series associated with the data. To be more precise, as the series shown in Fig. 2 shows a lot of variability, the first thing we did was to apply a transformation to the data. Then, using the programming language R [28] and the tseries library next to the Arima command, we obtained a two-differentiated AR(1) model [7], in which results are summarized in the following expression:

$$(1-B)^2 (1-B^6)(1-0.512B)Y_t=\varepsilon _t,\ \ \ \varepsilon _t\sim N(0,\sigma ^2),$$

where B is the lag operator. Remembering that \(BY_t=Y_{t-1}\), it turns out

$$\begin{aligned} Y_t= & {} 2.512Y_{t-1}-2.024Y_{t-2}+0.512Y_{t-3}+Y_{t-6} \nonumber \\&\qquad -2.512Y_{t-7}+2.024Y_{t-8}-0.512Y_{t-9}+\varepsilon _t, \end{aligned}$$
(4)

where \(\varepsilon _t\) is a white noise \(N(0,\sigma ^2)\).

Then, using this time series and an appropriate interpolation we construct the function \(I^{obs}(t)\) on [0, T].

We observe that model (4) corresponds to the synthetic data obtained by simulation of (3). Then for other particular cases of system (2), we proceed analogously to construct the corresponding time series model and the appropriate \(I^{obs}\) continuous function.

Fig. 1
figure 1

Plot of the number of infected population solution of (3)

Full size image
Fig. 2
figure 2

Plot of the adjustment of infected population solution of (3) by the time series to an ARIMA(1, 2, 0) \(\times \) (0, 1, 0)\(_6\) model

Full size image

We reformulate the inverse problem like an optimal control problem. The optimization problem is now formulated as follows: the objective function J depending on the variables \(\mu \) and \(\gamma \) is the least squares cost function and the restriction is the initial value problem for the system (2) with some parameters \(\mu \) and \(\gamma \). More precisely we have the following definition.

Definition 2

The inverse problem is defined by the optimization problem:

$$\begin{aligned} \text{ Minimize } \ \ J(\mu ,\gamma )=\delta \, \left\| I_{\mu ,\gamma }-I^{obs}\right\| ^2_{L_2(0,T)} :=\delta \int _0^T (I_{\mu ,\gamma }-I^{obs})^2(t)dt \end{aligned}$$
(5)

subject to \(I_{\mu ,\gamma }\) solution of system (2) a given initial condition \((S,I)(0)=(S_0,I_0)\), \(I^{obs}\) is the continuous observation constructed with a time series and an appropriate interpolation, and \( \delta \) a positive constant.

We remark two facts. First, the objective function J measures the distance between two functions, and therefore it must be minimized and is called cost. One of the functions involved in this cost is that which solves the initial value problem and the other is the one that adjusts the data through the series of time already found. Second, we observe that the existence of solutions for the inverse problem can be derived by applying the continuous dependence of (S, I) with respect to \((\mu ,\gamma )\). However, the uniqueness of the inverse problem solution or the proof of a unique global optimizer for J is difficult to get.

4 Methodology of the Solution for the Inverse Problem

In order to solve the optimization problem, we apply the gradient method where the gradient of the cost function is obtained by the introduction of an adjoint state. First, we deduce the gradient of the cost function when all data are continuous and then we mimic the process to introduce a discrete gradient.

4.1 Continuous Gradient

We apply the Lagrange multipliers method. We recall that the Lagrangian is a linear combination between the objective function and the constraints. As it must be scalar then the constraints, which are functions, are multiplied, respectively, by the functions p and q, and then integrated over the whole domain, obtaining the following function to be minimized:

$$\mathscr {L}\!\left( S_{\mu ,\gamma },I_{\mu ,\gamma };p,q\right) =J(\mu ,\gamma )-E\!\left( S_{\mu ,\gamma },I_{\mu ,\gamma };p,q\right) ,$$

where J is defined in (5) and \(E:=E(S_{\mu ,\gamma },I_{\mu ,\gamma };p,q)\) is given by

$$\begin{aligned} E=&-\int _{0}^{T}\left[ S\frac{dp}{dt} + \left( \varLambda -\mu S -\frac{\beta (t)S I }{1+kI}\right) p \right] d\tau +p(T)S(T)-p(0)S_0\\&-\int _{0}^{T}\!\left[ I\frac{dq}{dt}+ \left( \frac{\beta (t)S I }{1+kI} -(\mu +\gamma ) I -m\right) q\right] \!d\tau +q(T)I(T)-q(0)I_0. \end{aligned}$$

Thus, we have a classic minimization problem for \(\mathscr {L}\), and therefore we can apply the first-order optimal conditions to deduce the adjoint state, i.e., we calculate the gradient of the Lagrangian with respect to the variables \(\mu \) and \(\gamma \), and select the states (p, q) such that the gradient of \(\mathscr {L}\) vanishes. We note that

$$\begin{aligned} \frac{d\mathscr {L}}{d \mu }&= \frac{\partial \mathscr {L} }{\partial S}\,\frac{\partial S }{\partial \mu } +\frac{\partial \mathscr {L} }{\partial I}\,\frac{\partial I }{\partial \mu } +\frac{\partial \mathscr {L}}{\partial \mu } \equiv 0,\\ \frac{d\mathscr {L}}{d\gamma }&= \frac{\partial \mathscr {L} }{\partial S}\,\frac{\partial S }{\partial \gamma } +\frac{\partial \mathscr {L} }{\partial I}\,\frac{\partial I }{\partial \gamma } +\frac{\partial \mathscr {L}}{\partial \gamma } \equiv 0. \end{aligned}$$

The calculus of \(\partial _{\mu } S,\partial _{\mu } I,\partial _{\gamma } S,\) and \(\partial _{\gamma } I\) is difficult to develop directly since the functions S and I do not depend explicitly on \(\mu \) and \(\gamma \) and the strategy is to select p and q such that \(\partial _{S} \mathscr {L}=\partial _{I} \mathscr {L}=0\). We observe that

$$\begin{aligned} \frac{\partial \mathscr {L} }{\partial S}&=-\frac{\partial E }{\partial S} =\int _{0}^{T}\left[ \frac{dp}{dt} - \left( \mu +\frac{\beta (t) I }{1+kI}\right) p +\frac{\beta (t) I q }{1+kI} \right] d\tau -p(T) \\ \frac{\partial \mathscr {L} }{\partial I}&=\frac{\partial J }{\partial I}-\frac{\partial E }{\partial I} \\&=2\delta \int _0^T (I-I^{obs})+\frac{dq}{dt} -\left[ \frac{\beta (t)S }{(1+kI)^2}p+\frac{\beta (t)S }{(1+kI)^2}q +(\mu +\gamma )q \right] d\tau -q(T). \end{aligned}$$

Thus, a necessary condition for p and q such that \(\partial _{S} \mathscr {L}=\partial _{I} \mathscr {L}=0\) is given by

$$\begin{aligned} \left. \begin{array}{ll} \displaystyle \frac{dp}{dt} &{}= \mu \,p+\displaystyle \frac{\beta (t)\,I}{1+kI}\,(p-q), \\ \displaystyle \frac{dq}{dt} &{}= (\mu +\gamma )\,q+\displaystyle \frac{\beta (t)\,S}{\left( 1+kI\right) ^2}\,(p-q) +2\delta (I^{obs}-I),\\ p(T)&{}=q(T)=0. \end{array} \right\} \end{aligned}$$
(6)

The backward problem (6) is called the continuous adjoint state. It gives rise to the so-called continuous gradient, which arises equal to zero the derivatives of the Lagrangian, obtaining

$$\begin{aligned} \nabla J=\nabla E= - \int _{0}^{T}(Sp,Iq)d\tau . \end{aligned}$$
(7)

The gradient given in (7) can be used to solve numerically the optimization problem. However, there are several suggestions to use a discrete gradient obtained by a similar methodology instead of direct discretization for \(\nabla J\) in (7), see, for instance, [8, 10].

Fig. 3
figure 3

Scheme of the gradient calculus methodology. The definition of (S, I), J, (p, q), and \(\nabla J\) is given in (2), (5), (6), and (7), respectively. Now, the definition of \((S_\varDelta ,I_\varDelta ),J_\varDelta ,(p_\varDelta ,q_\varDelta )\), and \(\nabla J_\varDelta \) is presented in (8), (9), (11), and (12), respectively

Full size image

4.2 Discrete Gradient

The discretization of (7) typically develops numerical instabilities [8, 10]. Then, the strategy is to obtain a discrete gradient by a similar methodology to that applied to get (7). We recall that the three steps are the following: (i) construct the continuous cost function given on (5), (ii) apply a Lagrangian formulation to define the continuous adjoint state given on (6), and (iii) use the continuous and the adjoint state to define the continuous gradient given on (7), see the upper part on the scheme given on Fig. 3. Then, to obtain the discrete we discretize the continuous state variables and proceed analogously to the steps (i)–(iii), see the lower part on the scheme given on Fig. 3. The specific definitions of \((S_{\varDelta },I_{\varDelta }),J_{\varDelta },(p_{\varDelta },q_{\varDelta })\), and \(\nabla J_{\varDelta }\) are given below.

The numerical solution \((S_{\varDelta },I_{\varDelta })\) is calculated by a fourth-order Runge–Kutta method. Let us select \(N\in \mathbb {N}\) and define \(\varDelta t=T/N,\) \(t_n=n\varDelta t\) and

$$\begin{aligned} (S_{\varDelta },I_{\varDelta })(t) =(S^n,I^n), \quad t\in [t_n,t_{n+1}[, \end{aligned}$$

with \(\mathbf {x}^n:=(S^n,I^n)^t\) calculated as follows:

$$\begin{aligned} \left. \begin{array}{lcl} \mathbf {x}^{n+1} &{}=&{}\displaystyle \mathbf {x}^{n}+\frac{\varDelta t}{6} \Big (\mathbf {m}_1+2\mathbf {m}_2+2\mathbf {m}_3+\mathbf {m}_4\Big ),\\ \mathbf {m}_1&{}=&{} \displaystyle \mathbf {f}(\mathbf {x}^n,t_n), \qquad \mathbf {m}_2=\mathbf {f}\left( \mathbf {x}^n+\frac{\varDelta t}{2}\mathbf {m}^1, t_n+\frac{\varDelta t}{2}\right) ,\\ \mathbf {m}_3&{}=&{} \displaystyle \mathbf {f}\left( \mathbf {x}^n+\frac{\varDelta t}{2}\mathbf {m}^2, t_n+\frac{\varDelta t}{2}\right) , \qquad \mathbf {m}_4=\mathbf {f}\left( \mathbf {x}^n+\frac{\varDelta t}{2}\mathbf {m}^3, t_n+\varDelta t\right) , \\ \mathbf {x}^{0}&{}=&{}(S_0,I_0), \end{array} \right\} \end{aligned}$$
(8)

where \(\mathbf {f}\) is defined by

$$\begin{aligned} \mathbf {f} \left( \begin{array}{l} S\\ I\\ t \end{array} \right) = \left( \begin{array}{l} \varLambda -\mu \,S-\displaystyle \frac{\beta (t) S\,I}{1+kI}\\ \displaystyle \frac{\beta (t) S\,I}{1+kI}-(\mu +\gamma )\,I-m \end{array} \right) , \end{aligned}$$

i.e., \(\mathbf {f}\) is the right side of the system (2). Thus, (8) with \(\mathbf {x}^n:=(S^n,\) \(I^n)^t\) is the discretization of (2), which is called the discrete state.

The discrete cost function \(J_\varDelta \) is given by

$$\begin{aligned} J_{\triangle }(\mu ,\gamma ) =\delta \varDelta t\sum _{n=0}^N \left( I^{n}-I^{obs,n}\right) ^2, \end{aligned}$$
(9)

where \(I^{n}\) is obtained by the numerical scheme (8) and \(I^{obs,n}\) is the evaluation of the continuous observation on the nodes of the mesh, i.e., \(I^{obs,n}=I^{obs}(t_n)\). Note that \(J_{\triangle }\) given on (9) is the natural discretization of J given on (5). Thus, we have that

$$\begin{aligned} \text{ Minimize } \ \ J_\varDelta (\mu ,\gamma ) \;\; \text{ subject } \text{ to } I_{\varDelta } \text{ solution } \text{ of } \text{ the } \text{ numerical } \text{ scheme } \text{(2) } \end{aligned}$$
(10)

is the discrete version or the discretization of the optimization problem (5).

In order to define the discrete adjoint state \((p_\varDelta ,q_\varDelta )\), we apply the Lagrange multipliers method. We define the discrete Lagrangian

$$\mathscr {L}_\varDelta \!\left( S_\varDelta ,I_\varDelta ;p_\varDelta ,q_\varDelta \right) =J_\varDelta (\mu ,\gamma )-E_\varDelta \!\left( S_\varDelta ,I_\varDelta ;p_\varDelta ,q_\varDelta \right) ,$$

where \(J_\varDelta \) is defined in (9) and \(E_\varDelta :=E(S_\varDelta ,I_\varDelta ;p_\varDelta ,q_\varDelta )\) is given by

$$\begin{aligned} E_\varDelta =&\sum _{n=0}^{N-1}\left[ \mathbf {x}^n\Big (\mathbf {p}^{n-1}-\mathbf {p}^n\Big ) -\frac{\varDelta t}{6} \Big (\mathbf {m}_1+2\mathbf {m}_2+2\mathbf {m}_3+\mathbf {m}_4\Big ) \right] +\mathbf {x}^N\mathbf {p}^{N-1} -\mathbf {x}^0\mathbf {p}^{-1}. \end{aligned}$$

Thus, by analogous arguments to the continuous case, we need to determine \((p_\varDelta ,q_\varDelta )\) such that \(\partial _{S^n} \mathscr {L}_\varDelta =\partial _{I^n} \mathscr {L}_\varDelta =0\). Thus, from differentiation of \(\mathscr {L}_\varDelta \) we obtain that \(\mathbf {p}^n:=(p^n,q^n)^t\) can calculated by the scheme

$$\begin{aligned} \left. \begin{array}{lcl} \mathbf {p}^{n-1} &{}=&{}\displaystyle \mathbf {p}^{n}+\frac{\varDelta t}{6} \Big (\mathbf {n}_1+2\mathbf {n}_2+2\mathbf {n}_3+\mathbf {n}_4\Big )+ 2\delta \varDelta t\mathbf {g}(\mathbf {x}^n),\\ \mathbf {n}_1&{}=&{} \displaystyle \partial \mathbf {f}(\mathbf {x}^n,t_n), \qquad \mathbf {n}_2=\partial \mathbf {f}\left( \mathbf {x}^n+\frac{\varDelta t}{2}\mathbf {m}^1, t_n+\frac{\varDelta t}{2}\right) , \\ \mathbf {n}_3&{}=&{} \displaystyle \partial \mathbf {f}\left( \mathbf {x}^n+\frac{\varDelta t}{2}\mathbf {m}^2, t_n+\frac{\varDelta t}{2}\right) , \qquad \mathbf {n}_4=\partial \mathbf {f}\left( \mathbf {x}^n+\frac{\varDelta t}{2}\mathbf {m}^3, t_n+\varDelta t\right) , \\ \mathbf {p}^{N}&{}=&{}(0,0), \end{array} \right\} \end{aligned}$$
(11)

where

$$\begin{aligned} \partial \mathbf {f} \left( \begin{array}{l} S\\ I\\ t \end{array} \right) = \left( \begin{array}{l} -\mu \,-\displaystyle \frac{\beta (t) \,I}{1+kI} \\ \displaystyle \frac{\beta (t) S\,}{(1+kI)^2}-(\mu +\gamma )\, \end{array} \right) , \qquad \mathbf {g} \left( \begin{array}{l} S\\ I \end{array} \right) = \left( \begin{array}{l} 0 \\ I-I^{obs,n}\, \end{array} \right) , \end{aligned}$$

and \(\mathbf {x}^n\) is calculated by (8). The scheme (11) is called the discrete adjoint state.

The discrete gradient \(\nabla J_\varDelta \) is calculated by

$$\begin{aligned} \nabla J_\varDelta = \frac{\varDelta t}{6}\quad \sum _{n=0}^{N-1}\left[ \nabla _{\mu ,\gamma }\mathbf {m}_1 +2\nabla _{\mu ,\gamma }\mathbf {m}_2 +2\nabla _{\mu ,\gamma }\mathbf {m}_3 +\nabla _{\mu ,\gamma }\mathbf {m}_4 \right] , \end{aligned}$$
(12)

where \(\mathbf {m}_i\) for \(i=1,\ldots ,4\) are defined in (8). The gradient given in (12) is used to solve numerically the inverse problem.

Fig. 4
figure 4

Plot of the number of infected people using the real parameters and an initial estimate

Full size image

5 Numerical Results

In this section, we present a numerical result for estimating the value of parameters \(\mu \) and \(\gamma \) from synthetic observation data. We consider the system (3) and by a numerical simulation we obtain a discrete observation. Then, by the process indicated on Sect. 3 we construct \(I^{obs}\) on [0, T], see also Figs. 1 and 2. To be more precise, after processing the observation by a time series technique, we fit the discrete observation data by \(I^{obs}:[0,T]\in \mathbb {R}^+\) defined by

$$\begin{aligned} I^{obs}(t)&= a_1\sin (b_1t+c_1) +a_2\sin (b_2t+c_2) +a_3\sin (b_3t+c_3) \nonumber \\&\qquad \quad \quad \,+a_4\sin (b_4t+c_4) +a_5\sin (b_5t+c_5), \end{aligned}$$
(13)

where the values of \(a_i,b_i\), and \(c_i\) are given by

$$\begin{aligned}&a_1 = 2412,\quad a_2 = 1457,\quad a_3 = 430.7,\quad a_4 = 114.3,\quad a_5 = 40.3,\\&b_1 = 0.01641,\quad b_2 = 0.02814,\quad b_3 = 0.04432,\quad b_4 = 0.05374,\quad b_5 = 1.047,\\&c_1 = -0.3434,\quad c_2 = 1.491,\quad c_3 = 2.903,\quad c_4 = 5.065,\quad c_5 = -1.513. \end{aligned}$$

The graph of \(I^{obs}\) given in (13) is the curve labeled as real parameters in Figs. 4 and 5.

For identification, we use the gradient method where the gradient of the cost function is defined by (12). To be more precise, we proceed to the identification with the gradient method using the curvature information [2]:

$$\begin{aligned} \mathbf {e}^{k+1}= & {} \mathbf {e}^{k}-\lambda _k \nabla J(\mathbf {e}^{k}), \quad \text{ with }\quad \mathbf {e}^{k}=(\mu _k,\lambda _k),\\ \lambda _k= & {} \frac{\Vert \nabla J_\varDelta (\mathbf {e}^{k})\Vert \hat{\varepsilon }^2}{|J_\varDelta (\mathbf {e}^{k}-\hat{\varepsilon } \nabla J_\varDelta (\mathbf {e}^{k})) -2J_\varDelta (\mathbf {e}^{k}) +J_\varDelta (\mathbf {e}^{k}+\hat{\varepsilon } \nabla J_\varDelta (\mathbf {e}^{k}))|} \cdot \end{aligned}$$

Here \(J_\varDelta \) is calculated by (9). Moreover, we remark that in our numerical simulations we consider that \(\hat{\varepsilon }=10E-6\) in the definition of \(\lambda _k\) and \(\delta =10E-12\) in the definition of \(J_\varDelta \) and the discrete adjoint state. The numerical value of the parameters is given in Table 1. The infected curve for the initial guess parameters is labeled as initial estimate of the parameters as shown in Fig. 4. The infected curve for the identified parameters is labeled as final estimate of the parameters shown in Fig. 5.

Fig. 5
figure 5

Plot of the number of infected using the real parameters and a final estimate

Full size image
Table 1 Numerical value of the parameters
Full size table

Finally, Fig. 6 illustrates the path followed by the gradient method in order to descend the values in the cost function until reaching the point where the optimum is achieved.

Fig. 6
figure 6

Plot graph of the path traveled by the cost function until reaching the optimum

Full size image

6 Conclusions

In this paper, we have introduced a methodology, based on discrete gradient method and time series, for parameter identification or model calibration in ordinary differential equation systems. Although the content of this research focuses on a specific ordinary differential equations system, we can deduce that the proposed method can be generalized for identification of coefficients in other types of system. Moreover, in this study, we have applied the numerical identification for synthetic observation data and expect to apply the methodology in the model calibration when the experimental data is obtained in laboratory experiments.