Recent Advances in Stochastic Riemannian Optimization

Abstract

Stochastic and finite-sum optimization problems are central to machine learning. Numerous specializations of these problems involve nonlinear constraints where the parameters of interest lie on a manifold. Consequently, stochastic manifold optimization algorithms have recently witnessed rapid growth, also in part due to their computational performance. This chapter outlines numerous stochastic optimization algorithms on manifolds, ranging from the basic stochastic gradient method to more advanced variance reduced stochastic methods. In particular, we present a unified summary of convergence results. Finally, we also provide several basic examples of these methods to machine learning problems, including learning parameters of Gaussians mixtures, principal component analysis, and Wasserstein barycenters.

1 Introduction

In this chapter we outline first-order optimization algorithms used for minimizing the expected loss (risk) and its special case, finite-sum optimization (empirical risk). In particular, we focus on the setting where the parameters to be optimized lie on a Riemannian manifold. This setting appears in a variety of problems in machine learning and statistics, including principal components analysis [33], low-rank matrix completion [9, 39], fitting statistical models like Gaussian mixture models [17, 18, 38], Karcher mean computation [22, 33], Wasserstein barycenters [40], dictionary learning [12], low rank multivariate regression [27], subspace learning [28], and structure prediction [34]; see also the textbook [1].

Typical Riemannian manifolds used in applications can be expressed by a set of constraints on Euclidean manifolds. Therefore, one can view a Riemannian optimization problem as a nonlinearly constrained one, for which one could use classical approaches. For instance, if the manifold constitutes a convex set in Euclidean space, one can use gradient projection like methods,¹ or other nonlinear optimization methods [6]. These methods could suffer from high computational costs, or as a more fundamental weakness, they may fail to satisfy the constraints exactly at each iteration of the associated algorithm. Another problem is that the Euclidean gradient does not take into account the geometry of the problem, and even if the projection can be done and the constraints can be satisfied at each iteration, the numerical conditioning may be much worse than a method that respects geometry [1, 42].

Riemannian optimization has shown great success in solving many practical problems because it respects the geometry of the constraint set. The definition of the inner product in Riemannian geometry makes the direction of the gradient to be more meaningful than Euclidean gradients because it considers the geometry imposed by constraints on the parameters of optimization. By defining suitable retractions (geodesic like curves on manifolds), the constraint is always satisfied. Sometimes the inner product is defined to also take into account the curvature information of the cost function. The natural gradient is an important example of the Riemannian gradient shown to be successful for solving many statistical fitting problems [2]. The natural gradient was designed for fitting statistical models and it is a Riemannian gradient on a manifold where the metric is defined by the Fisher information matrix.

Additional Background and Summary

Another key feature of Riemannian optimization is the generalization of the widely important concept of convexity to geodesic convexity. We will see later in this chapter that geodesic convexity help us derive convergence results for accelerated gradient descent methods akin to their famous Euclidean counterpart: Nesterov’s accelerated gradient method. Similar to the Euclidean case, there are works that develop results for recognizing geodesic convexity of functions for some special manifolds [37]. Reformulating problems keeping an eye on geodesic convexity also yields powerful optimization algorithms for some practical problems [18].

After summarizing key concepts of Riemannian manifolds, we first sketch the Riemannian analogue of the widely used (Euclidean) stochastic gradient descent method. Though some forms of stochastic gradient descent (SGD) such as natural gradient were developed decades ago, the version of SGD studied here and its analysis has a relatively short history; Bonnabel [8] was the first to give a unifying framework for analyzing Riemannian SGD and provided an asymptotic analysis on its almost sure convergence. We recall his results after explaining SGD on manifolds. We then note how convergence results of [15] for Euclidean non-convex SGD generalize to the Riemannian case under similar conditions [18]. Among recent progress on SGD, a notable direction is that of faster optimization by performing variance reduction of stochastic gradients. We will later outline recent results of accelerating SGD on manifolds and give convergence analysis for geodesically non-convex and convex cases. Finally, we close by summarizing some applications drawn from machine learning that benefit from the stochastic Riemannian algorithms studied herein.

Apart from the algorithms given in this chapter, there exist several other methods that generalize well from the Euclidean to the Riemannian setting. For example in [4] the SAGA algorithm [13] is generalized to Riemannian manifolds along with convergence theory assuming geodesic convexity. In [23] a Riemannian stochastic quasi-Newton method is studied; in [21] an inexact Riemannian trust-region method is developed and applied to finite-sum problems. Adaptive stochastic gradient methods such as ADAM and RMSProp have also been generalized [5, 24, 25]. It was observed however that ADAM works inferior to plain SGD for fitting Gaussian mixture models [16], where momentum and Nesterov SGD offered the best variants that improve on the performance of plain SGD.

The convergence results presented in this chapter are for general Riemannian manifolds and hold for a fairly general class of cost functions. For specific manifolds and functions, one can obtain better convergence results for the algorithms. For example for the case of quadratic optimization with orthogonality constraint, the authors in [26] proved convergence results. The authors in [41] proved convergence for a block eigensolver.

2 Key Definitions

We omit standard definitions such as Riemannian manifolds, geodesics, etc.; and defer to a standard textbook such as [20]. Readers familiar with concepts from Riemannian geometry can skip this section and directly move onto Sect. 19.3; however, a quick glance will be useful for getting familiar with our notation.

A retraction is a smooth mapping $\operatorname {\mathrm {Ret}}$ from the tangent bundle $T\mathcal {M}$ to the manifold $\mathcal {M}$. The restriction of a retraction to $T_x\mathcal {M}$, $\operatorname {\mathrm {Ret}}_x:T_x\mathcal {M} \rightarrow \mathcal {M}$, is a smooth mapping that satisfies the following:

• 1. $\operatorname {\mathrm {Ret}}_x(0)=x$, where 0 denotes the zero element of $T_x\mathcal {M}$.

• 2. $D \operatorname {\mathrm {Ret}}_x(0)=\text{id}_{T_x\mathcal {M}}$, where $D \operatorname {\mathrm {Ret}}_x$ denotes the derivative of $\operatorname {\mathrm {Ret}}_x$ and $\text{id}_{T_x\mathcal {M}}$ denotes the identity mapping on $T_x\mathcal {M}$.

One possible candidate for retraction on Riemannian manifolds is the exponential map. The exponential map $\operatorname {\mathrm {Exp}}_x:T_x\mathcal {M}\rightarrow \mathcal {M}$ is defined as $\operatorname {\mathrm {Exp}}_x v = \gamma (1)$, where γ is the geodesic satisfying the conditions γ(0) = x and $\dot {\gamma }(0) = v$.

A vector transport $\mathcal {T}:\mathcal {M} \times \mathcal {M} \times T \mathcal {M}\rightarrow T \mathcal {M}, (x,y,\xi ) \mapsto \mathcal {T}_{x,y}(\xi )$ is a mapping that satisfies the following properties:

• 1. There exists an associated retraction $\operatorname {\mathrm {Ret}}$ and a tangent vector ν satisfying $\mathcal {T}_{x,y}(\xi ) \in T_{ \operatorname {\mathrm {Ret}}_x(\xi )}$, for all $\xi \in T_x\mathcal {M}$.

• 2. $\mathcal {T}_{x,x}\xi = \xi$, for all $\xi \in T_x\mathcal {M}$.

• 3. The mapping $\mathcal {T}_{x,y}(\cdot )$ is linear.

We use $\mathcal {T}_{x,y}^{ \operatorname {\mathrm {Ret}}_x}$ to denote the vector transport constructed by the differential of the retraction, i.e., $\mathcal {T}_{x,y}^{ \operatorname {\mathrm {Ret}}_x} (\xi ) = D \operatorname {\mathrm {Ret}}_{x}(\eta )[\xi ]$, wherein $\operatorname {\mathrm {Ret}}_x(\eta )=y$ (in the case of multiple η, we make it clear by writing the value of η), while $\mathcal {P}_{x,y}^{ \operatorname {\mathrm {Ret}}_x}$ denotes the parallel transport along the retraction curve (again, if there are multiple curves where $\operatorname {\mathrm {Ret}}_x(\eta )=y$, we make it clear from context which curve is meant).

The gradient on a Riemannian manifold is defined as the vector ∇f(x) in tangent space such that

$$\displaystyle \begin{aligned} Df(x)\xi = \langle {\nabla f(x)},\, {\xi} \rangle,\quad \text{for}\ \xi \in T_x\mathcal{M}, \end{aligned}$$

where 〈⋅, ⋅〉 is the inner product in the tangent space $T_x\mathcal {M}$. Df(x)ξ is the directional derivative of f along ξ. Let $\gamma :[-1,1]\to \mathcal {M}$ be a differentiable curve with γ(0) = x and $\dot {\gamma }(0)=\xi$ (for example $\gamma (t)= \operatorname {\mathrm {Exp}}(t\xi )$), then the directional derivative can be defined by

$$\displaystyle \begin{aligned} Df(x)\xi = \frac{d}{d\tau}f ( \gamma(\tau))\bigg\rvert_{\tau=0}. \end{aligned}$$

Differentials at each point on the manifold forms the cotangent space. The cotangent space on the smooth manifold $\mathcal {M}$ at point x is defined as the dual space of the tangent space. Elements of the cotangent space are linear functionals on the tangent space.

The Hessian of a function is a symmetric bilinear form $D^2 f(x):T_x\mathcal {M} \times T_x\mathcal {M} \to \mathbb {R},(\xi ,\eta )\to \langle {\nabla _\eta \nabla f(x)},\, {\xi } \rangle$, where ∇_η is the covariant derivative with respect to η [1]. The Hessian as a operator $\nabla ^2 f(x):T_x\mathcal {M}\to T_x\mathcal {M}$ is a linear operator that maps ν in $T_x\mathcal {M}$ onto the Riesz representation D ²f(x)(ν, .). Alternatively, the operator Hessian can be defined by

$$\displaystyle \begin{aligned} \frac{d}{d\tau} \langle {\nabla f ( \gamma(\tau))},\, {\nabla f ( \gamma(\tau))} \rangle\bigg\rvert_{\tau=0} = 2\langle {\nabla f(x)},\, {(\nabla^2 f)\xi} \rangle, \end{aligned}$$

where $\gamma :[-1,1]\to \mathcal {M}$ is a differentiable curve with γ(0) = x and $\dot {\gamma }(0)=\xi$. In the following, we give some conditions and definitions needed for the complexity analysis of the algorithms in this book chapter.

Definition 19.1 (ρ-Totally Retractive Neighborhood)

A neighborhood Ω of a point x is called ρ-totally retractive if for all y ∈ Ω, $\Omega \subset \mathbb {B}(0_y,\rho )$ and $\operatorname {\mathrm {Ret}}_y(\cdot )$ is a diffeomorphism on $\mathbb {B}(0_y,\rho )$.

All optimization algorithms given in this book chapter start from an initial point and the point is updated based on a retraction along a direction with a certain step size. The following condition guarantees that all points along retraction in all interactions stay in a set.

Definition 19.2 (Iterations Stay Continuously in $\boldsymbol {\mathcal {X}}$)

The iterate $x_{k+1}= \operatorname {\mathrm {Ret}}_{x_k}( \alpha _k \xi _k)$ is said to stay continuously in $\mathcal {X}$ if $\operatorname {\mathrm {Ret}}_{x_k}(t\xi _k)\in \mathcal {X}$ for all t ∈ [0, α _k].

Most of the optimization algorithms explained in this chapter need a vector transport. The convergence analysis for many of them is available for the specific case of parallel transport. Some works that go beyond parallel transport still need some extra conditions on the vector transport as explained below. These conditions hold a forteriori for parallel transport.

Definition 19.3 (Isometric Vector Transport)

The vector transport $\mathcal {T}$ is said to be isometric on $\mathcal {M}$ if for any $x,y\in \mathcal {M}$ and $\eta ,\xi \in T_x \mathcal {M}$, $\langle {\mathcal {T}_{x,y}(\eta )},\, {\mathcal {T}_{x,y}(\xi )} \rangle = \langle {\eta },\, {\xi } \rangle$.

Definition 19.4 (θ-Bounded Vector Transport)

The vector transport $\mathcal {T}$ with its associated retraction $\operatorname {\mathrm {Ret}}$ is said to be θ-bounded on $\mathcal {M}$ if for any $x,y = \operatorname {\mathrm {Ret}}_x(\xi )\in \mathcal {M}$ and $\xi \in T_x \mathcal {M}$,

$$\displaystyle \begin{aligned} \|{\mathcal{T}_{x,y} \eta - \mathcal{P}_{x,y}^{\operatorname{\mathrm{Ret}}_x} \eta}\| \leq \theta \|{\xi}\|\|{\eta}\|, \end{aligned} $$

(19.1)

where $\mathcal {P}$ is the parallel transport along this associated retraction curve.

Definition 19.5 (θ-Bounded Inverse Vector Transport)

The inverse vector transport with its associated retraction $\operatorname {\mathrm {Ret}}$ is said to be θ-bounded on $\mathcal {M}$ if for any $x,y = \operatorname {\mathrm {Ret}}_x(\xi )\in \mathcal {M}$ and $\xi \in T_x \mathcal {M}$,

$$\displaystyle \begin{aligned} \|{\left ( \mathcal{T}_{x,y}\right)^{-1} \chi - \left ( \mathcal{P}_{x,y}^{\operatorname{\mathrm{Ret}}_x}\right)^{-1} \chi}\| \leq \theta \|{\chi}\|\|{\xi}\|, \end{aligned}$$

where $\mathcal {P}$ is the parallel transport along this associated retraction curve.

The following proposition helps in checking if a vector transport satisfies some of the conditions expressed above.

Proposition 19.6 (Lemma 3.5 in Huang et al. [19])

Assume that there exists a constant c ₀ > 0 such that $\mathcal {T}$ satisfies $\|{\mathcal {T}_{x,y} -\mathcal {T}_{x,y}^{ \operatorname {\mathrm {Ret}}_x} }\| \leq c_0 \|{\xi }\|$, $\|{\left ( \mathcal {T}_{x,y}\right )^{-1} - \left ( \mathcal {T}_{x,y}^{ \operatorname {\mathrm {Ret}}_x}\right )^{-1} }\| \leq c_0 \|{\xi }\|$, for any $x,y\in \mathcal {M}$ and the retraction $y= \operatorname {\mathrm {Ret}}_x(\xi )$. Then, the vector transport and its inverse are θ-bounded on $\mathcal {M}$, for a constant θ > 0.

We note that if the vector transport is C ⁰, then the condition of this proposition holds.

For the convergence analysis of the algorithms in this chapter, the cost function needs to satisfy some of the properties given below.

Definition 19.7 (G-Bounded Gradient)

A function $f:\mathcal {X}\to \mathbb {R}$ is said to have a G-bounded gradient in $\mathcal {X}$ if ∥∇f(x)∥≤ G, for all $x \in \mathcal {X}$.

Definition 19.8 (H-Bounded Hessian)

A function $f:\mathcal {X}\to \mathbb {R}$ is said to have an H-bounded Hessian in $\mathcal {X}$ if ∥∇²f(x)∥≤ H, for all $x \in \mathcal {X}$.

Definition 19.9 (Retraction L-Smooth)

A function $f:\mathcal {X}\to \mathbb {R}$ is said to be retraction L-smooth if for any $x,y= \operatorname {\mathrm {Ret}}_x(\xi )$ in $\mathcal {X}$, we have

$$\displaystyle \begin{aligned} f(y) \leq f(x) + \langle {\nabla f(x)},\, {\xi} \rangle + \frac L2 \|{\xi}\|{}^2. \end{aligned}$$

If the retraction is the exponential map, then the function is called geodesically L-smooth.

Definition 19.10 (Retraction L-Upper-Hessian Bounded)

A function $f:\mathcal {X} \to \mathbb {R}$ is said to be upper-Hessian bounded in a subset $\mathcal {U} \subset \mathcal {X}$ if $\operatorname {\mathrm {Ret}}_x(t\xi )$ stays in $\mathcal {X}$ for all $x,y= \operatorname {\mathrm {Ret}}_x(\xi )$ in $\mathcal {U}$ and t ∈ [0, 1], and there exists a constant L > 0 such that $\frac {d^2 f( \operatorname {\mathrm {Ret}}_x(t\xi ))}{dt^2} \leq L$.

Definition 19.11 (Retraction μ-Lower-Hessian Bounded)

A function $f:\mathcal {X} \to \mathbb {R}$ is said to be lower-Hessian bounded in a subset $\mathcal {U} \subset \mathcal {X}$ if $\operatorname {\mathrm {Ret}}_x(t\xi )$ stays in $\mathcal {X}$ for all $x,y= \operatorname {\mathrm {Ret}}_x(\xi )$ in $\mathcal {U}$ and t ∈ [0, 1], and there exists a constant μ > 0 such that $\frac {d^2 f( \operatorname {\mathrm {Ret}}_x(t\xi ))}{dt^2} \geq \mu$.

Definition 19.12 (Retraction L _l-Lipschitz)

A function $f:\mathcal {X} \to \mathbb {R}$ is said to be retraction L _l-Lipschitz in $\mathcal {X}$, if there exists L _l > 0 such that for all $x,y \in \mathcal {X}$,

$$\displaystyle \begin{aligned} \|{\mathcal{P}_{x,y}^{\operatorname{\mathrm{Ret}}_x} \nabla f(x)- \nabla f(y)}\| \leq L_l \|{\xi}\|, {} \end{aligned} $$

(19.2)

where $\mathcal {P}$ is the parallel transport along this associated retraction curve $y = \operatorname {\mathrm {Ret}}_x(\xi )$.

If the retraction is the exponential map, then this condition is called geodesically L _l-Lipschitz. A function that is geodesically L _l-Lipschitz is also geodesically L-smooth with L = L _l [44].

In the following, we give two propositions and a theorem for checking if a function satisfies some of the conditions explained before. The following proposition is based on a Lemma in [22].

Proposition 19.13

Suppose that the function $f:\mathcal {X} \to \mathbb {R}$ is retraction L-upper-Hessian bounded in $\mathcal {U} \subset \mathcal {X}$. Then, the function is also retraction L-smooth in $\mathcal {U}$.

Proposition 19.14 (Lemma 3.8 in Kasai et al. [22])

Let $\operatorname {\mathrm {Ret}}$ be a retraction on $\mathcal {M}$ and the vector transport associated with the retraction and its inverse be θ-bounded. Assume a function is twice continuously differentiable with H-bounded Hessian. Then the function is retraction L _l-Lipschitz with L _l = H(1 + Ξθ) with Ξ being an upper bound for ∥ξ∥ in (19.2).

For showing retraction L-smoothness, we can use the following theorem.

Theorem 19.15 (Lemma 2.7 in Boumal et al. [11])

Let $\mathcal {M}$ be a compact Riemannian submanifold of a Euclidean space. Let $\operatorname {\mathrm {Ret}}$ be a retraction on $\cal M$ . If a function has a Euclidean Lipschitz continuous gradient in the convex hull of $\mathcal {M}$ , then the function is retraction L-smooth for some constant L for any retraction.

The aforementioned conditions of function are quite general. In the following we give some conditions on functions that help to develop stronger convergence results.

Definition 19.16 (g-Convex)

A set $\mathcal X$ is geodesically convex (g-convex) if for any $x,y\in \mathcal X$, there is a geodesic γ with γ(0) = x, γ(1) = y and $\gamma (t)\in \mathcal X$ for t ∈ [0, 1]. A function $f:\mathcal X \to R$ is called geodesically convex in this set if

$$\displaystyle \begin{aligned} f(\gamma(t))\leq (1-t) f(x) + t f(y). \end{aligned}$$

Definition 19.17 (μ-Strongly g-Convex)

A function $f:\mathcal X \to R$ is called geodesically μ-strongly convex if for any $x,y= \operatorname {\mathrm {Exp}}_x(\xi )\in \mathcal X$ and g _x subgradient of f at x (gradient if f is smooth), it holds

$$\displaystyle \begin{aligned} f(y)\geq f(x)+\langle {g_x},\, {\xi} \rangle+\frac \mu 2 \| \xi \|{}^2. \end{aligned}$$

Definition 19.18 (τ-Gradient Dominated)

A function $f:\mathcal X \to R$ is called τ-gradient dominated if x ^∗ is a global minimizer of f and for every $x\in \mathcal X$ we have

$$\displaystyle \begin{aligned} f(x) - f(x^*) \leq \tau \|\nabla f(x) \|{}^2. {} \end{aligned} $$

(19.3)

The following proposition shows that strongly convex functions are also gradient dominated. Therefore, the convergence analysis developed for gradient dominated functions also holds for strongly convex functions [44].

Proposition 19.19

τ-gradient domination is implied by $\frac {1}{2\tau }$ -strong convexity as in Euclidean case.

3 Stochastic Gradient Descent on Manifolds

In the most general form, consider the following constrained optimization problem:

$$\displaystyle \begin{aligned} \min_{x \in \mathcal{M}} f(x).\end{aligned} $$

(19.4)

We assume $\mathcal {M}$ is a Riemannian manifold and that at each step of SGD we obtain a noisy version of the Riemannian gradient. Riemannian SGD uses the following simple update rule:

$$\displaystyle \begin{aligned} x_{t+1} = \operatorname{\mathrm{Ret}}_{x_{t}}\bigl(-\eta_t \nabla f_{i_t}(x_t)\bigr),\end{aligned} $$

(19.5)

where $\nabla f_{i_t}$ is a noisy version of the Riemannian gradient at time step t and the noise terms at different time steps are assumed to be independent. Note that there is stochasticity in each update. Therefore, the value x _t can be seen as a sample from a distribution depending on the gradient noise until time step t. A sketch of Riemannian SGD is given in Algorithm 1. For providing convergence results for all algorithms, it is assumed the stochastic gradients in all iterations are unbiased, i.e.,

$$\displaystyle \begin{aligned} \mathbb{E}[\nabla f_{i_t}(x_t) -\nabla f(x_t) ] =0. \end{aligned}$$

This unbiasedness condition is assumed in all theorems and we do not state it explicitly in the statements of the theorems.

Algorithm 1 Riemannian SGD

Given: Smooth manifold $\mathcal {M}$ with retraction $\operatorname {\mathrm {Ret}}$; initial value x ₀; a differentiable cost function f; number of iterations T.

for t = 0,  1, …, T − 1 do

Obtain the direction ξ _t = ∇f _i(x _t), where ∇f _i(x _t) is the noisy version of the cost gradient

Use a step-size rule to choose the step-size α _t

Calculate $x_{t+1}= \operatorname {\mathrm {Ret}}_{x_t}(-\alpha _t \xi _t)$

end for

return x _T

The cost function used in many practical machine learning problems which is solved by SGD can be defined by

$$\displaystyle \begin{aligned} f(x) = \mathbb{E} [f(z;x)] = \int f(z;x)dP(z),\end{aligned} $$

(19.6)

where x denotes the parameters, dP is a probability measure and f(z;x) is the risk function. For this cost function $f_{i_t}=f(z_{i_t},x_t)$ is the risk evaluated at the current sample $z_{i_t}$ from the probability law dP. Apparently, the stochastic gradients for this cost function satisfy the condition that stochastic gradients are unbiased. A special case of the above-mentioned cost function is the following finite-sum problem:

$$\displaystyle \begin{aligned} f(x) = \frac 1n \sum_{i=1}^n f_i(z_i, x). \end{aligned} $$

(19.7)

If we assume to be our data, then the empirical distribution over the data $P(Z=z_i)=\frac {1}{n}$ gives rise to the above noted cost function. Therefore, the theoretical analysis for SGD works both for online-algorithms and also finite-sum optimization problems. To further elucidate this consider the following example.

Example: Maximum Likelihood Parameter Estimation

Consider we want to estimate the parameters of a model distribution given by the density q(z;x), where x denotes the parameters. In the online learning framework, we observe a sample z _t from the underlying distribution p(z) at each time step. Observing this new sample, the parameter set is updated by a rule. The update rule should be designed such that in the limit of observing enough samples, the parameters converge to the optimal parameters. The optimal parameters are commonly defined as the parameters that minimize the Kullback-Leibler divergence between the estimated and the true distributions. The following cost function minimizes this divergence:

$$\displaystyle \begin{aligned} f(x) = \mathbb{E} [-\log q(z;x)] = -\int \log q(z;x) p(z) dz, \end{aligned}$$

where q is the density of model distribution and p is the true density. Apparently, this cost function is in the form of cost function defined in (19.6). One of the common update rules for online learning is SGD. For Riemannian SGD, we have $\nabla f(z_t,x_t) = \nabla f_{i_t}(x_t)$ and we use the update rule as in (19.5).

In the finite sample case, consider to be i.i.d. samples from the underlying density q(z;x). A common approach for estimating the parameters is the maximum-likelihood estimate where we are minimizing the following cost function:

$$\displaystyle \begin{aligned} f(x) = \frac 1n \sum_{i=1}^n -\log q(z_i; x). \end{aligned}$$

The cost function is a finite-sum cost that can be minimized using SGD. Therefore, it is important to know the conditions under which SGD guarantees convergence.

The following theorem gives the convergence to stationary points of the cost function.

Theorem 19.20 (Theorem 2 in Bonnabel [8]) 

Consider the optimization problem in (19.4), where the cost function is the expected risk (19.6). Assume

• The manifold $\mathcal {M}$ is a connected Riemannian manifold with injectivity radius uniformly bounded from below by I > 0.

• The steps stay within a compact set.

• The gradients of the f _is are G-bounded.

Let the step-sizes in Algorithm 1 satisfy the following standard condition

$$\displaystyle \begin{aligned} \sum{\alpha_t^2} < \infty \mathit{\text{ and }} \sum{\alpha_t} = \infty, \end{aligned} $$

(19.8)

Then f(x _t) converges a.s. and ∇f(x _t) → 0 a.s.

Staying within a compact set of the previous theorem is a strong requirement. Under milder conditions, [18] were able to prove the rate of convergence.

Theorem 19.21 (Theorem 5 in Hosseini and Sra [18])

Assume that the following conditions hold

• The functions f _i are retraction L-smooth.

• The expected square norm of the gradients of the f _i s are G ² -bounded.

Then for the following constant step-size in Algorithm 1

$$\displaystyle \begin{aligned} \alpha_t= \frac{c}{\sqrt{T}}, \end{aligned}$$

we have

$$\displaystyle \begin{aligned} \min_{0\le t\le T{-}1}\mathbb{E}[\|{\nabla f(x_t)}\|{}^2] \leq \frac{1}{T}\sum_{t=0}^{T-1}\mathbb{E}[\|{\nabla f(x_t)}\|{}^2] {\le}\frac{1}{\sqrt{T}}\left( \frac{f(x_0){-}f(x^*)}{c} {+} \frac{Lc}{2}G^2\right). \end{aligned} $$

(19.9)

where f(x ₀) is the function value at the initial point and f(x ^∗) is the minimum function value.

The following theorem shows that it is possible to get a convergence rate without needing bounded gradients with a randomized rule. For this theorem, the stochastic gradients needs to have σ-bounded variance, i.e.,

$$\displaystyle \begin{aligned} \mathbb{E}[\|{\nabla f_{i_t}(x_t) - \nabla f(x_t)}\|{}^2] \leq \sigma^2,\qquad 0\le \sigma < \infty. \end{aligned}$$

The conditions and the resulting rate are similar to that of Euclidean case [15], and no further assumptions are necessary.

Theorem 19.22 (Theorem 4 in Hosseini and Sra [18])

Assume that the following conditions hold.

• The functions f _i are retraction L-smooth.

• The functions f _i have σ-bounded variance.

Assume a slightly modified version of SGD that outputs a point x _a by randomly picking one of the iterates, say x _t , with probability $p_t := (2\alpha _t-L\alpha _t^2)/Z_T$ , where $Z_T=\sum _{t=1}^T(2\alpha _t-L\alpha _t^2)$ . Furthermore, choose $\alpha _t = \min \{ L^{-1}, c\sigma ^{-1}T^{-1/2}\}$ in Algorithm 1 for a suitable constant c. Then, we obtain the following bound on $\mathbb {E}[\|{\nabla f(x_a)}\|{ }^2]$ , which measures the expected gap to stationarity:

$$\displaystyle \begin{aligned} \mathbb{E}[\|{\nabla f(x_a)}\|{}^2] \le \frac{2L\Delta_1}{T} + \bigl(c+c^{-1}\Delta_1\bigr)\frac{L\sigma}{\sqrt{T}} = \mathcal{O}\left(\frac 1T\right)+\mathcal{O}\left(\frac{1}{\sqrt{T}}\right). \end{aligned} $$

(19.10)

For Hadamard manifolds (complete, simply-connected Riemannian manifolds with nonpositive sectional curvature), one can prove a.s. convergence under milder conditions. Hadamard manifolds have strong properties, for example the exponential map at any point is globally invertible. Concerning convergence for Hadamard manifolds there is the following result requiring milder assumptions.

Theorem 19.23 (Theorem 3 in Bonnabel [8])

Consider the optimization problem in (19.4), where the cost function is the expected risk (19.6). Assume

• The exponential map is used for the retraction.

• The manifold $\mathcal {M}$ is a Hadamard manifold.

• There is a lower bound on the sectional curvature denoted by κ < 0.

• There is a point $y \in \mathcal {M}$ such that the negative gradient points towards y when d(x, y) becomes larger than s > 0, i.e.,

  $$\displaystyle \begin{aligned} \inf_{d(x,y)>s} \langle {\operatorname{\mathrm{Exp}}_x^{-1}(y)},\, {\nabla f(x)} \rangle<0 \end{aligned}$$

• There is a continuous function $g:\mathcal {M} \to \mathbb {R}$ that satisfies

  $$\displaystyle \begin{aligned} \begin{aligned} g(x) \geq \max & \big\{1, \mathbb{E}\big[ \|{\nabla f(z;x)}\|{}^2 (1+\sqrt{\kappa}(d(x,y) + \|{\nabla f(z;x)}\|))\big], \\ & \mathbb{E}\big[\big(2\|{\nabla f(z;x)}\|d(x,y)+\|{\nabla f(z;x)}\|{}^2\big)^2\big] \big\} \end{aligned} \end{aligned}$$

Then for the step size rule $\alpha _t = -\frac {\beta _t}{g(x_t)}$ in Algorithm 1, wherein β _t satisfying (19.8), f(x _t) converges a.s. and ∇f(x _t) → 0 a.s.

4 Accelerating Stochastic Gradient Descent

Mainly for finite-sum problems but also for expected risk (19.6) problems, accelerated algorithms have been developed with faster convergence rates than plain SGD. In this section, we review several popular accelerated algorithms that are based on variance reduction ideas. Stochastic variance reduced gradient (SVRG) is a popular variance reduction technique that has a superior convergence than plain SGD. A Riemannian version of SVRG (R-SVRG) was proposed in [33] and generalized to use retractions and vector transports in [36]. Variance reduction can be seen in the line 9 of Algorithm 2, where the average gradient is used for adjust the current gradient. Consider a stochastic gradient that has high variance; then subtracting the difference between this gradient and the average gradient at a reference point from this gradient in the current point reduces the effect of high variance. Because we are on a Riemannian manifold, gradients live in different tangent spaces, and a vector transport is needed to make the subtraction meaningful as can be seen in the line 9 of Algorithm 2.

Algorithm 2 Riemannian SVRG

• 1: Given: Smooth manifold $\mathcal {M}$ with retraction $\operatorname {\mathrm {Ret}}$ and vector transport $\mathcal {T}$; initial value x ₀; a finite-sum cost function f; update frequency m; number of epochs S and K.

• 2: for k = 0, …, K-1 do

• 3: $\tilde {x}^{0}= x_{k}$

• 4: for s = 0, …, S-1 do

• 5:      Calculate the full Riemannian gradient $\nabla f(\tilde {x}^{s})$

• 6:      Store $x_{0}^{s+1} = \tilde {x}^{s}$

• 7:      for t = 0, …, m − 1 do

• 8:         Choose uniformly at random

• 9:         Calculate $\xi _{t}^{s+1} = \nabla f_{i_t}({x}_{t}^{s+1}) - \mathcal {T}_{\tilde {x}^{s},x_{t}^{s+1}}(\nabla f_{i_t}(\tilde {x}^{s})-\nabla f(\tilde {x}^{s}))$

• 10:         Use a step-size rule to choose the step-size $\alpha _t^{s+1}$

• 11:         Calculate $x_{t+1}^{s+1}= \operatorname {\mathrm {Ret}}_{x_t^{s+1}}(-\alpha _t^{s+1} \xi _t^{s+1})$

• 12:      end for

• 13:      Option I-a: Set $\tilde {x}^{s+1} = x_m^{s+1}$

• 14:      Option II-a: Set $\tilde {x}^{s+1} = x_t^{s+1}$ for randomly chosen

• 15: end for

• 16: Option I-b: Set $x_{k+1} = \tilde {x}^{S}$

• 17: Option II-b: Set $x_{k+1} = \tilde {x}_t^{s}$ for randomly chosen and

• 18: end for

• 19: return x _K

The authors in [33] were able to prove that R-SVRG has the same convergence as in the Euclidean case [32]. Though, the statement on the convergence rate needs additional assumptions and a bound depending on the sectional curvature.

Theorem 19.24 (Theorem 2 in Zhang et al. [33]) 

Consider the optimization problem in (19.4), where the cost function is the finite sum (19.7). Consider, we run Riemannian SVRG to solve this problem with K = 1, Option I-a, Option II-b. Assume

• The exponential map is used for the retraction and the parallel transport is used for the vector transport.

• The iterations stay in a compact subset $\mathcal {X}$, and the diameter of $\mathcal {X}$ is bounded by D, that is $\max _{x,y \in \mathcal {X}}d(x,y) \leq D$.

• The exponential map on $\mathcal {X}$ is invertible.

• The sectional curvature is upper-bounded.

• There is a lower bound on the sectional curvature denoted by κ.

• The functions f _i are geodesically L-smooth.

• The function f attains its minimum at $x^* \in \mathcal {X}$.

Define ζ to be a constant that captures the impact of the manifold curvature.

(19.11)

Then there exist universal constants μ ₀ ∈ (0, 1), ν > 0 such that if we set $\alpha _t=\frac {\mu _0}{Ln^{\alpha _1} \zeta ^{\alpha _2}},\alpha _1 \in (0,1], \alpha _2 \in (0,2]$ and $m=\lfloor \frac {n^{3\alpha _1}}{3\mu _0\zeta ^{1-2\alpha _2}} \rfloor$ in Algorithm 2, we have

$$\displaystyle \begin{aligned} \mathbb{E}[\|{\nabla f(x_1)}\|{}^2] \leq \frac{Ln^{\alpha_1}\zeta^{\alpha_2} [f(x_0)-f(x^*)]}{T\nu}, \end{aligned}$$

where T = mS is the number of iterations.

The abovementioned theorem was stated based on the exponential map and the parallel transport that can be expensive making SVRG impractical for some applications. In [36] the following convergence result is proved when using retractions and vector transports.

Theorem 19.25 (Theorem 4.6 in Sato et al. [36])

Consider the optimization problem in (19.4), where the cost function is the finite sum (19.7). Consider, we run the Riemannian SVRG algorithm to solve this problem with K = 1, Option I-a and Option I-b. Assume

• The retraction is of the class C ².

• The iterations stay in a compact subset $\mathcal {X}$.

• For each s ≥ 0, there exists $\eta _t^{s+1}\in T_{\tilde {x}^s} \mathcal {M}$ such that $\operatorname {\mathrm {Ret}}_{\tilde {x}^s}(\eta _t^{s+1})=x_t^{s+1}$.

• There exists I > 0 such that, for any $x \in \mathcal {X}$, $\operatorname {\mathrm {Ret}}_x(.)$ is defined in a ball $\mathbb {B}(0_x,I)\in T_x \mathcal {M}$, which is centered at the origin 0_x in $T_x \mathcal {M}$ with radius I.

• The vector transport is continuous and isometric on $\mathcal {M}$.

• The functions f _i are twice-differentiable.

Assume the step-size $\alpha _t^s$ in Algorithm 2 is chosen by the rule (19.8). Then $f(x_t^s)$ converges a.s. and $\nabla f(x_t^s) \rightarrow 0$ a.s.

Note that existence of $\eta _t^{s+1}$ is guaranteed if $\operatorname {\mathrm {Ret}}_x$ has ρ-totally retractive neighborhood for all $x \in \mathcal {X}$. For the special case of the exponential map and the parallel transport, many of the conditions of the aforementioned theorem are automatically satisfied or simplified: The parallel transport is an isometry, the exponential map is of class C ², and the third and fourth conditions can be satisfied by having a connected manifold with the injectivity radius uniformly bounded from below by I > 0.

Stochastic recursive gradient (SRG) [29] is another variance reduction algorithm similar to SVRG proposed. It was recently shown that the algorithm achieves the optimal bound for the class of variance reduction methods that only assume the Lipschitz continuous gradients [30]. Recently, the Riemannian counterpart of this algorithm (R-SRG) shown in Algorithm 3 has also been developed [22]. The following theorem gives a convergence result with the minimalistic conditions needed for the proof.

Theorem 19.26 (Theorem 4.5 in Kasai et al. [22])

Consider the optimization problem in (19.4), where the cost function is the finite sum (19.7). Consider, we run the Riemannian SRG algorithm to solve this problem with S = 1. Assume

• The iterations stay continuously in a subset $\mathcal {X}$.

• The vector transport is θ-bounded.

• The vector transport is isometric on $\mathcal {X}$.

• The functions f _i are retraction L-smooth.

• The functions f _i are retraction L _l-Lipschitz.

• The gradients of the f _is are G-bounded.

• The function f attains its minimum at $x^* \in \mathcal {X}$.

Assume a constant step-size $\alpha \leq \frac {2}{L+\sqrt {L^2+8m(L_l^2+G^2\theta ^2)}}$ in Algorithm 3 . Then, we have

$$\displaystyle \begin{aligned} \mathbb{E}[\|{\nabla f(\tilde{x})}\|{}^2] \leq \frac{2}{\alpha(m+1)}[f(x_0)-f(x^*)]. \end{aligned}$$

Algorithm 3 Riemannian SRG

• 1: Given: Smooth manifold $\mathcal {M}$ with retraction $\operatorname {\mathrm {Ret}}$ and vector transport $\mathcal {T}$; initial value $\tilde {x}^0$; a finite-sum cost function f; update frequency m; number of epochs S.

• 2: for s = 0, …, S-1 do

• 3: Store $x_{0} = \tilde {x}^{s}$

• 4: Calculate the full Riemannian gradient ∇f(x ₀)

• 5: Store ξ ₀ = ∇f(x ₀)

• 6: Store $x_{1} = \operatorname {\mathrm {Ret}}_{x_0} (-\alpha _0 \xi _0)$

• 7: for t = 1, …, m − 1 do

• 8:      Choose uniformly at random

• 9:      Calculate $\xi _{t} = \nabla f_{i_t}(x_{t}) - \mathcal {T}_{x_{t-1},x_{t}}\bigl (\nabla f_{i_t}(x_{t-1})-\xi _{t-1}\bigr )$

• 10:      Use a step-size rule to choose the step-size α _t

• 11:      Calculate $x_{t+1}= \operatorname {\mathrm {Ret}}_{x_t}(-\alpha _t \xi _t)$

• 12: end for

• 13: Set $\tilde {x}^{s+1} = x_t$ for randomly chosen

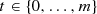
• 14: end for

• 15: return $\tilde {x}^{S}$

A very similar idea to R-SRG was used in another algorithm called Riemannian SPIDER (R-SPIDER) [45]. The Euclidean counterpart of the R-SPIDER algorithm was shown to have near optimal complexity bound. It can be applied to both the finite-sum and the stochastic optimization problems [14]. The details of the R-SPIDER method are given in Algorithm 4. The algorithm uses retraction and vector transport while the original algorithm and proofs of [45] were for the exponential mapping and the parallel transport. For the analysis of general non-convex functions in this section, we set T = 1 meaning that we have a single outer-loop.

Theorem 19.27 (Theorem 1 in Zhou et al. [45]) 

Consider the optimization problem in (19.4), where the cost function is the finite sum (19.7). Consider, we run the Riemannian SPIDER algorithm with option I to solve this problem. Assume

• The exponential map is used for the retraction and the parallel transport is used for the vector transport.

• The functions f _i are geodesically L-Lipschitz.

• The stochastic gradients have σ-bounded variance.

Let T = 1, $s=\min \bigl (n,\frac {16\sigma ^2}{\epsilon ^2}\bigr )$, $p=n_0s^{\frac 12}$, $\alpha _k=\min \bigl ( \frac {\epsilon }{2Ln_0},\frac {\|{\xi _k}\|}{4Ln_0}\bigr )$, $|\mathcal {S}_1|=s$, $|\mathcal {S}_2|=\frac {4s^{\frac 12}}{n_0}$ and $n_0 \in [1,4s^{\frac 12}]$ in Algorithm 4. Then, we achieve $\mathbb {E}[\|{\nabla f(\tilde {x}^1)}\|] \leq \epsilon$ in at most $K=\frac {14Ln_0\Delta }{\epsilon ^2}$ iterations in expectation, where Δ = f(x ₀) − f(x ^∗) with $x^*=\arg \min _{x\in \mathcal {M}} f(x)$.

For the online case, the following theorem considers the iteration complexity of the algorithm.

Theorem 19.28 (Theorem 2 in Zhou et al. [45])

Consider the optimization problem in (19.4), where the cost function is the expected risk (19.6). Assume the same conditions as in Theorem 19.27. Consider we run the Riemannian SPIDER algorithm with option I to solve this problem. Let T = 1, $p=\frac {n_0\sigma }{\epsilon }$, $\alpha _k=\min \bigl ( \frac {\epsilon }{2Ln_0},\frac {\|{\xi _k}\|}{4Ln_0}\bigr )$, $|\mathcal {S}_1|=\frac {64\sigma ^2}{\epsilon ^2}$, $|\mathcal {S}_2|=\frac {4\sigma }{\epsilon n_0}$ for $n_0 \in [1,4\frac \sigma \epsilon ]$ in Algorithm 4. Then, we achieve $\mathbb {E}[\|{\nabla f(\tilde {x}^1)}\|] \leq \epsilon$ in at most $K=\frac {14Ln_0\Delta }{\epsilon ^2}$ iterations in expectation, where Δ = f(x ₀) − f(x ^∗) with $x^*=\arg \min _{x\in \mathcal {M}} f(x)$.

The authors of [44] give the following convergence theorem for the same algorithm. The following theorems are for finite-sum and online settings.

Theorem 19.29 (Theorem 2 in Zhang et al. [44])

Consider the same problem and assume the same conditions as in Theorem 19.27. Consider, we run the Riemannian SPIDER algorithm with option II to solve this problem. Let T = 1, p = ⌈n ^1∕2⌉, $\alpha _k=\min \{\frac {1}{2L},\frac {\epsilon }{\|{\xi _k}\|L}\}$, $|\mathcal {S}_1|=n$, and $|\mathcal {S}_2|=\lceil n^{1/2} \rceil$ for each iteration in Algorithm 4. Then, we achieve $\mathbb {E}[\|{\nabla f(\tilde {x}^1)}\|{ }^2] \leq 10\epsilon ^2$ in at most $K=\frac {4L\Delta }{\epsilon ^2}$ iterations, where Δ = f(x ₀) − f(x ^∗) with $x^*=\arg \min _{x\in \mathcal {M}} f(x)$.

Theorem 19.30 (Theorem 1 in Zhang et al. [44])

Consider the same problem and assume the same conditions as in Theorem 19.28. Consider, we run the Riemannian SPIDER algorithm with option II to solve this problem. Let T = 1, $p=\frac {1}{\epsilon }$, $\alpha _k=\min \{\frac {1}{2L},\frac {\epsilon }{\|{\xi _k}\|L}\}$, $|\mathcal {S}_1|=\frac {2\sigma ^2}{\epsilon ^2}$, and $|\mathcal {S}_{2}|=\frac {2}{\epsilon }$ for each iteration in Algorithm 4. Then, we achieve $\mathbb {E}[\|{\nabla f(\tilde {x}^1)}\|{ }^2] \leq 10\epsilon ^2$ in at most $K=\frac {4L\Delta }{\epsilon ^2}$ iterations, where Δ = f(x ₀) − f(x ^∗) with $x^*=\arg \min _{x\in \mathcal {M}} f(x)$.

Among the convergence results presented in this section, R-SPIDER is the only algorithm that has strong convergence without the need for the strong condition that the iterates stay in a compact set. This condition is hard to ensure even for simple problems. Another important point to mention is that the step-sizes suggested by the theorems are very small, and in practice much larger step-sizes with some decaying rules are usually used.

Algorithm 4 Riemannian SPIDER

• 1: Given: Smooth manifold $\mathcal {M}$ with retraction $\operatorname {\mathrm {Ret}}$ and vector transport $\mathcal {T}$; initial value $\tilde {x}^0$; noisy version of the cost function f _i; iteration interval p ^t, mini-batch sizes $|\mathcal {S}_1^t|$ and $|\mathcal {S}_{2,k}^t|$; number of epochs T and K ^t.

• 2: for t = 0, …, T − 1 do

• 3: $x_0 = \tilde {x}^t$

• 4: for k = 0, …, K ^t − 1 do

• 5:      if mod(k, p ^t) = 0 then

• 6:         Draw minibatch size $|\mathcal {S}_1^t|$ and compute $\xi _k=\nabla f_{\mathcal {S}_1^t}(x_k)$

• 7:      else

• 8:         Draw minibatch size $|\mathcal {S}_2^t|$ and compute $\nabla f_{\mathcal {S}_2^t}(x_k)$

• 9:         Compute $\xi _k=\nabla f_{\mathcal {S}_2^t}(x_k) - \mathcal {T}_{x_{k-1},x_{k}}\bigl (\nabla f_{\mathcal {S}_2^t}(x_{k-1})-\xi _{k-1}\bigr )$

• 10:      end if

• 11:      if ξ _k ≤ 2𝜖 _k then

• 12:         Option II: $\tilde {x}^{t+1} = x_k$, break

• 13:      end if

• 14:      Use a step-size rule to choose the step-size $\alpha _k^t$

• 15:      Calculate $x_{k+1}= \operatorname {\mathrm {Ret}}_{x_k}(-\alpha _k^t \xi _k)$

• 16: end for

• 17: Option I: Output $\tilde {x}^{t+1} = x_k$ for randomly chosen

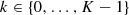
• 18: end for

• 19: return $\tilde {x}^{T}$

5 Analysis for G-Convex and Gradient Dominated Functions

For g-convex or gradient dominated functions, we obtain faster convergence rates for the algorithms explained in the previous sections. For plain SGD,  [43] proved faster convergence for g-convex functions as stated in the following theorem.

Theorem 19.31 (Theorem 14 in Zhang et al. [43]) 

Consider the R-SGD Algorithm for solving the optimization problem in (19.4), where the cost function is the expected risk (19.6). Assume

• The function f is g-convex.

• The exponential map is used for the retraction.

• The iterations stay in a compact subset $\mathcal {X}$, and the diameter of $\mathcal {X}$ is bounded by D, that is $\max _{x,y \in \mathcal {X}}d(x,y) \leq D$.

• There is a lower bound on the sectional curvature denoted by κ.

• The functions f _i are geodesically L-smooth.

• The function f attains its minimum at $x^* \in \mathcal {X}$.

• The functions f _i have σ-bounded variance.

• The manifold is Hadamard (Riemannian manifolds with global non-positive curvature).

Define ζ to be a constant that captures the impact of manifold curvature defined by

$$\displaystyle \begin{aligned} \zeta = \frac{\sqrt{|\kappa|}D}{\tanh\bigl(\sqrt{|\kappa|}D\bigr)}. {} \end{aligned} $$

(19.12)

Then the R-SGD algorithm with $\alpha _t = \frac {1}{L+\frac {\sigma }{D}\sqrt {(t+1)\zeta }}$ in Algorithm 1 satisfies

$$\displaystyle \begin{aligned} \mathbb{E} [ f(\bar{x}_T)-f(x^*)] \leq \frac{\zeta L D^2+2D\sigma\sqrt{\zeta T}}{2(\zeta+T-1)}, \end{aligned}$$

where $\bar {x}_1=x_1$, $\bar {x}_{t+1}= \operatorname {\mathrm {Exp}}_{\bar {x}_{t}}(\frac {1}{t+1} \operatorname {\mathrm {Exp}}^{-1}_{\bar {x}_{t}}(x_{t+1}))$, for 1 ≤ t ≤ T − 1 and $\bar {x}_T= \operatorname {\mathrm {Exp}}_{\bar {x}_{T-1}}(\frac {\zeta }{\zeta +T-1} \operatorname {\mathrm {Exp}}^{-1}_{\bar {x}_{T-1}}(x_{T}))$.

The aforementioned theorem shows that we need a decaying step size for obtaining faster convergence for the R-SGD algorithm, while Theorem 19.22 needed constant step size for getting a convergence rate for general non-convex functions. Decaying step-size is usually used in practice and the above theorem can be a motivation, because near local minima the function can be assumed to be g-convex. For the case of strongly g-convex functions, the authors of [43] proved a stronger convergence result stated below.

Theorem 19.32 (Theorem 12 in Zhang et al. [43])

Consider the R-SGD Algorithm for solving the optimization problem in (19.4), where the cost function is the expected risk (19.6). Assume

• The function f is μ-strongly g-convex.

• The exponential map is used for the retraction.

• The iterations stay in a compact subset $\mathcal {X}$, and the diameter of $\mathcal {X}$ is bounded by D, that is $\max _{x,y \in \mathcal {X}}d(x,y) \leq D$.

• There is a lower bound on the sectional curvature denoted by κ.

• The function f attains its minimum at $x^* \in \mathcal {X}$.

• The expected square norm of the gradients of the f _is are G ²-bounded.

• The manifold is Hadamard (Riemannian manifolds with global non-positive curvature).

Then the R-SGD algorithm with $\alpha _t = \frac {2}{\mu (t+2)}$ in Algorithm 1 satisfies

$$\displaystyle \begin{aligned} \mathbb{E} [ f(\bar{x}_T)-f(x^*)] \leq \frac{2\zeta G}{(T+2)}, \end{aligned}$$

where $\bar {x}_0=x_0$, $\bar {x}_{t+1}= \operatorname {\mathrm {Exp}}_{\bar {x}_{t}}(\frac {2}{t+2} \operatorname {\mathrm {Exp}}^{-1}_{\bar {x}_{t}}(x_{t+1}))$ and ζ is a constant given in (19.12).

For strongly g-convex functions, [33] proved a linear convergence rate for the R-SVRG algorithm given in the following theorem.

Theorem 19.33 (Theorem 1 in Zhang et al. [33])

Consider the optimization problem in (19.4), where the cost function is the finite sum (19.7). Consider, we run the Riemannian SVRG algorithm to solve this problem with K = 1, Option I-a and Option I-b. Assume the same conditions as in Theorem 19.24. Furthermore, assume that the function f is μ-strongly g-convex. If we use an update frequency and a constant step size in Algorithm 2 such that the following holds

$$\displaystyle \begin{aligned} a = \frac{3\zeta\alpha L^2}{\mu-2\zeta\alpha L^2}+\frac{(1+4\zeta\alpha^2-2\alpha\mu)^m(\mu-5\zeta\alpha L^2)}{\mu-2\zeta\alpha L^2}<1, \end{aligned}$$

then the iterations satisfy

$$\displaystyle \begin{aligned} \mathbb{E}[f(\tilde{x}^S)-f(x^*)] \leq \frac{L}{2} \mathbb{E}[d^2(\tilde{x}^S,x^*)]\leq \frac{L}{2}a^S d^2(x^0,x^*). \end{aligned}$$

For a class of functions more general than strongly g-convex functions, that is gradient-dominated functions, it is also possible to prove that R-SVRG has a strong linear convergence rate.

Theorem 19.34 (Theorem 3 in Zhang et al. [33])

Consider the optimization problem in (19.4), where the cost function is the finite sum (19.7). Consider, we run the Riemannian SVRG algorithm to solve this problem with Option II-a, Option I-b. Assume the same conditions as in Theorem 19.24. Furthermore, assume that the function f is τ-gradient dominated. If we use the parameters $\alpha =\frac {\mu _0}{Ln^{2/3}\zeta ^{1/3}}$, $m=\lfloor \frac {n}{3\mu _0}\rfloor$, $S=\lceil (6+\frac {18\mu _0}{n-3}) \frac {L \tau \zeta ^{1/2}\mu _0}{\nu n^{1/3}}\rceil$ for some universal constants μ ₀ ∈ (0, 1) and ν > 0 in Algorithm 2, then we have

$$\displaystyle \begin{aligned} \mathbb{E}[ \|{\nabla f(x^K)}\|{}^2] &\leq 2^{-K} \|{\nabla f(x^0)}\|{}^2,\\ \mathbb{E}[ f(x^K)-f(x^*)] &\leq 2^{-K} [ \|{f(x^0)-f(x^*)}\|]. \end{aligned} $$

The aforementioned strong convergence results for R-SVRG are valid when using the exponential map and the parallel transport. For the general retraction and the vector transport there is not any global rate of convergence result yet. However, the authors in [36, Theorem 5.14] proved a local linear convergence result for the R-SVRG algorithm.

For the R-SRG algorithm, [22] gives a convergence result for the g-convex case as stated in the following.

Theorem 19.35 (Theorem 4.1 in Kasai et al. [22])

Consider the optimization problem in (19.4), where the cost function is the finite sum (19.7). Assume the same conditions as in Theorem 19.26 hold, and furthermore assume that

$$\displaystyle \begin{aligned} \|{\mathcal{P}_{x,y}^{\operatorname{\mathrm{Ret}}_x} \nabla f_i(x)-\nabla f_i(y)}\|{}^2 \leq L \langle {\mathcal{P}_{x,y}^{\operatorname{\mathrm{Ret}}_x} \nabla f_i(x)-\nabla f_i(y)},\, {\operatorname{\mathrm{Exp}}_y^{-1}x} \rangle, \end{aligned}$$

where L is the constant for the retraction smooth function f. For the Euclidean case, this condition is equal to have a convex and L-smooth function. Consider, we run the Riemannian SRG algorithm to solve this problem using the parameters α and m in Algorithm 3 such that α < 2∕L and (β − L ²)α ² + 3Lα − 2 ≤ 0, where

$$\displaystyle \begin{aligned} \beta :=2\bigl((2L_l+2\theta G+L)\theta G +\nu L\bigr)m. {} \end{aligned} $$

(19.13)

Then for s > 0,

$$\displaystyle \begin{aligned} \mathbb{E}[\|{\nabla f(\tilde{x}^s)}\|{}^2] \leq \frac{2}{\alpha (m+1)} \mathbb{E}[\|{f(\tilde{x}^{s-1})-f(x^*) }\|] +\frac{\alpha L}{2-\alpha L} \mathbb{E}[\|{\nabla f(\tilde{x}^{s-1})}\|{}^2]. \end{aligned}$$

For μ-strongly g-convex functions, the authors of [22] proved linear convergence as stated below. The nice feature of the R-SRG algorithm is that it is the only method that achieves linear convergence without needing the exponential map and the parallel transport.

Theorem 19.36 (Theorem 4.3 in Kasai et al. [22])

Consider the optimization problem in (19.4), where the cost function is the finite sum (19.7). Assume the same conditions as in Theorem 19.35 and furthermore assume that the function f is μ-strongly convex. Consider, we run the Riemannian SRG algorithm to solve this problem using the parameters α and m in Algorithm 3 such that such that $\alpha _m := \frac {1}{\mu \alpha (m+1)}+\frac {\alpha L}{2-\alpha L} < 1$. Then,

$$\displaystyle \begin{aligned} \mathbb{E}[\|{\nabla f(\tilde{x}^s)}\|{}^2] \leq \sigma_m^s \mathbb{E}[\|{\nabla f(\tilde{x}^{0})}\|{}^2]. \end{aligned}$$

Similarly for τ gradient dominated functions, the authors of [22] obtained linear convergence.

Theorem 19.37 (Theorem 4.6 in Kasai et al. [22])

Consider the optimization problem in (19.4), where the cost function is the finite sum (19.7). Assume the same conditions as in Theorem 19.26 hold and furthermore assume that the function is τ-gradient dominated. Consider, we run Riemannian SRG algorithm to solve this problem with the same α in Algorithm 3 as that of Theorem 19.26 and assume $\bar \sigma _m:=\frac {2\tau }{\alpha (m+1)}<1$. Then for s > 0,

$$\displaystyle \begin{aligned} \mathbb{E}[\|{\nabla f(\tilde{x}^s)}\|{}^2] \leq \bar \sigma_m^s \mathbb{E}[\|{\nabla f(\tilde{x}^{0})}\|{}^2]. \end{aligned}$$

For τ-gradient dominated functions, [45] was able to prove stronger convergence results for the R-SPIDER algorithm. The following two theorems are convergence results for the finite-sum and online cases. Unlike the analysis for the general non-convex case, here the authors use a fixed step-size and adaptive batch sizes.

Theorem 19.38 (Theorem 3 in Zhou et al. [45])

Consider the finite sum problem (19.7) solved using the R-SPIDER algorithm with option I. Assume the same conditions as in Theorem 19.27, and furthermore assume that the function f is τ-gradient dominated. At iteration t of Algorithm 4, set $\epsilon _0=\frac {\sqrt {\Delta }}{2\sqrt {\tau }}$, $\epsilon _t=\frac {\epsilon _0}{2^t}$, $s_t=\min (n,\frac {32\sigma ^2}{\epsilon _{t-1}^2})$, $p^t=n_0^t s_t^{\frac 12}$, $\alpha _k=\frac {\|{\xi _k}\|}{2Ln_0}$, $|\mathcal {S}_1^t|=s_t$, $|\mathcal {S}_{2,k}^t|=\min \bigl (\frac {8p^t\|{\xi _{k-1}}\|{ }^2}{(n_0^{t})^2\epsilon _{t-1}^2},n\bigr )$ and $K^t=\frac {64Ln_o^t\Delta ^t}{\epsilon _{t-1}^2}$ where $n_0^t \in [1,\frac {8\sqrt {s}\|{\xi _{k-1}}\|{ }^2 }{\epsilon _{t-1}^2}]$ and Δ = f(x ₀) − f(x ^∗) with $x^*=\arg \min _{x\in \mathcal {M}} f(x)$. Then the sequence $\tilde {x}^t$ satisfies

$$\displaystyle \begin{aligned} \mathbb{E}[\|{\nabla f(\tilde{x}^t)}\|{}^2] \leq \frac{\Delta}{4^t\tau}. \end{aligned}$$

Theorem 19.39 (Theorem 4 in Zhou et al. [45])

Consider the optimization problem in (19.4) solved using the R-SPIDER algorithm with option I. Assume the same conditions as in Theorem 19.28, and furthermore assume that the function f is τ-gradient dominated. At iteration t of Algorithm 4, set $\epsilon _0=\frac {\sqrt {\Delta }}{2\sqrt {\tau }}$, $\epsilon _t=\frac {\epsilon _0}{2^t}$, $p^t=\frac {\sigma n_0^t}{\epsilon _{t-1}}$, $\alpha _k^t=\frac {\|{\xi _k}\|}{2L_ln_0^t}$, $|\mathcal {S}_1^t|=\frac {32\sigma ^2}{\epsilon _{t-1}^2}$, $|\mathcal {S}_{2,k}^t|=\frac {8\sigma \|{\xi _{k-1}}\|{ }^2}{n_0^{t}\epsilon _{t-1}^3}$ and $K^t=\frac {64Ln_o^t\Delta ^t}{\epsilon _{t-1}^2}$ where $n_0 \in [1,\frac {8\sigma \|{\xi _{k-1}}\|{ }^2 }{\epsilon _{t-1}^3}]$ and Δ = f(x ₀) − f(x ^∗) with $x^*=\arg \min _{x\in \mathcal {M}} f(x)$. Then the sequence $\tilde {x}^t$ satisties,

$$\displaystyle \begin{aligned} \mathbb{E}[\|{\nabla f(\tilde{x}^t)}\|{}^2] \leq \frac{\Delta}{4^t\tau}. \end{aligned}$$

The authors of [44] give the following analysis of the R-SPIDER algorithm for τ-gradient dominated functions.

Theorem 19.40 (Theorem 3 in Zhang et al. [44])

Consider the same problem and assume the same conditions as in Theorem 19.28. Consider, we run the Riemannian SPIDER algorithm with option II to solve this problem. Let p = ⌈n ^1∕2⌉, $\epsilon _t=\sqrt {\frac {M_0}{10\tau 2^t}}$, $\alpha _t=\frac {\epsilon _t}{L}$, $|\mathcal {S}_1|=n$, and $|\mathcal {S}_2|=\lceil n^{1/2} \rceil$ in each iteration of Algorithm 4, where M ₀ > f(x ₀) − f(x ^∗) with $x^*=\arg \min _{x\in \mathcal {M}} f(x)$. Then the algorithm returns $\tilde {x}^T$ that satisfies

$$\displaystyle \begin{aligned} \mathbb{E} [f(\tilde{x}^T) - f(x^*)] \leq \frac{M_0}{2^{T}}. \end{aligned}$$

The authors of [44] also give another proof for the R-SPIDER algorithm with different parameters that give better iteration complexity for τ-gradient dominated functions with respect to n.

Theorem 19.41 (Theorem 4 in Zhang et al. [44])

Consider the same problem and assume the same conditions as in Theorem 19.28. Consider, we run the Riemannian SPIDER algorithm with option II to solve this problem. In Algorithm 4, let T = 1, $p=\lceil 4L \tau \log (4) \rceil$, $\alpha =\frac {1}{2L}$, $|\mathcal {S}_1|=n$, and $|\mathcal {S}_{2,k}|=\lceil \min \biggl \{n,\frac {4\tau pL^2 \| \operatorname {\mathrm {Exp}}_{x_{k-1}}^{-1}(x_k)\|{ }^2 2^{\lceil k/p \rceil }}{ M_0}\biggr \}\rceil$, where M ₀ > f(x ₀) − f(x ^∗) with $x^*=\arg \min _{x\in \mathcal {M}} f(x)$. Then, the algorithm returns $\tilde {x}^K$ after K = pS iterations that satisfies

$$\displaystyle \begin{aligned} \mathbb{E} [f(\tilde{x}^K) - f(x^*)] \leq \frac{M_0}{2^{S}}.\end{aligned} $$

The theorems of the algorithms in the previous sections showing convergence speed of different algorithms are summarized in Tables 19.1 and 19.2. The incremental first order oracle (IFO) complexity for different algorithms are calculated by counting the number of evaluations needed to reach the 𝜖 accuracy of gradient ($\mathbb {E}[\|{\nabla f(x)}\|{ }^2 ] \leq \epsilon$) or function ($\mathbb {E}[ f(x)-f(x^*)]\leq \epsilon$) in the theorems given in the previous sections.

Table 19.1 Comparison of the IFO complexity for different Riemannian stochastic optimization algorithms under finite-sum and online settings

Table 19.2 Comparison of the IFO complexity for different Riemannian stochastic optimization algorithms under finite-sum and online settings

6 Example Applications

We list below a few finite-sum optimization problems drawn from a variety of applications. Riemannian stochastic methods turn out to be particularly effective for solving these problems. We only include the formulation, and refer the reader to the cited works for details about implementation and empirical performance. The manifolds occurring in the examples below are standard, and the reader can find explicit implementations of retractions, vector transport, etc., within the Manopt software [10], for instance.

Stochastic PCA

Suppose we have observations $z_1,\ldots ,z_n \in \mathbb {R}^d$. The stochastic PCA problem is to compute the top eigenvector of the matrix $\sum _{i=1}^n z_iz_i^T$. This problem can be written as a finite-sum optimization problem on the sphere $\mathbb {S}^{d-1}$ as follows

$$\displaystyle \begin{aligned} \min_{x^Tx=1}\quad -x^T\left(\sum\nolimits_{i=1}^nz_iz_i^T\right)x = -\sum\nolimits_{i=1}^n (z_i^Tx)^2. \end{aligned} $$

(19.14)

Viewing (21.100) as a Riemannian optimization problem was proposed in [33], who solved it using R-SVRG, in particular, by proving that the cost function satisfies a Riemannian gradient-dominated condition (probabilistically). One can extend this problem to solve for the top-k eigenvectors by considering is as an optimization problem on the Stiefel manifold.

A challenge for the methods discussed in the present paper, except R-SGD and R-SPIDER explained in Sect. 19.4 is the requirements for the iterates to remain within a predefined compact set. While the whole manifold is compact, for obtaining a precise theoretical characterization of the computational complexity of the algorithms involved, the requirement to remain within a compact set is important.

GMM

Let z ₁, …, z _n be observations in $\mathbb {R}^d$ that we wish to model using a Gaussian mixture model (GMM). Consider the mixture density

$$\displaystyle \begin{aligned} p(z; \{\mu_j,\Sigma_j\}_{j=1}^k) := \sum\nolimits_{j=1}^k \pi_j\mathcal{N}(z; \mu_j, \Sigma_j), \end{aligned}$$

where $\mathcal {N}(z; \mu , \Sigma )$ denotes the Gaussian density evaluated at z and parameterized by μ and Σ. This leads to the following maximum likelihood problem:

$$\displaystyle \begin{aligned} \max_{\{\pi_j,\mu_j,\Sigma_j\}_{j=1}^k}\sum\nolimits_{i=1}^n\log p(z_i; \{\mu_j,\Sigma_j\}_{j=1}^k). \end{aligned} $$

(19.15)

In [18], the authors reformulate (21.52) to cast it as a problem well-suited for solving using R-SGD. They consider the reformulated problem

$$\displaystyle \begin{aligned} \max_{\{\omega_j,S_j \succ 0\}_{j=1}^k} \sum_{i=1}^n \log\Bigl(\sum\nolimits_{j=1}^k\tfrac{\exp(\omega_j)}{\sum\nolimits_{k=1}^k \exp(\omega_k)} q(y_i; S_j)\Bigr), \end{aligned} $$

(19.16)

where y _i = [z _i;1], and q(y;S _j) is the centered normal distribution parameterized by $S_j = \begin {bmatrix} \Sigma _j + \mu _j\mu _j^T & \mu _j\\ \mu _j^T & 1\end {bmatrix}$. With these definitions, problem (21.61) can be viewed as an optimization problem on the product manifold $\bigl (\prod _{j=1}^k\mathbb {P}^{d+1}\bigr ) \times \mathbb {R}^{k-1}$.

Importantly, in [18] it was shown that SGD generates iterates that remain bounded, which is crucial, and permits one to invoke the convergence analysis without resorting to projection onto a compact set.

Karcher Mean

Let A ₁, …, A _n be hermitian (strictly) positive definite (hpd) matrices. This set is a manifold, commonly endowed with the Riemmanian metric 〈η, ξ〉 = tr(ηX ⁻¹ξX ⁻¹). This metric leads to the distance $d(X,Y) := \|\log (X^{-1/2}YX^{-1/2})\|{ }_F$ between hpd matrices X and Y . The Riemannian centroid (also called the “Karcher mean”) is defined as the solution to the following finite-sum optimization problem:

$$\displaystyle \begin{aligned} \min_{X \succ 0}\quad \sum\nolimits_{i=1}^n w_id^2(X,A_i), \end{aligned} $$

(19.17)

where the weights w _i ≥ 0 and $\sum _{i=1}^n w_i=1$. This problem is often used as a defacto benchmark problem for testing Riemannian optimization problems (see e.g., [33]). The objective function in (19.14) is both geodesically L-smooth as well as strongly convex, both properties can be exploited to obtain faster convergence [22, 33].

It is important to note that this problem is over the manifold of hpd matrices, which is a noncompact manifold. Hence, to truly invoke the convergence theorems (except for R-SGD and R-SPIDER explained in Sect. 19.4), we need to ensure lower bounds on the curvature as well as ensure that iterates remain within a compact set. Lower bounds on the curvature can be obtained in terms of $\min _{1\le i \le n}\lambda _{\min }(A_i)$; ensuring that the iterates remain within a compact set can be ensured via projection. Fortunately, for (19.17), a simple compact set containing the solution is known, since we know that (see e.g., [7]) its solution X ^∗ satisfies Hm(A ₁, …, A _n) ≼ X ^∗≼Am(A ₁, …, A _n), where Hm and Am denote the Harmonic and Arithmetic Means, respectively. A caveat, however, is that R-SVRG and related methods do not permit a projection operation and assume their iterates to remain in a compact set by fiat; R-SGD, however, allows metric projection and can be applied. Nevertheless, in practice, one can invoke any of the methods discussed in this chapter.

We note in passing here that the reader may also be interested in considering the somewhat simpler “Karcher mean” problems that arise when learning hyperbolic embeddings [35], as well as Fréchet-means on other manifolds [3, 31].

Wasserstein Barycenters

Consider two centered multivariate Gaussian distributions with covariance matrices Σ₁ and Σ₂. The Wasserstein W ₂ optimal transport distance between them is given by

(19.18)

The Wasserstein barycenter of n different centered Gaussians is then given by the solution to the optimization problem

$$\displaystyle \begin{aligned} \min_{X \succ 0}\quad \sum\nolimits_{i=1}^nw_id_W^2(X,\Sigma_i). \end{aligned} $$

(19.19)

While (21.83) is a (Euclidean) convex optimization problem, it lends itself to more efficient solution by viewing it as a Riemannian convex optimization problem [40]. A discussion about compact sets similar to the Karcher mean example above applies here too.

Riemannian Dictionary Learning

Dictionary learning problems seek to encode input observations using a sparse combination of an “overcomplete basis”. The authors of [12] study a Riemannian version of dictionary learning, where input hpd matrices must be encoded as sparse combinations of a set of hpd “dictionary atoms.” This problem may be cast as the finite-sum minimization problem

$$\displaystyle \begin{aligned} \min_{B, \alpha_1,\ldots,\alpha_n} \quad \sum\nolimits_{i=1}^n d^2\left(X_i,\sum\nolimits_{j=1}^m\alpha_{ij}B_j\right) + R(B,\alpha_1,\ldots,\alpha_n). \end{aligned} $$

(19.20)

In other words, we seek to approximate each input matrix $X_i \approx \sum _{j=1}^m \alpha _{ij}B_j$, using B _j ≻ 0 and nonegative coefficients α _ij. The function R(⋅) is a suitable regularizer on the tensor B and the coefficient matrix α, and d(⋅, ⋅) denotes the Riemannian distance.

For this particular problem, we can invoke any of the discussed stochastic methods in practice; though previously, results only for SGD have been presented [12]. By assuming a suitable regularizer R(⋅, ⋅) we can ensure that the problem has a solution, and that the iterates generated by the various methods remain bounded.