Shape Analysis of Functional Data

Abstract

Functional data is one of the most common types of data in our digital society. Such data includes scalar or vector time series, Euclidean curves, surfaces, or trajectories on nonlinear manifolds. Rather than applying past statistical techniques developed using standard Hilbert norm, we focus on analyzing functions according to their shapes. We summarize recent developments in the field of elastic shape analysis of functional data, with a perspective on statistical inferences. The key idea is to use metrics, with appropriate invariance properties, to register corresponding parts of functions and to use this registration in quantification of shape differences. Furthermore, one introduces square-root representations of functions to help simplify computations and facilitate efficient algorithms for large-scale data analysis. We will demonstrate these ideas using simple examples from common application domains.

1 Introduction

Statistical shape analysis aims to study the shapes of given geometric objects by statistical methods. It has wide applications in biology, computer vision, medical images, etc. For instance, in bioinformatics, it is important to associate the shapes of biological objects like RNAs and proteins with their functionality. Given a sample of shapes, one would like to use some statistical tools to summarize the information and make the inference. Some important techniques include an appropriate metric for quantifying shape difference, geodesics to study a natural deformation between two shapes, summary statistics (mean, covariance) of shapes, shape models to characterize shape populations and regression models using shapes as predictors or responses.

The object of interest varies depending on different applications. Examples include scalar functions, planar or 3D curves, surfaces, etc. As the result, shape analysis is naturally related to the subject of differential geometry. A typical framework for shape analysis starts with mathematical representations of objects and removes certain shape-preserving transformations as pre-processing. The remaining transformations that cannot be removed by pre-processing are dealt with equivalent classes defined by group actions. For example, since shape is invariant with respect to different rotations, an equivalent class defined by rotation of a specific shape is a set that contains all the possible rotations of that shape. And one treats this set as a specific observation in shape analysis.

Since shape analysis is an important branch of statistics, numerous methods have been developed in the literature. In the earlier works, shapes are represented by landmarks, a finite set of points [6, 9, 19]. One of the earliest formal mathematical frameworks is introduced in [9] where one removes rigid motions and global scaling from landmarks to reach final shape representations. Translation and scaling are first removed by centering and rescaling the landmarks, as a pre-processing. The space achieved is also called preshape space. The remaining transformation, rotation, is removed by forming orbits (equivalent classes) under the group action. A metric is then imposed on the space of orbits, which is also called quotient space, followed with rich methods in statistical analysis. More recently, there is a trend that shapes are more continuously represented other than using the finite, discrete points as landmarks.

One of the important challenges in shape analysis is the registration problem, which means finding the correspondence points between different objects. Historically, some shape analysis methods presume that objects have been already registered while others use different methods to register first and use this registration in subsequent own methods for analyzing shapes. However, both approaches are restrictive and questionable. A simultaneous registration and shape analysis called elastic shape analysis [20] has achieved significant recognition over the past few years. This is a class of Riemannian metrics based solutions that perform registration along with the process of shape analysis. The key idea is to equip the shape space with an elastic Riemannian metric that is invariant under the action of registration group. Such elastic metrics are often complicated if used directly. However, a square-root transformation can simplify them into the standard Euclidean metric and results in an efficient solution.

In this chapter, we summarize advances in elastic shape analysis. As mentioned earlier, there are different objects of shapes. For example, planar curves come from boundaries or silhouettes of objects in images [22]. 3D curves can be extracted from complex biomolecular structures like proteins or RNAs [13]. A special case of this problem is when the functional data is in $\mathbb {R}$, i.e., real numbers, which is also called functional data analysis (FDA) [17], where one analyzes shapes of scalar functions on a fixed interval [23]. The use of elastic Riemannian metrics and square-root transformations for curves were first introduced in [29, 30] although this treatment used complicated arithmetic and was restricted to planar curves. Later on, a family of elastic metrics are presented [16] that allowed for different levels of elasticity in shape comparisons. The works [21, 23] introduced a square-root representation that was applicable to curves in any Euclidean space. Subsequently, several other elastic metrics and square-root representations, each representing a different strength and limitation, have been discussed in the literature [2, 3, 11, 15, 31]. In this paper, we focus on the framework in [21, 23] and demonstrate that approach using a number of examples involving functional and curve data.

In addition to methods summarized in this chapter, we mention that elastic frameworks have also been developed for curves taking values on nonlinear domains also, including unit spheres [32], hyperbolic spaces [5], the space of symmetric positive definite (SPD) matrices [33], and some other manifolds. In the case where the data is a trajectory of functions or curves, for instance, the blood oxygenation level-dependent (BOLD) signal along tracts can be considered as trajectories of functions. A parallel transported square-root transformation in [24] can be used to effectively analyze and summarize the projection pathway. Additionally, elastic metrics and square-root representations have also been used to analyze shapes of surfaces in $\mathbb {R}^3$. These methods provide techniques for registration of points across objects, as well as comparisons of their shapes, in a unified metric-based framework. Applications include modeling parameterized surfaces of endometrial tissues that reconstructed from 2D MRI slices [12], shape changes of brain structures associated with Alzheimer [8], etc. For details, we refer to the textbook [7].

2 Registration Problem and Elastic Framework

We provide a comprehensive framework in a similar spirit of Kendall’s [9] approach for comparing shapes of functional objects. The essence is to treat them as parameterized objects and use an elastic metric to register them. The invariant property with respect to reparameterization of the elastic metric enable us to conduct registration and shape analysis simultaneously.

2.1 The Use of the $\mathbb {L}^2$ Norm and Its Limitations

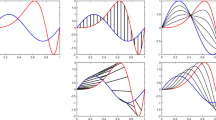
The problem of registration is fundamental for comparing shapes of functional data. To formulate the problem, we consider $\mathcal {F}$ as all the parameterized functional objects, whose elements are $f: D \rightarrow \mathbb {R}^n$ where D represents the domain of parameterization. As an example, for open planar curves, n = 2 and D is the unit interval [0, 1]. While for analyzing shapes of surfaces, D can be a unit sphere $\mathbb {S}^2$, unit disk, etc. The reparametrization of f is given by the composition with γ : f ∘ γ, where γ : D → D is a boundary-preserving diffeomorphism that is an invertible function maps from domain D to itself that both the function and its inverse are smooth. We denote Γ as all the boundary-preserving diffeomorphisms of domain D. One can show that Γ forms a group with action as composition and the identity element is γ _id(t) = t, t ∈ D. Therefore, for any two γ ₁, γ ₂ ∈ Γ, γ ₁ ∘ γ ₂ ∈ D is also a (cumulative) reparameterization. Reparametrization does not change the shape of $f \in \mathbb {R}^n, n \geq 2$, i.e., f and f ∘ γ, γ ∈ Γ has the exact same shape. For scalar functions $f \in \mathbb {R}$, the reparametrization is usually called time warping, and we will discuss details later. An example of reparametrization of 2D curves can be found in Fig. 13.1. The top row shows the sine functions in the plane in different reparametrizations plotted in the bottom row. The middle column shows the original parametrization while left and right columns visualize different reparametrizations. For any t ∈ D and any two functional object $f_1, f_2 \in \mathcal {F}$, f ₁(t) are registered to f ₂(t). Therefore, if we reparametrize f ₂ to f ₂ ∘ γ, we can change the registration between f ₁ and f ₂, controlled by the diffeomorphism γ.

Fig. 13.1

An illustration of reparametrization of a 2D open curve. Top row is the curve in different parametrization. Bottom row shows the corresponding γ (diffeomorphism)

In order to quantify the problem, one needs an objective function to measure the quality of registration. A seemingly natural choice is using L ² norm. Let ∥⋅∥ represents the L ² norm, i.e., $\|f\| = \sqrt {\int _D |f(t)|{ }^2 dt}$. Therefore, the corresponding objective function becomes inf_{γ ∈ Γ}∥f ₁ − f ₂ ∘ γ∥. There are several problems related to it. The main issue is that it leads to degeneracy solution. In other words, one can find a γ to reduce the cost to be infinitesimal even if f ₁, f ₂ are quite different. Such γ minimize the cost by eliminating the part of f ₂ that is greatly different from the part of f ₁, which is referred to pinching problem in the literature [20]. Figure 13.2 shows a simple example to illustrate the idea using two scalar functions. We have two scalar functions on the unit interval [0, 1] showed in the left panel. If we optimize the previous L ² based objective functions, the obtained time warping function γ is plotted on the right panel while the middle panel visualizes the reparameterization f ₂ ∘ γ. As we can see, it kills the height of f ₂ to get this degenerate solution. To avoid this, people proposed the modified solution that penalize large time warpings by some roughness penalties:

$$\displaystyle \begin{aligned} \inf_{\gamma \in \Gamma} (\|f_1 - f_2 \circ\gamma \| + \lambda \mathcal{R}(\gamma)) \ , \end{aligned} $$

(13.1)

where $\mathcal {R}(\gamma )$ represents the roughness of γ. For example, it can be the norm of the first or the second derivatives.

Fig. 13.2

Pinching effect when using $\mathbb {L}^2$ norm to align scalar functions. The rightmost is the time warping function

While this solution prevents the pinching problem, it introduces new issues. For example, the solution is not inverse consistent. That is, the registration of f ₂ to f ₁ is no longer equivalent with that of f ₁ to f ₂. We use Fig. 13.3 to explain this issue. The task is to align two scalar functions f ₁ and f ₂, shown in the top panel of Fig. 13.3. And in this example, we use the first order penalty $\mathcal {R}(\gamma ) = \int \dot {\gamma }(t)^{2} dt$ in Eq. (13.1). To study the property of symmetry, for each row, we perform registration using different template and target on a fixed λ, i.e., warping f ₂ to register to f ₁ to get γ ₁ and warping f ₁ to register to f ₂ to get γ ₂. Then, we compose the two obtained optimal warping functions. If the solution is symmetric, the composition $\gamma _1 \circ \gamma _2^{-1}$ should be the identity function: γ _id(t) = t. The last column shows the compositions. As we can see, when λ = 0, the solution is symmetric. However, it suffers the pinching problem. As λ increases, the pinching effect is reducing but the solution is no longer inverse consistent. In the last row, where λ is large, the pinching problem disappears. However, the alignment is also largely limited. It is not obvious to select the appropriate λ for this example. In reality, it is even difficult to tune this parameter.

Fig. 13.3

Example of penalized-$\mathbb {L}^2$ based alignment. The top row shows the two original functions. From the second row to the bottom row, the roughness tuning parameter is set to λ = 0, 0.03, 0.3, respectively. As λ increases, the solution becomes more and more asymmetric

In the following sections, we will go through the shape analysis in elastic framework for scalar functions, parametrized curves.

2.2 Elastic Registration of Scalar Functions

Among various functional objects one comes across in shape analysis, the simplest types are real-valued functions on a fixed interval. For simplicity, functional data in this section refers to the scalar functions. Examples include human activities collected by wearable devices, biological growth data, weather data, etc. Shape analysis on scalar functions is reduced to alignment problem in FDA. If one does not account for misalignment in the given data, which happens when functions are contaminated with the variability in their domain, this can inflate variance artificially and can overwhelm any statistical analysis. The task is warping the temporal domain of functions so that geometric features (peaks and valleys) of functions are well-aligned, which is also called curve registration or phase-amplitude separation [14]. While we have illustrated the limitation of L ² norm earlier, we will introduce a desirable solution in elastic framework as follows.

Definition 13.1

For a function $f(t): [0,1] \rightarrow \mathbb {R}$, define the square-root velocity function (SRVF) (or square-root slope function (SRSF)) q(t) as follows:

$$\displaystyle \begin{aligned} q(t) = sign (\dot{f}(t))\sqrt{|\dot{f}(t)|} \ . \end{aligned} $$

(13.2)

It can be shown if f(t) is absolutely continues, q(t) is square-integrable, i.e., q(t) ∈ L ². The representation is invertible given f(0): $f(t) = f(0) + \int _{0}^t q(s)|q(s)| ds$. If the function f is warped as f ∘ γ, then the SRVF becomes: $(q \circ \gamma )\sqrt {\dot {\gamma }}$, denoted by (q ∗ γ). One of the most import properties of the representation is isometry under the action of diffeomorphism: ∥q ₁ − q ₂∥ = ∥(q ₁ ∗ γ) − (q ₂ ∗ γ)∥, ∀γ ∈ Γ. In other words, L ² norm of SRVFs is preserved under time warping. One can show that the L ² metric of SRVF is non-parametric Fisher-Rao metric on f, given f is absolutely continuous and $\dot {f}>0$, and it can be extended to the larger space $\mathcal {F}_0 = \{f\in \mathcal {F}|f\text{ is absolute continuous}\}$ [20]. Then, in order to register f ₁ and f ₂, the problem becomes

$$\displaystyle \begin{aligned} \inf_{\gamma \in \Gamma} \| q_1 -(q_2 * \gamma) \|=\inf_{\gamma \in \Gamma} \| q_2 - (q_1 * \gamma)\| \ . \end{aligned} $$

(13.3)

One can efficiently solving above objective function using Dynamic Programming [4]. Gradient based algorithm or exact solutions [18] are also available.

For aligning multiple functions, one can easily extend the framework to align every function to their Karcher mean [20] by iteratively updating the following equations:

$$\displaystyle \begin{aligned} & \gamma_i = \arg \inf_{\gamma \in \Gamma} \| \mu - (q_i * \gamma) \| \ , \\ & \mu = \frac{1}{n} \sum_{i=1}^{n} (q_i * \gamma_i) \end{aligned} $$

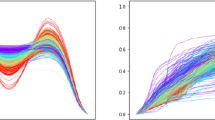
We demonstrate an application of function alignment using the famous Berkeley growth data [27], where observations are heights of human subjects in the age domain recorded from birth to age 18. In order to understand the growth pattern, we use a smoothed version of the first time derivative (growth velocity) of the height functions, instead of the height functions themselves, as functional data, plotted in (a) and (d) of Fig. 13.4 for male and female subjects, respectively. The task is to align the growth spurts of different subjects in order to make inferences about the number and placement of such spurts for the underlying population. The aligned functions are presented in (b) and (e) of Fig. 13.4. After alignment, it becomes much easier to estimate the location and size of the growth spurts in observed subjects, and make inferences about the general population.

Fig. 13.4

Alignment on Berkeley growth data. (a) Original male growth function. (b) Aligned male growth function. (c) Time warping functions for male. (d) Original female growth function. (e) Aligned female growth function. (f) Time warping functions for female

There are many studies related to the elastic functional analysis in the literature. For example, one can construct a generative model for functional data, in terms of both amplitude and phase parts [25]. One can also take account the elastic part into functional principal component analysis [26]. For regression models using elastic functions as predictors, readers can refer to [1].

2.3 Elastic Shape Analysis of Curves

2.3.1 Registration of Curves

As previously mentioned, square-root transformations were first proposed for planar curves [29, 30]. We can register curves in $\mathbb {R}^2$ and $\mathbb {R}^3$ using SRVFs as defined below.

Definition 13.2

Define SRVF of 2D or 3D parametrized curves:

$$\displaystyle \begin{aligned} q(t)= \begin{cases} \frac{\dot{f}(t)}{\sqrt{|\dot{f}(t)|}}, &|\dot{f}(t)| \neq 0 \\ 0 \ , & |\dot{f}(t)| = 0 \end{cases} \ . \end{aligned} $$

(13.4)

Here $f: [0,1] \rightarrow \mathbb {R}^n, n=2,3$, is an absolutely continuous parametrized curve. (For closed curves, $\mathbb {S}^1$ is a more appropriate domain.) It is worth noting that this definition is valid for $\mathbb {R}^n$. The L ² metric in the space of SRVFs is a special elastic metric in the space of curves, which measures the bending and stretching from the curves [20]. To register curves, we again use Eq. (13.3). An example of registering 2D curves is shown in Fig. 13.5, where we are registering signatures.

Fig. 13.5

Registration of signatures

2.3.2 Shape Space

Now we know how to align functions and to register curves using the SRVF framework. And these will now serve as fundamental tools for our ultimate goal: shape analysis. One has to note that shapes are invariant to some nuanced group actions: translation, scaling, rotation, and reparametrization. For example, Fig. 13.6 illustrates that using a bird shape. On the left panel, although the bird contour is shifted, scaled and rotated, the shape is keeping the same as the original one. One the right panel, two shapes have different reparametrizations but they need to be treated as the same shape. Therefore, it is important to identify what is the space that shapes reside in. We represent a curve f by its SRVF q and thus it is invariant to translation (because it is a derivative). The curve can be rescaled into unit length to remove scaling. Since the length of f is L[f] = ∥q∥, after rescaling, ∥q∥ = 1. As the result, the unit length q is on the unit Hilbert sphere. Let $\mathcal {C} = \{ q \in L^2 | \|q \| = 1 \}$ denote the unit Hilbert sphere inside L ², which is also called preshape space. The geometry of $\mathcal {C}$ is simple: the distance between any two point $q_1, q_2 \in \mathcal {C}$ is given by the arc length $d_{\mathcal {C}} (q_1,q_2) = \cos ^{-1}(\langle q_1,q_2 \rangle )$, where <, >  represents L ² inner product. The geodesic (shortest path) between q ₁ and q ₂ is $\alpha : [0,1] \rightarrow \mathcal {C}$ is the shortest arc length on the greater circle:

$$\displaystyle \begin{aligned}\alpha ( \tau ) = \frac{1}{\sin \theta} (\sin ((1 - \tau) \theta)q_1 + \sin{}(\tau \theta ) q_2 ), \tau \in [0,1] \end{aligned}$$

Fig. 13.6

Example of bird shapes

The remaining variability that has not been removed is rotation and reparametrization. We will remove them by using equivalent classes that are defined by group actions. Let SO(n) represent the set of all the rotation matrices in $\mathbb {R}^n$. For any O ∈ SO(n) and $q \in \mathcal {C}$, Oq has exactly same shape with q. (The SRVF of Of is Oq.) The same holds for a reparametrization (q ∗ γ), ∀γ ∈ Γ. We will treat them as the same object in the shape space as follows. Define the action of group SO(n) × Γ on $\mathcal {C}$ according to:

$$\displaystyle \begin{aligned}(SO(n) \times \Gamma) \times \mathcal{C} \rightarrow \mathcal{C}, (O,\gamma)*q = O (q * \gamma) \ , \end{aligned}$$

which leads to the equivalent classes or orbits:

$$\displaystyle \begin{aligned}{}[q] = \{ O (q * \gamma) | O \in SO(n), \gamma \in \Gamma \} \ . \end{aligned}$$

Therefore, each orbit [q] represents a unique shape of curves. The shape space (quotient space) $\mathcal {S}$ is the collection of all the orbits:

$$\displaystyle \begin{aligned}\mathcal{S} = \mathcal{C} / (SO(n) \times \Gamma) = \{[q] | q \in \mathcal{C} \} \ . \end{aligned}$$

As we mentioned earlier, the inner product or L ² norm of SRVF is preserved under reparametrization. This is also true for rotation actions: 〈q ₁, q ₂〉 = 〈Oq ₁, Oq ₂〉. As the result, we can inherit the metric from preshape space into shape space as follows:

Definition 13.3

For two representations of shapes [q ₁] and [q ₂], define the shape metric as:

$$\displaystyle \begin{aligned} d_{\mathcal{S}}([q_1],[q_2]) = \inf_{\gamma \in \Gamma, O \in SO(n)} d_{\mathcal{C}} (q_1 , O(q_2 *\gamma)) \ . \end{aligned} $$

(13.5)

The above equation is a proper metric in the shape space [20] and thus can be used for ensuing statistical analysis. The optimization over SO(n) is performed using Procrustes method [10]. For instance, for curves in 2D, the optimal rotation O ^∗ is given by

$$\displaystyle \begin{aligned} O*= \begin{cases} UV ^T& \text{if } det(A)>0\\ U \begin{bmatrix} 1 &0\\ 0 &-1 \end{bmatrix}V^T& \text{otherwise} \end{cases} \ , \end{aligned} $$

(13.6)

where $A = \int _0^1 q_1q_2^T dt$ and A = U ΣV ^T (singular value decomposition). While the optimization of γ can be implement by Dynamic Programming or gradient based methods [20]. For [q ₁] and [q ₂] in $\mathcal {S}$, the geodesic path is given by the geodesic between q ₁ and $\tilde {q}_2$, while $\tilde {q}_2$ is rotated and reparemetrized w.r.t. q ₁. We present an example geodesic in Fig. 13.7. The top row is the geodesic in $\mathcal {S}$. For comparison, we also plot the geodesic path in $\mathcal {C}$ in bottom row. It is clear to see that elastic registration makes a more reasonable deformation since it matches the corresponding parts.

Fig. 13.7

Comparison between geodesic and interpolation for a toy 2D open curve. (a) Geodesic in $\mathcal {S}$. (b) Geodesic in $\mathcal {C}$

Shape Spaces of Closed Curves

For parametrized closed curves, there is one more constraint: f(0) = f(1). Therefore, as we mentioned earlier, $\mathbb {S}^1$ is a more natural domain for parametrized closed curves. Let q denote the SRVF of a closed curve f, the above condition f(0) = f(1) becomes $\int _{\mathbb {S}^1}q(t)|q(t)|dt = 0$. As the result, the prespace $\mathcal {C}^c$ for unit length closed curve is:

$$\displaystyle \begin{aligned}\mathcal{C}^c = \left\{ q \in \mathbb{L}^2(\mathbb{S}^1, \mathbb{R}^n) | \int_{\mathbb{S}^1}|q(t)|dt = 1, \int_{\mathbb{S}^1}q(t)|q(t)|dt = 0 \right\} \subset \mathcal{C} \ . \end{aligned}$$

One can still use $d_{\mathcal {C}}$ as the extrinsic metric in $\mathcal {C}^c$ [20]. Unlike the open curves, the geodesics in $\mathcal {C}^c$ have no closed form. A numerical approximation method called path straightening [20] can be used to compute the geodesic. The shape space is $\mathcal {S}^c = \mathcal {C}^c / (SO(n) \times \Gamma )$. whose elements, equivalence classes or orbits, are $[q] = \{O(q*\gamma )|q \in \mathcal {C}^c, O \in SO(n), \gamma \in \Gamma \}$. Some examples of geodesic paths can be found in Fig. 13.8, where we can see natural deformations between two shapes.

Fig. 13.8

Some geodesic paths between two closed planar curves in $\mathcal {S}^c$

3 Shape Summary Statistics, Principal Modes and Models

The framework we have developed so far is able to define and compute several statistics for analysis of shapes. For instance, we may want to compute the mean shape from a sample of curves to represent the underlying population. The intrinsic sample mean on a nonlinear manifold is typically defined as the Fréchet mean or Karcher mean, defined as follows.

Definition 13.4 (Mean Shape)

Given a set of curves $f_1, f_2, \ldots , f_n \in \mathcal {F}_0$ with corresponding shapes [q ₁], [q ₂], …, [q _n], we define the mean shape [μ] as:

$$\displaystyle \begin{aligned}{}[\mu] = \arg\min_{[q]} \sum_{i=1}^n d^2_{\mathcal{S}} ([q], [q_i]) \ . \end{aligned}$$

The algorithm for computing a mean shape [20] is similar to the one described earlier in multiple function alignment. We iteratively find the best one from rotation, registration and average while fixing the other two, in way of coordinate descent [28]. Figure 13.9 illustrates some mean shapes. One the left hand side, there are some sample shapes: glasses and human beings. Their corresponding mean shapes are plotted on the right.

Fig. 13.9

Examples of mean shapes

Besides the Karcher mean, the Karcher covariance and modes of variation can be calculated to summarize the given sample shapes. As it is known that the shape space $\mathcal {S}$ is a non-linear manifold, we will use tangent PCA [20] to flatten the space. Let $T_{[\mu ]}\mathcal {S}$ denote the tangent space to $\mathcal {S}$ at the mean shape [μ] and log_[μ]([q]) denote the mapping from the shape space $\mathcal {S}$ to this tangent space using inverse exponential map. Let v _i =log_[μ]([q]), for i = 1, 2, …, n be the shooting vectors from the mean shape to the given shapes in the tangent space. Since these shooting vectors are in the linear space, we are able to compute the covariance matrix $C = \frac {1}{n-1} \sum _{i=1}^{n} v_i v^t_i$. Performing Principal Component Analysis (PCA) of C provides the directions of maximum variability in the given shapes and can be used to visualize (by projecting back to the shape space) the main variability in that set. Besides that, one can impose a Gaussian model on the principal coefficients s _i, i = 1, 2, …, n in the tangent space. To valid the model, one can generate a random vector r _i from the estimated model and project back to the shape space using exponential map exp_[μ](r _i), where random vectors become random shapes. We use Figs. 13.10 and 13.11 as illustrations. We have several sample shapes of apples and butterflies in panel (a) and the mean shapes are presented in panel (b). We perform tangent PCA as described above and show the results in panel (c). While the mean shapes are the red shapes in the shape matrix, the modes in first and second principal direction are plotted horizontally and vertically, respectively, which explain the first and second modes of variation in the given sample shapes. Finally, we generate some random shapes from the estimated tangent Gaussian model and show them in panel (d). The similarity between random shapes and given samples validates the fitness of the shape models.

Fig. 13.10

Principal modes and random samples of apple shapes. (a) Sample shapes. (b) Mean shapes. (c) Principal modes. (d) Random samples from Tangent Gaussian model

Fig. 13.11

Principal modes and random samples of butterfly shapes. (a) Sample shapes. (b) Mean shapes. (c) Principal modes. (d) Random samples from Tangent Gaussian model

4 Conclusion

In this chapter, we describe the elastic framework for shape analysis of scalar functions and curves in Euclidean spaces. The SRVF transformation simplifies the registration and makes the key point for the approach. Combining with L ² norm, it derives an appropriate shape metric that unifies registration with comparison of shapes. As the result, one can compute geodesic paths, summary statistics. Furthermore, these tools can be used in statistical modeling of shapes.