Abstract
Very generally speaking, statistical data analysis builds on descriptors reflecting data distributions. In a linear context, well studied nonparametric descriptors are means and PCs (principal components, the eigenorientations of covariance matrices). In 1963, T.W. Anderson derived his celebrated result of joint asymptotic normality of PCs under very general conditions. As means and PCs can also be defined geometrically, there have been various generalizations of PC analysis (PCA) proposed for manifolds and manifold stratified spaces. These generalizations play an increasingly important role in statistical dimension reduction of non-Euclidean data. We review their beginnings from Procrustes analysis (GPA), over principal geodesic analysis (PGA) and geodesic PCA (GPCA) to principal nested spheres (PNS), horizontal PCA, barycentric subspace analysis (BSA) and backward nested descriptors analysis (BNDA). Along with this, we review the current state of the art of their asymptotic statistical theory and applications for statistical testing, including open challenges, e.g. new insights into scenarios of nonstandard rates and asymptotic nonnormality.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
1 Introduction
The mean and the covariance are among the most elementary statistical descriptors describing a distribution in a nonparametric way, i.e. in the absence of a distributional model. They can be used for dimension reduction and for statistical testing based on their asymptotics. Extending these two quantities to non-Euclidean random deviates and designing statistical methods for these has been the subject of intense research in the last 50 years, beginning with Procrustes analysis introduced by Gower [23] and the strong law of large numbers for Fréchet means by Ziezold [51]. This chapter intends to provide a brief review of the development of this research until now and to put it into context.
We begin with the Euclidean version including classical PCA, introduce the more general concept of generalized Fréchet ρ-means, their strong laws and recover general Procrustes analysis (GPA) as a special case. Continuing with principal geodesic analysis we derive a rather general central limit theorem for generalized Fréchet ρ-means and illustrate how to recover from this Anderson’s asymptotic theorem for the classical first PC and the CLT for Procrustes means. Next, as another application of our CLT we introduce geodesic principal component analysis (GPCA), which, upon closer inspection, turns out to be a nested descriptor. The corresponding backward nested descriptor analysis (BNDA) requires a far more complicated CLT, which we state. We put the rather recently developed methods of principal nested spheres (PNS), horizontal PCA and barycentric subspace analysis (BSA) into context and conclude with a list of open problems in the field.
2 Some Euclidean Statistics Building on Mean and Covariance
Asymptotics and the Two-Sample Test
Let  be random vectors in
be random vectors in  ,
,  , with existing population mean \(\mathbb {E}[X]\). Denoting the sample mean by
, with existing population mean \(\mathbb {E}[X]\). Denoting the sample mean by

the strong law of large numbers (SLLN) asserts that (e.g. [8, Chapter 22])

Upon existence of the second moment \(\mathbb {E}[\|X\|{ }^2]\), the covariance cov[X] exists and the central limit theorem (CLT) asserts that the fluctuation between sample and population mean is asymptotically normal (e.g. [14, Section 9.5]), namely that

Using the sample covariance

as a plugin estimate for cov[X] in (10.1), asymptotic confidence bands for \(\mathbb {E}[X]\) can be obtained as well as corresponding tests.
A particularly useful test is the two-sample test, namely that for random vectors  in
in  and independent random vectors
and independent random vectors  in
in  with full rank population and sample covariance matrices, cov[X] and cov[Y ], \(\hat {\Sigma }_n^X\) and \(\hat {\Sigma }_m^Y\), respectively,
with full rank population and sample covariance matrices, cov[X] and cov[Y ], \(\hat {\Sigma }_n^X\) and \(\hat {\Sigma }_m^Y\), respectively,

follows a Hotelling distribution if X and Y are multivariate normal, cf. [40, Section 3.6.1]. More precisely,  follows a F
D,n+m−D−1-distribution. Remarkably, this holds also asymptotically under nonnormality of X and Y , if
follows a F
D,n+m−D−1-distribution. Remarkably, this holds also asymptotically under nonnormality of X and Y , if  or
or  , cf. [45, Section 11.3].
, cf. [45, Section 11.3].
Principal Component Analysis (PCA)
Consider again random vectors  in
in  ,
,  , with sample covariance matrix
, with sample covariance matrix  and existing population covariance
and existing population covariance  . Further let
. Further let  and
and  be spectral decompositions, i.e.
be spectral decompositions, i.e.  and
and  ,
,  with
with  and
and  , respectively. Then the vectors γ
j (j = 1, …, D) are called population principal components and \(\hat \gamma _j\) (j = 1, …, D) are called sample principal components, abbreviated as PCs. These PCs can be used for dimension reduction, namely considering instead of
, respectively. Then the vectors γ
j (j = 1, …, D) are called population principal components and \(\hat \gamma _j\) (j = 1, …, D) are called sample principal components, abbreviated as PCs. These PCs can be used for dimension reduction, namely considering instead of  their projections, also called scores,
their projections, also called scores,

to the first  PCs. The variance explained by the first J PCs is
PCs. The variance explained by the first J PCs is

Due to the seminal result by Anderson [1], among others, there is a CLT for  (
( ), stating that if X is multivariate normal,
), stating that if X is multivariate normal,  and λ
j simple,
and λ
j simple,

Here, we have assumed, w.l.o.g., that  .
.
This CLT has been extended to nonnormal X with existing fourth moment \(\mathbb {E}[\|X\|{ }^4]\) by Davis [11] with a more complicated covariance matrix in (10.3). With little effort we reproduce the above result in Corollary 10.4 for j = 1 in the context of generalized Fréchet ρ-means.
3 Fréchet ρ-Means and Their Strong Laws
What is a good analog to \(\mathbb {E}[X]\) when data are no longer vectors but points on a sphere, as are principal components, say? More generally, one may want to statistically assess points on manifolds or even on stratified spaces. For example, data on stratified spaces are encountered in modeling three-dimensional landmark-based shapes by Kendall [36] (cf. Sect. 10.4) or in modeling phylogenetic descendants trees in the space introduced by Billera et al. [7].
For a vector-valued random variable X in  , upon existence of second moments \(\mathbb {E}[\|X\|{ }^2]\) note that,
, upon existence of second moments \(\mathbb {E}[\|X\|{ }^2]\) note that,

For this reason, [21] generalized the classical Euclidean expectation to random deviates X taking values in a metric space (Q, d) via

In contrast to the Euclidean expectation, E(X) can be set-valued, as is easily seen by a symmetry argument for \(Q=\mathbb {S}^{D-1}\) equipped with the spherical metric d and X uniform on \(\mathbb {S}^{D-1}\). Then  .
.
Revisiting PCA, note that PCs are not elements of the data space  but elements of \(\mathbb {S}^{D-1}\), or more precisely, elements of real projective space of dimension D − 1
but elements of \(\mathbb {S}^{D-1}\), or more precisely, elements of real projective space of dimension D − 1

Moreover, the PCs (as elements in \(\mathbb {S}^{D-1}\)) are also solutions to a minimization problem, e.g. for the first PC we have

Since  , in case of \(\mathbb {E}[X]=0\), this motivates the following distinction between data space and descriptor space leading to Fréchet ρ-means.
, in case of \(\mathbb {E}[X]=0\), this motivates the following distinction between data space and descriptor space leading to Fréchet ρ-means.
Definition 10.1 (Generalized Fréchet Means)
Let Q, P be topological spaces and let  be continuous. We call Q the data space, P the descriptor space and ρ the link function. Suppose that
be continuous. We call Q the data space, P the descriptor space and ρ the link function. Suppose that  are random elements on Q with the property that
are random elements on Q with the property that

called the population and sample Fréchet functions, are finite for all  . Every minimizer of the population Fréchet function is called a population Fréchet mean and every minimizer of the sample Fréchet function is called a sample Fréchet mean. The corresponding sets are denoted by
. Every minimizer of the population Fréchet function is called a population Fréchet mean and every minimizer of the sample Fréchet function is called a sample Fréchet mean. The corresponding sets are denoted by

□
Remark
By construction, E n and E are closed sets, but they may be empty without additional assumptions. □
For the following we require that the topological space P is equipped with a loss function d, i.e.
-
1.
 , is a continuous function
, is a continuous function -
2.
that vanishes only on the diagonal, that is
 if and only if p = p′.
if and only if p = p′.
We now consider the following two versions of a set valued strong law,


In (10.7), N is random as well.
Ziezold [51] established (10.6) for separable P = Q and ρ = d a quasi-metric. Notably, this also holds in case of void E. Bhattacharya and Patrangenaru [5] proved (10.7) under the additional assumptions that  ,
,  is a metric and P = Q satisfies the Heine–Borel property (stating that every closed bounded subset is compact). Remarkably, (10.6) implies (10.7) for compact spaces P; this has been observed by Bhattacharya and Patrangenaru [5, Remark 2.5] for P = Q and ρ = d a metric and their argument carries over at once to the general case.
is a metric and P = Q satisfies the Heine–Borel property (stating that every closed bounded subset is compact). Remarkably, (10.6) implies (10.7) for compact spaces P; this has been observed by Bhattacharya and Patrangenaru [5, Remark 2.5] for P = Q and ρ = d a metric and their argument carries over at once to the general case.
For generalized Fréchet ρ-means we assume the following strongly relaxed analogs of the triangle inequality for (quasi-)metrics.
Definition 10.2
Let Q, P be topological spaces with link function ρ and let d be a loss function on P. We say that (ρ, d) is uniform if

Further, we say that (ρ, d) is coercive, if  and
and  with
with  ,
,

Theorem ([27])
With the notation of Definition 10.1 we have (10.6) if (ρ, d) is uniform and P is separable. If additionally (ρ, d) is coercive,  and
and  satisfies the Heine Borel property with respect to d then (10.7) holds true. □
satisfies the Heine Borel property with respect to d then (10.7) holds true. □
Let us conclude this section with another example. In biomechanics, e.g. traversing skin markers placed around the knee joint (e.g. [49]), or in medical imaging, modeling deformation of internal organs via skeletal representations (cf. [47]), typical motion of markers occurs naturally along small circles in \(\mathbb {S}^2\), c.f. [46]. For a fixed number  , considering k markers as one point
, considering k markers as one point  , define the descriptor space P of k concentric small circles p = (p
1, …, p
k) defined by a common axis
, define the descriptor space P of k concentric small circles p = (p
1, …, p
k) defined by a common axis  and respective latitudes 0 < θ
1 < … < θ
k < π. Setting
and respective latitudes 0 < θ
1 < … < θ
k < π. Setting

and

we obtain a link ρ and a loss d which form a uniform and coercive pair. Moreover, even P satisfies the Heine–Borel property.
4 Procrustes Analysis Viewed Through Fréchet Means
Long before the notion of Fréchet means entered the statistics of shape, Procrustes analysis became a tool of choice and has been ever after for the statistical analysis of shape.
Kendall’s Shape Spaces
Consider n geometric objects in  , each described by k landmarks (
, each described by k landmarks ( ), i.e. every object is described by a matrix
), i.e. every object is described by a matrix  (
( ), the columns of which are the k landmark vectors in
), the columns of which are the k landmark vectors in  of the j-th object. When only the shape of the objects is of concern, consider every
of the j-th object. When only the shape of the objects is of concern, consider every

equivalent with X
j, where λ
j ∈ (0, ∞) reflects size,  rotation and
rotation and  translation. Here, 1k is the k-dimensional column vector with all entries equal to 1. Note that the canonical quotient topology of
translation. Here, 1k is the k-dimensional column vector with all entries equal to 1. Note that the canonical quotient topology of  gives a non-Hausdorff space which is a dead end for statistics, because all points have zero distance from one another. For this reason, one projects instead to the unit sphere
gives a non-Hausdorff space which is a dead end for statistics, because all points have zero distance from one another. For this reason, one projects instead to the unit sphere  and the canonical quotient
and the canonical quotient

is called Kendall’s shape space, for details see [13].
Procrustes Analysis
Before the introduction of Kendall’s shape spaces, well aware that the canonical quotient is statistically meaningless, [23] suggested to minimize the Procrustes sum of squares

over  (
( ) under the constraining condition
) under the constraining condition

It turns out that the minimizing a
j are the mean landmarks, so for the following, we may well assume that every X
j is centered, i.e.  and dropping one landmark, e.g. via Helmertizing, i.e. by multiplying each X
j with a sub-Helmert matrix \(\mathcal {H}\)
and dropping one landmark, e.g. via Helmertizing, i.e. by multiplying each X
j with a sub-Helmert matrix \(\mathcal {H}\)

from the right, see [13], we may even more assume that  (j = 1, …, n). Further, with minimizing
(j = 1, …, n). Further, with minimizing  , every Procrustes mean
, every Procrustes mean

is also a representative of a Fréchet mean on \(Q=P=\Sigma _m^k\) using the canonical quotient  of the residual quasi-metric
of the residual quasi-metric

on  , in this context, called the pre-shape space, see [26] for a detailed discussion.
, in this context, called the pre-shape space, see [26] for a detailed discussion.
If μ is a Procrustes mean with minimizing λ
j, R
j (j = 1, …, n), notably, this implies  , then
, then

are called the Procrustes residuals. By construction they live in the tangent space  of
of  at μ. In particular, this is a linear space and hence, the residuals can be subjected to PCA. Computing the Procrustes mean and performing PCA for the Procrustes residuals is full Procrustes analysis as proposed by Gower [23].
at μ. In particular, this is a linear space and hence, the residuals can be subjected to PCA. Computing the Procrustes mean and performing PCA for the Procrustes residuals is full Procrustes analysis as proposed by Gower [23].
Note that at this point, we have neither a CLT for Procrustes means nor can we apply the CLT (10.3) because the tangent space is random.
This nested randomness can be attacked directly by nested subspace analysis in Sect. 10.7 or circumvented by the approach detailed in the Sect. 10.6. Let us conclude the present section by briefly mentioning an approach for Riemannian manifolds similar to Procrustes analysis.
Principal Geodesic Analysis
Suppose that Q = P is a Riemannian manifold with intrinsic geodesic distance  . Fréchet means with respect to ρ are called intrinsic means and [20] compute an intrinsic mean μ and perform PCA with the data mapped under the inverse exponential at μ to the tangent space
. Fréchet means with respect to ρ are called intrinsic means and [20] compute an intrinsic mean μ and perform PCA with the data mapped under the inverse exponential at μ to the tangent space  of Q at μ. Again, the base point of the tangent space is random, prohibiting the application of the CLT (10.3).
of Q at μ. Again, the base point of the tangent space is random, prohibiting the application of the CLT (10.3).
5 A CLT for Fréchet ρ-Means
For this section we require the following assumptions.
-
(A1)
 are random elements in a topological data space Q, which is linked to a topological descriptor space P via a continuous function
are random elements in a topological data space Q, which is linked to a topological descriptor space P via a continuous function  , featuring a unique Fréchet ρ-mean
, featuring a unique Fréchet ρ-mean  .
. -
(A2)
There is a loss function
 and P has locally the structure of a D-dimensional manifold near μ, i.e. there is an open set
and P has locally the structure of a D-dimensional manifold near μ, i.e. there is an open set  ,
,  and a homeomorphism
and a homeomorphism 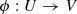 onto an open set
onto an open set  . W.l.o.g. assume that
. W.l.o.g. assume that  .
. -
(A3)
In local coordinates the population Fréchet function is twice differentiable at μ with non-singular Hessian there, i.e. for
 , x = ϕ
−1(p),
, x = ϕ
−1(p), 
-
(A4)
The gradient
 exists almost surely and there is a measurable function
exists almost surely and there is a measurable function  , satisfying
, satisfying  , such that the following Lipschitz condition
, such that the following Lipschitz condition 
holds for all
 .
.
Theorem 10.3
Under the above Assumptions (A1)–(A4), if
 is a measurable selection of sample Fréchet ρ-means with
is a measurable selection of sample Fréchet ρ-means with
 , then
, then

Proof
We use [17, Theorem 2.11] for r = 2. While this theorem has been formulated for intrinsic means on manifolds, upon close inspection, the proof utilizing empirical process theory from [50], rests only on the above assumptions, so that it can be transferred word by word to the situation of Fréchet ρ-means. □
Remark
Since the seminal formulation of the first version of the CLT for intrinsic means on manifolds by Bhattacharya and Patrangenaru [6] there has been a vivid discussion on extensions and necessary assumptions (e.g. [2,3,4, 19, 24, 25, 33, 37, 39, 41]). Recently it has been shown that the rather complicated assumptions originally required by Bhattacharya and Patrangenaru [6] could be relaxed to the above. Further relaxing the assumption H > 0 yields so-called smeary CLTs, cf. [17]. □
Classical PCA as a Special Case of Fréchet ρ -Means
As an illustration how asymptotic normality of PCs shown by Anderson [1] in an elaborate proof follows simply from Theorem 10.3 we give the simple argument for the first PC.
Corollary 10.4
Suppose that
 are random vectors in
are random vectors in
 with
\(\mathbb {E}[X]=0\)
, finite fourth moment and orthogonal PCs
with
\(\mathbb {E}[X]=0\)
, finite fourth moment and orthogonal PCs
 to descending eigenvalues
to descending eigenvalues
 . Further let
. Further let
 be a first sample PC with
be a first sample PC with
 and local coordinates
and local coordinates
 . Then, with
. Then, with
 ,
,

If X is multivariate normal then the covariance of the above r.h.s. is given by the r.h.s. of (10.3) for j = 1. □
Proof
With the representation  ,
,  , we have that the link function underlying (10.5) is given by
, we have that the link function underlying (10.5) is given by

From

and, with the unit matrix I,

verify that it satisfies Assumption (A4) with  and
and  for U sufficiently small, which is square integrable by hypothesis. Since
for U sufficiently small, which is square integrable by hypothesis. Since  , with
, with

which is, by hypothesis, positive definite in  , we obtain the first assertion of Theorem 10.3. Since in case of multivariate normality
, we obtain the first assertion of Theorem 10.3. Since in case of multivariate normality  with independent real random variables c
1, …, c
D, the second assertion follows at once. □
with independent real random variables c
1, …, c
D, the second assertion follows at once. □
The CLT for Procrustes Means
For  , Kendall’s shape spaces are stratified as follows. There is an open and dense manifold part \((\Sigma _m^k)^*\) and a lower dimensional rest \((\Sigma _m^k)^0\) that is similarly stratified (comprising a dense manifold part and a lower dimensional rest, and so on), e.g. [9, 32, 38]. For a precise definition of stratified spaces, see the following Sect. 10.6.
, Kendall’s shape spaces are stratified as follows. There is an open and dense manifold part \((\Sigma _m^k)^*\) and a lower dimensional rest \((\Sigma _m^k)^0\) that is similarly stratified (comprising a dense manifold part and a lower dimensional rest, and so on), e.g. [9, 32, 38]. For a precise definition of stratified spaces, see the following Sect. 10.6.
As a toy example one may think of the unit two-sphere  on which
on which  acts via
acts via

The canonical quotient space has the structure of the closed interval  in which (−1, 1) is an open dense one-dimensional manifold and {1, −1} is the rest, a zero-dimensional manifold.
in which (−1, 1) is an open dense one-dimensional manifold and {1, −1} is the rest, a zero-dimensional manifold.
Let  be random configurations of m-dimensional objects with k landmarks, with pre-shapes
be random configurations of m-dimensional objects with k landmarks, with pre-shapes  in \(\mathbb {S}^{m\times (k-1)-1}\) and shapes
in \(\mathbb {S}^{m\times (k-1)-1}\) and shapes  in \(\Sigma _m^k\) with the link function ρ given by the Procrustes metric from the pre-shape (i.e. residual) quasi-metric (10.8).
in \(\Sigma _m^k\) with the link function ρ given by the Procrustes metric from the pre-shape (i.e. residual) quasi-metric (10.8).
Theorem (Manifold Stability, cf. [28, 29])
If, with the above setup,  and if the probability that two shapes are maximally remote is zero then every Procrustes mean μ is assumed on the manifold part. □
and if the probability that two shapes are maximally remote is zero then every Procrustes mean μ is assumed on the manifold part. □
In consequence, for \(Q=P=\Sigma _m^k\), if the manifold part is assumed at all, Assumption (A1) implies Assumption (A2). With the same reasoning as in the proof of Corollary 10.4, Assumption (A4) is verified. This yields the following.
Corollary
Let
 be random configurations of m-dimensional objects with k landmarks, with pre-shapes
be random configurations of m-dimensional objects with k landmarks, with pre-shapes
 in
\(\mathbb {S}^{D\times (k-1)-1}\)
and shapes
in
\(\mathbb {S}^{D\times (k-1)-1}\)
and shapes
 in
\(\Sigma _m^k\)
such that
in
\(\Sigma _m^k\)
such that
-
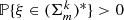 , the probability that two shapes are maximally remote is zero and
, the probability that two shapes are maximally remote is zero and
-
Assumptions (A1) and (A3) are satisfied.
Then, every measurable selection μ n of Procrustes sample means satisfies a CLT as in Theorem 10.3. □
6 Geodesic Principal Component Analysis
In this section we assume that random deviates  take values in a Riemann stratified space Q.
take values in a Riemann stratified space Q.
Definition (Stratified Space)
A stratified space Q of dimension m embedded in a Euclidean space can be defined as a direct sum

such that  , each \(Q_{d_j}\) is a d
j-dimensional manifold and
, each \(Q_{d_j}\) is a d
j-dimensional manifold and  for
for  .
.
A stratified space  is called Whitney stratified, if for every
is called Whitney stratified, if for every 
-
(i)
If
 then
then  .
. -
(ii)
For sequences
 and
and  which converge to the same point
which converge to the same point  such that the sequence of secant lines c
i between x
i and y
i converges to a line c as
such that the sequence of secant lines c
i between x
i and y
i converges to a line c as  , and such that the sequence of tangent planes
, and such that the sequence of tangent planes  converges to a d
l dimensional plane T as
converges to a d
l dimensional plane T as  , the line c is contained in T. We call a Whitney stratified space Riemann stratified, if
, the line c is contained in T. We call a Whitney stratified space Riemann stratified, if -
(iii)
for every
 and sequence
and sequence  which converges to the point
which converges to the point  the Riemannian metric tensors
the Riemannian metric tensors  converge to a rank two tensor
converge to a rank two tensor  and the Riemannian metric tensor
and the Riemannian metric tensor  is given by the restriction
is given by the restriction  .
.
□
Geodesics, i.e. curves of locally minimal length, exist locally in every stratum \(Q_{d_j}\). Due to the Whitney condition, a geodesic can also pass through strata of different dimensions if these strata are connected. Property (ii) is called Whitney condition B and it follows from this condition that  , which is called Whitney condition A, e.g. [22].
, which is called Whitney condition A, e.g. [22].
Of course, all Riemannian manifolds are stratified spaces. Typical examples for stratified spaces that are not Riemannian manifolds are Kendall’s shape spaces \(\Sigma _m^k\) for  dimensional objects with
dimensional objects with  landmarks or the BHV space of phylogenetic descendants trees \(\mathcal {T}_n\) with n ≥ 3 leaves.
landmarks or the BHV space of phylogenetic descendants trees \(\mathcal {T}_n\) with n ≥ 3 leaves.
Let Γ(Q) be the space of point sets of maximal geodesics in Q. With the intrinsic geodesic metric d Q on Q we have the link function

Further, we assume that Γ(Q) also carries a metric d
Γ. This can be either Hausdorff distance based on d
Q, or a quotient metric, e.g. induced from  with a suitable equivalence relation. An example for the latter is the identification of \(\Gamma (\mathbb {S}^{D-1})\) with G(D, 2), the Grassmannian structure of the space of two-dimensional linear subspaces in
with a suitable equivalence relation. An example for the latter is the identification of \(\Gamma (\mathbb {S}^{D-1})\) with G(D, 2), the Grassmannian structure of the space of two-dimensional linear subspaces in  (every geodesic on \(\mathbb {S}^{D-1}\) is a great circle which is the intersection with
(every geodesic on \(\mathbb {S}^{D-1}\) is a great circle which is the intersection with  of a plane through the origin).
of a plane through the origin).
Definition 10.5 (cf. [32])
With the above assumptions, setting P 0 = Γ(Q), every population Fréchet ρ-mean on P = P 0 is a first population geodesic principal component (GPC) and every such sample mean is a first sample GPC.
Given a unique first population GPC γ
1, setting  , every population Fréchet ρ-mean on P = P
1 is a second population GPC.
, every population Fréchet ρ-mean on P = P
1 is a second population GPC.
Higher order population GPCs are defined by requiring them to pass through a common point  and being orthogonal there to all previous unique population GPCs.
and being orthogonal there to all previous unique population GPCs.
Similarly, for the second sample GPC, for a given unique first GPC  use
use  and higher order sample GPCs are defined by requiring them to pass through a common point
and higher order sample GPCs are defined by requiring them to pass through a common point  and being orthogonal there to all previous unique sample GPCs.
and being orthogonal there to all previous unique sample GPCs.
The GPC scores are the orthogonal projections of X, or of the data, respectively, to the respective GPCs. □
Remark
In case of valid assumptions (A1) – (A4) the CLT from Theorem 10.3 yields asymptotic \(\sqrt {n}\)-normality for the first PC in a local chart. An example and an application to \(Q=\Sigma _2^k\)  ) can be found in [27]. □
) can be found in [27]. □
Obviously, there are many other canonical intrinsic generalizations of PCA to non-Euclidean spaces, e.g. in his horizontal PCA [48] defines the second PC by a parallel translation of a suitable tangent space vector, orthogonally along the first PC. One difficulty is that GPCs usually do not define subspaces, as classical PCs do, which define affine subspaces. However, there are stratified spaces which have rich sets of preferred subspaces.
Definition (Totally Geodesic Subspace)
A Riemann stratified space  with Riemannian metric induced by the Riemannian metric of a Riemann stratified space Q is called totally geodesic if every geodesic of S is a geodesic of Q. □
with Riemannian metric induced by the Riemannian metric of a Riemann stratified space Q is called totally geodesic if every geodesic of S is a geodesic of Q. □
The totally geodesic property is transitive in the following sense. Consider a sequence of Riemann stratified subspaces  where Q
1 is totally geodesic with respect to Q
2 and Q
2 is totally geodesic with respect to Q
3. Then Q
1 is also totally geodesic with respect to Q
3.
where Q
1 is totally geodesic with respect to Q
2 and Q
2 is totally geodesic with respect to Q
3. Then Q
1 is also totally geodesic with respect to Q
3.
In the following, we will use the term rich space of subspaces for a space of k-dimensional Riemann stratified subspaces of an m-dimensional Riemann stratified space, if it has dimension at least (m − k)(k + 1). This means that the space of k-dimensional subspaces has at least the same dimension as the space of affine k-dimensional subspaces in \(\mathbb {R}^m\). If a Riemann stratified space has a rich space of sequences of totally geodesic subspaces  where every Q
j is a Riemann stratified space of dimension j, a generalization which is very close in spirit to PCA can be defined. This is especially the case, if Q has a rich space of (m − 1)-dimensional subspaces which are of the same class as Q. For example, the sphere S
m has a rich space of great subspheres S
m−1, which are totally geodesic submanifolds. Therefore, spheres are well suited to introduce an analog of PCA, and [34, 35] have defined principal nested spheres (PNS) which even exist as principal nested small spheres, which are not totally geodesic, however. In the latter case the dimension of the space of k-dimensional submanifolds is even (m − k)(k + 2), cf. [30].
where every Q
j is a Riemann stratified space of dimension j, a generalization which is very close in spirit to PCA can be defined. This is especially the case, if Q has a rich space of (m − 1)-dimensional subspaces which are of the same class as Q. For example, the sphere S
m has a rich space of great subspheres S
m−1, which are totally geodesic submanifolds. Therefore, spheres are well suited to introduce an analog of PCA, and [34, 35] have defined principal nested spheres (PNS) which even exist as principal nested small spheres, which are not totally geodesic, however. In the latter case the dimension of the space of k-dimensional submanifolds is even (m − k)(k + 2), cf. [30].
Generalizing this concept [43], has introduced barycentric subspaces, cf. Chapter 18 of this book.
In the following penultimate section we develop an inferential framework for such nested approaches.
7 Backward Nested Descriptors Analysis (BNDA)
As seen in Definition 10.5, higher order GPCs depend on lower order GPCs and are hence defined in a nested way. More generally, one can consider sequences of subspaces of descending dimension, where every subspace is also contained in all higher dimensional subspaces. Here we introduce the framework of backward nested families of descriptors to treat such constructions in a very general way.
In Sect. 10.9 we introduce several examples of such backward nested families of descriptors.
Definitions and Assumptions 10.6
Let Q be a separable topological space, called the data space and let \(\{P_j\}_{j=0}^m\) be a family of separable topological spaces called descriptor spaces, each equipped with a loss function  (i.e. it is continuous and vanishes exactly on the diagonal) with
(i.e. it is continuous and vanishes exactly on the diagonal) with  (j = 1, …, m).
(j = 1, …, m).
Next, assume that every  (j = 1, …, m) is itself a topological space giving rise to a topological space
(j = 1, …, m) is itself a topological space giving rise to a topological space  with a continuous function
with a continuous function  called a link function.
called a link function.
Further, assume that for all  (j = 1, …, m) and
(j = 1, …, m) and  there exists a measurable mapping
there exists a measurable mapping  called projection.
called projection.
Then for  every
every

is a backward nested family of descriptors (BNFD) from P m to P j which lives in the space

with projection along each descriptor

For another BNFD  set
set

Definition
With the above Definitions and Assumptions 10.6, random elements  on the data space Q admitting BNFDs give rise to backward nested population and sample means (BN-means)
on the data space Q admitting BNFDs give rise to backward nested population and sample means (BN-means)  and
and  , respectively, recursively defined via
, respectively, recursively defined via  , i.e.
, i.e.  and for j = m, …, 2,
and for j = m, …, 2,

If all of the population minimizers are unique, we speak of unique BN-means.
Remark
A nested sequence of subspaces is desirable for various scenarios. Firstly, it can serve as a basis for dimension reduction as is also often done using PCA in Euclidean space. Secondly, the residuals of projections along the BNFD can be used as residuals of orthogonal directions in Euclidean space in order to achieve a “Euclideanization” of the data (e.g. [44]). Thirdly, lower dimensional representations of the data or scatter plots of residuals can be used for more comprehensible visualization.
Backward approaches empirically achieve better results than forward approaches, starting from a point and building up spaces of increasing dimension, in terms of data fidelity. The simplest example, determining the intrinsic mean first and then requiring the geodesic representing the one-dimensional subspace to pass through it, usually leads to higher residual variance than fitting the principal geodesic without reference to the mean. □
For a strong law and a CLT for BN-means we require assumptions corresponding to Definition 10.2 and corresponding to assumptions in [4]. Both sets of assumptions are rather complicated, so that they are only referenced here.
To the best knowledge of the authors, instead of (B2), more simple assumptions corresponding to (A1)–(A4) from Sect. 10.5 have not been derived for the backward nested descriptors scenario.
Theorem ([31])
If the BN population mean
 is unique and if
is unique and if
 is a measurable selection of BN sample means then under (B1),
is a measurable selection of BN sample means then under (B1),

i.e. there is
 measurable with
\(\mathbb {P}(\Omega ')=1\)
such that for all
measurable with
\(\mathbb {P}(\Omega ')=1\)
such that for all
 and
and
 , there is
, there is
 with
with

Theorem 10.7 ([31])
Under Assumptions (B2), with unique BN population mean  and local chart ϕ with ϕ
−1(0) = f, for every measurable selection f
n of BN sample means
and local chart ϕ with ϕ
−1(0) = f, for every measurable selection f
n of BN sample means  , there is a symmetric positive definite matrix B
ϕ such that
, there is a symmetric positive definite matrix B
ϕ such that

Remark 10.8
Under factoring charts as detailed in [31], asymptotic normality also holds for the last descriptor  ,
,

with a suitable local chart ϕ such that  and a symmetric positive definite matrix C
ϕ. □
and a symmetric positive definite matrix C
ϕ. □
8 Two Bootstrap Two-Sample Tests
Exploiting the CLT for ρ-means, BN-means or the last descriptor of BN-means (cf. Remark 10.8) in order to obtain an analog of the two-sample test (10.2), we inspect its ingredients. Suppose that  and
and  are independent random elements on Q. In case of ρ-means, we assume that Assumptions (A1)–(A4) from Sect. 10.5 are valid and in case of BN-means (or a last descriptor thereof) assume that Assumption (B2) from Sect. 10.7 is valid for X and Y , in particular that unique means μ
X and μ
Y lie within one single open set
are independent random elements on Q. In case of ρ-means, we assume that Assumptions (A1)–(A4) from Sect. 10.5 are valid and in case of BN-means (or a last descriptor thereof) assume that Assumption (B2) from Sect. 10.7 is valid for X and Y , in particular that unique means μ
X and μ
Y lie within one single open set  that homeomorphically maps to an open set
that homeomorphically maps to an open set  under ϕ. With measurable selections \(\hat {\mu }_{n}^X\) and \(\hat {\mu }_{m}^Y\) of sample means, respectively, replace
under ϕ. With measurable selections \(\hat {\mu }_{n}^X\) and \(\hat {\mu }_{m}^Y\) of sample means, respectively, replace  with
with  .
.
Obviously, \(\hat {\Sigma }_n^X\) and \(\hat {\Sigma }_m^Y\) are not directly assessable, however. If one had a large number B of samples {X
1,1, …, X
1,n}, …, {X
B,1, …, X
B,n}, one could calculate the descriptors  and estimate the covariance of these. But since we only have one sample, we use the bootstrap instead. The idea of the n out-of n non-parametric bootstrap (e.g. [12, 15]) is to generate a large number B of bootstrap samples
and estimate the covariance of these. But since we only have one sample, we use the bootstrap instead. The idea of the n out-of n non-parametric bootstrap (e.g. [12, 15]) is to generate a large number B of bootstrap samples  of the same size n by drawing with replacement from the sample X
1, …, X
n. From each of these bootstrap samples one can calculate estimators
of the same size n by drawing with replacement from the sample X
1, …, X
n. From each of these bootstrap samples one can calculate estimators  , which serve as so-called bootstrap estimators of μ. From these, one can now calculate the estimator for the covariance of \(\hat {\mu }_{n}^X\)
, which serve as so-called bootstrap estimators of μ. From these, one can now calculate the estimator for the covariance of \(\hat {\mu }_{n}^X\)

For the First Test
Perform B X times n out-of n bootstrap from X 1, …, X n to obtain Fŕechet ρ-means \(\mu ^{X,*1}_n,\ldots ,\mu ^{X,*B_X}_n\) and replace \(\hat {\Sigma }_n^X\) with the n-fold of the bootstrap covariance \(\Sigma _n^{X,*}\) as defined in Eq. (10.9). With the analog m out-of m bootstrap, replace \(\hat {\Sigma }^Y_m\) with \(m\Sigma _m^{Y,*}\).
Then, under  , if
, if  or
or  , under typical regularity conditions, e.g. [10], the statistic
, under typical regularity conditions, e.g. [10], the statistic

adapted from Eq. (10.2), is asymptotically Hotelling distributed as discussed in Sect. 10.2.
For the Second Test
Observe that, alternatively, the test statistic

can be used. Notably, this second test for  does not rely on
does not rely on  or equal covariances, as does the first. However, the test statistic is only approximately F distributed, even for normally distributed data and the parameters of the F distribution have to be determined by an approximation procedure.
or equal covariances, as does the first. However, the test statistic is only approximately F distributed, even for normally distributed data and the parameters of the F distribution have to be determined by an approximation procedure.
To enhance the power of either test, quantiles can be determined using the bootstrap. A naive approach would be to pool samples and use \(\widetilde {X}\) for the first n data points, \(\widetilde {Y}\) for the last m data points of bootstrapped samples from the pooled data X 1, …, X n, Y 1, …, Y m. However, it turns out that this approach suffers from significantly diminished power.
Instead, we generate the same number B of bootstrap samples from X
1, …, X
n and Y
1, …, Y
m separately, thus getting \(\mu _{n}^{X,*1},\ldots ,\mu _{n}^{X,*B}\) and \(\mu _{m}^{Y,*1},\ldots ,\mu _{m}^{Y,*B}\). Due to the CLT 10.7 and Remark 10.8, \(\phi ^{-1}(\mu _{n}^{X,*1}),\ldots ,\phi ^{-1}(\mu _{n}^{X,*B})\) are samples from a distribution which is close to normal with mean \(\phi ^{-1}(\hat {\mu }_{n}^{X})\). The analog holds for Y . As a consequence, the residuals  are close to normally distributed with mean 0. To simulate quantiles from the null hypothesis
are close to normally distributed with mean 0. To simulate quantiles from the null hypothesis  , we therefore only use the residuals \(d^X_{n,*j}\) and \(d^Y_{m,*j}\) and calculate
, we therefore only use the residuals \(d^X_{n,*j}\) and \(d^Y_{m,*j}\) and calculate

Then we order these values ascendingly and use them as (j − 1∕2)∕B-quantiles as usual for empirical quantiles. Tuning the corresponding test to the right level, its power is usually larger than using the F-quantiles corresponding to the Hotelling distribution.
9 Examples of BNDA
Scenarios of BNDA are given by flags, namely, by nested subspaces,

We give three examples.
The Intrinsic Mean on the First GPC
It is well known, that the intrinsic mean usually comes not to lie on the first GPC. For example a distribution on \(\mathbb {S}^2\) that is uniform on a great circle has this great circle as its first GPC with respect to the spherical metric. The Fréchet mean with respect to this metric is given, as is easily verified, by the two poles having this great circle as the equator. In order to enforce nestedness, we consider the first GPC on a Riemannian manifold and the intrinsic mean on it. The corresponding descriptor spaces are

with the tangent bundle TQ over Q, the maximal geodesic γ
q,v through q with initial velocity  and
and  if the two geodesics agree as point sets. Denoting the class of γ
q,v by [γ
q,v], it turns out that
if the two geodesics agree as point sets. Denoting the class of γ
q,v by [γ
q,v], it turns out that

where  and PQ denotes the projective bundle over Q. With the local trivialization of the tangent bundle one obtains a local trivialization of the projective bundle and thus factoring charts, so that, under suitable conditions, Theorem 10.7 and Remark 10.8 are valid. In fact, this construction also works for suitable Riemann stratified spaces, e.g. also for \(Q=\Sigma _m^k\) with
and PQ denotes the projective bundle over Q. With the local trivialization of the tangent bundle one obtains a local trivialization of the projective bundle and thus factoring charts, so that, under suitable conditions, Theorem 10.7 and Remark 10.8 are valid. In fact, this construction also works for suitable Riemann stratified spaces, e.g. also for \(Q=\Sigma _m^k\) with  , cf. [31].
, cf. [31].
Principal Nested Spheres (PNS)
For the special case of  let P
j be the space of all j-dimensional unit-spheres (j = 1, …, D − 1) and
let P
j be the space of all j-dimensional unit-spheres (j = 1, …, D − 1) and  . Note that P
j can be given the manifold structure of the Grassmannian G(D, j + 1) of (j + 1)-dimensional linear subspaces in
. Note that P
j can be given the manifold structure of the Grassmannian G(D, j + 1) of (j + 1)-dimensional linear subspaces in  . The corresponding BNDA has been introduced by Jung et al. [34, 35] as principal nested great spheres analysis (PNGSA) in contrast to principal nested small sphere analysis (PNSSA), when allowing also small subspheres in every step. Notably, estimation of small spheres involves a test for great spheres to avoid overfitting, cf. [18, 34].
. The corresponding BNDA has been introduced by Jung et al. [34, 35] as principal nested great spheres analysis (PNGSA) in contrast to principal nested small sphere analysis (PNSSA), when allowing also small subspheres in every step. Notably, estimation of small spheres involves a test for great spheres to avoid overfitting, cf. [18, 34].
Furthermore, PNSSA offers more flexibility than PNGSA because the family of all j-dimensional small subspheres in \(\mathbb {S}^{D-1}\) has dimension  , cf. [18].
, cf. [18].
As shown in [31], under suitable conditions, Theorem 10.7 and Remark 10.8 are valid for both versions of PNS.
Extensions of PNS to general Riemannian manifolds can be sought by considering flags of totally geodesic subspaces. While there are always geodesics, which are one-dimensional geodesic subspaces, there may be none for a given dimension j. And even, if there are, for instance on a torus, totally geodesic subspaces winding around infinitely are statistically meaningless because they approximate any given data set arbitrarily well. As a workaround, tori can be topologically and geometrically deformed into stratified spheres and on these PNS with all of its flexibility, described above, can be performed, as in [18]. Barycentric Subspace Analysis (BSA) by Pennec [43] constitutes another extension circumventing the above difficulties. Here P
j is the space of exponential spans of any j + 1 points in general position. More precisely, with the geodesic distance d on Q, for  , define their exponential span by
, define their exponential span by

For an m-dimensional manifold Q a suitable choice of m + 1 points  thus yields the flag
thus yields the flag

For the space of phylogenetic descendants tree by Billera et al. [7] in a similar approach by Nye et al. [42] the locus of the Fréchet mean of a given point set has been introduced along with corresponding optimization algorithms.
Barycentric subspaces and similar constructions are the subject of Chapter 11.
To the knowledge of the authors, there have been no attempts, to date, to investigate applicability of Theorem 10.7 and Remark 10.8 to BSA.
10 Outlook
Beginning with Anderson’s CLT for PCA, we have sketched some extensions of PCA to non-Euclidean spaces and have come up with a rather general CLT, the assumptions of which are more general than those of [4, 6]. Let us conclude with listing a number of open tasks, which we deem of high importance for the development of suitable statistical non-Euclidean tools.
-
1.
Formulate the CLT for BNFDs in terms of assumptions corresponding to Assumptions (A1)–(A4).
-
2.
Apply the CLT for BNFDs to BSA if possible.
-
3.
Formulate BNFD not as a sequential but as a simultaneous optimization problem, derive corresponding CLTs and apply them to BSA with simultaneous estimation of the entire flag.
-
4.
In some cases we have no longer \(\sqrt {n}\)-Gaussian CLTs but so-called smeary CLTs which feature a lower rate, cf. [17]. Extend the CLTs presented here to the general smeary scenario.
-
5.
Further reduce and generalize Assumptions (A1)–(A4), especially identify necessary and sufficient conditions for (A3).
References
Anderson, T.: Asymptotic theory for principal component analysis. Ann. Math. Statist. 34(1), 122–148 (1963)
Barden, D., Le, H., Owen, M.: Central limit theorems for Fréchet means in the space of phylogenetic trees. Electron. J. Probab. 18(25), 1–25 (2013)
Barden, D., Le, H., Owen, M.: Limiting behaviour of fréchet means in the space of phylogenetic trees. Ann. Inst. Stat. Math. 70(1), 99–129 (2018)
Bhattacharya, R., Lin, L.: Omnibus CLTs for Fréchet means and nonparametric inference on non-Euclidean spaces. Proc. Am. Math. Soc. 145(1), 413–428 (2017)
Bhattacharya, R.N., Patrangenaru, V.: Large sample theory of intrinsic and extrinsic sample means on manifolds I. Ann. Stat. 31(1), 1–29 (2003)
Bhattacharya, R.N., Patrangenaru, V.: Large sample theory of intrinsic and extrinsic sample means on manifolds II. Ann. Stat. 33(3), 1225–1259 (2005)
Billera, L., Holmes, S., Vogtmann, K.: Geometry of the space of phylogenetic trees. Adv. Appl. Math. 27(4), 733–767 (2001)
Billingsley, P.: Probability and Measure, vol. 939. Wiley, London (2012)
Bredon, G.E.: Introduction to Compact Transformation Groups. Pure and Applied Mathematics, vol. 46. Academic Press, New York (1972)
Cheng, G.: Moment consistency of the exchangeably weighted bootstrap for semiparametric m-estimation. Scand. J. Stat. 42(3), 665–684 (2015)
Davis, A.W.: Asymptotic theory for principal component analysis: non-normal case. Aust. J. Stat. 19, 206–212 (1977)
Davison, A.C., Hinkley, D.V.: Bootstrap Methods and Their Application, vol. 1. Cambridge University Press, Cambridge (1997)
Dryden, I.L., Mardia, K.V.: Statistical Shape Analysis. Wiley, Chichester (2014)
Durrett, R.: Probability: Theory and Examples. Cambridge University Press, Cambridge (2010)
Efron, B., Tibshirani, R.J.: An Introduction to the Bootstrap. CRC Press, Boca Raton (1994)
Eltzner, B., Huckemann, S.: Bootstrapping descriptors for non-Euclidean data. In: Geometric Science of Information 2017 Proceedings, pp. 12–19. Springer, Berlin (2017)
Eltzner, B., Huckemann, S.F.: A smeary central limit theorem for manifolds with application to high dimensional spheres. Ann. Stat. 47, 3360–3381 (2019)
Eltzner, B., Huckemann, S., Mardia, K.V.: Torus principal component analysis with applications to RNA structure. Ann. Appl. Statist. 12(2), 1332–1359 (2018)
Eltzner, B., Galaz-García, F., Huckemann, S.F., Tuschmann, W.: Stability of the cut locus and a central limit theorem for Fréchet means of Riemannian manifolds (2019). arXiv: 1909.00410
Fletcher, P.T., Lu, C., Pizer, S.M., Joshi, S.C.: Principal geodesic analysis for the study of nonlinear statistics of shape. IEEE Trans. Med. Imag. 23(8), 995–1005 (2004)
Fréchet, M.: Les éléments aléatoires de nature quelconque dans un espace distancié. Ann. Inst. Henri Poincare 10(4), 215–310 (1948)
Goresky, M., MacPherson, R.: Stratified Morse Theory. Springer, Berlin (1988)
Gower, J.C.: Generalized Procrustes analysis. Psychometrika 40, 33–51 (1975)
Hotz, T., Huckemann, S.: Intrinsic means on the circle: uniqueness, locus and asymptotics. Ann. Inst. Stat. Math. 67(1), 177–193 (2015)
Hotz, T., Huckemann, S., Le, H., Marron, J.S., Mattingly, J., Miller, E., Nolen, J., Owen, M., Patrangenaru, V., Skwerer, S.: Sticky central limit theorems on open books. Ann. Appl. Probab. 23(6), 2238–2258 (2013)
Huckemann, S.: Inference on 3D Procrustes means: Tree boles growth, rank-deficient diffusion tensors and perturbation models. Scand. J. Stat. 38(3), 424–446 (2011)
Huckemann, S.: Intrinsic inference on the mean geodesic of planar shapes and tree discrimination by leaf growth. Ann. Stat. 39(2), 1098–1124 (2011)
Huckemann, S.: Manifold stability and the central limit theorem for mean shape. In: Gusnanto, A., Mardia, K.V., Fallaize, C.J. (eds.) Proceedings of the 30th LASR Workshop, pp. 99–103. Leeds University Press, Leeds (2011)
Huckemann, S.: On the meaning of mean shape: Manifold stability, locus and the two sample test. Ann. Inst. Stat. Math. 64(6), 1227–1259 (2012)
Huckemann, S., Eltzner, B.: Polysphere PCA with applications. In: Proceedings of the Leeds Annual Statistical Research (LASR) Workshop, pp. 51–55. Leeds University Press, Leeds (2015)
Huckemann, S.F., Eltzner, B.: Backward nested descriptors asymptotics with inference on stem cell differentiation. Ann. Stat. 46(5), 1994–2019 (2018)
Huckemann, S., Hotz, T., Munk, A.: Intrinsic shape analysis: Geodesic principal component analysis for Riemannian manifolds modulo Lie group actions (with discussion). Stat. Sin. 20(1), 1–100 (2010)
Huckemann, S., Mattingly, J.C., Miller, E., Nolen, J.: Sticky central limit theorems at isolated hyperbolic planar singularities. Electron. J. Probab. 20(78), 1–34 (2015)
Jung, S., Foskey, M., Marron, J.S.: Principal arc analysis on direct product manifolds. Ann. Appl. Stat. 5, 578–603 (2011)
Jung, S., Dryden, I.L., Marron, J.S.: Analysis of principal nested spheres. Biometrika 99(3), 551–568 (2012)
Kendall, D.G.: The diffusion of shape. Adv. Appl. Probab. 9, 428–430 (1977)
Kendall, W.S., Le, H.: Limit theorems for empirical Fréchet means of independent and non-identically distributed manifold-valued random variables. Braz. J. Probab. Stat. 25(3), 323–352 (2011)
Kendall, D.G., Barden, D., Carne, T.K., Le, H.: Shape and Shape Theory. Wiley, Chichester (1999)
Le, H., Barden, D.: On the measure of the cut locus of a Fréchet mean. Bull. Lond. Math. Soc. 46(4), 698–708 (2014)
Mardia, K.V., Kent, J.T., Bibby, J.M.: Multivariate Analysis. Academic Press, New York (1980)
McKilliam, R.G., Quinn, B.G., Clarkson, I.V.L.: Direction estimation by minimum squared arc length. IEEE Trans. Signal Process. 60(5), 2115–2124 (2012)
Nye, T.M., Tang, X., Weyenberg, G., Yoshida, R.: Principal component analysis and the locus of the fréchet mean in the space of phylogenetic trees. Biometrika 104(4), 901–922 (2017)
Pennec, X.: Barycentric subspace analysis on manifolds. Ann. Stat. 46(6A), 2711–2746 (2018)
Pizer, S.M., Jung, S., Goswami, D., Vicory, J., Zhao, X., Chaudhuri, R., Damon, J.N., Huckemann, S., Marron, J.: Nested sphere statistics of skeletal models. In: Innovations for Shape Analysis, pp. 93–115. Springer, Berlin (2013)
Romano, J.P., Lehmann, E.L.: Testing Statistical Hypotheses. Springer, Berlin (2005)
Schulz, J.S., Jung, S., Huckemann, S., Pierrynowski, M., Marron, J., Pizer, S.: Analysis of rotational deformations from directional data. J. Comput. Graph. Stat. 24(2), 539–560 (2015)
Siddiqi, K., Pizer, S.: Medial Representations: Mathematics, Algorithms and Applications. Springer, Berlin (2008)
Sommer, S.: Horizontal dimensionality reduction and iterated frame bundle development. In: Geometric Science of Information, pp. 76–83. Springer, Berlin (2013)
Telschow, F.J., Huckemann, S.F., Pierrynowski, M.R.: Functional inference on rotational curves and identification of human gait at the knee joint (2016). arXiv preprint arXiv:1611.03665
van der Vaart, A.: Asymptotic Statistics. Cambridge University Press, Cambridge (2000)
Ziezold, H.: Expected figures and a strong law of large numbers for random elements in quasi-metric spaces. In: Transaction of the 7th Prague Conference on Information Theory, Statistical Decision Function and Random Processes, pp. 591–602. Springer, Berlin (1977)
Acknowledgements
The authors acknowledge support from the Niedersachen Vorab of the Volkswagen Foundation and support from DFG HU 1575-7.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Huckemann, S., Eltzner, B. (2020). Statistical Methods Generalizing Principal Component Analysis to Non-Euclidean Spaces. In: Grohs, P., Holler, M., Weinmann, A. (eds) Handbook of Variational Methods for Nonlinear Geometric Data. Springer, Cham. https://doi.org/10.1007/978-3-030-31351-7_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-31351-7_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-31350-0
Online ISBN: 978-3-030-31351-7
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)





 , is a continuous function
, is a continuous function if and only if p = p′.
if and only if p = p′. are random elements in a topological data space Q, which is linked to a topological descriptor space P via a continuous function
are random elements in a topological data space Q, which is linked to a topological descriptor space P via a continuous function  , featuring a unique Fréchet ρ-mean
, featuring a unique Fréchet ρ-mean  .
. and P has locally the structure of a D-dimensional manifold near μ, i.e. there is an open set
and P has locally the structure of a D-dimensional manifold near μ, i.e. there is an open set  ,
,  and a homeomorphism
and a homeomorphism 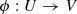 onto an open set
onto an open set  . W.l.o.g. assume that
. W.l.o.g. assume that  .
. , x = ϕ
−1(p),
, x = ϕ
−1(p), 
 exists almost surely and there is a measurable function
exists almost surely and there is a measurable function  , satisfying
, satisfying  , such that the following Lipschitz condition
, such that the following Lipschitz condition 
 .
.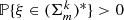 , the probability that two shapes are maximally remote is zero and
, the probability that two shapes are maximally remote is zero and
 then
then  .
. and
and  which converge to the same point
which converge to the same point  such that the sequence of secant lines c
i between x
i and y
i converges to a line c as
such that the sequence of secant lines c
i between x
i and y
i converges to a line c as  , and such that the sequence of tangent planes
, and such that the sequence of tangent planes  converges to a d
l dimensional plane T as
converges to a d
l dimensional plane T as  , the line c is contained in T. We call a Whitney stratified space Riemann stratified, if
, the line c is contained in T. We call a Whitney stratified space Riemann stratified, if and sequence
and sequence  which converges to the point
which converges to the point  the Riemannian metric tensors
the Riemannian metric tensors  converge to a rank two tensor
converge to a rank two tensor  and the Riemannian metric tensor
and the Riemannian metric tensor  is given by the restriction
is given by the restriction  .
.