Keywords

1 Introduction

Networks of mobile robots captured the attention of the distributed computing community, as they promise new application (rescue, exploration, surveillance) in potentially harmful environments. Originally introduced in 1999 by Suzuki and Yamashita [40], the model has been refined since by many authors while growing in popularity (see [28] for a comprehensive textbook). From a theoretical point of view, the interest lies in characterising, for each of these various refinements, the exact conditions that enable solving a particular task.

In the model we consider, all robots are anonymous and operate using the same embedded program through repeated Look-Compute-Move cycles. In each cycle, a robot first “looks” at its environment and obtains a snapshot containing some information about the locations of all robots, expressed in the robot’s own self-centred coordinate system, whose scale and orientation might not be consistent with the other robots’ coordinate systems (or even with the same robot’s coordinate system from a previous cycle). Then the robot “computes” a destination, still in its own coordinate system, based only on the snapshot it just obtained (which means the robot is oblivious, in the sense that its behaviour is independent of the past history of execution). Finally the robot “moves” towards the computed destination.

Different levels of synchronisation between robots have been considered. The weakest [28] (and most realistic) is the asynchronous model (ASYNC), where each robot performs its Look, Compute and Move actions at its own pace, which may not be consistent with that of other robots. The strongest [40] is the fully synchronous model (FSYNC), where all robots perform simultaneously and atomically all of these three steps. An intermediate level [40] is called semi-synchronous (SSYNC), where the computation is organised in rounds and only a subset of the robots are active at any given round; the active robots in a round performing exactly one atomic Look-Compute-Move cycle.

The general model is agnostic to the shape of the space where the robots operate, which can be the real line, a two dimensional Euclidean space, a discrete space (a.k.a. a graph), or even another space with a more intricate topology. To date, two independent lines of research focused on (i) continuous Euclidean spaces, and (ii) graphs, studying different sets of problems and using distinct algorithmic techniques.

1.1 Continuous vs. discrete spaces

The core problem to solve in the context of mobile robot networks that operate in bidimensional continuous spaces is pattern formation, where robots starting from distinct initial positions have to form a given geometric pattern. Arbitrary patterns can be formed when robots have memory [13, 40] or common knowledge [29], otherwise only a subset of patterns can be achieved [30, 42, 45]. Forming a point as the target pattern is known as gathering [3, 16, 17, 37, 40], where robots have to meet at a single point in space in finite time, not known beforehand. The problem is generally impossible to solve [17, 37, 40] unless the setting is fully synchronous [3] or robots are endowed with multiplicity detection [16]. Recently, researchers considered tridimensional Euclidean spaces [41, 43, 44], where robots must solve plane formation, that is, land on a common plane (not determined beforehand) in finite time. It turns out that robots cannot form a plane from most of the semi-regular polyhedra, while they can form a plane from every regular polyhedron (except a regular icosahedron). In the context of robots operating on graphs, typical problems are terminating exploration [15, 21,22,23, 26, 27, 35], where robots must explore all nodes of a given graph and then stop moving forever, exclusive perpetual exploration [5, 9,10,11, 20], where robots must explore all nodes of a graph forever without ever colliding, exclusive searching [8, 19, 20], where robots must capture an intruder in the graph without colliding, and gathering [12, 20, 32,33,34], where robots must meet at a given node in finite time, not determined beforehand.

Although some of the studied problems overlap (e.g. gathering), the algorithmic techniques that enable solving problems are substantially different. On the one hand, robots operating in continuous spaces may typically use fractional distance moves to another robot, or non-straight moves in order to make the algorithm progress, two options that are not possible in the discrete model. On the other hand, in the asynchronous continuous setting, a robot may be seen by another robot as it is moving, hence at some arbitrary position between its source and destination point within a cycle, something that is impossible to observe in the discrete setting. Indeed, all aforementioned works for robots on graph consider that their moves are atomic, even in the ASYNC setting, which may seem unrealistic to a practitioner.

1.2 Related Works

Designing and proving mobile robot protocols is notoriously difficult. Formal methods encompass a long-lasting path of research that is meant to overcome errors of human origin. Unsurprisingly, this mechanised approach to protocol correctness was successively used in the context of mobile robots [1, 3, 4, 6, 7, 10, 17, 21, 36, 38, 39].

In the discrete setting, model-checking proved useful to find bugs (usually in the ASYNC setting) in existing literature [7, 24, 25] and formally check the correctness of published algorithms [7, 21, 38]. Automatic program synthesis [10, 36] can be used to obtain automatically algorithms that are “correct-by-design”. However, those approaches are limited to small instances with few robots. Generalising to an arbitrary number of robots with similar approaches is doubtful as Sangnier et al. [39] proved that safety and reachability problems become undecidable in the parameterised case.

When robots move freely in a continuous bidimensional Euclidean space, to the best of our knowledge the only formal framework available is the Pactole framework.Footnote 1 Pactole enabled the use of higher-order logic to certify impossibility results [1, 4, 17] as well as certifying the correctness of algorithms [3, 18], possibly for an arbitrary number of robots (hence in a scalable manner). Pactole was recently extended by Balabonski et al. [4] to handle discrete spaces as well as continuous spaces, thanks to its modular design. However, to this paper, Pactole only allowed one to express specifications and proofs with the FSYNC and SSYNC models.

1.3 Our Contribution

In this paper, we explore the possibility of establishing a first bridge between the continuous movements and observation vs. discrete movements and observation in the context of autonomous mobile robots. Our position is that the continuous model reflects well the physicality of robots operating in some environment, while the discrete model reflects well the digital nature of autonomous robots, whose sensors and computing capabilities are inherently finite. For this purpose, we consider that robots make continuous, non atomic moves, but only sense in a discrete manner the position of robots. Our approach is certified using the Coq proof assistant and the Pactole framework.

In more details, we first extend the Pactole framework to handle the ASYNC model, preserving its modularity by keeping the operating space and the robots algorithm both abstract. This permits to retain the same formal framework for both continuous and discrete spaces, and the possibility for mobile robots to be faulty (even possibly malicious a.k.a. Byzantine). Then, as an application of the new framework, we formally prove the equivalence between atomic moves in a discrete space (the classical model for robots operating on graphs) and non-atomic moves in a continuous unidimensional space when robot vision sensors are discrete (that is, robots are only able to see another robot on a node when they perform the Look phase, but robots can move anywhere on a straight line between two adjacent nodes), irrespective of the problem being solved. Our effort consolidates the integration between the model, the problem specification, and its proof that is advocated by the Pactole framework.

Pactole and the formal developments of this work are available at https://pactole.liris.cnrs.fr.

2 The Asynchronous Look-Compute-Move Model

The complete lack of synchronisation makes reasoning in the ASYNC model particularly error prone. Nevertheless, being the most realistic model, it is widely used in the literature. In this section, we describe how to include the ASYNC model in the Pactole framework.

The formalisation of the Look-Compute-Move model in Pactole for FSYNC and SSYNC has been described in [1, 3, 18]. We briefly recall what we need here, and emphasise what characterises the ASYNC model.

2.1 Configurations

Locations. The notion of location is a parameter of the Pactole framework and is left abstract in this section, as it depends on the nature of the space in which the robots operate. In Sect. 3, we present two different spaces based on graphs, one in which the robots are only located on vertices of the graph, and the other in which the robots can also be located on edges.

Configurations associate a conformation to a robot. In the original Pactole model, robots were mapped to locations only. To reflect in ASYNC the lack of synchronisation and of uniformity of robot actions, and to add generality to the model, we enrich configurations to map a robot id to a conformation ( ) consisting of the current location, and information about movement: namely source and target locations. We can also add other information relating to individual robots such as their speeds or internal states. This allows for some robots to move while others are looking or computing. Note that integrating more information into the configuration does not give the robots extra power: they only “see” a configuration through their sensors, the result being what we call a spectrum in the sequel (see below).

figure b

We may now consider robots to be in two possible states summarised in Fig. 1: an Idle state and a Moving state. An idle robot is ready to start a new cycle with a simple Look/Compute action performing the usual Look and Compute phases. Merging these two actions is justified by the fact that the computation is based on the snapshot taken during the Look action only, thus its result cannot be changed by any other event taking place after the Look action. A robot is considered to be moving whenever its current and target locations are different, and becomes idle again when it reaches its target location (thus an idle robot that decides not to move stays idle).

Fig. 1.
figure 1

States and actions of the robots

Full size image

Spectra and Robograms. We call the embedded program the robots use to define their moves a robogram. It consists of a function that simply returns a destination location when given a perception (spectrum) of the environment and the robot’s perception of its current location. Spectra inhabit an arbitrary type that is part of the description of the model and contributes to its genericity. Indeed, depending on the robots’ capabilities, the perception usually contains less information that the complete configuration: anonymous robots cannot see names, they may lack detection of multiplicity, frames of reference may not be shared, vision can be limited, etc. In the case of ASYNC in particular, the robots generally do not perceive the additional information describing the ongoing movements of other robots. The forbidden information is pruned from the configuration, using the function which returns a spectrum, to be given as input to the robogram’s .

Depending on the space considered, the destination returned may be restricted, e.g., to locations that are close enough to the starting location. The pack of theses possible constraints with the declaration of the function constitutes what we call a robogram.

figure g

2.2 ASYNC Executions

For all synchronisation models, an execution is a sequence of configurations, each of which is deduced from the previous one, based on the robogram and on a scheduler (called a demon) that assigns a change (or not) of conformation to each robot and which is considered as an adversary. To mimic this behaviour, our formal model does not introduce any extra information: execution steps are completely characterised through a transition function by: (i) the current configuration, (ii) the demon’s choices for the step (a demonic action), and (iii) the considered protocol. Executions are simply streams of consecutive configurations for that function.

Demonic Actions. Formally, each demonic action can request a moving robot to travel further towards its target, or an idle robot to initiate a new move. In each of these cases the demon provides its choices through the action: either the distance travelled along an ongoing move for a Move action, or a frame of reference for the perception of a robot for a Look/Compute action.

figure h

This choice ( or ) is performed by the function . When relevant, demonic actions also relocate Byzantine robots in an arbitrary way (the regular states and actions being per se irrelevant for these robots).

We have no control on the choices made by the demon, which is why we call it an adversary. It must nonetheless still make meaningful choices, which we model by the following constraint: only idle robots (that is, robots that are at their target location) may receive an order to look and compute.

figure l

Transition Function. One obtains successive configurations by running the robogram according to the current demonic action and configuration.

This is done by the function computing new conformations ( ) in a configuration, for each robot identifier , according to a demonic action  :

  1. 1.

    If is Byzantine, it is relocated directly by  on actions, and ignores ones.

  2. 2.

    Else, if carries further its ongoing move ( action), its current location is updated to the location it reached during this move (the way this reached location is computed may depend on the underlying space). In the diagram in Fig. 1, this corresponds to:

    • the Move transition from Moving to Idle when reaches its target location,

    • the Move loop around Moving when does not reach its target location,

    • a Move loop (not shown) around Idle if was already at its target location.

  3. 3.

    Else, a new target location is defined as follows:

    1. (a)

      The local frame of reference provided by  is used to convert the configuration according to the relevant local point of view,

    2. (b)

      The resulting local configuration is transformed into a spectrum using ,

    3. (c)

      The obtained spectrum is passed as a parameter to the robogram, which returns the target location.

    4. (d)

      The target location is converted from the local frame to the global one.

    The robot’s conformation is updated with the obtained location as new target, and with the current location as new source. In the diagram in Fig. 1, this corresponds to:

    • the Look/Compute transition from Idle to Moving when ’s current and target locations are different,

    • the Look/Compute loop around Idle when ’s current and target location are equal.

To define a full execution, the function iterates starting from configuration , using robogram and demon . Note that a step in an ASYNC execution does not always imply a change in the multiset of inhabited locations, as some robots may undergo a change of state only.

3 Application: Formal Equivalence Between Discrete and Continuous Models

In a discrete setting, the simplest possible location type is discrete graphs where robots can only be located on vertices. A robogram takes as parameters a spectrum (perception) and a current location based on robots located on vertices, and returns a vertex as destination location. Travel along an edge is unnoticed as the target vertex is supposed to be reached instantaneously. Particularly simple, this model is convenient for reasoning; it may however be considered as rather artificial.

A more realistic point of view is given by continuous models, which take into account the continuous movements of the robots. We nevertheless restrict ourselves to discrete observations: each robot is only perceived as being close to some reference point. As a consequence, the space can still be seen as a graph (the graph of the chosen reference points) and the robots are always observed on the vertices. The movement of a robot between two vertices however is now continuous. The corresponding edge is parameterised by a travel ratio called , which is compared to the position of a robot along the edge to determine whether the robot is perceived at the source or target vertex. Computed destinations are still vertices.

We propose formalisations for these two models in our formal framework, and prove formally their equivalence in the context of oblivious robots with discrete observations, regardless of their actual observation capabilities.

3.1 Discrete Graphs

A formal model for graphs has been provided, and illustrated for SSYNC in [4] to which we refer for further details. Briefly, a graph is defined as a pair of two sets, the vertices and the edges. Each edge has a source vertex and a target vertex, given by functions and respectively. A change of frame of reference is supported by a graph isomorphism (the type of which is written in the formalisation). We want to extend this model by combining it with the ASYNC aspects presented above.

A graph and a set of robots of some size being given, we provide a model in which the ASYNC notions described above are blended.

figure ar

The locations are given by the set of vertices of the graph.

Given a spectrum, a robogram computes as destination a location that must be reachable from (i.e., adjacent to) the current location of the robot. It is thus required that the target is linked through an edge to the current location. This is simply an additional constraint to the definition of a robogram.

A moving robot travelling instantaneously between its source and target locations, the notion of travel distance degenerates into a Boolean choice: the robot either jumps to its destination, or stays at its current location. Hence the only effort in defining an ASYNC discrete graph in our formal model is to instantiate the parameter in the definition of the demonic action with .

Further note that for technical reasons we will use, in our case study, a version of these discrete graphs enriched with a field that will remain unused in the discrete case. This way both kinds of graphs will inhabit the same datatype, thus easing comparisons.

3.2 Continuous Graphs with Discrete Observations

As in the discrete model, a graph and a set of robots being given, we provide a model in which both ASYNC and continuous moves are embedded.

figure ay

The type of locations is richer, and distinguishes two cases: a robot is either on a vertex of the graph ( ) or at some position along an edge other than its source or target ( ). A position along an edge is given by a position ratio p of its length such that \(0<p<1\) (thus making actual lengths unnecessary in the model). We represent these ratios using arbitrary reals and a continuous bijection between reals and the interval ]0, 1[.

figure bb

Discrete observation is understood as a limitation (capability) of the robots’ sensors. As such, it is naturally included in the spectrum. For example, with anonymous robots enjoying multiplicity detection, the spectrum of a configuration is based on multisets of locations, however it does not show robots’ locations with accuracy. Instead, each robot is seen at the “nearest” vertex: a robot located at some position ratio p along an edge is perceived at its source if p is less than or equal to the edge , and at its target otherwise. For this, it is sufficient to use the following projection function in the construction of a spectrum from a configuration whenever the position of a robot is looked up.

figure bd

Thus the type of spectra is exactly the same as in the discrete model. Note that we also require the returned destination to be a vertex in the additional constraints embedded in the definition of a robogram.

The parameter provided by the demonic action in a transition is more precise than in the discrete setting: it can be any moving ratio m in the interval [0, 1]. The transition function then interprets this moving ratio the following way:

  • If the robot is on the source vertex of its ongoing move, \(m=0\) means staying there, \(m=1\) means going directly to the destination vertex, and \(0<m<1\) means going at the corresponding position along the edge between the current vertex and the destination vertex.

  • If the robot is at some position p on an edge, then it goes to the position \(m+p\) on the same edge. In case \(m+p\ge {}1\) the robot goes to the target vertex.

  • If the robot is already on the destination vertex, then it stays there.

For this model to make sense, the configurations must satisfy the following properties:

  • The source and target locations of robots are vertices, with an edge going from the source to the target.

  • If a robot is on a vertex, it is either its source or its target vertex.

  • If a robot is on an edge, the latter has the same source and target vertices as the robot.

These properties are collected in a property, which is shown to be preserved by the transition function .

figure bh

Hence we restrict our initial configurations to configurations in which these properties hold, and this ensures that the configurations will remain well-formed in any execution.

3.3 Simulation of the Discrete Model in the Continuous Model

To prove that the discrete model and the continuous model with discrete observation are equivalent for oblivious robots, we show that any given robogram produces the same executions in both models. We firstly establish in Theorem  that for any “discrete” execution, there is a demon such that this execution can take place in the continuous model with discrete observation context.

First remark that any robogram in one of the models can also be read as a robogram of the other model, thanks to the following facts:

  • the first parameter of a robogram is a spectrum, and the types of spectra are the same in both models,

  • the current position of the robot is always a vertex since the general model assumes that the robogram is applied only for idle robots, which are located on vertices,

  • the destination returned by a robogram is a vertex.

Technically the types are different and a translation has to be applied to see a discrete robogram as continuous or a continuous robogram as discrete, but the translation only casts \(\leftrightsquigarrow \) in both directions.

We define a translation from discrete to continuous configurations, and show that this translation relates any execution step in the discrete model with an execution step of the same robogram in the continuous model. Since for any given underlying graph the locations of the discrete model are a subset of the locations of the continuous model, the translation of the configurations is straightforward: mapping each vertex to the (continuous) location . 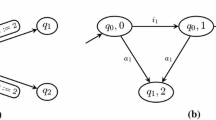The property then reads as follows: for any robogram , demonic action and configuration in the discrete model, there is a demonic action in the continuous model such that the diagram in Fig. 2 is satisfied.

Fig. 2.
figure 2

Bisimulation

Full size image
figure bs

The proof of this lemma requires to provide a demonic action in the continuous model, which is again obtained by quite a simple translation of the discrete action . In particular, the boolean parameter associated to a move action is canonically translated to either or , and the conversion to the local frame of reference needs not be translated (since both models have the same underlying graph). Note that, since demonic actions are associated to constraints (namely ), the definition of a new demonic action requires a proof that these constraints are satisfied. Once this witness is provided, the proof amounts to reasoning by cases on the various parameters of the transition function: is the robot Byzantine or not? is the scheduled action a move or a new activation? is the parameter of the move or ?

From this, we deduce that any execution in the discrete model can be simulated in the continuous model. The reciprocal property, which is more complex, is detailed in the next section.

3.4 Simulation of the Continuous Model in the Discrete Model

Configurations in the continuous model can also be translated to configurations in the discrete model. The translation uses the location projection function already defined in the description of spectra in the continuous model.

This translation allows us to state a second simulation result, similar to the previous one but relating continuous executions steps to discrete ones (that is, reading the diagram in Fig. 2 from bottom to top).

figure cc

The definition of the witness is subtler than in the previous lemma. The case where an idle robot is activated and computes a new destination ( action) is straightforward, since again we can use the same isomorphism. The case however cannot be treated using only the information in the continuous action : when a continuous demonic action provides a move ratio, we have to translate it into a boolean choice describing whether the move will end in the region of the source vertex or in the region of the target vertex. That is, we have to know whether the movement will pass the threshold or not. This requires knowing not only the demonic action , but also the configuration . The full definition then takes the following form:

figure cj

Again, the proof is by cases on all the parameters of the transition function, which are more numerous than in the previous case since the definition of the demonic action itself distinguishes many more cases.

These two simulation results, taken together, mean that any execution in any of the two models (discrete or continuous) can be related to an equivalent execution in the other model.

4 Concluding Remarks

Our work established the first formal bridge between two previously distinct models for oblivious mobile robots. From a practical point of view, the formal equivalence we provide between the discrete model and the continuous model with discrete sensors sheds new light about what is actually computable in real environments by limited capabilities robots. Furthermore, our work hints at possible new paths for future research:

  • The first issue we plan to tackle is that of realistic sensing models for mobile robots. Actual robots endowed with omnidirectional 3D visibility sensors typically use a digital camera with a set of parabolic mirrors [14], which implies that the accuracy of the localisation of a robot varies with the distance to its target robot. In our modeling, the threshold for a given edge e is the same for all participating robots, while a threshold that varies according to the distance of the observing robot to e would be more realistic. Adding this possibility to our framework is not difficult thanks to its modularity, but the equivalence proof is then likely to fail in the extended model.

  • Another important long-term open question raised by our work is that of model equivalence beyond oblivious mobile robots. Our approach considers the equivalence of executions and is hence agnostic with regards to the actual problem being solved; it also enables Byzantine robots. It would be interesting to consider model equivalences with other classical distributed computing models (e.g. Problem A in robot model m with f faulty robots is equivalent to problem B in asynchronous shared memory model \(m'\) with \(f'\) faulty processes). A natural candidate case study would be the Consensus vs. Robot Gathering problem [31].