Control of a Microturbine Using Neural Networks

Abstract

In many distributed generation applications, microturbines are used for energy conversion. On the other hand, neural networks are a suitable option for the control of complex non-linear systems. Thus, in this article is shown the speed control of a microturbine using neural networks. For this process, the identification of the microturbine using a neural network is carried out in order to subsequently perform the optimization of the other neural network used for control.

1 Introduction

Distributed resources of energy are an important alternative to supply electric power, the approach of distributed generation may allow the costs of generators and the production of electricity to be cheaper [1]. Some distributed resources of energy are: eolian generation, fuel cells, microturbines and photovoltaic systems [2]. According to [3] and [4], using appropriated control schemes is possible to improve the reliability and the power quality.

A microturbine (MT) generation system belongs to the type of thermal generation due to characteristics like lower cost, higher efficiency, more reliability and convenience; thus, MT system is considered one of the best forms of distributed generation. However, a microturbine is a complex thermal dynamic system which makes complicated to establish a precise model because of the manifested non-linearities and uncertainties [2, 5]. Some investigations addressing proper modeling for a MT can be seen in [2, 5,6,7] and [8].

Conventionally, a MT shows controls of velocity, acceleration, temperature, and fuel. According to [5], a microturbine is mainly adjusted by velocity which is regulated to a constant value close to nominal velocity in conditions of normal operation.

Meanwhile, neural networks (NN) offer an acceptable control alternative when having a highly complex system given by non-linearities, parameter variance, and saturation, among others [9].

A system of control to a microturbine using NN is proposed in this paper; the work is mainly focused on velocity controls, leaving the possibility of studying other control variables in further papers.

2 Microturbine Model

In relation of development models for a microturbine, in [6] a modular model of sixth order to a microturbine is presented. Moreover, [7] describes a simple model based on a transfer function.

According to [8], assuming the microturbine operates always close to its nominal velocity, and ignoring the start and off processes, it is then possible the construction of a simple model. In this regard, it is necessary to bear in mind that suppositions may arise uncertainties in the model [5].

Fig. 1.

Microturbine systems.

2.1 Microturbine Operation

In general, the following process are involved in the operation of a microturbine:

• 1. Air at atmospheric pressure enters to the gas turbine through the compressor.

• 2. Air is compressed to achieve the conditions to combustion.

• 3. The fuel (gas) is mixed with the air in the combustion chamber.

• 4. Then, combustion takes place. Hot gases are expanded through the turbine to generate mechanic energy.

During the combustion process, the chemical energy present in the combustion reagents is transferred to the gas flux. This energy is given by gas enthalpy such that it becomes into mechanic work by the gas expansion through the turbine. It also occurs that in the last stage of the combustion process a part of the flux is derivate to activate the compressor [10]. Figure 1 displays the interaction of these systems. From this view three components can be seen to a MT:

• 1. Combustion system.

• 2. Turbine and compressor system.

• 3. Thermal system.

Fuel System. Figure 2 shows the fuel system parts. Main components are the valve positioner and the flux dynamic behavior. In this figure $V_f$ is the fuel input signal, this is amplified via $K_f$ (gain) and compensated using $F_0$ which are the fuel flux without load in nominal velocity. Then, the signal passes through the valve and actuator positioner to produce the fuel flow signal $W_f$ [2].

Fig. 2.

Fuel subsystem.

According to [11] and [12], the transfer function associated to the valve is:

$$\begin{aligned} E_f = \frac{K_a}{T_bs+1}f_d \end{aligned}$$

(1)

Regarding the flux dynamics the respective transfer function is:

$$\begin{aligned} W_f = \frac{1}{T_fs+1}E_f \end{aligned}$$

(2)

where $K_a$ represents the gain associated with the valve positioner, $T_b$ and $T_f$ are time constant values for the valve positioner and the fuel system. Meanwhile, $f_d$, $E_1$ are the input and output positioner of the valve, and $W_{f}$ is the flux signal fuel.

Turbine and Compressor Systems. Figure 3 displays the block diagram of the gas turbine. Turbine input signals are the fuel flux $W_f$ and the angular velocity $w_r(t)$. Output signals are the turbine torque $\tau _m(t)$. According to [11] and [12], the transfer for the gas turbine is:

$$\begin{aligned} W_{C} = \frac{1}{T_{CD}s+1}W_{fC} \end{aligned}$$

(3)

where $T_{CD}$ is the constant time value associated with the dynamics of the gas turbine. The torque of the microturbine is described by:

$$\begin{aligned} F_C = a_{C}-b_{C}W_{C}+c_{C}(1-w_r) \end{aligned}$$

(4)

As observable, $F_C$ is a function of the fuel flux and the turbine velocity.

Fig. 3.

Turbine and compressor systems.

Thermal System. The fuel burnt (fuel flux) in the combustion chambers generates torque of the turbine and the gas escape temperature [11]. Figure 4 shows the block diagram of the thermal system.

Fig. 4.

Thermal system.

According to [11] and [12], the escape temperature of the gas is given by:

$$\begin{aligned} F_T = T_{ref} - a_{t}(1-W_{t})+b_{t}(1-w_r) \end{aligned}$$

(5)

where $F_T$ is a function whose entries consist of fuel flux with delay $W_{t}$, and the turbine velocity $w_r(t)$. Escape temperature is measured using a set of thermocouples which are assigned in the radiators.

On the other hand, $K_4$ and $K_5$ are constant values associated with the insulation transfer function (opposing to the radiation). $T_3$ and $T_4$ are values of constant time of the transfer functions of both the insulation and the thermocouple. In addition, $T_{ref}$ represents the escape temperature (reference temperature) [5, 8].

3 Permanent Magnet Synchronous Generator

In energy generation systems, the Permanent Magnet Synchronous Generator (PMSG) is widely used to obtain transformation from mechanical to electrical energy [13]. According to [14] and [15], permanent magnet synchronous generators need no feeding of direct current (DC) for the excitation circuit, neither have contact brushes.

The scheme for PMSG is shown in Fig. 5, where the input of the generator is the torque $\tau _m(t)$ and the output the angular velocity $w_r(t)$. Related works using PMSG and neural systems are presented in [16] and [17].

Fig. 5.

Scheme of a PSMG.

The dynamic model of a PMSG is composed of two parts, one mechanical and the other electrical that is obtained of the mobile synchronous framework of two signals $d-q$, where the axis q is $90^{\circ }$ ahead axis d regarding the direction of rotation [15]. The mechanical system is composed by the following equations:

$$\begin{aligned} \frac{dw_r}{dt}= & {} \frac{1}{J}(\tau _e-Fw_r-\tau _m ) \end{aligned}$$

(6)

$$\begin{aligned} \frac{d\theta }{dt}= & {} w_r \end{aligned}$$

(7)

where $w_r$ rotor angular velocity, $\theta$ angular position, J is the rotor inertia, F rotor viscous friction, and $\tau _m$ mechanical torque. For the electrical part the model equations in the coordinates $d-q$ are:

$$\begin{aligned} \frac{di_d}{dt}= & {} \frac{1}{L_d}v_d-\frac{R}{L_d}i_d+\frac{L_q}{L_d}pw_ri_q \end{aligned}$$

(8)

$$\begin{aligned} \frac{di_q}{dt}= & {} \frac{1}{L_q}v_q-\frac{R}{L_q}i_d-\frac{L_d}{L_q}pw_ri_d-\frac{\lambda pw_r}{L_q} \end{aligned}$$

(9)

$$\begin{aligned} \tau _e= & {} 1.5p[\lambda i_q+(L_d-L_q)i_di_q] \end{aligned}$$

(10)

in these equations $i_d$, $i_q$ are the currents, $v_d$, $v_q$ voltages, $L_d$, $L_q$ the inductances, R stator resistance, $\lambda$ amplitude of the flux induced by the permanent magnets, p number of pole pairs, and $\tau _e$ electromagnetic torque. For current and voltage conversions is used the parameter $\gamma =2\pi /3$. The current conversion from $d-q$ to abc axis is:

$$\begin{aligned} \left[ \begin{array}{c} i_a \\ i_b \\ i_c \\ \end{array} \right] = \left[ \begin{array}{cc} \cos (\theta ) &{} -\sin (\theta ) \\ \cos (\theta -\gamma ) &{} -\sin (\theta -\gamma ) \\ \cos (\theta +\gamma ) &{} -\sin (\theta +\gamma ) \\ \end{array} \right] \left[ \begin{array}{c} i_d \\ i_q \\ \end{array} \right] \end{aligned}$$

(11)

The voltage conversions from abc to $d-q$ corresponds to:

$$\begin{aligned} \left[ \begin{array}{c} v_d \\ v_q \\ \end{array} \right] = \frac{2}{3} \left[ \begin{array}{ccc} \cos (\theta ) &{} \cos (\theta -\gamma ) &{} \cos (\theta +\gamma ) \\ -\sin (\theta ) &{} -\sin (\theta -\gamma ) &{} -\sin (\theta +\gamma )\\ \end{array} \right] \left[ \begin{array}{c} v_a \\ v_b \\ v_c \\ \end{array} \right] \end{aligned}$$

(12)

4 Neural Networks

According to [18, 19] neural networks are a suitable alternative for the identification and control of dynamic systems when the system presents non-linearities. One of the advantages of neural networks is the flexibility of adaptation, association, evaluation and recognition of patterns [20].

The information is processed through inputs, a weight per connection and an output associated with an activation function as corresponds to equation (13), where each input $x_n$ is weighted using $w_n$ and added to be later evaluated by an activation function f to obtain the output y. Some activation functions are: sigmoid, gaussian, linear, saturated linear, and hard limit. The addition of network layers allows the increase of the adaptation capabilities [21].

$$\begin{aligned} y = f\left( \sum _{n=1}^{N} w_n x_n \right) \end{aligned}$$

(13)

In applications of identification and control can be used feed forward or backward networks. In recurrent networks (feed-backward networks) feedback is present among neurons as well as from the output to the inputs. In feed-forward the signals move forward only, therefore, it is necessary an additional feedback from the output to the inputs [22].

5 Neural Control System

Neural control system is proposed as an alternative to identify and to control dynamic systems, using its capacity as approximator for general functions [9]. Figure 6 shows the neural network control model.

Fig. 6.

Neural network control reference model.

In Fig. 6 it is shown two neural networks used for the neural control system, where y[n] is the measured signal of the process, u[n] is the control signal, r[n] the reference for the controller, $y_s[n]$ the simulated plant output, and $y_r[n]$ the desired output (reference-model).

The considered architecture uses two neural networks, one for the control and another to estimate the plant model. Thus, the identification of the plant is first carried out and subsequently the controller training. The plant identification is made using the Backpropagation algorithm, after carrying out the identification, the controller training is performed using the algorithm Dynamic Backpropagation in which it incorporates in a closed loop the dynamics of the neural-model plant and the dynamic behavior of the controller, thus, the parameters of the controller are optimized so that the output has the desired behavior (reference-model). After being trained the controller is put into operation with the plant [23, 24].

5.1 Identification Using Neural Networks

According to [25], when using neural networks, the classic methods for identifying dynamic systems are series-parallel and parallel, shown in Fig. 7. In the series-parallel identification scheme are directly used the inputs and outputs of the plant; under this approach, the Backpropagation method can be used as a training algorithm [26]. On the other hand, in the parallel identification scheme, inputs of the plant are used and the output of the network being feedback to the inputs, with this perspective, the Dynamic Backpropagation is employed as training algorithm [24]. In this paper is used series-parallel identification.

Fig. 7.

Series-parallel and parallel identification scheme.

6 Implementation and Results

Implementing the process of identification, together with microturbine control are made in MATLAB$^{\circledR }$ (version 7). The plant model used can be seen in Fig. 8; it can be noted that the input corresponds to the flux of fuel and the output to the angular velocity. A random signal is employed to obtain the data used in plant identification which allows to describe the different behaviors present in the system output (velocity). Figure 9 permits to see the neural controller architecture using MATLAB$^{\circledR }$.

Fig. 8.

Microturbine model used.

The general expressions for neural networks used for identification are given by $f_p$ and for control by $f_c$ functions. Taken p as the output delays, q as the input delays, m as reference delays, then the equations for plant model $y_s[n+1]$ and the control signal $u[n+1]$ are:

$$\begin{aligned} y_s[n+1]= & {} f_p(y[n],y[n-1],...,y[n-p+1],u[n],u[n-1],...\nonumber \\&,u[n-q+1]) \end{aligned}$$

(14)

$$\begin{aligned} u[n+1]= & {} f_c(y[n],y[n-1],...,y[n-p+1],r[n],r[n-1],...\nonumber \\&,r[n-m+1],u[n-1],...,u[n-q+1]) \end{aligned}$$

(15)

Fig. 9.

Neural control system scheme.

For control and identification process, different neural networks are used taking 2, 3, and 4 delays for the input as well as to output feedback. The neural networks used have two hidden layers, the first layer is set using 2, 3, and 5 neurons, and the second layer one neuron. For plant identification is used the function “TRAINLM” that implements the Levenberg-Marquardt Backpropagation, and for controller training is used “TRAINBFGC” corresponding to the BFGS (Broyden-Fletcher-Goldfarb-Shanno) quasi-Newton Backpropagation method. The additional configurations of neural controller are:

• Hidden layers: 2

• Activation functions layer 1: sigmoid

• Activation function layer 2: linear

• Training epoch for identification: 300

• Training epoch for controller: 50

• Number of training data for identification: 6000

• Number of training data for controller: 1000

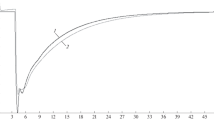
Each configuration is respectively executed 20 times to identification and control training; thus, obtaining the values of the Mean Squared Error (MSE) as shown in Table 1a for identification, and Table 1b for controller training. These tables present for each configuration the minimum, maximum, average and standard deviation (STD) values. To perform the controller training is used the configuration of 2 delays and 5 neurons obtained from the identification process (neural-model). Part of data used for identification can be seen in Fig. 10a; this figure also displays the results of the identification process made with the neural network.

Table 1. Results for identification and controller training.

Figure 10b shows the control system response after the training, as an example, it is taken a configuration using 1 delay and 3 neurons. This process includes the identified model (with the neural network) to train the controller which is implemented with another neural network.

Fig. 10.

Graphical results for identification and controller training. (Color figure online)

Finally, the results of the simulation of the neural controller with the plant model can be seen in Fig. 11; in this case, the microturbine model is used for simulation.

Fig. 11.

Simulation for microturbine control. (Color figure online)

These simulations allow to see the system behavior when it is performing the controller training and also the controller response operating with the microturbine model.

7 Conclusions

In this work, the identification and control of a microturbine were achieved using a neural network scheme. Observations show that the performance of the system is linked to the initial configuration of the neural network, which is made randomly.

The traditional Backpropagation algorithm was used to identify the plant, while the Dynamic Backpropagation algorithm was used for the optimization of the controller.

Taking the most suitable configuration obtained from the system, it is observable that the system can achieve the control for different speed values.

Plant parameter variations can be considered in a further work in such a way that an adaptive process may be implemented, as well as a neuro-fuzzy system in which random parameter initializations be needless in the neural system.