On a Simple Hedonic Game with Graph-Restricted Communication

Abstract

We study a hedonic game for which the feasible coalitions are prescribed by a graph representing the agents’ social relations. A group of agents can form a feasible coalition if and only if their corresponding vertices can be spanned with a star. This requirement guarantees that agents are connected, close to each other, and one central agent can coordinate the actions of the group. In our game everyone strives to join the largest feasible coalition. We study the existence and computational complexity of both Nash stable and core stable partitions. Then, we provide tight or asymptotically tight bounds on their quality, with respect to both the price of anarchy and stability, under two natural social functions, namely, the number of agents who are not in a singleton coalition, and the number of coalitions. We also derive refined bounds for games in which the social graph is restricted to be claw-free. Finally, we investigate the complexity of computing socially optimal partitions as well as extreme Nash stable ones.

1 Introduction

Coalition formation, that is the process by which agents gather into groups, is a fervent research topic at the intersection of Multi-Agent Systems, Computational Social Choice and Algorithmic Game Theory. One of the most studied models of coalition formation is that of hedonic games [6, 8, 13, 19], where agents have preferences over all possible coalitions they can belong to. As agents are usually assumed to be self-interested, an acceptable outcome for a hedonic game, that is a partition of agents into coalitions, needs to be resistant to agents’ deviations. Several notions of stability have been investigated in the literature, such as, individual stability, Nash stability, core stability (see, for instance, [1]).

In a recent paper, Igarashi and Elkind [20] add a further constraint to the definition of acceptable outcomes for hedonic games, by introducing the notion of feasible coalition: a coalition is feasible if and only if it complies with some prescribed properties. For instance, they assume that the set of agents corresponds to the vertex set V(G) of a social graph G and require a coalition to induce a connected subgraph of G.

In this work, we restrict the feasibility constraint of [20] to coalitions inducing a subgraph of G admitting a spanning star. This requirement guarantees that agents are connected, close to each other, and one central agent can coordinate the actions of the group. We apply this framework within a basic model, falling within the class of additive separable symmetric hedonic games, in which an agent’s utility is defined by the cardinality of the coalition she belongs to.

1.1 Game Model, Definitions and Notation

Given an unweighted and undirected graph $G=(V,E)$, a coalition is any non-empty subset of V. A partition of V is a set of pairwise disjoint coalitions whose union equals V. We denote by $\mathcal {F}\subseteq 2^V$ the set of feasible coalitions. We shall consider $\mathcal {F}=\{C\in 2^V\mid G[C] can be spanned with a star\},$ where G[C] is the subgraph of G induced by C and a star is a tree of depth at most 1. A star on one vertex is called trivial.

Given an undirected, unweighted and connected graph G, game $(G,\mathcal {F})$ is defined as follows. Each vertex of G is associated with an agent in the game. Let $\varPi$ be the set of partitions of V. For a partition $\pi \in \varPi$ and a vertex $i\in V$, denote as $\pi (i)$ the coalition in $\pi$ containing i. The utility of i in $\pi$ is defined as

$$\begin{aligned} {u}_{i}(\pi )=\left\{ \begin{array}{cl} |\pi (i)| &{} \text { if }\pi (i)\in \mathcal {F},\\ 0 &{} \text { otherwise.} \end{array} \right. \end{aligned}$$

(1)

We say that agent i has a profitable deviation in $\pi$ if either $\pi (i)\notin \mathcal{F}$, or there exists a coalition $C\in \pi$ such that $C\cup \{i\}\in \mathcal{F}$ and $|C|\ge |\pi (i)|$. In the first case agent i can form the singleton coalition $\{i\}$ which is feasible because it is spanned by a trivial star and yields a utility equal to $1>u_i(\pi )=0$. In the second case, agent i increases her utility by joining C. More generally, a set of agents S has a joint profitable deviation in $\pi$ if there exists a partition $\pi '$, obtained from $\pi$ by letting every agent $i\in S$ leave coalition $\pi (i)$ and either join another coalition in $\pi$ or form a new one, such that $u_i(\pi ')>u_i(\pi )$ for each $i\in S$.

A partition $\pi$ is Nash stable (resp. Strong Nash stable) if no agent (resp. no set of agents) has a profitable deviation (resp. a joint profitable deviation) in $\pi$. Nash and strong Nash stable partitions correspond to (pure) Nash and Strong equilibria respectively. We say that a partition is feasible if each of its coalitions belongs to $\mathcal F$. It is easy to see that, by definition, any Nash stable partition is feasible. In a core stable partition $\pi$, there is no coalition C for which all its members are better off by forming C. The set of core stable partitions (simply called the core) is a subset of the set of Nash stable ones. Strong Nash stability implies core stability but the converse is not always true. Nevertheless, because every agent only cares about the size of its coalition if it is feasible, like in anonymous hedonic games [6], strong Nash stability and core stability coincide in our game. We will use the word core instead of strong Nash for the rest of this article.

A social function is a function, defined from $\varPi$ to ${\mathbb {R}_{\ge 0}}$, measuring the social value of a partition. A social optimum is a partition $\pi ^{*}\in \mathcal{F}$ optimizing a given social function. We consider the following two social functions: sociality, defined as $soc(\pi )=|\{i\in V:|\pi (i)|>1\}|$, and fragmentation, defined as $frag(\pi )=|\pi |$. Sociality needs to be maximized, while fragmentation needs to be minimized.

We evaluate the efficiency of stable partitions by means of the well established notions of price of anarchy (PoA), price of stability (PoS) and their strong versions (SPoA and SPoS). The PoA (resp. PoS) of game $(G,\mathcal{F})$ with respect to sociality is defined as $\frac{soc(\pi ^*)}{soc(\pi )}$, where $\pi ^*$ is a social optimum and $\pi$ is a Nash stable partition of minimum (resp. maximum) sociality. The PoA (resp. PoS) of game $(G,\mathcal{F})$ with respect to fragmentation is defined as $\frac{frag(\pi )}{frag(\pi ^*)}$, where $\pi ^*$ is a social optimum and $\pi$ is a Nash stable partition of maximum (resp. minimum) fragmentation. By substituting the notion of Nash stable partition with that of core stable one, we obtain the definition of both the SPoA and SPoS. Observe that, for a given game $(G,\mathcal{F})$ and independently of the chosen social function, PoS$(G,\mathcal{F})\le$ SPoS$(G,\mathcal{F})\le$ SPoA$(G,\mathcal{F})\le$ PoA$(G,\mathcal{F})$.

1.2 Some Motivations

Requiring subgraphs spanned by a star can be interpreted as restricting the model of [20] to communication patterns of small length. In comparison, unbounded multi-hop communication may be costlier, slower, and prone to errors or misunderstandings. Therefore, distant communication should be avoided. These observations provide both theoretical and practical motivations for the constraint considered in this work. Moreover, our game, complemented with a suitable social function, naturally models several interesting scenarios, some of which are outlined in the following.

Unions. Assume that V(G) models a set of workers of a given company, the edge set E(G) the ideological acquaintance, and that the power of a union is measured by its size. Thus, workers want to join the largest unions. However, a union can survive only if it has a leader who is ideologically close to its partners. For this model, it makes sense considering the fragmentation social function that aims at minimizing the number of unions representing the workers and augmenting their negotiation power.

Group Buying. Assume that V(G) models a set of buyers, all interested in the same product, and E(G) their knowledge/trust relationships. Buyers enjoy flowing into large buying groups, as the larger the group, the better the purchasing conditions they can fetch. However, negotiation with the seller is carried out by one group member only, who then gets also in charge of redistributing what is bought to the others. Thus, this agent needs to be trusted by everybody. If one considers the case in which the product has a fixed price and the share each agent pays is equal to the price divided by the cardinality of her buying group, fragmentation becomes equal to the sum of the costs of all players, i.e., to the utilitarian social function.

Sport Tournaments. Assume that V(G) models a set of teams and there is an edge between two teams if they are close enough to meet and practice a given sport (e.g. football). The participants gather into groups in such a way that a central member can host all teams of its group and organize a tournament. Teams will prefer larger tournaments to small ones in order to maximize the number of opponents against which they can play a match. Sociality, here, aims at involving as many teams as possible into the organization of local tournaments, no matter how big those events are.

1.3 Contribution

We focus on the complexity and efficiency of both Nash stable and core stable partitions. Some proofs are omitted due to space constraints.

As to complexity results, we provide two constructive evidences showing existence of core stable partitions, and so also of Nash stable ones. In particular, any sequence of joint profitable deviations converges to a core stable partition, while Theorem 1 characterizes the core as the set of all possible outputs of a polynomial time greedy algorithm. These two facts complement each other, as the first does not need any coordination among the agents, but provides no guarantees of fast convergence, whereas the second, while requiring centralized coordination (dictated by the greedy choices of the proposed algorithm), guarantees efficient computation. We then provide bounds on the PoA, PoS, SPoA and SPoS under social functions sociality and fragmentation. In particular, we consider games induced by general (unrestricted) graphs and games induced by claw-free graphs. These results are summarized in Fig. 1.

Fig. 1.

Bounds on the efficiency of both Nash stable and core stable partitions with respect to social functions sociality and fragmentation. In the last column $k=\sqrt{n+4}-2$.

It turns out that the presence of claws in the social graph defining the game is a provable source of inefficiency that has to be taken into account, for instance, whenever mechanisms for coping with selfish behavior can be designed and applied.

Finally, we also address the problem of computing outcomes with prescribed welfare guarantees. In particular, we consider the computation of social optima and extreme (i.e., either best or worst) Nash stable partitions under both social functions. We design a polynomial time algorithm to compute a social optimum for sociality and prove that all other problems are NP-hard, except for that of computing a worst Nash stable partition under fragmentation whose complexity remains open.

1.4 Related Work

The language for describing which coalitions are feasible, and how agents value them, is a critical feature in hedonic games. Like in [9, 12], feasible coalitions and their values can be described with the help of a (directed) graph. Igarashi and Elkind [20] and Peters [27] have considered hedonic games defined over graphs: agents are the vertices and feasible coalitions satisfy a given graph property. Regarding the worth of a coalition, a simple and compact representation is given by additively separable functions [6]: each agent i assigns a value $\nu _{ij}$ to agent j and agent i’s worth for a coalition C is $\sum _{j \in C}\nu _{ij}$. See, for example, [23] for a simple hedonic game where $\nu _{ij} \in \{0,1\}$. Our work falls in this framework, as everybody wants to be part of the largest coalition ($\nu _{ij}$ is always 1), and a coalition is feasible if and only if the vertices representing the agents can be covered with a star.

Regarding existing games defined over graphs, Panagopoulou and Spirakis [25] and Escoffier et al. [14] studied a game where the vertices of a graph have to select a color (each color corresponds to a coalition), and a vertex’s payoff is the number of agents with the same color, provided that it constitutes an independent set.

In many works including the famous stable marriage problem, the coalitions form a matching of a graph (see for example [19]).

For bounds on the price of anarchy and the price of stability in some classes of hedonic games, one can see [4, 7, 15, 21, 22]. The computation of socially optimal partitions in hedonic games, according to different social functions, has been treated in [5, 9,10,11, 16]. Finally, we refer the reader to [2, 3, 24, 26] for an extensive treatment of the computational complexity of both decision and search problems related to stable partitions in hedonic games.

2 On Core Stable Partitions

Given a partition $\pi$, a strong Nash dynamics of length $\ell$ starting from $\pi$ is a sequence of partitions $\langle \pi =\pi _0,\pi _1,\ldots ,\pi _\ell \rangle$ such that, for each $j\ge 1$, $\pi _j$ is obtained as a result of a joint profitable deviation of some set of agents in $\pi _{j-1}$.

A game has the lexicographical improvement property (LIP) [18], if every joint profitable deviation strictly decreases the lexicographical order of a certain function defined on $\varPi$. It is not difficult to see that for any graph G, game $(G,\mathcal{F})$ has the LIP property if one considers the n-dimensional vector consisting of the values $u_i(\pi )$ for each $i\in V$, sorted in non-increasing order. Thus, a core stable partition always exists as the length of every strong Nash dynamics is finite.

We now prove that, if centralized coordination is allowed, a core stable partition can be computed in polynomial time. This is done by proving that the core is completely characterized by the set of all possible outputs of Algorithm 1.

Theorem 1

A partition is core stable if and only if it is the output of Algorithm 1 (according to some specific tie breaking rule).

Proof

The algorithm outputs a feasible partition $\pi$. First we show that $\pi$ is core stable. Assume, by way of contradiction, that $\pi$ is not core stable. Then, there exists a joint profitable deviation in $\pi$ for a coalition S such that $|S|\ge 1$. Let i be the agent getting the highest utility in $\pi$ among the ones belonging to S. As i improves, she will end up in a coalition $C\in \mathcal{F}$ such that $|C|>|\pi (i)|$. If C is created by the algorithm before $\pi (i)$, then i should belong to C in $\pi$: a contradiction to the greedy choice. Hence, either C is created by the algorithm after $\pi (i)$ or it is a new coalition created by the joint deviation. As i gets the highest utility in S, C only contains vertices belonging to coalitions created by the algorithm at the step $\pi (i)$ is created or after. This implies that, at the step in which $\pi (i)$ is created, C could have been created too, thus contradicting the greedy choice.

Now, we show that any core stable partition $\pi$ can be the output of the above algorithm. List the coalitions in $\pi$ by non-increasing cardinality and define a tie breaking rule R that gives priority to the coalitions in $\pi$ according to the given ordering, and gives higher priority to a coalition in $\pi$ with respect to any coalition not in $\pi$. Run the algorithm according to rule R to obtain a partition $\pi '$. Assume, by way of contradiction, that $\pi \ne \pi '$. List the coalitions in $\pi '$ by non-increasing cardinality, breaking ties according to R. Let j be the first index at which the two sequences become different and denote as C and $C'$ the j-th coalition in the ordering defined on $\pi$ and $\pi '$, respectively. By the definition of R, it must be $|C'|>|C|$ which implies that all vertices in $C'$ can perform a joint profitable deviation in $\pi$. This contradicts the assumption that $\pi$ is a core stable partition.   $\square$

3 Efficiency of Core/Nash Stable Partitions

In this section, we focus on the efficiency of Nash or core stable partitions with respect to both social functions sociality and fragmentation. Before characterizing the price of anarchy, we prove some preliminary lemmas.

Lemma 1

If G admits a spanning star, then any Nash stable partition for game $(G,\mathcal{F})$ is formed by a unique coalition V(G).

Lemma 2

If G is connected with $n\ge 3$, then any Nash stable partition for game $(G,\mathcal{F})$ contains either 2 coalitions of size at least 2 or a coalition of size at least 3.

We are now ready to characterize the PoA. As it is equal to 1 for any game with three players (by Lemma 1), in the remaining of the section we shall assume $n\ge 4$.

Theorem 2

For any game with n players, the price of anarchy is n/3 with respect to sociality and $(n-2)/2$ with respect to fragmentation. Both bounds are tight.

Proof

Fix a Nash stable partition $\pi$. By Lemma 2, $soc(\pi )\ge 3$. As the sociality of any partition is upper bounded by n, we obtain an upper bound of n/3 on the price of anarchy. By Lemma 1, if the fragmentation of the social optimum is 1, then the price of anarchy is 1, hence assume that its fragmentation is at least 2. By Lemma 2, $frag(\pi )\le n-2$ which yields the desired upper bound on the price of anarchy.

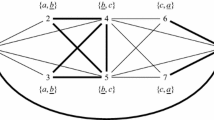
A matching lower bound for both social functions can be obtained by considering the game induced by the graph G depicted in Fig. 2. The partition $\pi$ such that $\pi (v_1)=\{v_1,v_2,v_3\}$ and $\pi (v_i)=\{v_i\}$ for $i>3$ is Nash stable and has $soc(\pi )=3$ and $frag(\pi )=n-2$. On the other hand, the partition $\pi ^*$ such that $\pi ^*(v_1)=\{v_1,v_2\}$ and $\pi ^*(v_3)=\{v_3,\ldots ,v_n\}$ has a sociality of n and a fragmentation of 2. Comparing the two partitions yields the desired lower bounds.   $\square$

Fig. 2.

A graph yielding a game with worst-case price of anarchy.

It is also possible to give an upper bound on the price of anarchy with respect to both social functions which depends on the stability number $\alpha (G)$ of graph G, where $\alpha (G)$ is the largest size of an independent set.

Theorem 3

The price of anarchy of game $(G,\mathcal{F})$ is at most $\frac{n}{n-\alpha (G)+1}$ with respect to sociality and at most $\frac{\alpha (G)}{2}$ with respect to fragmentation.

Proof

Fix a Nash stable partition $\pi$. As the set of centres of the stars spanning the subgraph induced by each coalition in $\pi$ forms an independent set in G, it follows that $frag(\pi )\le \alpha (G)$. Thus, by Lemma 2, it follows that the price of anarchy with respect to fragmentation is at most $\frac{\alpha (G)}{2}$. Moreover, as G has at least one edge, the number of singleton coalitions in $\pi$ can be at most $frag(\pi )-1\le \alpha (G)-1$. So, $soc(\pi )\ge n-\alpha (G)+1$.   $\square$

For the efficiency of core stable outcomes, we have the following results.

Theorem 4

For any game $(G,\mathcal {F})$ with n players $SPoS(G,\mathcal {F}) \in \left[ \frac{n}{2+\sqrt{n-2}}, \frac{n}{1+\sqrt{n-1}}\right]$ and $SPoA (G,\mathcal {F}) = \frac{n}{1+\sqrt{n-1}}$ hold for the sociality function.

Proof

For the upper bound, consider a coalition C in a core stable partition $\pi$ with $|C|=k>2$ and let c be the center of the spanning star of G[C]. No vertex i belonging to a singleton coalition can be adjacent to c, otherwise i would have a profitable deviation in $\pi$. Any vertex $i\in C$, with $i\ne c$ can be adjacent to at most $k-2$ vertices belonging to a singleton coalition, otherwise these vertices, together with i and c would have a joint profitable deviation in $\pi$. It follows that for any coalition in $\pi$ with $k>2$ vertices, there can be at most $(k-1)(k-2)$ singleton coalitions in $\pi$. Let $s_k$ be the number of coalitions in $\pi$ with k vertices for $k\ge 1$. We deduce $\sum _{k=3}^n\left( s_k(k^2-3k+2)\right) \ge s_1$ which gives $\sum _{k=2}^n\left( s_k(k^2-2k+2)\right) \ge n$ by adding $\sum _{k=2}^n k s_k$ on both sides.

As the sociality in a social optimum is upper bounded by n and $soc(\pi )=\sum _{k=2}^n(s_k k)$, we obtain that the strong price of anarchy is at most $\frac{n}{\sum _{k=2}^n(s_k k)} \le \frac{\overline{k}^2-2{\overline{k}}+2}{\overline{k}}$, where $\overline{k}=\max \{k:s_k>0\}$. Moreover, as $soc(\pi )\ge \overline{k}$, the strong price of anarchy is trivially upper bounded by $n/\overline{k}$. It follows that the minimum of the two derived bounds is maximized for $\overline{k}^2-2\overline{k}+2=n \Leftrightarrow \overline{k}=1+\sqrt{n-1}$, which yields the desired upper bound on both $SPoA (G,\mathcal {F})$ and $SPoS (G,\mathcal {F})$.

For the lower bound on the strong price of anarchy, consider the game induced by a tree G rooted at vertex $x_0$ which has $\ell$ children denoted as $x_1,\ldots ,x_\ell$. For each $i\in [\ell ]$, $x_i$ has $\ell -1$ children, so that G has $n=\ell ^2+1$ vertices. By using the characterization of core stable partitions given in Theorem 1, it follows that the partition $\pi$ whose unique non-singleton coalition is $\{x_0,x_1,\ldots ,x_\ell \}$ is a core stable partition for game $(G,\mathcal{F})$. As $soc(\pi )=\ell +1$ and there is a partition with sociality n, we get that the strong price of anarchy is lower bounded by $\frac{n}{\ell +1}$. By using $n=\ell ^2+1$, it follows that $\frac{n}{\ell +1}=\frac{n}{1+\sqrt{n-1}}$ and this provides the desired lower bound.

For the lower bound on the strong price of stability, add a vertex y to the previous instance which is solely connected to $x_0$, so that G now has $n=\ell ^2+2$ vertices. In this case, the partition $\pi$ whose unique non-singleton coalition is $\{x_0,x_1,\ldots ,x_\ell ,y\}$ is the unique core stable partition for game $(G,\mathcal{F})$. As $soc(\pi )=\ell +2$, we get that the strong price of stability is lower bounded by $\frac{n}{\ell +2}$. By using $n=\ell ^2+2$, it follows that $\frac{n}{\ell +2}=\frac{n}{2+\sqrt{n-2}}$ and this provides the desired lower bound.   $\square$

Theorem 5

For any instance $(G,\mathcal{F})$ of the game with n players and the fragmentation function, it holds that $\lceil n/2 \rceil /2 \le PoS(G,\mathcal{F}) \le SPoA(G,\mathcal{F}) \le n/4+11/20$.

Proof

Let $\pi$ be a core stable partition and set $k=\Delta (G)+1$, where $\Delta (G)$ is the maximum degree of G. It follows that the fragmentation of the social optimum is at least $\lceil n/k\rceil$. From Theorem 1, we know that there is a coalition of size k in $\pi$. Thus $frag (\pi ) \le 1+n-k$, and $SPoA(G,\mathcal {F}) \le \frac{k(1+n-k)}{n}$. If n is even then $\frac{k(1+n-k)}{n} \le n/4+1/2$, otherwise $\frac{k(1+n-k)}{n} \le \frac{(n+1)^2}{4n}=\frac{n}{4}+\frac{1}{2}+\frac{1}{4n} \le \frac{n}{4}+\frac{11}{20}$, where the last inequality is due to the hypothesis $n \ge 4$ (the smallest odd n is 5).

To show the lower bound when n is even, consider the game induced by the graph depicted in Fig. 3. We have a social optimum $\pi ^*$ such that $\pi ^*(x_1)=\{x_1,\ldots ,x_{\lfloor n/2 \rfloor }\}$ and $\pi ^*(y_1)=V\setminus \pi ^*(x_1)$ and yielding $frag(\pi ^*)=2$. There are only two Nash stable partitions, namely $\pi _1$ and $\pi _2$, both having fragmentation equal to $\lceil n/2 \rceil$. In particular, $\pi _1$ is such that $\pi _1(x_1)=\{x_1,\ldots ,x_{\lfloor n/2 \rfloor },y_1\}$ and $\pi _1(y_i)=\{y_i\}$ for $i>1$, while $\pi _2$ flips the roles of x and y. When n is odd, take the same instance and add a new vertex solely connected to $x_1$ to get the lower bound of $\lceil n/2 \rceil /2$.    $\square$

Fig. 3.

A graph yielding a game with worst-case price of stability with respect to fragmentation.

We conclude the section with a lower bound on the price of stability for the sociality social function showing that the quality of the best Nash stable partition cannot be better than twice that of the worst core stable one.

Theorem 6

For any game with n players, the price of stability with respect to sociality is at least $\frac{n}{2\sqrt{n}-1}$.

Proof

Consider the game yielded by the graph $G=(V,E)$ such that $V=X \cup Y_1 \cup \ldots \cup Y_\ell$, with $X=\{x_1,\ldots ,x_\ell \}$ and, for each $i\in [\ell ]$, $Y_i=\{y_{i,1},\ldots ,y_{i,\ell -1}\}$. The set of edges E is such that $G[X]=K_\ell$ (i.e. complete graph on $\ell$ vertices) and, for each $i\in [\ell ]$ each vertex in $Y_i$ is connected to $x_i$ only. Note that, by setting $\ell =\sqrt{n}$, we obtain $|V|=n$. We shall prove that, in any Nash stable partition, the sociality is at most $2\sqrt{n}-1$. Given that there is a partition of sociality n, this will yield the corresponding lower bound. Fix a Nash stable partition $\pi$. We claim that $\pi$ contains a unique non-singleton coalition containing X. This easily follows from the fact that X defines a clique and that, by the topology of G, in any feasible coalition C containing a vertex of $x\in X$, C induces a subgraph of G admitting a spanning star centred at x. Moreover, as $\pi$ is Nash stable, we shall have that the unique non-singleton coalition in $\pi$ will also contain all vertices in $Y_i$ for a certain $i\in [\ell ]$. No other vertices of G can be added to the coalition without violating the feasibility constraint and no other non-singleton coalition can be constructed as the remaining vertices yield an independent set of G. Hence, the sociality of $\pi$ is $2\sqrt{n}-1$.   $\square$

3.1 Claw-Free Graphs

In this subsection, we consider the case in which the graph G is claw-free, i.e., it does not contain an induced $K_{1,3}$ (i.e. complete bipartite graph with 1 and 3 vertices on the respective sides). It will turn out that the presence of claws in graph G is a provable source of inefficiency as the price of anarchy with respect to both social functions (and so also all the other metrics) for games played on claw-free graphs drops to a value which never exceeds 2. Claws (and more generally induced stars with a large number of leaves) are problematic for our social functions when the center c of a claw belongs to a partition $\pi (c)$ which does not admit a spanning star of center c. In this case some leaves of the claw are isolated: they cannot join $\pi (c)$ or group themselves because they are disconnected. For the social function sociality, the following two theorems provide an asymptotically tight characterization.

Theorem 7

For any game with n players, the price of anarchy with respect to sociality is at most $\frac{n}{n-\lfloor \frac{n-1}{2} \rfloor }$, that is $\frac{2n}{n+2}$ and $\frac{2n}{n+1}$ when n is even and odd, respectively.

Proof

Fix a Nash stable partition $\pi$ and let i be a vertex belonging to a singleton coalition in $\pi$. Clearly, i cannot be adjacent to a vertex being a center of a spanning star of any subgraph induced by a coalition in $\pi$. So, i can only be adjacent to leaves of spanning stars of any subgraph induced by coalitions in $\pi$. Assume that there exists a vertex j also belonging to a singleton coalition in $\pi$ and sharing a neighbour k with i. Let c be the center of a star spanning $G[\pi (k)]$. As $\{i,j,c\}$ is independent, we find that the set of vertices $\{i,j,k,c\}$ induces a claw in G: a contradiction. Two vertices forming a singleton coalition cannot share the same leaf of a star spanning a non-singleton coalition. Thus, denote by $\alpha$ the number of vertices that are centres of a star spanning the subgraph induced by a non-singleton coalition in $\pi$, we get that the number of vertices forming singleton coalitions in $\pi$, which is integral, is upper bounded by $\lfloor \frac{n-\alpha }{2} \rfloor \le \lfloor \frac{n-1}{2} \rfloor$. This implies that $soc(\pi )\ge n-\lfloor \frac{n-1}{2} \rfloor$, which yields the desired upper bound because the optimal sociality $soc(\pi ^*)$ is n.   $\square$

Theorem 8

For any game with n players, the price of stability with respect to sociality is at least $\frac{n}{n-\lfloor \frac{n-1}{2} \rfloor }$.

Proof

Suppose $n=2p$ and consider the graph $G_{2p}=(V_{2p},E_{2p})$ such that $V_{2p}=X_p\cup Y_p$, where $X_p=\{x_1,\ldots ,x_{p}\}$, $Y_p=\{y_1,\ldots ,y_{p}\}$, $X_p$ forms a clique, and each vertex $y_i$ is adjacent to vertex $x_i$. One can see that $G_{2p}$ is claw-free, and $X_p\subseteq \pi (x_i)$ for any Nash stable partition $\pi$. Moreover, to have feasibility, a coalition C can contain at most one vertex from $Y_p$. It follows that the sociality of any Nash stable partition is at most $p+1$. As there exists a partition with sociality 2p, the claimed lower bound follows. For $n=2p+1$, use the same construction with $Y_p=\{y_1,\ldots ,y_{p-1}\}$.    $\square$

For the fragmentation social function, a slightly different situation occurs.

Theorem 9

For any game with n players, the price of anarchy with respect to fragmentation is at most 2.

Proof

Fix a Nash stable partition $\pi$. If $frag(\pi )\le 2$, we are done. If $frag(\pi )\ge 3$, consider three distinct coalitions $C_1,C_2,C_3\in \pi$ and let $c_1$, $c_2$ and $c_3$ be the centres of the spanning stars of $G[C_1]$, $G[C_2]$ and $G[C_3]$, respectively. As $\pi$ is Nash stable, the set of vertices $U=\{c_1,c_2,c_3\}$ induces an independent set of G. We claim that these vertices cannot belong to a same cluster in some social optimum $\pi ^*$. Assume, by way of contradiction, that there exists a cluster $C^*\in \pi ^*$ containing U. As U induces an independent set of G no vertex in U can be the center of the star spanning $G[C^*]$. So, there exists $c^*\in C^*$ which is adjacent to all vertices in U. But $U\cup \{c^*\}$ induces a claw: a contradiction. Hence, for every two coalitions in $\pi$, there must exist a distinct coalition in $\pi ^*$ which yields the desired upper bound.   $\square$

Theorem 10

For any positive integer k, there exists a game whose strong price of stability with respect to fragmentation is at least $\frac{2k}{k+1}$.

Proof

For an integer $k\ge 1$, define the following graph $G_k$. The set of vertices is $V=X_1\cup \ldots \cup X_k\cup Y\cup Z$, with $Y=\{y_1,\ldots ,y_k\}$ and $Z=\{z^a_1,z^b_1,\ldots ,z^a_k,z^b_k\}$ so that $|Z|=2k$. As to sets $X_i$ for $i\in [k]$, we have that $|X_i|=2i$, $G_k(X_i)$ induces a clique and $X_i$ contains two special vertices, namely $\overline{x}_i$ and $\underline{x}_i$, which are the only vertices adjacent to vertices in $V\setminus X_i$. In particular, $\overline{x}_i$ is adjacent to both $z^a_i$ and $z^b_i$, while $\underline{x}_i$ is adjacent to $y_i$ and, for $i<k$, to both $z^a_{i+1}$ and $z^b_{i+1}$. Finally, for each $i\in [k]$, $z^a_i$ and $z^b_i$ are adjacent and, for $i>1$, they are both adjacent to $y_{i-1}$. Again, we show two fundamental properties:

Property 1

(i) $G_k$ is claw-free, (ii) $(X_i\cup \{z^a_i,z^b_i\},\{y_i\}\mid i\in [k])$ is a core stable partition.

Consider the feasible partition $\pi ^*$ containing the following coalitions: $X_k\cup \{y_k\}$, $X_i\cup \{y_i\}\cup \{z^a_{i+1},z^b_{i+1}\}$ for each $i\in [k-1]$ and $\{z^a_1,z^b_1\}$. As $frag(\pi )=k+1$, the claimed lower bound follows.   $\square$

Theorem 11

For any game with n players, the price of stability with respect to fragmentation is 1.

Proof

Our aim is to show that, given a partition $\pi$, it is possible to schedule profitable deviations so as to obtain a Nash dynamics starting from $\pi$ and ending up to a Nash stable partition $\pi _\ell$ such that $frag(\pi _\ell )\le frag(\pi )$. Choosing a social optimum as starting partition will yield the claim. Our scheduling algorithm is defined as follows: given a partition $\pi$, if more than one player have a profitable deviation in $\pi$, break ties in favour of a player who does not constitute a center for any spanning star of the subgraph induced by the coalition she belongs to. By the LIP property, we are guaranteed that the Nash dynamics defined by this scheduling algorithm always ends to a Nash stable partition $\pi _\ell$ for any starting partition $\pi$.

Assume, by way of contradiction, that $frag(\pi _\ell )>frag(\pi )$. This implies that there are two partitions $\pi ,\pi '\in \varPi$ and a player i such that $\pi '$ is obtained as a result of a profitable deviation of i in $\pi$ and $frag(\pi )<frag(\pi ')$. The latter condition can happen only if $G[\pi (i)\setminus \{i\}]$ does not admit a spanning star, which implies that $G[\pi (i)]$ admits only one spanning star centred at i. So, there are at least two distinct vertices u and v other than i belonging to $\pi (i)$. Let $C\in \pi$ be the coalition joined by i and let $j\ne i$ be the center of a spanning star for $G[C\cup \{i\}]$. Clearly it must be $\{i,j\}\in E$. If $\{u,j\}\in E$, then $C\cup \{u\}\in \mathcal{F}$. But as $u_u(\pi )=u_i(\pi )=|\pi (i)|<u_i(\pi ')=|C\cup \{i\}|=|C\cup \{u\}|,$ it follows that u has a profitable deviation in $\pi$ and, by the definition of the scheduling algorithm, i should have not been chosen. The same argument holds for v. Thus, we have detected a set of vertices $\{i,j,u,v\}$ inducing a claw in G: a contradiction.   $\square$

4 Computing Partitions with Prescribed Properties

In this section, we address the complexity of computing partitions with some prescribed properties, such as, for example, being a social optimum or being a Nash stable partition either maximizing or minimizing a given social function.

4.1 Computing a Social Optimum

Proposition 1

Computing a social optimum with respect to fragmentation is NP-hard, even for claw-free graphs.

The following result relies on the efficient computation of a minimum edge-cover.

Proposition 2

For connected graphs on n vertices, computing a social optimum $\pi ^*$ with respect to sociality is polynomial and $soc(\pi ^*)=n$.

4.2 Computing an Extreme Stable Partition

Using Theorem 11 and Proposition 1, we deduce that computing a best Nash stable partition with respect to fragmentation is NP-hard, even for claw-free graphs. We now show that hardness holds also for the sociality social function.

Theorem 12

Computing the best Nash stable partition with respect to sociality is NP-hard when the input graph G has maximum degree equal to 5.

Proof

We propose a reduction from 3-dimensional matching (3-DM in short). An instance of 3-DM consists of a collection $\mathcal {C}=\{s_1,\dots ,s_m\}\subseteq X\times Y\times Z$ of m triples, where $X=\{x_1,\dots ,x_n\}$, $Y=\{y_1,\dots ,y_n\}$ and $Z=\{z_1,\dots ,z_n\}$ are 3 pairwise disjoint sets of size n. A matching is a subset $M\subseteq \mathcal {C}$ such that no two elements in M agree in any coordinate, and the purpose of 3-DM is to answer the question: does there exist a perfect matching M on $\mathcal {C}$, that is, a matching of size n? This problem is known to be NP-complete (problem [SP1] p. 221 in [17]), even if each element $t\in X\cup Y \cup Z$ appears in at most 3 triples. We start from such an instance $I=(\mathcal {C},X\cup Y \cup Z)$ of 3-DM and we build a game $(G,\mathcal {F})$, where $G=(V,E)$ is as follows. Vertex set contains $L\cup R$ where $L=\{l_1,\dots ,l_{m}\}$ corresponds to the different triples of $\mathcal {C}$ and $R=R^x\cup R^y\cup R^z$ where $R^t=\{r^t_1,\dots ,r^t_{n}\}$ for $t=x,y,z$, corresponds to elements of $X\cup Y \cup Z$. Moreover for $t=x,y,z$, $l_ir^t_j\in E$ if and only if $t_j$ is an element of triplet $s_i$. This particular bipartite graph is usually called representative bipartite graph. We use gadget $H(l_i)$ for each $l_i\in L$ to characterize triplets of $\mathcal {C}$. This gadget is illustrated in Fig. 4 (on the left of the drawing).

The construction of G is complete and its maximum degree is 5. We claim that I admits a perfect matching if and only if there exists a Nash stable partition $\pi$ of $(G,\mathcal {F})$ with $soc(\pi )\ge 5m+n$. Actually, we will prove that $5m+n$ is the best value reachable by any Nash stable partition $\pi$.

Clearly, if $\mathcal {C}'\subseteq \mathcal {C}$ is a set of n triples forming a perfect matching, then consider the following partition $\pi$. For $s_i=(x_{i_1},y_{i_2},z_{i_3})\in \mathcal {C}'$, set $\pi (d_i)=\{d_i\}$, $\pi (e_i)=\{e_i\}$ and $\pi (l_i)=\{b_i,c_i,l_i,r^x_{i_1},r^y_{i_2},r^z_{i_3}\}$; an illustration of these 3 coalitions is proposed in Fig. 4 (on the right of the drawing). Otherwise, for $s_i\notin \mathcal {C}'$, set $\pi (l_i)=\{l_i,b_i,c_i,d_i,e_i\}$. It is easy to see that $\pi$ is a Nash stable partition with $soc(\pi ) = 6n+5(m-n) = 5m+n$.

Fig. 4.

On the left: Gadget $H(l_i)$. On the right: a possible Nash stable partition for agents in $H(l_i)$.

Conversely, let $\pi$ be a Nash stable partition. If $\{l_i,r^t_j\}\subseteq \pi (r^t_j)$ for some $j\in [n]$ and $t=x,y,z$, then:

Property 2

(i) $\forall i'\ne i$, $l_{i'}\notin \pi (r^t_j)$, (ii) $\{b_i,c_i\}\subseteq \pi (r^t_j)$ and $\{d_i,e_i\}\cap \pi (r^t_j)=\emptyset$.

Let $Cov=\{l_i\in L : |\pi (l_i)|=6\}$ and $p=|Cov|$. By Property 2, for every $l_i\in Cov$, it must be $\pi (e_i)=\{e_i\}$ and $\pi (d_i)=\{d_i\}$ (see right picture of Fig. 4 for an illustration); actually, these collations correspond to a (3-dimensional) matching of size p. Using Property 2, we know that we also loose in the sociality function, as many trivial stars as the number of vertices of $R\setminus \left( \cup _{l_i\in Cov}\pi (l_i)\right)$. Hence, $soc(\pi )\le 5m+3n-(2p+3n-3p)=5m+p\le 5m+n$ and the last inequality is tight only when $|Cov|=n$ or equivalently when $\mathcal {C}'=\{s_i|l_i\in Cov\}$ is a perfect matching.   $\square$

Corollary 1

Computing the best Nash stable partition with respect to either sociality or fragmentation is NP-hard even for planar graphs.

As to the problem of computing a worst Nash stable partition, we give a hardness result with respect to sociality, while the case of the fragmentation social function remains open.

Theorem 13

Computing the worst Nash stable partition with respect to sociality is NP-hard when the input graph G has maximum degree equal to 11.

5 Conclusion

Two problems are left open: closing the gap between upper and lower bounds on the PoS with respect to sociality for games played on general graphs, and determining the complexity of computing a worst Nash stable partition with respect to fragmentation. Addressing the problem of computing extreme core stable partition is also worth to be investigated.

Applying our feasibility constraint (i.e. imposing a spanning star) to hedonic games having agents’ preferences other than the ones considered in this paper is clearly an interesting research direction. Other graph patterns are appealing in our opinion: the largest distance between any pair of agents, or the distance to some agent of the coalition can be upper bounded by a given number (for the latter the distance to some agent is 1 in this paper).