Abstract
This paper explores a particular type of model, a cyclic model, in which there are sequences of observable actions separated by discrete time intervals, introduces a novel implementation relation and studies some properties of this relation. Implementation relations formalise what it means for an unknown model of the system under test (SUT) to be a correct implementation of a specification. Many implementation relations are variants of the well known ioco implementation relation, and this includes several timed versions of ioco. It transpires that the timed variants of ioco are not suitable for cyclic models. Our implementation relation encapsulates the discrete nature of time in cyclic models and takes into account not only the actions that models can perform but also the ones that they can refuse at each point of time. We prove that our implementation relation is a conservative extension of trace containment and present two alternative characterisations.
This work has been supported by EPSRC grant EP/R025134/2 RoboTest: Systematic Model-Based Testing and Simulation of Mobile Autonomous Robots, the Spanish MINECO-FEDER (grant numbers DArDOS, TIN2015-65845-C3-1-R and FAME, RTI2018-093608-B-C31) and the Region of Madrid (grant number FORTE-CM, S2018/TCS-4314).
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
1 Introduction
Robotic systems form the basis for advances in a number of areas such as manufacturing, healthcare, and transport but also in home assistance. In fact, their use is steadily increasing in all sectors: sales increased by 30% in 2017, a new peak for the fifth year in a row [12], and according to a UK government reportFootnote 1 it is expected that the value of the global market for robotics and autonomous systems will be £13 billion by 2025. A number of the areas where robotic systems are becoming ubiquitous are safety-critical and so there is a need for robotic systems that are safe, reliable and trusted.
In practice, developers of robotic systems produce a state-based model and then separately develop a simulation model, which is used to validate the original model and potentially also to test the system developed. Concerning time, these simulations have discrete time and are cyclic in nature, with each time slot containing a sequence of actions (see, for example, [19]). Unfortunately, there is no guarantee that the simulation model is consistent with the original model. In addition, the actual choice of simulations (test cases) to run is typically ad hoc.
This paper relates to a line of research regarding the development process for robotic systems. As usual, a state-based model (in a language, RoboChart [16], similar to those used by roboticists) is produced but the model is given a formal semantics. The model is also automatically mapped to a simulation model, in a language called RoboSim [4], that is consistent with the original model. The simulation models are also given a formal semantics, making it possible to automatically analyse or reason about them. A formal semantics for RoboSim [5] is given by mapping a RoboSim model to a variant of CSP, called tock-CSP [20, Chapter 14]. One of the benefits of this approach is that we can analyse the semantics of a RoboSim model using formal tools and methodologies available for CSP. In particular, and this is the main goal of this paper, we can formally define when an SUT conforms to a specification of the system, in this case the robot, that we would like to build. It will then be possible to systematically and automatically derive test cases from a tock-CSP model, which provides the semantics of a RoboSim model, and map it back to define simulation runs (test cases) for the simulation. As a result, we would obtain systematic test generation algorithms for automating the validation of specifications of robotic systems through simulation. This should make the development of robotic systems more efficient and effective, through removing the need for several manual, error prone activities.
The above is motivated by the observation that software testing [1, 17] is the main validation technique to increase the reliability of software governing the behaviour of systems. Initially, testing was considered to be an informal activity but it is currently well-known that formal methods and testing can be successfully combined. There are many complementary approaches to testing, supported by tools [15, 22], with a formal basis [2, 6, 10, 11]. Formal approaches to testing usually rely on state-based models, that is, models that are in the form of labelled transition systems (LTSs); these models have states and labelled transitions between the states. LTSs have typically been used to define the operational semantics of a number of specification languages including different variants of CSP [20]. In testing from an LTS, it is normal to assume that the SUT behaves like an unknown LTS (this is called the test hypothesis [13]) and so testing involves comparing two LTSs. More generally, if we want to reason about the correctness of one model (a design) with respect to another model (specification) then we need to define what we mean by correctness and such notions are described as implementation relations. There are many implementation relations for LTSs, with different implementation relations typically differing in the observational power of the observer [7]. An observer might only be allowed to observe the actions in which the system participates. However, we can increase the capabilities of the observers. For example, we might consider situations in which they are also able to observe the refusal of a set of actions; it is possible that the system cannot participate in some set X of actions. In the scope of testing, this is a well-known and classical approach [18] and typically a refusal of a set X is observed through the tester only offering the actions in X and a deadlock occurring.
In this paper we present an implementation relation for timed systems where time is discrete, we are interested in using refusals while testing and do not assume that SUTs are input-enabled. Essentially, this is the framework underlying the LTSs generated by the operational semantics of tock-CSP [20] which, in turn, is the formal language to which RoboSim descriptions are translated [5]. We consider an LTS corresponding to tock-CSP rather than just RoboSim in order to aid generality. For example, there is potential to adapt the research reported in this paper for use with other simulation languages and also languages, such as Statecharts [8], that have a cyclic nature and a step semantics. The work should thus be relevant to the testing of many classes of control systems.
The rest of the paper is organised as follows. In Sect. 2 we explain the testing context and discuss related work. In Sect. 3 we introduce the main definitions and give a preliminary implementation relation: trace inclusion. In Sect. 4 we introduce our implementation relation and show that it is strictly stronger than trace inclusion. In Sect. 5 we present two alternative characterisations of our implementation relation. Finally, in Sect. 6 we give our conclusions and describe some lines for future work.
2 Testing Context and Related Work
In testing we distinguish between inputs and outputs since these play different roles and this has led to additional implementation relations. The best known implementation relation is ioco [23]. In classical ioco, there is only one type of refusal, called quiescence, that can be observed if the system is in a state where it cannot evolve via an internal action and, in addition, the system cannot produce an output without first receiving an input. If we are testing an SUT, then quiescence is typically observed through a timeout. Note that there is an extension of ioco to include refusals [9] that we will discuss later on.
While implementation relations such as ioco are widely used, they usually do not take into account time. Time is not a normal action: it is not like an input, since the tester does not control it, and it is not like an output since the SUT does not control it (the SUT cannot, for example, stop time). As a result, there are now several timed variants of ioco (all are typically called tioco) [3, 14, 21]. The versions of tioco differ in a number of ways, including whether quiescence is a possible observation. However, time is typically continuous and these implementation relations either do not consider refusals or they only consider one simple type of refusal (quiescence).
As previously mentioned, we were motivated by an interest in certain types of simulations (in the context of robotics). These simulations are cyclic, where each cycle is of the form of a finite sequence of observations followed by the passing of a unit of time. In addition, outputs are urgent: time cannot pass if an output is possible. An agent (robot) might potentially be in a situation in which it cannot engage in certain actions and it is desirable to model this, which can be achieved through using refusals. As a result of the above factors, we require that time is discrete and refusals can be observed. The observation of the refusal of a set A is typically represented by the situation in which the environment chooses to only engage in the actions in A and the composition of the environment and SUT deadlocks. The observation of a deadlock takes time and is usually observed through a timeout, similar to what is usually done to observe quiescence. As a result, the observation of a deadlock (and so also a refusal) should precede a duration (an action representing a unit of time passing). In this paper we develop implementation relations for timed LTSs that capture the scenario described above.
A last point of divergence with respect to ioco and its variants is that they usually assume that the SUT is input-enabled. Essentially, this means that the SUT should be able to react to any input provided by the tester. This assumption makes sense for a range of systems and is based on the observation that the SUT will not block input. However, there are also systems that are not input-enabled and where this is deliberate. For example, certain options/fields might be greyed-out on a webpage or simply not available; consider, for instance, the options available to an editor and to an author in a journal’s manuscript system. In the context of autonomous systems, and more related to the topic of this paper, a system might switch off sensors and, in addition, sensors might fail. It is well-known that one might convert a model that is not input-enabled into one that is. However, in the type of systems that we are considering in this paper, such a completed model would less appropriately model an SUT in which certain inputs are disabled and could lead to the generation of test cases that either do not make sense from a testing perspective or contain redundancy.
Concerning related work, it might be possible to use some versions of tioco with discrete time and in some situations this will be sufficient but we prefer a native discrete time tioco (in addition, previous work does not consider refusals). There is a variant of ioco that we initially considered because it includes refusals and systems need not be input-enabled [9]. We depart from this work in several lines (in addition to including time). First, our refusals are observed only in stable statesFootnote 2 and this has some implications. Specifically, an internal choice between outputs is equivalent to the same external choice while if we consider inputs then we obtain semantically different processes. Using a process algebraic notation, we have \((\tau ; !o_1;stop) + (\tau ; !o_2;stop) \sim (!o_1;stop) + (!o_2;stop)\) while \((\tau ; ?i_1;stop) + (\tau ; ?i_2;stop) \not \sim (?i_1;stop) + (?i_2;stop)\), where actions preceded by ? and ! denote, respectively, an input and an output, and \(\tau \) denotes an internal action. Second, their notion of input-enabledness is more restrictive than ours: at a certain port, either all the inputs are enabled or none of them is. In their notation, we have only one port and we allow several inputs to be enabled and several to not be.
3 Background and Models
In this section we define the models and notation used in this paper.
3.1 Traces and Automata
Observations made in testing will be in the form of sequences and we use \(\epsilon \) for the empty sequence. Given a set A, \(A^*\) denotes the set of finite sequences of elements from A and \(A^{\omega }\) denotes the set of infinite sequences of elements from A.
A system will interact with its environment through inputs and outputs. Throughout the paper, I and O will represent the (disjoint) input and output alphabets and we let \(L = I \cup O\) denote the set of actions.
The basic, untimed, type of model we consider is an automaton in which, as usual in Automata Theory and in contrast to the standard notion of LTS, we have the concept of a final state.
Definition 1
(Automaton). We say that \(p = (Q, q_0, L, T, F)\) is an automaton where
-
Q is a countable, non-empty set of states;
-
\(q_0 \in Q\) is the initial state;
-
L is a countable set of actions;
-
\(T \subseteq Q \times (L \cup \{\tau \}) \times Q\) is the transition relation, where \( \tau \notin L\) represents an internal action;
-
\(F \subseteq Q\) is the set of final states.
At any time, an automaton p is in a particular state \(q \in Q\). If \((q,a,q') \in T\) for action \(a \in L \cup \{\tau \}\) then p can move to state \(q'\) through action a. We will sometimes use an alternative notation: a transition \((q,a,q') \in T\) can be expressed as  . We will also write
. We will also write  if there does not exist \(q'\) such that \((q,a,q') \in T\). The transition relation can be extended as follows.
if there does not exist \(q'\) such that \((q,a,q') \in T\). The transition relation can be extended as follows.
Definition 2
Let \(p = (Q, q_0, L, T, F)\) be an automaton with states \(q, q' \in Q\), visible actions \(a, a_1,\ldots ,a_n \in L\), with \(n > 1\), and sequence of visible actions \( \sigma \in L^*\).

As usual, we will not always distinguish between a model and its initial state. If \(p = (Q, q_0, L, T, F)\), then we will identify p with its initial state \(q_0\), and, for example, we will usually write  instead of
instead of  . The automaton \(p = (Q, q_0, L, T, F)\) defines the language L(p) of finite sequences that take p to a final state.
. The automaton \(p = (Q, q_0, L, T, F)\) defines the language L(p) of finite sequences that take p to a final state.
Definition 3
Given automaton \(p = (Q, q_0, L, T, F)\), the language \(L(p) \subseteq L^*\) is defined as  .
.
3.2 Timed Models
We now describe our timed model, which is an LTS in which there is a special action, \(\circleddash \), that denotes the passing of a unit of time. We call this action ‘tock’ in order to be consistent with tock-CSP [20, Chapter 14].
Definition 4
(tockLTS, timed traces). A labelled transition system with tock (or tockLTS) is a tuple \(p= (Q, q_0, I, O, T)\) where
-
Q is a countable, non-empty set of states;
-
\(q_0 \in Q\) is the initial state;
-
I and O are countable disjoint sets of inputs and outputs respectively, with \(L=I\cup O\) being the set of visible actions;
-
\(T \subseteq Q \times (L \cup \{ \tau , \circleddash \} ) \times Q\) is the transition relation, where \( \tau \notin L\) represents the internal action, and \(\circleddash \) represents a tock action denoting the passage of a unit of time.
We use \( TockLTS (I,O)\) to denote the set of tockLTS with input set I and output set O.
The definition of the  relation is similar to the one given in Definition 2, with the only difference that \(\sigma \in (L \cup \{ \circleddash \})^* \) and, therefore, we omit it. The set of timed traces of p is defined as
relation is similar to the one given in Definition 2, with the only difference that \(\sigma \in (L \cup \{ \circleddash \})^* \) and, therefore, we omit it. The set of timed traces of p is defined as

As usual, we expect processes to have certain properties. First, processes should not have forced inputs, that is, for each state of a process there exists at least an outgoing transition that is not an input. Second, we should have the urgency of internal actions and outputs (to be consistent with how simulations operate). Third, processes should not show Zeno behaviour, that is, processes in which an infinite sequence of actions can occur in finite time should not be allowed. Finally, processes should have time determinism: processes do not branch as a result of time passing (a \(\circleddash \)), though a process can branch through internal actions that occur after a \(\circleddash \).
Definition 5
(No forced inputs, urgency, Zeno behaviour, time determinism). Let \(p = (Q, q_0, I, O, T) \) be a tockLTS. Then
-
p has no forced inputs if for all \(q \in Q\) there exists \(a\in O\cup \{\tau ,\circleddash \}\) such that
 .
. -
p has urgent internal actions and output if for all \(q \in Q\) and \(a \in O \cup \{\tau \}\), if
 then
then  .
. -
p has Zeno behaviour if there exists a state \(q \in Q\) and an infinite path from q with finitely many tock actions.
-
p has time determinism if for all states \(q_1, q_2, q_3 \in Q\) we have that
 implies \(q_2 = q_3 \).
implies \(q_2 = q_3 \).
If a tockLTS fulfills the previous properties then it also has a very interesting property: processes cannot stop time. In other words, it is always possible for time to progress (though certain actions might first happen). The proof of the following is a straightforward consequence of the absence of Zeno behaviour and the assumption of no forced inputs.
Proposition 1
Let \(p = (Q, q_0, I, O, T) \) be a tockLTS. We have that for all \(q \in Q\) there exists an infinite path \(\sigma =\mu _1 \circleddash \mu _2 \circleddash \mu _3 \ldots \in ((I\cup O)^*\{\circleddash \})^{\omega }\) such that  and \(\forall i, \mu _i \in (I \cup O)^*\).
and \(\forall i, \mu _i \in (I \cup O)^*\).
3.3 A First Implementation Relation
If the environment can only observe traces of visible actions and time (i.e. it cannot observe refusals) then we have one natural implementation relation: the requirement that all observations (traces) that can be made when interacting with the SUT are also observations that can be made when interacting with the specification.
Definition 6
Let p and q be two tockLTSs. We say that p conforms to q under timed trace inclusion if and only if \(\mathtt {{\mathcal T}\! traces}(p) \subseteq \mathtt {{\mathcal T}\! traces}(q)\).
The following property is immediate from the definition.
Proposition 2
The timed trace inclusion relation is reflexive and transitive but need not be symmetric.
Although this initial implementation relation has some nice properties, in addition to its simplicity, it also has some drawbacks. First, it does not consider refusals, so that its discriminatory power can be enhanced. Second, there are some systems that are related but that, intuitively, should not be.
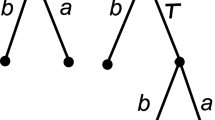
Example 1
Let us consider the fragments of models given in Fig. 1(top and bottom). These two pairs of models conform to each other under timed trace inclusion because we have \(\mathtt {{\mathcal T}\! traces}(p) \subseteq \mathtt {{\mathcal T}\! traces}(q)\) and \(\mathtt {{\mathcal T}\! traces}(q) \subseteq \mathtt {{\mathcal T}\! traces}(p)\), \(\mathtt {{\mathcal T}\! traces}(r) \subseteq \mathtt {{\mathcal T}\! traces}(s)\) and \(\mathtt {{\mathcal T}\! traces}(s) \subseteq \mathtt {{\mathcal T}\! traces}(r)\). However, often we will want to be able to distinguish between such processes. On the one hand, we expect both conformances between p and q because outputs cannot be controlled by the environment. In other words, a choice between outputs should work exactly as the corresponding internal choice. For example, even though \(?o_1\) and \(?o_2\) are available at \(p_0\), a user/tester cannot choose which of them will be performed (testers cannot block output). On the other hand, r and s should not be equivalent. The issue is that the tester or user can choose between two inputs in the same way that one can choose among the available options in a vending machine. If we have the corresponding internal choice and we reach, for example, state \(s_1\) then input \(?i_2\) is not available. The implementation relation that we present in the next section satisfies all of these properties.
4 An Implementation Relation Including Refusals
So far, the discussion has only allowed inputs, outputs, and the passing of time to be observed. In this section we explore the notion of refusals in our setting and how they can be added as observations, with this leading to a stronger implementation relation.
Recall that we are interested in models that are cyclic/have a step semantics: a sequence of actions occurs without time (in the model) passing and then there is a tock action. A refusal of a set \(X \subseteq L\) is typically observed through the tester only being willing to engage in the actions in X and the composition of the tester and the SUT deadlocking. Since deadlocks are observed (in testing) through timeouts, the observation of a refusal takes time and so we only allow a refusal to be observed immediately before a tock action. Since outputs and internal actions are urgent, this means that a refusal can only be observed in a stable state. Note that we might have combined a refusal with the \(\circleddash \) that follows this; we chose not to because this is not the usual use of refusals and also because we would like to have the potential to extend the work to allow an observation to end with a refusal.
Definition 7
(Stable state). Let \(p = (Q, q_0, I, O, T)\) be a tockLTS, with \(L=I\cup O\). We say that the state \(q\in Q\) is stable if for all \(a \in O \cup \{\tau \}\) we have that  .
.
Given a set \(X \subseteq L\) of actions, we use R(X) to denote the refusal of set X. Further, we let \({\mathcal R}(L) = \{R(X) | X \subseteq L\} \) denote the set of all possible refusals.
We can extend the transition relation of a tockLTS with refusals as follows.
Definition 8
(Refusal). Let \(p = (Q, q_0, I, O, T)\) be a tockLTS and \(X \subseteq I\cup O\). For all \(q\in Q\) we write  if the following hold:
if the following hold:
-
1.
q is stable and
-
2.
for all \(x\in X\) we have that
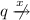 .
.
This constitutes the observation of the refusal R(X), that is, at a given stable state the model cannot perform the actions belonging to X.
It follows that the observation of a refusal R(X) implies that no element \(a \in X \cup O \cup \{ \tau \}\) can be accepted in state q:  .
.
Note also that the second condition from the definition implies that we include R(X) as a refusal if all the actions in X can be refused, even if there are other actions from \(L \setminus X\) that can be refused. Therefore, we do not only include maximal refusals. In fact, doing this would lead to some undesirable effects (this will be clearer after we give our implementation relation using refusals).
We can then give the set of refusal traces of a tockLTS in which, as we already said,  is defined in terms of
is defined in terms of  , in the usual way. Recall, however, that a refusal can only be observed immediately before a tock action. We therefore obtain a set of potential refusal traces (those that satisfy this condition) and we call these timed refusal traces. Also note that a timed refusal trace cannot end in a refusal since the observation of a refusal takes time (and so must be followed by a \(\circleddash \)). As a result, this set is not prefix closed.
, in the usual way. Recall, however, that a refusal can only be observed immediately before a tock action. We therefore obtain a set of potential refusal traces (those that satisfy this condition) and we call these timed refusal traces. Also note that a timed refusal trace cannot end in a refusal since the observation of a refusal takes time (and so must be followed by a \(\circleddash \)). As a result, this set is not prefix closed.
Definition 9
(Timed refusal traces). Let L be a set of actions. We define the set of timed refusal traces over L as \(RT(L) = (L^* \cup ({\mathcal R}(L)\{ \circleddash \}))^*\).
Let \(p = (Q, q_0, I, O, T)\) be a tockLTS, with \(L=I\cup O\). The set of timed refusal traces of p is defined as

We then obtain a second implementation relation in the natural way: we do not require the inclusion of (timed) traces but the inclusion of timed refusal traces.
Definition 10
Let I and O be countable disjoint sets of inputs and outputs, respectively. Let p and q be two elements of \( TockLTS (I,O)\). We say that p conforms to q under timed refusal trace inclusion if and only if \(\mathtt {{\mathcal T}\!{\mathcal R}traces}(p) \subseteq \mathtt {{\mathcal T}\!{\mathcal R}traces}(q)\).
First, we present an example showing some relations between models and why maximal refusals do not provide the expected implementation relation.
Example 2
Consider again the fragments of models p and q given in Fig. 1(top). We have that we cannot add refusals to traces in states \(p_0\), \(q_0\), \(q_1\) and \(q_3\) because they are not stable. Therefore, we have \(\mathtt {{\mathcal T}\!{\mathcal R}traces}(p) \subseteq \mathtt {{\mathcal T}\!{\mathcal R}traces}(q)\) and \(\mathtt {{\mathcal T}\!{\mathcal R}traces}(q) \subseteq \mathtt {{\mathcal T}\!{\mathcal R}traces}(p)\).
Consider now r and s given in Fig. 1(bottom). Assuming that \(I=\{?i_1,?i_2\}\) and \(O=\emptyset \), we have that s has the timed refusal traces \(R(\{?i_1\})\circleddash \) and \(R(\{?i_2\})\circleddash \) and these are not timed refusal traces of r. Essentially, the \(\tau \) transitions mean that s moves to a state in which it can refuse one input (\(?i_2\) in \(s_1\) and \(?i_1\) in \(s_2\)) before performing a \(\circleddash \).
We have \(\mathtt {{\mathcal T}\!{\mathcal R}traces}(r) \subseteq \mathtt {{\mathcal T}\!{\mathcal R}traces}(s)\), so that r conforms to s under timed refusal trace inclusion, but the converse is not the case. This shows that an external choice between inputs is a good implementation of the internal choice between the same inputs.
These last two fragments are also useful to show why we cannot restrict ourselves to compute only maximal refusal sets. If we would do this, we would have that the timed refusal traces of r would be the same but the ones corresponding to s would be \(R(\{?i_2\})?i_1\cdots , R(\{?i_1\})?i_2\cdots , R(\{?i_1\})\circleddash , R(\{?i_2\})\circleddash ,\ldots \) and we would not have timed trace inclusion.
We can now compare this implementation relation with trace inclusion introduced in Definition 6. The proof of the following result follows from the fact that, for a process r, \(\mathtt {{\mathcal T}\! traces}(r) = \mathtt {{\mathcal T}\!{\mathcal R}traces}(r) \cap L^*\).
Proposition 3
Let I and O be countable disjoint sets of inputs and outputs, respectively. Let p and q be two elements of \( TockLTS (I,O)\). If p conforms to q under timed refusal trace inclusion then p conforms to q under timed trace inclusion.
However, the converse is not the case as the following result shows.
Proposition 4
Let I and O be countable disjoint sets of inputs and outputs, respectively. There exist p and q in \( TockLTS (I,O)\) such that p conforms to q under timed trace inclusion but p does not conform to q under timed refusal trace inclusion.
Proof
In order to prove this it is sufficient to give an example of such tockLTSs. Consider r and s depicted in Fig. 1(bottom). In Example 1 we showed that \(\mathtt {{\mathcal T}\! traces}(r) = \mathtt {{\mathcal T}\! traces}(s)\). Therefore, s conforms to r under timed trace inclusion. On the contrary, in Example 2 we showed that \(\mathtt {{\mathcal T}\!{\mathcal R}traces}(s) \not \subseteq \mathtt {{\mathcal T}\!{\mathcal R}traces}(r)\). Therefore, s does not conform to s under refusal timed trace inclusion.
To summarise, r conforms to s under timed trace inclusion but not under timed refusal trace inclusion. The result therefore holds.
We therefore obtain the following.
Theorem 1
Timed refusal trace inclusion is strictly stronger than timed trace inclusion.
This tells us that if we can observe timed refusal traces in testing then we have a more powerful implementation relation than just timed trace inclusion. It is also the case that if the environment (e.g. the user) can observe timed refusal traces (through, for example, the refusal of actions being observed as a result of options not being available on a screen) then it is insufficient to test for trace inclusion: the user might consider an SUT p to be faulty with respect to a specification q even though they have the same sets of timed traces.
5 Alternative Characterisations
In this section we provide two alternative characterisations of timed refusal trace inclusion. First, we develop an approach in which a tockLTS p is transformed into an automaton whose language describes the set of timed refusal traces of p. This gives us the potential to use automata theory and algorithms when reasoning about timed refusal trace inclusion. We then show how we can model timed refusal trace inclusion in terms of observers and the observations they can make. This shows that our definition of timed refusal trace inclusion corresponds to what can be observed, with respect to the SUT, in our setting and so confirms that it is the right implementation relation for our context.
5.1 Using an Automaton
Trace inclusion corresponds to a relation between the languages defined by the automata corresponding to two LTS. The benefit is that it is possible to use standard results and algorithms from formal language theory. This is particularly useful if the processes are deterministic finite state automata since there are efficient algorithms for many standard problems, including language inclusion (that is, trace inclusion in our setting). We now show how we can generate an automaton whose traces are exactly the timed refusal traces of a tockLTS q.
In order to explore one approach that might be used to achieve this, consider the fragment of a model in Fig. 2(a). This can refuse all actions other than ?b when in state \(q_1\). It might seem that we can simply add a self-loop transition, with such a refusal, in state \(q_1\). However, we would then have the problem that such a self-loop need not be followed by a \(\circleddash \) action. For example, the inclusion of such a self-loop in state \(q_1\) would allow refusal traces such as \(?a R(\{?a\}) ?b\). Such a refusal trace should not be allowed since it has a refusal followed by an action other than \(\circleddash \).
One possible solution is outlined in Fig. 2(b). Rather than adding a self-loop, we include a transition, to a new state \(\widetilde{q_1}\), that is labelled with the refusal. From \(\widetilde{q_1}\) there is only one possible action, which is \(\circleddash \). We also require that \(\widetilde{q_1}\) is not a final state of the automaton. As a result, any path that reaches a final state and includes the transition from \(q_1\) to \(\widetilde{q_1}\) must follow this transition by a transition with label \(\circleddash \). Note that we require the notion of a final state and so the model is an automaton and not a tockLTS.
We now formally define the automaton \({\mathcal M}(p)\) that includes these refusals.
Definition 11
Let \(p= (Q, q_0, I, O, T)\) be a tockLTS. Let us consider the subset of states that can evolve by performing \(\circleddash \), that is,  . We define a set of fresh states \(\tilde{Q} = \{\tilde{q} | q \in Q_\circleddash \}\) (i.e. \(Q \cap \tilde{Q} = \emptyset \)). The new set of states \(\tilde{Q}\) has a state for each state of \(Q_\circleddash \).
. We define a set of fresh states \(\tilde{Q} = \{\tilde{q} | q \in Q_\circleddash \}\) (i.e. \(Q \cap \tilde{Q} = \emptyset \)). The new set of states \(\tilde{Q}\) has a state for each state of \(Q_\circleddash \).
We let \({\mathcal M}(p)\) denote the automaton \((Q\cup \tilde{Q}, q_0, I \cup O \cup {\mathcal R}(L), T', F)\) where
-
 .
. -
\(F = Q\).
The following result shows that the previous construction is correct.
Theorem 2
Let \(p= (Q, q_0, I, O, T)\) be a tockLTS. We have that \(\mathtt {{\mathcal T}\!{\mathcal R}traces}(p) = L({\mathcal M}(p))\).
Proof
First, observe that both sets are subsets of RT(L), where \(L=I\cup O\). We will prove a slightly stronger result than the one stated before. Specifically, we will prove that for all \(\sigma \in RT(L)\), we have that \(\sigma \) takes p to state q if and only if q is a final state of \({\mathcal M}(p)\) and \(\sigma \) takes \({\mathcal M}(p)\) to state q.
We use proof by induction on the length of \(\sigma \). The base case, with \(\sigma \) being the empty sequence, is immediate.
Inductive hypothesis: the result holds if \(\sigma \) has length less than k (\(k>0\)). Let us suppose that \(\sigma \) has length k and \(\sigma \) takes one of p and \({\mathcal M}(p)\) to state q. By the definition of RT(L), \(\sigma = \sigma _1 a\) for some \(a \in L \cup \{\circleddash \}\) (i.e. sequences in RT(L) cannot end in refusals). There are two cases to consider. First, if \(\sigma _1\) does not end with a refusal then, by the inductive hypothesis, we have that \(\sigma _1\) reaches the same states in p and \({\mathcal M}(p)\). In addition, by construction we have that a takes p and \({\mathcal M}(p)\) to the same state and so the result follows. The second case is where \(\sigma _1\) ends in a refusal and so \(\sigma = \sigma _2 R(X) \circleddash \) for some \(X \subseteq L\) and \(\sigma _2 \in RT(L)\). By the inductive hypothesis, \(\sigma _2\) takes p and \({\mathcal M}(p)\) to the same state \(q_1\). By construction, \(R(X) \circleddash \) takes p and \({\mathcal M}(p)\) to the same state q and so the result follows.
5.2 Using Observers
Implementation relations should correspond to the ability of the environment, or a tester, to distinguish between processes, with it typically being the case that we require that all observations that can be made of the SUT are also observations that can be made when interacting with the specification (see, for example, [23]). In this section we define the notion of an observer, in our context, and how such an observer interacts with a tockLTS. This will provide an alternative, but equivalent, characterisation of timed refusal trace inclusion.
We follow the classical approach of ioco [23], in which a special action \(\theta \) is included in an observer to denote the observation of a refusal. An observer will be placed in parallel with the SUT, with the two synchronising on common actions in \(I \cup O \cup \{\circleddash \}\); \(\theta \) synchronises with refusals. Before we include a formal definition, we informally explain the properties we expect an observer to have in order to observe the refusal of X in state u.
-
1.
There is a transition from u labelled by \(\theta \), with the parallel composition being defined so that the other transitions are given priority over this (if the SUT and observer are both able to take an action \(a \ne \theta \) then they take such an action, in preference to communicating through a \(\theta \)).
-
2.
For all \(x \in X\), there is a transition from u that has label x. This ensures that if p can engage in an action \(x \in X\) when in the current state then the parallel composition of p and the observer can engage in action x and so a refusal will not be observed (since x is given priority over \(\theta \)).
-
3.
For all \(a \in O\), there is a transition from u labelled with a. Similar to the previous case, the prioritisation of such actions over \(\theta \) means that this ensures that a \(\theta \) transition cannot occur if p can perform an internal action or an output. As a result, if the process (with which u is interacting) is not in a stable state then a refusal cannot happen.
-
4.
There are no transitions from u labelled with an action from \(L {\setminus } (X \cup O)\). This ensures that the observer can only change state by engaging in an action from X or through taking a transition with label \(\theta \).
The combination of the above ensures that the observer can only take the transition with label \(\theta \) if the process p is in a stable state and also no actions from X are possible - i.e. if and only if p can refuse X. In order to ensure that a refusal can only be observed in a stable state we will require observers to have the following property.
Definition 12
(Observer). Let I and O be countable disjoint sets of inputs and outputs, respectively. An observer u is an automaton with action set \(L = I \cup O \cup \{\circleddash , \theta \}\) that satisfies the following properties for each state q of u:
-
1.
 ;
; -
2.
if
 then for all \(a \in O\) we have that
then for all \(a \in O\) we have that  ;
; -
3.
if
 then for all \(a \in O\) we have that
then for all \(a \in O\) we have that  ;
; -
4.
if \((q,\theta ,q')\) is a transition of u then \(\circleddash \) is the only action available in state \(q'\).
We let \(\mathcal {U}(I,O)\) denote the set of observers with input set I and output set O.
The last rule ensures that a refusal must be followed by a \(\circleddash \). The second rule is the standard condition that a tester is able to observe outputs; the exception is because the observation of a refusal takes time and so a \(\theta \) must be followed by a \(\circleddash \).
We can now define a parallel composition operator \(\ \rceil | \ \) between a process \(p \in TockLTS (I,O)\) and an observer \(u \in \mathcal {U}(I,O)\). This is similar to the operators for LTS [23] but we choose to enrich the observations made with refusal sets.
Definition 13
(Synchronised parallel communication). Let I and O be countable disjoint sets of inputs and outputs, respectively. Let \(p=(Q, q_0, I, O, T)\in TockLTS (I,O)\) and \(u= (Q', q_0', I \cup O\cup \{\circleddash , \theta \}, T',Q')\in \mathcal {U}(I,O)\). The composition of the observer u and the model p, denoted by \(u\ \rceil | \ p\), is an automaton \((Q\times Q', (q_0,q'_0), I\,\cup \,O\,\cup \,{\mathcal R}(I\,\cup \,O)\,\cup \,\{\circleddash \}, T'',F)\) in which \(F = Q\times Q'\) and \(T''\) is defined as follows:
-
If \((q_1,\tau ,q_2)\in T\) then for all \(q'\in Q'\) we have \(((q_1,q'),\tau ,(q_2,q'))\in T''\).
-
If \((q_1,a,q_2)\in T\) and \((q_1',a,q_2')\in T'\), with \(a \in I \cup O \cup \{\circleddash \}\), then we have \(((q_1,q_1'),a,(q_2,q_2'))\in T''\).
-
Let \(X \subseteq I\, \cup \, O\). If \((q_1,\circleddash ,q_2)\in T\), \((q_1',\theta ,q_2') \in T'\) then \(((q_1,q_1'),R(X),(q_1,q_2'))\) \(\in T''\) is the case if the following conditions hold:
-
for all \(a \in I\cup O\) we have that either there does not exist \(q_3\) such that \((q_1,a,q_3)\in T\) or there does not exist \(q_3'\) such that \((q_1',a,q_3')\in T'\).
-
for all \(a \in X\) we have that there exists \(q_3'\) such that \((q_1',a,q_3')\in T'\).
Note that, since \(p \in TockLTS (I,O)\) and \((q_1,\circleddash ,q_2)\in T\), we know that \(q_1\) is a stable state.
-
The sets of observations that the observer u can make of p, denoted by \(obs^\theta (u,p)\), are given by the following:

Note that in the last rule of the composition, since \(q_1\) may evolve via \(\circleddash \) then we have that it must be a stable state (for all \(a \in O \cup \{\tau \}\) we have that  ); this follows from the fact that p is a tockLTS and tockLTSs have urgent outputs and internal actions (Definition 5). In this rule, also note that we discard the state reached after the performance of \(\circleddash \) from \(q_1\): the composition makes p remains in the same state, according to how refusals are added as transitions to tockLTSs (Definition 8).
); this follows from the fact that p is a tockLTS and tockLTSs have urgent outputs and internal actions (Definition 5). In this rule, also note that we discard the state reached after the performance of \(\circleddash \) from \(q_1\): the composition makes p remains in the same state, according to how refusals are added as transitions to tockLTSs (Definition 8).
The following shows how observations relate to timed refusal traces and is a result of the definition of \(u \ \rceil | \ p\) and the definition of timed refusal traces (Definition 9).
Proposition 5
Let I and O be countable disjoint sets of inputs and outputs, respectively. Given \(\sigma \in (I\cup O\cup \{\circleddash \} \cup {\mathcal R}(L))^*\) and p in \( TockLTS (I,O)\), there is an observer \(u \in \mathcal {U}(I,O)\) such that \(\sigma \in obs^\theta (u,p)\) if and only if \(\sigma \) is a prefix of a timed refusal trace of p.
Note that in the above result \(\sigma \) need not be a timed refusal trace of p since \(\sigma \) could end in a refusal; to make this a timed refusal trace it would be necessary to add the \(\circleddash \) that follow this refusal. The following result is immediate from Proposition 5.
Theorem 3
Let I and O be countable disjoint sets of inputs and outputs, respectively. Given p and q in \( TockLTS (I,O)\) we have that p conforms to q under timed refusal trace inclusion if and only if, for all \(u \in \mathcal {U}(I,O)\) we have that \(obs^\theta (u,p) \subseteq obs^\theta (u,q)\).
Since the observers capture the observations that can be made, this tells us that timed refusal trace inclusion is a suitable implementation relation for our scenario.
6 Conclusions and Future Work
There has been significant interest in testing from formal models since this brings the potential for automated systematic testing. In order to test from a formal model one requires an implementation relation that says what it means for the system under test (SUT) to be a correct implementation of the specification. This paper considered cyclic models, in which behaviours are of the form of sequences of observable actions separated by discrete time intervals. The work was motivated by the use of cyclic simulators in a number of areas, including robotic systems.
Although many implementation relations are variants of the well known ioco implementation relation, ioco and its timed versions were not suitable for cyclic models. As a result, there was a need to define novel implementation relations that take into account the discrete nature of time in cyclic models and also not only the actions that models can perform but also the ones that they can refuse at each point of time. We introduced the notion of a timed refusal trace and also our main implementation relation: timed refusal trace inclusion. We introduced two alternative characterisations of timed refusal trace inclusion. First, we showed how one can define an automaton whose language is exactly the set of timed refusal traces of a model; this allows one to express correctness in terms of formal language containment for automata. We also showed how one can define timed refusal trace inclusion in terms of the observations that can be made by an observer interacting with processes (the specification and SUT); this demonstrates that timed refusal trace inclusion corresponds to the notion of observation for our models.
There are several possible lines of future work. It should be possible to extend classical test generation algorithms to test for timed refusal trace inclusion. There is also the potential to enrich models to include, for example, probabilities or continuous variables (i.e. hybrid systems). Finally, we plan to carry out case studies with robotic systems.
Notes
- 1.
- 2.
We will say that a state is stable if it is not possible to take a transition whose label is an output or an internal action.
References
Ammann, P., Offutt, J.: Introduction to Software Testing, 2nd edn. Cambridge University Press, Cambridge (2017)
Binder, R.V., Legeard, B., Kramer, A.: Model-based testing: where does it stand? Commun. ACM 58(2), 52–56 (2015)
Briones, L.B., Brinksma, E.: A test generation framework for quiescent real-time systems. In: Grabowski, J., Nielsen, B. (eds.) FATES 2004. LNCS, vol. 3395, pp. 64–78. Springer, Heidelberg (2005). https://doi.org/10.1007/978-3-540-31848-4_5
Cavalcanti, A., Ribeiro, P., Miyazawa, A., Sampaio, A., Conserva Filho, M., Didier, A.: RoboSim reference manual. Technical report, University of York (2019)
Cavalcanti, A., et al.: Verified simulation for robotics. Sci. Comput. Program. 174, 1–37 (2019)
Cavalli, A.R., Higashino, T., Núñez, M.: A survey on formal active and passive testing with applications to the cloud. Ann. Telecommun. 70(3–4), 85–93 (2015)
van Glabbeek, R.: The linear time-branching time spectrum I. The semantics of concrete, sequential processes. In: Bergstra, J.A., Ponse, A., Smolka, S.A. (eds.) Handbook of Process Algebra, chapter 1, North Holland (2001)
Harel, D.: Statecharts: a visual formulation for complex systems. Sci. Comput. Program. 8(3), 231–274 (1987)
Heerink, L., Tretmans, J.: Refusal testing for classes of transition systems with inputs and outputs. In: 19th Joint International Conference on Protocol Specification, Testing, and Verification and Formal Description Techniques, FORTE/PSTV 1999, pp. 23–38. Chapman & Hall (1997)
Hierons, R.M., et al.: Using formal specifications to support testing. ACM Comput. Surv. 41(2), 9:1–9:76 (2009)
Hierons, R.M., Bowen, J.P., Harman, M. (eds.): Formal Methods and Testing. LNCS, vol. 4949. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78917-8
World Robotics 2018: International Federation of Robotics. Statistical Department (2018)
ISO/IEC JTCI/SC21/WG7, ITU-T SG 10/Q.8: Information Retrieval, Transfer and Management for OSI; Framework: Formal Methods in Conformance Testing. Committee Draft CD 13245–1, ITU-T proposed recommendation Z.500. ISO - ITU-T (1996)
Krichen, M., Tripakis, S.: Conformance testing for real-time systems. Form. Methods Syst. Des. 34(3), 238–304 (2009)
Marinescu, R., Seceleanu, C., Le Guen, H., Pettersson, P.: A research overview of tool-supported model-based testing of requirements-based designs. In: Advances in Computers, chapter 3, vol. 98, pp. 89–140. Elsevier (2015)
Miyazawa, A., Ribeiro, P., Li, W., Cavalcanti, A., Timmis, J., Woodcock, J.: RoboChart: modelling and verification of the functional behaviour of robotic applications. Softw. Syst. Model. (2019, to appear)
Myers, G.J., Sandler, C., Badgett, T.: The Art of Software Testing, 3rd edn. Wiley, Hoboken (2011)
Phillips, I.: Refusal testing. Theor. Comput. Sci. 50(3), 241–284 (1987)
Rohmer, E., Singh, S.P., Freese, M.: V-REP: aversatile and scalable robot simulation framework. In: 26th IEEE/RSJ International Conference on Intelligent Robots and Systems, IROS 2013, vol. 1, pp. 1321–1326. IEEE Computer Society (2013)
Roscoe, A.W.: Understanding Concurrent Systems. Texts in Computer Science. Springer, London (2010). https://doi.org/10.1007/978-1-84882-258-0
Schmaltz, J., Tretmans, J.: On conformance testing for timed systems. In: Cassez, F., Jard, C. (eds.) FORMATS 2008. LNCS, vol. 5215, pp. 250–264. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85778-5_18
Shafique, M., Labiche, Y.: A systematic review of state-based test tools. Int. J. Softw. Tools Technol. Transf. 17(1), 59–76 (2015)
Tretmans, J.: Model based testing with labelled transition systems. In: Hierons, R.M., Bowen, J.P., Harman, M. (eds.) Formal Methods and Testing. LNCS, vol. 4949, pp. 1–38. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-78917-8_1
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Lefticaru, R., Hierons, R.M., Núñez, M. (2019). An Implementation Relation for Cyclic Systems with Refusals and Discrete Time. In: Ölveczky, P., Salaün, G. (eds) Software Engineering and Formal Methods. SEFM 2019. Lecture Notes in Computer Science(), vol 11724. Springer, Cham. https://doi.org/10.1007/978-3-030-30446-1_21
Download citation
DOI: https://doi.org/10.1007/978-3-030-30446-1_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-30445-4
Online ISBN: 978-3-030-30446-1
eBook Packages: Computer ScienceComputer Science (R0)




 .
. then
then  .
. implies
implies 
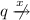 .
.
 .
. ;
; then for all
then for all  ;
; then for all
then for all  ;
;