Abstract
In 2012, Tim Güneysu, et al. proposed the GLP signature scheme, a practical and efficient post-quantum signature scheme. It is built on the modification of Vadim Lyubashevsky’s idea of constructing previous signature schemes. It has a significantly smaller signature and key size than prior signature scheme. The design of the GLP is a foundation to construct newer signature schemes such as Bai-Galbraith, Dilithium. However, Tim Güneysu has only given the description of the GLP signature scheme that has not yet given a detailed security proof for this scheme. Therefore, in this paper, we will present a full security proof for the GLP signature scheme. Specifically, we show that the GLP signature scheme is EU-CMA secure in the random oracle model.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The security of currently popular signature schemes is based on hard problems in number theory, such as integer factorization or discrete logarithm problem. More than 20 years ago, Peter Shor proposed an efficient algorithm to solve these hard arithmetic problems on a quantum computer [Sho99]. Therefore, as soon as quantum computers achieve sufficient computational power, widely-used signature schemes will be insecure. This urges researchers to search for new cryptography primitives resistant to quantum computing-based attacks. Due to the recent innovative development of quantum computers, post-quantum cryptography becomes more and more crucial. Among the candidates for post-quantum cryptography, lattice-based cryptography is the most potential candidates.
The last few years have witnessed surprising development of lattice-based cryptography, especially constructions of new signatures schemes. At present, lattice-based signatures have become more practical and competitive with classical signatures related to efficiency and security level. Among the methods of constructing signatures, Fiat-Shamir technique is attracting the attention of the cryptography community for its effectiveness and practicality. The first Fiat-Shamir lattice-based signature was introduced by Lyubashevsky [Lyu08] in 2008. This scheme based on the hardness of the shortest vector problem. Later, several improved schemes was proposed in [Lyu12, DDLL13, BG14, DLL+17]. One of them, the Dilithium signature scheme, has been submitted to NIST to standardize as a post-quantum signature.
The GLP signature scheme [GLP12]Footnote 1 is constructed by adapting the idea from [Lyu12] and [Lyu08]. Concretely, GLP follows the idea that ephemeral values in signing algorithm are chosen randomly from a uniform distribution over a set the same as in [Lyu08], instead of from a Gaussian distribution in [Lyu12]. Moreover, the way how to select a valid signature of GLP is the same as the proposed way in [Lyu08] (in [Lyu08] the signatures is simply checked to be in some interval or not, while [Lyu12] uses rejection sampling to output a valid signature). However, due to the usage of optimized parameters to reduce the signature size and key size, the security proof of GLP was founded on the proof in [Lyu12]. Key size and signature size of GLP is significantly smaller than those of other signature schemes in [Lyu12, Lyu08]. Besides, the construction idea of GLP is a foundation to construct later improved scheme such as [BG14, DLL+17].
Our contribution: In [GLP12], the authors described the GLP signature scheme but did not prove its security in details (concretely, [GLP12] provided a guideline to prove based on [Lyu12]). Therefore, our main contribution is to present a full security proof for the GLP signature scheme based on previous technique in [Lyu08, Lyu12]. We show that the GLP signature scheme is EU-CMA secure in the random oracle model under assuming the hardness of the worst-case lattice problems.
Organization of the paper: In Sect. 2, we recall the definitions of SIS problem and its hardness on ideal lattices. The description of GLP is recalled in Sect. 3. In Sect. 4, we present a security proof of the GLP signature scheme in the random oracle model. Finally, the conclusion of this paper is described in Sect. 5.
2 Preliminaries
Throughout the paper, we will assume that \(n={{2}^{\alpha }}\) where \(\alpha \) is a positive integer, \(p\equiv 1\bmod 2n\) and \(R^{p^n}={{{\mathbb {Z}}_{p}}\left[ x \right] }/{\left\langle {{x}^{n}}+1 \right\rangle }\). Each element of \(R^{p^n}\) can be presented as a polynomial of which the degree is at most \(n-1\) and the coefficients are in \(\left[ -\frac{p\,-\,1}{2},\frac{p\,-\,1}{2} \right] \). We let \(R_{k}^{p^n}\) be a subset of the ring \(R^{p^n}\) in which the elements of \(R_{k}^{p^n}\) can be presented as polynomials with degree at most \(n-1\) and the coefficients in \(\left[ -k,k \right] \), where \(|k|<\frac{p\,-\,1}{2}\). For any set S, let  mean that s is chosen uniformly at random from S. We denote U(0, 1) to be the uniform distribution on (0, 1). Let \(\mathbf {s}=s_0+s_1x+\ldots +s_{n-1}x^{n-1}\) be a polynomial, we denote \(\left\| \mathbf {s} \right\| _{\infty }=\max _{i=0}^{n-1}|s_i|\).
mean that s is chosen uniformly at random from S. We denote U(0, 1) to be the uniform distribution on (0, 1). Let \(\mathbf {s}=s_0+s_1x+\ldots +s_{n-1}x^{n-1}\) be a polynomial, we denote \(\left\| \mathbf {s} \right\| _{\infty }=\max _{i=0}^{n-1}|s_i|\).
Definition 1
(\(\mathbf{R}\)-\(\mathbf{SIS}_{p,n,\gamma ,\beta }\) problem, [Lyu12]). Given the polynomials \(\mathbf {a}_{1}, \mathbf {a}_2, \ldots , \mathbf {a}_{\gamma }\) are chosen uniformly random from \({{R}^{p^n}}\), find the polynomials \({{\mathbf {s}}_{1}},{{\mathbf {s}}_{2}},\ldots ,{{\mathbf {s}}_{\gamma }} \ne 0\) in \(R_{\beta }^{p^n}\) such that \({{\mathbf {a}}_{1}}{{\mathbf {s}}_{1}}+{{\mathbf {a}}_{2}}{{\mathbf {s}}_{2}}+\ldots +{{\mathbf {a}}_{\gamma }}{{\mathbf {s}}_{\gamma }}=0\).
Definition 2
(\(\mathbf{R}\)-\(\mathbf{SIS}_{p,n,\gamma ,k}\) distribution, [Lyu12]). The \(\text {R-SIS}_{p,n,\gamma ,k}\) distribution is sampled by choosing \({{\mathbf {a}}_{1}},{{\mathbf {a}}_{2}},\ldots ,{{\mathbf {a}}_{\gamma }}\) uniformly random from \({{R}^{p^n}}\), the polynomials \({{\mathbf {s}}_{1}},{{\mathbf {s}}_{2}},\ldots ,{{\mathbf {s}}_{\gamma }}\) uniformly random from \(R_{k}^{p^n}\) and outputting \(({{\mathbf {a}}_{1}},{{\mathbf {a}}_{2}},\ldots ,{{\mathbf {a}}_{\gamma }},\mathbf {t}={{\mathbf {a}}_{1}}{{\mathbf {s}}_{1}}+{{\mathbf {a}}_{2}}{{\mathbf {s}}_{2}}+\ldots +{{\mathbf {a}}_{\gamma }}{{\mathbf {s}}_{\gamma }})\).
Definition 3
(\(\mathbf{R}\)-\(\mathbf{SIS}_{p,n,\gamma ,k}\) decision problem, [Lyu12]). Given \(({{\mathbf {a}}_{1}},{{\mathbf {a}}_{2}}, \ldots , {{\mathbf {a}}_{\gamma }}, \mathbf {t})\), distinguish whether \(({{\mathbf {a}}_{1}},{{\mathbf {a}}_{2}},\ldots ,{{\mathbf {a}}_{\gamma }},\mathbf {t})\) are generated from the \(\text {R-SIS}_{p,n,\gamma ,k}\) distribution or chosen uniformly random from \(( \underbrace{R^{{p}^{n}}\times .\ldots \times R^{{p}^{n}}}_{\gamma },R^{{p}^{n}})\).
The \(\text {R-SIS}_{p,n,\gamma ,\beta }\) problem is consider as a hard problem. Solving the problem \(\text {R-SIS}_{p,n,\gamma ,\beta }\) have the hardness as solving worst-case lattice problems in ideal lattices [LM06].
Definition 4
(\(\mathbf {DCK}_{p,n}\) problem, [GLP12]). Distinguish between the uniform distribution over \({{R}^{p^n}}\times {{R}^{p^n}}\) and the distribution \(\left( \mathbf {a},\mathbf {a}{{\mathbf {s}}_{1}}+{{\mathbf {s}}_{2}} \right) \), where \({{\mathbf {s}}_{i}}\) are uniformly random in \(R_{1}^{p^n}\) and \(\mathbf {a}\) is uniformly random in \({{R}^{p^n}}\).
As in [GLP12], the \(\text {DCK}_{p,n}\) problem is also considered as a hard problem. The following lemma indicates a reduction from the \(\text {DCK}_{p,n}\) problem to the \(\text {R-SIS}_{p,n,2,3\alpha +1}\) decision problem. In other words, if one can solve the \(\text {R-SIS}_{p,n,2,3\alpha +1}\) decision problem, then one can solve the \(\text {DCK}_{p,n}\) problem.
Lemma 1
[Lyu12]. Let \(\alpha \) be a non-negative integer such that \(GCD(2\alpha +1,p)=1\), then there exists a polynomial-time reduction from the \(DCK _{p,n}\) problem to the \(R-SIS _{p,n,2,3\alpha +1}\) decision problem.
Proof
See [Lyu12], Lemma 3.6, p. 7. \(\square \)
The following lemma shows that, with suitable parameters, if one can solve the \(\text {R-SIS}_{p,n,2,\beta }\) problem then one can solve the \(\text {DCK}_{p,n}\) problem.
Lemma 2
Footnote 2 If \(8\beta n\le p\) then there is a polynomial-time randomized reduction from the \(\text {DCK} _{p,n}\) problem to the \(R-SIS _{p,n,2,\beta }\) problem.
Proof
Given an instance \(\left( \mathbf {a},\mathbf {t} \right) \) of the \(\text {DCK}_{p,n}\) problem. Using the \(\text {R-SIS}_{p,n,2,\beta }\) oracle on \((\mathbf {a},1)\) to find  such that
such that  . If \(\mathbf {t}=\mathbf {a}{{\mathbf {s}}_{1}}+{{\mathbf {s}}_{2}}\) then
. If \(\mathbf {t}=\mathbf {a}{{\mathbf {s}}_{1}}+{{\mathbf {s}}_{2}}\) then

Since \({{\left\| {{\mathbf {s}}_{1}} \right\| }_{\infty }},{{\left\| {{\mathbf {s}}_{2}} \right\| }_{\infty }}\le 1\),  , and [Lyu08], Lemma 2.8], we have
, and [Lyu08], Lemma 2.8], we have

Hence  . On the other hand, if \(\mathbf {t}\) is uniformly random \({{R}^{{{p}^{n}}}}\) then
. On the other hand, if \(\mathbf {t}\) is uniformly random \({{R}^{{{p}^{n}}}}\) then  will also be uniformly random in \({{\mathbb {Z}}_{p}}\). Hence, in order to solve the \(\text {DCK}_{p,n}\) problem, distinguisher simply looks at the value
will also be uniformly random in \({{\mathbb {Z}}_{p}}\). Hence, in order to solve the \(\text {DCK}_{p,n}\) problem, distinguisher simply looks at the value  . If
. If  then he says that \(\left( \mathbf {a},\mathbf {t} \right) \) is an instance of the \(\text {DCK}_{p,n}\) problem. Otherwise, he says that \(\left( \mathbf {a},\mathbf {t} \right) \) is chosen uniformly from \({{R}^{{{p}^{n}}}}\times {{R}^{{{p}^{n}}}}\). In the case \(\left( \mathbf {a},\mathbf {t} \right) \) is an instance of the \(\text {DCK}_{p,n}\) problem, the distinguisher will be correct. However, in the case of the uniform distribution \(\left( \mathbf {a},\mathbf {t} \right) \) is uniformly on \({{R}^{{{p}^{n}}}}\times {{R}^{{{p}^{n}}}}\), he will make an error with probability \(\frac{1}{2}\) (because \(\mathbf {t}\) is chosen uniformly from \({{R}^{{{p}^{n}}}}\), the probability that
then he says that \(\left( \mathbf {a},\mathbf {t} \right) \) is an instance of the \(\text {DCK}_{p,n}\) problem. Otherwise, he says that \(\left( \mathbf {a},\mathbf {t} \right) \) is chosen uniformly from \({{R}^{{{p}^{n}}}}\times {{R}^{{{p}^{n}}}}\). In the case \(\left( \mathbf {a},\mathbf {t} \right) \) is an instance of the \(\text {DCK}_{p,n}\) problem, the distinguisher will be correct. However, in the case of the uniform distribution \(\left( \mathbf {a},\mathbf {t} \right) \) is uniformly on \({{R}^{{{p}^{n}}}}\times {{R}^{{{p}^{n}}}}\), he will make an error with probability \(\frac{1}{2}\) (because \(\mathbf {t}\) is chosen uniformly from \({{R}^{{{p}^{n}}}}\), the probability that  is \(\frac{1}{2}\)). \(\square \)
is \(\frac{1}{2}\)). \(\square \)
A signature scheme includes three algorithms: \(\textsf {Keygen}\), \(\textsf {Sign}\) and \(\textsf {Verify}\). \(\textsf {Keygen}\) takes as input a security parameter and outputs a public key pk and secret key sk. \(\textsf {Sign}\) takes as input a message \(\mu \) and a secret key sk, outputs a signature \(\varSigma \). \(\textsf {Verify}\) takes as input a message \(\mu \), signature \(\varSigma \) and public key pk, output valid (1) or invalid (0). We require that, with the non-negligible probability, \(\textsf {Verify}\left( \mu ,\varSigma ,pk \right) =1\).
The standard security notion for signatures is existential unforgeability under chosen message attacks (EU-CMA). Consider the following game of challenger \(\mathcal {C}\) and forger \(\mathcal {F}\). Firstly, the challenger generates a key pair \(\left( sk,pk \right) \) and sends pk to \(\mathcal {F}\). The forger takes as input public key pk. Besides, the forger can make the polynomial queries for signatures on messages \({{\mu }_{1}},\ldots ,{{\mu }_{Q}}\) of its choice. For the i-th query, the challenger answers \(\left( {{\mu }_{i}},{{\varSigma }_{i}} \right) \). The output of the forger is \(\left( {{\mu }^{*}},{{\varSigma }^{*}} \right) \). It wins the game if \(\textsf {Verify}\left( {{\mu }^{*}},{{\varSigma }^{*}},pk \right) =1\), and \(\mu ^* \ne \mu _i \) for any \(i=1,\ldots ,Q\). The signature scheme is called EU-CMA secure if there is no polynomial-time \(\mathcal {F}\) whose success probability in the above game is non-negligible.
3 The GLP Signature Scheme
The signature scheme has three main algorithms: key generation, signing and verifying. In particular, the signing and verifying algorithm can access to the random oracle H is defined in [GLP12] as follows: \(H:\{ 0,1\}^{*}\rightarrow \{ \mathbf {v}:\mathbf {v}\in R_{1}^{p^n},\sum \limits _{i=0}^{n-1}{\left| {{v}_{i}} \right| }=32 \}\), where \(\mathbf {v}={{v}_{0}}+{{v}_{1}}x+\ldots +{{v}_{n-1}}{{x}^{n-1}}\in R_{1}^{p^n}\).
Key Generation Algorithm
Input: Parameters (n, p).
Output: Secret key  and public key \(( \mathbf {a},\mathbf {t})\).
and public key \(( \mathbf {a},\mathbf {t})\).
-
1.
Choose secret key
 .
. -
2.
Choose
 .
. -
3.
Compute
 .
. -
4.
Return secret key
 and public key \(( \mathbf {a},\mathbf {t})\).
and public key \(( \mathbf {a},\mathbf {t})\).
Signing Algorithm
Input: Parameters (n, p, k), message \(\mu \), secret key  and \(\mathbf {a}\).
and \(\mathbf {a}\).
Output: A signature for message \(\mu \).
-
1.
Choose
 .
. -
2.
Compute
 .
. -
3.
Compute
 .
. -
4.
If \({{\mathbf {z}}_{1}},{{\mathbf {z}}_{2}}\in R_{k-32}^{{{p}^{n}}}\) then
-
5.
Output \(( {{\mathbf {z}}_{1}},{{\mathbf {z}}_{2}},\mathbf {c})\)
-
6.
Else return to Step 1.
Verifying Algorithm
Input: The parameters (n, p, k), public key \(( \mathbf {a},\mathbf {t})\), message \(\mu \) and signature \(( {{\mathbf {z}}_{1}},{{\mathbf {z}}_{2}},\mathbf {c})\).
Output: The signature is valid or invalid.
-
1.
If \({{\mathbf {z}}_{1}},{{\mathbf {z}}_{2}}\in R_{k-32}^{p^n}\) and \(\mathbf {c}=H( \mathbf {a}{{\mathbf {z}}_{1}}+{{\mathbf {z}}_{2}}-\mathbf {tc},\mu )\) then
-
2.
The signature is valid.
-
3.
Else
-
4.
The signature is invalid.
The secret keys are random polynomials  . The public key is \((\mathbf {a},\mathbf {t})\), where
. The public key is \((\mathbf {a},\mathbf {t})\), where  and
and  .
.
To sign message \(\mu \), firstly, the signer chooses random polynomials  . Then the signer compute
. Then the signer compute  and
and  . Before outputting the signature for the message \(\mu \), the signer will check if \({{\mathbf {z}}_{1}},{{\mathbf {z}}_{2}}\) has belong to \(R_{k-32}^{p^n}\) or not. If \({{\mathbf {z}}_{1}},{{\mathbf {z}}_{2}}\in R_{k-32}^{p^n}\) then signer will output \(( {{\mathbf {z}}_{1}},{{\mathbf {z}}_{2}},\mathbf {c})\) as the signature for \(\mu \). Otherwise, the signer regenerate
. Before outputting the signature for the message \(\mu \), the signer will check if \({{\mathbf {z}}_{1}},{{\mathbf {z}}_{2}}\) has belong to \(R_{k-32}^{p^n}\) or not. If \({{\mathbf {z}}_{1}},{{\mathbf {z}}_{2}}\in R_{k-32}^{p^n}\) then signer will output \(( {{\mathbf {z}}_{1}},{{\mathbf {z}}_{2}},\mathbf {c})\) as the signature for \(\mu \). Otherwise, the signer regenerate  and recalculate the signature. The signer will perform the signing algorithm until it can give \({{\mathbf {z}}_{1}},{{\mathbf {z}}_{2}}\in R_{k-32}^{p^n}\). With the parameters chosen as in Table 1, Lemma 3 will show that the average signer needs to make approximately 7 times to generate a valid signature.
and recalculate the signature. The signer will perform the signing algorithm until it can give \({{\mathbf {z}}_{1}},{{\mathbf {z}}_{2}}\in R_{k-32}^{p^n}\). With the parameters chosen as in Table 1, Lemma 3 will show that the average signer needs to make approximately 7 times to generate a valid signature.
To verify the signature \(( {{\mathbf {z}}_{1}},{{\mathbf {z}}_{2}},\mathbf {c})\), the verifier simply checks that \({{\mathbf {z}}_{1}},{{\mathbf {z}}_{2}} \in R_{k-32}^{p^n}\) and that \(\mathbf {c}=H( \mathbf {a}{{\mathbf {z}}_{1}}+{{\mathbf {z}}_{2}}-\mathbf {tc},\mu )\). If \({{\mathbf {z}}_{1}},{{\mathbf {z}}_{2}}\) are generated from the signing algorithm then we have \({{\mathbf {z}}_{1}},{{\mathbf {z}}_{2}}\in R_{k-32}^{p^n}\) and

The Table 1 [GLP12] shows the parameters n, p, k, the average number of executions to generate a valid signature, signature size and keys size used in the GLP signature scheme.
The parameter k controls the trade-off between the security and the run time of the scheme. The smaller k gets, the more secure the scheme becomes and the shorter the signatures get but the time to sign will increase. The authors of the implementation of [GLP12] suggest \(k=2^{14},n=512\) and \(p=8383489\) for \({\approx }\! 80\) bits of security and \(k=2^{15},n=1024\) and \(p=16760833\) for \({>}\! 256\) bits of security.
The size of the signature is the number of bits used to represent  . Since
. Since  ,
,  can be represented by \(2n\log \left( 2(k-32)+1 \right) \). And \(\mathbf {c}\) can be represented by n bits. Therefore, the signature size can be represented by \(2n\log \left( 2(k-32)+1 \right) +n\) bits.
can be represented by \(2n\log \left( 2(k-32)+1 \right) \). And \(\mathbf {c}\) can be represented by n bits. Therefore, the signature size can be represented by \(2n\log \left( 2(k-32)+1 \right) +n\) bits.
Since  , the size of secret key can be represented by \(2n\log (3)\). The public key consists of two polynomials \(\left( \mathbf {a},\mathbf {t} \right) \), where \(\mathbf {a}\) is shared by all users (therefore, can be viewed as part of the signature scheme) and \(\mathbf {t}\) is the individual component of each user. Therefore, the public key size with each user is just a component \(\mathbf {t} \in R^{p^n}\) and can be represented by \(n\log p\).
, the size of secret key can be represented by \(2n\log (3)\). The public key consists of two polynomials \(\left( \mathbf {a},\mathbf {t} \right) \), where \(\mathbf {a}\) is shared by all users (therefore, can be viewed as part of the signature scheme) and \(\mathbf {t}\) is the individual component of each user. Therefore, the public key size with each user is just a component \(\mathbf {t} \in R^{p^n}\) and can be represented by \(n\log p\).
Lemma 3
Footnote 3 For any \(\mathbf {w} \in R^{p^n}\) such that \({{\left\| \mathbf {w} \right\| }_{\infty }}\le 32\),

Proof
Let some \(\mathbf {w} \in R^{p^n}\) such that \({{\left\| \mathbf {w} \right\| }_{\infty }}\le 32\) and consider \(\mathbf {w}\) as a vector of dimension n with coefficients \({{w}_{j}}\) (for \(1\le j\le n\)) having absolute value at most 32. Then the sum \(\mathbf {w}+\mathbf {y}\) will belong to \(R_{k-32}^{p^n}\) if for every coefficient \({{w}_{i}}\) the corresponding coefficient of \(\mathbf {y}\) (denoted \({{y}_{j}}\)) is in the range
Since every coefficient \(y_j\) is generated randomly in the range \(\left[ -k,k \right] \) and \(\left| {{w}_{j}} \right| \le 32\), the range (1) is contained in the range of possible coefficient \({{y}_{j}}\) of \(\mathbf {y}\). The probability that \({{y}_{j}}\) is in the range (1) is \(\frac{2\left( k\,-\,32 \right) \,+\,1}{2k\,+\,1}=1\,-\,\frac{64}{2k\,+\,1}\). Therefore,

\(\square \)
Since  and \(\left\| \mathbf {c} \right\| _1\le 32\), we have
and \(\left\| \mathbf {c} \right\| _1\le 32\), we have  and
and  . Hence, we have
. Hence, we have

and

Moreover,  and
and  , the probability that
, the probability that  belong to \(R_{k-32}^{p^n}\) is
belong to \(R_{k-32}^{p^n}\) is

We can see that if k is too small then the probability that  is very low. The below table show the relationship between n, k and the average number of executions to generate a valid signature (Table 2).
is very low. The below table show the relationship between n, k and the average number of executions to generate a valid signature (Table 2).
4 Security Proof of the GLP Signature Scheme
In this section, we show that the GLP signature scheme is EU-CMA secure in the random oracle model, assuming the hardness of the \(\text {DC}{{\text {K}}_{p,n}}\) problem and the \(\text {R-SI}{{\text {S}}_{q,n,2,\beta }}\) problem. In [GLP12], it’s a bit confusing when saying that the security of the GLP signature scheme is based only on the hardness of the \(\text {DC}{{\text {K}}_{p,n}}\) problem. Because [GLP12] assumes that there is a polynomial-time reduction from the \(\text {DC}{{\text {K}}_{p,n}}\) problem to the \(\text {R-SI}{{\text {S}}_{q,n,2,\beta }}\) problem as Lemma 2. However, we can easily see that if the parameters n, p, k chosen as in [GLP12] (Table 1) then the condition \(8\beta n\le p\) in Lemma 2 is not satisfied. In other words, there is no polynomial-time reduction from the \(\text {DC}{{\text {K}}_{p,n}}\) problem to the \(\text {R-SI}{{\text {S}}_{q,n,2,\beta }}\) problem with the parameters chosen as in [GLP12] by using Lemma 2.
Firstly, we see that if a adversary can derive the secret key \((\mathbf {s}_1, \mathbf {s}_2)\) from the public key \((\mathbf {a},\mathbf {t})\) then he can be used to solve \(\text {DCK}_{p,n}\) problem. Therefore, the security of the GLP signature scheme must be based on \(\text {DCK}_{p,n}\) problem.
The following theorem shows the security of the GLP signature scheme also need to be based on \(\text {R-SI}{{\text {S}}_{q,n,2,\beta }}\) problem. Assume, for contradiction, that there exists a polynomial-time forger \(\mathcal {F}\) breaking the EU-CMA security of the signature scheme with non-negligible advantage. Then, we can use \(\mathcal {F}\) to solve the \(\text {R-SI}{{\text {S}}_{q,n,2,\beta }}\) problem.
Theorem 1
Footnote 4 If there is a polynomial-time adversary who can produce a valid signature with success probability \(\delta \) after making s queries to the signing oracle and h queries to the random oracle H, then there exists a polynomial-time algorithm to solve \(R-SIS _{p,n,2,\beta }\) problem, where \(\beta =\left( 2(k-32)+64{k}^{\prime } \right) \), \({k}'=3\left\lceil \frac{{{2}^{\frac{100}{n}-1}\sqrt{p}}-1}{3} \right\rceil +1\), with probability at least \({\approx }\! \frac{{{\delta }^{2}}}{2(h\,+\,s)}.\)
Proof
This theorem is proven through Lemmas 5 and 6 using the hybrid arguments. To be more precise, Lemma 5 shows that the actual signing algorithm and the actual key generation algorithm can be replaced by the key generation algorithm Hybrid 3 and the signing algorithm Hybrid 3 (those are obtained from the actual key generation algorithm and the actual signing algorithm. The advantage of the adversary in distinguishing the actual algorithms and the Hybrid 3 algorithms is negligible). Therefore, if the adversary is able to produce a valid signature with probability \(\delta \) for the actual key generation algorithm and actual signing algorithm, then he can also produce a valid signature with probability \(\delta \) for the key generation algorithm Hybrid 3 and signing algorithm Hybrid 3.
In Lemma 6, we show that if an adversary is able to produce a valid signature with probability \(\delta \) for the key generation algorithm Hybrid 3 and signing algorithm Hybrid 3, then we can use that signature to solve the \(\text {R-SIS}_{p,n,2,\beta }\) problem, where \(\beta =\left( 2(k-32)+64{k}^{\prime } \right) \), \({k}'=3\left\lceil \frac{{{2}^{\frac{100}{n}-1}\sqrt{p}}-1}{3} \right\rceil +1\), with success probability at least
\(\square \)
The Hybrid algorithms are described as follows.
Key Generation Algorithm Hybrid 1 and Hybrid 2
Input: Parameters (n, p).
Output: Secret key  and public key \(\left( \mathbf {a},\mathbf {t} \right) \).
and public key \(\left( \mathbf {a},\mathbf {t} \right) \).
-
1.
Choose secret key
 .
. -
2.
Choose
 .
. -
3.
Compute
 .
. -
4.
Return secret key
 and public key \(\left( \mathbf {a},\mathbf {t} \right) \).
and public key \(\left( \mathbf {a},\mathbf {t} \right) \).
Signing Algorithm Hybrid 1
Input: Parameters (n, p, k), message \(\mu \), secret key  and \(\mathbf {a}\).
and \(\mathbf {a}\).
Output: A signature for \(\mu \).
-
1.
Choose
 .
. -
2.
Choose

-
3.
Compute
 .
. -
4.
If
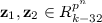 then
then -
5.
Output a signature

-
6.
ProgramFootnote 5

-
7.
Else return to Step 1.
Signing Algorithm Hybrid 2 and Hybrid 3
Input: Parameters (n, p, k), message \(\mu \), secret key  and \(\mathbf {a}\)
and \(\mathbf {a}\)
Output: A signature for \(\mu \).
-
1.
Choose

-
2.
Choose
 .
. -
3.
Choose

-
4.
Set \(M \leftarrow \left( 1-\frac{64}{2k\,+\,1}\right) ^{2n}\)
-
5.
If \(u\le M\) then
-
6.
Output a signature

-
7.
Program

-
8.
Else return to Step 1.
Key Generation Algorithm Hybrid 3
Input: Parameters \((n,p,k^{\prime })\), where \({k}'=3\alpha +1,\alpha =\left\lceil \frac{{{2}^{\frac{100}{n}-1}\sqrt{p}}-1}{3} \right\rceil \).
Output: Secret key  and public key \(\left( \mathbf {a},\mathbf {t} \right) \).
and public key \(\left( \mathbf {a},\mathbf {t} \right) \).
-
1.
Choose secret key
 .
. -
2.
Choose
 .
. -
3.
Compute
 .
. -
4.
Return secret ket
 and public key \(\left( \mathbf {a},\mathbf {t} \right) \).
and public key \(\left( \mathbf {a},\mathbf {t} \right) \).
The following lemma shows that, if  is randomly chosen from \(R_{k^{\prime }}^{p^n}\times R_{k^{\prime }}^{p^n}\) in which \({k}^{\prime }\) is reasonably chosen, then with high probability, there exists \(\left( \mathbf {s}_1^{\prime },\mathbf {s}_2^{\prime } \right) \in R_{k^{\prime }}^{p^n}\times R_{k^{\prime }}^{p^n}\) different from
is randomly chosen from \(R_{k^{\prime }}^{p^n}\times R_{k^{\prime }}^{p^n}\) in which \({k}^{\prime }\) is reasonably chosen, then with high probability, there exists \(\left( \mathbf {s}_1^{\prime },\mathbf {s}_2^{\prime } \right) \in R_{k^{\prime }}^{p^n}\times R_{k^{\prime }}^{p^n}\) different from  satisfying
satisfying  .
.
Lemma 4
Footnote 6 For any  and
and  randomly chosen from \(R_{k^{\prime }}^{p^n}\times R_{k^{\prime }}^{p^n}\), in which \({k}^{\prime }\ge {{2}^{\frac{100}{n}-1}\sqrt{p}}\). Then, with probability at least \(1-{{2}^{-200}}\), there exists \(\left( \mathbf {s}_1^{\prime },\mathbf {s}_2^{\prime } \right) \) different from
randomly chosen from \(R_{k^{\prime }}^{p^n}\times R_{k^{\prime }}^{p^n}\), in which \({k}^{\prime }\ge {{2}^{\frac{100}{n}-1}\sqrt{p}}\). Then, with probability at least \(1-{{2}^{-200}}\), there exists \(\left( \mathbf {s}_1^{\prime },\mathbf {s}_2^{\prime } \right) \) different from  satisfying
satisfying  .
.
Proof
For any \(\mathbf {a} \in R^{p^n}\), consider the map \(f_{\mathbf {a}}\) defined as follows:

We see that the cardinality of \(R^{p^n}\) is \(\left| R^{p^n} \right| ={{p}^{n}}\) and the cardinality of \(R_{k^{\prime }}^{p^n}\times R_{k^{\prime }}^{p^n}\) is \({{\left( 2{k}^{\prime }+1 \right) }^{2n}}\). Therefore, the probability of choosing \(\left( \mathbf {s}_1, \mathbf {s}_2 \right) \in R_{k^{\prime }}^{p^n}\times R_{k^{\prime }}^{p^n}\) such that there are no collisions is at least
In other words, with probability at least \(1-{{2}^{-200}}\), there exists \(\left( \mathbf {s}_1^{\prime },\mathbf {s}_2^{\prime } \right) \) different from  such that
such that  . \(\square \)
. \(\square \)
Lemma 5
Let \(\mathcal {D}\) be a distinguisher who can querry to the random oracle H. Moreover, \(\mathcal {D}\) can query the actual key generation algorithm, the actual signing algorithm, the key generation algorithm Hybrid 3 and the signing algorithm Hybrid 3. If \(\mathcal {D}\), after making h queries to the random oracle H and s queries to the signing algorithm (either actual or Hybrid 3), then the advantage of \(\mathcal {D}\) in distinguishing the actual key generation algorithm and the actual signing algorithm with the key generation algorithm Hybrid 3 and the signing algorithm Hybrid 3 is less than \(s\left( s-1+2h \right) {{2}^{-(n+1)}}\).
Proof
We will use the hybrid arguments to prove the Lemma. Specifically, we will use three Hybrid key generation and signing algorithms (the verification algorithms are the same to the actual one, so we do not mention them here). The key generation algorithm Hybrid 1 and Hybrid 2 are similar to the actual key generation algorithm while the key generation Hybrid 3 is different from the actual one in that  is uniformly chosen from \(R_{k^{\prime }}^{p^n}\times R_{k^{\prime }}^{p^n}\) instead of \(R_{1}^{p^n}\times R_{1}^{p^n}\). The signing algorithm Hybrid 1 is different from the actual one in that \(\mathbf {c}\) is randomly chosen from \(\{ \mathbf {v}\in R_{1}^{p^n}:\sum \limits _{i=0}^{n-1}{\left| {{v}_{i}} \right| =32}\}\) instead of being computed by
is uniformly chosen from \(R_{k^{\prime }}^{p^n}\times R_{k^{\prime }}^{p^n}\) instead of \(R_{1}^{p^n}\times R_{1}^{p^n}\). The signing algorithm Hybrid 1 is different from the actual one in that \(\mathbf {c}\) is randomly chosen from \(\{ \mathbf {v}\in R_{1}^{p^n}:\sum \limits _{i=0}^{n-1}{\left| {{v}_{i}} \right| =32}\}\) instead of being computed by  . The signing algorithm Hybrid 2 is different from the Hybrid 1 in that in the Hybrid 2,
. The signing algorithm Hybrid 2 is different from the Hybrid 1 in that in the Hybrid 2,  are uniformly chosen from \(R_{k-32}^{p^n}\) instead of being computed as
are uniformly chosen from \(R_{k-32}^{p^n}\) instead of being computed as  . The signing algorithm Hybrid 3 is similar to the Hybrid 2 one. We will show that with a suitable choice of parameters, the advantage of the distinguisher \(\mathcal {D}\) in distinguishing the Hybrid algorithms is negligible.
. The signing algorithm Hybrid 3 is similar to the Hybrid 2 one. We will show that with a suitable choice of parameters, the advantage of the distinguisher \(\mathcal {D}\) in distinguishing the Hybrid algorithms is negligible.
First of all, we show that the distinguisher \(\mathcal {D}\) has advantage less than \(s(s-1+2h){{2}^{-(n+1)}}\) in distinguishing the actual signing algorithm with the Hybrid 1 one. The only difference between those two algorithms is that in the Hybrid 1 algorithm, the output of the random oracle H is randomly chosen from \(\{ \mathbf {v}\in R_{1}^{p^n}:\sum \limits _{i=0}^{n-1}{\left| {{v}_{i}} \right| =32} \}\) and then is programmed as the answer of  without checking whether the hash value
without checking whether the hash value  has been queried to H or not. Therefore, in the signing algorithm Hybrid 1, there may be the case that with the same input, two queries to H may produce two different outputs, while with the actual algorithm one gets the same output. And this is the only point that the distinguisher can distinguish between the actual signing algorithm with the Hybrid 1 algorithm. In other words, the advantage of the distinguisher in distinguishing these two algorithms is the probability that the signing algorithm Hybrid 1 produces two outputs with the same query to H.
has been queried to H or not. Therefore, in the signing algorithm Hybrid 1, there may be the case that with the same input, two queries to H may produce two different outputs, while with the actual algorithm one gets the same output. And this is the only point that the distinguisher can distinguish between the actual signing algorithm with the Hybrid 1 algorithm. In other words, the advantage of the distinguisher in distinguishing these two algorithms is the probability that the signing algorithm Hybrid 1 produces two outputs with the same query to H.
Since \(\mathcal {D}\) makes h queries to H and s queries to the signing algorithm, there are at most \(s+h\) values  established. Now, we show that for every call to the signing algorithm Hybrid 1, the probability of generating
established. Now, we show that for every call to the signing algorithm Hybrid 1, the probability of generating  such that
such that  is equal to the previous queried value is less than \({{2}^{-n}}\). Given \(\mathbf {t}\) arbitrarily in \(R^{p^n}\), we have
is equal to the previous queried value is less than \({{2}^{-n}}\). Given \(\mathbf {t}\) arbitrarily in \(R^{p^n}\), we have

By hypothesis \(k\ll p\), then

We see that the previous queried value can be generated in the random oracle H or in signing algorithm Hybrid 1. Hence, the probability of getting a collision after making s queries is at
Now, we need to show that outputs of the signing algorithms Hybrid 1 and Hybrid 2 are indistinguishable. Indeed, the element \(\mathbf {c}\) in both algorithms are computed in a similar way. The main difference is the way  are computed. In the Hybrid 1 algorithm,
are computed. In the Hybrid 1 algorithm,  and
and  are output only if
are output only if  . By Lemma 3, the probability that the Hybrid 1 algorithm produces a valid signature is \({{\left( 1-\frac{64}{2k\,+\,1} \right) }^{2n}}\), whereas the Hybrid 2 chooses
. By Lemma 3, the probability that the Hybrid 1 algorithm produces a valid signature is \({{\left( 1-\frac{64}{2k\,+\,1} \right) }^{2n}}\), whereas the Hybrid 2 chooses  uniformly from \(R_{k-32}^{p^n}\) and the probability of producing a valid signature is
uniformly from \(R_{k-32}^{p^n}\) and the probability of producing a valid signature is

Therefore, \(\mathcal {D}\) cannot distinguish whether  is outputted by the Hybrid 1 algorithm or the Hybrid 2 algorithm.
is outputted by the Hybrid 1 algorithm or the Hybrid 2 algorithm.
Next, we show that \(\mathcal {D}\) cannot distinguish the public keys generated by the key generation algorithm Hybrid 3 and the Hybrid 2 algorithm. Indeed, by the hardness of \(\text {DCK}_{p,n}\), the distinguisher \(\mathcal {D}\) cannot distinguish between the outputs of the Hybrid 2 algorithm and the uniform distribution on \(R^{p^n}\times R^{p^n}\). By Lemma 1, there is a reduction from solving \(\text {DCK}_{p,n}\) to solving the \(\text {R-SIS}_{p,n,2,(3\alpha +1)}\) decision problem. Hence \(\mathcal {D}\) cannot distinguish between the outputs the Hybrid 3 algorithm with the uniform distribution on \(R^{p^n}\times R^{p^n}\) (if it does then it is possible to solve the \(\text {R-SIS}_{p,n,2,(3\alpha +1)}\) decision problem, from which one can solve the \(\text {DCK}_{p,n}\) problem). Therefore, \(\mathcal {D}\) cannot distinguish between the outputs by the Hybrid 3 algorithm and the Hybrid 2 algorithm.
As a conclusion, we see that the actual key generation algorithm and the actual signing algorithm can be replaced by the corresponding Hybrid 3 algorithms. The advantage of the distinguisher in distinguishing between the actual algorithms and the Hybrid 3 algorithms is less than \(s(s-1+2h)2^{-(n+1)}.\) \(\square \)
Lemma 6
Assume that there exists a polynomial-time forger \(\mathcal {F}\) who can produce a valid signature with success probability \(\delta \) after making at most s queries to the signing algorithm Hybrid 3 and at most h queries to the random oracle H. Then there exists a polynomial-time algorithm to efficiently solve the \(R-SIS _{p,n,2,\beta }\) problem, in which \(\beta =\left( 2(k-32)+64{k}^{\prime } \right) \), \({k}'=3\left\lceil \frac{{{2}^{\frac{100}{n}-1}\sqrt{p}}-1}{3} \right\rceil +1\) with success probability at least
Proof
Denote by \({{D}_{H}}:=\{ \mathbf {v}\in R_{1}^{p^n}:\sum \limits _{i=0}^{n-1}{\left| {{v}_{i}} \right| =32}\}\) the range of the random oracle H. Given \(\mathbf {a}\in R^{p^n}\), choose  to be the secret key and compute
to be the secret key and compute  . The public key is \(\left( \mathbf {a},\mathbf {t} \right) \). Set \(t=h+s\) to be the upper bound of the total number of times that H is queried or programmed by \(\mathcal {F}\). One query to H can be made by the forger or H can be programmed by the signing algorithm Hybrid 3 when the forger requests a signature of some message. Next we choose a random coins \(\phi \) for the forger, a random coins \(\psi \) for the signer (using Hybrid 3) and choose
. The public key is \(\left( \mathbf {a},\mathbf {t} \right) \). Set \(t=h+s\) to be the upper bound of the total number of times that H is queried or programmed by \(\mathcal {F}\). One query to H can be made by the forger or H can be programmed by the signing algorithm Hybrid 3 when the forger requests a signature of some message. Next we choose a random coins \(\phi \) for the forger, a random coins \(\psi \) for the signer (using Hybrid 3) and choose  to be the answers of the random oracle.
to be the answers of the random oracle.
Now, we consider a sub-algorithm \(\mathcal {A}\) with input \(\left( \mathbf {a},\mathbf {t},\phi ,\psi ,{{\mathbf {r}}_{1}},\ldots ,{{\mathbf {r}}_{t}} \right) \). The algorithm \(\mathcal {A}\) will run \(\mathcal {F}\) by supplying to \(\mathcal {F}\) the public key \(\left( \mathbf {a},\mathbf {t} \right) \) and the random coins \(\phi \) as input. Whenever \(\mathcal {F}\) requests a signature of a message, \(\mathcal {A}\) runs the signing algorithm Hybrid 3 and uses the random coins \(\psi \) to generate a signature. During the signing process, the random oracle H is programmed and answers the first value in \(\left( {{\mathbf {r}}_{1}},\ldots ,{{\mathbf {r}}_{t}} \right) \) which has not been used before. Here \(\mathcal {A}\) will save a table consisting of all queries to H, and when a same query is requested again, the random oracle will output the same answer. The forger can also make queries to the random oracle. In this case, the answer is done in the same way. Whenever \(\mathcal {F}\) stops and produces a forgery (with probability \(\delta \)), the algorithm \(\mathcal {A}\) will take the output of \(\mathcal {F}\) as its output.
With probability \(\delta \), the forger \(\mathcal {F}\) will produce a message \(\mu \) and a signature ( ) satisfying
) satisfying  and
and  . Note that if the random oracle was not queried or programmed with input
. Note that if the random oracle was not queried or programmed with input  then the probability that \(\mathcal {F}\) produces \(\mathbf {c}\) with \(\mathbf {c}=H\left( \mathbf {w},\mu \right) \) is \({1}/{\left| {{D}_{H}} \right| }\). Hence, with probability \(1-{1}/{\left| {{D}_{H}} \right| }\), \(\mathbf {c}\) has to be one of the values \({{\mathbf {r}}_{i}}\) with \(1\le i\le t\). Thus the probability that \(\mathcal {F}\) succeeds in a forgery and \(\mathbf {c}\) is one of the values \({{\mathbf {r}}_{i}}\) (with \(1\le i\le t\)) is at least \(\delta -{1}/{\left| {{D}_{H}} \right| }\;\). Indeed, let A be the event that \(\mathcal {F}\) succeeds in a forgery and B be the event that \(\mathbf {c}\) is one of the values \({{\mathbf {r}}_{i}}\). Then we have
then the probability that \(\mathcal {F}\) produces \(\mathbf {c}\) with \(\mathbf {c}=H\left( \mathbf {w},\mu \right) \) is \({1}/{\left| {{D}_{H}} \right| }\). Hence, with probability \(1-{1}/{\left| {{D}_{H}} \right| }\), \(\mathbf {c}\) has to be one of the values \({{\mathbf {r}}_{i}}\) with \(1\le i\le t\). Thus the probability that \(\mathcal {F}\) succeeds in a forgery and \(\mathbf {c}\) is one of the values \({{\mathbf {r}}_{i}}\) (with \(1\le i\le t\)) is at least \(\delta -{1}/{\left| {{D}_{H}} \right| }\;\). Indeed, let A be the event that \(\mathcal {F}\) succeeds in a forgery and B be the event that \(\mathbf {c}\) is one of the values \({{\mathbf {r}}_{i}}\). Then we have
Assume that j is the index such that \(\mathbf {c}={{\mathbf {r}}_{j}}\), with \(1\le j\le t\). Then there are two possibilities as follows:
-
Either \({{\mathbf {r}}_{j}}\) is an answer of a query of \(\mathcal {F}\) to the random oracle,
-
or \({{\mathbf {r}}_{j}}\) is programmed in the signing process.
In the second case, assume that, when signs a message \({\mu }^{\prime }\), the signer programs the random oracle as \(H\left( \left( \mathbf {a}\mathbf {z}_1^{\prime }+\mathbf {z}_2^{\prime }-\mathbf {tc} \right) ,{\mu }^{\prime } \right) =\mathbf {c}\). If the forger produces a valid signature  for \(\mu \) then \(\mu \ne {\mu }^{\prime }\) or
for \(\mu \) then \(\mu \ne {\mu }^{\prime }\) or  (or both are different). Because if \(\mu ={\mu }^{\prime }\) and
(or both are different). Because if \(\mu ={\mu }^{\prime }\) and  , the adversary just outputs a message with a signature that he already saw. If \(\mu \ne {\mu }'\) then we have a collision for H, since
, the adversary just outputs a message with a signature that he already saw. If \(\mu \ne {\mu }'\) then we have a collision for H, since

If \(\mu =\mu ^{\prime } \) then  and
and

Thus if  then we find a collision for H. On the other hand, if
then we find a collision for H. On the other hand, if  then
then

Since  , one has
, one has  . Therefore we can solve the \(\text {R-SIS}_{p,n,2,\beta }\) problem where \(\beta =2(k-32)\) with success probability at least \(\delta -1/{\left| {{D}_{H}} \right| }\).
. Therefore we can solve the \(\text {R-SIS}_{p,n,2,\beta }\) problem where \(\beta =2(k-32)\) with success probability at least \(\delta -1/{\left| {{D}_{H}} \right| }\).
Now we come back to the first case, i.e., \({{\mathbf {r}}_{j}}\) is an answer when \(\mathcal {F}\) makes a query to the random oracle. In this case, first we save the signature  of the forger \(\mathcal {F}\) for \(\mu \). Then, we generate new random elements
of the forger \(\mathcal {F}\) for \(\mu \). Then, we generate new random elements  . Next we run again the algorithm \(\mathcal {A}\) with input \(\left( \mathbf {a},\mathbf {t},\phi ,\psi ,{{\mathbf {r}}_{1}},\ldots ,{{\mathbf {r}}_{j-1}},{{{\mathbf {{r}'}}}_{j}},\ldots ,{{{\mathbf {{r}'}}}_{t}} \right) \). By the General Forking Lemma [BN06], Lemma 1], the probability that \({{\mathbf {{r}'}}_{j}}\ne {{\mathbf {r}}_{j}}\) and the forger uses \({{\mathbf {{r}'}}_{j}}\) as an answer for a query to the random oracle is at least
. Next we run again the algorithm \(\mathcal {A}\) with input \(\left( \mathbf {a},\mathbf {t},\phi ,\psi ,{{\mathbf {r}}_{1}},\ldots ,{{\mathbf {r}}_{j-1}},{{{\mathbf {{r}'}}}_{j}},\ldots ,{{{\mathbf {{r}'}}}_{t}} \right) \). By the General Forking Lemma [BN06], Lemma 1], the probability that \({{\mathbf {{r}'}}_{j}}\ne {{\mathbf {r}}_{j}}\) and the forger uses \({{\mathbf {{r}'}}_{j}}\) as an answer for a query to the random oracle is at least
and so with the above probability, \(\mathcal {F}\) produces a signature  for \(\mu \) and
for \(\mu \) and

where \(\mathbf {c}={{\mathbf {r}}_{j}}\) and \(\mathbf {{c}'}={{\mathbf {{r}'}}_{j}}\). Plug  into (2), we obtain
into (2), we obtain

Since  and
and  , one gets
, one gets

Set  and
and  . If \({{\mathbf {u}}_{1}},{{\mathbf {u}}_{2}}\ne 0\) then we can solve the \(\text {R-SIS}_{p,n,2,\beta }\) problem with \(\beta =\left( 2(k-32)+64{k}^{\prime } \right) \). Therefore, it suffices to show that \({{\mathbf {u}}_{1}},{{\mathbf {u}}_{2}}\ne 0\) with probability at least \(\frac{1}{2}-{{2}^{-200}}\). By Lemma 4, with probability at least \(1-{{2}^{-200}}\), there exists
. If \({{\mathbf {u}}_{1}},{{\mathbf {u}}_{2}}\ne 0\) then we can solve the \(\text {R-SIS}_{p,n,2,\beta }\) problem with \(\beta =\left( 2(k-32)+64{k}^{\prime } \right) \). Therefore, it suffices to show that \({{\mathbf {u}}_{1}},{{\mathbf {u}}_{2}}\ne 0\) with probability at least \(\frac{1}{2}-{{2}^{-200}}\). By Lemma 4, with probability at least \(1-{{2}^{-200}}\), there exists  such that
such that  . If
. If  then
then  . Indeed, assume that
. Indeed, assume that

Then  . Hence
. Hence

Because \({{\left\| \mathbf {c} \right\| }_{1 }},{{\left\| {\mathbf {{c}^{\prime }}} \right\| }_{1 }}\le 32\) and  , we have
, we have  . By the choice of parameters, \(256{k}^{\prime }<p\). Thus if
. By the choice of parameters, \(256{k}^{\prime }<p\). Thus if  over \(R^{p^n}={{{\mathbb {Z}}_{p}}\left[ x \right] }/{\left\langle {{x}^{n}}\,+\,1 \right\rangle }\;\) then
over \(R^{p^n}={{{\mathbb {Z}}_{p}}\left[ x \right] }/{\left\langle {{x}^{n}}\,+\,1 \right\rangle }\;\) then  over \({\mathbb {Z}\left[ x \right] }/{\left\langle {{x}^{n}}\,+\,1 \right\rangle }\). Since n is a power of 2, \({{x}^{n}}\,+\,1\) is irreducible in \(\mathbb {Z}\left[ x \right] \). Hence \({\mathbb {Z}\left[ x \right] }/{\left\langle {{x}^{n}}\,+\,1 \right\rangle }\) is an integral domain. Then,
over \({\mathbb {Z}\left[ x \right] }/{\left\langle {{x}^{n}}\,+\,1 \right\rangle }\). Since n is a power of 2, \({{x}^{n}}\,+\,1\) is irreducible in \(\mathbb {Z}\left[ x \right] \). Hence \({\mathbb {Z}\left[ x \right] }/{\left\langle {{x}^{n}}\,+\,1 \right\rangle }\) is an integral domain. Then,  which implies \(\mathbf {c}\,-\,\mathbf {{c}^{\prime }}=0\) or
which implies \(\mathbf {c}\,-\,\mathbf {{c}^{\prime }}=0\) or  . So \(\mathbf {c}\ne \mathbf {{c}^{\prime }}\) and hence
. So \(\mathbf {c}\ne \mathbf {{c}^{\prime }}\) and hence  (which contradicts to
(which contradicts to  above). Similarly, if
above). Similarly, if  then
then  . On the other hand, at the beginning, we do not know whether
. On the other hand, at the beginning, we do not know whether  and
and  or
or  and
and  . Therefore, the probability that
. Therefore, the probability that  and
and  is exactly the probability that the secret key is \(\left( \mathbf {s}_1^{\prime },\mathbf {s}_2^{\prime } \right) \). Denote by E the event that there exists a related key \(\left( \mathbf {s}_1^{\prime },\mathbf {s}_2^{\prime } \right) \) and by F the event that the secret key is \(\left( \mathbf {s}_1^{\prime },\mathbf {s}_2^{\prime } \right) \). Then the probability that
is exactly the probability that the secret key is \(\left( \mathbf {s}_1^{\prime },\mathbf {s}_2^{\prime } \right) \). Denote by E the event that there exists a related key \(\left( \mathbf {s}_1^{\prime },\mathbf {s}_2^{\prime } \right) \) and by F the event that the secret key is \(\left( \mathbf {s}_1^{\prime },\mathbf {s}_2^{\prime } \right) \). Then the probability that  and
and  is
is
Therefore, the probability that  and
and  is at least \(\frac{1}{2}\,-\,{{2}^{-200}}\). Moreover, since \(\mathcal {A}\) does not use the secret keys as input and does not use those secret keys for signing, the forger cannot know which secret key used in signing is
is at least \(\frac{1}{2}\,-\,{{2}^{-200}}\). Moreover, since \(\mathcal {A}\) does not use the secret keys as input and does not use those secret keys for signing, the forger cannot know which secret key used in signing is  or \(\left( \mathbf {s}_1^{\prime },\mathbf {s}_2^{\prime } \right) \).
or \(\left( \mathbf {s}_1^{\prime },\mathbf {s}_2^{\prime } \right) \).
Hence in case \({{\mathbf {r}}_{j}}\) is an answer for a query of \(\mathcal {F}\) to the random oracle, we can solve the \(\text {R-SIS}_{p,n,2,\beta }\) problem where \(\beta =\left( 2(k-32)+64{k}^{\prime } \right) \) with probability at least
Since \(\beta =2(k-32)\) in the first case is less than \(\beta =\left( 2(k-32)+64{k}^{\prime } \right) \) in the later case and the success probability of solving the \(\text {R-SIS}_{p,n,2,\beta }\) problem in the first case is greater than the success probability of solving the \(\text {R-SIS}_{p,n,2,\beta }\) problem in the second case, the success probability will be the small one. Therefore, if there exists a polynomial-time forger \(\mathcal {F}\) with success probability \(\delta \) after making s queries to the signing algorithm Hybrid 3 and h queries to the random oracle H, then there exists a polynomial-time algorithm to solve the \(\text {R-SIS}_{p,n,2,\beta }\) problem, where \(\beta =\left( 2(k-32)+64{k}^{\prime } \right) \), with success probability at least
Since \(\left| {{D}_{H}} \right| ={{2}^{32}}\left( \begin{matrix} n \\ 32 \\ \end{matrix} \right) \). For \(n=512\), we have \(\left| {{D}_{H}} \right| \approx {{2}^{200}}\) and for \(n=1024\), we have \(\left| {{D}_{H}} \right| \approx {{2}^{233}}\). \(\square \)
5 Conclusion
In this paper, we present a full security proof for the GLP signature scheme. Concretely, we show that the GLP signature scheme is EU-CMA secure in the random oracle model, assuming the hardness of the \(\text {DCK}_{p,n}\) problem and the \(\text {R-SIS}_{q,n,2,\beta }\) problem. Based on the statements and arguments in [Lyu12, Lyu08], we gave the Lemmas 2, 4, Lemmas 5, 6 and Theorem 1. The optimal version of the GLP digital signature scheme can be proved in the same way as this paper.
Notes
- 1.
A later scheme version is given in [GLP15]. But, it still does not contain a full security proof.
- 2.
This lemma is stated based on Lemma 3.7 in [Lyu12]. Namely, we give a reduction for the hard problems on the ideal lattices instead of the lattice in \(\mathbb {R}^n\) as in Lemma 3.7.
- 3.
This lemma is stated based on Lemma 6.1 in [Lyu08].
- 4.
This theorem is stated based on Theorem 5.1 in [Lyu12]. Namely, we provide an additional algorithms Hybrid 3 to prove the security of the GLP signature scheme.
- 5.
When it is queried, the oracle H is programmed to return a random \(\mathbf {c}\in \{ \mathbf {v}\in R_{1}^{p^n}:\sum \limits _{i=1}^{n}{\left| {{v}_{i}} \right| =32} \}\) without checking whether that value has been used before.
- 6.
This lemma is stated based on Lemma 5.2 in [Lyu12].
References
Bai, S., Galbraith, S.D.: An improved compression technique for signatures based on learning with errors. In: Benaloh, J. (ed.) CT-RSA 2014. LNCS, vol. 8366, pp. 28–47. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-04852-9_2
Bellare, M., Neven, G.: New multi-signatures and a general forking lemma. Full version of this paper (2006). http://www.cs.ucsd.edu/users/mihir
Ducas, L., Durmus, A., Lepoint, T., Lyubashevsky, V.: Lattice signatures and bimodal gaussians. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 40–56. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_3
Ducas, L., Lepoint, T., Lyubashevsky, V., Schwabe, P., Seiler, G., Stehlé, D.: Crystals-dilithium: digital signatures from module lattices. Technical report, Cryptology ePrint Archive, Report 2017/633 (2017)
Güneysu, T., Lyubashevsky, V., Pöppelmann, T.: Practical lattice-based cryptography: a signature scheme for embedded systems. In: Prouff, E., Schaumont, P. (eds.) CHES 2012. LNCS, vol. 7428, pp. 530–547. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-33027-8_31
Güneysu, T., Lyubashevsky, V., Pöppelmann, T.: Lattice-based signatures: optimization and implementation on reconfigurable hardware. IEEE Trans. Comput. 64(7), 1954–1967 (2015)
Lyubashevsky, V., Micciancio, D.: Generalized compact Knapsacks are collision resistant. In: Bugliesi, M., Preneel, B., Sassone, V., Wegener, I. (eds.) ICALP 2006. LNCS, vol. 4052, pp. 144–155. Springer, Heidelberg (2006). https://doi.org/10.1007/11787006_13
Lyubashevsky, V.: Towards Practical Lattice-Based Cryptography. University of California, San Diego (2008)
Lyubashevsky, V.: Lattice signatures without trapdoors. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 738–755. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-29011-4_43
Shor, P.W.: Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Rev. 41(2), 303–332 (1999)
Acknowledgements
The authors are grateful to Duong Hoang Dung and Trieu Quang Phong for helpful comments and discussions on drafts of this paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 ICST Institute for Computer Sciences, Social Informatics and Telecommunications Engineering
About this paper
Cite this paper
Khuc, T.X., Bui, M.K., Chu, H. (2019). A Security Proof of the GLP Signature Scheme. In: Duong, T., Vo, NS., Nguyen, L., Vien, QT., Nguyen, VD. (eds) Industrial Networks and Intelligent Systems. INISCOM 2019. Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering, vol 293. Springer, Cham. https://doi.org/10.1007/978-3-030-30149-1_21
Download citation
DOI: https://doi.org/10.1007/978-3-030-30149-1_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-30148-4
Online ISBN: 978-3-030-30149-1
eBook Packages: Computer ScienceComputer Science (R0)





 .
. .
. .
. and public key
and public key  .
. .
. .
. .
. .
. .
. and public key
and public key  .
.
 .
.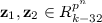 then
then


 .
.


 .
. .
. .
. and public key
and public key