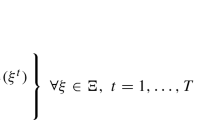Exploiting Counterfactuals for Scalable Stochastic Optimization

Abstract

We propose a new framework for decision making under uncertainty to overcome the main drawbacks of current technology: modeling complexity, scenario generation, and scaling limitations. We consider three NP-hard optimization problems: the Stochastic Knapsack Problem (SKP), the Stochastic Shortest Path Problem (SSPP), and the Resource Constrained Project Scheduling Problem (RCPSP) with uncertain job durations, all with recourse. We illustrate how an integration of constraint optimization and machine learning technology can overcome the main practical shortcomings of the current state of the art.

1 Introduction

Optimization relies on data. To solve a knapsack problem we need to know the profits and weights of the items, as well as the knapsack’s capacity. To solve a shortest path or travelling salesperson problem, we need to know the lengths of the links in the network. To solve a revenue optimization problem, we need to know demand and how prices affect demand. In practice, we often lack perfect knowledge of the situation we ultimately needed to plan for. Profits, transition times, price sensitivity, and demands frequently have to be estimated.

One simple and still widely used approach is to optimize for point estimates of the data: We estimate demand, profits, transition times, etc, and optimize for the resulting optimization problem. The problem with using only one set of estimates, even if they represented the maximum likelihood scenario, is that the probability of exactly this scenario taking place is close to zero, and performance of the solution that is optimal for this one scenario may decline steeply across a range of scenarios that, together, would have a reasonable probability mass. In other words, a solution that is sub-optimal for all scenarios but works with good performance for a large number of potential futures will lead to much better expected performance than the solution that is provably optimal for the maximum likelihood scenario yet abysmal otherwise.

1.1 Stochastic Optimization

The brittleness of solutions obtained by optimizing for one, point-estimated scenario only is well-studied in the field of stochastic optimization (SO). The objective of SO is to provide a solution that optimizes the expected returns over all possible futures.

This led to the idea of two-stage stochastic optimization: In the first stage, we need to take certain decisions based on uncertain data. After taking these decisions, the uncertainties are revealed and we can take the remaining decisions based on certain data. This allows us first to make up for certain inconsistencies our initial decisions might have created (note that the constraints are also based on estimates) and thus exercise certain recourse actions to regain feasibility, and second to optimize the second-stage decisions that can wait to be taken until we know the real data. An overview of two-stage stochastic integer programming problems can be found in [4], and [21] present a method to solve two-stage problems using the special form of these problems.

One crucial step in stochastic optimization is the generation of a representative set of potential futures (scenarios). Many methods exist to generate scenarios, and [13] points out that quality scenario generation is critical to the success using SO. [12] recommend that a number of different data sources should be used for scenario generation.

Obviously, solving SO problems to optimality gets harder the more scenarios are considered. Sample average approximation [14] has been developed to generate a small random sample of scenarios and approximate the expected value function. This technique has been be applied to a variety of problems (see, e.g., [16, 20, 22]) and can help the method scale a bit better. However, the fundamental problem remains that SO relies on a representative set of scenarios to be considered, and that it must make optimal first and second stage decisions for every scenario under consideration.

1.2 Multi-stage Stochastic Optimization

One practical aspect that we also need to take into account is that the execution of a planned solution is frequently disrupted by outside events: equipment or crew assumed to be available may suddenly go out of service, requiring adjustment of a plan during operations. Consequently, the plan may need to be adjusted multiple times.

This leads to the idea of multi-stage stochastic optimization. In multi-stage SO, uncertainty is revealed in multiple consecutive steps, and more decisions need to be taken at each stage. In these problems, random variables in later stages depend on the decisions taken in the earlier stages. Models and solutions to these problems are therefore structured in the form of a tree [7], with independent decisions at the root node, and dependencies between decisions modeled with parent-child relationships in the tree.

Due to their richer modeling power, these types of SO models are especially relevant for real-world decision making, but unfortunately explode in complexity very quickly, even when employing advanced decomposition techniques like presented by [3] who extend the work of [21]. Furthermore, the problem of scenario generation is even more daunting in this more realistic setting, as conditional scenarios need to be generated, and often the data needed for this purpose may not be available. An overview of scenario generation methods for multi-stage stochastic programs is provided in [7].

1.3 Simulation-Based Optimization

Modeling dynamic recourse and managing a meaningful number of scenarios in stochastic optimization is often cumbersome. An alternative is to employ a simulator that can evaluate a given plan on a number of scenarios, whereby the algorithm to generate recourse actions is built into the simulation. The recourse policy employed by a real-world organization may involve solving nested optimization problems on the go, as SO assumes, but oftentimes the real-world operational constraints may not allow for a full-fledged optimization, for example because the data needed is not readily available, or because re-optimization would be too time-consuming. A simulator can easily reflect the real recourse actions that would be taken, which are usually locally optimal only, or maybe just best-effort heuristics.

Simulation-based optimization is thus an alternative to stochastic optimization [1, 9]. In this setting, a simulation is constructed to provide a stochastic evaluation of a provided solution. The search for good solutions can then be conducted by employing a meta-heuristic procedure. For example, [10] employs tabu search for this purpose.

An alternative to using a general local search heuristic is to apply bandit theory and to conduct a search based on Bayesian optimization [19]. In this method, the search space is traversed in a statistically principled way which balances exploitation and exploration by considering new solutions for simulation next which combine high expected performance with high uncertainty of this performance.

No matter which search method is employed, to compute an objective function value for an instance, we need to expose it to certain futures. In SO these were called scenarios, in simulation-based optimization the “scenario generation” is hidden in the simulator. However, both methods rely on an adequate representation of potential futures of the world as it currently presents itself.

2 Technology Gaps

In practice, many organizations do not take the uncertainty in their forecasts into account when devising their operational plans. In fact, this observation even holds for those organizations that would stand to benefit the most, because events disrupting their plans frequently ruin all operational success. Airlines are one prototypical example. Over decades, the airline industry has spent billions of dollars on optimization technology to improve their operational planning (e.g., in crew planning [17]). There is certainly no lack of affinity to optimization technology, nor a lack of understanding that their current optimized plans are very brittle. The question is, why then is decision-making under uncertainty not employed?

We believe there are three main factors that prevent current decision making under uncertainty technology from being applied in practice:

• Complexity of modeling the base problem

• Inability to generate meaningful future scenarios for the current situation

• Computational limitations preventing the scale-up to real-world numbers of primary and recourse decisions

Take the example of an airline again. Flights may be delayed due to weather or traffic. Gates may be occupied and have to be changed. Crew may be out of service because of sickness or because they are delayed and past their maximum allowed service time. Equipment may not be available because of technical issues or because other issues in the network prevented the plane from being at the airport where it was planned to be.

Modeling the operation of an airline is extremely complex to begin with, which is why airlines break down the original problem into network design, revenue management, fleet assignment, crew pairing, tail assignment, and crew scheduling problems. There are literally millions of decision variables to consider. Secondly, there are frequently no models available for assessing the probabilities of disruptions with any meaningful accuracy. This is especially true for the joint distributions of disruptions which are frequently correlated. And finally, the number of recourse decisions taken during operation is staggering: Airlines literally run their recovery solvers every minute to adjust their plans to ever new, thankfully usually minor, disruptions.

Stochastic optimization is not applicable, because computation times are prohibitively long, and the number of recourse decisions far exceeds efficient modeling capabilities. However, simulation-based optimization cannot handle the millions of decision variables or the complex constraints that govern whether solutions are even feasible.

This analysis is the starting point for our research. In the following, we propose a framework for decision making under uncertainty that overcomes the limitations of existing technology. In a nutshell, we propose a paradigm shift away from trying to anticipate the future and towards discovering structures in the solutions that correlate with historically good performance. In doing so, we trade dual bounds (i.e., a guarantee of the relative quality of the solution provided by SO) for scalability and easier modeling.

3 Learning from Counterfactuals

A key limitation of stochastic optimization is the need to model every decision. Not only does this put an enormous burden on the modeler and the optimization, it often also falsely assumes that we were able to optimize recourse decisions during operation. Another problem that both simulation-based optimization and stochastic optimization share is that they need to generate meaningful scenarios how the execution of a solution may unfold in the future. Finally, both methods scale to a hundreds, maybe a few thousand decision variables, before computation times become impractically long.

Our proposal is to combine both what disruptions are likely, as well as how well the initial solution is adjusted during execution, into one data-driven forecast.

Consider a model that, given two solutions to an optimization problem can provide a classification as to which of the two solutions will fare better when they are executed. Consider solving this problem in two stages. In the first stage, we solve the problem as if there were no uncertainty using the expected costs in the objective function, and generate multiple near-optimal solutions. The goal of the second stage is to determine which of the near-optimal solutions will likely lead to better results when executed. We train a model that compares these solutions on a pairwise basis and choose the solution that wins the most times against the other solutions. This general method alleviates many of the problems existing approaches encounter:

• The first-stage problem is as easy to model as the optimization problem without uncertainties.

• There is no need to generate future scenarios for the current data at hand.

• There is no complexity blow-up, no matter how many recourse actions are needed.

All of the complexity is off-loaded into the second stage model. The crucial question is, of course: How can we obtain a model that, given two solutions, can predict which one will fare better in operations?

Thesis: We can learn such a model from historical data.

We argue that all that is needed to learn such a model is to keep track of our estimates over time, and what eventually happened. Consider, e.g., the Stochastic Shortest Path Problem (SSPP), a problem that [5] argue is particularly difficult when there are no assumptions about the uncertain travel times. We can track how the arc transit time estimates for the entire network have evolved over time, and what they ended up being. Or, for the Stochastic Knapsack Problem (SKP), we can examine what our weight and profit estimates were before each decision for historical solutions and what they turned out to be in reality. That is to say: Historical data often enables us to compare multiple historical solutions, even though only one of them was actually executed in reality, whereas all others are essentially counterfactuals.

Please note a subtle but very important difference; the historical data is enough to compare two potential solutions for the optimization problem as it presented itself in the past. It would, however, not enable us to simulate two solutions for a new instance of our underlying optimization problem. Take the SSPP as an example. We may have a historic example where we needed to go from some node s to node t. We know how our estimated arc transition times evolved over time and the resulting values on all arcs in the network. With this, we can compare two paths $P_1$ and $P_2$ that connect s and t.

Now imagine we currently need a solution to go from node s to node t again. Our initial estimates are of course completely different from those in the historic example. Consequently, we cannot just simulate two paths $Q_1$ and $Q_2$ in the old scenario and assume that their relative performance would remain the same under the current conditions. In fact, if this were the case, we should forget our estimates altogether and just always go from s to t using the exact same route all the time.

However, if we could capture estimate-dependent characteristics, or features, of pairs of paths $P_1$ and $P_2$, and associate these characteristics with the relative performance of these paths, then, by repeating this exercise many times, we just might be able to learn to tell which of any given pairs of paths will probably execute better – albeit with no guarantees.

Through this framework, we have now decomposed the problem of making primary decisions based on uncertain forecasts and assumptions regarding estimate distributions and recourse policies into two tasks: We first need to model the primary optimization problem. Second, we need to use historical data to build a supervised set of examples of pairs of solutions, recording which one fared, or would have fared, better. Crucially, we need to devise a set of features to characterize the solutions in the context of the problem instance they were generated for.

We formalize our framework as follows. We are given a deterministic optimization problem P with decision variables $\mathbf {x}$. Let $f(\mathbf {x})$ be the objective function of the deterministic problem, and $f'(\mathbf {x}, \omega )$ be the objective function when the decisions are evaluated under scenario $\omega$.

1. Training set generation: We first generate n solutions $\mathbf {x}_{i1},\dots ,\mathbf {x}_{in}$ to the problem instance i in a set of training instances I, where all uncertain parameters take their expected value. The choice of such solutions is up to the user of this framework, but we recommend high quality solutions with some diversity. We associate a label $y_{ij} = \sum _{\omega \in \varOmega _i} f'(\mathbf {x}_{ij},\omega )/|\varOmega _i|$ with each solution of each instance for a set of counterfactual scenarios $\varOmega _i$ that are derived from the true scenario that unfolded for the historic problem instance i. Finally, we compute problem dependent feature vectors $\mathbf {u}_{ij}\in \mathbb {R}^f$ describing each solution j of instance i.

2. Learning a classifier: Next, we train a binary classifier M that, given two solutions j, k to a problem instance i, forecasts which of the two solutions will likely perform better when executed. The training input for this cost-sensitive learning task are triples ($u'_{ijk}$, $y_{ij}$, $y_{ik}$), where $u'_{ijk}\in \mathbb {R}^{3f}$ consists of a concatenation of feature vectors $u_{ij}$, $u_{ik}$, and $u_{ij} - u_{ik}$. We use the technique from [18] for this purpose.

3. Deployment: Given a problem instance i, we generate n solutions using the deterministic optimization model with expected values for uncertain parameters. We then compute the features $u'_{ijk}$ for each pair of solutions j, k. Then, we query the model M for all such pairs and choose the solution that “wins” the most times.

In the following, we will exercise the above steps for three optimization problems: the SKP, the SSPP, and the Resource Constrained Project Scheduling Problem (RCPSP), each with recourse. The objective of this study is to investigate whether we can effectively learn which solution for a problem instance will perform better.

4 Stochastic Knapsack

The SKP is the stochastic variant of the well-known optimization problem: Given $n\in \mathbb {N}$ items $\{1,\dots ,n\}$ with profits $p_1,\dots ,p_n\in \mathbb {N}$, expected weights $w_1,\dots ,w_n\in \mathbb {N}$, and a capacity $C\in \mathbb {N}$, the objective is to find a subset of items $I\subseteq \{1,\dots ,n\}$ such that $\sum _{i\in I'} w'_i \le C$ and $P=\sum _{i\in I'} p_i$ is maximized, where $w'_1,\dots ,w'_n$ are the actual weights incurred, and $I'$ is the set of items we ultimately include in our knapsack.

4.1 Stochastic Environment

To complete the setup of our problem, we need to determine how the weights $w'_i$ are derived from the expected weights $w_i$, and how $I'$ derives from I during operations. This is precisely the task of determining the distributions of stochastic data, and the incorporation of recourse policies that we aim to avoid estimating and modeling when solving the stochastic variant of the underlying optimization problem. However, for the sake of experimentation, we obviously need to fix the stochastic environment.

We will assume that items have to be decided for inclusion or exclusion in sequence 1 to n.¹ That is, we first decide if we want to insert item 1 in the knapsack. If not, we can directly move on to the next item. If yes, then we add the actual weight $w'_1$ to our knapsack, the remaining capacity is reduced accordingly, and the profit $p_1$ is achieved. We consider all items in sequence. At stage i, we sample $w'_i$ from a Pareto distribution with mean $w_i$ (note: the nature of this distribution is not known to the optimization approach). In our variant of the problem, should the new item overload the knapsack, the item is automatically not inserted and we proceed as if we had never decided to include the item. However, if the item fits into the remaining capacity, we have to take it, even if the actual weight of the item is much larger than we had anticipated.

In terms of recourse, whenever during the sequential consideration of items our remaining capacity deviates from the anticipated capacity at that point in the sequence by more than a given percentage threshold p, we are allowed to reconsider our original plan and change the tail of our plan. However, if we include an item that was originally not planned to be included, we incur a profit penalty b (late buy penalty). Similarly, we incur a penalty s for items we do not include in our knapsack that we had originally committed to include (restocking fee). Finally, we cannot change the original plan for the next r items (minimum reaction time).

The recourse policy is to re-optimize the rest of the knapsack based on the profits adjusted for penalties, the originally estimated weights, and the remaining items and capacity. The selection of the next r items is fixed.

To support our introductory claim that existing technology is not feasible even for such a simple practical setting, we invite the reader to try to model this problem as an n-stage stochastic optimization problem or as a simulation-based optimization problem with n variables and an uncertain side constraint.

4.2 Winner Forecasting

In stage 1 of our approach, we consider the original knapsack problem with the given capacity, profits, and estimated weights. We solve the problem to optimality using dynamic programming and generate a desired number of solutions that are either optimal or as close to optimal as possible.

In stage 2, we need to characterize each solution with respect to the given problem instance. Before we list the features we introduce for this purpose, we define a number of quantities we can compute for any sequences of numbers.

For monotonically increasing (or decreasing) sequences, we define the following quantities (leading to 3q + 2 quantities for q quantiles considered):

• The mean, and the mean of the second moment.

• The median and the median of the second moment.

• For a desired number q of quantiles over the range of the sequence, the percentage of numbers in the sequence before each quantile is first reached, depending on whether the sequence is increasing or decreasing (including the last quantile).

• For a desired number q of quantiles, the value of the sequence at each quantile of items in the sequence, and the corresponding values in the second moment (excluding the last quantile).

For general sequences, we define the following 8 quantities:

• The mean and the mean of the second moment.

• The median and the median of the second moment.

• The minimum and maximum, and the corresponding values of the second moment.

Now, to characterize a given solution to a knapsack instance, we consider the following five monotone sequences, and the six general sequences thereafter:

• M 1: For each item i in the sequence, the total profits achieved so far, as a percentage of the maximum achievable profit (here and in the following per the given solution).

• M 2: For each item i in the sequence, the remaining capacity as a percent of the total capacity.

• M 3: For each item i in the sequence, the linear programming upper bound for the remaining items and the remaining capacity, as percentage of the optimum profit.

• M 4: For each item i in the sequence, the linear programming upper bound for the remaining items and the total original capacity C, as percentage of the optimum profit achievable.

• M 5: For each item i in the sequence, we compute the number $d_i$ of items since the last item that was included in the solution. We aggregate and normalize these numbers by setting $D_i=\sum _{k\le i}d_i/n$ and considering the monotone sequence $(D_i)_i$.

• G 1–3: For each item selected in the given solution, its profit (as percentage of maximum profit), weight (as percentage of total capacity), and efficiency (the ratio of profit over weight).

• G 4–6: The same three values as above, but over the items not selected in the solution.

We consider 5 quantiles, therefore the above yields $5 (3 * 5 + 2) + 6 * 8 = 133$ features. We add two more by also computing the total efficiency of the solution, defined by the ratio of total profit divided by total capacity, and finally the LP/IP gap as percentage of maximum achievable profit. In total, for each solution we thus obtain 135 features. For a given pair of solutions, we concatenate the features of each solution, as well as the difference of the features of the two solutions. Our machine learning approach thus has access to $3 * 135 = 405$ features to decide which of the two solutions given is likely to perform better than the other.

To complete the data-driven part of our approach, we choose binary cost-sensitive classification to rank the solutions, in particular, the cost-sensitive hierarchical clustering approach from [18]. We use this technique in all following test cases.

4.3 Numerical Results

We generate knapsack instances with 1,000 items and (expected) weights drawn between 1 and 100 uniformly at random. The capacity is set to 10% of the total expected weights of all 1,000 items. Weakly correlated knapsack instances are generated by choosing the profit of item i with weight $w_i$ in the interval $[w_i-3,w_i+3]$. Strongly correlated instances are generated by setting the profits to $w_i+5$. Furthermore, almost strongly correlated instances are generated by choosing the profits in $[w_i+4,w_i+6]$ uniformly at random.

We build a simulation environment where the weight of an item i is drawn from a random variable following a Pareto distribution with mean $w_i$ and minimum value $0.95 w_i$. Note that the Pareto distribution is heavy-tailed: With the given parameters, there is only about a 20% chance of seeing a value larger than the mean, but a 1.5% chance to see a value of at least 1.5 times the mean, and about a 0.3% chance of encountering values of twice the mean or more.

We set the recourse threshold $p=5\%$, the restocking fee and late buying fee $s=b=10$, and the minimum reaction time $r=5$. Whenever the remaining capacity in the knapsack deviates by more than $p=5\%$, we solve a new knapsack problem (with adjusted profits to reflect the respective restocking and late buying fees) to determine our recourse action for the remaining items beyond the minimum reaction threshold.

Using this environment, we generate 100 instances of each knapsack type (weakly, strongly, and almost strongly correlated). To build our test benchmarks, we solve each knapsack to optimality using dynamic programming and choose ten near-optimal solutions. We then run each of these solutions through our simulation environment twenty times, so that each solution is exposed to the exact same twenty simulations. We then record the average performance for each near-optimal solution over the twenty simulations to grade them. In practice, there would only be one reality the selected solution would be exposed to, of course. We run each test solution through twenty potential futures to lower the possibility that we are just lucky with the scenario we encountered.

The task for our data-driven solution selector is to pick a solution from the set of ten that exhibits very good performance in the simulated environment. To train this assessor, we generate training data as follows: For each knapsack type, we generate 500 instances. For each instance, we generate twenty near-optimal solutions. Moreover, for each of these instances, we generate one, and only one, vector of weights for each item. Note that, in practice, we would equally have access to our originally expected weights $w_i$, and the actual weights $w'_i$.

Next, we need to counter-factually assess the performance of each solution. To lower the variance in these labels, we proceed as follows: First, we build twenty derived scenarios from each real scenario, by choosing weights $w''_i\in [w'_i - \alpha , w'_i+ \alpha ]$, where $\alpha ={|w_i-w'_i|\over 2}$, uniformly at random. That is, we derive scenarios from the historical examples without any assumptions regarding, or knowledge of, any distributions. We merely consider the actually encountered deviations from our original estimates and derive scenarios by varying these deviations a little. Please note that these changes do not affect the direction of the deviations: A weight that was under-estimated, remains under-estimated in each derived scenario, and each weight that was over-estimated remains over-estimated.

Table 1. SKP results

Finally, we execute each of our twenty near-optimal solutions under each derived scenario (including the recourse actions we would have taken) and label each with the average performance observed. Note that all that is needed to conduct this counterfactual assessment of additional solutions is the knowledge about our original estimates and the real item weights that were encountered.

Test results on all three classes of knapsacks are shown in Table 1. In the first column we denote the parameters of the experiment: The number of training scenarios vs number of test scenarios (usually 500-100), late-buying and restocking fees on train vs test (usually 10-10 or 5-5), and the knapsack capacity on train vs test (usually 10% or 20% of the weight of all items for both).

Next, we show the average of the worst of the ten solutions we generated for each test instance, the expected performance, and the performance if we chose the best of the ten solutions generated. Note that the latter is the maximum gain we can hope to achieve by selecting among the ten solutions generated. The numbers represent percentages above an imaginary best solution (since the ten we generated may obviously not include the optimum under uncertainty), which we set at three standard deviations below the average of the ten solutions, and whose performance itself we measure as percent above the best omniscient solution. In absolute terms, the numbers presented are thus percentages over percentages over the true profits.

Finally, we show the performance of counterfactual selection (ML), as well as the percent gap closed (GC) between the average performance and the best performance that is achievable by selecting among those select ten solutions for each instance.

Overall, we close between 22% and 47% of the gap between the average performance and the best solution available to us. That means that our forecasting models are certainly not optimal, but nevertheless effective at choosing solutions which are expected to perform better than the average near-optimal solution. This holds for varying knapsack types as well as different capacities and recourse penalties.

To assess how critical the amount of historical scenarios is, we lowered the training set to only 100 scenarios. On all knapsack types, this leads to a reduction in effectiveness, but the approach still works: We close 26%, 32% and 27% for the three knapsack types using only 20% of scenarios.

Encouragingly, we see that counterfactual forecasting can also be reasonably effective when the historical scenarios used were gathered under a different regime. For example, assume that, historically, the late-buy and restocking fees were 5, but now they are 10. Please note that what should be done when operational parameters change is to re-run the historical scenarios under the new penalties and to generate a new counterfactual training set this way. For experimental purposes only, we did not do that here so we can assess how robust our forecasting models are under varying parameters. Under [500-100 5–10 10%-10%] we see that we achieve 26%, 42% and 29% gap closed for weakly, strongly, and almost strongly correlated knapsacks, respectively.

Finally, we generated a benchmark which consists, in equal parts, of weakly, strongly, and almost strongly correlated knapsack instances, both for training and for testing. As the table shows, the counterfactuals-based predictive models work for heterogeneous mixes of different knapsack types as well.

Overall, we conclude that, for the SKP, we can learn an effective, though sub-optimal, data-driven model to predict which near-optimal solution has greater chances of performing well in an uncertain future.

5 RCPSP with Uncertain Job Durations

The RCPSP with uncertain job durations involves the scheduling of a set of jobs J given a set of resources R and a set of time periods T. Each job j consumes $u_{jr}$ units of resource r in each time period the job is running. Each resource has a maximum capacity $k_r$ that may be consumed in each time period. A precedence graph $P = J \times J$ specifies an order in which jobs are executed, i.e., for $(i,j) \in P$ job i must be completed before j can start. In the deterministic case, each job j has a fixed duration $d_j$. We consider a version of the problem where the job duration is uncertain, and assume that, if a job takes longer than planned, it continues to consume $u_{jr}$ resources in each additional time period. This version of the problem corresponds closely with real-world RCPSPs, such as construction or software projects in which delays are common, and resource consumption of jobs continues even if they take longer than expected.

The (deterministic) RCPSP can be modeled with the following constraint program [2], in which the start time of each job is given by $S_j$:

$$\begin{aligned} \min \;&\max _{j \in J} S_j + d_j&\end{aligned}$$

(1)

$$\begin{aligned} \text {subject to} \;&S_i + d_i \le S_j&\forall (i,j) \in P \end{aligned}$$

(2)

$$\begin{aligned}&\texttt {cumulative}(\mathbf {S}, \mathbf {d}, \mathbf {u}_{.r}, k_r)&\forall r \in R \end{aligned}$$

(3)

5.1 Stochastic Environment

We sample the job durations $d'_j$ from a Pareto distribution with the expected value $d_j$. The simulation starts at time period 0 and iterates through each time period until the maximum time is reached or all jobs have been executed. For some time period $t'$, all jobs ending in that period ($t' = S_j + d'_j$) are ended and the resources they are consuming freed. We then start jobs that have a start time of the current time period, if their precedence constraints are satisfied and their resource consumption requirements can be met. If job j with $S_j = t'$ cannot start in $t'$, $S_j \leftarrow S_j + 1$, i.e., we delay its start by one time period.

If significant delays occur, it may be appropriate to do recourse planning and find new start times for the remaining jobs based on the current forecast. The recourse planning involves simply fixing the start times of jobs that are finished, or running and updating the job durations with either the real duration for finished/running jobs or the current forecast for scheduled jobs. This deterministic problem can then be solved by any RCPSP algorithm, based on the CP model above.

We forecast job durations by assuming that, when a job i that must precede j is finished (i.e., $(i,j) \in P$), we know more about the duration of j than we did before i finished. We construct a graph with the same nodes and arcs as in the precedence graph, and assign the true duration $d'_i$ to every arc (i, j). Let $a_{ij}$ be the shortest path between all pairs of jobs on the newly constructed graph with Dijkstra’s algorithm. We then compute the forecast as $f_{ij} := \text {round}(d_j + (1 - a_{ij} / \max _{k \in J}\{a_{ik}\})(d'_j - d_j))$, such that $f_{ij}$ is the forecast for job j when job i is finished, assuming j is reachable from i in P. While simulating, when job i finishes we check $f_{ij}$, and if it is closer to the true duration of j, we update our expected duration.

5.2 Winner Forecasting

We propose the following groups of features to describe solutions to the RCPSP with uncertain job durations.

• 1. The expected makespan of the solution divided by the maximum time.

• 2. Let $B_{ij} := S_j - S_i$ for all $(i,j) \in P$ be the buffer between jobs with precedence relations. We compute the mean, median, standard deviation, skew, 25% quantile, and 75% quantile of the values in B.

• 3. Let $B^T_{ij} := B_{ij}(S_j / |T|)$. We compute the mean and skew of $B^T$.

• 4. We execute the solution with the expected durations and compute the percentage residual resource usage $\hat{k}_{tr}$ for each resource at each time period, and aggregate this into $\hat{k}_t := \sum _{r\in R} \hat{k}_{tr} / |R|$. We compute the mean, standard deviation, 25% quantile and 75% quantile over all values of $\hat{k}_t$.

• 5. Let $m^1$ and $m^2$ be the number of jobs directly affected (we do not examine network effects here) due to insufficient available resources if a job j starts 1 or 2 time periods later than planned, respectively.

• 6. Let a delay chain be a path in the precedence graph which forms a sequence of jobs that are separated with buffer less than the 25% quantile of B. We compute the maximum length delay chain and divide it by the total number of jobs.

5.3 Numerical Results

We test our approach on the well-known instances from the PSPLIB [15]. We use the j30 and j60 categories, which have 30 and 60 jobs, respectively, and split each into 320 training instances and 160 testing instances. The maximum job duration in these categories is 10 time units, so we add two more instance categories containing randomly generated job durations with a maximum of 50 and 100 time units, respectively.

We solve the constraint programming model in (1) through (3) with Google OR Tools CP-SAT solver version 7.0 [11]. We first generate the optimal expected values solution. We note that, in the RCPSP, shifting the buffer of a few jobs results in a “new” solution, but this is not desirable for our approach, as the realized performance will be nearly the same. Therefore, to generate $k - 1$ solutions in addition to the optimal solution, we begin an iterative process. After a solution $S'$ is found, we append the following constraints to require that a given percentage of the jobs have a different order than the previously found solution:

$$\begin{aligned} o_{ij} = 1 \Leftrightarrow S_i \circ S_j&\qquad \forall S'_i \star S'_j, \; (\circ ,\star ) \in \{(>,<), (<,>), (\ne ,=)\} \end{aligned}$$

(4)

$$\begin{aligned} \sum _{i,j \in J, i < j} o_{ij} \ge h \end{aligned}$$

(5)

where the decision variable $o_{ij} \in \{0,1\}$ for $i,j \in J, i < j$ is 1 iff jobs i and j have a different order than in the previous solution. We require the number of job order changes in (5) to be greater than a threshold h, which we set to 5% of the unique job pairs ($|J||J-1|$).

Table 2. RCPSP results

As for the SKP and SSPP, we test our approach on 20 simulations per instance, simulating training and testing instances the same way as the previous two problems, with training simulations being derived from only one real simulation without knowledge of the actual distributions of job delays, and test simulations running 20 real scenarios for proper evaluation. Table 2 shows the results in the same format as the SKP and SSPP, with the addition of columns indicating the number of training and testing instances.

We are able to achieve modest gains over using the expected value solution, except in the case of j30 with a maximum expected duration of 10. On this instance set, the learning algorithm failed to find a good way of identifying superior solutions. This may be due to our features, which focus closely on buffer, and this may not be sufficient when the durations are low.

On the j60 instances, we are able to close between 15% and 30% of the gap to the best available solution. Even though the absolute gain may seem small, as with many optimization under uncertainty problems, real-world RCPSP problems can involve expensive resources (specialized digging equipment, etc.), and even small absolute improvements often translate into significant cost savings, as well as time savings for the overall plan. Therefore, even though our method is heuristic in nature, it can be of high value in practice.

6 Stochastic Shortest Path Problem

In the SSPP, we are given a graph $G = (V,A)$ of nodes V and arcs A. Every arc $(i,j) \in A$ has an uncertain cost with an expected value of $c_{ij}$. The objective is to find a minimal cost path through the graph between a source node s and destination node t. The SSPP can model problems such as the routing of ships under the influence of weather, or routing a vehicle through a road network considering traffic delays.

6.1 Stochastic Environment

We base the stochastic environment for the SSPP on the one described for the SKP with a few problem-specific modifications. Given a solution to an SSPP instance, we first sample the realized costs $c'_{ij}$ for each arc from a Pareto distribution with mean $c_{ij}$ and the minimum at 90% of $c_{ij}$. We then begin executing the path given to us as one of the ten solutions, using $c'_{ij}$ for each realized arc. If the accumulated delay exceeds 10% of the expected costs, we allow recourse planning every 5 nodes.

In the recourse planning, we adjust our forecast based on the current node. The assumption is that arcs close to this node have a more accurate forecast than those far away, since we would traverse these arcs in the nearer future. To assemble our forecast, let $a_{ij}$ be the number of arcs between nodes i and j. Then, let the forecast cost for (i, j) be $f_{ij} := \text {round}(c_{ij} + (1 - a_{ij} / \varDelta \})(c'_{ij} - c_{ij}))$ if $a_{ij} < 5$, and $c_{ij}$ otherwise. We set $\varDelta$ to 7 to keep the forecasts from becoming too accurate when we get close, but keep them inaccurate when we are far away.

6.2 Winner Forecasting

We introduce the following features to characterize an SSPP solution. For each feature set, we compute the minimum, maximum, mean, standard deviation, skew and kurtosis of the array of values. For features using arc costs, we divide the costs by the average arc cost of the graph, and for features using node degrees, we use the average node degree of the entire graph.

• 1. Array of arc costs on the path

• 2. Array of arc costs over the set of arcs leaving nodes of the path going to nodes not on the path

• 3. Array of arc costs over the set of arcs leaving nodes that are connected to the path by a single node (excluding any arcs to nodes directly connected to the path or nodes on the path)

• 4. Array of node degrees in the path

• 5. Array of node degrees of nodes that are connected to nodes on the path

• 6. Array of node degrees over the set of nodes that are connected to the path by a single node (excluding any nodes directly connected to the path)

Table 3. SSPP results

As in the case of the SKP, we concatenate the features for two given solutions with the difference between the features of both solutions, which are then used by the machine learning approach to determine the most promising solution.

6.3 Numerical Results

We build a dataset of SSPP instances consisting of graphs based on one of three graph types: $G_{nm}$ [8], “bottleneck”, and Watts-Strogatz small-world graphs. The bottleneck instances consist of five $G_{nm}$ graphs of equal size connected sequentially with 5 links between each graph. We create 300 instances of each graph type and size and select random source and sink nodes for the path, splitting the instances into 200 train and 100 test. The expected arc costs $c_{ij}$ are drawn uniformly random between 1 and 100. We further ensure that all graphs have no isolated components by adding arcs between such components and the rest of the graph.

For each SSPP graph, we generate the ten shortest paths for a given graph between s and t using Yen’s algorithm [23]. We simulate using the same scenario structure as in the SKP. The “true” arc costs $c'_{ij}$ are drawn from a Pareto distribution with an expected value $c_{ij}$, shifted so that the minimum is at $0.9c_{ij}$. Training instances are evaluated on 20 scenarios that are all variations of a single scenario (using the exact same scenario variation as in the SKP), and test instances are evaluated on 20 scenarios generated independently of each other. Every 5 nodes we check if the accumulated delay is more than 10% of the expected cost, and if it is, we run a recourse algorithm that tries to replan the shortest path to t from the current node.

Table 3 shows the results of our computational experiments. We compute the gap to the optimal shortest path considering $c'_{ij}$ and average it over 20 scenarios as described above. Note that, for many graph instances, paths that were near optimal for the point-estimated scenario may perform much worse than the shortest path had we known the true arc distances beforehand. This leads to relatively high values in our table, but is really more a reflection of the inherent cost of uncertainty in this particular problem than the absolute performance of the particular algorithm used to optimize under the uncertainty. Looking closer at our data, we find that the expected path lengths of the solutions is usually about the same, with the bottleneck graphs exhibiting slightly higher variance than for the other graph types.

Despite the simplicity of our features (we just measure arc costs and node degrees), we are able to close the gap by around 50% in all graph types and 64% for the mixed setting. This provides further support that we can learn from historical data which solution features are favorable for later execution under stochastic disruption.

7 Conclusion

We have introduced a new methodology for modeling and heuristically solving stochastic optimization problems. The key idea is to move away from trying to accurately forecast the uncertainty in the problem instance at hand. Instead, we propose to use logs of historical estimates and the realities that followed for comparing various counterfactual solutions. Our thesis is that we can devise features that capture instance-dependent characteristics of the solutions that allow us to predict which solution from a solution pool will likely perform well for a new problem instance at hand.

The objective of this paper was to provide a proof of concept. We considered three stochastic optimization problems that would each be extremely hard to model and solve with existing approaches, even heuristically. For all three problems, we were able to quickly devise sets of features that were effective enough to choose solutions that were superior to picking an average solution from our pool of optimal (with respect to the underlying point-estimated optimization problem) or near-optimal solutions.

Note that we did not spend any time to optimize hyper-parameters of our learning approaches, or to engineer more effective features. Providing a general set of features and pairing it with off-the-shelf machine learning methods was enough to tackle each of the three optimization problems. We believe that the experimental results provided strongly support our thesis that we can learn from data which solutions will exhibit superior performance in an uncertain future. However, this is of course not to say that, in practice, one should not conduct feature engineering and hyper-parameter optimization to achieve even better results.

The ability to tackle complex stochastic optimization problems with thousands of recourse stages comes at a cost, though. The framework presented gives no guarantees regarding the quality of the solutions achieved, and dual bounds are not provided. Therefore, whenever traditional stochastic optimization is applicable and full online-reoptimization is feasible during real-world operations, we would recommend this approach. The framework introduced here is meant for situations when the traditional methods break down.

In the future, we intend to investigate if the models trained on historic counterfactuals can be mined to infer constraints to guide the search for less brittle solutions directly: solutions that are not only near-optimal for the “fair weather” data, but also have high probability of performing well under stochastic disruption. In this sense, the new framework opens the door for a comprehensive new research agenda for stochastic constraint optimization.