Viscoelastoplastic Damage with Maximum Rate of Dissipation-Based Growth Criterion and Tri-Component Lie Rate Decomposition

Abstract

Maximization of the rate of dissipation is applied to develop a viscoelastoplastic damaging material model with anisotropic properties and finite deformation. The thermodynamic framework suggests a new damage activation criterion based on the sum of stress and an energy release rate based on a damage-based strain measure. The framework combines the usually disjointed ideas of effective stress and damage strain kinematics to track the dimensional changes attributed to damage while retaining the physical link to load-bearing area reduction. Potential applications include large volume change oxidation of SiC CMC composites, high temperature creep and relaxation influences on damage processes in reinforced polymers and ceramics, and opening/closing of cracks via natural elastic behavior as opposed to treatments based on loading criteria.

Maximum rate of dissipation analysis is applied to develop a framework corresponding to a material model incorporating three strain elements characterized by viscoelastic, damage, and viscoplastic behaviors. A push-pull framework associates these behaviors with respective multiplicative deformation gradients with rates determined by Lie material derivatives.

Kinematic/Kinetic Definitions

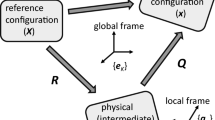
The present study considers materials which may undergo viscoelastoplastic damage under finite strains. The configurations and associated deformation gradients are depicted in Fig. 1, where F ^c is viscoplastic/creep, F ^d is damage, and F ^veis viscoelastic, with F = F ^eF ^dF ^c the multiplicative decomposition of the total deformation. τ is the Kirchhoff stress.

Fig. 1

Body configurations κ _R (reference), $\overline{\kappa}$, $\tilde{\kappa}$ and κ _t (current time). X _K, ${\overline{x}}_{\Lambda}$, ${\tilde{x}}_{\alpha }$, x _j are coordinates

Denoting also F ^dc = F ^dF ^cfor convenience and with F ^e = F ^ve and E ^e = E ^ve (Voigt assumption), strain measures are given by, strain measures are given by

$$ \mathbf{E}=\frac{1}{2}\left({\mathbf{F}}^T\mathbf{F}-\mathbf{I}\right)={\mathbf{F}}^T\mathbf{eF},\kern1em \mathbf{e}=\frac{1}{2}\Big(\mathbf{I}-{\left({\mathbf{F}}^e{\mathbf{F}}^{dc}\right)}^{-T}{\left({\mathbf{F}}^e{\mathbf{F}}^{dc}\right)}^{-1} $$

$$ {\overline{\mathbf{E}}}^d=\frac{1}{2}\left({\mathbf{F}}^{dT}{\mathbf{F}}^d-\mathbf{I}\right),\kern1em {\overline{\mathbf{e}}}^c=\frac{1}{2}\left(\mathbf{I}-{\mathbf{F}}^{c-T}{\mathbf{F}}^{c-1}\right) $$

$$ {\tilde{\mathbf{E}}}^d={\mathbf{F}}^{d-T}{\overline{\mathbf{E}}}^d{\mathbf{F}}^{d-1},\kern1em {\tilde{\mathbf{e}}}^c={\mathbf{F}}^{d-T}{\overline{\mathbf{e}}}^c{\mathbf{F}}^{d-1},\kern1em {\tilde{\mathbf{E}}}^e=\frac{1}{2}\left({\mathbf{F}}^{eT}{\mathbf{F}}^e-\mathbf{I}\right), $$

$$ \tilde{\mathbf{E}}={\tilde{\mathbf{E}}}^e+{\tilde{\mathbf{E}}}^d+{\tilde{\mathbf{e}}}^c. $$

It can be noted that while ${\tilde{\mathbf{E}}}^e={\tilde{\mathbf{E}}}^e\left[{\mathbf{F}}^e\right]$ and ${\tilde{\mathbf{e}}}^d={\tilde{\mathbf{e}}}^d\left[{\mathbf{F}}^d\right]$, ${\tilde{\mathbf{e}}}^c$ has the mixed dependency ${\tilde{\mathbf{e}}}^c\left[{\mathbf{F}}^c,{\mathbf{F}}^d\right]$, but ${\tilde{\mathbf{e}}}^c=0$ when F ^c = 0 and ${\tilde{\mathbf{e}}}^c$ pushes/pulls properly with the deformation.

The Lie derivatives employed for tensors associated with $\tilde{\kappa}$ are material derivatives of these tensors when pulled back to the reference configuration κ _R, then pushed back to $\tilde{\kappa}$, as illustrated by that of $\tilde{\mathbf{E}}$:

$$ \overset{\varDelta }{\tilde{\mathbf{E}}}={\mathbf{\mathcal{L}}}^{dc}\tilde{\mathbf{E}}={\mathbf{F}}^{dc-T}\overset{\cdotp }{\overline{\left({\mathbf{F}}^{dc T}\tilde{\mathbf{E}}{\mathbf{F}}^{dc}\right)}}{\mathbf{F}}^{dc-1}={\mathbf{F}}^{dc-T}\dot{\mathbf{E}}{\mathbf{F}}^{dc-1}={\mathbf{F}}^{eT}{\mathbf{d}\mathbf{F}}^e=\tilde{\mathbf{d}}=\dot{\tilde{\mathbf{E}}}+{\left({\tilde{\mathbf{l}}}^{dc}\right)}^T\tilde{\mathbf{E}}+{\tilde{\mathbf{E}}\tilde{\mathbf{l}}}^{dc} $$

$$ \mathbf{d}=\frac{1}{2}\left({\left(\dot{\mathbf{F}}{\mathbf{F}}^{-1}\right)}^T+\dot{\mathbf{F}}{\mathbf{F}}^{-1}\right),\kern1em {\tilde{\mathbf{l}}}^{dc}={\dot{\mathbf{F}}}^{dc}{\mathbf{F}}^{dc-1}. $$

Stress measures and stress power combinations are given by:

$$ \mathbf{S}={\mathbf{F}}^{-1}{\boldsymbol\uptau \mathbf{F}}^{-T}={\mathbf{F}}^{dc-1}\tilde{\mathbf{S}}{\mathbf{F}}^{dc-T}={\mathbf{F}}^{c-1}\overline{\mathbf{S}}{\mathbf{F}}^{c-T}\kern1em \tilde{\mathbf{S}}={\mathbf{F}}^{e-1}{\boldsymbol\uptau \mathbf{F}}^{e-T}\kern1em \overline{\mathbf{S}}={\mathbf{F}}^{ed-1}{\boldsymbol\uptau \mathbf{F}}^{ed-T} $$

$$ \tilde{\mathbf{S}}\cdot \overset{\varDelta }{\tilde{\mathbf{E}}}=\tilde{\mathbf{S}}\cdot \tilde{\mathbf{d}}=\boldsymbol\uptau \cdot \mathbf{d}=\mathbf{S}\cdot \dot{\mathbf{E}} $$

with

$$ \mathrm{tr}\left(\mathbf{TS}\right)={\mathbf{T}}_{ij}{\mathbf{S}}_{ji}=\mathbf{T}\cdot \mathbf{S}. $$

A similar kinematic/kinetic framework with one intermediate configuration is detailed by Stumpf [1].

Thermodynamics/Constitutive Development

The reduced energy dissipation equation, assuming a split of the entropy production into mechanical and thermal components, is given by (ψ, ρ _o, η, θ, q ₀ are respectively Helmholtz energy, reference density, specific entropy, temperature, and heat flux referred to the reference configuration):

$$ -{\rho}_0\dot{\psi}-{\rho}_0\eta \dot{\theta}+\tilde{\mathbf{S}}\cdot \overset{\triangle }{\tilde{\mathbf{E}}}-{\mathbf{q}}_0\cdot \frac{\nabla_0\theta }{\theta }={\rho}_0\theta \zeta \equiv \xi $$

$$ -{\rho}_0\dot{\psi}+\tilde{\mathbf{S}}\cdot \overset{\triangle }{\tilde{\mathbf{E}}}={\xi}^{mech},\kern1em -{\rho}_0\eta \dot{\theta}-{\mathbf{q}}_0\cdot \frac{\nabla_0\theta }{\theta }={\xi}^{thermal} $$

Assuming $\psi =\tilde{\psi}\left[{\tilde{\mathbf{E}}}^{ve},{\tilde{\mathbf{e}}}^d,{\tilde{\mathbf{e}}}^c\right]$ with the chain rule for $\overset{\triangle }{\psi }$ it follows:

$$ \mathrm{tr}\left[\tilde{\mathbf{S}}\left(\overset{\triangle \kern0.5em }{{\tilde{\mathbf{E}}}^{ve}}+\overset{\triangle \kern0.5em }{{\tilde{\mathbf{e}}}^d}+\overset{\triangle \kern0.5em }{{\tilde{\mathbf{e}}}^c}\right)\right]-{\rho}_0\overset{\triangle }{\psi }={\xi}^{mech}\ge 0 $$

$$ \left(\tilde{\mathbf{S}}-{\tilde{\mathbf{S}}}^e\right)\cdot \overset{\triangle \kern0.5em }{{\tilde{\mathbf{E}}}^{ve}}+\left(\tilde{\mathbf{S}}+\tilde{\mathbf{Y}}\right)\cdot \overset{\triangle \kern0.5em }{{\tilde{\mathbf{e}}}^d}+\left(\tilde{\mathbf{S}}-{\tilde{\mathbf{S}}}^{c\ast}\right)\cdot \overset{\triangle \kern0.5em }{{\tilde{\mathbf{e}}}^c}={\xi}^{mech}\ge 0 $$

$$ {\tilde{\mathbf{S}}}^e={\rho}_0{\left(\frac{\partial \tilde{\psi}}{\partial {\tilde{\mathbf{E}}}^{ve}}\right)}^T\kern1em \tilde{\mathbf{Y}}=-{\rho}_0{\left(\frac{\partial \tilde{\psi}}{\partial {\tilde{\mathbf{e}}}^d}\right)}^T\kern1em {\tilde{\mathbf{S}}}^{c\ast }={\rho}_0{\left(\frac{\partial \tilde{\psi}}{\partial {\tilde{\mathbf{e}}}^c}\right)}^T $$

Based on the dissipation relation, the following are adopted as inelastic activation criteria:

$$ \left(\tilde{\mathbf{S}}-{\tilde{\mathbf{S}}}^e\right)\overset{\triangle \kern0.5em }{\cdot {\tilde{\mathbf{E}}}^{ve}}={\xi}^{ve}\ge 0,\kern1em \left(\tilde{\mathbf{S}}+\tilde{\mathbf{Y}}\right)\cdot \overset{\triangle \kern0.5em }{{\overline{\mathbf{e}}}^d}={\xi}^d\ge 0,\kern1em \left(\tilde{\mathbf{S}}-{\tilde{\mathbf{S}}}^{c\ast}\right)\cdot \overset{\triangle \kern0.5em }{{\overline{\mathbf{e}}}^c}={\xi}^c\ge 0 $$

$$ {\xi}^{mech}={\xi}^{ve}+{\xi}^d+{\xi}^c $$

The second activation criterion is noteworthy. ${\tilde{\mathbf{e}}}^d$ is a strain-based measure of damage; $\tilde{\mathbf{Y}}$ is thus called here the damage strain energy release rate, and appropriately reflects the loss of stored energy occurring with damage. The combination of $\tilde{\mathbf{Y}}$with the stress $\tilde{\mathbf{S}}$ is thus thermodynamically implied to drive damage in accordance with the dissipation eq.

A Lagrange function is defined for application of assumed maximization of the rate of dissipation (cf. [2, 3]), where $s=\left\{{\tilde{\mathbf{E}}}^{ve},{\tilde{\mathbf{e}}}^d,{\tilde{\mathbf{e}}}^c\right\}$is the state and λ is a Lagrange multiplier constraining the assumed dissipation function ${\tilde{\xi}}^{mech}\left[\overset{\triangle \kern0.75em }{{\tilde{\mathbf{E}}}^{ve}},\overset{\triangle \kern0.5em }{{\tilde{\mathbf{e}}}^d},\overset{\triangle \kern1.75em }{{\tilde{\mathbf{e}}}^c;s}\right]={\tilde{\xi}}^{ve}\left[\overset{\triangle \kern0.5em }{{\tilde{\mathbf{E}}}^{ve}};s\right]+{\tilde{\xi}}^d\left[\overset{\triangle \kern0.5em }{{\tilde{\mathbf{e}}}^d};s\right]+{\tilde{\xi}}^c\left[\overset{\triangle \kern1.75em }{{\tilde{\mathbf{e}}}^c;s}\right]$ to obey the derived dissipation equation:

$$ \Phi ={\tilde{\xi}}^{mech}\left[\overset{\triangle \kern0.75em }{{\tilde{\mathbf{E}}}^{ve}},\overset{\triangle \kern0.5em }{{\tilde{\mathbf{e}}}^d},\overset{\triangle \kern1.75em }{{\tilde{\mathbf{e}}}^c;s}\right]-\lambda \left\{\left(\tilde{\mathbf{S}}-{\tilde{\mathbf{S}}}^e\right)\cdot \overset{\triangle \kern0.75em }{{\tilde{\mathbf{E}}}^{ve}}+\left(\tilde{\mathbf{S}}+\tilde{\mathbf{Y}}\right)\cdot \overset{\triangle \kern0.5em }{{\tilde{\mathbf{e}}}^d}+\left(\tilde{\mathbf{S}}-{\tilde{\mathbf{S}}}^{c\ast}\right)\cdot \overset{\triangle \kern0.5em }{{\tilde{\mathbf{e}}}^c}-{\tilde{\xi}}^{mech}\left[\overset{\triangle \kern0.75em }{{\tilde{\mathbf{E}}}^{ve}},\overset{\triangle \kern0.5em }{{\tilde{\mathbf{e}}}^d},\overset{\triangle \kern1.75em }{{\tilde{\mathbf{e}}}^c;s}\right]\right\} $$

Maximization of Φ leads to

$$ \mu \frac{\partial {\tilde{\xi}}^{ve}}{\partial \overset{\triangle \kern0.5em }{{\tilde{\mathbf{E}}}^{ve}}}=\tilde{\mathbf{S}}-{\tilde{\mathbf{S}}}^e,\kern1em \mu \frac{\partial {\tilde{\xi}}^d}{\partial \overset{\triangle \kern0.5em }{{\tilde{\mathbf{e}}}^d}}=\tilde{\mathbf{S}}+\tilde{\mathbf{Y}},\kern1em \mu \frac{\partial {\tilde{\xi}}^c}{\partial \overset{\triangle \kern0.5em }{{\tilde{\mathbf{e}}}^c}}=\tilde{\mathbf{S}}-{\tilde{\mathbf{S}}}^{c\ast },\kern1em \mu =\frac{1+\lambda }{\lambda } $$

Assuming simple quadratic dissipation relations for each of ${\tilde{\xi}}^{ve},{\tilde{\xi}}^d,{\tilde{\xi}}^c$ leads to the following integrable relations:

$$\stackrel{△}{{\tilde{\mathbf{E}}}^{\mathit{ve}}}={\mathbf{N}}^{v-1}\left[s\right]\left(\tilde{\mathbf{S}}-{\tilde{\mathbf{S}}}^e\left[s\right]\right)\stackrel{△}{{\tilde{\mathbf{e}}}^d}={\mathbf{H}}^{d-1}\left[s\right]\left(\tilde{\mathbf{S}}+\tilde{\mathbf{Y}}\left[s\right]\right)\stackrel{△}{{\tilde{\mathbf{e}}}^c}={\mathbf{K}}^{c-1}\left[s\right]\left(\tilde{\mathbf{S}}-{\tilde{\mathbf{S}}}^{c_{\ast }}\left[s\right]\right)$$

Conclusion

The described model corresponds to a Voigt viscoelastic element in combination with damage and viscoplastic elements. The stress employed in the above relations is obtained via an effective stress continuum damage argument, e.g [4]. A fourth-order damage measure connected to the damage strain ${\tilde{\mathbf{e}}}^d$ permits memory of the accrued damage state while ${\tilde{\mathbf{e}}}^d$fluctuates with deformation. Work continues on further defining the detailed constitutive relations and computational implementations.