Abstract
In work of Connes and Consani, Γ-spaces have taken a new importance. Segal introduced Γ-spaces in order to study stable homotopy theory, but the new perspective makes it apparent that also information about the unstable structure should be retained. Hence, the question naturally presents itself: to what extent are the commonly used invariants available in this context? We offer a quick survey of (topological) cyclic homology and point out that the categorical construction is applicable also in an \({\mathbb N}\)-algebra (aka. semi-ring or rig) setup.
Access provided by Autonomous University of Puebla. Download chapter PDF
Similar content being viewed by others
Keywords
- Cyclic homology
- Ring spectra
- Topological cyclic homology
- Special gamma spaces
- Unstable homology
- Group completion
Mathematical Subject Classification (2010)
On the occasion of Alain Connes’ 70 year celebration.
Alain Connes introduced cyclic homology in 1981 as a generalization of de Rham homology suitable for non-commutative geometry. Boris Tsygan reintroduced it in 1983 as an “additive” version of algebraic K-theory (see Section 1 for a brief overview with citations of the part of the theory relevant for our considerations). Almost immediately it became apparent that cyclic homology was a very good invariant for studying K-theory, at least rationally. However, for torsion information one needed to extend the construction from rings to so-called \(\mathbb S\)-algebras (i.e., replacing the ring \({\mathbb Z}\) of integers with the sphere spectrum \(\mathbb S\)), resulting in Bökstedt, Hsiang, and Madsen’s topological cyclic homology  . A possible framework for extending cyclic homology in this direction is Segal’s category of Γ-spaces, generalizing the concept of abelian groups in a way that also allows objects where the axioms of an abelian group are perhaps only true up to some notion of equivalence—see Section 2.1 for an elementary introduction to Γ-spaces where we try to explain why the structure is virtually forced upon us from the algebraic origins.
. A possible framework for extending cyclic homology in this direction is Segal’s category of Γ-spaces, generalizing the concept of abelian groups in a way that also allows objects where the axioms of an abelian group are perhaps only true up to some notion of equivalence—see Section 2.1 for an elementary introduction to Γ-spaces where we try to explain why the structure is virtually forced upon us from the algebraic origins.
Actually, in many of these examples there is one axiom that does not hold at all—the existence of negatives. For instance, at the outset there are no sets with a negative number of elements or vector spaces of negative dimension. However, experience—starting in elementary school—has taught us that we get a much more effective theory if we adjoin negatives.
Stable homotopy theory is the study of such examples after adjoining negatives by a process dubbed stabilization. This is an enormously successful theory: the sphere spectrum sees much more combinatorial data than the ring of integers does, and some of this combinatorial data is reflected in the number theory revealed by algebraic K-theory. In fact, Thomason [60] showed that algebraic K-theory can be viewed as a localization from the category \(\mathcal {S}\mathcal {M}\mathcal {C}\) of small symmetric monoidal categories to the homotopy category (with respect to stable equivalences) of Γ-spaces.
One crucial difference between abelian groups and stable homotopy theory is how symmetries behave. For instance, if A is an \(\mathbb S\)-algebra we can consider the smash A∧A—the analog of the tensor product or, in algebraic geometry, a product X × X. The cyclic group of order two acts and we can consider the fixed points \((A{\wedge } A)^{C_2}\)—analog to the symmetric product (X × X)∕C 2.
What does not have an analog in the algebraic or geometric situation is that in stable homotopy theory \((A{\wedge } A)^{C_2}\) is much like a form of Witt vectors: there is a “restriction” map \((A{\wedge } A)^{C_2}\to A\) (it is not any sort of multiplication! At the level of path components it is the extension of the group π
0A by (π
0A ⊗ π
0A)∕C
2 by the cocycle (x, y)↦ − x ⊗ y) which often is the first step of a lift, either from finite characteristic to infinite characteristic or higher up in the so-called chromatic tower of stable homotopy theory. The restriction map is essential for the construction of  in Section 1.5 and can be viewed as the source of most of the verifications we know of the so-called “red-shift conjecture” in algebraic K-theory.
in Section 1.5 and can be viewed as the source of most of the verifications we know of the so-called “red-shift conjecture” in algebraic K-theory.
The restriction map reappears below in a special context as a composite of the geometric diagonal of Section 2.3.4 and isotropy separation in Section 2.2.1.
However, algebraic K-theory kills much information one might be interested in. For a ring A, the Grothendieck group K 0(A) is obtained from the isomorphism classes of finitely generated projective A-modules by introducing objects of “negative rank.” For many situations this is a rather innocent operation (from the natural numbers one obtains the integers), but in other situations group completion can drastically alter the object at hand.
If k is a field, consider the category \(\mathrm {Vect}_k^{\text{count}}\) of all k-vector spaces of countable dimension. Then k n ⊕ k ∞≅k ∞ for all n ≤∞, and if you group complete with respect to sum—essentially introducing negative dimensions—you have cancellation, leaving you with the rather uninformative trivial group. This sorry state of affairs is sometimes referred to as the Eilenberg swindle. This is in stark contrast with the situation where you only consider finite dimensional vector spaces which leads to the usual algebraic K-theory, which is far from trivial and (the higher homotopy) contains much information about the field.
For all its categorical defects, the category \(\mathcal {S}\mathcal {M}\mathcal {C}\) of small symmetric monoidal categories is in many ways the natural philosophical relaxation of the category of abelian groups. We must perhaps live without negatives and that laws like commutativity only hold up to isomorphism. While we want to retain as much information about \({\mathcal S}{\mathcal M}{\mathcal C}\) as possible, in order to obtain a situation we can calculate with, some localization seems necessary.
One choice is to study the localization of \(\mathcal {S}\mathcal {M}\mathcal {C}\) with respect to the unstable equivalences: a symmetric monoidal functor f : c → d in \(\mathcal {S}\mathcal {M}\mathcal {C}\) is a weak equivalence if the map of nerves Nc → Nd is a weak equivalence in spaces. Mandell [46] improves on Thomason’s result by showing that the localization of \(\mathcal {S}\mathcal {M}\mathcal {C}\) with respect to unstable equivalences is equivalent to the localization of the category of Γ-spaces with respect to the special equivalences (we will discuss these in Section 2.2.3).
Forty years after Segal’s discovery, Γ-spaces reappear in work of Connes and Consani [18] where it becomes clear that this generalization of abelian groups fits as a common framework for many of the current efforts of understanding the “field with one element.” The rôle of the field with one element is taken by the sphere spectrum \(\mathbb S\) and the rôle of the tensor product is taken by the smash product ∧, see Section 2 for further details. However, for Connes and Consani it is vital that we do not adjoin negative elements; we are no longer in the realm of stable homotopy theory and many of the identifications we are used to no longer hold. A priori this has serious consequences for invariants—we may have used identifications that only hold after having adjoined negatives.
What follows is a tentative study of to what extent we can hope to extend invariants to a context that handles symmetric monoidal categories well without adjoining negatives by treating (successfully) the case of topological cyclic homology, see Section 3. Central to this is that the underlying machinations of the restriction map of Example 0.0.1 carry through.
The reader should be aware of the fact that this is only a tentative study: ultimately we are after a theory that better reflects the intuition of how modules over the field with one element should behave. In order to achieve this, there are reasons to not take spaces as our primitive notion, but rather quasi-categories (i.e., the Joyal model structure on the category of spaces). However, this theory is more technical and not at all suited for a survey-type paper of this sort. While most things follow a path very similar to the one sketched below, we have not yet written down all the details and hope to return to it in a future paper.
In Section 1 we give a quick overview of the history and some results pertaining to cyclic homology that are relevant to our discussion.
In Section 2 we study the equivariant theory you get from Γ-spaces when you stop short of group completing. This is the so-called special model and the most important output is that the categorical model adapts to the current situation. The category of Γ-spaces is in many ways a much less friendly world than most of its competitors modeling stable homotopy theory, but it is almost finitely generated (a technical term of Voevodsky’s) which means that we retain just enough control also over the special situation.
In Section 3 we see that the equivariant control we obtained in Section 2 is exactly what is needed in order to set up  in the special situation.
in the special situation.
Lastly we collect some results on modules and monoids that are of interest, but require input that did not fit with the equivariant focus of the rest of the paper. In particular, one of the examples Connes and Consani pay special attention to is the so-called Boolean algebra B = {0, 1} with 1 + 1 = 1. In Section 4 we show that B is “specially solid”: the multiplication map B∧LB →B is a special equivalence. This can be seen as a disappointment: although we have devised a theory that avoids the Scylla of group completing the monoidal structure of a symmetric monoidal category, we still must deal with the Charybdis of weak equivalences which is akin to inverting the morphisms. In this example these processes are much the same (not quite: otherwise everything would be zero). One fix is to consider the Joyal structure referred to above, but this is as mentioned postponed to another day.
FormalPara Notational conventions-
1.
The category of symmetric monoids is symmetric monoidal with unit \({\mathbb N}=\{0,1,2,\dots \}\) and tensor \(\otimes _{\mathbb N}\) (defined exactly as the usual tensor product). To avoid the rig/semi-ring controversy (we find neither alternative particularly attractive, but we really dislike “semi-rings”) we call the monoids with respect to the tensor in symmetric monoids \({\mathbb N}\)-algebras.
-
2.
If \({\mathcal C}\) is a category and c, c′ are objects, then \({\mathcal C}(c,c')\) is the set (or space according to flavor) of morphisms c → c′ in \({\mathcal C}\). The functor \(c'\mapsto {\mathcal C}(c,c')\) is denoted \({\mathcal C}(c,-)\).
-
3.
If X and Y are pointed sets, then the wedge X ∨ Y ⊆ X × Y is the subset where one of the coordinates is the base point and the smash product is the quotient X∧Y = X × Y∕X ∨ Y .
-
4.
We use “k +” as shorthand for the set {0, 1, …, k} pointed at 0 and [k] for the ordered set {0 < 1 < ⋯ < k}. The category of pointed finite sets is called Γo and the category of nonempty totally ordered finite sets is called Δ.
-
5.
Objects in the category \(\mathcal S_*\) of pointed simplicial sets will be referred to as spaces. A Γ-space is a pointed functor from Γo to \(\mathcal S_*\).
-
6.
If X is an object on which a group G acts, then X G → X is the “inclusion of fixed points” (as defined e.g., by a categorical limit over G).
1 Cyclic homology
1.1 Prehistory
The connection between algebraic K-theory and de Rham cohomology was pointed out already in the early days of higher algebraic K-theory (ca. 1972). For a commutative ring A, Gersten provided a map to the Kähler differentials
and Bloch [5] proved that the “tangent space” \(TK_n(A)=\ker \{K_n(A[\epsilon ]/\epsilon ^2)\to K_n(A)\}\) contains \(\Omega ^{n-1}_A\) as a split summand when A is local, 1∕2 ∈ A and n > 0. Also other connections between algebraic K-theory and homological theories were investigated, for instance the Dennis trace map to Hochschild homology  .
.
1.2 Cyclic homology
In 1980 Alain Connes was searching for a cohomology theory of de Rham type [14] suitable for non-commutative algebras and introduced cyclic homology the year after [15, 17]. A few years later, Tsygan [61] rediscovered cyclic homology and in parallel with Loday and Quillen [42] proved that in characteristic zero, cyclic homology  is isomorphic to the primitive part of the homology of the Lie algebra \(\mathfrak {gl}(A)\). Goodwillie completed the picture by showing [31] that in the context of a nilpotent extension of associative rings, the relative algebraic K-theory agrees, rationally and up to a shift in grading, with relative cyclic homology.
is isomorphic to the primitive part of the homology of the Lie algebra \(\mathfrak {gl}(A)\). Goodwillie completed the picture by showing [31] that in the context of a nilpotent extension of associative rings, the relative algebraic K-theory agrees, rationally and up to a shift in grading, with relative cyclic homology.
It is tempting to think of the map used by Goodwillie between relative K-theory and cyclic homology as a “logarithm” from the general linear group GL(A) to its “tangent space,” the Lie algebra \(\mathfrak {gl}(A)\). In this interpretation the rationality assumption is necessary for the coefficients in the Taylor expansion of the logarithm to be defined, the nilpotence assures convergence and finally the need for taking primitives stems from the correspondence in rational stable homotopy between homology and homotopy. See [19] and [63] for ideas along this line.
Connes demonstrated [16] that the Hochschild homology is a cyclic object and its associated spectrum  comes with an action by the circle \(\mathbb T\) (see Section 3.1 for more on cyclic objects). In this interpretation, cyclic homology corresponds to the homotopy orbits
comes with an action by the circle \(\mathbb T\) (see Section 3.1 for more on cyclic objects). In this interpretation, cyclic homology corresponds to the homotopy orbits  (the double complex is a concrete algebraic representation of the fact that the classifying space \(B\mathbb T\cong {\mathbb C}\mathrm P^\infty \) of the circle \(\mathbb T\) has a single cell in each even dimension). Goodwillie (and Jones [38]) showed that the Dennis trace factors through the homotopy fixed points
(the double complex is a concrete algebraic representation of the fact that the classifying space \(B\mathbb T\cong {\mathbb C}\mathrm P^\infty \) of the circle \(\mathbb T\) has a single cell in each even dimension). Goodwillie (and Jones [38]) showed that the Dennis trace factors through the homotopy fixed points  (which was dubbed “negative cyclic homology”). The difference between the homotopy orbits and fixed points is measured by the “norm map”
(which was dubbed “negative cyclic homology”). The difference between the homotopy orbits and fixed points is measured by the “norm map”  (note the suspension which is responsible for the above observed shift in grading) which is part of a fiber sequence
(note the suspension which is responsible for the above observed shift in grading) which is part of a fiber sequence

The last term—the “Tate-construction” on  and whose homotopy groups are referred to as periodic homology—is defined by this sequence and vanishes in certain key situations. Most notably, in the rational nilpotent situation the relative periodic homology vanishes.
and whose homotopy groups are referred to as periodic homology—is defined by this sequence and vanishes in certain key situations. Most notably, in the rational nilpotent situation the relative periodic homology vanishes.
1.3 The “topological” version
However, as Goodwillie and Waldhausen pointed out, Hochschild homology in itself contains much too little information to be a useful starting point for measuring algebraic K-theory and they conjectured the existence of a version built on the sphere spectrum \(\mathbb S\) instead of the integers \({\mathbb Z}\) and the smash product ∧ instead of the tensor product ⊗. This idea was realized by Bökstedt and dubbed “topological Hochschild homology,”  or—emphasizing that this is nothing but Hochschild homology over \(\mathbb S\)—
or—emphasizing that this is nothing but Hochschild homology over \(\mathbb S\)— .
.
Topological Hochschild homology has a richer inner life than Hochschild homology over the integers , and Bökstedt et al. [10] used this to define topological cyclic homology and prove an algebraic K-theory version of the Novikov conjecture. Although predating the first fully adequate setups for \(\mathbb S\)-algebras, their approach critically used the ability to move freely between \(\mathbb S\) and \({\mathbb Z}\) as ground rings and that rationally the difference is very small.
Topological Hochschild homology gained further credibility from the fact [62, 56, 27, 26] that it agreed with stable K-theory as predicted by Goodwillie and Waldhausen. Stable K-theory is a version of Bloch’s tangent space, where the dual numbers \(A\ltimes \epsilon A=A[\epsilon ]/\epsilon ^2\) is replaced by a square zero extension \(A\ltimes M\) where the connectivity of M is allowed to tend to infinity—it is the differential of algebraic K-theory in a way made precise by Goodwillie’s calculus of functors. Related to early ideas of Goodwillie, Lindenstrauss, and McCarthy [41] show that it actually is (relatively) fair to think of  as the Taylor tower of K-theory. This also sheds light on the nature of the action by cyclic group \(C_n\subseteq \mathbb T\): it is a remnant of the action by the symmetric group hiding behind the denominator n! in the usual Taylor series. Much of this insight was clear already at the time of [47].
as the Taylor tower of K-theory. This also sheds light on the nature of the action by cyclic group \(C_n\subseteq \mathbb T\): it is a remnant of the action by the symmetric group hiding behind the denominator n! in the usual Taylor series. Much of this insight was clear already at the time of [47].
It is not only the connection to algebraic K-theory that makes topological cyclic homology and its relatives interesting. Topological cyclic homology carries interesting information from an algebro-geometric and number theoretic point of view, as a theory with close connections to motivic, étale, crystalline and de Rham cohomology. Some of this was clear from the very start, but some aspects have become apparent more recently, see e.g., [33] and [34].
1.4 The cyclotomic trace
The cyclotomic trace  , first defined by Bökstedt et al. [10], refined in [22] and beautifully pinned down in [6] and [7], is of crucial importance for two reasons:
, first defined by Bökstedt et al. [10], refined in [22] and beautifully pinned down in [6] and [7], is of crucial importance for two reasons:
-
1.
 has surprisingly often been possible to calculate
has surprisingly often been possible to calculate -
2.
the homotopy fiber K inv of the cyclotomic trace
 is very well behaved.
is very well behaved.
The starting point for many applications is that the K-theory of finite fields is known by Quillen [50] and that topological cyclic homology is possible to calculate in a number of difficult situations. From there the following omnibus theorem will take you a long way.
Theorem 1.4.1
Let A → B be a map of connective \(\mathbb S\)-algebras such that the map π 0A → π 0B is a surjection with kernel I.
- Locally constant :
-
If I is nilpotent, then the map K invA → K inv(B) is a stable equivalence [ 22]
- Rigidity :
-
If π 0A and π 0B are commutative and (π 0A, I) is a Henselian pair, then the map K inv(A) → K inv(B) is a stable equivalence with mod-n coefficients for \(n\in {\mathbb N}\) [ 13]
- Closed excision :
-
If C → B is a map of connective \(\mathbb S\)-algebras and \(D=A\times ^h_BC\) the homotopy pullback, then

is a homotopy pullback square [ 40].
□
Closed excision was proved rationally by Cortiñas [20], after completion by Geisser and Hesselholt [28] for rings and in general by Dundas–Kittang [23]. Land and Tamme’s preprint [40] removes an unnecessary surjectivity condition from the integral result of [24].
The combined outcome of the calculations of  and Theorem 1.4.1 has been that a vast range of calculations in algebraic K-theory has become available, at least after profinite completion, but also integrally when coupled with motivic calculations. Even a somewhat random and very inadequate listing of results would include [10, 9, 35, 52, 4, 53, 54, 51, 36, 29, 30, 3, 49, 32, 2, 1, 43]. See [45] and [22] for more background on these methods.
and Theorem 1.4.1 has been that a vast range of calculations in algebraic K-theory has become available, at least after profinite completion, but also integrally when coupled with motivic calculations. Even a somewhat random and very inadequate listing of results would include [10, 9, 35, 52, 4, 53, 54, 51, 36, 29, 30, 3, 49, 32, 2, 1, 43]. See [45] and [22] for more background on these methods.
1.5 The original construction of 
Bökstedt et al. [10] relied on equivariant stable homotopy theory to produce a “naively invariant” theory out of categorical fixed points with respect to the finite cyclic subgroups C
m of the circle. In particular, if m|n the model for  provided by Bökstedt comes with a hands-on restriction map
provided by Bökstedt comes with a hands-on restriction map

related to the restriction map in Example 0.0.1. The restriction map has very good homotopical properties; for instance, if p is a prime, it fits into the “fundamental cofibration sequence”

i.e., the homotopy fiber of the restriction map \(R_{p^n}^{p^{n-1}}\) is naturally equivalent to the homotopy orbits  . The algebraic analog of the restriction map is the restriction map of truncated Witt vectors, and the inclusion of fixed points
. The algebraic analog of the restriction map is the restriction map of truncated Witt vectors, and the inclusion of fixed points

turns out to mirror the Frobenius. Focusing on one prime p, one defines

Note that one has full homotopic control of this construction. For instance, if a map A → B induces an equivalence  , the fundamental cofibration sequences guarantee that the same is true for all \(C_{p^n}\)-fixed points and ultimately
, the fundamental cofibration sequences guarantee that the same is true for all \(C_{p^n}\)-fixed points and ultimately  is an equivalence too.
is an equivalence too.
After p-completion, the inclusion of the p-power roots of unity induces an equivalence of classifying spaces  , and so the target of the natural map
, and so the target of the natural map

(given by restricting to the Frobenius maps and mapping the fixed points to the homotopy fixed points) is equivalent after p-completion to  , and one defines integral topological cyclic homology by the pullback
, and one defines integral topological cyclic homology by the pullback

Hesselholt and Madsen packaged in [35] the information about the nature of the restriction map in the language of stable equivariant homotopy theory via their notion of cyclotomic spectra by focusing on the so-called geometric fixed points ΦN (which we will discuss more extensively in Sections 2.2 and 2.3) and one way of stating this is that there is an equivalence between  and its C
p-geometric fixed points
and its C
p-geometric fixed points  , see Lemma 3.3.1.
, see Lemma 3.3.1.
1.6 The Nikolaus–Scholze approach
The fundamental cofibration sequence/cyclotomic structure implies that the categorical fixed points of topological Hochschild homology is a homotopy invariant (for instance,  is the homotopy pullback of a diagram of the form
is the homotopy pullback of a diagram of the form  ). Nikolaus and Scholze [48] showed that this gives rise to an extremely elegant formula expressing topological cyclic homology in terms of functors that are manifestly homotopy invariant; namely as the homotopy fiber of a certain map
). Nikolaus and Scholze [48] showed that this gives rise to an extremely elegant formula expressing topological cyclic homology in terms of functors that are manifestly homotopy invariant; namely as the homotopy fiber of a certain map

from the homotopy fixed points to the profinite completion of the Tate-construction of topological Hochschild homology.
2 The special version
We have seen that there are many reasons to consider Γ-spaces. If we are especially careful (as we will be) it models symmetric monoidal categories very faithfully but still has very good algebraic properties and is a common framework for various points of view of the “vector spaces over the field with one element.” In what follows, we explore how we can formulate some important invariants in this special context.
2.1 Γ-spaces as a generalization of symmetric monoids
Graeme Segal introduced Γ-spaces as an infinite delooping machine in [58], and Manos Lydakis [44] realized that this very down-to-earth approach actually possessed very good properties. Other useful sources for the properties of Γ-spaces are Bousfield and Friedlander [11] and Schwede [57]. As we try to elucidate below, apart from being very concrete, one of the benefits of Γ-spaces is that their algebraic origin is very clear.
A symmetric monoid is a set M together with a multiplication and a unit element so that any two maps M ×j → M obtained by composing maps in the diagram

are equal. The diagram is mirrored by the diagram of sets

We will need to encode the two projections M × M → M as well, and for this purpose we add a basepoint and consider the category Γo of finite pointed sets (the functions must preserve the base point), so that the diagram governing the axioms of a monoid looks like

where k + = {0, 1, …, k}. Segal realized that if one wants to relax the axioms for symmetric monoids so that they only are true up to some sort of equivalence (as for instance is the case for symmetric monoidal categories) it is fruitful to extend this diagram to all finite pointed sets: send k + to HM(k +) = M ×k and a pointed function ϕ: k + → l + to
This is the so-called Eilenberg–Mac Lane construction which identifies the category of symmetric monoids with a combinatorially easily recognizable subcategory of the category of Γ-sets (pointed functors from the category Γo of finite pointed sets to pointed sets): we get an isomorphism between the categories of symmetric monoids and of the full category of Γ-sets sending ∨ to × strictly (e.g.,3+ = 1+ ∨ 1+ ∨ 1+ must be sent to the triple product of the values at 1+). The projections HM(k +) = M ×k → M = HM(1+) are given by the characteristic functions
for i = 1, …k and the multiplication M × M → M is given by ∇: 2+ → 1+ with ∇(1) = ∇(2) = 1.
We want to be able to handle not only symmetric monoids but also symmetric monoidal categories, so we allow a simplicial direction to harbor morphisms: Let
-
\(\mathcal S_*=\) pointed simplicial sets (“spaces”),
-
Γo = pointed finite sets,
-
\(\Gamma {\mathcal S_*}=\) “Γ-spaces” = pointed functors \(\Gamma ^o\to \mathcal S_*\).
Note that (up to natural isomorphism) it is enough to specify a Γ-space on the skeletal subcategory containing the objects of the form k + only.
2.1.1 Smash as a generalization of tensor
The smash product—even more than its sibling the tensor product—is often shrouded in mystery, but I insists it is a natural object forced on us by bilinearity and can be motivated as follows: Fiddling with the functoriality of the Eilenberg–Mac Lane construction

defined above we see that a transformation HM → HN is uniquely given by its value on 1+: it comes from a unique homomorphism M → N, and the canonical map  is an isomorphism (actually, of spaces, but you may ignore this enrichment if you just want to understand the smash of Γ-sets). However,
is an isomorphism (actually, of spaces, but you may ignore this enrichment if you just want to understand the smash of Γ-sets). However,  is obviously itself a symmetric (simplicial) monoid and
is obviously itself a symmetric (simplicial) monoid and

(where \(k^{\prime }_+{\wedge } k_+\cong k'k_+\) is the smash of finite pointed sets), so if we define the internal morphism object by \( \underline {\Gamma {\mathcal S_*}}(X,Y)=\{k_+\mapsto \Gamma {\mathcal S_*}(X,Y(-{\wedge } k_+))\}\in \Gamma {\mathcal S_*}\) for arbitrary \(X,Y\in \Gamma {\mathcal S_*}\) we get a natural isomorphism of Γ-spaces

Now, we want the smash product to be the adjoint:
and the usual Yoneda yoga “solving the equation with respect toX∧Y ” gives us the smash product by means of a concrete coend formula
i.e., as the “weighted average of all pointwise smash products.” Even more concretely, we have an identification between maps \(X{\wedge } Y\to Z\in \Gamma {\mathcal S_*}\) and transformations X(m +)∧Y (n +) → Z(m +∧n +) natural in m +, n + ∈ Γo, specifying X∧Y up to unique isomorphism.
This affords \(\Gamma {\mathcal S_*}\) the structure of a closed symmetric monoidal category. This categorical construction is a special case of the Day construction known since the 1970s but it was Lydakis who realized that it actually was the relevant construction for stable homotopy theory [44].
The unit for the smash is the inclusion \(\Gamma ^o\subseteq \mathcal S_*\) denoted either by \(\mathbb S\) or Γo(1+, −) and often referred to as the sphere spectrum (since under the equivalence between the stable homotopy categories of Γ-spaces and connective spectra \(\mathbb S\) corresponds to the actual sphere spectrum).
Hence it makes sense to talk about monoids with respect to the smash products, and we refer to these as \(\mathbb S\)-algebras. By design, the Eilenberg–Mac Lane construction is lax symmetric monoidal from  to \((\Gamma {\mathcal S_*},{\wedge },\mathbb S)\) and so takes \({\mathbb N}\)-algebras (aka. rigs or semi-rings—they do not necessarily have additive inverses but otherwise satisfy the axioms of rings) to \(\mathbb S\)-algebras.
to \((\Gamma {\mathcal S_*},{\wedge },\mathbb S)\) and so takes \({\mathbb N}\)-algebras (aka. rigs or semi-rings—they do not necessarily have additive inverses but otherwise satisfy the axioms of rings) to \(\mathbb S\)-algebras.
2.1.2 Special Γ-spaces
Although simplicial monoids are too restrictive for our purposes, some Γ-spaces are more important than others (in particular those that arise from symmetric monoidal categories) and we consider Segal’s “up to homotopy” notion.
A Γ-space \(X\in \Gamma {\mathcal S_*}\) is isomorphic to the Eilenberg–Mac Lane construction of a symmetric monoid if and only if
is an isomorphism for all k ≥ 0. The “up to homotopy” notion is the following
Definition 2.1.3
A Γ-space X is special if δ k: X(k +) → X(1+)×k is a weak equivalence for all k.
An equivalent, and for our purposes better, way of expressing this is as follows. For k + ∈ Γo, consider the inclusion
Under the Yoneda isomorphisms \(X(k_+)\cong \Gamma {\mathcal S_*}(\Gamma ^o(k_+,-),X)\) and \(X(1_+)^{\times k}\cong \Gamma {\mathcal S_*}(\Gamma ^o(1_+,-){\wedge } k_+,X)\) we see that δ k corresponds to \(s_k^*\colon \Gamma {\mathcal S_*}(\Gamma ^o(k_+,-),X)\to \Gamma {\mathcal S_*}(\Gamma ^o(1_+,-){\wedge } k_+,X) \). Let
Example 2.1.4
Among examples of special Γ-spaces we have those that arise from symmetric monoidal categories: The Eilenberg–Mac Lane construction extends from symmetric monoids to symmetric monoidal categories—and in this guise it is often referred to as algebraic K-theory
by incorporating automorphisms into the construction (functorially rectifying the pseudo-functor you get by taking the formula for monoids either through one of the standard machines or by hand ), and all special Γ-spaces are unstably equivalent to something in its image [46].
This is yet another manifestation of the idea that \(\Gamma {\mathcal S_*}\) represents the categorification of the category of symmetric monoids. Driving home this message, de Brito and Moerdijk [8] prove a special refinement of the famous Barratt–Priddy–Quillen theorem: “the canonical map \(\mathbb S\to H\Sigma \) is a fibrant replacement in the special structure,” where Σ is the category of finite sets and isomorphisms.
The problem is that standard operations of special Γ-spaces give output that is not special (case in point: the smash product), and the standard remedy is to allow for all Γ-spaces, but localize with respect to\({\mathcal L}\). We will need to do this in the presence of extra symmeries, so we will bake this into the presentation from the start.
2.2 Symmetries on Γ-spaces
From now on, let G be a finite group. A pointed G-set is a pointed set together with an action of G preserving the base point. Let (deleting “the category of” for convenience)
-
\(\Gamma ^o_G\): finite pointed G-sets and all (not necessarily equivariant) pointed maps
-
\(\mathcal S_G\): pointed simplicial G-sets and all (not necessarily equivariant) pointed maps;
\(G\mathcal S_*\): pointed simplicial G-sets and pointed G-equivariant maps
-
\(\Gamma _{G}\mathcal {S}_G\): pointed G-functors \(\Gamma ^o_G\to \mathcal S_G\) and G-natural transformations; \(\Gamma G\mathcal S_*\): pointed functors \(\Gamma ^o\to G\mathcal S_*\) and natural transformations; in other words, G-objects in \(\Gamma {\mathcal S_*}\).
To elucidate the distinctions, let us list some functors connecting these (see Shimakawa [59])
-
the inclusion \(\nu \colon \Gamma ^o\subseteq \Gamma ^o_G\) giving a finite pointed set the trivial G-action is an equivalence of categories with retraction \(\Gamma ^o_G\to \Gamma ^o\) the forgetful functor.
-
sending \(X\in \Gamma _{G}\mathcal S_G\) to \(\{k_+\to X(\nu k_+)\}\in G\mathcal S_*\) induces an equivalence \(\nu ^*\colon \Gamma _{G}\mathcal S_G\to \Gamma G\mathcal S_*\) with inverse \(\Gamma G\mathcal S_*\to \Gamma _{G}\mathcal S_G\) sending \(Y\in \Gamma G\mathcal S_*\) to \(\{A\mapsto Y(A)=\int ^{k_+}\Gamma ^o(k_+,A){\wedge } Y(k_+)\}\in \Gamma _{G}\mathcal S_G\) (with G acting diagonally on Γo(k +, A)∧Y (k +)).
Analogous to the set of maps \({\mathcal L}\) determining the special Γ-spaces we have the set \({\mathcal L}_G\) of inclusions
(where A is a G-set which for the sake of keeping \({\mathcal L}_G\) a set is of the form k + for some \(k\in {\mathbb N}\) and some homomorphism G → Σk) and we say that \(X\in \Gamma _{G}\mathcal S_G\) is special if the maps \(\Gamma _{G}\mathcal S_G(s_A,X)\in G\mathcal S_*\) are G-equivalences (i.e., for every subgroup H ⊆ G, the map of H-fixed points \(\Gamma _{G}\mathcal S_G(s_A,X)^H=\Gamma {\mathcal S_*}(s_A,X)^H\) is a weak equivalence
of simplicial sets).
2.2.1 Fixed points
If \(f\colon G\twoheadrightarrow J\) is a surjective group homomorphism with kernel N we let
be the categorical and geometric fixed point functors sending \(X\in \Gamma _{G}\mathcal S_G\) to the objects in \(\Gamma _{J}\mathcal S_J\) sending \(V\in \Gamma ^o_J\) to
(with the two maps in the coequalizer given by functoriality Γo(W′, W)∧X(W′) → X(W) and composition Γo(W N, V )∧ Γo(W′, W)N → Γo([W′]N, V )). Although weird-looking when presented like this without any motivation, the geometric fixed points are in many ways more convenient. In particular, ΦN preserves much structure, like colimits and smash; a fact that becomes particularly potent when coupled with the isomorphism
(for \(A\in \Gamma ^o_G\) and \(K\in \mathcal S_G\)) obtained from the dual Yoneda lemma plus the fact that for G-spaces fixed points commute with smash. This isomorphism is the Γ-space version of “geometric fixed points commute with forming the suspension spectrum.”
By writing out the definitions we see that ΦN has a very special effect on the elements of \({\mathcal L}_G\):
Lemma 2.2.2
If \(f\colon G\twoheadrightarrow J\) is a surjective group homomorphism with kernel N and \(A\in \Gamma ^o_G\) , then

commutes.
Note that since [f ∗V ]N = V , we have a canonical isotropy separation map
2.2.2 Model structures
We record a minimum of the model theoretic properties that we need. Readers unfamiliar with this technology can for a large part ignore this and the next section at the price of accepting as black boxes the special equivalences and the few references to (co)fibrant replacements occurring later (in particular to Lemma 2.2.9).
The projective model structure on \(\Gamma _{G}\mathcal S_G\) is the one where a map X → Y is a fibration (resp. weak equivalence) if for every subgroup H ⊆ G and \(V\in \Gamma ^o_G\), the induced map X(V )H → Y (V )H is a (Kan) fibration (resp. weak equivalence) in \(\mathcal S_*\).
As sets of generating cofibrations and generating acyclic cofibrations for the projective structure on \(\Gamma _{G}\mathcal S_G\) we may choose
where A varies over \(\Gamma ^o_G\) and H over the subgroups of G and \(\Lambda ^n_k\subseteq \Delta [n]\) is the k-th horn in the n-simplex. The source and targets of the maps in I G and J G are finitely presented, and so the projective structure is finitely generated. The internal morphism object is
Cell induction implies that smashing with a cofibrant object preserves projective equivalences.
Definition 2.2.4
The special model structure on \(\Gamma _{G}\mathcal S_G\) is the one obtained from the projective model structure by (left Bousfield) localizing with respect to\({\mathcal L}_G\). The weak equivalences and fibrations in the special structure are referred to as special equivalences and special fibrations, whereas—since the cofibrations are the same in the projective structure and its localizations—we refer to the cofibrations simply as cofibrations without any qualifications.
Note 2.2.5
Even if we started with the Joyal structure, the cofibrations would remain the same.
Explicitly, a map \(A\to B \in \Gamma _{G}\mathcal S_G\) with A, B cofibrant is a special equivalence if and only if for all specially fibrant (special and projectively fibrant) \(Z\in \Gamma _{G}\mathcal S_G\), the induced map
is a weak equivalence on all fixed points. In general, a map is a special equivalence if its (projective) cofibrant replacement is.
Lemma 2.2.6
Smashing with a cofibrant object preserves special equivalences.
Proof
Let \(C\in \Gamma _{G}\mathcal S_G\) be cofibrant. Since smashing with cofibrant objects preserves projective equivalences, we may consider the case of a special equivalence A → B with A and B cofibrant. If Z is specially fibrant and \(V\in \Gamma ^o_G\), then the map \(Z(V{\wedge }-)\to \mathcal S_*(V,Z)\in \Gamma _{G}\mathcal S_G\) is a projective equivalence and so the internal morphism object \( \underline {\Gamma _{G}\mathcal S_G}(C,Z)\) is specially fibrant. By the adjointness of smash and internal morphism object, this implies that A∧C → B∧C is a special equivalence. □
2.2.3 Special fibrant replacements and geometric fixed points
We need some control over special fibrant replacements in \(\Gamma _{G}\mathcal S_G\), so for the moment we allow ourselves to be a bit technical. For \(s_A\colon \Gamma ^o(1_+,-){\wedge } A\to \Gamma ^o(A,-)\in {\mathcal L}_G\), let
be the result of applying the simplicial mapping cylinder construction to s A, so that \(\tilde s_A\) is a cofibration while localizing with respect to\(\tilde {\mathcal L}_G=\{\tilde s_A\}\) still gives the special structure on \(\Gamma _{G}\mathcal S_G\). Finally, we let \(\Lambda ({\mathcal L}_G)\,{=}\,\{\tilde s_A\square i\,|\,\tilde s_A\,{\in }\,\tilde {\mathcal L}_G,i\,{\in }\, I_G\}\). Here \(\square \) is the “pushout product”: if f : X → X′ and g : Y → Y ′, then \(f\square g\) is the universal map form the pushout to the final vertex X′∧ Y ′ in

The following results show that we have good control over the specially fibrant objects.
Lemma 2.2.8
Consider a map \(f\colon X\to Y\in \Gamma _{G}\mathcal S_G\) with Y specially fibrant. Then f is a special fibration if and only if f has the right lifting property with respect to \(\Lambda ({\mathcal L}_G)\cup J_G\). In particular, X is specially fibrant if X →∗ has the right lifting property with respect to \(\Lambda ({\mathcal L}_G)\cup J_G\).
By the small object argument, we construct a specially fibrant replacement functor X → X fG as a relative \((\Lambda ({\mathcal L}_G)\cup J_G)\)-cell. A cell induction using Lemma 2.2.2 then gives that
Lemma 2.2.9
If \(f\colon G\twoheadrightarrow J\) is a surjection of groups with kernel N and \(X\in \Gamma _{G}\mathcal S_G\) then the geometric N-fixed points applied to the specially fibrant replacement, Φ N(X) → Φ N(X fG), is a special equivalence in \(\Gamma _{J}\mathcal S_J\).
Note 2.2.10
There is a slight variant that is occasionally useful. Note that the source and targets in \(\Lambda ({\mathcal L}_G)\cup J_G\) are cofibrant, so smashing one of these with a projective equivalence \(X\overset {\sim }{\rightarrow } Y\in \Gamma _{G}\mathcal S_G\) gives a projective equivalence. Since cofibrant replacements are projective equivalences we get that all the maps in \((\Lambda ({\mathcal L}_G)\cup J_G){\wedge } \Gamma _{G}\mathcal S_G\) are special equivalences. Applying this to the construction in [25, 3.3.2] we get a fibrant replacement \(\Gamma _{G}\mathcal S_G\)-functor
In particular, we get an induced map of internal morphism objects
R GX is specially fibrant and X → R GX is a special equivalence (it may not be a cofibration).
2.3 Fixed points of smash powers
The (co)domains of the generating cofibrations behave nicely with respect to the smash product:
Lemma 2.3.1
If \(A,A'\in \Gamma ^o_G\) and \(K,K'\in \mathcal S_G\) , then the smash
(for \(B,B'\in \Gamma ^o_G\) ) induces an isomorphism
2.3.1 Smash powers
If \(X\in \Gamma _{G}\mathcal S_G\) we can form smash indexed over arbitrary finite sets S:
(either by choosing orderings on every S and coherently sticking to these choices or defining the S-fold smash in a symmetric fashion from scratch as we did for S = {1, 2}). This will at the outset only be functorial with respect to bijections of sets, but if X has more structure (if for instance X is an \(\mathbb S\)-algebra) then we obtain more functoriality as in [12]. However, the functoriality in mere bijections means that all the symmetries of S are present in the smash: ∧SX is an Aut(S)-object in \(\Gamma _{G}\mathcal S_G\), or equivalently, an element in \(\Gamma ^o(\mathrm {Aut}(S)\times G)\mathcal S_*\simeq \Gamma _{\mathrm {Aut}(S)\times G}\mathcal S_{\mathrm {Aut}(S)\times G}\).
For some applications one may want to consider cases where S varies over sets with some prescribed group interacting with G. However, for our current purposes, it even suffices to focus on the symmetries of S, not on the symmetries of the incoming Γ-spaces. So, for simplicity we will start with \(X\in \Gamma {\mathcal S_*}\) and since then “G” is freed from its duties and is such a good letter for a group, we let G be a group acting on S and view the S-fold smash as a functor
Note that
is cofibrant (where A ∧S is considered as an object in \(\Gamma ^o_G\) and K ∧S an object in \(\mathcal S_G\)) and a cell induction yields
Lemma 2.3.3
If S is a finite G-set, then the S-fold smash \(\bigwedge _S\colon \Gamma {\mathcal S_*}\to \Gamma _{G}\mathcal S_G\) preserves cofibrations.
2.3.2 The Geometric diagonal
The geometric fixed points treat smash powers of cofibrant objects like fixed points of sets treat Cartesian power. The beginning of the induction needed to show this is
Lemma 2.3.5
If \(f\colon G\twoheadrightarrow J\) is a surjection of groups with kernel N, then the dual Yoneda lemma gives isomorphisms
Inspired by the observation 2.3.5 we define, following the pattern laid out in e.g., [12, 37, 39], a chain of natural (in \(X\in \Gamma {\mathcal S_*}\)) transformations connecting ∧S∕NX and ΦN∧SX, which in the case when X is cofibrant(!) gives an isomorphism
called the geometric diagonal. The tricky part is the functoriality in S. For Example 0.0.1 there is no requirement, and for topological Hochschild homology, as discussed in Section 3.3, when X is an \(\mathbb S\)-algebra and G is a cyclic group we only need functoriality with respect to the structure maps in the (subdivisions of the simplicial) circle. For commutative \(\mathbb S\)-algebras this is much more demanding since we have to be more careful with our cofibration hypotheses and typically we want functoriality with respect to a wide range of functions of finite sets.
3
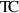 in a special world
in a special world
It is relatively straightforward to express (topological) Hochschild homology in Γ-spaces: you simply do exactly as Goodwillie and Walhausens envisioned: in the standard complex replace the tensor with the smash (tensor over \(\mathbb S\)). Just as in the algebraic case there are flatness concerns, but that is all you need to worry about (and taken care of by the unproblematic demand that the input being cofibrant).
However, if you want to make further refinements like cyclic homology you need to take a right derived version (aka a fibrant replacement). Magically, Bökstedt’s topological Hochschild homology is an explicit version of such a right derived version: its very construction has built in deloopings with respect to all finite subgroups of the circle. This extremely fortunate state of affairs is crucially used in [10] for the definition of topological cyclic homology; most importantly the restriction map is simply obtained by restricting an equivariant map to the fixed points.
Since we want to avoid group completion we do not want to deloop, but we do want to retain homotopical control. Luckily, the categorical approach works wonderfully, as we now will sketch.
3.1 Cyclic objects
Connes’ cyclic category Λ and its variants Λa (for a = 1, 2, …, ∞ with Λ = Λ1) can be obtained as follows. Fixing a there is an object [n]a ∈ Λa for each n = 0, 1, …. For fixed m and n the set of morphisms Λ∞([m]∞, [n]∞) is the set of order preserving functions \(f\colon \frac 1{m+1}{\mathbb Z}\to \frac 1{n+1}{\mathbb Z}\) with \(f\left (\frac {i}{m+1}+1\right )=f\left (\frac {i}{n+1}\right )+1\) for all i. Fixing a < ∞, we let Λa([m]a, [n]a) be the quotient of Λ∞([m]∞, [n]∞) by the equivalence relation generated by f ∼ f + a. Composition in Λa is composition of functions.
The cyclic group C a of order a acts on Λa by the identity on objects and by f↦f − 1 on Λa([m]a, [n]a). This means that functors from Λa comes with a natural C a-action. The group of automorphisms \(\mathrm {Aut}_{\Lambda _a}([n]_a)\) is cyclic of order a(n + 1) generated by the class t a,n of the function \(\frac 1{n+1}{\mathbb Z}\to \frac 1{n+1}{\mathbb Z}\) given by \(i\mapsto i+\frac 1{n+1}\). The faithful inclusion j a: Δ → Λa is given by j[n] = [n]a and by sending ϕ ∈ Δ([m], [n]) to the class of the function \(\frac 1{m+1}{\mathbb Z}\to \frac 1{n+1}{\mathbb Z}\) with \(\frac {i}{m+1}\mapsto \frac {\phi (i)}{n+1}\) for 0 ≤ i ≤ m.
A functor X from \(\Lambda ^{{ }^o}=\Lambda _1^{{ }^o}\) to some category is called a cyclic object in that category and the composite j ∗X = Xj = Xj 1 is referred to as the underlying simplicial object.
A particularly important example is the cyclic set S 1 = Λ[0] modeling the circle. An element in \(S^1_n=\Lambda ([n],[0])\) can be composed uniquely into an automorphism of [n] followed by the unique map [n] → [0] coming from Δ. Hence, \(S^1_n\) is identified with the cyclic group AutΛ([n]) of order n + 1. Restricting to Δop we have the usual simplicial circle: j ∗S 1 = Δ[1]∕∂ Δ[1].
3.2 Edgewise subdivision
Essentially because |S 1| is homeomorphic to the circle, the geometric realization of cyclic object comes equipped with an action by the circle group \(\mathbb T=|S^1|\). Bökstedt, Hsiang, and Madsen [10] introduced the edgewise subdivision as a way of making the action of the finite cyclic subgroups of \(\mathbb T\) combinatorial. Let sd r: Δ → Δ be the r-fold concatenation S↦S ⊔⋯ ⊔ S. Note that sd r[k − 1] = [kr − 1] and that sd rsd s = sd rs. This extends to the cyclic situation

by setting sd r(t ar) = t a. Precomposing any cyclic object X with sd r gives sd rX = X ∘ sd r, the r-fold edgewise subdivision of X, giving us a functor from cyclic objects to Λr-objects. We note that (sd rX)k−1 = X kr−1 and that
From [10] we know that there is a natural C r-equivariant homeomorphism \(D\colon |sd_{C_r}X|\cong |X|\), where the C r-action on \(|sd_{C_r}X|\) comes from the C r-action on \(sd_{C_r}X\), and the action on |X| comes from the cyclic structure on X. The resulting homeomorphism \(|sd_{C_r}X^{C_r}|\cong |X|{ }^{C_r}\) is \(\mathbb T\)-equivariant if we let \(\mathbb T\) act on \(|sd_{C_r}X^{C_r}|\) via the cyclic structure, and on \(|X|{ }^{C_r}\) through the isomorphism \(\mathbb T\cong \mathbb T/C_r\).
3.3 (Topological) Hochschild homology
Topological cyclic homology makes sense in the special world. This is not obvious since the classical construction relies on various objects being equivalent, and when the meaning of “equivalent” is changed not all constructions translate. There is much to be said, for instance in regard to compatibility, but we present only what is needed for setting up the framework.
(Topological) Hochschild homology for \(\mathbb S\)-algebras is defined exactly as ordinary Hochschild homology, with \(({{\mathcal Ab}},\otimes ,{\mathbb Z})\) replaced by \((\Gamma {\mathcal S_*},{\wedge },\mathbb S)\): if A is an \(\mathbb S\)-algebra then  is the cyclic Γ-space
is the cyclic Γ-space
with face maps induced by multiplication, degeneracy maps by insertion of identities, and the cyclic operator acting by cyclic permutation. As in the algebraic case where the analogous definition is problematic unless the ring is flat, we really only ever use this definition for sufficiently flat A—being cofibrant is more than enough. We have chosen to use the notation  rather than
rather than  to emphasize that we are using the categorical smash powers.
to emphasize that we are using the categorical smash powers.
Recall the discussion of the smash powers and geometric fixed points from Section 2.3. When A is a cofibrant, then the geometric diagonal \(\Phi ^{C_p}\bigwedge _{S^{\sqcup p}}A\cong \bigwedge _{S}A\) is an isomorphism 2.3.4 which is natural in A and natural enough in S to give an isomorphism on the level of Hochschild homology:
Lemma 3.3.1
If A is a cofibrant \(\mathbb S\) -algebra, then the geometric diagonal yields an isomorphism

Hence the considerations of Section 2.2.1 give an isotropy separation or “restriction” map

and an inclusion of fixed points “Frobenius”  and we want to build the theory from here.
and we want to build the theory from here.
Note 3.3.2
There are technicalities regarding fibrant replacements that we for the sake of exposition have glossed over, but which can be handled as follows. If X is a \(C_{p^n}\)-Γ-space (simplicial or topological) we let \(X\to X^{f_n}\) be the specially \(C_{p^n}\)-fibrant replacement. Note that if \(i\colon C_{p^k}\subseteq C_{p^n}\), then \(i^*X\to i^*(X^{f_n})\) is a special \(C_{p^k}\)-fibrant replacement, and so naturally equivalent (but not equal) to \(i^*X\to i^*(X)^{f_k}\). In all honesty, the “restriction map” is the chain

given by composing the map

induced by fibrant replacement with \((-)^{f_{n-1}C_{p^{n-1}}}\) of

(the unmarked equivalences are annoying but innocent jugglings with fibrant replacements written out in its most primitive form), whereas the Frobenius is the inclusion of fixed points (and change of fibrant replacement)

3.4 Topological cyclic homology
We define  as the homotopy limit over the R and F-maps (which makes sense since the arrows pointing in the “wrong” directions are equivalences and we can choose an explicit model taking this into account).
as the homotopy limit over the R and F-maps (which makes sense since the arrows pointing in the “wrong” directions are equivalences and we can choose an explicit model taking this into account).
Note that for any \(\mathbb T\)-space X, there is a chain \(X^{f_nC_{p^n}}\to X^{f_n\, hC_{p^n}}\overset {\sim }{\leftarrow } X^{hC_{p^n}} \) compatible with the inclusion of fixed points (we use \(E\mathbb T\) for all the \(EC_{p^n}\)s occurring in the homotopy fixed points), so that we get a map

where after p-completion the latter object is naturally equivalent to the homotopy \(\mathbb T\)-fixed points  . Ultimately, this leads us to the same definition for
. Ultimately, this leads us to the same definition for  as in the stable case.
as in the stable case.
Definition 3.4.1
Let A be a cofibrant \(\mathbb S\)-algebra. Then the topological cyclic homology  is the homotopy pullback of
is the homotopy pullback of

Note 3.4.2
I do not know whether the setup of Nikolaus and Scholze of Section 1.6 translates well to the special situation since the nature of the Tate-construction is somewhat mysterious in this case.
Note 3.4.3
The extension from \(\mathbb S\)-algebras to categories enriched in Γ-spaces is straightforward and left to the reader.
4 On modules and monoids
We end by discussing some algebraic properties. In particular we show that if B is the Boolean \({\mathbb N}\)-algebra, then HB-modules are specially homotopy discrete. For this purpose we first give a more concrete characterization of special equivalences. Recall that a map A → B of cofibrant Γ-spaces is a special equivalence if for all special and projectively fibrant \(Z\in \Gamma {\mathcal S_*}\) the induced map \(\Gamma {\mathcal S_*}(B,Z)\to \Gamma {\mathcal S_*}(A,Z)\in \mathcal S_*\) is a weak equivalence. In general, a map A → B is a special equivalence if its cofibrant replacement is a special equivalence.
Using the fibrant replacement \(\Gamma {\mathcal S_*}\)-functor of 2.2.10 (we use the enriched fibrant replacement in order to apply it to modules) we can simplify this to the statement that A → B is a special equivalence if and only if RA → RB is a projective equivalence, which in view of the fact that RA and RB are special is the same as saying that RA(1+) → RB(1+) is a weak equivalence of simplicial sets.
4.1 Linearization
The Eilenberg–Mac Lane construction has a left adjoint  with LX given as the coequalizer in
with LX given as the coequalizer in  of the two maps
of the two maps
where \({\mathbb N}[-]\) is free functor adjoint to the forgetful functor from symmetric monoids to pointed sets. Adapting the argument in [57, Lemma 1.2] we get
Lemma 4.1.1
The unit of adjunction A → LHA is an isomorphism. The adjunction is enriched in the sense that it extends to a natural isomorphism

and L is strong symmetric monoidal: the maps induced by the enriched adjunction are isomorphisms \({\mathbb N}\cong L(\mathbb S)\) , \(LX\otimes _{\mathbb N} LY\cong L(X{\wedge } Y)\) . Furthermore, L preserves finite products.
Lemma 4.1.2
The Eilenberg–Mac Lane functor  is a right Quillen map, both with respect to the projective and the special structures on \(\Gamma {\mathcal S_*}\).
is a right Quillen map, both with respect to the projective and the special structures on \(\Gamma {\mathcal S_*}\).
Proof
It is enough to show that H preserves acyclic fibrations and fibrations between fibrant objects (see [21]). Since finite products preserve fibrations and equivalences, H sends fibrations/weak equivalences to projective fibrations/equivalences. Since acyclic fibrations in the projective and special structures coincide, it is enough to show that if  is a fibration between fibrant objects then HM → HN is a special fibration. This follows since HM, HN are specially fibrant and HM → HN projectively fibrant. □
is a fibration between fibrant objects then HM → HN is a special fibration. This follows since HM, HN are specially fibrant and HM → HN projectively fibrant. □
Note that, contrary to what is the case in other formalisms the Eilenberg–Mac Lane functor very rarely takes cofibrant values.
Lemma 4.1.3
If M is a nontrivial simplicial symmetric monoid, then \(HM\in \Gamma {\mathcal S_*}\) is not cofibrant.
Proof
If \(HM\in \Gamma {\mathcal S_*}\) is cofibrant, then LHM≅M is cofibrant in  with the projective structure ((L, H) is a Quillen pair), which is equivalent to M being a retraction of a free (in the sense of Quillen) simplicial symmetric monoid. Hence, it is enough to consider the case where M is free simplicial symmetric monoid. In that case, if n is the smallest dimension in which M
n is nontrivial (here we use that M ≠ 0), then M
n is actually a nontrivial free symmetric monoid, and so contains \({\mathbb N}\) as a retract. By Schwede [57, A3], if HM were cofibrant then HM
n—and hence \(H{\mathbb N}\)—would be a wedge of representables.
with the projective structure ((L, H) is a Quillen pair), which is equivalent to M being a retraction of a free (in the sense of Quillen) simplicial symmetric monoid. Hence, it is enough to consider the case where M is free simplicial symmetric monoid. In that case, if n is the smallest dimension in which M
n is nontrivial (here we use that M ≠ 0), then M
n is actually a nontrivial free symmetric monoid, and so contains \({\mathbb N}\) as a retract. By Schwede [57, A3], if HM were cofibrant then HM
n—and hence \(H{\mathbb N}\)—would be a wedge of representables.
However, \(H{\mathbb N}\) has no proper retracts: if \(X\subseteq H{\mathbb N}\to X\) is a retract, then \(LX\subseteq {\mathbb N}\to LX\) is a retract (of symmetric monoids), implying that either LX = 0 or \(LX={\mathbb N}\). In the first case, the inclusion \(X\subseteq H{\mathbb N}\) factors over HLX = 0, so that X = 0, and in the second case the composite \(H{\mathbb N}\to X\to HLX\) is an isomorphism implying that the surjection \(H{\mathbb N}\to X\) is an injection too.
Combining this information, we get that if \(H{\mathbb N}\) were cofibrant, \(H{\mathbb N}\) would be representable, which is nonsense given that representables are finite. □
4.1.1 The special path monoid
The special analog of the set of path components is the following.
Definition 4.1.5
If X is a Γ-space, then the special path monoid of X is the symmetric monoid \(\pi ^{\mathrm {special}}_0X=\pi _0RX(1_+)\).
It can alternatively be seen as the monoid of all maps \(\mathbb S\to X\) in the special homotopy category, but for our purposes the characterization in terms of linearization is more useful.
Lemma 4.1.6
A special equivalence X → Y (of not necessarily cofibrant Γ-spaces) induces an isomorphism π 0LX≅π 0LY . If Z is special, then the map π 0Z(1+) → π 0LZ induced by the unit Z → HLZ is an isomorphism. Hence, for any \(X\in \Gamma {\mathcal S_*}\) we have a chain of natural isomorphisms
Proof
Since L is a left Quillen functor, it sends special equivalences between cofibrant objects to weak equivalences, so we need to show that π 0L sends projective equivalences to isomorphisms. This is true since π 0 commutes with colimits.
Likewise, if Z is special, then π 0Z(1+) inherits a monoid structure and π 0LZ is a coequalizer of a diagram
exactly recovering the generators \(\pi _0Z(1_+)\subseteq {\mathbb N}\pi _0 Z(1_+)\) □
Corollary 4.1.7
The isomorphism of Lemma 4.1.6 and the monoidality of L of Lemma 4.1.1 induce isomorphisms
In particular, if  , then \(\pi ^{\mathrm {special}}_0(HA{\wedge }^L HB)\cong \pi ^{\mathrm {special}}_0(HA{\wedge } HB)\cong \pi _0A\otimes _{\mathbb N}\pi _0B\).
, then \(\pi ^{\mathrm {special}}_0(HA{\wedge }^L HB)\cong \pi ^{\mathrm {special}}_0(HA{\wedge } HB)\cong \pi _0A\otimes _{\mathbb N}\pi _0B\).
The superscript L signifies the derived smash, where the factors are functorially replaced by cofibrant objects. For instance we could use the standard simplicial replacement (symmetric version, Hochschild-style structure maps) for X∧LY with Γ-space of q-simplices
Generally, X∧Y and X∧LY are not specially equivalent but, as we see, their path monoids coincide. On the other hand, allowing a simplicial direction offers no real advantage (or disadvantage) when considering B-modules (or for that matter modules over other rigs where 1 + ⋯ + 1 = 1).
Example 4.1.8
Consider the Boolean algebra B = {0, 1} (0 is “false” and 1 is “true”) with the operation + being “or” ((B, +) is isomorphic to \({\mathbb Z}/2^\times \), the integers mod 2 under multiplication) and ⋅ being “and”. This is the \({\mathbb N}\)-algebra on {0, 1} defined by 1 + 1 = 1. If we force all elements to have negatives, then we can cancel 1 on each side of the expression 1 + 1 = 1 resulting in 1 = 0: the group completion is the trivial group.
The advantage of the special world is that we do not group complete and so the theory is not trivialized, but the special theory of HB-modules is of an essentially discrete nature unless we change the underlying weak equivalences on simplicial sets (e.g., by using quasi-categories instead of Kan complexes as our fibrant objects).
The fact that HB-modules are specially homotopy discrete can be seen as follows. It is enough to consider specially fibrant HB-modules M and show that the map
is a projective equivalence, or equivalently, that M(1+) → π 0M(1+) is a weak equivalence. Consider the part of the functoriality of the multiplication map HB∧M → M expressed in the diagram

Choosing a basepoint x ∈ M(1+) we see that for i > 0 the lower row defines a group homomorphism +: π i(M(1+), x) × π i(M(1+), x) → π i(M(1+), x). If α ∈ π i(M(1+), x) and 0 ∈ π i(M(1+), x) is the constant loop, then tracing through the diagram we see that α = 0 + α = α + 0, so that Eckmann–Hilton forces + to be the usual group operation in π i(M(1+), x), but also α + α = α, which means that π i(M(1+), x) = 0.
This is somewhat disappointing. For instance, it means that multiplication B∧LB →B is a special equivalence. Since topological Hochschild homology  is a B-module it also means that
is a B-module it also means that  is a special equivalence. This is a good motivation for not only to moving from the stable to the special world, but also from Kan simplicial sets to quasi-categories (where not all paths have homotopy inverses, and so the argument about homotopy discreteness fails).
is a special equivalence. This is a good motivation for not only to moving from the stable to the special world, but also from Kan simplicial sets to quasi-categories (where not all paths have homotopy inverses, and so the argument about homotopy discreteness fails).
If A is an \(\mathbb S\)-algebra, then the fixed points of the smash powers and  are generally not an A-module since it is built out of non-split extensions (for instance, \(\pi ^{\mathrm {special}}_0(H{\mathbb F}_2{\wedge }^LH{\mathbb F}_2)^{C_2}\cong {\mathbb Z}/4{\mathbb Z}\) is not an \({\mathbb F}_2\)-algebra), but Example 4.1.8 still makes it clear that the presence of elements killed by group completion puts severe restrictions on the theory. In addition, even when such a theory is set up, it is by no means clear that is has any of the calculational power that the original setup of Bökstedt, Hsiang, and Madsen had.
are generally not an A-module since it is built out of non-split extensions (for instance, \(\pi ^{\mathrm {special}}_0(H{\mathbb F}_2{\wedge }^LH{\mathbb F}_2)^{C_2}\cong {\mathbb Z}/4{\mathbb Z}\) is not an \({\mathbb F}_2\)-algebra), but Example 4.1.8 still makes it clear that the presence of elements killed by group completion puts severe restrictions on the theory. In addition, even when such a theory is set up, it is by no means clear that is has any of the calculational power that the original setup of Bökstedt, Hsiang, and Madsen had.
Note 4.1.9
Example 4.1.8 showed that if 1 + 1 = 1 in an \({\mathbb N}\)-algebra, then its modules are specially discrete. It should however be noted that the ∞ + 1 = ∞ encountered in Example 0.0.2 for the category \(\mathrm {Vect}_k^{\text{count}}\) of countable vector spaces is less dramatic. The associated Γ-space (wrt. ⊕) is specially fibrant with value at 1+ (the nerve of) the groupoid \(\mathrm {Vect}_k^{\text{count}}\). This groupoid has a lot of automorphisms and so is not homotopy discrete.
References
Vigleik Angeltveit. On the K-theory of truncated polynomial rings in non-commuting variables. Bull. Lond. Math. Soc., 47(5):731–742, 2015.
Vigleik Angeltveit, Teena Gerhardt, Michael A. Hill, and Ayelet Lindenstrauss. On the algebraic K-theory of truncated polynomial algebras in several variables. J. K-Theory, 13(1):57–81, 2014.
Christian Ausoni. On the algebraic K-theory of the complex K-theory spectrum. Invent. Math., 180(3):611–668, 2010.
Christian Ausoni and John Rognes. Algebraic K-theory of topological K-theory. Acta Math., 188(1):1–39, 2002.
S. Bloch. On the tangent space to Quillen K-theory. In AlgebraicK-theory, I: HigherK-theories (Proc. Conf., Battelle Memorial Inst., Seattle, Wash., 1972), pages 205–210. Lecture Notes in Math., Vol. 341. Springer, Berlin, 1973.
Andrew J. Blumberg, David Gepner, and Gonçalo Tabuada. A universal characterization of higher algebraic K-theory. Geom. Topol., 17(2):733–838, 2013.
Andrew J. Blumberg, David Gepner, and Gonçalo Tabuada. Uniqueness of the multiplicative cyclotomic trace. Adv. Math., 260:191–232, 2014.
P. Boavida de Brito and I. Moerdijk. Dendroidal spaces, Γ-spaces and the special Barratt-Priddy-Quillen theorem. ArXiv e-prints, January 2017.
M. Bökstedt, G. Carlsson, R. Cohen, T. Goodwillie, W. C. Hsiang, and I. Madsen. On the algebraic K-theory of simply connected spaces. Duke Math. J., 84(3):541–563, 1996.
M. Bökstedt, W. C. Hsiang, and I. Madsen. The cyclotomic trace and algebraic K-theory of spaces. Invent. Math., 111(3):465–539, 1993.
A. K. Bousfield and E. M. Friedlander. Homotopy theory of Γ-spaces, spectra, and bisimplicial sets. In Geometric applications of homotopy theory (Proc. Conf., Evanston, Ill., 1977), II, volume 658 of Lecture Notes in Math., pages 80–130. Springer, Berlin, 1978.
M. Brun, B. I. Dundas, and M. Stolz. Equivariant Structure on Smash Powers. ArXiv e-prints, April 2016.
D. Clausen, A. Mathew, and M. Morrow. K-theory and topological cyclic homology of henselian pairs. ArXiv e-prints, March 2018.
Alain Connes. C ∗ algèbres et géométrie différentielle. C. R. Acad. Sci. Paris Sér. A-B, 290(13):A599–A604, 1980.
Alain Connes. Spectral sequence and homology of currents for operator algebras. Math. Forschungsinstitut Oberwolfach Tagungsbericht, 42/81, 1981.
Alain Connes. Cohomologie cyclique et foncteurs Extn. C. R. Acad. Sci. Paris Sér. I Math., 296(23):953–958, 1983.
Alain Connes. Noncommutative differential geometry. Inst. Hautes Études Sci. Publ. Math., (62):257–360, 1985.
Alain Connes and Caterina Consani. Absolute algebra and Segal’s Γ-rings: au dessous de \(\overline {\mathrm {Spec}(\mathbb {Z})}\). J. Number Theory, 162:518–551, 2016.
Alain Connes and Max Karoubi. Caractère multiplicatif d’un module de Fredholm. C. R. Acad. Sci. Paris Sér. I Math., 299(19):963–968, 1984.
Guillermo Cortiñas. The obstruction to excision in K-theory and in cyclic homology. Invent. Math., 164(1):143–173, 2006.
Daniel Dugger. Replacing model categories with simplicial ones. Trans. Amer. Math. Soc., 353(12):5003–5027, 2001.
Bjørn Ian Dundas, Thomas G. Goodwillie, and Randy McCarthy. The local structure of algebraic K-theory, volume 18 of Algebra and Applications. Springer-Verlag London, Ltd., London, 2013.
Bjørn Ian Dundas and Harald Øyen Kittang. Excision for K-theory of connective ring spectra. Homology Homotopy Appl., 10(1):29–39, 2008.
Bjørn Ian Dundas and Harald Øyen Kittang. Integral excision for K-theory. Homology Homotopy Appl., 15(1):1–25, 2013.
Bjørn Ian Dundas, Oliver Röndigs, and Paul Arne Østvær. Enriched functors and stable homotopy theory. Doc. Math., 8:409–488, 2003.
Bjørn Ian Dundas. Relative K-theory and topological cyclic homology. Acta Math., 179(2):223–242, 1997.
Bjørn Ian Dundas and Randy McCarthy. Stable K-theory and topological Hochschild homology. Ann. of Math. (2), 140(3):685–701, 1994.
Thomas Geisser and Lars Hesselholt. Bi-relative algebraic K-theory and topological cyclic homology. Invent. Math., 166(2):359–395, 2006.
Thomas Geisser and Lars Hesselholt. On the K-theory and topological cyclic homology of smooth schemes over a discrete valuation ring. Trans. Amer. Math. Soc., 358(1):131–145, 2006.
Thomas Geisser and Lars Hesselholt. On the vanishing of negative K-groups. Math. Ann., 348(3):707–736, 2010.
Thomas G. Goodwillie. Relative algebraic K-theory and cyclic homology. Ann. of Math. (2), 124(2):347–402, 1986.
Lars Hesselholt. On the K-theory of planar cuspical curves and a new family of polytopes. In Algebraic topology: applications and new directions, volume 620 of Contemp. Math., pages 145–182. Amer. Math. Soc., Providence, RI, 2014.
Lars Hesselholt. The big de Rham-Witt complex. Acta Math., 214(1):135–207, 2015.
Lars Hesselholt. Topological Hochschild homology and the Hasse-Weil zeta function. In An alpine bouquet of algebraic topology, volume 708 of Contemp. Math., pages 157–180. Amer. Math. Soc., Providence, RI, 2018.
Lars Hesselholt and Ib Madsen. On the K-theory of finite algebras over Witt vectors of perfect fields. Topology, 36(1):29–101, 1997.
Lars Hesselholt and Ib Madsen. On the K-theory of local fields. Ann. of Math. (2), 158(1):1–113, 2003.
Michael A. Hill, Michael J. Hopkins, and Douglas C. Ravenel. On the non-existence of elements of Kervaire invariant one. In Proceedings of the International Congress of Mathematicians—Seoul 2014. Vol. II, pages 1219–1243. Kyung Moon Sa, Seoul, 2014.
John D. S. Jones. Cyclic homology and equivariant homology. Invent. Math., 87(2):403–423, 1987.
T. A. Kro. Involutions on S[ ΩM]. ArXiv Mathematics e-prints, October 2005.
M. Land and G. Tamme. On the K-theory of pullbacks. ArXiv e-prints, 2018.
Ayelet Lindenstrauss and Randy McCarthy. On the Taylor tower of relative K-theory. Geom. Topol., 16(2):685–750, 2012.
Jean-Louis Loday and Daniel Quillen. Cyclic homology and the Lie algebra homology of matrices. Comment. Math. Helv., 59(4):569–591, 1984.
Wolfgang Lück, Holger Reich, John Rognes, and Marco Varisco. Algebraic K-theory of group rings and the cyclotomic trace map. Adv. Math., 304:930–1020, 2017.
Manos Lydakis. Smash products and Γ-spaces. Math. Proc. Cambridge Philos. Soc., 126(2):311–328, 1999.
Ib Madsen. Algebraic K-theory and traces. In Current developments in mathematics, 1995 (Cambridge, MA), pages 191–321. Internat. Press, Cambridge, MA, 1994.
Michael A. Mandell. An inverse K-theory functor. Doc. Math., 15:765–791, 2010.
Randy McCarthy. Relative algebraic K-theory and topological cyclic homology. Acta Math., 179(2):197–222, 1997.
T. Nikolaus and P. Scholze. On topological cyclic homology. ArXiv e-prints, July 2017.
Crichton Ogle. On the homotopy type of A( ΣX). J. Pure Appl. Algebra, 217(11):2088–2107, 2013.
Daniel Quillen. Cohomology of groups. In Actes du Congrès International des Mathématiciens (Nice, 1970), Tome 2, pages 47–51. Gauthier-Villars, Paris, 1971.
J. Rognes and C. Weibel. Two-primary algebraic K-theory of rings of integers in number fields. J. Amer. Math. Soc., 13(1):1–54, 2000. Appendix A by Manfred Kolster.
John Rognes. Algebraic K-theory of the two-adic integers. J. Pure Appl. Algebra, 134(3): 287–326, 1999.
John Rognes. Two-primary algebraic K-theory of pointed spaces. Topology, 41(5):873–926, 2002.
John Rognes. The smooth Whitehead spectrum of a point at odd regular primes. Geom. Topol., 7:155–184 (electronic), 2003.
Rekha Santhanam. Units of equivariant ring spectra. Algebr. Geom. Topol., 11(3):1361–1403, 2011.
Roland Schwänzl, Ross Staffeldt, and Friedhelm Waldhausen. Stable K-theory and topological Hochschild homology of A ∞ rings. In AlgebraicK-theory (Poznań, 1995), volume 199 of Contemp. Math., pages 161–173. Amer. Math. Soc., Providence, RI, 1996.
Stefan Schwede. Stable homotopical algebra and Γ-spaces. Math. Proc. Cambridge Philos. Soc., 126(2):329–356, 1999.
Graeme Segal. Categories and cohomology theories. Topology, 13:293–312, 1974.
Kazuhisa Shimakawa. A note on ΓG-spaces. Osaka J. Math., 28(2):223–228, 1991.
R. W. Thomason. Symmetric monoidal categories model all connective spectra. Theory Appl. Categ., 1:No. 5, 78–118 (electronic), 1995.
B. L. Tsygan. Homology of matrix Lie algebras over rings and the Hochschild homology. Uspekhi Mat. Nauk, 38(2(230)):217–218, 1983.
Friedhelm Waldhausen. Algebraic K-theory of spaces, concordance, and stable homotopy theory. In Algebraic topology and algebraicK-theory (Princeton, N.J., 1983), volume 113 of Ann. of Math. Stud., pages 392–417. Princeton Univ. Press, Princeton, NJ, 1987.
Charles A. Weibel. Nil K-theory maps to cyclic homology. Trans. Amer. Math. Soc., 303(2):541–558, 1987.
Acknowledgements
Apart from obvious input from Alain Connes this tribute has benefitted from enlightening conversations with M. Brun, K. Consani, L. Hesselholt, M. Hill, and C. Schlichtkrull. Also, the preprint [8] by de Brito and Moerdijk and the papers of Santhanam [55] and Mandell [46] were inspirational. The author also wants to thank an anonymous referee for correcting an unfortunate misconception about events in the early 1980s.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
Dundas, B.I. (2019). Cyclic homology in a special world. In: Chamseddine, A., Consani, C., Higson, N., Khalkhali, M., Moscovici, H., Yu, G. (eds) Advances in Noncommutative Geometry. Springer, Cham. https://doi.org/10.1007/978-3-030-29597-4_5
Download citation
DOI: https://doi.org/10.1007/978-3-030-29597-4_5
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-29596-7
Online ISBN: 978-3-030-29597-4
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)




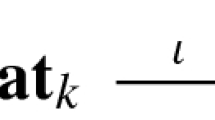
 has surprisingly often been possible to calculate
has surprisingly often been possible to calculate is very well behaved.
is very well behaved.

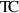 in a special world
in a special world