Abstract
We present two methods for proving confluence of left-linear term rewrite systems. One is hot-decreasingness, combining the parallel/development closedness theorems with rule labelling based on a terminating subsystem. The other is critical-pair-closing system, allowing to boil down the confluence problem to confluence of a special subsystem whose duplicating rules are relatively terminating.
Supported by JSPS KAKENHI Grant Number 17K00011 and Core to Core Program.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
We present two results for proving confluence of first-order left-linear term rewrite systems, which extend and generalise three classical results: Knuth and Bendix’ criterion [19] and strong and parallel closedness due to Huet [17]. Our idea is to reduce confluence of a term rewrite system \(\mathcal {{R}}\) to that of a subsystem \(\mathcal {{C}}\) comprising rewrite rules needed for closing the critical pairs of \(\mathcal {{R}}\). In Sect. 3 we introduce hot-decreasingness, requiring that critical pairs can be closed using rules that are either below those in the peak or in a terminating subsystem \(\mathcal {{C}}\). In Sect. 4 we introduce the notion of a critical-pair-closing system and present a confluence-preservation result based on relative termination \(\mathcal {{C}}_{ d }/\mathcal {{R}}\) of the duplicating part \(\mathcal {{C}}_{ d }\) of \(\mathcal {{C}}\). For the left-linear systems we consider, our first criterion generalises both Huet’s parallel closedness and Knuth and Bendix’ criterion, and the second Huet’s strong closedness. In Sect. 5, we assess viability of the new techniques, reporting on their implementation and empirical results.
Huet’s parallel closedness result relies on the notion of overlap whose geometric intuition is subtle [1, 24], and reasoning becomes intricate for development closedness as covered by Theorem 2. We factor the classical theory of overlaps and critical pairs through the encompassment lattice in which overlapping redex-patterns is taking their join and the amount of overlap between redex-patterns is computed via their meet, thus allowing to reason algebraically about overlaps. Methodologically, our contribution here is the introduction of the lattice-theoretic language itself, relevant as it allows one to reason about occurrences of patternsFootnote 1 and their amount of (non-)overlap, omnipresent in deduction. Technically, whereas Huet’s critical pair lemma [17] is well-suited for proving confluence of terminating TRSs, it is ill-suited to do so for orthogonal TRSs. Our lattice-theoretic results remedy this, allowing to decompose a reduction R both horizontally (as  ) and vertically (as \(R_1^{[x\mathbin {{:}{=}}R_2]}\)), enabling both termination and orthogonality reasoning in confluence proofs (Theorem 2).
) and vertically (as \(R_1^{[x\mathbin {{:}{=}}R_2]}\)), enabling both termination and orthogonality reasoning in confluence proofs (Theorem 2).
In the last decade various classical confluence results for term rewrite systems have been factored through the decreasing diagrams method [28, 30] for proving confluence of abstract rewrite systems, often leading to generalisations along the way: e.g. Felgenhauer’s multistep labelling [13] generalises Okui’s simultaneous closedness [27], the layer framework [12] generalises Toyama’s modularity [33], critical pair systems [16] generalise both orthogonality [31] and Knuth and Bendix’ criterion [19], and Jouannaud and Liu generalise, among others [20], parallel closedness, but in a way we do not know how to generalise to development closedness [29]. This paper fits into this line of research.Footnote 2
We assume the reader is familiar with term rewriting [1, 9, 32] in general and confluence methods [17, 19, 30] in particular. Notions not explicitly defined in this paper can all be found in those works.
2 Preliminaries on Decreasingness and Encompassment
We recall the key ingredients of the decreasing diagrams method for proving confluence, see [20, 26, 30, 32], and revisit the classical notion of critical pair, recasting its traditional account [1, 17, 19] based on redexes (substitution instances of left-hand sides) into one based on redex-patterns (left-hand sides).
Decreasingness. Consider an ARS comprising an I-indexed relation \({\rightarrow } = \bigcup _{{\ell }\in I} {\rightarrow _{\ell }}\) equipped with a well-founded strict order \(\succ \). We refer to \(\{ {\kappa }\in I \mid {\ell }\succ {\kappa }\}\) by \({{\curlyvee }{\ell }}\), and to \({{\curlyvee }{\ell }} \cup {{\curlyvee }{\kappa }}\) by \({{\curlyvee }{\ell },{\kappa }}\). For a subset J of I we define \(\rightarrow _J\) as \(\bigcup _{{\ell }\in J} {\rightarrow _{\ell }}\).
Definition 1
A diagram for a peak  is decreasing if its closing conversion has shape
is decreasing if its closing conversion has shape  . An ARS in this setting is called decreasing if every peak can be completed into a decreasing diagram.
. An ARS in this setting is called decreasing if every peak can be completed into a decreasing diagram.
One may think of decreasing diagrams as combining the diamond property [25, Theorem 1] (via the steps in the closing conversion with labels \({\ell }\), \({\kappa }\)) at the basis of confluence of orthogonal systems [6, 31], with local confluence diagrams [25, Theorem 3] (via the conversions with labels \({{\curlyvee }{\ell },{\kappa }}\)) at the basis of confluence of terminating systems [19, 21].
Theorem 1
([28, 30]). An ARS is confluent if it is decreasing. Conversely, every countable ARS that is confluent, is decreasing for some set of indices I.
For the converse part it suffices that the set of labels I is a doubleton, a result that can be reformulated without referring to decreasing diagrams, as follows.
Lemma 1
([11]). A countable confluent rewrite relation has a spanning forest.
Here a spanning forest for \({\rightarrow }\) is a relation  that is spanning (
that is spanning ( ) and a forest, i.e. deterministic (
) and a forest, i.e. deterministic ( implies \({b}\mathrel {{=}}{c}\)) and acyclic.
implies \({b}\mathrel {{=}}{c}\)) and acyclic.
Critical Peaks Revisited. We introduce clusters as the structures obtained after the matching of the left-hand side of a rule in a rewrite step, but before its replacement by the right-hand side. When proving the aforementioned results in Sects. 3 and 4, we use them as a tool to analyse overlaps and critical peaks. To illustrate our notions we use the following running example. We refer to [16, 32] for the notion of multistep.
Example 1
In the TRS \(\mathcal {{R}}\) with \({\varrho }(x) \mathbin {:}f(f(x))\mathbin {{\rightarrow }}g(x)\) the term \({t}=f(f(f(f(a))))\) allows the step \(f({\varrho }(f(a))) \mathbin {:}{t}\mathrel {{\rightarrow }}f(g(f(a)))\) and multistep  .
.
Here \(f({\varrho }(f(a)))\) and \({\varrho }({\varrho }(a))\) are so-called proofterms, terms representing proofs of rewritability in rewriting logic [22, 32]. The source of a proofterm can be computed by the 2nd-order substitution  of the left-hand side of the rule for the rule symbolFootnote 3 \(f({\varrho }(f(a)))^{\mathsf {src}} =f({\varrho }(f(a)))^{\llbracket {\varrho }\mathbin {{:}{=}}\lambda x.f(f(x))\rrbracket } \mathrel {{=}}f(f(f(f(a)))) \), and, mutatis mutandis, the same for the target via \(\mathsf {tgt}\). Proofclusters, introduced here, abstract from such proofterms by allowing to represent the matching and substitution phases of multisteps as well, by means of let-expressions.
of the left-hand side of the rule for the rule symbolFootnote 3 \(f({\varrho }(f(a)))^{\mathsf {src}} =f({\varrho }(f(a)))^{\llbracket {\varrho }\mathbin {{:}{=}}\lambda x.f(f(x))\rrbracket } \mathrel {{=}}f(f(f(f(a)))) \), and, mutatis mutandis, the same for the target via \(\mathsf {tgt}\). Proofclusters, introduced here, abstract from such proofterms by allowing to represent the matching and substitution phases of multisteps as well, by means of let-expressions.
Example 2
The multistep in Example 1 comprises three phases [28, Chapter 4]:
-
1.
 denotes matching f(f(x)) twice;
denotes matching f(f(x)) twice; -
2.
 denotes replacing by \({\varrho }\) twice;
denotes replacing by \({\varrho }\) twice; -
3.
 denotes substituting g(x) twice.
denotes substituting g(x) twice.
To represent these we assume to have proofterms \({t}, {s}, {u}, \ldots \) over a signature comprising function symbols \({f}, {g}, {h}, \ldots \), rule symbols \({\varrho }, {\theta }, {\eta }, \ldots \), 2nd-order variables  , all having natural number arities, and 1st-order variables \({x}, {y}, {z}, \ldots \) (with arity \({0}\)).We call proofterms without 2nd-order variables or rule symbols, 1st-order proofterms respectively terms, ranged over by \({M}\), \({N}\), \({L}\), \(\ldots \).
, all having natural number arities, and 1st-order variables \({x}, {y}, {z}, \ldots \) (with arity \({0}\)).We call proofterms without 2nd-order variables or rule symbols, 1st-order proofterms respectively terms, ranged over by \({M}\), \({N}\), \({L}\), \(\ldots \).
Definition 2
A proofcluster is a let-expression  , where
, where
-
 is a vector
is a vector  of (pairwise distinct) second-order variables;
of (pairwise distinct) second-order variables; -
\(\varvec{Q}\) is a vector of length \({n}\) of closed \(\lambda \)-terms \(Q_{{i}} = \lambda \varvec{{x}_{{i}}}.{s}_{{i}}\), where \({s}_{{i}}\) is a proofterm and the length of the vector \(\varvec{{x}_{{i}}}\) of variables is the arity of
 ; and
; and -
\({t}\) is a proofterm, the body, with its 2nd-order variables among
 .
.
Its denotation  is
is  . It is a cluster if \({s}_{{1}},\ldots ,{s}_{{n}},{t}\) are terms.
. It is a cluster if \({s}_{{1}},\ldots ,{s}_{{n}},{t}\) are terms.
We let \({\varsigma }\), \({\zeta }\), \({\xi }\), \(\ldots \) range over (proof)clusters. They denote (proof)terms.
Example 3
Using \({\varsigma }\), \({\zeta }\), \({\xi }\) for the three let-expressions in Example 2, each is a proofcluster and \({\varsigma }\), \({\xi }\) are clusters. Their denotations are the term \(\llbracket {\varsigma }\rrbracket =f(f(f(f(a))))\mathrel {{=}}{t}\), proofterm \(\llbracket {\zeta }\rrbracket ={\varrho }({\varrho }(a))\), and term \(\llbracket {\xi }\rrbracket =g(g(a))\).
We assume the usual variable renaming conventions, both for the 2nd-order ones in let-binders and the 1st-order ones in \(\lambda \)-abstractions. We say a proofcluster \({\varsigma }\) is linear if every (let or \(\lambda \)) binding binds exactly once, and canonical [23] if, when a binding variable occurs to the left of another such (of the same type), then the first bound occurrence of the former occurs before that of the latter in the pre-order walk of the relevant proofterm.
Example 4
Let \({\zeta }'\) and \({\xi }'\) be the clusters  and
and  . Each of \({\varsigma }\), \({\zeta }'\), \({\xi }'\) denotes \({t}\) in Example 1. The cluster \({\varsigma }\) is linear and canonical, \({\zeta }'\) is canonical but not linear (
. Each of \({\varsigma }\), \({\zeta }'\), \({\xi }'\) denotes \({t}\) in Example 1. The cluster \({\varsigma }\) is linear and canonical, \({\zeta }'\) is canonical but not linear ( occurs twice in the body), and \({\xi }'\) is neither linear (z does not occur in f(y)) nor canonical (
occurs twice in the body), and \({\xi }'\) is neither linear (z does not occur in f(y)) nor canonical ( occurs outside of
occurs outside of  in the body).
in the body).
We adopt the convention that absent \(\lambda \)-binders are inserted linearly, canonically;  is \({\zeta }'\). Clusters witness encompassment
is \({\zeta }'\). Clusters witness encompassment  [9].
[9].
Proposition 1
 iff
iff  s.t.
s.t.  and
and  occurs once in \({u}\).
occurs once in \({u}\).
We define the size \({\parallel }{t}{\parallel }\) of a proofterm \({t}\) in a way that is compatible with encompassment. Formally, \({\parallel }{t}{\parallel }\) is the pair comprising the number of non-1st-order-variable symbols in \({t}\), and the sum over the 1st-order variables \({x}\), of the square of the number of occurrences of \({x}\) in \({t}\). Then  if
if  , where we (ab)use \({>}\) to denote the lexicographic product of the greater-than relation with itself, e.g.
, where we (ab)use \({>}\) to denote the lexicographic product of the greater-than relation with itself, e.g.  . For a proofcluster \({\varsigma }\) given by
. For a proofcluster \({\varsigma }\) given by  its pattern-size
its pattern-size  is \({\sum }_{{i}}{\parallel }{s}_{{i}}{\parallel }\) (adding component-wise, with empty sum \(({0}{,}{0})\)) and its body-size
is \({\sum }_{{i}}{\parallel }{s}_{{i}}{\parallel }\) (adding component-wise, with empty sum \(({0}{,}{0})\)) and its body-size  is \({\parallel }{t}{\parallel }\). Encompassment
is \({\parallel }{t}{\parallel }\). Encompassment  is at the basis of the theory of reducibility [7, Section 3.4.2]: \({t}\) is reducible by a rule \({\ell }\mathbin {{\rightarrow }}{r}\) iff
is at the basis of the theory of reducibility [7, Section 3.4.2]: \({t}\) is reducible by a rule \({\ell }\mathbin {{\rightarrow }}{r}\) iff  . For instance,
. For instance,  is a witness to reducibility of \({t}\) in Example 1. We call it, or simply f(f(x)), a pattern in \({t}\).
is a witness to reducibility of \({t}\) in Example 1. We call it, or simply f(f(x)), a pattern in \({t}\).
Definition 3
Let \({\varsigma }\) be a canonical linear proofcluster  with term \({t}\). We say \({\varsigma }\) is a multipattern if each \({s}_{{i}}\) is a non-variable 1st-order term, and \({\varsigma }\) is a multistep if each \({s}_{{i}}\) has shape \({\varrho }(\varvec{{x}})\), i.e. a rule symbol applied to a sequence of pairwise distinct variables. If
with term \({t}\). We say \({\varsigma }\) is a multipattern if each \({s}_{{i}}\) is a non-variable 1st-order term, and \({\varsigma }\) is a multistep if each \({s}_{{i}}\) has shape \({\varrho }(\varvec{{x}})\), i.e. a rule symbol applied to a sequence of pairwise distinct variables. If  has length \({1}\) we drop the prefix ‘multi’.
has length \({1}\) we drop the prefix ‘multi’.
We use \({\varPhi },{\varPsi },{\varOmega },\ldots \) to range over multisteps, and \({\phi },{\psi },{\omega },\ldots \) to range over steps. Taking their denotation yields the usual multistep [16, 32] and step ARSs  and \({\rightarrow }\) underlying a TRS \(\mathcal {{R}}\). These can be alternatively obtained by first applying \(\mathsf {src}\) and \(\mathsf {tgt}\) (of which only the former is guaranteed to yield a multipattern, by left-linearity) and then taking denotations: \(\llbracket {\varPhi }^{\mathsf {src}}\rrbracket \mathrel {{=}}\llbracket {\varPhi }\rrbracket ^{\mathsf {src}} \) and \(\llbracket {\varPhi }^{\mathsf {tgt}}\rrbracket \mathrel {{=}}\llbracket {\varPhi }\rrbracket ^{\mathsf {tgt}} \). Pattern- and body-sizes of multipatterns are compositional.
and \({\rightarrow }\) underlying a TRS \(\mathcal {{R}}\). These can be alternatively obtained by first applying \(\mathsf {src}\) and \(\mathsf {tgt}\) (of which only the former is guaranteed to yield a multipattern, by left-linearity) and then taking denotations: \(\llbracket {\varPhi }^{\mathsf {src}}\rrbracket \mathrel {{=}}\llbracket {\varPhi }\rrbracket ^{\mathsf {src}} \) and \(\llbracket {\varPhi }^{\mathsf {tgt}}\rrbracket \mathrel {{=}}\llbracket {\varPhi }\rrbracket ^{\mathsf {tgt}} \). Pattern- and body-sizes of multipatterns are compositional.
Proposition 2
For multipatterns \({\varsigma }\),\(\varvec{{\varsigma }}\) if \({\varsigma }\mathrel {{=}}{\varsigma }_{{0}}^{[\varvec{{x}}\mathbin {{:}{=}}\varvec{{\varsigma }}]}\) with each variable among \(\varvec{{x}}\) occurring once in the body of \({\varsigma }_{{0}}\), then  , and
, and  for all \({i}\), with strict inequality holding in case the substitution is not a bijective renaming. Here multipattern-substitution substitutes in the body and combines let-bindings.
for all \({i}\), with strict inequality holding in case the substitution is not a bijective renaming. Here multipattern-substitution substitutes in the body and combines let-bindings.
Multipatterns are ordered by refinement \({\sqsubseteq }\).
Definition 4
Let \({\varsigma }\) and \({\zeta }\) be multipatterns  and
and  . We say \({\varsigma }\) refines \({\zeta }\) and write \({\varsigma }\mathrel {{\sqsubseteq }}{\zeta }\), if there is a 2nd-order substitution \({\sigma }\) on
. We say \({\varsigma }\) refines \({\zeta }\) and write \({\varsigma }\mathrel {{\sqsubseteq }}{\zeta }\), if there is a 2nd-order substitution \({\sigma }\) on  with \({w}^{{\sigma }}\mathrel {{=}}{t}\) and
with \({w}^{{\sigma }}\mathrel {{=}}{t}\) and  for all \({i}\), with \(\varvec{{y}_{{i}}}\) the variables of \({u}_{{i}}\).
for all \({i}\), with \(\varvec{{y}_{{i}}}\) the variables of \({u}_{{i}}\).
Example 5
We have \({\varsigma }\mathrel {{\sqsubseteq }}{\varsigma }'\) with \({\varsigma }'\) being  , and \({\varsigma }\) as in Example 3, as witnessed by the 2nd-order substitution mapping
, and \({\varsigma }\) as in Example 3, as witnessed by the 2nd-order substitution mapping  to
to  .
.
Lemma 2
\({\sqsubseteq }\) is a finite distributive lattice [8] on multipatterns denoting a 1st-order term \({t}\), with least element \({\bot }\) the empty let-expression  , and greatest element \({\top }\) of shape
, and greatest element \({\top }\) of shape  with \(\varvec{{x}}\) the vector of variables in \({t}\).
with \(\varvec{{x}}\) the vector of variables in \({t}\).
Proof
(Idea). Although showing that \({\sqsubseteq }\) is reflexive and transitive is easy, showing anti-symmetry or existence of/constructions for meets \({\sqcap }\) and joins \({\sqcup }\), directly is not. Instead, it is easy to see that each multipattern  is determined by the set of the (non-empty, convex,Footnote 4 pairwise disjoint) sets of node positions of its patterns \({s}_{{i}}\) in \({t}\), and vice versa. For instance, the multipatterns \({\varsigma }\) and \({\varsigma }'\) in Example 5 are determined by
is determined by the set of the (non-empty, convex,Footnote 4 pairwise disjoint) sets of node positions of its patterns \({s}_{{i}}\) in \({t}\), and vice versa. For instance, the multipatterns \({\varsigma }\) and \({\varsigma }'\) in Example 5 are determined by  and
and  . Viewing multipatterns as sets in that way \({\varsigma }\mathrel {{\sqsubseteq }}{\zeta }\) iff \(\forall P\mathbin {{\in }}{\varsigma }\), \(\exists Q\mathbin {{\in }}{\zeta }\) with
. Viewing multipatterns as sets in that way \({\varsigma }\mathrel {{\sqsubseteq }}{\zeta }\) iff \(\forall P\mathbin {{\in }}{\varsigma }\), \(\exists Q\mathbin {{\in }}{\zeta }\) with  . Saying \(P,Q\mathbin {{\in }}{\varsigma }\mathbin {{\cup }}{\zeta }\) have overlap if
. Saying \(P,Q\mathbin {{\in }}{\varsigma }\mathbin {{\cup }}{\zeta }\) have overlap if  , denoted by \(P\mathrel {{\between }}Q\), characterising meets and joins now also is easy:
, denoted by \(P\mathrel {{\between }}Q\), characterising meets and joins now also is easy:
 , and
, and
 , where \(P_{{\between }} =\{Q\mathbin {{\in }}{\varsigma }\mathbin {{\cup }}{\zeta }\mathrel {|}P\mathrel {{\between }^{{*}}}Q\}\), i.e. the sets connected to \(P\) by successive overlaps. On this set-representation \({\sqsubseteq }\) can be shown to be a finite distributive lattice by set-theoretic reasoning, using that the intersection of two overlapping patterns is a pattern againFootnote 5. For instance, \({\bot }\) is the empty set and \({\top }\) is the singleton containing the set of all non-variable positions in \({t}\). \(\square \)
, where \(P_{{\between }} =\{Q\mathbin {{\in }}{\varsigma }\mathbin {{\cup }}{\zeta }\mathrel {|}P\mathrel {{\between }^{{*}}}Q\}\), i.e. the sets connected to \(P\) by successive overlaps. On this set-representation \({\sqsubseteq }\) can be shown to be a finite distributive lattice by set-theoretic reasoning, using that the intersection of two overlapping patterns is a pattern againFootnote 5. For instance, \({\bot }\) is the empty set and \({\top }\) is the singleton containing the set of all non-variable positions in \({t}\). \(\square \)
The (proof of the) lemma allows to freely switch between viewing multisteps and multipatterns as let-expressions and as sets of sets of positions, and to reason about (non-)overlap of multipatterns and multisteps in lattice-theoretic terms. We show any multistep  can be decomposed horizontally as
can be decomposed horizontally as  followed by
followed by  for any step
for any step  [16, 29], and vertically as some vector
[16, 29], and vertically as some vector  substituted in a prefix
substituted in a prefix  of \({\varPhi }\), and that peaks can be decomposed correspondingly.
of \({\varPhi }\), and that peaks can be decomposed correspondingly.
Definition 5
For a pair of multipatterns \({\varsigma }\),\({\zeta }\) denoting the same term its amount of overlapFootnote 6 and non-overlap is  respectively
respectively  , we say
, we say  ,
, is overlapping if
is overlapping if  , and critically overlapping if moreover
, and critically overlapping if moreover  and
and  is linear. This extends to peaks
is linear. This extends to peaks  via
via  and
and  .
.
Note \({\varsigma }\),\({\zeta }\) is overlapping iff \({\varsigma }\mathbin {{\Cap }}{\zeta }\mathrel {{\ne }}({0}{,}{0})\). Critical peaks  are classified by comparing the root-positions \(p_{{\phi }}\), \(p_{{\psi }}\) of their patterns with respect to the prefix order \(\prec _{ o }\), into being outer–inner (
are classified by comparing the root-positions \(p_{{\phi }}\), \(p_{{\psi }}\) of their patterns with respect to the prefix order \(\prec _{ o }\), into being outer–inner ( ), inner–outer (
), inner–outer ( ), or overlay (
), or overlay ( ), and induce the usual [1, 9, 17, 19, 26, 32] notion of critical pair
), and induce the usual [1, 9, 17, 19, 26, 32] notion of critical pair  .Footnote 7
.Footnote 7
Definition 6
A pair \(({\varsigma }'{,}{\zeta }')\) of overlapping patterns such that \({\varsigma }'\), \({\zeta }'\) are in the multipatterns \({\varsigma }\), \({\zeta }\) with  , is called inner, if it is minimal among all such pairs, comparing them in the lexicographic product of \(\prec _{ o }\) with itself, via the root-positions of their patterns, ordering these themselves first by \(\preceq _{ o }\). This extends to pairs of steps in peaks of multisteps via \(\mathsf {src}\).
, is called inner, if it is minimal among all such pairs, comparing them in the lexicographic product of \(\prec _{ o }\) with itself, via the root-positions of their patterns, ordering these themselves first by \(\preceq _{ o }\). This extends to pairs of steps in peaks of multisteps via \(\mathsf {src}\).
Proposition 3
If \(({\phi }{,}{\psi })\) is an inner pair for a critical peak  , and \({\phi }\mathbin {{{{\in }}}}{\varPhi }\), \({\psi }\mathbin {{{{\in }}}}{\varPsi }\) contract redexes at the same position, then
, and \({\phi }\mathbin {{{{\in }}}}{\varPhi }\), \({\psi }\mathbin {{{{\in }}}}{\varPsi }\) contract redexes at the same position, then  and
and  .
.
For patterns and peaks of ordinary steps, their join being top, entails they are overlapping, and the patterns in a join are joins of their constituent patterns.
Proposition 4
Linear patterns \({\varsigma }\),\({\zeta }\) are critically overlapping iff  .
.
Lemma 3
If \({\xi }={\varsigma }\mathbin {{\sqcup }}{\zeta }\) and \({\varsigma },{\zeta }\mathrel {{\sqsubseteq }}{\xi }\) are witnessed by the 2nd-order substitutions \({\sigma }\), \({\tau }\), for multipatterns \({\varsigma }\) and \({\zeta }\) given by  and
and  , then for all let-bindings
, then for all let-bindings  of \({\xi }\),
of \({\xi }\),  .
.
Lemma 4
(Vertical). A peak  of overlapping multisteps either is critical or it can be vertically decomposed as:
of overlapping multisteps either is critical or it can be vertically decomposed as:

for peaks  with
with  and
and  , for all \({i}\).
, for all \({i}\).
Let \({\varPhi }\), \({\varPsi }\) in  be given by
be given by  and
and  , for rules \({\varrho }_{{i}}(\varvec{{x}_{{i}}}) \mathbin {:}{\ell }_{{i}}\mathbin {{\rightarrow }}{r}_{{i}}\) and \({\theta }_{{j}}(\varvec{{y}_{{j}}}) \mathbin {:}{g}_{{j}}\mathbin {{\rightarrow }}{d}_{{j}}\). Lemma 2 entails that if
, for rules \({\varrho }_{{i}}(\varvec{{x}_{{i}}}) \mathbin {:}{\ell }_{{i}}\mathbin {{\rightarrow }}{r}_{{i}}\) and \({\theta }_{{j}}(\varvec{{y}_{{j}}}) \mathbin {:}{g}_{{j}}\mathbin {{\rightarrow }}{d}_{{j}}\). Lemma 2 entails that if  ,
,  are non-overlapping their patterns are (pairwise) disjoint, so that the join
are non-overlapping their patterns are (pairwise) disjoint, so that the join  is given by taking the (disjoint) union of the let-bindings:
is given by taking the (disjoint) union of the let-bindings:  for some \({L}\) such that
for some \({L}\) such that  and
and  . We define the joinFootnote 8
. We define the joinFootnote 8  and residual
and residual  by
by  respectively
respectively  , where, as substituting the right-hand sides \(\varvec{{d}}\) may lose being linear and canonical, we implicitly canonise and linearise the latter by reordering and replicating let-bindings. Then
, where, as substituting the right-hand sides \(\varvec{{d}}\) may lose being linear and canonical, we implicitly canonise and linearise the latter by reordering and replicating let-bindings. Then  , giving rise to the classical residual theory [2, 4, 6, 18], see [32, Section 8.7]. We let \({\phi }\mathbin {{{{\in }}}}{\varPhi }\) abbreviate
, giving rise to the classical residual theory [2, 4, 6, 18], see [32, Section 8.7]. We let \({\phi }\mathbin {{{{\in }}}}{\varPhi }\) abbreviate  .
.
Example 6
The steps \({\phi }\) and \({\psi }\) given by  respectively
respectively  , are non-overlapping, \({\phi },{\psi }\mathbin {{{{\in }}}}{\zeta }\),
, are non-overlapping, \({\phi },{\psi }\mathbin {{{{\in }}}}{\zeta }\),  , and
, and  , for \({\zeta }\) and \({\varrho }\) as in Example 3.
, for \({\zeta }\) and \({\varrho }\) as in Example 3.
Lemma 5
(Horizontal). A peak  of multisteps either
of multisteps either
-
1.
is non-overlapping and then
 , with the rule symbols occurring in \({\varPsi }{/}{\varPhi }\) contained in \({\varPsi }\) (and those in \({\varPhi }{/}{\varPsi }\) contained in \({\varPhi }\)); or
, with the rule symbols occurring in \({\varPsi }{/}{\varPhi }\) contained in \({\varPsi }\) (and those in \({\varPhi }{/}{\varPsi }\) contained in \({\varPhi }\)); or -
2.
it can be horizontally decomposed:
 for some peak
for some peak  of overlapping steps
of overlapping steps  .
.
The above allows to refactor the proof of the critical pair lemma [17, Lemma 3.1] for left-linear TRSs, as an induction on the amount of non-overlap between the steps in the peak, such that the critical peaks form the base case:
Lemma 6
A left-linear TRS is locally confluent if all critical pairs are joinable.
Proof
We show every peak  of empty or single steps is joinable, by induction on the amount of non-overlap (\({\phi }\mathbin {{\Cup }}{\psi }\)) ordered by \({>}\). We distinguish cases on whether \({\phi }\), \({\psi }\) are overlapping (\({\phi }\mathbin {{\Cap }}{\psi }\mathrel {{\ne }}({0}{,}{0})\)) or not. If \({\phi }\), \({\psi }\) do not have overlap, in particular when either \({\phi }\) or \({\psi }\) is empty, then we conclude by Lemma 5(1). If \({\phi }\), \({\psi }\) do have overlap, then by Lemma 4 the peak either
of empty or single steps is joinable, by induction on the amount of non-overlap (\({\phi }\mathbin {{\Cup }}{\psi }\)) ordered by \({>}\). We distinguish cases on whether \({\phi }\), \({\psi }\) are overlapping (\({\phi }\mathbin {{\Cap }}{\psi }\mathrel {{\ne }}({0}{,}{0})\)) or not. If \({\phi }\), \({\psi }\) do not have overlap, in particular when either \({\phi }\) or \({\psi }\) is empty, then we conclude by Lemma 5(1). If \({\phi }\), \({\psi }\) do have overlap, then by Lemma 4 the peak either
-
is critical and we conclude by assumption; or
-
can be (vertically) decomposed into smaller such peaks
 . Since these are \({>}\)-smaller, the induction hypothesis yields them joinable, from which we conclude by reductions and joins being closed under composition. \(\square \)
. Since these are \({>}\)-smaller, the induction hypothesis yields them joinable, from which we conclude by reductions and joins being closed under composition. \(\square \)
Remark 1
Apart from enabling our proof of Theorem 2 below, we think this refactoring is methodologically interesting, as it extends to (parallel and) simultaneous critical pairs, then yielding, we claim, simple statements and proofs of confluence results [13, 27] based on these and their higher-order generalisations.
3 Confluence by Hot-Decreasingness
Linear TRSs have a critical-pair criterion for so-called rule-labelling [16, 30, 35]: If all critical peaks are decreasing with respect to some rule-labelling, then the TRS is decreasing, hence confluent. We introduce the hot-labelling extending that result to left-linear TRSs. To deal with non-right-linear rules we make use of a rule-labelling for multisteps that is invariant under duplication, cf. [13, 35].
Remark 2
Naïve extensions fail. Non-left-linear TRSs need not be confluent even without critical pairs [32, Exercise 2.7.20]. That non-right-linear TRSs need not be confluent even if all critical peaks are decreasing for rule-labelling, is witnessed by [16, Example 8].
Definition 7
For a TRS \(\mathcal {{R}}\), terminating subsystem \(\mathcal {{C}}\subseteq \mathcal {{R}}\), and labelling of  -rules into a well-founded order \({\succ }\), hot-labelling \(\mathring{\mathcal {L}}\) maps a multistep
-rules into a well-founded order \({\succ }\), hot-labelling \(\mathring{\mathcal {L}}\) maps a multistep 
-
to the term \({t}\) if \({\varPhi }\) contains \(\mathcal {{C}}\)-rules only; and
-
to the set of \({\succ }\)-maximal
 -rules in \({\varPhi }\) otherwise.
-rules in \({\varPhi }\) otherwise.
The hot-order \(\mathring{{\succ }}\) relates terms by \({\rightarrow }^{{+}}_{\mathcal {{C}}}\), sets by \({\succ }_{{\mathsf {mul}}}\), and all sets to all terms.
Note \(\mathring{{\succ }}\) is a well-founded order as series composition [3] of \({\rightarrow }^{{+}}_{\mathcal {{C}}}\) and \({\succ }_{{\mathsf {mul}}}\), which are well-founded orders by the assumptions on \(\mathcal {{C}}\) and \({\succ }\). Taking the set of maximal rules in a multistep makes hot-labelling invariant under duplication. As with the notation \({{\curlyvee }{\ell }}\), we denote \(\{ {\kappa }\mid {\ell }\mathrel {\mathring{{\succ }}}{\kappa } \}\) by \({\mathring{{\curlyvee }}{\ell }}\), and \(\{ {\kappa }\mid {\ell }\mathrel {\mathring{{\succeq }}}{\kappa } \}\) by \({{{\shortmid }\!\mathring{{\curlyvee }}}{\ell }}\).
Definition 8
A TRS \(\mathcal {{R}}\) is hot-decreasing if its critical peaks are decreasing for the hot-labelling, for some \(\mathcal {{C}}\) and \({\succ }\), such that each outer–inner critical peak  for label \({\ell }\), is decreasing by a conversion of shape (oi):
for label \({\ell }\), is decreasing by a conversion of shape (oi):  .
.
Theorem 2
A left-linear TRS is confluent, if it is hot-decreasing.
Before proving Theorem 2, we give (non-)examples and special cases.
Example 7
Consider the left-linear TRS \(\mathcal {{R}}\):

By taking \(\mathcal {{C}}={{\emptyset }}\), labelling rules by themselves, and ordering \({\varrho }_{4}\mathrel {{\succ }}{\varrho }_{1},{\varrho }_{3},{\varrho }_{6}\) the only critical peak  can be completed into the decreasing diagram:
can be completed into the decreasing diagram:

Since the peak is outer–inner, the closing conversion must be of (oi)-shape  . It is, so the system is confluent by Theorem 2.
. It is, so the system is confluent by Theorem 2.
Example 8
Consider the left-linear confluent TRS \(\mathcal {{R}}\):

Since b is an \(\mathcal {{R}}\)-normal form, the only way to join the outer–inner critical peak  is by a conversion starting with a step
is by a conversion starting with a step  . As its label must be identical to the same step in the peak, not smaller, whether we choose \({\varrho }_{1}\) to be in \(\mathcal {{C}}\) or not, the peak is not hot-decreasing, so Theorem 2 does not apply.
. As its label must be identical to the same step in the peak, not smaller, whether we choose \({\varrho }_{1}\) to be in \(\mathcal {{C}}\) or not, the peak is not hot-decreasing, so Theorem 2 does not apply.
That hot-decreasingness in Theorem 2 cannot be weakened to (ordinary) decreasingness, can be seen by considering \(\mathcal {{R}}'\) obtained by omitting \({\varrho }_5\) from \(\mathcal {{R}}\). Although \(\mathcal {{R}}'\) is not confluent [16, Example 8], by taking \(\mathcal {{C}}= \varnothing \) and \({\varrho }_{1}\mathrel {{\succ }}{\varrho }_{3},{\varrho }_{4}\), we can show that all critical peaks of \(\mathcal {{R}}'\) are decreasing for the hot-labelling.
A special case of Theorem 2, is that a left-linear terminating TRS is confluent [19], if each critical pair is joinable, as can be seen by setting \(\mathcal {{C}}=\mathcal {{R}}\).
Corollary 1
A left-linear development closed TRS is confluent [29, Corollary 24].
Proof
A TRS is development closed if for every critical pair  such that
such that  is obtained by an outer step,
is obtained by an outer step,  holds. Taking
holds. Taking  and labelling all rules the same, say by 0, yields that each outer–inner or overlay critical peak is labelled as
and labelling all rules the same, say by 0, yields that each outer–inner or overlay critical peak is labelled as  , and can be completed as
, and can be completed as  , yielding a hot-decreasing diagram of (oi)-shape. We conclude by Theorem 2. \(\square \)
, yielding a hot-decreasing diagram of (oi)-shape. We conclude by Theorem 2. \(\square \)
The proof of Theorem 2 uses the following structural properties of decreasing diagrams specific to the hot-labelling. The labelling was designed so they hold.
Lemma 7
-
1.
If the peak
 is hot-decreasing, then it can be completed into a hot-decreasing diagram of shape
is hot-decreasing, then it can be completed into a hot-decreasing diagram of shape  such that the 1st-order variables in all terms in the diagram are contained in those of \({t}\).
such that the 1st-order variables in all terms in the diagram are contained in those of \({t}\). -
2.
If the multisteps \({\varPhi }\), \({\varPsi }\) in the peak
 are non-overlapping, then the valley
are non-overlapping, then the valley  completes it into a hot-decreasing diagram.
completes it into a hot-decreasing diagram. -
3.
If the peak
 and vector of peaks
and vector of peaks  have hot-decreasing diagrams, so does the composition
have hot-decreasing diagrams, so does the composition  .
.
The proof of Theorem 2 refines our refactored proof (see Lemma 6) of Huet’s critical pair lemma, by wrapping the induction on the amount of non-overlap (\({\Cup }\)) between multisteps, into an outer induction on their amount of overlap (\({\Cap }\)).
Proof
(of Theorem 2). We show that every peak  of multisteps \({\varPhi }\) and \({\varPsi }\) can be closed into a hot-decreasing diagram, by induction on the pair \(({\varPhi }\mathbin {{\Cap }}{\varPsi }{,}{\varPhi }\mathbin {{\Cup }}{\varPsi })\) ordered by the lexicographic product of \({>}\) with itself. We distinguish cases on whether or not \({\varPhi }\) and \({\varPsi }\) have overlap.
of multisteps \({\varPhi }\) and \({\varPsi }\) can be closed into a hot-decreasing diagram, by induction on the pair \(({\varPhi }\mathbin {{\Cap }}{\varPsi }{,}{\varPhi }\mathbin {{\Cup }}{\varPsi })\) ordered by the lexicographic product of \({>}\) with itself. We distinguish cases on whether or not \({\varPhi }\) and \({\varPsi }\) have overlap.
If \({\varPhi }\) and \({\varPsi }\) do not have overlap, Lemma 5(1) yields  . This valley completes the peak into a hot-decreasing diagram by Lemma 7(2).
. This valley completes the peak into a hot-decreasing diagram by Lemma 7(2).
If \({\varPhi }\) and \({\varPsi }\) do have overlap, then we further distinguish cases on whether or not the overlap is critical.
If the overlap is not critical, then by Lemma 4 the peak can be vertically decomposed into a number of peaks between multisteps \({\varPhi }_{{i}}\), \({\varPsi }_{{i}}\) that have an amount of overlap that is not greater,  , and a strictly smaller amount of non-overlap
, and a strictly smaller amount of non-overlap  . Hence the I.H. applies and yields that each such peak can be completed into a hot-decreasing diagram. We conclude by vertically recomposing them yielding a hot-decreasing diagram by Lemma 7(3).
. Hence the I.H. applies and yields that each such peak can be completed into a hot-decreasing diagram. We conclude by vertically recomposing them yielding a hot-decreasing diagram by Lemma 7(3).
If the overlap is critical, then by Lemma 5 the peak can be horizontally decomposed as  for some peak
for some peak  of overlapping steps \({\phi }\mathbin {{{{\in }}}}{\varPhi }\) and \({\psi }\mathbin {{{{\in }}}}{\varPsi }\), i.e. such that
of overlapping steps \({\phi }\mathbin {{{{\in }}}}{\varPhi }\) and \({\psi }\mathbin {{{{\in }}}}{\varPsi }\), i.e. such that 
 for some \({\varPhi }'\), \({\varPsi }'\). We choose \(({\phi }{,}{\psi })\) to be inner among such overlapping pairs (see Definition 6), assuming w.l.o.g. that \(p_{{\phi }}\mathrel {\preceq _{ o }}p_{{\psi }}\) for the root-positions \(p_{{\phi }}\),\(p_{{\psi }}\) of their patterns. We distinguish cases on whether or not \(p_{{\phi }}\) is a strict prefix of \(p_{{\psi }}\).
for some \({\varPhi }'\), \({\varPsi }'\). We choose \(({\phi }{,}{\psi })\) to be inner among such overlapping pairs (see Definition 6), assuming w.l.o.g. that \(p_{{\phi }}\mathrel {\preceq _{ o }}p_{{\psi }}\) for the root-positions \(p_{{\phi }}\),\(p_{{\psi }}\) of their patterns. We distinguish cases on whether or not \(p_{{\phi }}\) is a strict prefix of \(p_{{\psi }}\).
If \(p_{{\phi }}\mathbin {{=}}p_{{\psi }}\), then  and
and  by Proposition 3, so the peak is overlay, from which we conclude since such peaks are hot-decreasing by assumption.
by Proposition 3, so the peak is overlay, from which we conclude since such peaks are hot-decreasing by assumption.
Suppose \(p_{{\phi }}\mathrel {\prec _{ o }}p_{{\psi }}\). We will construct a hot-decreasing diagram D for the peak  out of several smaller such diagrams as illustrated in Fig. 1, using the multipattern \({\varsigma }={\varPhi }^{\mathsf {src}}\mathbin {{\sqcup }}{\psi }^{\mathsf {src}}\) as a basic building block; it has as patterns those of \({\varPhi }'\) and the join of the patterns of \({\phi }\), \({\psi }\). To make \({\varsigma }\) explicit, unfold \({\varPhi }\) and \({\varPsi }\) to let-expressions
out of several smaller such diagrams as illustrated in Fig. 1, using the multipattern \({\varsigma }={\varPhi }^{\mathsf {src}}\mathbin {{\sqcup }}{\psi }^{\mathsf {src}}\) as a basic building block; it has as patterns those of \({\varPhi }'\) and the join of the patterns of \({\phi }\), \({\psi }\). To make \({\varsigma }\) explicit, unfold \({\varPhi }\) and \({\varPsi }\) to let-expressions  respectively
respectively  , for rules of shapes \({\varrho }_{{i}}(\varvec{{x}_{{i}}}) \mathbin {:}{\ell }_{{i}}\mathbin {{\rightarrow }}{r}_{{i}}\) and \({\theta }_{{j}}(\varvec{{y}_{{j}}}) \mathbin {:}{g}_{{j}}\mathbin {{\rightarrow }}{d}_{{j}}\). We let
, for rules of shapes \({\varrho }_{{i}}(\varvec{{x}_{{i}}}) \mathbin {:}{\ell }_{{i}}\mathbin {{\rightarrow }}{r}_{{i}}\) and \({\theta }_{{j}}(\varvec{{y}_{{j}}}) \mathbin {:}{g}_{{j}}\mathbin {{\rightarrow }}{d}_{{j}}\). We let  and
and  be such that
be such that  and
and  are the 2nd-order variables corresponding to \({\phi }\mathbin {{{{\in }}}}{\varPhi }\) and \({\psi }\mathbin {{{{\in }}}}{\varPsi }\) for rules \({\varrho }(\varvec{{x}}) \mathbin {:}{\ell }\mathbin {{\rightarrow }}{r}\) and \({\theta }(\varvec{{y}}) \mathbin {:}{g}\mathbin {{\rightarrow }}{d}\). By the choice of \(({\phi }{,}{\psi })\) as inner, \({\phi }^{\mathsf {src}}\) is the unique pattern in \({\varPhi }^{\mathsf {src}}\) overlapping \({\psi }^{\mathsf {src}}\). As a consequence we can write \({\varsigma }\) as
are the 2nd-order variables corresponding to \({\phi }\mathbin {{{{\in }}}}{\varPhi }\) and \({\psi }\mathbin {{{{\in }}}}{\varPsi }\) for rules \({\varrho }(\varvec{{x}}) \mathbin {:}{\ell }\mathbin {{\rightarrow }}{r}\) and \({\theta }(\varvec{{y}}) \mathbin {:}{g}\mathbin {{\rightarrow }}{d}\). By the choice of \(({\phi }{,}{\psi })\) as inner, \({\phi }^{\mathsf {src}}\) is the unique pattern in \({\varPhi }^{\mathsf {src}}\) overlapping \({\psi }^{\mathsf {src}}\). As a consequence we can write \({\varsigma }\) as  , for some pattern \(\hat{{t}}\), the join of the patterns of \({\phi }\),\({\psi }\), such that \({\sigma }\) maps
, for some pattern \(\hat{{t}}\), the join of the patterns of \({\phi }\),\({\psi }\), such that \({\sigma }\) maps  to a term of shape
to a term of shape  as \({\phi }\) is the outer step, and \({\tau }\) maps it to a term of shape
as \({\phi }\) is the outer step, and \({\tau }\) maps it to a term of shape  ,Footnote 9 where \({\sigma }\), \({\tau }\) witness \({\varPhi }^{\mathsf {src}},{\psi }^{\mathsf {src}}\mathrel {{\sqsubseteq }}{\varsigma }\). That the other 2nd-order variables are
,Footnote 9 where \({\sigma }\), \({\tau }\) witness \({\varPhi }^{\mathsf {src}},{\psi }^{\mathsf {src}}\mathrel {{\sqsubseteq }}{\varsigma }\). That the other 2nd-order variables are  follows by \({\sigma }\) being the identity on them (their patterns do not overlap \({\psi }\)), and that these are bound to the patterns
follows by \({\sigma }\) being the identity on them (their patterns do not overlap \({\psi }\)), and that these are bound to the patterns  by \({\tau }\) mapping them to 1st-order terms (only
by \({\tau }\) mapping them to 1st-order terms (only  can be mapped to a non-1st-order term).
can be mapped to a non-1st-order term).
We start with constructing a hot-decreasing diagram \(\mathring{D}\) for the critical peak  encompassed by the peak between \({\phi }\) and \({\psi }\), as follows. We set \(\hat{{\phi }}\) and \(\hat{{\psi }}\) to
encompassed by the peak between \({\phi }\) and \({\psi }\), as follows. We set \(\hat{{\phi }}\) and \(\hat{{\psi }}\) to  respectively
respectively  . This yields a peak as desired, which is outer–inner as \(p_{\hat{{\phi }}}\mathrel {\prec _{ o }}p_{\hat{{\psi }}}\) by \(p_{{\phi }}\mathrel {\prec _{ o }}p_{{\psi }}\), and critical by Lemma 3, hence by the hot-decreasingness assumption, it can be completed into a hot-decreasing diagram \(\hat{D}\) by a conversion of (oi)-shape:
. This yields a peak as desired, which is outer–inner as \(p_{\hat{{\phi }}}\mathrel {\prec _{ o }}p_{\hat{{\psi }}}\) by \(p_{{\phi }}\mathrel {\prec _{ o }}p_{{\psi }}\), and critical by Lemma 3, hence by the hot-decreasingness assumption, it can be completed into a hot-decreasing diagram \(\hat{D}\) by a conversion of (oi)-shape:  . Below we refer to its conversion and multistep as \(\hat{{\varPsi }}\) and \(\hat{{\varPhi }}\). Based on \(\hat{D}\) we construct a hot-decreasing diagram \(D'\) (Fig. 1, left) for the peak
. Below we refer to its conversion and multistep as \(\hat{{\varPsi }}\) and \(\hat{{\varPhi }}\). Based on \(\hat{D}\) we construct a hot-decreasing diagram \(D'\) (Fig. 1, left) for the peak  by constructing a conversion \(\hat{{\varPsi }}{\uparrow } \mathbin {:}{s}\mathrel {{\leftrightarrow }^{{*}}}{w}'' \) and a multistep
by constructing a conversion \(\hat{{\varPsi }}{\uparrow } \mathbin {:}{s}\mathrel {{\leftrightarrow }^{{*}}}{w}'' \) and a multistep  , with their composition (reversing the latter) of (oi)-shape.
, with their composition (reversing the latter) of (oi)-shape.
The conversion \(\hat{{\varPsi }}{\uparrow } \mathbin {:}{s}\mathrel {{\leftrightarrow }^{{*}}}{w}'' \) is constructed by lifting the closing conversion \(\hat{{\varPsi }}\) of the diagram \(\hat{D}\) back into \({\varsigma }\). Formally, for any multistep \(\hat{{\varOmega }}\) given by  for rules \({\eta }_{{k}}(\varvec{{w}_{{k}}})\), occurring anywhere in \(\hat{{\varPsi }}\) , we define its lifting \(\hat{{\varOmega }}{\uparrow }\) to be
for rules \({\eta }_{{k}}(\varvec{{w}_{{k}}})\), occurring anywhere in \(\hat{{\varPsi }}\) , we define its lifting \(\hat{{\varOmega }}{\uparrow }\) to be  . That is, we update \({\varsigma }\) by substitutingFootnote 10 both \(\hat{{\varOmega }}\) (for
. That is, we update \({\varsigma }\) by substitutingFootnote 10 both \(\hat{{\varOmega }}\) (for  , instead of binding that to \(\hat{{t}}\)) and the right-hand sides \(\varvec{{r}}'\) in its body. Because right-hand sides \(\varvec{{r}}\) need not be linear, the resulting proofclusters may have to be linearised (by replicating let-bindings) first to obtain multisteps. This extends to terms \({p}\) by
, instead of binding that to \(\hat{{t}}\)) and the right-hand sides \(\varvec{{r}}'\) in its body. Because right-hand sides \(\varvec{{r}}\) need not be linear, the resulting proofclusters may have to be linearised (by replicating let-bindings) first to obtain multisteps. This extends to terms \({p}\) by  . That this yields multisteps and terms that connect into a conversion
. That this yields multisteps and terms that connect into a conversion  as desired follows by computation. E.g.,
as desired follows by computation. E.g.,  using that \({\sigma }\) witnesses \({\varPhi }^{\mathsf {src}}\mathrel {{\sqsubseteq }}{\varsigma }\) so that
using that \({\sigma }\) witnesses \({\varPhi }^{\mathsf {src}}\mathrel {{\sqsubseteq }}{\varsigma }\) so that  and
and  . That the labels in \(\hat{{\varPsi }}{\uparrow }\) are strictly below \(\mathring{\mathcal {L}}({\varPhi })\) follows for set-labels from that lifting clearly does not introduce rule symbols and from that labels of rule symbols in \(\hat{{\varPsi }}\) are, by assumption, strictly below the label of the rule \({\varrho }\) of \({\phi }\). In case \({\varPhi }\) is term-labelled, by \({t}\), it follows from closure of \({\rightarrow }_{\mathcal {{C}}}\)-reduction under lifting (which also contracts \({\varPhi }'\)).
. That the labels in \(\hat{{\varPsi }}{\uparrow }\) are strictly below \(\mathring{\mathcal {L}}({\varPhi })\) follows for set-labels from that lifting clearly does not introduce rule symbols and from that labels of rule symbols in \(\hat{{\varPsi }}\) are, by assumption, strictly below the label of the rule \({\varrho }\) of \({\phi }\). In case \({\varPhi }\) is term-labelled, by \({t}\), it follows from closure of \({\rightarrow }_{\mathcal {{C}}}\)-reduction under lifting (which also contracts \({\varPhi }'\)).
The multistep  is the combination of the multisteps \({\varPhi }'\) (the redex-patterns in \({\varPhi }\) other than \({\phi }\)) and \(\hat{{\varPhi }}\), lifting the latter into \({\varsigma }\). For
is the combination of the multisteps \({\varPhi }'\) (the redex-patterns in \({\varPhi }\) other than \({\phi }\)) and \(\hat{{\varPhi }}\), lifting the latter into \({\varsigma }\). For  given by
given by  , it is defined as
, it is defined as  . Per construction it only contracts rules in \({\varPhi }'\), \(\hat{{\varPhi }}\), so has a label in \({{{\shortmid }\!\mathring{{\curlyvee }}}\mathring{\mathcal {L}}({\varPhi })}\) by
. Per construction it only contracts rules in \({\varPhi }'\), \(\hat{{\varPhi }}\), so has a label in \({{{\shortmid }\!\mathring{{\curlyvee }}}\mathring{\mathcal {L}}({\varPhi })}\) by  and the label of \(\hat{{\varPhi }}\) is in \({{{\shortmid }\!\mathring{{\curlyvee }}}\mathring{\mathcal {L}}(\hat{{\phi }})}\) by the (oi)-assumption. That
and the label of \(\hat{{\varPhi }}\) is in \({{{\shortmid }\!\mathring{{\curlyvee }}}\mathring{\mathcal {L}}(\hat{{\phi }})}\) by the (oi)-assumption. That  follows again by computation, e.g.
follows again by computation, e.g.  .
.
Finally, applying the I.H. to the peak  yields some hot-decreasing diagram \(D_{\text {IH}}\) (Fig. 1, right). Prefixing \(\hat{{\varPsi }}{\uparrow }\) to its closing conversion between \({w}''\) and \({u}\), then closes the original peak
yields some hot-decreasing diagram \(D_{\text {IH}}\) (Fig. 1, right). Prefixing \(\hat{{\varPsi }}{\uparrow }\) to its closing conversion between \({w}''\) and \({u}\), then closes the original peak  into a hot-decreasing diagram D, because labels of steps in \(\hat{{\varPsi }}{\uparrow }\) are in \({\mathring{{\curlyvee }}\mathring{\mathcal {L}}({\varPhi })}\), \(\mathring{\mathcal {L}}({\varPhi })\mathrel {\mathring{{\succeq }}}\mathring{\mathcal {L}}({\varPhi }'\oplus \hat{{\varPhi }}) \) as seen above, and \(\mathring{\mathcal {L}}({\varPsi })\mathrel {\mathring{{\succeq }}}\mathring{\mathcal {L}}({\varPsi }{/}{\psi }) \). The I.H. applies since \({\varPhi }\mathbin {{\Cap }}{\varPsi } > ({\varPhi }'\oplus \hat{{\varPhi }})\mathbin {{\Cap }}({\varPsi }{/}{\psi })\): To see this, we define
into a hot-decreasing diagram D, because labels of steps in \(\hat{{\varPsi }}{\uparrow }\) are in \({\mathring{{\curlyvee }}\mathring{\mathcal {L}}({\varPhi })}\), \(\mathring{\mathcal {L}}({\varPhi })\mathrel {\mathring{{\succeq }}}\mathring{\mathcal {L}}({\varPhi }'\oplus \hat{{\varPhi }}) \) as seen above, and \(\mathring{\mathcal {L}}({\varPsi })\mathrel {\mathring{{\succeq }}}\mathring{\mathcal {L}}({\varPsi }{/}{\psi }) \). The I.H. applies since \({\varPhi }\mathbin {{\Cap }}{\varPsi } > ({\varPhi }'\oplus \hat{{\varPhi }})\mathbin {{\Cap }}({\varPsi }{/}{\psi })\): To see this, we define  and
and  and collect needed ingredients (the joins are disjoint):
and collect needed ingredients (the joins are disjoint):

Using these one may reason with sets of patterns (not let-expressions as \({t}\mathrel {{\ne }}{s}'\); the sets are positions in both \({t}\),\({s}'\)) as follows, relying on distributivity:

where \(F\) is the singleton  having all positions in \({\phi }\) not below \({\psi }\)’s root, \(D_{-} ={\varPhi }'^{\mathsf {src}} \mathbin {{\sqcup }}F\), and
having all positions in \({\phi }\) not below \({\psi }\)’s root, \(D_{-} ={\varPhi }'^{\mathsf {src}} \mathbin {{\sqcup }}F\), and  . \(\square \)
. \(\square \)
4 Confluence by Critical-Pair Closing Systems
We introduce a confluence criterion based on identifying for a term rewrite system \(\mathcal {{R}}\) a subsystem \(\mathcal {{C}}\) such that every \(\mathcal {{R}}\)-critical peak can be closed by means of \(\mathcal {{C}}\)-conversions, rendering the rules used in the peak redundant.
Definition 9
A TRS \(\mathcal {{C}}\) is critical-pair closing for a TRS \(\mathcal {{R}}\), if \(\mathcal {{C}}\) is a subsystem of \(\mathcal {{R}}\) (namely \(\mathcal {{C}}\subseteq \mathcal {{R}}\)) and  holds for all critical pairs \((s{,}t)\) of \(\mathcal {{R}}\).
holds for all critical pairs \((s{,}t)\) of \(\mathcal {{R}}\).
We phrase the main result of this section as a preservation-of-confluence result. We write \(\rightarrow _{\mathcal {{S}}/\mathcal {{R}}}\) for \(\twoheadrightarrow _\mathcal {{R}}\cdot \rightarrow _\mathcal {{S}}\cdot \twoheadrightarrow _\mathcal {{R}}\), and if it is terminating, \(\mathcal {{S}}/\mathcal {{R}}\) is said to be (relatively) terminating. By \(\mathcal {{C}}_{ d }\) we denote the set of all duplicating rules in \(\mathcal {{C}}\).
Theorem 3
If \(\mathcal {{C}}\) is a critical-pair-closing system for a left-linear TRS \(\mathcal {{R}}\) such that \(\mathcal {{C}}_{ d }/\mathcal {{R}}\) is terminating, then \(\mathcal {{R}}\) is confluent if \(\mathcal {{C}}\) is confluent.
Any left-linear TRS is critical-pair-closing for itself. However, the power of the method relies on choosing small \(\mathcal {{C}}\). Before proving Theorem 3, we illustrate it by some (non-)examples and give a special case.
Example 9
Consider again the TRS \(\mathcal {{R}}\) in Example 7. As we observed, the only critical pair originating from \({\varrho }_{4}\) and \({\varrho }_{1}\) is closed by  . So the subsystem \(\mathcal {{C}}=\{ {\varrho }_1, {\varrho }_3, {\varrho }_6 \}\) is a critical-pair-closing system for \(\mathcal {{R}}\). As all \(\mathcal {{C}}\)-rules are linear, \(\mathcal {{C}}_{ d }/\mathcal {{R}}\) is vacuously terminating. Thus, by Theorem 3 it is sufficient to show confluence of \(\mathcal {{C}}\). Because \(\mathcal {{C}}\) has no critical pairs, the empty TRS \({\emptyset }\) is a critical-pair-closing TRS for \(\mathcal {{C}}\). As \({\emptyset }/\mathcal {{C}}\) is terminating, confluence of \(\mathcal {{C}}\) follows from that of \({\emptyset }\), which is trivial.
. So the subsystem \(\mathcal {{C}}=\{ {\varrho }_1, {\varrho }_3, {\varrho }_6 \}\) is a critical-pair-closing system for \(\mathcal {{R}}\). As all \(\mathcal {{C}}\)-rules are linear, \(\mathcal {{C}}_{ d }/\mathcal {{R}}\) is vacuously terminating. Thus, by Theorem 3 it is sufficient to show confluence of \(\mathcal {{C}}\). Because \(\mathcal {{C}}\) has no critical pairs, the empty TRS \({\emptyset }\) is a critical-pair-closing TRS for \(\mathcal {{C}}\). As \({\emptyset }/\mathcal {{C}}\) is terminating, confluence of \(\mathcal {{C}}\) follows from that of \({\emptyset }\), which is trivial.
Observe how confluence was shown by successive applications of the theorem.
Remark 3
In our experiments (see Sect. 5), \(\frac{3}{4}\) of the TRSs proven confluent by means of Theorem 3 used more than 1 iteration, with the maximum number of iterations being 6. For countable ARSs (see Corollary 2 below) 1 iteration suffices, which can be seen by setting \(\mathcal {{C}}\) to the spanning forest obtained by Lemma 1. This provides the intuition underlying rule specialisation in Example 15 below.
Example 10
Although confluent, the TRS \(\mathcal {{R}}\) in Example 8 does not have any confluent critical-pair-closing subsystem \(\mathcal {{C}}\) such that \(\mathcal {{C}}_{ d }/\mathcal {{R}}\) is terminating, not even \(\mathcal {{R}}\) itself: Because of b being in normal form in the critical pair induced by  , any such subsystem must contain \({\varrho }_4\), as one easily verifies, but \({\varrho }_4\) is both duplicating and non-terminating (looping).
, any such subsystem must contain \({\varrho }_4\), as one easily verifies, but \({\varrho }_4\) is both duplicating and non-terminating (looping).
Note that the termination condition of \(\mathcal {{C}}_{ d }/\mathcal {{R}}\) cannot be omitted from Theorem 3. Although the TRS \(\mathcal {{R}}'\) in Example 8 is not confluent, it admits the confluent critical-pair-closing system \(\{ {\varrho }_1, {\varrho }_3, {\varrho }_4 \}\).
Remark 4
The example is taken from [16] where it was used to show that decreasingness of critical peaks need not imply that of all peaks, for rule labelling. That example, in turn was adapted from Lévy’s TRS in [17] showing that strong confluence need not imply confluence for left-linear TRSs.
Example 11
For self-joinable rules, i.e. rules that are self-overlapping and whose critical pairs need further applications of the rule itself to join, Theorem 3 is not helpful since the critical-pair-closing system \(\mathcal {{C}}\) then contains the rule itself. Examples of self-joinable rules are associativity  and self-distributivity
and self-distributivity  , with confluence of the latter being known to be hard (currently no tool can handle it automatically).Footnote 11
, with confluence of the latter being known to be hard (currently no tool can handle it automatically).Footnote 11
The special case we consider is that of TRSs that are ARSs, i.e. where all function symbols are nullary. The identification is justified by that any ARS in the standard sense [26, 32] can be presented as \({\rightarrow }_{\mathcal {{R}}}\) for the TRS \(\mathcal {{R}}\) having a nullary symbol for each object, and a rule for each step of the ARS. Since ARSs have no duplicating rules, Theorem 3 specialises to the following result.
Corollary 2
If \(\mathcal {{C}}\) is critical-pair-closing for ARS \(\mathcal {{R}}\), \(\mathcal {{R}}\) is confluent if \(\mathcal {{C}}\) is.
Example 12
Consider the TRS \(\mathcal {{R}}\) given by \({c}\mathrel {{\rightarrow }}{a}'\mathrel {{\rightarrow }}{a}\mathrel {{\rightarrow }}{b}\) and \({a}\mathrel {{\rightarrow }}{a}'\mathrel {{\rightarrow }}{c}\). It is an ARS having the critical-pair-closing system \(\mathcal {{C}}\) given by the first part \({c}\mathrel {{\rightarrow }}{a}'\mathrel {{\rightarrow }}{a}\mathrel {{\rightarrow }}{b}\). Since \(\mathcal {{C}}\) is orthogonal it is confluent by Corollary 2, so \(\mathcal {{R}}\) is confluent by the same corollary. In general, a confluent ARS may have many non-confluent critical-pair-closing systems. Requiring local confluence is no impediment to that: The subsystem \(\mathcal {{C}}'\) of \(\mathcal {{R}}\) obtained by removing \({c}\mathrel {{\rightarrow }}{a}'\) allows to join all \(\mathcal {{R}}\)-critical peaks, but is not confluent; it simply is Kleene’s example [32, Figure 1.2] showing that local confluence need not imply confluence.
For \(\mathcal {{C}}_{ d }/\mathcal {{R}}\) to be vacuously terminating it is sufficient that all rules are linear.
Example 13
Consider the linear TRS \(\mathcal {{R}}\) consisting of \(\rho _1:f(x) \rightarrow f(f(x))\), \(\rho _2:f(x) \rightarrow g(x)\), and \(\rho _3:g(x) \rightarrow f(x)\). The subsystem \(\mathcal {{C}}= \{ \rho _1, \rho _3 \}\) is critical-pair-closing and has no critical pairs, so \(\mathcal {{R}}\) is confluent.
From the above it is apparent that, whereas usual redundancy-criteria are based on rules being redundant, the theorem gives a sufficient criterion for peaks of steps being redundant. This allows one to leverage the power of extant confluence methods. Here we give a generalisation of Huet’s strong closedness theorem [17] as a corollary of Theorem 3.
Definition 10
A TRS \(\mathcal {{R}}\) is strongly closed [17] if  and
and  hold for all critical pairs \((s{,}t)\).
hold for all critical pairs \((s{,}t)\).
Corollary 3
A left-linear TRS \(\mathcal {{R}}\) is confluent if there exists a critical-pair-closing system \(\mathcal {{C}}\) for \(\mathcal {{R}}\) such that \(\mathcal {{C}}\) is linear and strongly closed.
Example 14
Consider the linear TRS \(\mathcal {{R}}\):

\(\mathcal {{C}}= \{ {\varrho }_1,\ldots ,{\varrho }_5 \}\) is critical-pair-closing for \(\mathcal {{R}}\), since the \(\mathcal {{R}}\)-critical peak between \({\varrho }_6\) and \({\varrho }_7\) can be \(\mathcal {{C}}\)-closed: \(h(f(x,k(y,z))) \mathrel {{\rightarrow }_{{\varrho }_1 }}f(h(r(x)),k(y,z)) \mathrel {{\rightarrow }_{{\varrho }_2 }}g(p(y),q(z,h(r(x)))) \). Because \(\mathcal {{C}}\) is strongly closed and also linear, confluence of \(\mathcal {{R}}\) follows by Corollary 3.
Remark 5
Neither of the TRSs in Examples 13 and 14 is strongly closed. The former not, because  does not hold, and the latter not because
does not hold, and the latter not because  does not hold.
does not hold.
Having illustrated the usefulness of Theorem 3, we now present its proof. In TRSs there are two types of peaks: overlapping and non-overlapping ones. As Example 10 shows, confluence criteria only addressing the former need not generalise from ARSs to TRSs. Note that one of the peaks showing non-confluence of \(\mathcal {{R}}'\), the one between \({\varrho }_2\) and \({\varrho }_3\) (\({\varrho }_4\)), is non-overlapping. Therefore, restricting to a subsystem without \({\varrho }_2\) can only provide a partial analysis of confluence of \(\mathcal {{R}}'\); the (non-overlapping) interaction between \(\mathcal {{C}}\) and  is not accounted for, and indeed that is fatal here. The intuition for our proof is that the problem is that the number of such interactions is unbounded due to the presence of the duplicating and non-terminating rule \({\varrho }_3\) (and \({\varrho }_4\)) in \(\mathcal {{C}}\), and that requiring termination of \(\mathcal {{C}}_{ d }/\mathcal {{R}}\) bounds that number and suffices to regain confluence. This is verified by showing that
is not accounted for, and indeed that is fatal here. The intuition for our proof is that the problem is that the number of such interactions is unbounded due to the presence of the duplicating and non-terminating rule \({\varrho }_3\) (and \({\varrho }_4\)) in \(\mathcal {{C}}\), and that requiring termination of \(\mathcal {{C}}_{ d }/\mathcal {{R}}\) bounds that number and suffices to regain confluence. This is verified by showing that  has the diamond property.
has the diamond property.
Lemma 8
Let \({\rightarrow _\mathcal {A}} = \bigcup _{a \in I} {\rightarrow _a}\) be a relation equipped with a well-founded order \(\succ \) on a label set I, and let \(\rightarrow _\mathcal {B}\) be a confluent relation with \({\rightarrow _\mathcal {B}} \subseteq {\twoheadrightarrow _\mathcal {A}}\). The relation \({\rightarrow _\mathcal {A}}\) is confluent if
-
1.
 for all \(a, b \in I\); and
for all \(a, b \in I\); and -
2.
 for all \(a \in I\).
for all \(a \in I\).
Here \(\succ _{\mathsf {mul}}\) stands for the multiset extension of \(\succ \).
Proof
(Sketch). Let  . We claim that
. We claim that  holds for all labels a, b and numbers \(m, n \geqslant 0\). The claim is shown by well-founded induction on \((\{a,b\}, m + n)\) with respect to the lexicographic product of \(\succ _{\mathsf {mul}}\) and the greater-than order \({>}\) on \(\mathbb {N}\). Thus, the diamond property of \({\rightarrowtail }\) follows from the claim and confluence of \(\mathcal {B}\). As \({\rightarrow _\mathcal {A}} \subseteq {\rightarrowtail } \subseteq {\twoheadrightarrow _\mathcal {A}}\), we conclude confluence of \(\mathcal {A}\) by e.g. [32, Proposition 1.1.11].
holds for all labels a, b and numbers \(m, n \geqslant 0\). The claim is shown by well-founded induction on \((\{a,b\}, m + n)\) with respect to the lexicographic product of \(\succ _{\mathsf {mul}}\) and the greater-than order \({>}\) on \(\mathbb {N}\). Thus, the diamond property of \({\rightarrowtail }\) follows from the claim and confluence of \(\mathcal {B}\). As \({\rightarrow _\mathcal {A}} \subseteq {\rightarrowtail } \subseteq {\twoheadrightarrow _\mathcal {A}}\), we conclude confluence of \(\mathcal {A}\) by e.g. [32, Proposition 1.1.11].
Proof
(of Theorem 3 by Lemma 8). Let I comprise pairs of a term and a natural number, and define \({t}\mathrel {{\rightarrow }_{(\hat{{t}}{,}{n})}}{s}\) if  with \({n}\) the maximal length of a development of the multistep,Footnote 12 and
with \({n}\) the maximal length of a development of the multistep,Footnote 12 and  , in Lemma 8. As well-founded order
, in Lemma 8. As well-founded order  on indices we take the lexicographic product of
on indices we take the lexicographic product of  and greater-than
and greater-than  . We only present the interesting case, leaving the others to the reader:
. We only present the interesting case, leaving the others to the reader:
-
Suppose
 where the steps do not have overlap. Then by Lemma 5(1),
where the steps do not have overlap. Then by Lemma 5(1),  , so
, so  . Distinguish cases on the type of the \(\mathcal {{C}}\)-rule employed in \({t}\mathrel {{\rightarrow }_{\mathcal {{C}}}}{u}\). If the rule is duplicating, then
. Distinguish cases on the type of the \(\mathcal {{C}}\)-rule employed in \({t}\mathrel {{\rightarrow }_{\mathcal {{C}}}}{u}\). If the rule is duplicating, then  for
for  the maximal length of a development of the
the maximal length of a development of the  -step from
-step from  , and condition 2 is satisfied as
, and condition 2 is satisfied as  implies
implies  . If the rule is non-duplicating, then
. If the rule is non-duplicating, then  as
as  by assumption and the length of the maximal development of the residual multistep does not increase when projecting over a linear rule. Again, condition 2 is satisfied. \(\square \)
by assumption and the length of the maximal development of the residual multistep does not increase when projecting over a linear rule. Again, condition 2 is satisfied. \(\square \)
5 Implementation and Experiments
The presented confluence techniques have been implemented in the confluence tool Saigawa version 1.12 [14]. We used the tool to test the criteria on 432 left-linear TRSs in COPS [15] Nos. 1–1036, where we ruled out duplicated problems. Out of 432 systems, 224 are known to be confluent and 173 are non-confluent.
We briefly explain how we automated the presented techniques. As illustrated in Example 9, Theorem 3 can be used as a stand-alone criterion. The condition  of strong closedness is tested by
of strong closedness is tested by  . For a critical peak \(s \leftarrow \cdot \rightarrow t\) of \(\mathcal {{C}}\), hot-decreasingness is tested by \(s \twoheadrightarrow _\mathcal {{C}}\cdot \mathrel {_{\mathcal {{C}}}{\twoheadleftarrow }} t\). For any other critical peak \(s \mathrel {_{{\ell }}{\leftarrow }} \cdot \rightarrow t\), we test the disjunction of
. For a critical peak \(s \leftarrow \cdot \rightarrow t\) of \(\mathcal {{C}}\), hot-decreasingness is tested by \(s \twoheadrightarrow _\mathcal {{C}}\cdot \mathrel {_{\mathcal {{C}}}{\twoheadleftarrow }} t\). For any other critical peak \(s \mathrel {_{{\ell }}{\leftarrow }} \cdot \rightarrow t\), we test the disjunction of  and
and  if it is outer–inner one, and if it is overlay, the disjunction of
if it is outer–inner one, and if it is overlay, the disjunction of  and \(s \twoheadrightarrow _\mathcal {{C}}\cdot \mathrel {_{\mathcal {{C}}}{\twoheadleftarrow }} t\) is used. Order constraints for hot-labeling are solved by SMT solver Yices [10]. For proving (relative) termination we employ the termination tool NaTT version 1.8 [34]. Finally, suitable subsystems \(\mathcal {{C}}\) used in our criteria are searched by enumeration.
and \(s \twoheadrightarrow _\mathcal {{C}}\cdot \mathrel {_{\mathcal {{C}}}{\twoheadleftarrow }} t\) is used. Order constraints for hot-labeling are solved by SMT solver Yices [10]. For proving (relative) termination we employ the termination tool NaTT version 1.8 [34]. Finally, suitable subsystems \(\mathcal {{C}}\) used in our criteria are searched by enumeration.
Table 1 gives a summary of the results.Footnote 13 The tests were run on a PC equipped with Intel Core i7-8500Y CPU (1.5 GHz) and 16 GB memory using a timeout of 60 seconds. For the sake of comparison we also tested Knuth and Bendix’ theorem (kb), the strong closedness theorem (sc), and development closedness theorem (dc). As theoretically expected, they are subsumed by their generalizations.
6 Conclusion and Future Work
We presented two methods for proving confluence of TRSs, dubbed critical-pair-closing systems and hot-decreasingness. We gave a lattice-theoretic characterisation of overlap. Since many results in term rewriting, and beyond, are based on reasoning about overlap, which is notoriously hard [24], we expect that formalising our characterisation could simplify or even enable formalising them. We expect that both methods generalise to commutation, extend to HRSs [21], and can be strengthened by considering rule specialisations.
Example 15
Analysing the TRS \(\mathcal {{R}}\) of Example 10 one observes that for closing the critical pairs only (non-duplicating) instances of the duplicating rules \({\varrho }_3\) and \({\varrho }_4\) are used. Adjoining these specialisations allows the method to proceed: Adjoining \({\varrho }_{3}(a) \mathbin {:}f(c,a)\mathbin {{\rightarrow }}f(a,a)\) and \({\varrho }_{4}(a) \mathbin {:}f(a,c)\mathbin {{\rightarrow }}f(a,a)\) to \(\mathcal {{R}}\) yields a (reduction-equivalent) TRS having critical-pair-closing system \(\{ {\varrho }_1, {\varrho }_{3}(a), {\varrho }_{4}(a), {\varrho }_5 \}\). Since this is a linear system without critical pairs, it is confluent, so \(\mathcal {{R}}\) is as well.
Notes
- 1.
- 2.
For space reasons we have omitted the proof by decreasing diagrams of Theorem 3.
- 3.
\(\mathsf {src}\) can be viewed as tree homomorphism [7], or as a term algebra \({\varrho }^{\mathcal {Lhs}}(\varvec{{t}}) ={\ell }^{[\varvec{{x}}\mathbin {{:}{=}}\varvec{{t}}]}\).
- 4.
Here convex means that for each pair of positions \(p\),\(q\) in the set, all positions on the shortest path from \(p\) to \(q\) in the term tree are also in the set, cf. [32, Definition 8.6.21].
- 5.
This fails for, e.g., connected graphs; these may fall apart into non-connected ones.
- 6.
- 7.
We exclude neither overlays of a rule with itself nor pairs obtained by symmetry.
- 8.
This does not create ambiguity with joins of multipatterns since if
 , then
, then  unless the let-bindings of both are empty, so both are bottom.
unless the let-bindings of both are empty, so both are bottom. - 9.
\(C\) is a prefix of the left-hand side \({\ell }\) of \({\varrho }\). For instance, for a peak from f(g(a)) between
 and
and  ,
, 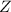 is mapped by
is mapped by  to
to  and by
and by  to
to  .
. - 10.
- 11.
See problem 127 of http://cops.uibk.ac.at/results/?y=2019-full-run&c=TRS.
- 12.
By the Finite Developments Theorem lengths of such developments are finite [32].
- 13.
Detailed data are available from: http://www.jaist.ac.jp/project/saigawa/19cade/.
References
Baader, F., Nipkow, T.: Term Rewriting and All That. Cambridge University Press, Cambridge (1998)
Barendregt, H.: The Lambda Calculus: Its Syntax and Semantics, Studies in Logic and the Foundations of Mathematics, vol. 103. North-Holland (1985)
Bechet, D., de Groote, P., Retoré, C.: A complete axiomatisation for the inclusion of series-parallel partial orders. In: Comon, H. (ed.) RTA 1997. LNCS, vol. 1232, pp. 230–240. Springer, Heidelberg (1997). https://doi.org/10.1007/3-540-62950-5_74
Boudol, G.: Computational semantics of term rewriting systems. In: Nivat, M., Reynolds, J. (eds.) Algebraic Methods in Semantics, pp. 169–236. Cambridge University Press (1985)
Bundy, A., Basin, D., Hutter, D., Ireland, A.: Rippling: meta-level guidance for mathematical reasoning. In: Cambridge Tracts in Theoretical Computer Science, Cambridge University Press (2005). https://doi.org/10.1017/CBO9780511543326
Church, A., Rosser, J.: Some properties of conversion. Transact. Am. Math. Soc. 39, 472–482 (1936)
Comon, H., et al.: Tree Automata Techniques and Applications (2007). http://www.grappa.univ-lille3.fr/tata
Davey, B., Priestley, H.: Introduction to Lattices and Order. Cambridge University Press, Cambridge (1990)
Dershowitz, N., Jouannaud, J.P.: Rewrite systems. In: van Leeuwen, J. (ed.) Handbook of Theoretical Computer Science, vol. B, Formal Models and Semantics, pp. 243–320. Elsevier (1990)
Dutertre, B.: Yices 2.2. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 737–744. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08867-9_49
Endrullis, J., Klop, J., Overbeek, R.: Decreasing diagrams with two labels are complete for confluence of countable systems. In: Proceedings of 3rd FSCD. LIPIcs, vol. 108, pp. 14:1–14:15 (2018). https://doi.org/10.4230/LIPIcs.FSCD.2018.14
Felgenhauer, B., Middeldorp, A., Zankl, H., van Oostrom, V.: Layer systems for proving confluence. ACM Transact. Computat. Logic 16, 1–32 (2015)
Felgenhauer, B.: Labeling multi-steps for confluence of left-linear term rewrite systems. In: Tiwari, A., Aoto, T. (eds.) Proceedings of 4th IWC, pp. 33–37 (2015)
Hirokawa, H., Klein, D.: Saigawa: A confluence tool. In: Proceedings of 1st IWC, p. 49 (2012). http://www.jaist.ac.jp/project/saigawa/
Hirokawa, N., Nagele, J., Middeldorp, A.: Cops and CoCoWeb: infrastructure for confluence tools. In: Galmiche, D., Schulz, S., Sebastiani, R. (eds.) IJCAR 2018. LNCS (LNAI), vol. 10900, pp. 346–353. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-94205-6_23
Hirokawa, N., Middeldorp, A.: Decreasing diagrams and relative termination. J. Autom. Reasoning 47(4), 481–501 (2011)
Huet, G.: Confluent reductions: abstract properties and applications to term rewriting systems. J. ACM 27(4), 797–821 (1980)
Huet, G., Lévy, J.J.: Computations in orthogonal rewriting systems, I. In: Lassez, J.L., Plotkin, G. (eds.) Computational Logic: Essays in Honor of Alan Robinson, chap. 11. The MIT Press (1991)
Knuth, D.E., Bendix, P.B.: Simple word problems in universal algebras. In: Leech, J. (ed.) Computational Problems in Abstract Algebra, Proceedings of a Conference held at Oxford under the Auspices of the Science Research Council Atlas Computer Laboratory, 29 August–2 September 1967. pp. 263–297 (1970)
Liu, J.L.: Propriétés de Confluence des Règles de Réécriture par des Diagrammes Décroissants. Ph.D. thesis, Tsinghua University and l’Université Paris-Saclay préparée à l’École Polytechnique (2016)
Mayr, R., Nipkow, T.: Higher-order rewrite systems and their confluence. Theoret. Comput. Sci. 192(1), 3–29 (1998). https://doi.org/10.1016/S0304-3975(97)00143-6
Meseguer, J.: Conditional rewriting logic as a unified model of concurrency. Theoret. Comput. Sci. 96, 73–155 (1992)
Métivier, Y.: About the rewriting systems produced by the Knuth–Bendix completion algorithm. Inf. Process. Lett. 16(1), 31–34 (1983)
Nagele, J., Middeldorp, A.: Certification of classical confluence results for left-linear term rewrite systems. In: Blanchette, J.C., Merz, S. (eds.) ITP 2016. LNCS, vol. 9807, pp. 290–306. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-43144-4_18
Newman, M.: On theories with a combinatorial definition of equivalence. Ann. Math. 43(2), 223–243 (1942)
Ohlebusch, E.: Advanced Topics in Term Rewriting. Springer, Heidelberg (2002). https://doi.org/10.1007/978-1-4757-3661-8
Okui, S.: Simultaneous critical pairs and Church-Rosser property. In: Nipkow, T. (ed.) RTA 1998. LNCS, vol. 1379, pp. 2–16. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0052357
van Oostrom, V.: Confluence for Abstract and Higher-Order Rewriting. Ph.D. thesis, Vrije Universiteit, Amsterdam, March 1994
van Oostrom, V.: Developing developments. Theoret. Comput. Sci. 175(1), 159–181 (1997)
van Oostrom, V.: Confluence by decreasing diagrams. In: Voronkov, A. (ed.) RTA 2008. LNCS, vol. 5117, pp. 306–320. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-70590-1_21
Rosen, B.: Tree-manipulating systems and Church-Rosser theorems. J. ACM 20, 160–187 (1973)
Terese: Term Rewriting Systems. Cambridge University Press (2003)
Toyama, Y.: On the Church-Rosser property for the direct sum of term rewriting systems. J. ACM 34(1), 128–143 (1987)
Yamada, A., Kusakari, K., Sakabe, T.: Nagoya termination tool. In: Dowek, G. (ed.) RTA 2014. LNCS, vol. 8560, pp. 466–475. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-08918-8_32
Zankl, H., Felgenhauer, B., Middeldorp, A.: Labelings for decreasing diagrams. J. Autom. Reasoning 54(2), 101–133 (2015)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Hirokawa, N., Nagele, J., van Oostrom, V., Oyamaguchi, M. (2019). Confluence by Critical Pair Analysis Revisited. In: Fontaine, P. (eds) Automated Deduction – CADE 27. CADE 2019. Lecture Notes in Computer Science(), vol 11716. Springer, Cham. https://doi.org/10.1007/978-3-030-29436-6_19
Download citation
DOI: https://doi.org/10.1007/978-3-030-29436-6_19
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-29435-9
Online ISBN: 978-3-030-29436-6
eBook Packages: Computer ScienceComputer Science (R0)





 denotes matching f(f(x)) twice;
denotes matching f(f(x)) twice; denotes replacing by
denotes replacing by  denotes substituting g(x) twice.
denotes substituting g(x) twice. is a vector
is a vector  of (pairwise distinct) second-order variables;
of (pairwise distinct) second-order variables; ; and
; and .
. , with the rule symbols occurring in
, with the rule symbols occurring in  for some peak
for some peak  of overlapping steps
of overlapping steps  .
. . Since these are
. Since these are  -rules in
-rules in  is hot-decreasing, then it can be completed into a hot-decreasing diagram of shape
is hot-decreasing, then it can be completed into a hot-decreasing diagram of shape  such that the 1st-order variables in all terms in the diagram are contained in those of
such that the 1st-order variables in all terms in the diagram are contained in those of  are non-overlapping, then the valley
are non-overlapping, then the valley  completes it into a hot-decreasing diagram.
completes it into a hot-decreasing diagram. and vector of peaks
and vector of peaks  have hot-decreasing diagrams, so does the composition
have hot-decreasing diagrams, so does the composition  .
.
 for all
for all  for all
for all  where the steps do not have overlap. Then by Lemma
where the steps do not have overlap. Then by Lemma  , so
, so  . Distinguish cases on the type of the
. Distinguish cases on the type of the  for
for  the maximal length of a development of the
the maximal length of a development of the  -step from
-step from  , and condition 2 is satisfied as
, and condition 2 is satisfied as  implies
implies  . If the rule is non-duplicating, then
. If the rule is non-duplicating, then  as
as  by assumption and the length of the maximal development of the residual multistep does not increase when projecting over a linear rule. Again, condition 2 is satisfied.
by assumption and the length of the maximal development of the residual multistep does not increase when projecting over a linear rule. Again, condition 2 is satisfied.  , see e.g. [
, see e.g. [ , then
, then  unless the let-bindings of both are empty, so both are bottom.
unless the let-bindings of both are empty, so both are bottom. and
and  ,
,  is mapped by
is mapped by  to
to  and by
and by  to
to  .
.